Экология жизни
Задание 1
Дан треугольник АВС. Требуется найти
1) Длину стороны АВ
2) Уравнение стороны АВ и ее
угловой коэффициент
) Уравнение медианы,
проведенной из вершины В
) Координаты точки
пересечения медиан
) Уравнение высоты, опущенной
из вершины С на сторону АВ
) Расстояние от вершины С до
стороны АВ
) Уравнение окружности, для
которой АВ есть диаметр А (5; 3); В (2; - 1); С (-4; 7).
Решение
1) Расстояние d между двумя точками A(x1; y1) и B(x2; y2) плоскости определяется
по формуле
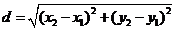
Применяя эту формулу,
найдем длину стороны АВ
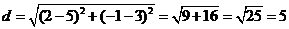
АВ=5
2) Уравнение прямой, проходящей
через точки A(x1; y1) и B(x2; y2) имеет вид
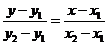
Подставляя вместо x1; y1;
x2; y2 координаты
точек А и В, получаем
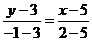 ,
,
Отсюда
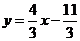
Искомое уравнение прямой
мы привели к уравнению с угловым коэффициентом, т.е. к уравнению вида 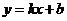 .
.
Таким образом, угловой
коэффициент искомой прямой 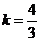 .
.
3) Пусть точка D - середина отрезка АС. Для
определения координат точки D применяем формулы деления отрезка пополам:
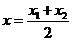 ;
; 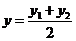 .
.
Находим координаты точки
D:
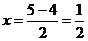 ;
; 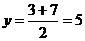
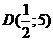
Подставив координаты
точек В и D в уравнение 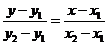 ,
находим уравнение медианы ВD:
,
находим уравнение медианы ВD:
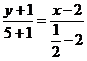
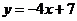
4)
Чтобы найти координаты точки пересечения медиан, необходимо написать уравнение
еще какой-нибудь одной медианы, например, СК. Для этого сначала найдем середину
отрезка АВ (координаты точки К) по формулам:
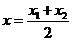 ;
; 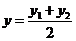 .
.
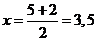 ;
; 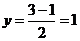
К (3,5; 1).
Напишем уравнение
медианы СК:
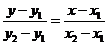
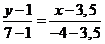
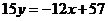
Теперь найдем точку
пересечения медиан. Для этого необходимо решить систему уравнений:
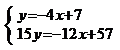
Получаем x=1; y=3. Следовательно, точка
пересечения медиан M (1; 3).
) Нам необходимо
написать уравнение высоты, опущенной из вершины С на сторону АВ. Уравнение
стороны АВ (из п. 2): 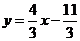 .
Поскольку высота перпендикулярна стороне АВ, то их угловые коэффициенты
.
Поскольку высота перпендикулярна стороне АВ, то их угловые коэффициенты 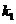 и
и
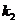 удовлетворяют
условию перпендикулярности двух прямых, т.е.
удовлетворяют
условию перпендикулярности двух прямых, т.е. 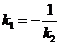 .
.
Так как 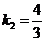 ,
то
,
то 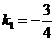 .
Зная координаты точки С (-4; 7) и угловой коэффициент
.
Зная координаты точки С (-4; 7) и угловой коэффициент 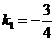 и
пользуясь уравнением прямой
и
пользуясь уравнением прямой 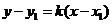 , проходящую через данную точку,
составляем уравнение искомой прямой
, проходящую через данную точку,
составляем уравнение искомой прямой 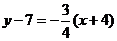 ;
; 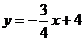 .
.
6) Чтобы найти расстояние от
точки С до стороны АВ, нам необходимо найти точку пересечения высоты СS со стороной АВ. Для этого решим
систему уравнений:
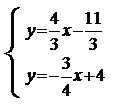
Получаем x=3,68; y=1,24. То есть S (3,68; 1,24). Теперь можем определить CS
по формуле
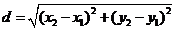
получим
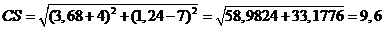 .
.
7) Уравнение окружности с
центром O (a, b) и радиусом R имеет вид
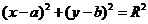
Так как по условию
АВ-диаметр, то середина отрезка АВ, то есть точка 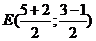 ;
;
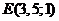 является
центром окружности.
является
центром окружности.
Кроме того, АВ=5 (из п.
1), поэтому АЕ=ЕВ=2,5. Следовательно, радиус окружности R=2,5.
Подставив в уравнение R=2,5; а=3,5; b=1,
получим уравнение искомой окружности
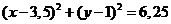
Задание 2
Найти область
определения функции
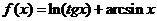
Решение
Функция определена при
тех значениях х, для которых
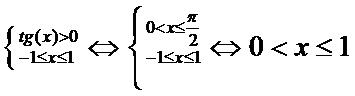
То есть D(y)=(0; 1).
Задание 3
Найти предел
Решение
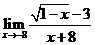
Здесь мы имеем
неопределенность вида 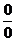 .
Чтобы ее раскрыть, умножаем числитель и знаменатель на выражение, сопряженное
числителю. После этого можно будет сократить на (x+8)
и воспользоваться теоремой о пределе дроби.
.
Чтобы ее раскрыть, умножаем числитель и знаменатель на выражение, сопряженное
числителю. После этого можно будет сократить на (x+8)
и воспользоваться теоремой о пределе дроби.
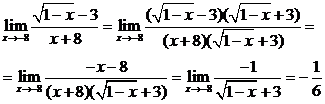
1. 
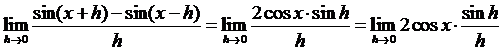
Поскольку 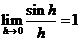 (замечательный
предел), то имеем
(замечательный
предел), то имеем
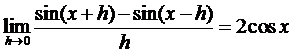
Задание 4
Найти производную
функции
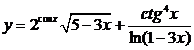
Решение
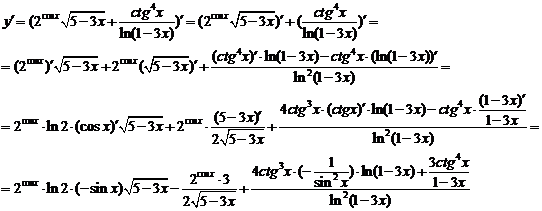
Задание 5
Сумма длин высоты и
диаметра основания конуса равна 6. При какой длине радиуса основания объем
конуса будет наибольшим?
Решение
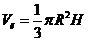
Где Vк-объем конуса, R-радиус
основания конуса, H - его высота. Так как
сумма высоты и диаметра основания конуса равна 6, то
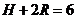 .
.
Тогда
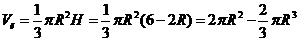
Исследуем функцию 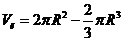 на
максимум:
на
максимум:
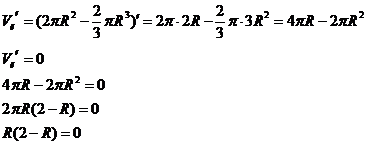
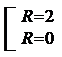
То есть R=2.
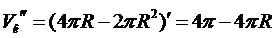
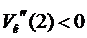
То есть в точке R=2 функция Vк(R) имеет максимум.
Значит, при R=2 объем конуса будет наибольшим.
Задание 6
Найти неопределенный
интеграл
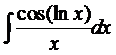
Решение
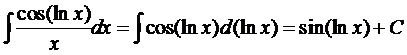
уравнение производная
функция площадь
Задание 7
Вычислить площадь
фигуры, ограниченной заданными линиями
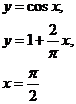
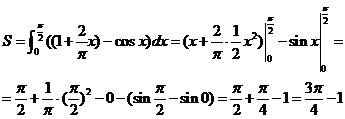
Задание 8
В партии, содержащей 20
изделий, имеется 4 изделия с дефектами. Наудачу отобрали 3 изделия для проверки
их качества. Случайная величина Х - число дефектных изделий, содержащихся в
указанной выборке. Найти закон распределения случайной величины Х и ее функцию
распределения F(x). Вычислить математическое ожидание М(х), дисперсию D(x) и среднее квадратичное отклонение 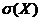 . Построить график функции
распределения F(x).
. Построить график функции
распределения F(x).
Решение
В выборке из трех
изделий может не оказаться ни одного дефектного изделия, может появиться одно,
два или три дефектных изделия. Следовательно, случайная величина Х может
принимать только 4 значения: x1=0;
x2=1; x3=2;
x4=3. Найдем вероятность этих значений:
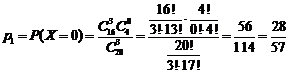
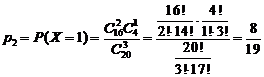
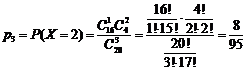
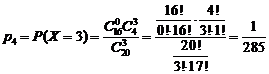
Следовательно, данная
случайная величина X имеет закон
распределения:
Отметим, что 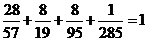 .
.
Найдем функцию
распределения этой случайной величины.
. При 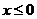 F(x)=0
F(x)=0
. При 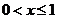 F(x)=
F(x)= 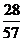
. При 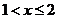 F(x)=
F(x)= 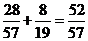
. При 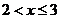 F(x)=
F(x)= 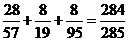
. При 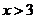 F(x)=
F(x)= 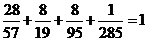
Вычислим математическое ожидание
M(X)= 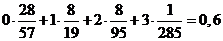
Найдем дисперсию
D(X)= 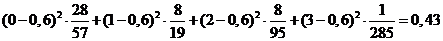
Вычислим среднее
квадратичное отклонение
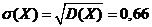
Задание 9
Имеются результаты
измерения роста 100 студентов:
|
Рост (см)
|
154-158
|
158-162
|
162-166
|
166-170
|
174-178
|
178-182
|
182-186
|
|
Число студентов
|
5
|
12
|
25
|
36
|
12
|
6
|
3
|
1
|
Преобразовать данную таблицу в
таблицу частот. Выбрав середины интервалов за значения роста, составить
дискретную таблицу частот и построить полигон.
Решение
|
Рост (см)154-158158-162162-166166-170170-174174-178178-182182-186
|
|
|
|
|
|
|
|
|
|
Число студентов
|
5
|
12
|
25
|
36
|
12
|
6
|
3
|
1
|
Общее количество студентов =100
Составим таблицу частот
|
Рост (см)
|
154-158
|
158-162
|
162-166
|
166-170
|
170-174
|
174-178
|
178-182
|
182-186
|
|
Частоты
|
5/100
|
12/100
|
25/100
|
36/100
|
12/100
|
6/100
|
3/100
|
1/100
|
Дискретная таблица частот
|
Рост (см)156160164168172176180184
|
|
|
|
|
|
|
|
|
|
Частоты
|
5/100
|
12/100
|
25/100
|
36/100
|
12/100
|
6/100
|
3/100
|
1/100
|