Экзаменационные билеты по курсу Биология (9 класс сш)
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ПОЯСНИТЕЛЬНАЯ
ЗАПИСКА К КУРСОВОЙ РАБОТЕ
По
дисциплине
«Математические
основы теории систем»
Подготовила: студентка Заочного факультета
Гр. СУА-09з
Шифр 95243
Гассиева Н.С.
Проверил: проф. Ткаченко В.Н.
Донецк
2012
Задание на курсовую
работу:
Задана нелинейная свободная система второго
порядка, описываемая следующим обыкновенным дифференциальным уравнением
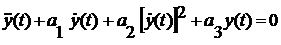 .
.
.Представить исходную систему в виде системы
дифференциальных уравнений первого порядка (в пространстве состояний).
. Определить положение равновесия системы.
. Выполнить численный расчет исходного
нелинейного уравнения и получить график y(t)
для начальных условий 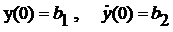 .
.
. Провести линеаризацию системы.
.Получить аналитическое решение линеаризованной
системы и построить его график y(t)
для тех же начальных условий 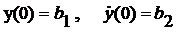 .
.
. Выполнить численный расчет линеаризованной
системы уравнений и получить график y(t)
для тех же начальных условий.
. Построить фазовый портрет системы.
. Исследовать асимптотическую устойчивость
состояния равновесия системы в соответствии с первым методом Ляпунова и сделать
выводы по работе.
Исходные данные:
|
№
вар.
|
a1
|
a2
|
a3
|
b1
|
b2
|
|
1
|
0,5
|
0,1
|
1
|
1
|
1
|
РЕФЕРАТ
Курсовая работа: 44 страницы,
6
рисунков, 5 таблиц, 9 источников.
Объект исследования: Нелинейная свободная
система второго порядка, описываемая обыкновенным дифференциальным уравнением.
Цель работы: С помощью математических средств,
провести анализ и синтез заданной системы по нескольким параметрам.
Выполнено: Исходная система представлена в виде
системы дифференциальных уравнений первого порядка (в пространстве состояний).
Определено положение равновесия системы. Выполнен численный расчет исходного
нелинейного уравнения и получен график y(t)
для заданных начальных условий. Проведена линеаризация системы. Получено
аналитическое решение линеаризованной системы и построен его график y(t)
для тех же начальных условий.
Выполнен численный расчет линеаризованной
системы уравнений и получен график y(t)
для тех же начальных условий. Построен фазовый портрет системы. Исследована
асимптотическая устойчивость состояния равновесия системы в соответствии с
первым методом Ляпунова.
СИСТЕМА, УРАВНЕНИЕ, ПРОСТРАНСТВО СОСТОЯНИЙ,
ПОЛОЖЕНИЕ РАВНОВЕСИЯ, ЧИСЛЕННЫЙ РАСЧЕТ, ЛИНЕАРИЗАЦИЯ, ФАЗОВЫЙ ПОРТРЕТ,
УСТОЙЧИВОСТЬ
СОДЕРЖАНИЕ
1. ВВЕДЕНИЕ
. ОТЧЕТ О ВЫПОЛНЕНИИ ЗАДАНИЯ
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
. ЗАКЛЮЧЕНИЕ
. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Введение
Математическая теория систем, которой посвящена
данная работа, занимается выяснением свойств формального описания (моделей)
реальности, которые позволяют ставить задачи и решать их. К числу таких
важнейших свойств относятся понятия наблюдаемости, управляемости, реализуемости
и минимальности.
При изучении математической теории систем саму
теорию систем рассматривают как теорию динамических взаимосвязей. Здесь
система, а точнее, динамическая система - это строгое математическое понятие.
Поэтому теория систем в основном, хотя и не полностью, является областью
математики. Вместе с тем изучение математической теории систем позволяет
получить важнейшие результаты, относящиеся к задаче регулирования классической
теории управления.
Теория автоматического управления и
регулирования - наука, которая изучает процессы управления, методы их
исследования и основы проектирования автоматических систем, работающих по
замкнутому циклу, в любой области техники. Особую роль для специалиста в данной
области играет даже не создание и проектирование технических средств, а задача
построения законов управления, которая и является основной проблемой общей
теории автоматического управления. Причина такого особого внимания заключается
не только в важности задачи, но и в существовании общего пути её решения. Этот
путь заключается в использовании математического описания, математической
модели как самого объекта, так и функциональных блоков схемы управления,
позволяющих прогнозировать поведение объекта и возможность достижения
поставленных целей при различных внешних условиях.
2. Отчёт о выполнении задания
. Представить исходную
систему в виде системы дифференциальных уравнений первого порядка (в
пространстве состояний)
Рассмотрим заданную нелинейную свободную систему
второго порядка, описываемую следующим обыкновенным дифференциальным
уравнением:
ӱ(t)
+ 0,5ẏ(t)
+ 0,1[ ẏ(t)
]2 + y(t)
= 0)
Данное уравнение представляет собой нелинейное
уравнение второго порядка. Общий вид обыкновенного дифференциального уравнения
второго порядка, разрешенного относительно старшей производной:
y′′xx
= f (x,
y, y′x)
Если уравнения системы разрешены относительно
старшей производной, то их всегда можно преобразовать к системе уравнений 1-го
порядка. Например, пусть система описывается уравнением
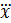
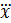 = F(x, ẍ, t)
= F(x, ẍ, t)
Его можно преобразовать к виду
ẋ1
=
x2
ẋ2
=
x3
ẋ3
=
F(x1,
x2,
x3,
t),
где x1
= x, x2
= ẋ, x3
= ẍ.
Аналогичное преобразование можно произвести и в
том случае, когда система описывается несколькими уравнениями.
В общем случае уравнения управляемой системы
можно представить в виде
ẋ1
= f1 (x1, x2, …, xn, u1, u2,…, ur, t)
ẋ2
= f2 (x1, x2, …, xn, u1, u2,…, ur, t)
…………………………………….
ẋn
= fn (x1, x2, …, xn, u1, u2,…, ur, t)= h1 (x1, x2, …, xn, u1, u2,…, ur, t)= h2
(x1, x2, …, xn, u1, u2,…, ur, t)
…………………………………….= hm (x1, x2, …, xn,
u1, u2,…, ur, t)
Здесь x1,
x2, …, xn
- фазовые координаты, или фазовые переменные; u1,
u2,…, ur
- управляющие параметры, или управления; y1,
y2,…, ym
- выходные переменные; t
- время.
Уравнения, записанные в виде системы
дифференциальных уравнений 1-го порядка, разрешенных относительно производной,
называются нормальной формой Коши или просто нормальной формой.
В векторной форме приведённые уравнения
принимают вид
ẋ = f
(x, u,
t) , (1.2а)
ẏ = h
(x, u,
t). (1.2б)
Здесь x
называют фазовым вектором или вектором состояний, u
- вектором управления или просто управлением, а также входной переменной или
просто входом, y - выходным
вектором или просто выходом. Множество всех векторов состояний (фазовых
векторов) называют пространством состояний или фазовым пространством.
Уравнение (1.2а) называют уравнением состояний,
а уравнение (1.2б) - уравнением выхода или уравнением наблюдений.
Если вход и выход системы являются скалярными
величинами, то такие системы называют одномерными. Если хотя бы одна из
указанных переменных является векторной, то такие системы называют
многомерными.
Итак, разрешая заданное уравнение (1.1)
относительно старшей производной, получаем:
ӱ(t)
= − 0,5ẏ(t)
− 0,1[ ẏ(t)
]2 − y(t)
Положив y
= x1, ẏ
= x2, получим
уравнения в нормальной форме:
ẋ1 = x2,
ẋ2 = − x1 - 0,1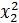
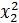 - 0,5x2
- 0,5x2
y = x1
Полная модель объекта в пространстве
состояний называется моделью вход-состояние-выход и содержит два уравнения -
уравнение входа и выхода:
ẋ(t) = A∙x(t) + B∙u(t)
y(t) = C∙x(t) + D∙u(t),
где через x(t) принято
обозначать вектор состояния, через u(t) - вход
объекта (сигнал управления), через y(t) - выход
объекта.
2. Определить положение равновесия
системы
Автономной системой для функций x(t), y(t) называется
система дифференциальных уравнений
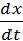
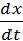 = P(x, y),
= P(x, y), 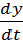
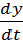 = Q(x, y), (2.1)
= Q(x, y), (2.1)
где правые части не зависят от переменной
t.
Пусть x = f(t), y = g(t) - решение
(2.1).
Положением равновесия, или точкой
покоя, автономной системы дифференциальных уравнений (2.1) называется её
решение вида x = x0, y = y0.
Отметим, что траектория положения
равновесия - точка, и P(x0, y0) = Q(x0, y0) = 0.
В простейшем случае, когда P, Q - линейны,
т.е. P(x, y) = ax + by, Q(x, y) = cx + dy, где a, b, c, d -
постоянные, система принимает вид
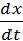
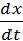 = ax + by,
= ax + by, 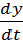
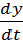 = cx + dy. (2.2)
= cx + dy. (2.2)
Итак, находим положение равновесия
системы
ẋ1 = x2,
ẋ2 = − x1 - 0,1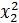
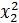 - 0,5x2
- 0,5x2
Здесь P(ẋ1, ẋ2) =
x2, Q(ẋ1, ẋ2) = − x1 - 0,1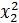
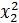 - 0,5x2.
- 0,5x2.
Положение равновесия находим из
системы уравнений
P(ẋ1, ẋ2) =
0
Q(ẋ1, ẋ2) = 0
Или
x2 = 0
− x1 - 0,1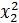
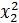 - 0,5x2 = 0
- 0,5x2 = 0
Решая её, находим
x2 = 0
x1 = 0
Таким образом, получаем положение
равновесия M(0,0).
3.
Выполнить численный расчет исходного нелинейного уравнения и получить график y(t) для начальных условий
y(0) = 1, ẏ(0) = 1
Если задачу об отыскании решений
дифференциального уравнения удаётся свести к конечному числу алгебраических
операций, операций дифференцирования и интегрирования известных функций, то
говорят, что дифференциальное уравнение интегрируется в квадратурах. На
практике редко встречаются уравнения, интегрируемые в квадратурах. Для
исследования и решения уравнений, которые не интегрируются в квадратурах,
используются численные методы решения задачи Коши.
Численное решение задачи Коши y′ = f(x, y), y(a) = y0 на отрезке
[a, b] состоит в
построении таблицы приближенных значений y0, y1,…, yi,…, yN решения y = y(x), y(xi) ≈ yi в узлах
сетки a = x0 < x1 < …
< xi < … <
xN = b.
Если xi = a + ih, h = (b - a)/N, то сетка
называется равномерной.
Численный метод решения задачи Коши
называется одношаговым, если для вычисления решения в точке x0 + h
используется информация о решении только в точке x0. Если же
используются несколько предыдущих значений - многошаговым.
Методы, в
которых для вычисления приближенного решения в очередном i-ом узле необходимо
дополнительно решать некоторые уравнения (линейные или нелинейные), называются
неявными методами. В противоположность этому методы, в которых приближенное
решение в очередном i-ом узле явно выражается через предыдущие значения,
называются явными методами.
Простейший одношаговый явный метод
численного решения задачи Коши - метод Эйлера. В методе Эйлера величины yi вычисляются
по формуле yi+1 = yi + h∙f(xi, yi) :
y′ =
f(x, y), y(a) = y0, x ∈ [a, b],= a
+ ih, h = (b - a)/N, i = 0, 1, 2, … , N,(xi) ≈ yi ,+1 = yi + h ∙
f(xi, yi).
Для погрешности метода Эйлера на
одном шаге справедлива оценка
max1≤i≤N | y(xi) − yi| ≤ Ch2,
а для оценки погрешности решения на
всём отрезке [a, b]
справедливо
max1≤i≤N | y(xi) − yi| ≤ C(|b−a|)∙h
Для практической оценки погрешности
удобнее всего использовать правило Рунге: производятся вычисления с шагом h - вычисляют
значения y(h)i , затем
производятся вычисления с половинным шагом h/2 -
вычисляют значения y(h/2)i . За оценку
погрешности с шагом h/2 принимают величину
maxi | yi(h) - y2i(h/2)|.
Если соединить точки (xi, yi)
прямолинейными отрезками, получим ломаную Эйлера - ломаную линию, каждое звено
которой с началом в точке (xi, yi) имеет
угловой коэффициент, равный f(xi, yi).
Итак, выполним численный расчет
исходного нелинейного уравнения
ӱ(t) + 0,5ẏ(t) + 0,1[ ẏ(t) ]2 + y(t) = 0
и построим график y(t) для
начальных условий y(0)=1, ẏ(0)=1.
Приведем исходное уравнение к
уравнению первого порядка, для удобства заменив
y(t) = z
y′(t) = u
y′′(t) = u′
Получаем уравнение первого порядка:
u′ = −
0,5u − 0,1u2 - z
Зададим шаг интегрирования -
расстояние h между
узлами интегрирования - равным 0,01.
Согласно условию задания, z0 = y(0) = 1, u0 = ẏ(0) = 1.
Последовательные значения ui и zi , согласно
методу Эйлера, будем вычислять по формулам
= ui-1∙h + zi-1
ui = ui-1 + h∙(−
0,5 ui-1 −
0,1 ui-12 − zi-1)
Находим:
z1= u0 h+ z0 = 1∙0,01
+ 1 = 1,01
u1 = u0+ h∙(−
0,5 u0− 0,1
u02 - z0) =
1+0,01(-0,5∙1-0,1∙12-1) = 0,984
Аналогично проводим расчёты u2,
u3, …, u100
и z2, z3,
…, z100. Результаты
расчётов, выполненных
с помощью программы Microsoft
Excel,
приведены
в таблице 3.1.
Для оценки погрешности используем правило Рунге:
произведём вычисления с шагом h/2=0,005.
Результаты расчётов приведены в таблице 3.2. Погрешность вычисляем по формуле
maxi | zi(h)
- z2i(h/2)|
= | z50(h)
- z100(h/2)|
= |1,308-1,3067| = 0,0013
Таблица 3.1. Результаты численного расчёта
исходного нелинейного уравнения методом Эйлера с шагом интегрирования 0,01.
|
ui
|
zi
|
yi
|
h
|
i
|
|
1
|
1
|
1
|
0,01
|
0
|
|
0,9840000000
|
1,010
|
0,990
|
0,01
|
1
|
|
0,9680117440
|
1,020
|
0,980
|
0,01
|
2
|
|
0,9520362385
|
1,030
|
0,970
|
0,01
|
3
|
|
0,9360744832
|
1,039
|
0,960
|
0,01
|
4
|
|
0,9201274705
|
1,048
|
0,950
|
0,01
|
5
|
|
0,9041961864
|
1,058
|
0,940
|
0,01
|
6
|
|
0,8882816097
|
1,067
|
0,930
|
0,01
|
7
|
|
0,8723847128
|
1,076
|
0,920
|
0,01
|
8
|
|
0,8565064614
|
1,084
|
0,910
|
0,01
|
9
|
|
0,8406478145
|
1,093
|
0,900
|
0,01
|
10
|
|
0,8248097248
|
1,101
|
0,890
|
0,01
|
11
|
|
0,8089931384
|
1,109
|
0,880
|
0,01
|
12
|
|
0,7931989952
|
1,118
|
0,870
|
0,01
|
13
|
|
0,7774282286
|
1,125
|
0,860
|
0,01
|
14
|
|
0,7616817660
|
1,133
|
0,850
|
0,01
|
15
|
|
0,7459605283
|
1,141
|
0,840
|
0,01
|
16
|
|
0,7302654307
|
1,148
|
0,830
|
0,01
|
17
|
|
0,7145973821
|
1,156
|
0,820
|
0,01
|
18
|
|
0,6989572853
|
1,163
|
0,810
|
0,01
|
19
|
|
0,6833460374
|
1,170
|
0,800
|
0,01
|
20
|
|
0,6677645295
|
1,177
|
0,790
|
0,01
|
21
|
|
0,6522136468
|
1,183
|
0,780
|
0,01
|
22
|
|
0,6366942690
|
1,190
|
0,770
|
0,01
|
23
|
|
0,6212072697
|
1,196
|
0,760
|
0,01
|
24
|
|
0,6057535171
|
1,202
|
0,750
|
0,01
|
25
|
|
0,5903338737
|
1,208
|
0,740
|
0,01
|
26
|
|
0,5749491964
|
1,214
|
0,730
|
0,01
|
27
|
|
0,5596003366
|
1,220
|
0,720
|
0,01
|
28
|
|
0,5442881402
|
1,226
|
0,710
|
0,01
|
29
|
|
0,5290134478
|
1,231
|
0,700
|
0,01
|
30
|
|
0,5137770943
|
1,236
|
0,690
|
0,01
|
31
|
|
0,4985799096
|
1,242
|
0,680
|
0,01
|
32
|
|
0,4834227181
|
1,247
|
0,670
|
0,01
|
33
|
|
0,4683063389
|
1,251
|
0,660
|
0,01
|
34
|
|
0,4532315861
|
1,256
|
0,650
|
0,01
|
35
|
|
0,4381992683
|
1,261
|
0,640
|
0,01
|
36
|
|
0,4232101892
|
1,265
|
0,630
|
0,01
|
|
0,4082651474
|
1,269
|
0,620
|
0,01
|
38
|
|
0,3933649362
|
1,273
|
0,610
|
0,01
|
39
|
|
0,3785103439
|
1,277
|
0,600
|
0,01
|
40
|
|
0,3637021541
|
1,281
|
0,590
|
0,01
|
41
|
|
0,3489411450
|
1,285
|
0,580
|
0,01
|
42
|
|
0,3342280900
|
1,288
|
0,570
|
0,01
|
43
|
|
0,3195637577
|
1,291
|
0,560
|
0,01
|
44
|
|
0,3049489117
|
1,295
|
0,550
|
0,01
|
45
|
|
0,2903843107
|
1,298
|
0,540
|
0,01
|
46
|
|
0,2758707086
|
1,301
|
0,530
|
0,01
|
47
|
|
0,2614088544
|
1,303
|
0,520
|
0,01
|
48
|
|
0,2469994926
|
1,306
|
0,510
|
0,01
|
49
|
|
0,2326433625
|
1,308
|
0,500
|
0,01
|
50
|
|
0,2183411989
|
1,311
|
0,490
|
0,01
|
51
|
|
0,2040937318
|
1,313
|
0,480
|
0,01
|
52
|
|
0,1899016866
|
1,315
|
0,470
|
0,01
|
53
|
|
0,1757657839
|
1,317
|
0,460
|
0,01
|
54
|
|
0,1616867395
|
1,319
|
0,450
|
0,01
|
55
|
|
0,1476652648
|
1,320
|
0,440
|
0,01
|
56
|
|
0,1337020663
|
1,322
|
0,430
|
0,01
|
57
|
|
0,1197978461
|
1,323
|
0,420
|
0,01
|
58
|
|
0,1059533015
|
1,324
|
0,410
|
0,01
|
59
|
|
0,0921691253
|
1,325
|
0,400
|
0,01
|
60
|
|
0,0784460056
|
1,326
|
0,390
|
0,01
|
61
|
|
0,0647846260
|
1,327
|
0,380
|
0,01
|
62
|
|
0,0511856653
|
1,328
|
0,370
|
0,01
|
63
|
|
0,0376497981
|
1,328
|
0,360
|
0,01
|
64
|
|
0,0241776941
|
1,329
|
0,350
|
0,01
|
65
|
|
0,0107700186
|
1,329
|
0,340
|
0,01
|
66
|
|
-0,0025725677
|
1,329
|
0,330
|
0,01
|
67
|
|
-0,0158494087
|
1,329
|
0,320
|
0,01
|
68
|
|
-0,0290598528
|
1,329
|
0,310
|
0,01
|
69
|
|
-0,0422032531
|
1,328
|
0,300
|
0,01
|
70
|
|
-0,0552789670
|
1,328
|
0,290
|
0,01
|
71
|
|
-0,0682863566
|
1,328
|
0,280
|
0,01
|
72
|
|
-0,0812247887
|
1,327
|
0,270
|
0,01
|
73
|
|
-0,0940936344
|
1,326
|
0,260
|
0,01
|
74
|
|
-0,1068922696
|
1,325
|
0,250
|
0,01
|
75
|
|
-0,1196200745
|
1,324
|
0,240
|
0,01
|
76
|
|
-0,1322764343
|
1,323
|
0,230
|
0,01
|
77
|
|
-0,1448607383
|
1,321
|
0,220
|
0,01
|
78
|
|
-0,1573723807
|
1,320
|
0,210
|
0,01
|
79
|
|
-0,1698107602
|
1,318
|
0,200
|
0,01
|
80
|
|
-0,1821752803
|
1,317
|
0,190
|
0,01
|
81
|
|
-0,1944653488
|
1,315
|
0,180
|
0,01
|
82
|
|
-0,2066803784
|
1,313
|
0,170
|
0,01
|
83
|
|
-0,2188197863
|
1,311
|
0,160
|
0,01
|
84
|
|
-0,2308829944
|
1,309
|
0,150
|
0,01
|
85
|
|
-0,2428694294
|
1,306
|
0,140
|
0,01
|
86
|
|
-0,2547785226
|
1,304
|
0,130
|
0,01
|
87
|
|
-0,2666097098
|
1,301
|
0,120
|
0,01
|
88
|
|
-0,2783624319
|
1,299
|
0,110
|
0,01
|
89
|
|
-0,2900361343
|
1,296
|
0,100
|
0,01
|
90
|
|
-0,3016302673
|
1,293
|
0,090
|
0,01
|
91
|
|
-0,3131442859
|
1,290
|
0,080
|
0,01
|
92
|
|
-0,3245776498
|
1,287
|
0,070
|
0,01
|
93
|
|
-0,3359298239
|
1,284
|
0,060
|
0,01
|
94
|
|
-0,3472002775
|
1,280
|
0,050
|
0,01
|
95
|
|
-0,3583884850
|
1,277
|
0,040
|
0,01
|
96
|
|
-0,3694939257
|
1,273
|
0,030
|
0,01
|
97
|
|
-0,3805160839
|
1,270
|
0,020
|
0,01
|
98
|
|
-0,3914544485
|
1,266
|
0,010
|
0,01
|
99
|
|
-0,4023085139
|
1,262
|
0,000
|
0,01
|
100
|
Таблица 3.2. Результаты численного расчёта
исходного нелинейного уравнения методом Эйлера с шагом интегрирования 0,005.
|
ui
|
zi
|
yi
|
h
|
i
|
|
1
|
1
|
1
|
0,005
|
0
|
|
0,9920000000
|
1,0050
|
0,995
|
0,005
|
1
|
|
0,9840029680
|
1,0100
|
0,990
|
0,005
|
2
|
|
0,9760090297
|
1,0149
|
0,985
|
0,005
|
3
|
|
0,9680183102
|
1,0198
|
0,980
|
0,005
|
4
|
|
0,9600309344
|
1,0246
|
0,975
|
0,005
|
|
0,9520470266
|
1,0294
|
0,970
|
0,005
|
6
|
|
0,9440667107
|
1,0342
|
0,965
|
0,005
|
7
|
|
0,9360901103
|
1,0389
|
0,960
|
0,005
|
8
|
|
0,9281173483
|
1,0436
|
0,955
|
0,005
|
9
|
|
0,9201485474
|
1,0482
|
0,950
|
0,005
|
10
|
|
0,9121838298
|
1,0528
|
0,945
|
0,005
|
11
|
|
0,9042233173
|
1,0574
|
0,940
|
0,005
|
12
|
|
0,8962671312
|
1,0619
|
0,935
|
0,005
|
13
|
|
0,8883153925
|
1,0664
|
0,930
|
0,005
|
14
|
|
0,8803682218
|
1,0708
|
0,925
|
0,005
|
15
|
|
0,8724257391
|
1,0752
|
0,920
|
0,005
|
16
|
|
0,8644880642
|
1,0796
|
0,915
|
0,005
|
17
|
|
0,8565553164
|
1,0839
|
0,910
|
0,005
|
18
|
|
0,8486276145
|
1,0882
|
0,905
|
0,005
|
19
|
|
0,8407050771
|
1,0924
|
0,900
|
0,005
|
20
|
|
0,8327878223
|
1,0966
|
0,895
|
0,005
|
21
|
|
0,8248759677
|
1,1008
|
0,890
|
0,005
|
22
|
|
0,8169696306
|
1,1049
|
0,885
|
0,005
|
23
|
|
0,8090689280
|
1,1090
|
0,880
|
0,005
|
24
|
|
0,8011739763
|
1,1130
|
0,875
|
0,005
|
25
|
|
0,7932848917
|
1,1170
|
0,870
|
0,005
|
26
|
|
0,7854017898
|
1,1210
|
0,865
|
0,005
|
27
|
|
0,7775247860
|
1,1249
|
0,860
|
0,005
|
28
|
|
0,7696539953
|
1,1288
|
0,855
|
0,005
|
29
|
|
0,7617895322
|
1,1327
|
0,850
|
0,005
|
30
|
|
0,7539315110
|
1,1365
|
0,845
|
0,005
|
31
|
|
0,7460800453
|
1,1403
|
0,840
|
0,005
|
32
|
|
0,7382352486
|
1,1440
|
0,835
|
0,005
|
33
|
|
0,7303972340
|
1,1477
|
0,830
|
0,005
|
34
|
|
0,7225661141
|
1,1513
|
0,825
|
0,005
|
35
|
|
0,7147420013
|
1,1549
|
0,820
|
0,005
|
36
|
|
0,7069250074
|
1,1585
|
0,815
|
0,005
|
37
|
|
0,6991152441
|
1,1621
|
0,810
|
0,005
|
38
|
|
0,6913128224
|
1,1655
|
0,805
|
0,005
|
39
|
|
0,6835178533
|
1,1690
|
0,800
|
0,005
|
40
|
|
0,6757304471
|
1,1724
|
0,795
|
0,005
|
41
|
|
0,6679507141
|
1,1758
|
0,790
|
0,005
|
42
|
|
0,6601787638
|
1,1791
|
0,785
|
0,005
|
43
|
|
0,6524147058
|
1,1824
|
0,780
|
0,005
|
44
|
|
0,6446586489
|
1,1857
|
0,775
|
0,005
|
45
|
|
0,6369107019
|
1,1889
|
0,770
|
0,005
|
46
|
|
0,6291709731
|
1,1921
|
0,765
|
0,005
|
47
|
|
0,6214395704
|
1,1953
|
0,760
|
0,005
|
48
|
|
0,6137166014
|
1,1984
|
0,755
|
0,005
|
49
|
|
0,6060021733
|
1,2014
|
0,750
|
0,005
|
50
|
|
0,5982963932
|
1,2045
|
0,745
|
0,005
|
51
|
|
0,5905993674
|
1,2075
|
0,740
|
0,005
|
52
|
|
0,5829112023
|
1,2104
|
0,735
|
0,005
|
53
|
|
0,5752320038
|
1,2133
|
0,730
|
0,005
|
54
|
|
0,5675618772
|
1,2162
|
0,725
|
0,005
|
55
|
|
0,5599009278
|
1,2190
|
0,720
|
0,005
|
56
|
|
0,5522492605
|
1,2218
|
0,715
|
0,005
|
57
|
|
0,5446069797
|
1,2246
|
0,710
|
0,005
|
58
|
|
0,5369741896
|
1,2273
|
0,705
|
0,005
|
59
|
|
0,5293509941
|
1,2300
|
0,700
|
0,005
|
60
|
|
0,5217374966
|
1,2326
|
0,695
|
0,005
|
61
|
|
0,5141338003
|
1,2353
|
0,690
|
0,005
|
62
|
|
0,5065400081
|
1,2378
|
0,685
|
0,005
|
63
|
|
0,4989562223
|
1,2404
|
0,680
|
0,005
|
64
|
|
0,4913825453
|
1,2429
|
0,675
|
0,005
|
65
|
|
0,4838190788
|
1,2453
|
0,670
|
0,005
|
66
|
|
0,4762659244
|
1,2477
|
0,665
|
0,005
|
67
|
|
0,4687231832
|
1,2501
|
0,660
|
0,005
|
68
|
|
0,4611909561
|
1,2525
|
0,655
|
0,005
|
69
|
|
0,4536693437
|
1,2548
|
0,650
|
0,005
|
70
|
|
0,4461584461
|
1,2570
|
0,645
|
0,005
|
71
|
|
0,4386583633
|
1,2593
|
0,640
|
0,005
|
72
|
|
0,4311691948
|
1,2615
|
0,635
|
0,005
|
73
|
|
0,4236910400
|
1,2636
|
0,630
|
0,005
|
74
|
|
0,4162239977
|
1,2657
|
0,625
|
0,005
|
75
|
1,2678
|
0,620
|
0,005
|
76
|
|
0,4013236449
|
1,2699
|
0,615
|
0,005
|
77
|
|
0,3938905307
|
1,2719
|
0,610
|
0,005
|
78
|
|
0,3864689217
|
1,2738
|
0,605
|
0,005
|
79
|
|
0,3790589152
|
1,2758
|
0,600
|
0,005
|
80
|
|
0,3716606083
|
1,2777
|
0,595
|
0,005
|
81
|
|
0,3642740977
|
1,2795
|
0,590
|
0,005
|
82
|
|
0,3568994798
|
1,2813
|
0,585
|
0,005
|
83
|
|
0,3495368508
|
1,2831
|
0,580
|
0,005
|
84
|
|
0,3421863066
|
1,2849
|
0,575
|
0,005
|
85
|
|
0,3348479425
|
1,2866
|
0,570
|
0,005
|
86
|
|
0,3275218539
|
1,2883
|
0,565
|
0,005
|
87
|
|
0,3202081355
|
1,2899
|
0,560
|
0,005
|
88
|
|
0,3129068821
|
1,2915
|
0,555
|
0,005
|
89
|
|
0,3056181879
|
1,2931
|
0,550
|
0,005
|
90
|
|
0,2983421468
|
1,2946
|
0,545
|
0,005
|
91
|
|
0,2910788526
|
1,2961
|
0,540
|
0,005
|
92
|
|
0,2838283987
|
1,2975
|
0,535
|
0,005
|
93
|
|
0,2765908781
|
1,2990
|
0,530
|
0,005
|
94
|
|
0,2693663836
|
1,3003
|
0,525
|
0,005
|
95
|
|
0,2621550078
|
1,3017
|
0,520
|
0,005
|
96
|
|
0,2549568427
|
1,3030
|
0,515
|
0,005
|
97
|
|
0,2477719802
|
1,3043
|
0,510
|
0,005
|
98
|
|
0,2406005120
|
1,3055
|
0,505
|
0,005
|
99
|
|
0,2334425294
|
1,3067
|
0,500
|
0,005
|
100
|
График y(t)
строим тоже в инструментах программы Microsoft
Excel. Он представлен на
рисунке 3.1.
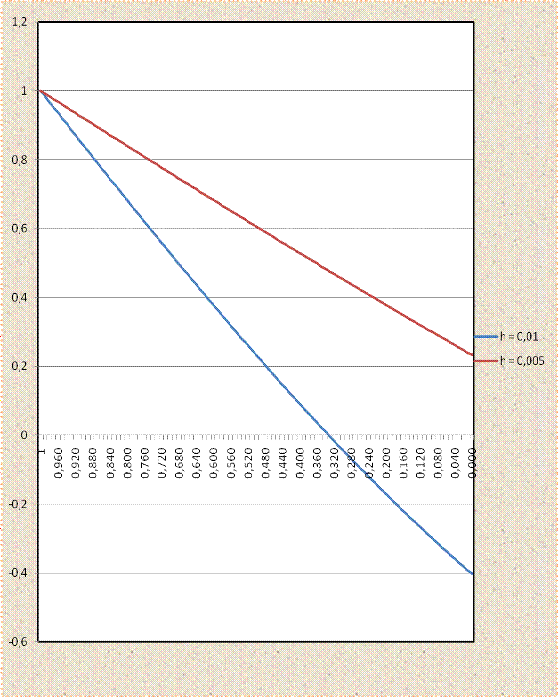
Рисунок 3.1. Кривые Эйлера для исходного
нелинейного дифференциального уравнения.
4. Провести
линеаризацию системы
Во многих случаях нелинейные дифференциальные
уравнения, описывающие большинство систем управления, можно линеаризовать, т.е.
заменить исходные нелинейные уравнения линейными. Процесс преобразования
нелинейных уравнений в линейные называют линеаризацией.
Назначение систем управления - это поддержание
некоторого заданного режима. При этом режиме входные и выходные переменные
звеньев системы изменяются по определенному закону. В частности, в системах
стабилизации они принимают определенные постоянные значения. Но из-за различных
возмущающих факторов фактический режим отличается от требуемого, и текущие
значения входных и выходных переменных не равны значениям, соответствующим
заданному режиму. Обычно систему управления проектируют таким образом, чтобы
реальный процесс мало отличался от требуемого режима, т.е. чтобы отклонения от
заданного режима были малы. Это позволяет производить линеаризацию, разлагая
нелинейные функции, входящие в уравнения, в ряд Тейлора в точке,
соответствующей заданному режиму, и отбрасывая нелинейные относительно
отклонений и их производных слагаемые.
Рассмотрим подробно процесс линеаризации.
Исходное нелинейное дифференциальное уравнение
ӱ(t)
+ 0,5ẏ(t)
+ 0,1[ ẏ(t)
]2 + y(t)
= 0,
т.о. динамическое уравнение системы имеет
нелинейный вид
F (y,
ẏ, ӱ)
= 0
Для удобства представим данную систему в простом
виде, положив y = x1,
ẏ = x2
и получив уравнение в нормальной форме:
ẋ2 = − x1 - 0,1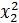
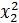 - 0,5x2
- 0,5x2
Тогда динамическое уравнение системы
в общей форме имеет нелинейный вид
F (x1, x2, ẋ2) = 0 (4.1)
Допустим, что установившийся процесс
в системе имеет место при некоторых постоянных значениях x1=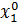
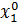 и x2=
и x2=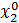
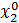 . Тогда уравнение установившегося состояния для
данной системы согласно (4.1) будет
. Тогда уравнение установившегося состояния для
данной системы согласно (4.1) будет
(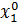
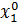 ,
, 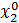
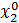 , 0) = 0 (4.2)
, 0) = 0 (4.2)
В основе линеаризации нелинейных
уравнений лежит предположение о том, что в исследуемом динамическом процессе
переменные (в данном случае x1, x2)
изменяются так, что их отклонения от установившихся значений (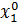
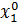 ,
, 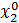
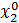 ) остаются всё время достаточно малыми.
) остаются всё время достаточно малыми.
Обозначим указанные отклонения через
∆x1, ∆x2. Тогда в
динамическом процессе
x1(t) = 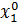
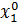 + ∆x1(t)
+ ∆x1(t)
x2(t) = 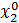
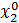 + ∆x2(t) (4.3)
+ ∆x2(t) (4.3)
ẋ2 = ∆ ẋ2
Условие достаточной малости динамических
отклонений переменных от некоторых установившихся значений для системы
автоматического управления обычно выполняется. Этого требует сама идея работы
замкнутой автоматической системы.
Внешнее же воздействие f
(правая часть уравнения) не зависит от работы автоматической системы, изменение
его может быть произвольным, и поэтому правая часть уравнения (4.1) обычно
линеаризации не подлежит (в отдельных случаях и она может быть линеаризована).
Далее выполняем линеаризацию.
Разложим функцию F,
стоящую в левой части уравнения (4.1) в ряд по степеням указанных выше малых
отклонений, рассматривая все производные тоже как самостоятельные переменные.
Тогда уравнение (4.1) примет вид:
F (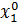
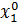 ,
, 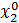
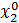 , 0) +
, 0) + 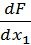
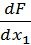 0 ∙∆x1 +
0 ∙∆x1 + 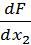
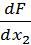 0 ∙∆x2 +
0 ∙∆x2 + 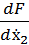
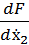 0 ∙∆ẋ2 = 0, (4.4)
0 ∙∆ẋ2 = 0, (4.4)
Где через 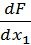
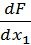 0 обозначена величина
0 обозначена величина 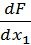
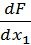 , взятая при x1 =
, взятая при x1 = 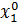
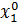 , x2 =
, x2 = 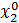
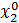 , ẋ2 = 0 (т.е. сначала
берется в общем виде частная производная от функции F по x1, после
чего в неё вместо всех переменных подставляются их постоянные значения
, ẋ2 = 0 (т.е. сначала
берется в общем виде частная производная от функции F по x1, после
чего в неё вместо всех переменных подставляются их постоянные значения 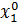
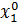 ,
, 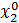
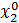 , 0).
, 0).
Следовательно, все частные
производные в полученном уравнении (4.4) представляют собой некоторые
постоянные коэффициенты. Они будут переменными во времени, если функция F будет
содержать t в явном
виде или если установившийся процесс в системе будет определяться переменными
значениями 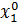
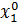 (t),
(t), 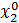
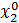 (t).
(t).
Находим:
система дифференциальный
уравнение равновесие
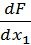
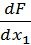 ∙ ∆x1 = 1∙
∆x1 = ∆x1
∙ ∆x1 = 1∙
∆x1 = ∆x1
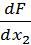
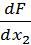 ∙ ∆x2 = 0,5∙∆x2 + 0,1∙2∙∆x2 = 0,7∆x2
∙ ∆x2 = 0,5∙∆x2 + 0,1∙2∙∆x2 = 0,7∆x2
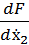
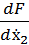 ∙ ∆ẋ2 = 1∙∆ẋ2 = ∆ẋ2
∙ ∆ẋ2 = 1∙∆ẋ2 = ∆ẋ2
Вычтя из уравнения (4.4) почленно
уравнение установившегося состояния (4.2), получим искомое линеаризованное
уравнение динамики данной системы:
x1 + 0,1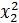
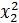 + 0,5x2 + ẋ2 + ∆x1 + 0,7∆x2 + ∆ẋ2 = 0
+ 0,5x2 + ẋ2 + ∆x1 + 0,7∆x2 + ∆ẋ2 = 0
Подставляя заданные начальные
условия y(0) = x1 = 1, ẏ(0) = x2 = 1,
получаем:
+ 0,1∙12 + 0,5∙1 + 1′
+ ∆x1 + 0,7∆x2 + ∆ẋ2 = 0
∆ẋ2 + 0,7∆x2 + ∆x1 + 1,6 = 0
- искомое линеаризованное уравнение. (4.5)
Это дифференциальное уравнение, так
же, как и (4.1), описывает тот же динамический процесс в том же звене
автоматической системы. Отличие этого уравнения от прежнего состоит в
следующем:
1) это уравнение будет являться
приближенным, если в процессе его вывода будут отброшены малые высшего порядка;
2) неизвестными функциями
времени в этом уравнении являются не прежние полные величины x1, x2, а их
отклонения ∆x1, ∆x2 от
некоторых установившихся значений 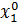
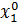 ,
, 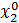
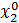 ;
;
3) полученное
уравнение является линейным относительно отклонений ∆x1, ∆x2, ∆ẋ2 с
постоянными коэффициентами 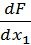
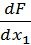 0 ,
0 , 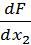
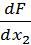 0 ,
0 , 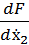
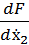 0 (или с переменными коэффициентами, если F содержит t в явном
виде, а также когда установившийся процесс определяется переменными величинами
0 (или с переменными коэффициентами, если F содержит t в явном
виде, а также когда установившийся процесс определяется переменными величинами 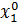
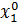 (t),
(t), 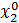
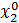 (t), например, при программном
управлении).
(t), например, при программном
управлении).
Таким образом, цель получения линейного
дифференциального уравнения взамен прежнего нелинейного достигнута. Уравнение
(4.5) называется дифференциальным уравнением звена в отклонениях.
5. Получить
аналитическое решение линеаризованной системы и построить его график y(t) для
тех же начальных условий y(0) = 1, ẏ(0) = 1
Полученная линеаризованная система имеет вид
y′′ + 0,7y′
+ y + 1,6 = 0 (5.1)
и представляет собой однородное линейное
дифференциальное уравнение второго порядка с постоянными коэффициентами, общий
вид которого
a2y′′
+ a1y′
+ a0y
= 0.
Данное уравнение интегрируется следующим
способом.
Составляют характеристическое уравнение
a2л2 + a1л
+ a0 = 0,
D = a12
- 4a2a0
- дискриминант.
Вид общего решения зависит от значения
дискриминанта D:
) при D
> 0 уравнение имеет два различных вещественных корня
л1,2 = б1,2 = 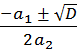
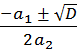
и общее решение имеет вид
y(t) = С1 ∙ eб1∙t + С2 ∙ eб2∙t
где С1,
С2
- произвольные постоянные.
) при D
= 0 уравнение имеет два совпадающих вещественных корня
л1 = л2 = б = 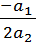
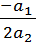
и общее решение имеет вид
y(t)
= С1 ∙ eб∙t
+ С2 ∙ eб∙t
) при D
< 0 уравнение имеет два комплексно сопряженных корня
л1,2 = б ± iв = 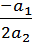
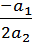 ± i ∙
± i ∙ 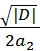
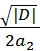
и общее решение имеет вид
y(t)
= С1 ∙ eб∙t
∙
cos(вt)
+ С2 ∙ eб∙t
∙
sin(вt)
Итак, составляем характеристическое уравнение из
исходного (5.1) (свободный член обнуляем):
y2 + 0,7y + 1 = 0
Здесь a2 = 1, a1
= 0,7, a0 = 1.
Вычисляем дискриминант:
= a12 - 4a2a0 = 0,72 − 4∙1∙1
= 0,49−4 = −3,51
Дискриминант - отрицательное число,
следовательно, наше уравнение имеет два комплексно сопряженных корня
л1,2 = б ± iв
= 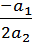
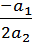 ± i ∙
± i ∙ 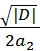
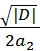
л1,2 = 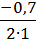
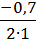 ± i ∙
± i ∙ 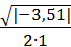
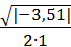
л1,2 = −
0,35 ± i ∙ 0,937,
откуда
б = −0,35,
в
= 0,937
Общий вид уравнения
(t) = С1
∙ e-0,35t
∙ cos(0,937t)
+ С2
∙ e-0,35t
∙ sin(0,937t)
(5.2)
Мы получили общее решение линейного
однородного дифференциального уравнения второго порядка с постоянными
коэффициентами.
Далее нам необходимо найти решение
уравнения (5.2), удовлетворяющее начальным условиям y(0) = 1, ẏ(0) = 1,
т.е. решить задачу Коши.
Подставляя значение t=0 в
уравнение (5.2), получаем первое условие:
y(0) = С1 ∙ e-0,35∙0 ∙ cos(0,937∙0) + С2 ∙ e-0,35∙0 ∙ sin(0,937∙0)
y(0)
= С1 ∙ 1 ∙ 1 +
С2 ∙ 1 ∙ 0 = С1
y(0) = 1
=> С1 = 1
Второе условие ẏ(0) = 1:
y′(0) =
[С1 ∙ e-0,35t ∙ cos(0,937t) + С2 ∙ e-0,35t ∙ sin(0,937t)]′
y′(0) =
[С1 ∙ e-0,35t ∙ cos(0,937t)]′ + [С2 ∙ e-0,35t ∙ sin(0,937t)]′
y′(0) =
[С1 ∙ e-0,35t ∙ cos(0,937t)]′ + [С2 ∙ e-0,35t ∙ sin(0,937t)]′
y′(0) =
(С1 ∙ e-0,35t )′ ∙
cos(0,937t) + С1 ∙ e-0,35t ∙[cos(0,937t)′] + (С2 ∙ e-0,35t)′∙
∙sin(0,937t) + [sin(0,937t)′]∙ С2 ∙ e-0,35t
y′(0) =
−0,35
С1
∙ e-0,35t cos(0,937t) −
0,937sin(0,937t)∙
С1
∙ e-0,35t + [(−0,35С2 ∙ e-0,35t ∙ sin(0,937t)] + 0,937 cos(0,937t)∙
С2
∙ e-0,35t
y′(0) =
cos(0,937t)∙(−0,35 С1 ∙ e-0,35t + 0,937С2 ∙ e-0,35t ) -
− sin(0,937t)∙(0,937С1 ∙ e-0,35t + 0,35С2 ∙ e-0,35t )
Подставляем t = 0:
y′(0) =
cos(0,937∙0)∙(−0,35 С1 ∙ e-0,35∙0 +
0,937С2 ∙ e-0,35∙0 ) -
− sin(0,937∙0)∙(0,937С1 ∙ e-0,35∙0 +
0,35С2 ∙ e-0,35∙0 )
y′(0) =
−0,35C1 + 0,937C2
Зная y′(0) =
1 по условию и рассчитанное С1 = 1, получаем
−0,35 + 0,937C2 = 1
С2 = 1,44
Тогда окончательное решение
линеаризованной системы для начальных условий y(0) = 1, ẏ(0) = 1
имеет вид
y(t) = e-0,35t
∙ cos(0,937t)
+ 1,44e-0,35t
∙ sin(0,937t)
График y(t)
аналитического решения линеаризованной системы построен с помощью инструментов
программы Microsoft Excel и приведен
на рисунке 5.1.
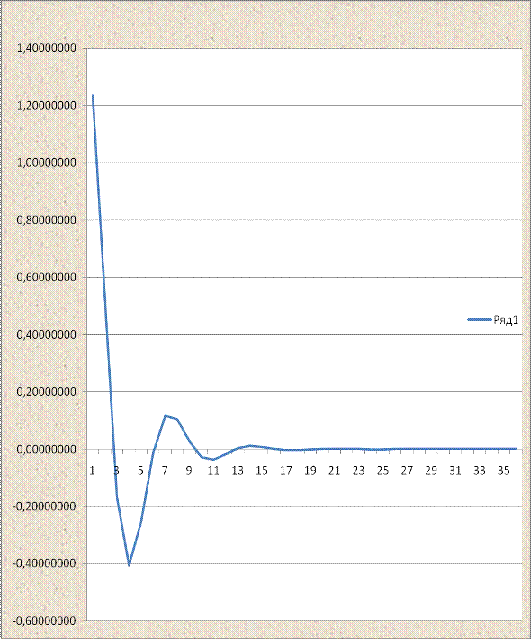
Рисунок 5.1. График y(t)
аналитического решения линеаризованной системы
6. Выполнить численный
расчет линеаризованной системы уравнений и получить график y(t) для
начальных условий y(0)=1, ẏ(0)=1
Будем выполнять численный расчет линеаризованной
системы
′′ + 0,7y′
+ y + 1,6 = 0 (6.1)
Аналогично пункту 3 данной работы, расчёт будем
выполнять методом Эйлера.
Итак, имеем уравнение
y′′ = −
0,7y′
− y
−
1,6
Приведем исходное уравнение к уравнению первого
порядка, для удобства заменив
y(t)
= z
y′(t)
= u
y′′(t)
= u′
Получаем уравнение первого порядка:
u′ = −
0,7u - z
- 1,6
Зададим шаг интегрирования - расстояние h
между узлами интегрирования - равным 0,01.
Согласно условию задания, z0
= y(0) = 1, u0
= y′(0) = 1.
Последовательные значения ui
и zi , согласно методу
Эйлера, будем вычислять по формулам
zi = ui-1∙h
+ zi-1
ui = ui-1
+ h∙(− 0,5
ui-1 − 0,1 ui-12
− zi-1)
Находим:
1= u0
h+ z0
= 1∙0,01 + 1 = 1,01
u1 = u0+
h∙(− 0,7u0
- z0 −1,6) =
1+0,01(−0,7∙1−1−1,6) = 0,967
Аналогично проводим расчёты u2,
u3, …, u100
и z2, z3,
…, z100. Результаты
расчётов, выполненных
с помощью программы Microsoft
Excel,
приведены
в таблице 6.1.
Для оценки погрешности используем правило Рунге:
произведём аналогичные вычисления с шагом h/2=0,005.
Результаты расчётов приведены в таблице 6.2. Погрешность вычисляем по формуле
maxi | zi(h)
- z2i(h/2)|
= | z50(h)
- z100(h/2)|
= |1,123-1,126| = 0,003
Таблица 6.1. Результаты численного расчёта
линеаризованной системы методом Эйлера с шагом интегрирования 0,01.
|
ui
|
zi
|
yi
|
h
|
i
|
|
1
|
1
|
1
|
0,01
|
0
|
|
0,9670000000
|
1,010
|
0,990
|
0,01
|
1
|
|
0,9341310000
|
1,020
|
0,980
|
0,01
|
2
|
|
0,9013953830
|
1,029
|
0,970
|
0,01
|
3
|
|
0,8687955022
|
1,038
|
0,960
|
0,01
|
4
|
|
0,8363336811
|
1,047
|
0,950
|
0,01
|
5
|
|
0,8040122131
|
1,055
|
0,940
|
0,01
|
6
|
|
0,7718333621
|
1,063
|
0,930
|
0,01
|
7
|
|
0,7397993617
|
1,071
|
0,920
|
0,01
|
8
|
|
0,7079124161
|
1,078
|
0,910
|
0,01
|
9
|
|
0,6761746991
|
1,085
|
0,900
|
0,01
|
10
|
|
0,6445883550
|
1,092
|
0,890
|
0,01
|
11
|
|
0,6131554977
|
1,099
|
0,880
|
0,01
|
12
|
|
0,5818782116
|
1,105
|
0,870
|
0,01
|
13
|
|
0,5507585510
|
1,110
|
0,860
|
0,01
|
14
|
|
0,5197985402
|
1,116
|
0,850
|
0,01
|
15
|
|
0,4890001736
|
1,121
|
0,840
|
0,01
|
16
|
|
0,4583654157
|
1,126
|
0,830
|
0,01
|
17
|
|
0,4278962011
|
0,820
|
0,01
|
18
|
|
0,3975944344
|
1,135
|
0,810
|
0,01
|
19
|
|
0,3674619905
|
1,139
|
0,800
|
0,01
|
20
|
|
0,3375007143
|
1,143
|
0,790
|
0,01
|
21
|
|
0,3077124208
|
1,146
|
0,780
|
0,01
|
22
|
|
0,2780988953
|
1,149
|
0,770
|
0,01
|
23
|
|
0,2486618932
|
1,152
|
0,760
|
0,01
|
24
|
|
0,2194031402
|
1,154
|
0,750
|
0,01
|
25
|
|
0,1903243324
|
1,156
|
0,740
|
0,01
|
26
|
|
0,1614271358
|
1,158
|
0,730
|
0,01
|
27
|
|
0,1327131873
|
1,160
|
0,720
|
0,01
|
28
|
|
0,1041840936
|
1,161
|
0,710
|
0,01
|
29
|
|
0,0758414323
|
1,162
|
0,700
|
0,01
|
30
|
|
0,0476867512
|
1,163
|
0,690
|
0,01
|
31
|
|
0,0197215687
|
1,164
|
0,680
|
0,01
|
32
|
|
-0,0080526262
|
1,164
|
0,670
|
0,01
|
33
|
|
-0,0356343739
|
1,164
|
0,660
|
0,01
|
34
|
|
-0,0630222441
|
1,163
|
0,650
|
0,01
|
35
|
|
-0,0902148357
|
1,163
|
0,640
|
0,01
|
36
|
|
-0,1172107770
|
1,162
|
0,630
|
0,01
|
37
|
|
-0,1440087252
|
1,161
|
0,620
|
0,01
|
38
|
|
-0,1706073667
|
1,159
|
0,610
|
0,01
|
39
|
|
-0,1970054168
|
1,158
|
0,600
|
0,01
|
40
|
|
-0,2232016199
|
1,156
|
0,590
|
0,01
|
41
|
|
-0,2491947489
|
1,153
|
0,580
|
0,01
|
42
|
|
-0,2749836059
|
1,151
|
0,570
|
0,01
|
43
|
|
-0,3005670215
|
1,148
|
0,560
|
0,01
|
44
|
|
-0,3259438548
|
1,145
|
0,550
|
0,01
|
45
|
|
-0,3511129935
|
1,142
|
0,540
|
0,01
|
46
|
|
-0,3760733539
|
1,138
|
0,530
|
0,01
|
47
|
|
-0,4008238804
|
1,135
|
0,520
|
0,01
|
48
|
|
-0,4253635460
|
1,131
|
0,510
|
0,01
|
49
|
|
-0,4496913515
|
1,126
|
0,500
|
0,01
|
50
|
|
-0,4738063260
|
1,122
|
0,490
|
0,01
|
51
|
|
-0,4977075265
|
1,117
|
0,480
|
0,01
|
52
|
|
-0,5213940380
|
1,112
|
0,470
|
0,01
|
53
|
|
-0,5448649732
|
1,107
|
0,460
|
0,01
|
54
|
|
-0,5681194724
|
1,101
|
0,450
|
0,01
|
55
|
|
-0,5911567036
|
1,096
|
0,440
|
0,01
|
56
|
|
-0,6139758623
|
1,090
|
0,430
|
0,01
|
57
|
|
-0,6365761712
|
1,084
|
0,420
|
0,01
|
58
|
|
-0,6589568803
|
1,077
|
0,410
|
0,01
|
59
|
|
-0,6811172668
|
1,071
|
0,400
|
0,01
|
60
|
|
-0,7030566350
|
1,064
|
0,390
|
0,01
|
61
|
|
-0,7247743159
|
1,057
|
0,380
|
0,01
|
62
|
|
-0,7462696673
|
1,050
|
0,370
|
0,01
|
63
|
|
-0,7675420738
|
1,042
|
0,360
|
0,01
|
64
|
|
-0,7885909465
|
1,034
|
0,350
|
0,01
|
65
|
|
-0,8094157229
|
1,027
|
0,340
|
0,01
|
66
|
|
-0,8300158668
|
1,019
|
0,330
|
0,01
|
67
|
|
-0,8503908681
|
1,010
|
0,320
|
0,01
|
68
|
|
-0,8705402428
|
1,002
|
0,310
|
0,01
|
69
|
|
-0,8904635328
|
0,993
|
0,300
|
0,01
|
70
|
|
-0,9101603057
|
0,984
|
0,290
|
0,01
|
71
|
|
-0,9296301549
|
0,975
|
0,280
|
0,01
|
72
|
|
-0,9488726991
|
0,966
|
0,270
|
0,01
|
73
|
|
-0,9678875825
|
0,956
|
0,260
|
0,01
|
74
|
|
-0,9866744744
|
0,947
|
0,250
|
0,01
|
75
|
|
-1,0052330693
|
0,937
|
0,240
|
0,01
|
76
|
|
-1,0235630866
|
0,927
|
0,230
|
0,01
|
77
|
|
-1,0416642705
|
0,916
|
0,220
|
0,01
|
78
|
|
-1,0595363898
|
0,906
|
0,210
|
0,01
|
79
|
|
-1,0771792378
|
0,895
|
0,200
|
0,01
|
80
|
|
-1,0945926322
|
0,885
|
0,190
|
0,01
|
81
|
|
-1,1117764150
|
0,874
|
0,180
|
0,01
|
82
|
|
-1,1287304520
|
0,863
|
0,170
|
0,01
|
83
|
|
-1,1454546331
|
0,851
|
0,160
|
0,01
|
84
|
|
-1,1619488719
|
0,840
|
0,150
|
0,01
|
85
|
|
-1,1782131056
|
0,828
|
0,140
|
0,01
|
86
|
|
-1,1942472947
|
0,816
|
0,130
|
0,01
|
87
|
|
-1,2100514233
|
0,804
|
0,01
|
88
|
|
-1,2256254981
|
0,792
|
0,110
|
0,01
|
89
|
|
-1,2409695494
|
0,780
|
0,100
|
0,01
|
90
|
|
-1,2560836297
|
0,768
|
0,090
|
0,01
|
91
|
|
-1,2709678145
|
0,755
|
0,080
|
0,01
|
92
|
|
-1,2856222016
|
0,742
|
0,070
|
0,01
|
93
|
|
-1,3000469112
|
0,730
|
0,060
|
0,01
|
94
|
|
-1,3142420857
|
0,717
|
0,050
|
0,01
|
95
|
|
-1,3282078892
|
0,703
|
0,040
|
0,01
|
96
|
|
-1,3419445079
|
0,690
|
0,030
|
0,01
|
97
|
|
-1,3554521495
|
0,677
|
0,020
|
0,01
|
98
|
|
-1,3687310432
|
0,663
|
0,010
|
0,01
|
99
|
|
-1,3817814393
|
0,649
|
0,000
|
0,01
|
100
|
Таблица 6.1. Результаты численного расчёта
линеаризованной системы методом Эйлера с шагом интегрирования 0,005.
|
ui
|
zi
|
yi
|
h
|
i
|
|
1
|
1
|
1
|
0,005
|
0
|
|
0,9835000000
|
1,005
|
0,995
|
0,005
|
1
|
|
0,9670327500
|
1,010
|
0,990
|
0,005
|
2
|
|
0,9505985479
|
1,015
|
0,985
|
0,005
|
3
|
|
0,9341976896
|
1,020
|
0,980
|
0,005
|
4
|
|
0,9178304694
|
1,024
|
0,975
|
0,005
|
5
|
|
0,9014971796
|
1,029
|
0,970
|
0,005
|
6
|
|
0,8851981105
|
1,033
|
0,965
|
0,005
|
7
|
|
0,8689335507
|
1,038
|
0,960
|
0,005
|
8
|
|
0,8527037869
|
1,042
|
0,955
|
0,005
|
9
|
|
0,8365091039
|
1,046
|
0,950
|
0,005
|
10
|
|
0,8203497847
|
1,050
|
0,945
|
0,005
|
11
|
|
0,8042261105
|
1,055
|
0,940
|
0,005
|
12
|
|
0,7881383603
|
1,059
|
0,935
|
0,005
|
13
|
|
0,7720868116
|
1,063
|
0,930
|
0,005
|
14
|
|
0,7560717399
|
1,066
|
0,925
|
0,005
|
15
|
|
0,7400934187
|
1,070
|
0,920
|
0,005
|
16
|
|
0,7241521199
|
1,074
|
0,915
|
0,005
|
17
|
|
0,7082481133
|
1,078
|
0,910
|
0,005
|
18
|
|
0,6923816669
|
1,081
|
0,905
|
0,005
|
19
|
|
0,6765530469
|
1,085
|
0,900
|
0,005
|
20
|
|
0,6607625175
|
1,088
|
0,895
|
0,005
|
21
|
|
0,6450103411
|
1,091
|
0,890
|
0,005
|
22
|
|
0,6292967783
|
1,094
|
0,885
|
0,005
|
23
|
|
0,6136220877
|
1,098
|
0,880
|
0,005
|
24
|
|
0,5979865261
|
1,101
|
0,875
|
0,005
|
25
|
|
0,5823903484
|
1,104
|
0,870
|
0,005
|
26
|
|
0,5668338077
|
1,107
|
0,865
|
0,005
|
27
|
|
0,5513171551
|
1,109
|
0,860
|
0,005
|
28
|
|
0,5358406399
|
1,112
|
0,855
|
0,005
|
29
|
|
0,5204045096
|
1,115
|
0,850
|
0,005
|
30
|
|
0,5050090098
|
1,117
|
0,845
|
0,005
|
31
|
|
0,4896543841
|
1,120
|
0,840
|
0,005
|
32
|
|
0,4743408743
|
1,122
|
0,835
|
0,005
|
33
|
|
0,4590687205
|
1,125
|
0,830
|
0,005
|
34
|
|
0,4438381607
|
1,127
|
0,825
|
0,005
|
35
|
|
0,4286494311
|
1,129
|
0,820
|
0,005
|
36
|
|
0,4135027662
|
1,131
|
0,815
|
0,005
|
37
|
|
0,3983983983
|
1,133
|
0,810
|
0,005
|
38
|
|
0,3833365581
|
1,135
|
0,805
|
0,005
|
39
|
|
0,3683174745
|
1,137
|
0,800
|
0,005
|
40
|
|
0,3533413742
|
1,139
|
0,795
|
0,005
|
41
|
|
0,3384084823
|
1,141
|
0,790
|
0,005
|
42
|
|
0,3235190220
|
1,143
|
0,785
|
0,005
|
43
|
|
0,3086732146
|
1,144
|
0,780
|
0,005
|
44
|
|
0,2938712796
|
1,146
|
0,775
|
0,005
|
45
|
|
0,2791134345
|
1,147
|
0,770
|
0,005
|
46
|
|
0,2643998950
|
1,149
|
0,765
|
0,005
|
47
|
|
0,2497308752
|
1,150
|
0,760
|
0,005
|
48
|
|
0,2351065869
|
1,151
|
0,755
|
0,005
|
49
|
|
0,2205272403
|
1,152
|
0,750
|
0,005
|
50
|
|
0,2059930438
|
1,154
|
0,745
|
0,005
|
51
|
|
0,1915042038
|
1,155
|
0,740
|
0,005
|
52
|
|
0,1770609249
|
1,156
|
0,735
|
0,005
|
53
|
|
0,1626634098
|
1,156
|
0,730
|
0,005
|
54
|
|
0,1483118596
|
1,157
|
0,725
|
0,005
|
55
|
|
0,1340064732
|
1,158
|
0,005
|
56
|
|
0,1197474478
|
1,159
|
0,715
|
0,005
|
57
|
|
0,1055349789
|
1,159
|
0,710
|
0,005
|
58
|
|
0,0913692600
|
1,160
|
0,705
|
0,005
|
59
|
|
0,0772504826
|
1,160
|
0,700
|
0,005
|
60
|
|
0,0631788368
|
1,161
|
0,695
|
0,005
|
61
|
|
0,0491545105
|
1,161
|
0,690
|
0,005
|
62
|
|
0,0351776898
|
1,161
|
0,685
|
0,005
|
63
|
|
0,0212485591
|
1,161
|
0,680
|
0,005
|
64
|
|
0,0073673010
|
1,161
|
0,675
|
0,005
|
65
|
|
-0,0064659040
|
1,162
|
0,670
|
0,005
|
66
|
|
-0,0202508769
|
1,161
|
0,665
|
0,005
|
67
|
|
-0,0339874407
|
1,161
|
0,660
|
0,005
|
68
|
|
-0,0476754204
|
1,161
|
0,655
|
0,005
|
69
|
|
-0,0613146424
|
1,161
|
0,650
|
0,005
|
70
|
|
-0,0749049352
|
1,161
|
0,645
|
0,005
|
71
|
|
-0,0884461292
|
1,160
|
0,640
|
0,005
|
72
|
|
-0,1019380563
|
1,160
|
0,635
|
0,005
|
73
|
|
-0,1153805505
|
1,159
|
0,630
|
0,005
|
74
|
|
-0,1287734476
|
1,159
|
0,625
|
0,005
|
75
|
|
-0,1421165850
|
1,158
|
0,620
|
0,005
|
76
|
|
-0,1554098021
|
1,157
|
0,615
|
0,005
|
77
|
|
-0,1686529401
|
1,157
|
0,610
|
0,005
|
78
|
|
-0,1818458418
|
1,156
|
0,605
|
0,005
|
79
|
|
-0,1949883520
|
1,155
|
0,600
|
0,005
|
80
|
|
-0,2080803173
|
1,154
|
0,595
|
0,005
|
81
|
|
-0,2211215860
|
1,153
|
0,590
|
0,005
|
82
|
|
-0,2341120082
|
1,152
|
0,585
|
0,005
|
83
|
|
-0,2470514359
|
1,151
|
0,580
|
0,005
|
84
|
|
-0,2599397229
|
1,149
|
0,575
|
0,005
|
85
|
|
-0,2727767245
|
1,148
|
0,570
|
0,005
|
86
|
|
-0,2855622982
|
1,147
|
0,565
|
0,005
|
87
|
|
-0,2982963029
|
1,145
|
0,560
|
0,005
|
88
|
|
-0,3109785995
|
1,144
|
0,555
|
0,005
|
89
|
|
-0,3236090507
|
1,142
|
0,550
|
0,005
|
90
|
|
-0,3361875209
|
1,141
|
0,545
|
0,005
|
91
|
|
-0,3487138762
|
1,139
|
0,540
|
0,005
|
92
|
|
-0,3611879845
|
1,137
|
0,535
|
0,005
|
93
|
|
-0,3736097156
|
1,135
|
0,530
|
0,005
|
94
|
|
-0,3859789410
|
1,134
|
0,525
|
0,005
|
95
|
|
-0,3982955338
|
1,132
|
0,520
|
0,005
|
96
|
|
-0,4105593691
|
1,130
|
0,515
|
0,005
|
97
|
|
-0,4227703236
|
1,128
|
0,510
|
0,005
|
98
|
|
-0,4349282758
|
1,125
|
0,505
|
0,005
|
99
|
|
-0,4470331058
|
1,123
|
0,500
|
0,005
|
100
|
График y(t)
строим также в инструментах программы Microsoft
Excel. Он представлен на
рисунке 6.1.
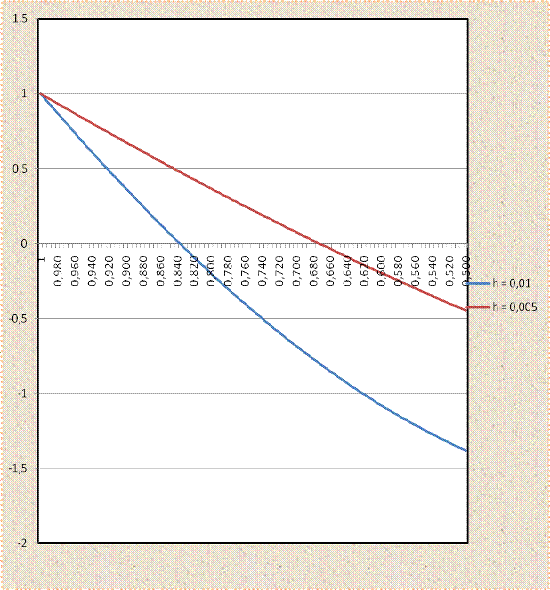
Рисунок 6.1. Ломаные Эйлера для линеаризованной
системы.
7. Построить фазовый
портрет системы
Если уравнения системы представлены в нормальной
форме, то вектор состояния системы однозначно определяет её состояние. Каждому
состоянию системы в пространстве состояний соответствует точка. Точка,
соответствующая текущему состоянию системы, называется изображающей точкой. При
изменении состояния изображающая точка описывает траекторию. Эта траектория
называется фазовой траекторией. Совокупность фазовых траекторий,
соответствующая всевозможным начальным условиям, называется фазовым портретом.
Наглядно фазовую траекторию и фазовый портрет
можно представить в случае двухмерного фазового пространства. Двухмерное
фазовое пространство называется фазовой плоскостью.
Фазовая плоскость - это координатная плоскость,
в которой по осям координат откладываются две переменные (фазовые координаты),
однозначно определяющие состояние системы второго порядка. Метод анализа и
синтеза системы управления, основанный на построении фазового портрета,
называют методом фазовой плоскости.
Рассмотрим общий порядок построения фазового
портрета динамической системы
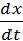
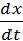 = ax + by
= ax + by
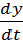
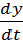 = cx + dy (1)
= cx + dy (1)
1. Выписать матрицу коэффициентов системы
(1):
M = 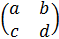
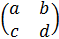 ,
,
найти её след tr M (a + d) и
определитель матрицы det M (ad - bc)
2. Используя рисунок 7.1, определить тип
особой точки.
3. Найти уравнения особых
управлений 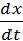
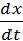 = 0 и
= 0 и 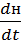
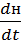 = 0.
= 0.
y = − 
 x = −
x = − 
 x.
x.
4. Если особая точка является седлом или
узлом, то найти асимптоты, используя подстановку y
= kx.
. Определить направление фазовых
траекторий.
Кроме описанного выше способа определения типа
особой точки, тип особой точки можно определить, зная корни характеристического
уравнения.
В таблице 7.1 приведены временные
характеристики, фазовые портреты и типы особых точек при различных корнях
характеристического уравнения.
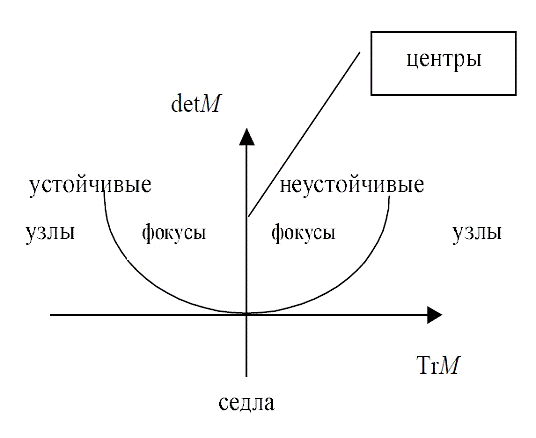
Рисунок 7.1. Зависимость типа особой точки от
определителя и следа матрицы коэффициентов динамической системы.
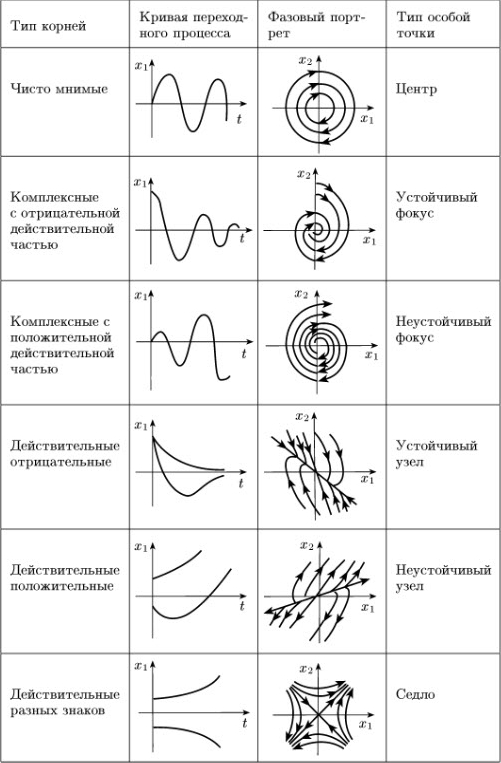
Таблица 7.1. Временные характеристики, фазовые
портреты и типы особых точек при различных корнях характеристического
уравнения.
Итак, рассмотрим найденную в п.4 данной работы
линеаризованную систему
u′ + 0,7u
+ z + 1,6 = 0,
где z
= y(t),
u = z′
= y′(t),
u′ = y′′(t).
Запишем эквивалентную систему дифференциальных
уравнений
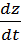
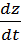 = u
= u
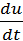
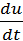 = − 0,7u - z
= − 0,7u - z
(свободный член обнуляем).
. Записываем матрицу коэффициентов
системы
M = 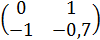
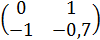
Определитель матрицы det M = 0∙(−0,7)
− 1∙(−1) = 1
След матрицы tr M = 0 + (−0,7)
= −0,7
. Поскольку определитель матрицы
положителен, а след матрицы = −0,7, и выполняется условие det M > (tr M / 2)2 , то
особая точка является устойчивым фокусом (см. Рисунок 7.1).
Сравнивая с зависимостью особой
точки от корней характеристического уравнения (л1,2 = − 0,35 ± i ∙ 0,937), можно
подтвердить, что особая точка - устойчивый фокус.
. Уравнения особых направлений
y = − 
 x = − 0/1 ∙ x = 0
x = − 0/1 ∙ x = 0
y = − 
 x = − (
x = − (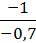
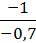 ) ∙ x = −1,429x
) ∙ x = −1,429x
Первую прямую фазовые траектории
пересекают в вертикальном направлении, а вторую - в горизонтальном.
. Поскольку особая точка является
устойчивым фокусом, то фазовые траектории направлены к точке (0;0). Необходимо
выяснить, в каком направлении происходит закручивание фазовой траектории: по
или против часовой стрелки.
Вычислим вектор скорости ( 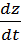
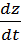 ;
; 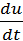
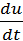 ) в точке (1;0).
) в точке (1;0).
u′ = 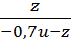
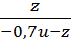
Координаты вектора x = 0, у = −0,7∙0−1=
−1. Имеем вектор скорости (-1;1). Таким образом, вектор скорости
направлен вверх, и, следовательно, спираль закручивается по часовой стрелке.
На рисунке 7.2 представлены графики
прямых y = 0 и y = −1,429x, на рисунке
7.3 представлены
фазовые
траектории устойчивого фокуса.
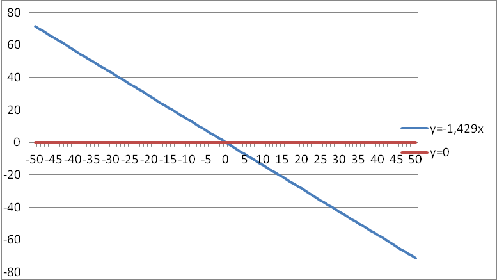
Рисунок 7.2. Графики прямых y = 0 и y = −1,429x
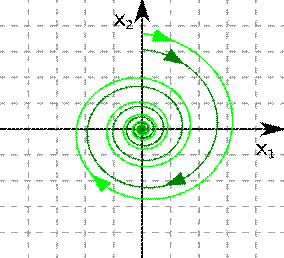
Рисунок 7.3. Фазовый портрет
устойчивого фокуса.
8.
Исследовать асимптотическую устойчивость состояния равновесия системы в
соответствии с первым методом Ляпунова
Назначением систем управления
является поддержание некоторого заданного режима, называемого невозмущенным
движением. Если на систему действует возмущение, то фактическое движение
(которое называется возмущенным движением) будет отличаться от невозмущенного
движения. Невозмущенное движение называется асимптотически устойчивым, если после
окончания действия возмущения возмущенное движение y(t) с течением
времени стремится к невозмущенному движению yн(t): y(t) → yн(t) при t → ∞.
Линейная система управления
называется устойчивой или асимптотически устойчивой, если любое её
невозмущенное движение, определяемое задающим воздействием, асимптотически
устойчиво.
Как уже отмечалось выше, практически
все системы управления являются нелинейными, а линейные системы управления
следует рассматривать как приближенные, линеаризованные модели нелинейных
систем.
Линеаризация производится
относительно заданного номинального режима y0(t),
называемого в теории устойчивости невозмущенным движением. Невозмущенное
движение y0(t) нелинейной
системы называется асимптотически устойчивым, если существует некоторая
окрестность вокруг невозмущенного движения такая, что любое возмущенное
движение y(t),
начинающееся в момент времени t0 окончания действия возмущения в
этой окрестности, в дальнейшем не выходит из этой окружности и y(t) → y0(t) при t → ∞.
Вопрос о том, можно ли судить об
асимптотической устойчивости невозмущенного движения нелинейной системы на
основании исследования устойчивости её линеаризованной модели, впервые был
поставлен и решён А.М. Ляпуновым в 1892 г. в его диссертационной работе.
Для исследования устойчивости систем
А.М. Ляпунов разработал два метода. Под первым методом Ляпунова понимают
совокупность приемов и средств исследования устойчивости решений систем
дифференциальных уравнений, основанных непосредственно на анализе общих или
частных решений этих систем, а также использующих определенные характеристики
указанных решений. Второй метод Ляпунова основан на исследовании системы с
помощью функции Ляпунова.
Итак, исследуем линейную систему
вида
y′′
+ 0,7y′ + y + 1,6 = 0,
(8.1)
которая представляет собой
линеаризованною форму заданной исходной системы, полученную в п.4 данной
работы.
Систему (8.1) можно представить в
виде
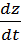
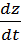 = u
= u
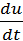
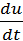 = - z − 0,7u, (8.2)
= - z − 0,7u, (8.2)
где z
= y(t),
u = z′
= y′(t),
u′ = y′′(t)
(свободный член обнуляется).
В общем виде данная система может описываться
как
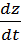
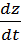 = a11z + a12u
= a11z + a12u
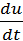
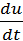 = a21z + a22 ,
= a21z + a22 ,
где a11, a12,
a21, a22 - элементы матрицы А:
А = 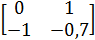
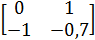
Записываем характеристическое
уравнение для матрицы:
det(A - лE)
= det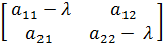
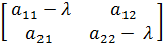 = det
= det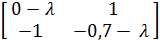
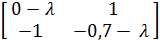 =0,
=0,
где Е - единичная матрица. Раскрывая
этот определитель, получаем уравнение второго порядка
(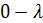
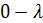 )∙(
)∙(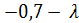
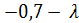 ) − 1∙(−1) = 0
) − 1∙(−1) = 0
л2 + 0,7л +1 = 0 (8.3)
В п.5 данной работы корни данного
характеристического уравнения уже рассчитаны нами:
л1,2 = − 0,35 ± i ∙ 0,937,
где действительная часть корня равна
(−0,35), мнимая равна 0,937.
А. М. Ляпуновым были доказаны
следующие теоремы, определяющие условия устойчивости линейных систем.
Теорема 4. Если все действительные
части корней характеристического уравнения (8.3) для дифференциальных уравнений
(8.2) отрицательны, то невозмущенное движение системы асимптотически устойчиво.
Теорема 5. Если среди корней
характеристического уравнения (8.3) для дифференциальных уравнений (8.2)
имеется хотя бы один с положительной действительной частью, то невозмущенное
движение системы не устойчиво.
Теорема 6. Если уравнение (8.3) не
имеет корней с положительной вещественной частью, но имеется часть корней с
нулевой вещественной частью, то положение равновесия системы будет устойчивым
(не асимптотически).
Таким образом, согласно
произведенным расчётам и утверждению Теоремы 1, невозмущенное движение
линеаризованного уравнения, или уравнения первого приближения, асимптотически
устойчиво.
Представленные выше теоремы А. М.
Ляпунова имеют важное значение в теории автоматического управления, так как они
позволяют судить об устойчивости нелинейных систем по уравнениям первого
приближения в соответствии со следующими условиями:
. Если линейная система первого
приближения устойчива, то соответствующее состояние равновесия нелинейной
системы также устойчиво.
. Если линейная система первого
приближения неустойчива, то соответствующее состояние равновесия нелинейной
системы также неустойчиво.
. Если линейная система первого приближения
находится на границе устойчивости, то судить об устойчивости исходной
нелинейной системы по уравнениям первого приближения нельзя. В этом случае
необходимо рассматривать исходную нелинейную систему.
Таким образом, состояние равновесия
исходной нелинейной системы (1.1) асимптотически устойчиво.
Это же следствие вытекает из еще
одних теорем Ляпунова:
) Если все корни характеристического
уравнения линеаризованной модели являются левыми, то невозмущенное движение
соответствующей нелинейной системы асимптотически устойчиво.
) Если среди корней
характеристического уравнения линеаризованной модели имеется правый корень, то
невозмущенное движение соответствующей нелинейной системы неустойчиво.
) Случай, когда среди корней
характеристического уравнения линеаризованной модели имеются нейтральные корни
(корни на мнимой оси), но нет правых корней, называют критическим. В
критическом случае по линеаризованной модели нельзя судить об устойчивости
невозмущенного движения нелинейной системы.
Как мы рассчитали, корни
характеристического уравнения (8.3) равны л1,2 = − 0,35 ± i ∙ 0,937, т.е. они оба
являются левыми: исходя из расположения на комплексной плоскости, корни с
отрицательными вещественными частями называются левыми, с положительными -
правыми.
Итак, невозмущенное движение
(состояние равновесия) нелинейной системы асимптотически устойчиво.
3.
Заключение
В данной работе была рассмотрена
нелинейная свободная система второго порядка, описанная её математической
моделью - обыкновенным дифференциальным уравнением. На основе проведённого
анализа и расчетов, исходную систему можно описать следующими характеристиками:
1. Уравнения исходной системы в нормальной
форме:
ẋ1 = x2,
ẋ2 = − x1 - 0,1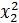
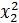 - 0,5x2
- 0,5x2
y = x1
2. Положение равновесия системы М(0,0).
. Линеаризованное уравнение исходной
системы:
′′ + 0,7y′ + y
+1,6 = 0.
. Общее аналитическое решение
линеаризованной системы:
y(t)
= С1 ∙ e-0,35t
∙
cos(0,937t)
+ С2 ∙ e-0,35t
∙
sin(0,937t)
5. Фазовый портрет исходной системы
представляет собой устойчивый фокус.
. Состояние равновесия исходной системы
асимптотически устойчиво.
4. Список
использованной литературы
1.
Васильева А. В., Медведев Г. Н., Тихонов Н.А., Уразгильдина Т. А.
Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и
задачах. - М.: ФИЗМАТЛИТ, 2003. - 432 с.
.
Ким Д. П. Теория автоматического управления. Т. 1. Линейные системы. - М.:
ФИЗМАТЛИТ, 2003. - 288 с.
.
Ким Д. П. Теория автоматического управления. Т. 2. Многомерные, нелинейные,
оптимальные и адаптивные системы: Учеб. пособие. - М.: ФИЗМАТЛИТ, 2004. - 464
с.
.
Математическая теория конструирования систем управления: Учеб. для вузов. / В.
Н. Афанасьев, В. Б. Колмановский, В. Р. Носов. - 3-е изд., испр. И доп. - М.:
Высш. шк., 2003. - 614 с.: ил
.
Мирошник И. В. Теория автоматического управления. Нелинейные и оптимальные
системы. - СПб.: Питер, 2006. - 272 с.: ил.
.
Первозванский А. А. Курс теории автоматического управлении: Учеб. пособ. - М.:
Наука. Гл. ред. физ.-мат. лит., 1986. - 616 с.
.
Поляков К. Ю. Теория автоматического управления для «чайников»: Методич.
пособие. - СПб, 2008. - 80 с.: ил.
.
Романко В. К. Курс дифференциальных уравнений и вариационного исчисления. - 2-е
изд. - М.: Лаборатория Базовых Знаний, 2001 - 344 с: ил.
.
Справочник по теории автоматического управления / Под ред. А. А. Красовского. -
М.: Наука. Гл. ред. физ.-мат. лит., 1987. - 712 с.