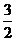Физиология человеческой памяти
Геометричні
системи Келі-Клейна
геометрія ріман
метричний
Вступ
Геометрії які можна отримати, коли
ввести на проектуючій площині метрику,способом який вказав Келі, цей спосіб
аналогічний побудовам проективних моделей геометрії Рімана і Лобачевського,
називається геометріями Келі-Клейна.
Працюючи над одним і тим же питанням
у Келі і Клейна виникла спільна ідея яка полягала у тому, що вони хотіли
виділити певні групи проєктуючих перетворень, які відіграють роль
"руху" відповідної геометриї.
Ідеї
Келі
привели до трьох видів вимірювання величин - до трьох геометричних систем в
образах першого степеня, які відповідають трьом видам інваріанта двох
елементів. З переходом до образів другого степеня в них з'являються два
незалежні типи образів першого степеня (або одновимірних образів). Так,
наприклад, в площині є ряди колінеарних точок (прямі лінії) і пучки прямих. У
кожному з цих образів першого степеня, незалежно від іншого, може бути
встановлене три типи вимірювання величин і, отже, всього можливим є дев'ять
комбінацій, які і приводять до дев'яти геометричних систем, що суттєво
відрізняються одна від одної. Розчленування і класифікація цих систем була
вперше опублікована Соммервилем в 1910 р. (D.
М. Sommerville
). Ці ідеї (у недостатньо розгорнутому вигляді) містилися вже в
лекціях Клейна, які він читав у
Геттингенському університеті ще в 1889-1890 роках. Лекції ці, раніше
літографовані, були опубліковані його учнем В. Роземаном (W. Rosemann)
після тривалої і ретельної їх переробки; вони з'явилися після смерті Клейна у
1928 р. Російський їх переклад вийшов у світ 1936 року. Класифікація
геометричних систем, побудованих за ідеями Келі, становить основний зміст цієї
дипломної.
Метою дипломного дослідження є більш
глибоке ознайомлення з дев'ятьма геометричними системами, що істотно
відрізняються одна від одної.
Завданнями є: систематизувати даний
матеріал, з'ясувати відмінність геометричних систем Келі-Клейна.
Під час написання дипломної роботи
було використано ряд навчальних посібників. В підручнику Гильберт Д. «Основания
геометрии» краще поданий матеріа про геометрію
Келі-Клейна поза круговим абсотутом, ніж в підручнику Костип
В.И."Основания геометрии". А також таку літературу як: Костип В.И.
"Основания геометри", Эйзенхарт А.П. "Риманова геометрия".
Рошевський П.К. "Введение в риманову геометрию и тензорный аналіз".
Букреев Б.А. "Планиметрия Лобачевського в аналитическом изложения". Шатуповский
С.О.
"Введение в анализ".
Дипломна робота складається з трьох
розділів, висновків, додатків і списку використаної літератури.
В першому розділі розглядається
геомертія Келі-Клейна з невиродженим абсолютом, в другому розділі геометрія
Келі-Клейна з виродженим абсолютом.
В третьому розділі викладено основні
образи планіметрії Лобачевського в інтерпритації Келі- Клейна.
1. Геометрія келі-клейна з
невиродженим абсолютом
.1 Геометрія Келі-Клейна поза
круговим абсолютом I
З'ясуємо відмінність геометричних
систем, побудованих за ідеями Келі, повернемося до простого двовимірного
абсолюту і пов'язаної з ним геометрії
-
до кругового абсолюту і до геометрії Лобачевського. Інтерпретація гіперболічної
геометрії була побудована всередині одиничного круга; це було пов'язано з тим,
що перетворення Келі-Клейна не тільки перетворюють в себе коло кругового
абсолюту, але й залишають інваріантним весь обмежений ним круг, тобто внутрішні
точки цього круга перетворюються у внутрішні точки. Разом з тим частина
площини, що розміщена поза абсолютом, також перетворюється в себе, і виникає
питання, чи не можна цю частину площини також зробити субстратом геометрії,
зберігаючи як рухи ту ж групу Келі- Клейна, і якою буде ця геометрія.
Звернемо перш за все увагу на
ту обставину, що прямі, які лежать в цій області, природно, розбиваються на дві
категорій: на прямі, що перетинають абсолют, і прямі, що не перетинають
абсолют, тобто повністю лежать поза ним. Ця відмінність є істотною, так як
перетворення, яке залишає абсолют інваріантним, перетворює прямі однієї
категорії в прямі тієї ж самої категорії (оскільки точки, в яких пряма
перетинає абсолют, переходять в точки, в яких абсолют перетинає образ прямої).
Прямі першої категорії (IІ ), тобто що
перетинає абсолют, будемо називати гіперболічними; прямі другої категорії (ІІ
), тобто що
перетинає абсолют, будемо називати гіперболічними; прямі другої категорії (ІІ ), що не
перетинає абсолюта, називатимемо еліптичними. З числа гіперболічних прямих
природно виділити ще прямі третьої категорії, такі що дотикаються до абсолюту.
Їх будемо називати ізотропними. Це відповідає, як встановленому вище значенню
цього терміну.
), що не
перетинає абсолюта, називатимемо еліптичними. З числа гіперболічних прямих
природно виділити ще прямі третьої категорії, такі що дотикаються до абсолюту.
Їх будемо називати ізотропними. Це відповідає, як встановленому вище значенню
цього терміну.
Будуємо двоїсту геометрію
поза круговим абсолютом, а саме: до першої віднесемо тільки гіперболічні прямі,
до другої тільки еліптичні. Всі точки розміщені поза абсолютом, відноситься як
до однієї, так і до іншої геометрії. При цьому не кожну пару точок в геометрії 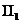 і в
геометрі
і в
геометрі
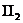 можна
з'єднати прямою, що відноситься до цієї геометрії.
У
можна
з'єднати прямою, що відноситься до цієї геометрії.
У
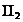 пару точок
пару точок  і
і  можна
з’єднати прямою тільки в тому випадку, якщо
можна
з’єднати прямою тільки в тому випадку, якщо 
 перетинає абсолют (гіперболічна
пара точок). Навпаки, в геометрії
перетинає абсолют (гіперболічна
пара точок). Навпаки, в геометрії 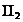 пару точок
пару точок  і
і  можна
з'єднати прямою тільки в тому випадку, якщо
можна
з'єднати прямою тільки в тому випадку, якщо 
 не
перетинає абсолюту (еліптична пара точок). Ця обставина може спочатку здаватися
дивною: у знайомих до цих пір геометричних системах (у геометрії Евкліда і в
геометрії Лобачевського) кожні дві точки можна з'єднати прямою, тобто які б не
були точки
не
перетинає абсолюту (еліптична пара точок). Ця обставина може спочатку здаватися
дивною: у знайомих до цих пір геометричних системах (у геометрії Евкліда і в
геометрії Лобачевського) кожні дві точки можна з'єднати прямою, тобто які б не
були точки 
 завжди
існує пряма m, що проходить як через точку
завжди
існує пряма m, що проходить як через точку  так і через точку
так і через точку  . Проте,
саме по собі таке положення зовсім не є єдино можливим. І геометрія Евкліда, і
геометрія Лобачевського мають ту властивість, що пари прямих не завжди
перетинається в одній точці: для даних двох прямих m
. Проте,
саме по собі таке положення зовсім не є єдино можливим. І геометрія Евкліда, і
геометрія Лобачевського мають ту властивість, що пари прямих не завжди
перетинається в одній точці: для даних двох прямих m і m
і m може і не
існувати такої точки. Ця обставина в деякому розумінні близька до особливостей
геометрій
може і не
існувати такої точки. Ця обставина в деякому розумінні близька до особливостей
геометрій 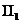 і
і 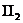 . Забігаючи
наперед, варто зауважити, що на противагу геометрії Евкліда і Лобачевського,
геометрична система
. Забігаючи
наперед, варто зауважити, що на противагу геометрії Евкліда і Лобачевського,
геометрична система 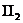 має ту
властивістю, що в ній кожні дві прямі m
має ту
властивістю, що в ній кожні дві прямі m і m
і m перетинаються в деякій точці
перетинаються в деякій точці 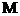 .
.
Таким чином, у порівнянні з
геометрією Лобачевського, тут прямі і точки ніби «обмінялися ролями» (у системі
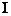 для кожних
двох точок можна знайти спільну для них пряму, але не для кожних двох прямих -
спільну точку; в системі
для кожних
двох точок можна знайти спільну для них пряму, але не для кожних двох прямих -
спільну точку; в системі 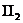 навпаки,
для кожних двох прямих можна знайти спільну їх точку, але не для кожних двох
точок - спільну пряму). Після цих попередніх зауважень розглянемо детальніше
систему
навпаки,
для кожних двох прямих можна знайти спільну їх точку, але не для кожних двох
точок - спільну пряму). Після цих попередніх зауважень розглянемо детальніше
систему 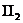 . На кожної
прямої введемо лінійний абсолют для вимірювання відстаней між точками цієї
прямої і в кожному пучку кутовий абсолют для вимірювання кутів між прямими
цього пучка. Нехай
. На кожної
прямої введемо лінійний абсолют для вимірювання відстаней між точками цієї
прямої і в кожному пучку кутовий абсолют для вимірювання кутів між прямими
цього пучка. Нехай 
 - гіперболічна пара точок така, що
пряма
- гіперболічна пара точок така, що
пряма 
 перетинає абсолют у двох точках
перетинає абсолют у двох точках 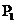 і
і  (які ми
будемо вважати різними. Серед перетворень групи, Келі - Клейна («рухів») є
одночленна група, що залишає точки
(які ми
будемо вважати різними. Серед перетворень групи, Келі - Клейна («рухів») є
одночленна група, що залишає точки 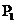 і
і  без змін. Розглядаючи точки
без змін. Розглядаючи точки 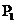 і
і  як лінійний
абсолют визначення довжин на прямій
як лінійний
абсолют визначення довжин на прямій 
 (яку ми зараз розглядаємо тільки
для тієї її частині, яка лежить на круговому абсолюті). Встановимо на цій
прямій гіперболічній величині; відстань
(яку ми зараз розглядаємо тільки
для тієї її частині, яка лежить на круговому абсолюті). Встановимо на цій
прямій гіперболічній величині; відстань 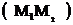 між точками
між точками  і
і  , буде
визначена ангармонічним відношенням
, буде
визначена ангармонічним відношенням 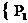
 ,
, 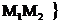 . Точніше, оскільки точки
. Точніше, оскільки точки  і
і  , не
розділяють точок
, не
розділяють точок 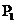 ,
,  , то
ангармонічні відносини
, то
ангармонічні відносини 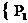
 ,
, 
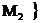 і
і 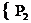
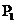 ,
, 
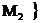 додатні; похідні їх рівні 1. Тому
одне з них більше 1, а друге менше. Логарифм того з цих двох ангармонічних
відношень, яке більше 1 (ангармонічного відношення
додатні; похідні їх рівні 1. Тому
одне з них більше 1, а друге менше. Логарифм того з цих двох ангармонічних
відношень, яке більше 1 (ангармонічного відношення 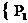
 ,
, 
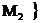 ), взятий з незмінним для всієї
області сталим множником
), взятий з незмінним для всієї
області сталим множником 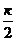 , береться
за відстань (
, береться
за відстань (
 ) між точками
) між точками  і
і  .
Встановлене таким чином гіперболічне визначення довжин для прямих системи II
.
Встановлене таким чином гіперболічне визначення довжин для прямих системи II , очевидно
буде інваріантим відносно «рухів» цієї геометрії: якщо перетворення
Келі - Клейна переводить точки
, очевидно
буде інваріантим відносно «рухів» цієї геометрії: якщо перетворення
Келі - Клейна переводить точки  ,
, в точки
в точки 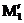 ,
, то точки
то точки 
 , перейдуть в точки Р
, перейдуть в точки Р ′, Р
′, Р ′, у
яких перетинається абсолют з прямою
′, у
яких перетинається абсолют з прямою 
 тому
тому
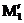
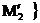 =
=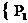
 ,
, 
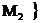 i
i 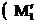
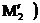 =
= 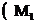
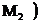 . Якщо пряма
. Якщо пряма 
 дотикаються до абсолюта в єдиній
точці Р, то точки
дотикаються до абсолюта в єдиній
точці Р, то точки 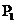 і Р
і Р слід
вважати такими, що співпали. В цьому випадку
слід
вважати такими, що співпали. В цьому випадку 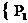
 ,
, 
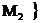 =1 і, отже (
=1 і, отже ( ,
, ) = =
) = =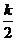 ln
ln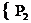
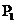 ,
, 
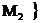 = 0. Таким чином, в системі II
= 0. Таким чином, в системі II відстань
між будь-якими двома точками ізотропної прямої рівна нулю. Ця обставина може
бути виправданням самого терміну «ізотропна пряма». Нарешті, якщо пара точок
відстань
між будь-якими двома точками ізотропної прямої рівна нулю. Ця обставина може
бути виправданням самого терміну «ізотропна пряма». Нарешті, якщо пара точок 
 є еліптичною (тобто пряма
є еліптичною (тобто пряма 
 не перетинає абсолюту), то точки
не перетинає абсолюту), то точки  і
і  в геометрії
в геометрії
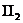 не можна
з'єднати прямою. В цьому випадку треба вважати, що відстань
не можна
з'єднати прямою. В цьому випадку треба вважати, що відстань 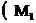
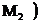 не існує (аналогічно тому як в
геометрії Лобачевського не існує кута між прямими що, не перетинаються в жодній
точці).
не існує (аналогічно тому як в
геометрії Лобачевського не існує кута між прямими що, не перетинаються в жодній
точці).
Перейдемо тепер до питання
про вимірювання кутів в геометрії 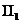 . Зауважимо перш за все, що дві
прямі цієї геометрії можуть не перетинатися-такими ми повинні вважати дві
гіперболічні прямі, які перетинаються у середині абсолюту або на абсолюті,
оскільки до геомeтрії
. Зауважимо перш за все, що дві
прямі цієї геометрії можуть не перетинатися-такими ми повинні вважати дві
гіперболічні прямі, які перетинаються у середині абсолюту або на абсолюті,
оскільки до геомeтрії 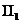 відносяться
лише точки, зовнішні відносно абсолюта. (Аналогічно до цього дві прямі
геометрії Лобачевського - вважали такими, що перетинаються в тому випадку, якщо
вони перетинаються у середині абсолюту.) Нехай тепер Q
відносяться
лише точки, зовнішні відносно абсолюта. (Аналогічно до цього дві прямі
геометрії Лобачевського - вважали такими, що перетинаються в тому випадку, якщо
вони перетинаються у середині абсолюту.) Нехай тепер Q , Q
, Q - дві прямі
геометрії
- дві прямі
геометрії  (тобто
прямі, що перетинають абсолют), що виходять з точки Q, зовнішньої відносно
абсолюта. Проведемо з точки Q ще дотичні Q
(тобто
прямі, що перетинають абсолют), що виходять з точки Q, зовнішньої відносно
абсолюта. Проведемо з точки Q ще дотичні Q i Q
i Q до абсолюту. Прямі Q
до абсолюту. Прямі Q i Q
i Q лежатимуть
в середині кута
лежатимуть
в середині кута  . Встановимо
в пучку прямих з вершиною Q величини кутів, кутовим абсолютом яких є дотичні Q
. Встановимо
в пучку прямих з вершиною Q величини кутів, кутовим абсолютом яких є дотичні Q i Q
i Q ; точніше,
нехай кут
; точніше,
нехай кут  Q
Q буде
пропорційним логарифму одного з ангармонічних відншень { Q
буде
пропорційним логарифму одного з ангармонічних відншень { Q , Q
, Q , Q
, Q , Q
, Q } і { Q
} і { Q , Q
, Q , Q
, Q , Q
, Q }, яке
більше 1 (ці ангармонічні відношення обидва додатні, оскільки прямі Q
}, яке
більше 1 (ці ангармонічні відношення обидва додатні, оскільки прямі Q i Q
i Q , не
розділяють прямих Q
, не
розділяють прямих Q , Q
, Q ; похідна їх
рівна 1). Ця міра визначення кутів гіперболічна.
; похідна їх
рівна 1). Ця міра визначення кутів гіперболічна.
Очевидно, що кут між прямими
Q i Q
i Q вимірюється
тим же числом, що і відстань між точками
вимірюється
тим же числом, що і відстань між точками  і
і  перетину цих прямих з прямою
перетину цих прямих з прямою 
 , Значення кута наближається до
нескінченності, коли одна з прямих Q
, Значення кута наближається до
нескінченності, коли одна з прямих Q , Q
, Q залишається нерухомою до однієї з
ізотропних прямих Q
залишається нерухомою до однієї з
ізотропних прямих Q i Q
i Q пучка.
Дійсно, якщо Q
пучка.
Дійсно, якщо Q незмінюється, а Q
незмінюється, а Q наближається до Q
наближається до Q ,то {Q
,то {Q , Q
, Q , Q
, Q , Q
, Q } (а отже, і
кут
} (а отже, і
кут  Q
Q )
нескінченно зростає. У геометричній системі
)
нескінченно зростає. У геометричній системі  як міра визначчення відстаней між
точками прямої, так і міра визначчення кутів між прямими пучка є гіперболічними.
Тому систему
як міра визначчення відстаней між
точками прямої, так і міра визначчення кутів між прямими пучка є гіперболічними.
Тому систему
 , будемо
позначати двома буквами НН.
, будемо
позначати двома буквами НН.
1.2 Геометрія Келі-Клейна поза
круговим абсолютом II;
система ЕН
Розглянемо тепер область поза
круговим абсолютом, приймаючи, проте, за прямі тільки ті прямі евклідової
площини, які не перетинають абсолют (система 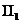 ). У цій системі вимірювaння
відстаней між точками прямої буде еліптичним; лінійним абсолютом для цієї міри
будуть дві спряжені уявні точки перетину прямої з абсолютом. При цьому тут, як
і в системі
). У цій системі вимірювaння
відстаней між точками прямої буде еліптичним; лінійним абсолютом для цієї міри
будуть дві спряжені уявні точки перетину прямої з абсолютом. При цьому тут, як
і в системі 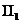 , відстань
, відстань 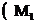
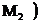 між точками
між точками  і
і  визначена
не для всіх пар точок: якщо
визначена
не для всіх пар точок: якщо  ,
, 
 - гіперболічна пара точок, та
відстань
- гіперболічна пара точок, та
відстань 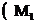
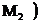 не буде існувати (це пов'язано з
тим, що гіперболічну пару точок в геометрії
не буде існувати (це пов'язано з
тим, що гіперболічну пару точок в геометрії 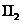 не можна з'єднати прямою).
Вимірювання кутів в системі
не можна з'єднати прямою).
Вимірювання кутів в системі 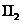 буде гіперболічним: кутовим
абсолютом будуть дві дійсні дотичні, проведені з вершини кута до абсолюта;
еліптичні прямі, які входять в субстрат цієї геометрії (прямі Q
буде гіперболічним: кутовим
абсолютом будуть дві дійсні дотичні, проведені з вершини кута до абсолюта;
еліптичні прямі, які входять в субстрат цієї геометрії (прямі Q Q
Q ), проходять
всередині кутів
), проходять
всередині кутів 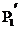 Q
Q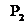 і
і 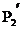 Q
Q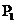 . При цьому
кожні дві пряма геометрія
. При цьому
кожні дві пряма геометрія 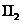 утворюють
між собою деякий кут (бо кожні дві еліптичні прямі перетинаються в точці,
зовнішній відносно до абсолюта, оскільки обидві вони цілком складаються з таких
точок). Систему
утворюють
між собою деякий кут (бо кожні дві еліптичні прямі перетинаються в точці,
зовнішній відносно до абсолюта, оскільки обидві вони цілком складаються з таких
точок). Систему  доцільно
позначати через ЕН (еліптичне вимірювання відстаней і гіперболічне вимірювання
кутів)
доцільно
позначати через ЕН (еліптичне вимірювання відстаней і гіперболічне вимірювання
кутів)
Мал. 3
Отже, область поза круговим
абсолютом є субстратом двох нових геометрій НН і ЕН, що істотно відрізняються
від геометрії Лобачевського.
1.3 Вирази
для довжин і кутів в геометричних системах з круговим абсолютом (I, II , ІІ
, ІІ )
)
Розглянуті три системи
усередині кругового абсолюту  і поза ним
і поза ним  і
і  , можуть
бути без зміни їх геометричного змісту побудовані для абсолюта, що є будь-яким
невиродженим конічним перерізом: дійсне коло, еліпс, гіпербола, парабола.
Система, що побудована в цьому порядку ідей всередині абсолюта, є геометрію
Лобачевського. Дві інші не відрізняються від системи
, можуть
бути без зміни їх геометричного змісту побудовані для абсолюта, що є будь-яким
невиродженим конічним перерізом: дійсне коло, еліпс, гіпербола, парабола.
Система, що побудована в цьому порядку ідей всередині абсолюта, є геометрію
Лобачевського. Дві інші не відрізняються від системи  і
і  . Розглянемо
аналітичний вираз для відстаней і кутів у кожній з розглянутих трьох систем,
враховуючи для спрощення абсолют колом.
. Розглянемо
аналітичний вираз для відстаней і кутів у кожній з розглянутих трьох систем,
враховуючи для спрощення абсолют колом.
Геометрія, побудована
всередині абсолюта  , є
геометрією Лобачевського. Формула відстані між двома точками в цій геометрії
виведена на підставі тригонометричних міркувань
, є
геометрією Лобачевського. Формула відстані між двома точками в цій геометрії
виведена на підставі тригонометричних міркувань
Трохи інакший підхід до
вираження значення кута між двома прямими в гіперболічній геометрії. Розглянемо
міркування Клейна для знаходження даної формули вони полягають на основі
властивостей «рухів», встановлених в цій інтерпретації.
Якщо
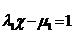
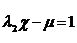 (1)
(1)
є дві прямі в площині
абсолюту, то рівняння
(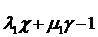 )+m(
)+m(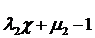 )=0 (1′)
)=0 (1′)
виражає пучок прямих, що
проходять через точку перетину прямих (1);, m- однорідні координати прямої
цього пучка. Відстань (евклідова) цієї прямої від початку виражається числом
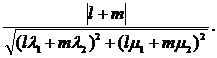 (2)
(2)
Якщо ця пряма дотикається до
кругового абсолюта, тобто кола радіуса 1 з центром в початку координат, то ця
відстань рівна 1. Отже умову, дотику прямої (l,m )
пучка до абсолюта, можна виразити рівністю
(l+m) =(lλ
=(lλ +mλ
+mλ )
) +(lμ
+(lμ +mμ
+mμ )
) , (3)
, (3)
або, покладаючи
λ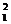 +μ
+μ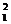 -1=ν
-1=ν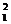 , λ
, λ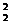 +μ
+μ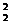 -1=ν
-1=ν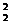 , і λ
, і λ λ
λ +μ
+μ μ
μ -1=ν
-1=ν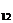 ,
,
рівністю
l ν
ν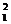 +2lmν
+2lmν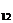 +m
+m ν
ν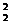 =0 (ν
=0 (ν >0, ν
>0, ν >0). (3′)
>0). (3′)
Яким би не був пучок, існують
дві його прямі (дійсні або уявні зв'язані), які дотикаються до абсолюта. Ці
дотичні - уявні, якщо ν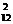 < ν
< ν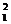 ν
ν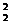 дійсні,
якщо ν
дійсні,
якщо ν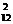 > ν
> ν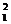 ν
ν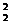 ; і вони
співпадають, якщо ν
; і вони
співпадають, якщо ν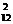 = ν
= ν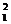 ν
ν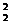 .
.
Зупинимося на першому
випадку. Прямі (1) перетинаються в цьому випадку усередині абсолюта. Точка їх
перетину належить геометрії Лобачевського  , що має
місце всередині абсолюта. Дві уявні зв'язані дотичні утворюють кутовий абсолют
вимірювання в цьому пучку . За схемою Келі прямі пучка утворюють кут. Отже, в
геометрії Лобачевського кути мають еліптичну міру величини; за прийнятою схемою
цю геометрію слід позначити НЕ, відповідно в цій системі має місце гіперболічне
вимірювання відстаней і еліптичне вимірювання кутів. Вимірювання відстаней і
кутів у геометрії Лобачевського здійснюється за схемою Келі-Клейна.
, що має
місце всередині абсолюта. Дві уявні зв'язані дотичні утворюють кутовий абсолют
вимірювання в цьому пучку . За схемою Келі прямі пучка утворюють кут. Отже, в
геометрії Лобачевського кути мають еліптичну міру величини; за прийнятою схемою
цю геометрію слід позначити НЕ, відповідно в цій системі має місце гіперболічне
вимірювання відстаней і еліптичне вимірювання кутів. Вимірювання відстаней і
кутів у геометрії Лобачевського здійснюється за схемою Келі-Клейна.
Звертаючись тепер до того
випадку, коли ν >ν
>ν ν
ν , і т.д.
коли прямі (1) перетинаються поза круговим абсолютом, потрібно відносити їх до
системи НН
, і т.д.
коли прямі (1) перетинаються поза круговим абсолютом, потрібно відносити їх до
системи НН 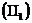 або до
системи ЕН
або до
системи ЕН 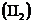 . Якщо ці
прямі перетинають абсолют, то вони входять до складу системи НН
. Якщо ці
прямі перетинають абсолют, то вони входять до складу системи НН 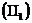 . Міра
визначення кутів складається з двох дійсних дотичних. Саме вимірювання величин
кутів виконується за формулою :
. Міра
визначення кутів складається з двох дійсних дотичних. Саме вимірювання величин
кутів виконується за формулою :
θ = 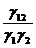 (4)
(4)
При цьому радикали, що
виражаються через ν і ν
і ν потрібно
взяти з такими знаками, щоб похідні ν
потрібно
взяти з такими знаками, щоб похідні ν ν
ν мали знак числа v
мали знак числа v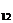 , яке в
цьому випадку може бути як додатнім, так і від’ємним.
, яке в
цьому випадку може бути як додатнім, так і від’ємним.
Дві прямі можуть належати
куту 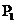 Q
Q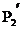 , суміжному
з
, суміжному
з 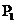 Q
Q .
Вимірювання кутів залишається гіперболічним (і формула (4) зберігається), але
вимірювання довжини стає еліптичним (система ЕН).
.
Вимірювання кутів залишається гіперболічним (і формула (4) зберігається), але
вимірювання довжини стає еліптичним (система ЕН).
Розглянуті три системи
характеризуються тим, що абсолютом геометрії служить дійсна, не вироджена крива
другого порядку. Рівняння цієї кривої може бути зведене до вигляду
х + у
+ у - 1 = 0
- 1 = 0
або в однорідних координатах
х + у
+ у - z
- z = 0.
= 0.
Іншими словами, форма, що
визначає конічний переріз, має ранг 3.
1.4
Геометрія уявного невиродженого абсолюту (геометрія Рімана)
За задумом Келі-Клейна можна
будувати геометрію також на базі уявного конічного перерізу. Якщо це уявна
невироджена крива другого порядку, то її рівняння може бути зведене до вигляду
х +у
+у +1=0 (5)
+1=0 (5)
або в однорідних координатах
 + у
+ у + z
+ z =0; (5a)
=0; (5a)
ця форма має ранг 3 і
сигнатуру 3.
Оскільки уявна крива не
ділить дійсну площину на частини, то за субстрат цієї геометрії слід прийняти
всю проективну площину, точніше, сукупність всіх дійсних точок площини. Прямими
в цій геометрії будемо вважати всі прямі площини. Під рухами в цій геометрії
відповідно до задуму Келі- Клейна будемо розуміти проєктивні перетворення:
х′=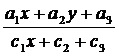 , у′=
, у′=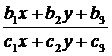 , (6)
, (6)
що залишають інваріантним
рівняння (5). Легко бачити, що для цього необхідно і достатньо, щоб коефіцієнти
перетворення (6), позв'язані рівняннями:
a + b
+ b + c
+ c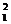 = 1; a
= 1; a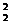 + b
+ b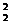 + c
+ c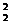 = 1; a
= 1; a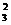 + b
+ b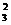 + c
+ c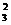 = 1;
= 1;
a a
a +b
+b b
b +c
+c c
c =0; a
=0; a a
a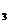 +b
+b b
b +c
+c c
c =1; a
=1; a a
a +b
+b b
b +c
+c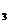 c
c =1. (7)
=1. (7)
утворювали ортогональну
систему. Будь-яку пряму слід в цій геометрії називати еліптичною, оскільки вона
перетинає абсолют у двох уявних зв'язаних точках.
Нехай  (
(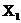 ,
,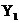 ) і
) і  (
(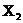 ,
,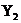 ) - дві
дійсні точки площини. Тоді координати будь-якої точки, прямої
) - дві
дійсні точки площини. Тоді координати будь-якої точки, прямої 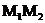 можуть бути
виражені рівняннями:
можуть бути
виражені рівняннями:
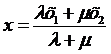 ,
, 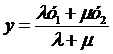 . (8)
. (8)
Значення λ і μ
відповідні точкам перетину прямої 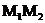 з абсолютом (5), визначаються
рівнянням
з абсолютом (5), визначаються
рівнянням
(λх +μх
+μх )
) +(λу
+(λу +μу
+μу )
) + (λ+μ)
+ (λ+μ) = 0.
= 0.
λ (х
(х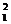 +у
+у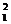 +1)+2λμ(х
+1)+2λμ(х х
х +у
+у у
у +1)+μ
+1)+μ (х
(х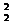 +у
+у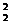 +1)=0 (9)
+1)=0 (9)
Вважаючи тепер
х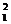 + y
+ y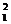 + 1= u
+ 1= u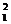 ; x
; x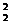 + y
+ y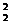 + 1 = u
+ 1 = u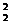 ; x
; x x
x + y
+ y y
y + 1 = u
+ 1 = u ;
;
u >0,u
>0,u >0,
(10)
>0,
(10)
напишемо його у вигляді
λ u
u + 2λμu
+ 2λμu + μ
+ μ u
u = 0. (9')
= 0. (9')
Формула Келі встановлює, що
вимірювання відстаней у цьому випадку буде еліптичним; відстань  =
=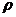 визначається співвідношенням
визначається співвідношенням
сos 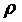 =
= 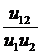 . (11)
. (11)
Аналогічно до цього, якщо
рівняння
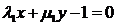 і
і  (12) виражають дві прямі
площини, то
(12) виражають дві прямі
площини, то
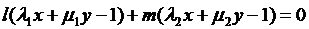 (13)
(13)
є прямою, що проходить через
точку перетину прямих (12); при змінних l і m це
є пучок прямих, які проходять через цю точку. Пряма (13) є дотичною до уявного
кола (5), якщо
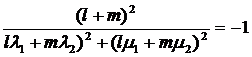 ,
,
якщо
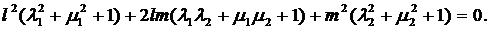 (14)
(14)
Це є рівняння двох уявних
дотичних до абсолюту (5). Приймаючи їх за абсолют визначення міри кутів і поклавши
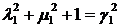 ,
, 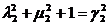 ,
, 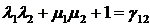 ,
, 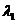 ›0,
›0, 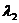 ›0, (15)
›0, (15)
напишемо рівняння (14) у
вигляді
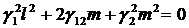 (14′)
(14′)
Так само як вище,
переконаємося, що 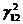 <
<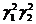 ; тому для
міри кута між прямими (12) отримаємо за Келі
; тому для
міри кута між прямими (12) отримаємо за Келі
cos θ = 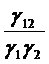 . (16)
. (16)
Отже, міра визначення кутів в
цій системі теж є еліптичною.
Ця геометрія, яку будемо
рахувати під номером III або позначати двома буквами (ЕЕ), була з інших
міркувань вказана Ріманом і зазвичай носить його ім'я. Як і геометричні системи
Лобачевського і Евкліда, вона має важливе значення.
1.5
Диференціальні метричні форми геометрії Рімана
Щоб знайти основну метричну
форму (квадрат елемента довжини) в рімановій
геометричній системі, покладемо у формулі (11)
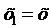 ,
,  ,
, 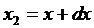 ,
, 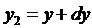 .
.
Відстань між цими точками
позначимо через dρ,
так що з точністю до нескінченно малих другого порядку відносно dp
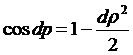 . (17)
. (17)
З іншого боку
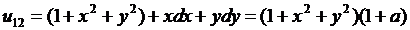 ,
,
Де
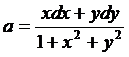 ,
,
а
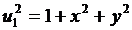 ,
,
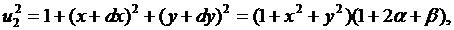
де
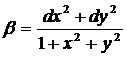 ,
,
Отже,
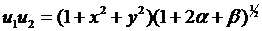
 .
.
Разом з тим рівність (11)
набирає вигляду
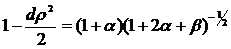 (18)
(18)
Нехтуючи нескінченно малими,
порядок яких вище двох, отримуємо:
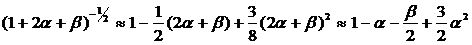 ;
;
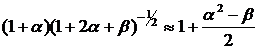 . (19)
. (19)
Тоді з тим рівність (18) має
вигляд
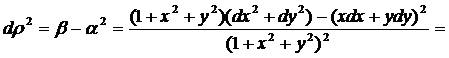
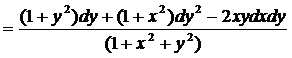 . (18′)
. (18′)
Відповідно таким же
обчисленням можемо з формули (16) отримати для елемента кута (тобто для
нескінченно малого кута dθ між двома
прямими λ, μ і λ+dμ, μ+dμ)
вираз
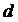 θ
θ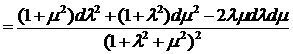 .
.
Отже, звіряючи вираз (18') з
основною метричною формою сфери в бельтрамієвих координатах при радіусі,
рівному 1 (K =
1), ми бачимо, що геометрія ріманової площини, принаймні локально, не
відрізняється від геометрії сфери.
По-друге, звіряючи вирази
(18') і (20), бачимо, що одним переходить в інше при заміні координат точок (х,
у) координатами прямої (λ,μ); відстань між двома
нескінченно близькими точками (х, у) і (x + dx, y+dy) виражається в координатах
точки і їх диференціалах так само, як кут між двома нескінченно близькими
прямими (λ,μ) і (λ+dλ, μ+dμ) в
координатах прямої і їх диференціалах.
Це при належному розвитку
висновків, що випливають звідси, приводить до так званої «подвійності» в
побудові метричної геометрії.
.6
Порівняння формул для вимірювання відстаней і кутів в геометричних системах I, II , II
, II III
III
При обчисленні відстані між
двома точками  ,
,  в геометрії
Лобачевського НЕ, побудованої всередині кругового абсолюта, шукаємо точки
в геометрії
Лобачевського НЕ, побудованої всередині кругового абсолюта, шукаємо точки 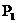 ,
, перетину
прямої
перетину
прямої 
 з абсолютом і обчислюємо
ангармонічне відношення
з абсолютом і обчислюємо
ангармонічне відношення 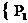
 ,
,
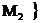 ; у бельтрамієвих координатах воно
виражається числом
; у бельтрамієвих координатах воно
виражається числом
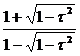 (21)
(21)
Де
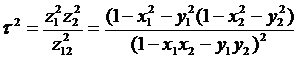 (22)
(22)
При цьому вираз (21) є
дійсним числом, більшим за 1; число, пропорційне його логарифму, приймаємо за
відстань s між точками  і
і  :
:
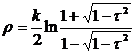 ,
, 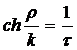 . (23)
. (23)
Число k
залежить від вибору одиниці міри; 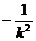 є кривизною метричної форми
двовимірної геометрії I.
є кривизною метричної форми
двовимірної геометрії I.
При переході до еліптичного
(ріманового) вимірювання величин на площині слід дійсне коло 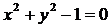 замінити
уявним колом
замінити
уявним колом 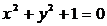 ; точки
; точки  ,
,  перетину
цього кола з прямою
перетину
цього кола з прямою 
 стають уявними. Не проводячи тут
повністю відповідних обчислень, зауважимо, що в цьому випадку число (22)
замінюється на
стають уявними. Не проводячи тут
повністю відповідних обчислень, зауважимо, що в цьому випадку число (22)
замінюється на
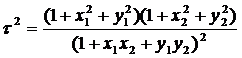 (22')
(22')
З тотожності
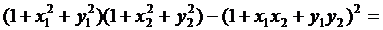
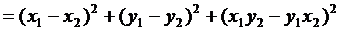
бачимо, що тепер 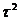 >l.
Ангармонічне відношення (21) стає комплексним числом з модулем, рівним 1. Його
логарифм є чисто уявним числом, і, щоб відстань р між двома точками
>l.
Ангармонічне відношення (21) стає комплексним числом з модулем, рівним 1. Його
логарифм є чисто уявним числом, і, щоб відстань р між двома точками  ,
,  виражалося
все ж таки дійсним числом, ми необхідно покласти
виражалося
все ж таки дійсним числом, ми необхідно покласти
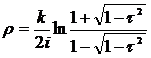 або
або 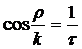 . (24)
. (24)
Таким чином, перехід від
гіперболічного вимірювання до еліптичного зводиться до того, що гіперболічна
функція ch у вирази
для відстані між двома точками замінюється тригонометричною функцією cos
у вирази
для відстані між двома точками замінюється тригонометричною функцією cos  .
.
Обчислення кутів за схемою
Келі-Клейна виконується таким чином. При дійсному круговому абсолюті для
встановлення кута θ між двома прямими m , m
, m
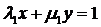 і
і 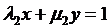 ,
,
які перетинаються в точці М
всередині абсолюту, з точки М проводять дві (уявні) дотичні р , р
, р до абсолюта
і складається ангармонічне відношення { p
до абсолюта
і складається ангармонічне відношення { p p
p , m
, m m
m }. Воно теж
виражається формулою, аналогічною (21):
}. Воно теж
виражається формулою, аналогічною (21):
Тут
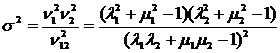 . (25′)
. (25′)
Оскільки,
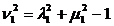 >0,
>0, 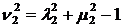 >0,
>0,
а за умови перетину прямих m , m
, m всередині
абсолюту має місце нерівність σ > 1.
Тому вираз (25) є комплексним числом, яке рівне за модулем одиниці, і ми можемо
покласти
всередині
абсолюту має місце нерівність σ > 1.
Тому вираз (25) є комплексним числом, яке рівне за модулем одиниці, і ми можемо
покласти
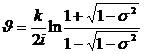 ,
,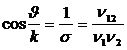 ; (26)
; (26)
Якщо ж прямі m , m
, m перетинаються поза абсолютом, як це має місце в системах НH і ЕH, то
число σ,
вибране формулою (25'), менше від 1. Тому у цих геометричних системах слід
покласти
перетинаються поза абсолютом, як це має місце в системах НH і ЕH, то
число σ,
вибране формулою (25'), менше від 1. Тому у цих геометричних системах слід
покласти
 .
.
Отже, ми бачимо, що і перехід
від еліптичної міри визначення кутів до гіперболічної приводить до заміни
тригонометричних функцій гіперболічними. Вказані закономірності є загальними і
знаходять віддзеркалення в багатьох формулах геометрії 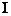 ,
, 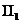 і
і 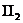 .
.
2. Геометрія
Келі-Клейна з виродженим абсолютом
.1
Геометричні системи з афінною групою
Чотири геометричні системи,
розглянуті вище, характеризуються тим, що абсолютом для них є невироджений
конічний переріз. Відповідно до цього проективні перетворення, що виражають
рухи в кожній з цих геометричних систем, не мають загальної інваріантної
прямої, тобто не вироджуються в афінні перетворення (які можна визначити як
проективні перетворення, що залишають на місці певну пряму проективної площини,
(умовно названу «нескінченно віддаленою» прямою)). Розглянемо тепер геометричні
системи, в яких роль рухів відіграють афінні перетворення.
Загальна група афінних
перетворень площини виражається рівняннями:
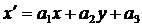 ,
, 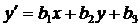 ,
, 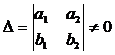 ; (1)
; (1)
вона залежить від шести
параметрів а , а
, а , а
, а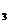 ; b
; b , b
, b , b
, b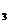 , тоді як
групи рухів у кожній з раніше розглянутих геометричних систем залежать всього
від трьох параметрів. Взагалі, якщо геометрична система на площині аналогічна
евклідовій або гіперболічній геометрії в тому розумінні, що існує єдиний «рух»,
що переводить дану точку, задану в ній пряму і одну з двох обмежених цією
прямою півплощин, в інші довільно задані точки, задані в ній пряму і
обмежену цією прямою півплощину, то група «рухів» геометричної системи
залежатиме від трьох параметрів. Тому займаючись геометричними системами, в
яких «рухами» є афінні перетворення, ми маємо тим або іншим способом виділити
три параметричні підгрупи загальної афінної групи. Але,це вимагає ще якихось
додаткових обмежень.
, тоді як
групи рухів у кожній з раніше розглянутих геометричних систем залежать всього
від трьох параметрів. Взагалі, якщо геометрична система на площині аналогічна
евклідовій або гіперболічній геометрії в тому розумінні, що існує єдиний «рух»,
що переводить дану точку, задану в ній пряму і одну з двох обмежених цією
прямою півплощин, в інші довільно задані точки, задані в ній пряму і
обмежену цією прямою півплощину, то група «рухів» геометричної системи
залежатиме від трьох параметрів. Тому займаючись геометричними системами, в
яких «рухами» є афінні перетворення, ми маємо тим або іншим способом виділити
три параметричні підгрупи загальної афінної групи. Але,це вимагає ще якихось
додаткових обмежень.
Всі афінні перетворення
залишають інваріантною одну і ту ж пряму проективної площини - «нескінченно
віддалену» пряму.
Кожне афінне перетворення
залишає нерухомими дві точки цієї прямої-дійсні різні або, ті, що співпадають
або комплексні зв'язані. Дійсно, «точка нескінченно віддаленої прямої» є з
точки зору афінної геометрії просто напрямом, який характеризується
відношенням, 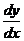 . Для всіх
прямих у = f(х)
(f(х)
- лінійна функція), що мають цей напрям, відношення
. Для всіх
прямих у = f(х)
(f(х)
- лінійна функція), що мають цей напрям, відношення 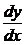 зберігає
одне і те ж значення. Але з рівнянь (1) виходить
зберігає
одне і те ж значення. Але з рівнянь (1) виходить
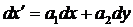 ,
,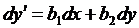 . (2)
. (2)
Звідси, якщо через 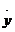 і
і 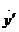 позначити
похідні
позначити
похідні 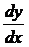 i
i 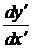 , то
отримаємо:
, то
отримаємо:
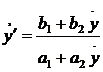 . (3)
. (3)
Тому значення у, що
відповідає інваріантній точці «нескінченно віддаленої» прямої (тобто інваріантному
напряму афінного перетворення), визначається з квадратного рівняння
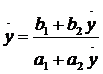 , (4)
, (4)
Або
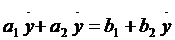 , (4')
, (4')
що завжди має два (дійсні, різні
або однакові комплексні) корені.
Розглянемо тепер геометричні
системи, в яких рухи, виражаються афінними перетвореннями, що залишають
інваріантними фіксовані точки нескінченно віддаленої прямої (дійсні різні, або
однакові, або комплексні зв'язані), тобто системи, абсолютом яких є пара точок
прямої (пряму треба спеціально вказувати, якщо точки співпадають). При цьому
приходимо до деяких нових цікави і важливи геометрій.
2.2
Евклідова геометрія в системі Келі-Клейна
Розглянемо спочатку той
випадок, коли афінне перетворення залишає незмінними дві уявні зв'язані
нескінченно віддалені точки; які можемо завжди звести до того, що 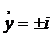 (це
означає, що дійсним афінним перетворенням завжди можна досягти того, що пучки,
для яких
(це
означає, що дійсним афінним перетворенням завжди можна досягти того, що пучки,
для яких 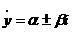 , перейдуть
в пучки, для яких
, перейдуть
в пучки, для яких 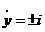 ).
).
Рівняння (4') набуває при
цьому вигляду:
± 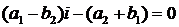 ,
,
а отже, якщо коефіцієнти
перетворення дійсні, то 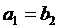 ,
, 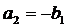 ; то
перетворення (1) набуває вигляду:
; то
перетворення (1) набуває вигляду:
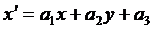 ,
,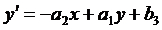 ;
; 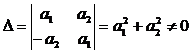 .
.
Ми можемо покласти
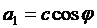 ,
, 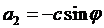 , c> 0.
, c> 0.
Таке афінне перетворення
набуває вигляду:
х' = c (х
cos 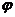 - у sin
- у sin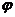 ) + а, у' =c (x
sin
) + а, у' =c (x
sin 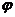 + у
cos
+ у
cos 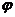 ) + b.
(5)
) + b.
(5)
Сукупність всіх таких
перетворень, що відповідають різним значенням а, b, 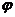 і c, є
чотиричленною групою перетворень подібності. Покладаючи с лише значення 1,
отримуємо групу евклідових рухів:
і c, є
чотиричленною групою перетворень подібності. Покладаючи с лише значення 1,
отримуємо групу евклідових рухів:
х' =x cos - у sin
- у sin + а, у' = х
sin
+ а, у' = х
sin  + у cos
+ у cos  + b. (6)
+ b. (6)
Точки, в яких прямі пучка 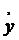 = ± і,
прямі
= ± і,
прямі 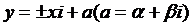 ,
перетинають нескінченно віддалену пряму, спільні нескінченно віддалені точки
цього пучка називають циклічними точками площини. Абсолют в розглянутому
випадку складається з двох циклічних точок. Оскільки циклічні точки залишаються
інваріантами, то залишається незмінною вся нескінченно віддалена пряма площини,
так як це має місце в рухах евклідової геометрії. Геометрія Келі - Клейна, для
якої абсолютом є циклічні точки площини, зводиться до геометрії Евкліда, яка,
таким чином, займає відповідне місце в системі Кели- Клейна. Потрібно,
відзначити що абсолют, який складається з двох циклічних точок площини, строго
кажучи, визначає чотиричленну групу подібну (5). Перехід до евклідової
геометрії потребує додаткової умова - виділення тричленної підгрупи рухів за
допомогою умови с = 1.
,
перетинають нескінченно віддалену пряму, спільні нескінченно віддалені точки
цього пучка називають циклічними точками площини. Абсолют в розглянутому
випадку складається з двох циклічних точок. Оскільки циклічні точки залишаються
інваріантами, то залишається незмінною вся нескінченно віддалена пряма площини,
так як це має місце в рухах евклідової геометрії. Геометрія Келі - Клейна, для
якої абсолютом є циклічні точки площини, зводиться до геометрії Евкліда, яка,
таким чином, займає відповідне місце в системі Кели- Клейна. Потрібно,
відзначити що абсолют, який складається з двох циклічних точок площини, строго
кажучи, визначає чотиричленну групу подібну (5). Перехід до евклідової
геометрії потребує додаткової умова - виділення тричленної підгрупи рухів за
допомогою умови с = 1.
У розглянутій нами
класифікації будемо позначати евклідову геометрію номером IV . Відомо, що
в ній вимірювання відстаней є параболічним , а вимірювання кутів - еліптичним;
відповідно до цього евклідову геометрію доцільно також позначати символом РЕ.
Це видно також з характеру інваріантних образів; якщо візьмемо будь-які дві
точки, то пряма, що їх сполучає, перетинає нескінченно віддалену пряму
(абсолют) в одній точці; тому вимірювання відстаней до прямої параболічне.
Квадрат відстані між двома точками виражається евклідовою формулою
. Відомо, що
в ній вимірювання відстаней є параболічним , а вимірювання кутів - еліптичним;
відповідно до цього евклідову геометрію доцільно також позначати символом РЕ.
Це видно також з характеру інваріантних образів; якщо візьмемо будь-які дві
точки, то пряма, що їх сполучає, перетинає нескінченно віддалену пряму
(абсолют) в одній точці; тому вимірювання відстаней до прямої параболічне.
Квадрат відстані між двома точками виражається евклідовою формулою
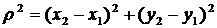
і є - інваріантом
перетворення (6). Якщо обидві точки лежать на осі абсцис, то відстань між ними
виразиться різницею х - х
- х ; це
відповідає формулі Клейна для параболічного вимірювання на прямій.
; це
відповідає формулі Клейна для параболічного вимірювання на прямій.
Дві прямі площини, що
виходять з якої-небудь (дійсної) точки М, і проходять через циклічні точки,
уявні спряжені. Прийнявши їх як абсолют для вимірювання кутів в пучку прямих,
що виходять з точки М, прийдемо до еліптичного вимірювання для кутів. Таким
чином, кут між прямими m m
m евклідової
площини визначається за допомогою ангармонічного відношення чотирьох прямих:
прямих m
евклідової
площини визначається за допомогою ангармонічного відношення чотирьох прямих:
прямих m , m
, m і прямих p
і прямих p , p
, p , що
сполучають точку перетину m
, що
сполучають точку перетину m , m
, m з циклічними точками площини. Це
визначення кута було вперше введене Лагером.
з циклічними точками площини. Це
визначення кута було вперше введене Лагером.
2.3
Псевдоєвклідова геометрія
Розглянемо афінні
перетворення, які залишають на нескінченно віддаленій прямій інваріантними
які-небудь дві фіксовані різні дійсні точки. Пряма, що сполучає які-небудь дві
(дійсні) точки площини, перетинає нескінченно віддалену пряму в одній точці;
абсолют відповідного лінійного виміру буде параболічним і, отже, вимірювання
відстаней буде параболічним. З іншого боку, прямі, що проходять через дійсну
точку М площини інваріантні точкам нескінченно, віддаленою прямою, дійсні;
прийнявши їх за абсолют, ми отримаємо гіперболічну міру визначення кутів.
За нерухомі точки на
нескінченно віддаленій прямій приймаємо ті, які відповідають значенням 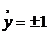 ; у
евклідової площині, інтерпретацією, такої геометрії, є точки перетину
нескінченно віддаленої прямої з прямими, які утворюють з віссю абсцис з того чи
з іншого боку кути 45°, з рівняння (4) в цьому випадку маємо
; у
евклідової площині, інтерпретацією, такої геометрії, є точки перетину
нескінченно віддаленої прямої з прямими, які утворюють з віссю абсцис з того чи
з іншого боку кути 45°, з рівняння (4) в цьому випадку маємо
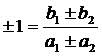 . (7)
. (7)
Розглядаючи це рівняння
відповідно до знаків, отримаємо:
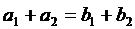 ,
, 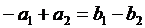 ,
,
Звідки
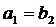 ,
, 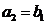 .
.
Рівняння перетворення (1)
набирають вигляду:
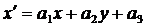 , (8)
, (8)
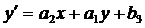 ,
,
 ;
;
Вважаючи тут (при 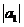 >
>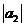 )
)
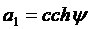
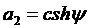 ,
,
отримуємо:
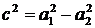 ,
,
а рівняння перетворення (8)
остаточно наберуть вигляду:
х' = з (х ch 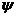 + у
sh
+ у
sh 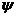 ) + а,
у' = c (х
sh
) + а,
у' = c (х
sh 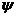 + у
ch
+ у
ch 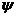 ) +b.
) +b.
Група перетворень в цьому
випадку буде чотиричленною; вважаючи с=1, приходимо до її тричленної підгрупи,
і приймаємо за рухи в нашій геометричній системі:
х' = х ch 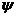 + у
sh
+ у
sh 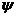 + а, у' =
х sh
+ а, у' =
х sh 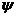 + y ch
+ y ch 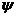 + b. (10)
+ b. (10)
Вони дають для двох точок
інваріант
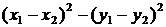 , (11)
, (11)
який і вважають квадратом
відстані між точками.
У цій геометрії через кожну
точку х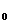 , у
, у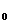 площини
проходять дві прямі:
площини
проходять дві прямі:
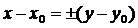 (12)
(12)
(В евклідовій площині - це
прямі, паралельні бісектрисам координатних кутів; відстань між двома точками на
кожній з цих прямих рівна нулю. Це ізотропні прямі площини; вони містять одну
або другу з нерухомих точок нескінченно віддаленої прямої. У кожній точці 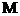 ізотропні
прямі утворюють дві пари вертикальних кутів. При цьому вираз (11), складений
для двох точок
ізотропні
прямі утворюють дві пари вертикальних кутів. При цьому вираз (11), складений
для двох точок 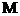 і
і 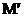 , буде
рівний нулю, якщо
, буде
рівний нулю, якщо 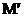 лежить на
ізотропній прямій, що проходить через точку
лежить на
ізотропній прямій, що проходить через точку 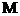 ; інакше в її додатній або від’ємний
залежно від того, в якій з двох пар вертикальних кутів лежить точка
; інакше в її додатній або від’ємний
залежно від того, в якій з двох пар вертикальних кутів лежить точка 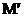 . Пари точок,
таким чином можуть бути розбиті на три категорії: для пари точок однієї
категорії вираз (11) має додатнє значення, для пари точок інший категорії -
від’ємне (і тут доводиться вважати, що відстань між точками є уявною або що
вираз (11) протилежний за знаком квадрату відстані між точками); для пари
точок, які лежать на ізотропній лінії, вона рівна нулю.
. Пари точок,
таким чином можуть бути розбиті на три категорії: для пари точок однієї
категорії вираз (11) має додатнє значення, для пари точок інший категорії -
від’ємне (і тут доводиться вважати, що відстань між точками є уявною або що
вираз (11) протилежний за знаком квадрату відстані між точками); для пари
точок, які лежать на ізотропній лінії, вона рівна нулю.
Цю геометрію позначимо
номером IV і будемо
називати псевдоєвклідовою. Така назва обумовлюється виразом (11), відстані між
двома точками. За характером вимірювання відстаней і кутів її слід позначити
через РН.
і будемо
називати псевдоєвклідовою. Така назва обумовлюється виразом (11), відстані між
двома точками. За характером вимірювання відстаней і кутів її слід позначити
через РН.
В евклідовій та
псевдоєвклідової геометрії роль абсолюту відіграють дві точки, дійсні або уявні
зв'язані, вони містяться на нескінченно віддаленій прямій, яка разом з ними
залишається інваріантною. За принцип двоїстості їм відповідають дві системи в
яких абсолютом є дві прямі, дійсні або уявні, зв'язані; разом з ними інваріантною
залишається точка їх перетину (завжди дійсна).
Цю точку перетину можна
проективним перетворенням перевести в будь-яку нескінченно віддалену точку.
Візьмемо її на осі ординат; в тому і в іншому з цих випадків абсолютом по суті
є дві паралельні прямі, уявні (геометрична система V ) або дійсні
(система V
) або дійсні
(система V ).
Розглянемо спочатку систему V
).
Розглянемо спочатку систему V . Якщо
. Якщо 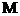 і
і 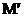 - дві
дійсні точки площини, то пряма
- дві
дійсні точки площини, то пряма 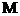
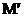 , взагалі кажучи, перетинає абсолют
у двох дійсних точках
, взагалі кажучи, перетинає абсолют
у двох дійсних точках 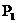 ,
,  . Таким
чином, для визначення відстані між двома точками
. Таким
чином, для визначення відстані між двома точками  ,
,  маємо лінійний абсолют, що
складається з двох дійсних точок
маємо лінійний абсолют, що
складається з двох дійсних точок 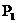 ,
,  ; він визначає гіперболічну міру
визначення відстаней на прямій. В тому окремому випадку, коли пряма
; він визначає гіперболічну міру
визначення відстаней на прямій. В тому окремому випадку, коли пряма 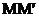 паралельна
прямим які є абсолютом, вона їх перетинає в одній нескінченно віддаленої точці.
Ця пряма ізотропна, відстань між кожними двома точками ізотропної прямої рівна
нулю. Таким чином, в системі V
паралельна
прямим які є абсолютом, вона їх перетинає в одній нескінченно віддаленої точці.
Ця пряма ізотропна, відстань між кожними двома точками ізотропної прямої рівна
нулю. Таким чином, в системі V є один пучок ізотропних прямих у
такій інтерпретації, де прямі абсолюту паралельні - це є пучок паралельних
прямих.
є один пучок ізотропних прямих у
такій інтерпретації, де прямі абсолюту паралельні - це є пучок паралельних
прямих.
Для вимірювання кутів, що
мають вершину в точці 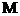 , абсолютом
має бути пряма, що йде від точки М до нескінченно віддаленої точки
, абсолютом
має бути пряма, що йде від точки М до нескінченно віддаленої точки 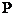 ; абсолют
вироджений; вимірювання кутів параболічне. Систему потрібно позначити символом
НP; її
можна розглядати як двоїсту до псевдоєвклідової.
; абсолют
вироджений; вимірювання кутів параболічне. Систему потрібно позначити символом
НP; її
можна розглядати як двоїсту до псевдоєвклідової.
У випадку, коли абсолютом є
пара зв'язаних уявних прямих (система V ), пряма ММ' перетинає абсолют у
двох уявних зв'язаних точках; міра визначення відстаней -
еліптична. Для вимірювання кутів, що мають вершину в точці М, абсолютом міри
визначення пучка прямих є одна пряма
), пряма ММ' перетинає абсолют у
двох уявних зв'язаних точках; міра визначення відстаней -
еліптична. Для вимірювання кутів, що мають вершину в точці М, абсолютом міри
визначення пучка прямих є одна пряма 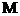
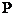 ; цьому відповідає параболічна міра
визначення кутів. Систему потрібно позначити ЕР; її можна розглядати як двоїсту
до евклідової
геометрії.
; цьому відповідає параболічна міра
визначення кутів. Систему потрібно позначити ЕР; її можна розглядати як двоїсту
до евклідової
геометрії.
.5
Аналітичні обчислення, що відносяться до системи V
За дійсні паралельні прямі,
що є абсолютом системи V приймемо
прямі
приймемо
прямі
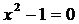 , (13)
, (13)
що не порушує загальності
міркувань. Пряма, що проходить через точки 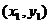 і
і 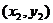 ,
,
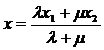 ,
,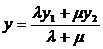 , (14)
, (14)
перетинає прямі абсолюту в
точках, для яких
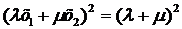 , (15)
, (15)
або
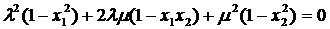 . (15')
. (15')
Дискримінант форми від
змінних λ, μ, що
міститься в лівій частині цього рівняння, рівний
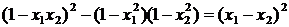 ,
,
має додатне значення;
відстань між точками визначається за формулою
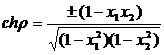 . (16)
. (16)
Якщо, в цьому виразі потрібно
взяти знак «плюс» і коли знак «мінус». Абсолют ділить площину паралельними
прямими на дві області: одна з них - це частина площини, що міститься між
паралелями, і друга - частина площини, поза ними. Якщо обидві точки  ,
,  лежать між
паралелями або обидві розташовані поза ними, то вираз, що стоїть під радикалом,
має додатне значення; інакше підкореневий вираз є від’ємним і відстань між
точками
лежать між
паралелями або обидві розташовані поза ними, то вираз, що стоїть під радикалом,
має додатне значення; інакше підкореневий вираз є від’ємним і відстань між
точками 
 слід вважати такою, що не існує. Що
стосується чисельника, то він має додатнє значення, коли точки
слід вважати такою, що не існує. Що
стосується чисельника, то він має додатнє значення, коли точки  і
і  лежать між
паралелями або обидві поза паралелями по різні боки від них; формула (16) при
цьому записується у вигляді:
лежать між
паралелями або обидві поза паралелями по різні боки від них; формула (16) при
цьому записується у вигляді:
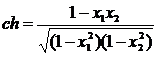 . (16')
. (16')
Якщо ж точки  і
і  лежать поза
паралелями по один бік від них, то у виразі (16)
лежать поза
паралелями по один бік від них, то у виразі (16) 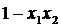 має від’ємне
значення і формулу (16) потрібно записати у вигляді:
має від’ємне
значення і формулу (16) потрібно записати у вигляді:
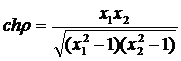 . (16˝)
. (16˝)
У геометричній системі V доцільно
обмежитися розглядом точок, які знаходяться в смузі між паралельними прямими.
доцільно
обмежитися розглядом точок, які знаходяться в смузі між паралельними прямими.
Якщо дві точки лежать на
одній прямій, паралельній осі ординат (тобто якщо х = х
= х ), то
формула (16') або (16") дасть
), то
формула (16') або (16") дасть 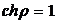 ,
, 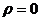 . Прямі, паралельні осі ординат
(паралельні абсолюту), є ізотропними прямими: дві ізотропні прямі знаходяться
на рівних відстанях одна від одної в тому сенсі, що відстань будь-якої точки
одній з них від будь-якої точки іншої має одне і те ж значення (рівне відстані
їх проекцій на осі абсцис).
. Прямі, паралельні осі ординат
(паралельні абсолюту), є ізотропними прямими: дві ізотропні прямі знаходяться
на рівних відстанях одна від одної в тому сенсі, що відстань будь-якої точки
одній з них від будь-якої точки іншої має одне і те ж значення (рівне відстані
їх проекцій на осі абсцис).
Припустимо, що через одну
точку, яка лежить всередині смуги, обмеженої розглянутими паралельними прямими,
проходять прямі
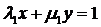 і
і 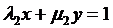 . (17)
. (17)
Кожна пряма, що проходить
через точку їх перетину, виражається рівнянням
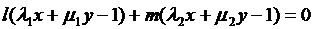 , (18)
, (18)
або
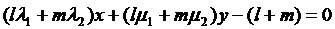 . (18')
. (18')
Щоб знайти точки перетину
цієї прямої з абсолютом х =1,
виключаємо з цих рівнянь х для визначення відповідних значень у. В результаті
отримуємо для у рівняння
=1,
виключаємо з цих рівнянь х для визначення відповідних значень у. В результаті
отримуємо для у рівняння
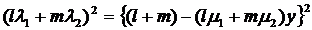 (19)
(19)
яке має двократний корінь
тільки, якщо
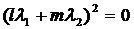 .
.
Це дає, відповідно до
загальних міркувань Келі, міру кута, пропорційну різниці
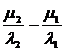 . (20)
. (20)
До цього зводиться в даному
випадку параболічне вимірювання кутів. Коли пряма повертається від положення,
паралельного осі абсцис, до положення, паралельного осі ординат, то кут
повороту зростає від куля до нескінечності.
2.6
Обчислення, що стосуються системи V
Розглянемо тепер випадок,
коли абсолют складається з двох уявних спряжених прямих, спільна точка яких
лежить на нескінченно віддаленій прямій; інакше кажучи, дійсний абсолют 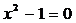 замінюється
уявним
замінюється
уявним 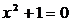 . В цьому
випадку абсолют не ділить дійсної площини на частини; субстратом геометрії є
вся евклідова площина.
. В цьому
випадку абсолют не ділить дійсної площини на частини; субстратом геометрії є
вся евклідова площина.
Пряма, що сполучає дійсні
точки 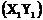 і
і 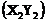 перетинає
абсолют
перетинає
абсолют 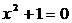 в точках, в
яких
в точках, в
яких
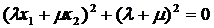 . (21)
. (21)
Це рівняння відрізняється від
рівняння (15) лише знаком другої частини і в розглянутому вигляді може бути
записано так:
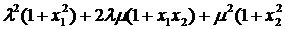 ). (22)
). (22)
Його дискримінант
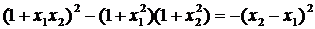 (23)
(23)
завжди має від’ємне значення;
це відповідає тому, що пряма перетинає абсолют у двох уявних зв'язаних точках.
Відстань визначається за формулою
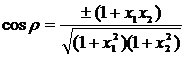 . (24)
. (24)
Ця міра визначення відстаней
еліптична; відстань визначена двозначно і перетворюється в нуль (або в π),
коли х = х
= х . Тут, це не
означає, що точки співпадають, а лише що дві точки лежать на одній прямій,
паралельній осі ординат; ці прямі і в цьому випадку є ізотропними.
. Тут, це не
означає, що точки співпадають, а лише що дві точки лежать на одній прямій,
паралельній осі ординат; ці прямі і в цьому випадку є ізотропними.
Звертаючись тепер до
вимірюванню кутів, шукаємо перетин абсолюту 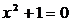 з будь-якою прямою (18) або (18');
для визначення у отримуємо рівняння, яке відрізняється від рівняння (19) тільки
знаком другої частини:
з будь-якою прямою (18) або (18');
для визначення у отримуємо рівняння, яке відрізняється від рівняння (19) тільки
знаком другої частини:
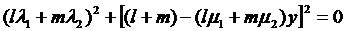 . (25)
. (25)
Таким чином
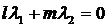 ,
, 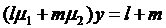 .
.
Відповідна пряма єдина; вона
паралельна осі абсцис і проходить від неї на відстані
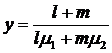 .
.
Міра визначення кутів і в
цьому випадку параболічна: кутовий абсолют виражається рівнянням
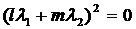 .
.
Міра кутів виражається
різницею
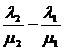 . (26)
. (26)
.7 Система з
подвійною параболічною метрикою
Звернемося тепер до
геометричної системи VI, в основі якої лежить група афінних перетворень. В
цьому випадку рівняння (4') не повинно мати кратні корені: отже
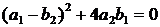 .
.
Якщо вважати, що інваріантна
точка нескінченно видаленої прямої відповідає напряму осі ординат, то рівняння
(4') повинно мати подвійний корінь 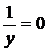 . Це відповідає тому, що в рівнянні
(4')
. Це відповідає тому, що в рівнянні
(4') 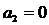 ,
, 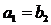 . Таким
чином, тут приходимо до чотиричленної групи афінних перетворень:
. Таким
чином, тут приходимо до чотиричленної групи афінних перетворень:
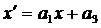 ,
, 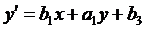 ;
;
її тричленну підгрупу, що
відповідає значенню 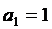 , групу
, групу
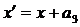 ,
, 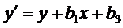 ,
,
приймаємо за рухи в
геометричній системі VI. Будь-яка пряма перетинає нескінченно віддалену пряму в
єдиній точці; тому абсолют довжин на прямій буде являти собою подвійну точку -
вимірювання довжин буде параболічним. Відстань між двома точками в наший
інтерпретація буде рівна 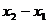 ; для
прямих, паралельних осі ординат, відстань між кожними двома їх точками буде
рівна нулю (ізотропні прямі, що проходять через інваріантну точку нескінченно
видаленої прямої). Так само абсолютом вимірювання кутів в пучку з вершиною
; для
прямих, паралельних осі ординат, відстань між кожними двома їх точками буде
рівна нулю (ізотропні прямі, що проходять через інваріантну точку нескінченно
видаленої прямої). Так само абсолютом вимірювання кутів в пучку з вершиною 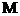 буде
(подвійна) пряма, що сполучає
буде
(подвійна) пряма, що сполучає 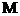 з інваріантною точкою (у нашій
інтерпретації пряма х = const). Міра кутів також буде параболічною; міра кута
виражається різницею
з інваріантною точкою (у нашій
інтерпретації пряма х = const). Міра кутів також буде параболічною; міра кута
виражається різницею 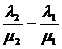 . За
прийнятою вище системою позначень таку геометрію VI потрібно позначати буквами
PP.
. За
прийнятою вище системою позначень таку геометрію VI потрібно позначати буквами
PP.
3. Основні образи планіметрії
Лобачевського в інтерпретації Келі-Клейна
Розглянемо геометрії Лобачевського в
інтерпретації Келі - Клейна.
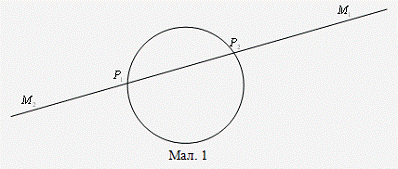
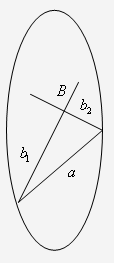
Паралельні прямі.
Паралельні прямі на площині
Лобачевського визначаються як граничні прямі, тобто як прямі, які в пучку
прямих із центром 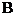 (рис.4)
відокремлюють прямі, що перетинають пряму
(рис.4)
відокремлюють прямі, що перетинають пряму 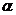 , від прямих, які її не перетинають.
Самі такі прямі не перетинають прямої
, від прямих, які її не перетинають.
Самі такі прямі не перетинають прямої 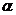 . Такими прямими є прямі, що
сполучають точку
. Такими прямими є прямі, що
сполучають точку 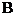 з
нескінченно віддаленими точками прямої
з
нескінченно віддаленими точками прямої 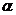 (рис. 4).
Взагалі паралельними є такі прямі, які перетинаються на абсолюті.
(рис. 4).
Взагалі паралельними є такі прямі, які перетинаються на абсолюті.
Взаємно перпендикулярні прямі.
У геометрії Евкліда
симетричним відображенням відносно прямої називається такий рух, який залишає
всі точки прямої нерухомими і переставляє між собою півплощини. Прямі, що
сполучають відповідні точки в цьому русі, є перпендикулярними до прямої (осі
симетричного відображення). Те саме матимемо і в геометрії Лобачевського.
Візьмемо за вісь симетрії в інтерпретації Келі - Клейна пряму UV (рис.
5). Нехай W -
точка перетину дотичних до абсолюта в точках U,V .
Ця точка є, очевидно, полюсом прямої UV відносно абсолюта. Нехай
деяка пряма  на (рис5),
що проходить через точку W, перетинає
абсолют у точках
на (рис5),
що проходить через точку W, перетинає
абсолют у точках  і
і  . Очевидно,
автоморфізм, який визначається чотирма парами UU, VV, WW,
. Очевидно,
автоморфізм, який визначається чотирма парами UU, VV, WW, 
 , є
симетричне відображення відносно прямої UV -
він залишає нерухомими точки прямої UV і
переставляє між собою півплощини UV
, є
симетричне відображення відносно прямої UV -
він залишає нерухомими точки прямої UV і
переставляє між собою півплощини UV і UV
і UV . Цей
автоморфізм є інволютивна гомологія з центром W і
віссю UV.
Кожна пряма, що сполучає відповідні точки в цій гомології, проходить через
центр гомології W. Отже, кожна така пряма
перпендикулярна до прямої UV. Таким
чином, взаємно перпендикулярними прямими в інтерпретації Келі - Клейна є
прямі, спряжені відносно абсолюта,
тобто
прямі, кожна з яких проходить через полюс другої прямої. ( Коли одна з двох
прямих проходить через полюс другої, то й друга пряма проходить через полюс
першої).
. Цей
автоморфізм є інволютивна гомологія з центром W і
віссю UV.
Кожна пряма, що сполучає відповідні точки в цій гомології, проходить через
центр гомології W. Отже, кожна така пряма
перпендикулярна до прямої UV. Таким
чином, взаємно перпендикулярними прямими в інтерпретації Келі - Клейна є
прямі, спряжені відносно абсолюта,
тобто
прямі, кожна з яких проходить через полюс другої прямої. ( Коли одна з двох
прямих проходить через полюс другої, то й друга пряма проходить через полюс
першої).
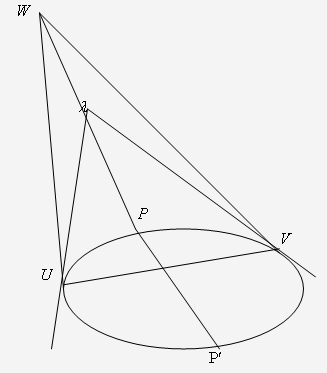
Рис .5
Еквідистанти
Дві прямі на площині Лобачевського,
які не є паралельними і не перетинаються, називаються, як відомо, розбіжними.
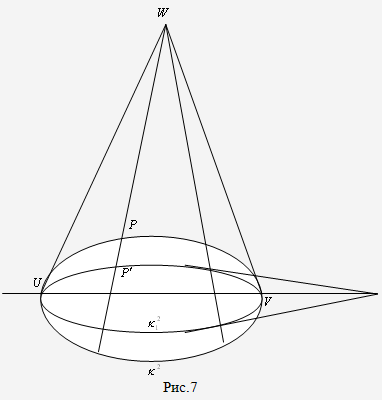
На проективній площині такі прямі перетинаються поза абсолютом (рис 6). Точка
їх перетину є полюс їх спільного перпендикуляра. Усі прямі, що проходять через
цей полюс, мають спільний перпендикуляр, тобто утворюють гіперболічний пучок (рис. 6).
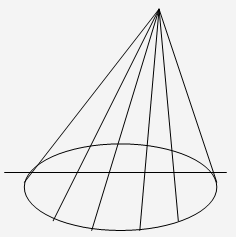
Рис.6
Якщо UV -
деяка пряма і W - її
полюс відносно абсолюта
(рис7), то, вибравши
деяку точку  на абсолюті
і точку
на абсолюті
і точку  на прямій WP в
середині абсолюта,
ми
гомологією з центром W, віссю UV і
парою відповідних точок
на прямій WP в
середині абсолюта,
ми
гомологією з центром W, віссю UV і
парою відповідних точок  ,
, перетворимо
абсолют у деяку криву другого порядку
перетворимо
абсолют у деяку криву другого порядку  . Ця гомологія
не є, очевидно, автоморфізмом відносно абсолюта (рис.7).
Крива
. Ця гомологія
не є, очевидно, автоморфізмом відносно абсолюта (рис.7).
Крива  дотикається
до абсолюта
в
точках U, V.
дотикається
до абсолюта
в
точках U, V.
З властивостей полюсів і
поляр відомо, що дотичні до кривої в точках її перетину з прямими, що проходять
через деяку точку, завжди перетинаються на полярі цієї точки. Таку саму
властивість мають і дотичні до абсолюта. А оскільки криву 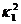 ми
дістаємо з абсолюта
за допомогою
деякої гомології з віссю UV , то
зазначена властивість справджується і для кривої
ми
дістаємо з абсолюта
за допомогою
деякої гомології з віссю UV , то
зазначена властивість справджується і для кривої 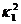 Але за означенням
перпендикулярності це означає, що дотичні до кривої
Але за означенням
перпендикулярності це означає, що дотичні до кривої 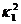 перпендикулярні
до прямих пучка W (гіперболічнного пучка), які
проходять через точки дотику. Отже, крива
перпендикулярні
до прямих пучка W (гіперболічнного пучка), які
проходять через точки дотику. Отже, крива 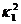 є ортогональною траєкторією
гіперболічного пучка прямих, тобто вона є еквідистантою. Пряма UV є
базою цієї еквідистанти. Отже, еквідистантою є будь-яка крива другого порядку,
яка розташована в середині абсолюта і дотикається до абсолюта в двох його
точках. Базою такої еквідистанти є пряма, що проходить через точки дотику.
Кожну таку криву можна дістати з абсолюта за допомогою
гомології з віссю на зазначеній прямій і центром в її полюсі.
є ортогональною траєкторією
гіперболічного пучка прямих, тобто вона є еквідистантою. Пряма UV є
базою цієї еквідистанти. Отже, еквідистантою є будь-яка крива другого порядку,
яка розташована в середині абсолюта і дотикається до абсолюта в двох його
точках. Базою такої еквідистанти є пряма, що проходить через точки дотику.
Кожну таку криву можна дістати з абсолюта за допомогою
гомології з віссю на зазначеній прямій і центром в її полюсі.
Орицикли
Якщо за вісь гомології взяти пряму
s, дотичну
до абсолюта в деякій
точці S (рис.
8), то за допомогою такої гомології з (центром) абсолют перетворюється в криву  , яка
дотикається до абсолюта
в точці S. У
випадку, коли ця крива розташована в середині абсолюта, вона
є орициклом.
Справді,
якщо
, яка
дотикається до абсолюта
в точці S. У
випадку, коли ця крива розташована в середині абсолюта, вона
є орициклом.
Справді,
якщо  - деяка
пряма, що проходить через точки S, U, V -
точки її перетину відповідно з абсолютом і кривою
- деяка
пряма, що проходить через точки S, U, V -
точки її перетину відповідно з абсолютом і кривою  , то
дотичні до кривих у точках U, V перетинають
пряму s у
точці W
-
полюсі прямої
, то
дотичні до кривих у точках U, V перетинають
пряму s у
точці W
-
полюсі прямої 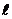 як відносно
абсолюта,
так і
відносно кривої
як відносно
абсолюта,
так і
відносно кривої 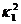 . Але
це означає, що пряма VW перпендикулярна
до
. Але
це означає, що пряма VW перпендикулярна
до 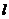 у точці V. Таким
чином, крива
у точці V. Таким
чином, крива 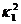 є
ортогональна траєкторія прямих, що проходять через нескінченно віддалену точку S, тобто
прямих параболічного пучка, а це доводить, що
вона є орицикл.
є
ортогональна траєкторія прямих, що проходять через нескінченно віддалену точку S, тобто
прямих параболічного пучка, а це доводить, що
вона є орицикл.
Зауважимо, що орициклом є не
кожна крива другого порядку, яка дотикається
до абсолюта в одній точці. Можна показати, що орицикл має з абсолютом у точці
дотику дотик третього порядку, тобто в точці дотику збігаються чотири
нескінченно близькі точки абсолюта і орицикла. Орицикл можна було б уявити собі
як граничний випадок еквідистанти, коли обидві точки еквідистанти, що належать
абсолюту, зливаються з однією точкою абсолюта.
Рис.8
Кола
Якщо за центр гомології взяти
яку - небудь
внутрішню точку абсолюта,а за
вісь гомології поляру
цього
центра відносно абсолюта,
то після
перетворення абсолют перейде в деяку криву другого порядку  . Якщо
ця крива міститься в середині абсолюта, то, вона буде
колом. Справді, якщо U, V дві
точки перетину якої-небудь прямої, що проходить через центр гомології S, з
абсолютом, то дотичні до абсолюта
в цих
точках обов'язково перетинаються на осі s. Те
саме справедливе і для точок перетину прямої UV з
кривою
. Якщо
ця крива міститься в середині абсолюта, то, вона буде
колом. Справді, якщо U, V дві
точки перетину якої-небудь прямої, що проходить через центр гомології S, з
абсолютом, то дотичні до абсолюта
в цих
точках обов'язково перетинаються на осі s. Те
саме справедливе і для точок перетину прямої UV з
кривою  (
рис.8). Точка перетину W зазначених
дотичних є полюс прямої UV, але це
означає, що дотичні до кривої у точках її перетину з прямою UV перпендикулярні
до цієї прямої. Таким чином, крива
(
рис.8). Точка перетину W зазначених
дотичних є полюс прямої UV, але це
означає, що дотичні до кривої у точках її перетину з прямою UV перпендикулярні
до цієї прямої. Таким чином, крива  є ортогональна траєкторія прямих
еліптичного пучка (пучка прямих з центром S), отже,
вона є колом (рис. 9).
є ортогональна траєкторія прямих
еліптичного пучка (пучка прямих з центром S), отже,
вона є колом (рис. 9).
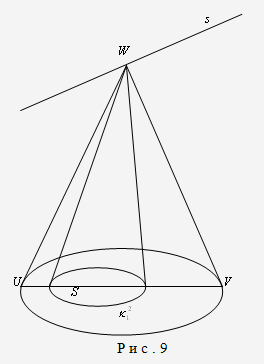
Рис.9
Відстань між двома точками
Відстань між двома точками на
площині Лобачевського є інваріант цих точок відносно всіляких рухів на цій
площині. За допомогою методів теорії груп можна довести, що цей інваріант є
єдиний незалежний інваріант цих точок, що будь-який інший їх інваріант є
функція від цього інваріанта.
Позначимо віддаль між точками
А і В символом 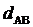 . З усіх
інваріантів, як відомо, віддаль є єдиний інваріант (з точністю до сталого
множника), який має таку властивість: якщо А, В, С три точки, що належать одній
прямій, і точка В розташована між точками А і С, то
. З усіх
інваріантів, як відомо, віддаль є єдиний інваріант (з точністю до сталого
множника), який має таку властивість: якщо А, В, С три точки, що належать одній
прямій, і точка В розташована між точками А і С, то
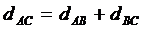 . (27)
. (27)
Коли точка В лежить між точками А і С,
то можна записати АС = АВ + ВС,
роглядаючи суму просто як суму двох відрізків, незалежно від того, чи мають
вони якусь міру, чи ні. Тоді рівність (27) можна записати у вигляді
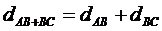 ,
,
отже, довжина відрізка є розв'язком
такого функціонального рівняння
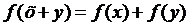 . (28)
. (28)
Єдиним розв'язком цього рівняння є
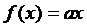 , (29)
, (29)
а - деякий коефіцієнт
пропорційності. Але з цього випливає, Що коли ми знайдемо яку - небудь функцію
відрізка, яка є довжиною цього відрізка, то будь-яка інша довжина повинна бути
пропорційною цій функції.
Нехай А, В - дві які-небудь точки на
площині Лобачевського (рис. 10).
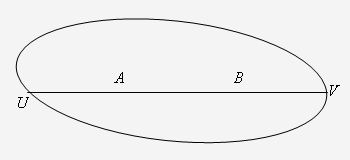
Рис.10
Пряма АВ перетинає абсолют у
точках U, V.
Четвірка точок А, В, U, V має
позитивне складне відношення  ), яке не змінюватиметься при
будь-яких автоморфізмах відносно абсолюта. Отже, це складне відношення є
інваріант таких автоморфізмів. Але його не можна брати за довжину відрізка АВ,
бо для нього не виконується рівність (27). Проте, розглядаючи рівності
), яке не змінюватиметься при
будь-яких автоморфізмах відносно абсолюта. Отже, це складне відношення є
інваріант таких автоморфізмів. Але його не можна брати за довжину відрізка АВ,
бо для нього не виконується рівність (27). Проте, розглядаючи рівності
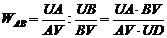 ,
,
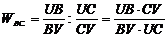 ,
,
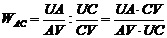 ,
,
бачимо, що
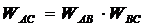 . (30)
. (30)
Звідси
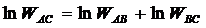 . (31)
. (31)
Ми дістали рівність (27), яка
характеризує довжину відрізка. Згідно з тим, що було сказано вище, за довжину
ми можемо взяти також величини, пропорційні логарифмам відповідних складних
відношень. Покажемо
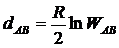 . (32)
. (32)
Коефіцієнт R,
який входить у цю формулу, відіграє дуже важливу роль у геометрії
Лобачевського. Він має назву радіуса кривизни простору Лобачевського.
Зауважимо, що формула (32)
дає для довжини відрізка завжди дійсну величину, бо складне відношення 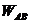 при не
розділяючих парах АВ і UV, завжди є
додатним.
при не
розділяючих парах АВ і UV, завжди є
додатним.
Формула (32) є формула
довжини відрізка в геометрії Лобачевського. Згідно з сказаним вище, ніякої
іншої довжини, крім тієї, що пропорційна правій частині формули (32), не існує.
Кут між прямими. Кут між
двома прямими також можна визначити як інваріант групи рухів на площині
Лобачевського. Якщо a, b -
дві прямі на площині, що мають спільну точку О, то кут між ними позначимо 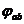 . Як і для
відрізків, для будь-яких трьох прямих, що проходять через точку О, ми повинні
мати
. Як і для
відрізків, для будь-яких трьох прямих, що проходять через точку О, ми повинні
мати
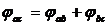 (33)
(33)
Зауважимо, що рівність (27) , як і
рівність (33), при відповідній умові щодо знаків відрізків або кутів можна
розглядати при будь-якому розташуванні точок А, В, С
на
прямій або прямих а, b, с в
пучку О.
Можна довести також методами
теорії груп, що будь-які дві прямі а, b, які проходять через деяку точку, мають
один і тільки один незалежний інваріант, а всі інші інваріанти будуть деякими
функціями від цього інваріанта. Але один з інваріантів відомий безпосередньо. Справді,
проведемо через точку 0 дві дотичні до абсолюта. Оскільки
точка О є
внутрішня точка абсолюта,
а
абсолют є дійсний, то обидві дотичні є уявно спряженими. Нехай ці прямі є и і v.
Складемо складне відношення 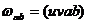 . Оскільки a, b -
дійсні прямі, а и, v - уявно
спряжені, то величина
. Оскільки a, b -
дійсні прямі, а и, v - уявно
спряжені, то величина  є
уявне число, модуль якого дорівнює одиниці, тобто число
є
уявне число, модуль якого дорівнює одиниці, тобто число
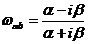 (34)
(34)
Логарифм такого числа є суто
уявне число, 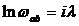
Як і у випадку точок на
прямій, для прямих одного пучка маємо 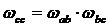 , звідки
, звідки 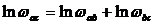 . Отже,
величина In
. Отже,
величина In 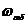 задовольняє
рівність (33), а тому її можна було б узяти за міру кута між прямими. Проте, як
було вже сказано, ця величина є уявною, а тому, щоб вимірювати кути дійсними
числами, покладають
задовольняє
рівність (33), а тому її можна було б узяти за міру кута між прямими. Проте, як
було вже сказано, ця величина є уявною, а тому, щоб вимірювати кути дійсними
числами, покладають
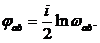 (35)
(35)
Ця формула є формула Лагерра, вона
точно збігається з формулою за
допомогою якої вимірюють кути в евклідовій геометрії.
Якщо прямі а і b полярно
спряжені відносно абсолюта,
то 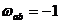 . У
цьому випадку
. У
цьому випадку 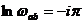 , а
тому
, а
тому 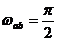 , тобто
прямий кут має величину
, тобто
прямий кут має величину 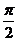 . Саме з цих
обставин ми поклали у формулі (35) множник
пропорційності, що дорівнює
. Саме з цих
обставин ми поклали у формулі (35) множник
пропорційності, що дорівнює 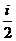 . При іншому множнику прямій кут
дорівнював би числу, відмінному від
. При іншому множнику прямій кут
дорівнював би числу, відмінному від 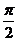 .
.
Висновки
Ми розглянули дев'ять різновидів
нєєвклідової геометрії в просторі двох вимірів; та їх відображення (оригінал
моделі, інтерпретації) на евклідовій площині. Перші три системи: (геометрія
Лобачевського (НЕ) та її найближчі різновиди (НН) і (ЕН) справедливі при
дійсному невиродженому абсолюті всередині або поза ним; система ЕЕ будується
при уявному абсолюті, а абсолют решти п'яти геометрій можна разглядати як вироджений
конічний переріз. Остаточно приходимо до наступної таблиці:Геометрія
Лобачевського (НЕ); дійсний невироджений абсолют: внутрішня його область.
IІ Геометрія з
гіперболічним виміром як відстаней, так і довжин (НН); дійсний невироджений
абсолют; зовнішня його область; прямі - гіперболічні прямі.
Геометрія з
гіперболічним виміром як відстаней, так і довжин (НН); дійсний невироджений
абсолют; зовнішня його область; прямі - гіперболічні прямі.
ІІ Геометрія,
двоїста геометрії Лобачевського (ЕН); дійсний невироджений абсолют; зовнішня
його область; прямі- еліптичні прямі.
Геометрія,
двоїста геометрії Лобачевського (ЕН); дійсний невироджений абсолют; зовнішня
його область; прямі- еліптичні прямі.
III Геометрія Рімана (ЕЕ); абсолютом
є уявна невироджена
крива другого порядку.
IV Геометрія
Евкліда (РЕ); абсолютом є дві циклічні точки площині-уявні спряжені точки
нескінченно віддаленої прямії.
Геометрія
Евкліда (РЕ); абсолютом є дві циклічні точки площині-уявні спряжені точки
нескінченно віддаленої прямії. Псевдоєвклідова геометрія (РН);
абсолютом є дві дійсні нескінченно віддалені точки площини.
Псевдоєвклідова геометрія (РН);
абсолютом є дві дійсні нескінченно віддалені точки площини. Геометрія,
двоїста евклідовій геометрії (ЕР); абсолютом є дві паралельні уявні зв'язані
прямі.
Геометрія,
двоїста евклідовій геометрії (ЕР); абсолютом є дві паралельні уявні зв'язані
прямі. Геометрія,
двоїста до псевдоєвклідової геометрії (HP); абсолютом є дві дійсні паралельні
прямі.
Геометрія,
двоїста до псевдоєвклідової геометрії (HP); абсолютом є дві дійсні паралельні
прямі.
VI Геометрія з параболічним виміром
як відстаней так і довжин (РР); абсолютом є нескінченно віддалена пряма з
виділеною дійсною точкою на ній.
У тривимірному просторі до колишніх
об'єктів першого ступеня, об’єкту вимірюванню (до прямолінійних відрізків і
лінійних кутів), додається ще один об'ект-двогранні кути. Оскільки кожен з цих
об'єктів може допускати різного роду вимірювання (еліптичне, гіперболічне або
параболічне), то тут можливі 27 комбінацій, тобто двадцять сім різних геометрій.
Найважливіші типи цих систем вказані, хоча і не розглянуті повністю. Вважаємо,
що ідея, за якою ці системи розрізняють і класифікують, достатньо з'ясована.
Проте Клейн неодноразово зауважував,
що справа зовсім не лише в тому, щоб перерахувати можливі системи; потрібно
дійсно побудувати геометрію для кожної з цих систем, встановити її аксіоматику,
з цієї аксіоматики дедуктивно вивести саму геометрію кожної системи і її
метрику. Але це в необхідному об'ємі ще не виконано і на теперішній час.
Література
.Гильберт
Д., Основания геометрии м. - л., Гостехиздат, 1948.
.Костип
В.И.,Основания геометрии м. - л., Гостехиздат, 1946.
.Несторович
Н.М., Геометрические построения в плоскости Лобачевського. м. - л.,
Гостехиздат, 1951.
.Глаголев
Н.А., Проэктивная геометрия. м. - л., ОНТИ, 1936.
.Эйзенхарт
А.П., Риманова геометрия. м. - л., ИЛ., 1948.
.Рошевський
П.К., Введение в риманову геометрию и тензорный аналіз. м. - л., ОНТИ, 1936.
.Букреев
Б.А., Планиметрия Лобачевського в аналитическом изложения. м. - л.,
Гостехиздат, 1951.
.Шатуповский
С.О., Введение в анализ. Одесса, Матерес, 1923.
.Дубров
Я.С., Векторное исчиление. ч., м. - л., Гостехиздат, 1950.
.Каган
В.Ф., Основы теории поверхностей. тт. 1, 2, м. - л., Гостехиздат, 1947, 1948.
Додатки
Додаток 1
Історична довідка
Фелікс Клейн відомий за його роботу
в неевклідової геометрії, та за роботу зв'язку між геометрією і теорія груп. Він
народився 25 квітня 1849
і насолоджувався вказавши, що кожен день,
місяць і рік був квадрат простого числа. Батько Клейна був секретарем глави
уряду. Існуть барвисті
описи народження Фелікса в його некролог у "Працях Королівського
товариства: Без, гармати гриміли на барикадах піднятих повсталого проти
ненависних правителів Пруссії. У рамках, хоча все було підготовлено для
польоту, не було думки вильоту; з цієї ночі народився син, на корму секретаря
Пруссії. Цей син був Фелікс Клейн. Революція проти пруссаків, в результаті яких
такі драматичні народження для Фелікса
Клейна, був абсолютно
пригнічений до літа 1849 року.
Клейн поступив
до
гімназії в Дюссельдорфі. Отримавши диплом, він вступив до Боннський університет
і вивчав математику і фізику протягом 1865-1866. Він почав свою кар'єру з
наміром стати фізиком. Ще навчаючись в університеті Бонна, він був призначений
на посаду лаборанта в Плюккер в 1866 році. Плюккереві
інтереси досить міцно
вкоренилася в геометрії. Клейн одержав докторський ступінь, якою керував
Плюккер з Університету Бонна в 1868 році, з дисертацією Про групи перетворень.
Однак
цього року Клейн одержав доктора наук.
Плюккер помер, залишивши свою головну працю з основ геометрії.
Клейн був очевидна
особа для завершення другої частини Плюккера
і ця робота його познайомила
з
Клебшом. Клебш переїхав до
Геттінген, в 1868 році і протягом 1869, Клейн зробив відвідувань в Берліні,
Парижі та Геттінгені. У липні 1870 Клейн
був у Парижі, коли Бісмарк, прусський канцлер, опублікував провокаційні
повідомлення, спрямовані на гнів французького уряду. Франція оголосила війну
Пруссії 19 липня,
і Клейн відчув він не міг більше залишатися в Парижі і повернувся. Потім,
протягом короткого періоду він зробив військову службу,
був
санітаром до свого
призначення лектора в Геттінгені на початку 1871 року.
Клейн
був призначений професором в Ерланген, в Баварії на півдні Німеччини, у 1872
році. Він рішуче підтримує Клебша, які розглядали його як провідного
математика свого часу.
Клейн хотів побудувати школу в
Ерланген, де було лише кілька студентів, але
йому це не вдалося тому він був радий запропонованому
місці
в Мюнхені в 1875 році. Там він і його колега Брілл, викладав курси для великого
числа студентів-відмінників і великий
талант Клейна в
навчанні було повністю
виражено. Серед студентів, що Клейн вчив
в той час як у Мюнхені були Гурвіца, фон
Дейка, Рон, Рунге, Планка, Бианки і Річчі-Курбастро.
Після п'яти років в Мюнхені, Клейн
був призначений на кафедру геометрії в Лейпцигу. Разом
із
колегами, талановитими
молодими викладачами,
у тому числі фон Дейка, Рон і Енгель.
З
1880
до
1886 , що Клейн провів у Лейпцигу багато часу, де
докорінно змінив своє життя. Клейн
пішов на кафедру в
Геттінгенському університеті в 1886 році. Він викладав у Геттінгені, поки не
вийшов на пенсію у 1913, але тепер він прагне до відновлення як провідного
дослідницького центру математики у світі. Свою роль як лідера геометричній
школі в Лейпцігську,
був
переведений в Геттінгену. У
Геттінгені викладав широкий вибір курсів, головним чином, на рубежі
математики і фізики, таких, як механіка і теорія потенціалу.
Клейном
був створений дослідний центр в Геттінгені який
повиннен був
служити в якості моделі для кращого
математично науково-дослідницького центра
по всьому світу. Він вносив
на щотижневих нарадах обговорення математичних читальний зал з математичної
бібліотеки. Клейн запросив
Гільберта з Кенігсберга, щоб приєднатися до його дослідницької групи в
Геттінгені в 1895 році. Клейн подав
у відставку у зв'язку з поганим здоров'ям в 1913 році. Проте він продовжував
викладати математику в своєму будинку в роки Першої світової війни.
Вклад
Клейна в геометрію
стало
такою ж невід'ємною частиною нашої сучасної математичної думки, що це нам важко
зрозуміти, новизну отриманих
результатів.
Під час перебування в Геттінгені в 1871 році
Клейн зробив великі відкриття відносно геометрії. Він опублікував два документи
з неевклідової геометрії, в якій він показав, що можна було розглянути питання
про геометрії Евкліда і неевклідової геометрії, як особливі випадки проективної
поверхні з конкретними конічними
перетинами. Це світліло про те, що неевклідова
геометрія була послідовною, якщо і геометрія Евкліда була послідовною. Той
факт, що в неевклідової
геометрії, в той час ще були суперечливі
теми зараз зникли. Його статус був зроблений на основі до ідентичних геометрії
Евкліда. Келі ніколи не приймав
ідеї Клейна вірячи своїм аргументам кругової
геометриї.
Ці перетворення
відігравали важливу
роль у сучасній математиці і Клейн показав,
як істотні властивості даної геометрії можуть
бути представлені групою перетворень,
які зберігають ці властивості. Таким чином, визначена програма геометрії
з тим щоб вона включає як геометрію
Евкліда так і неевклідову
геометрію.
Також клейн
розглянув рівняння ступеня вище 4 і була особливо зацікавленій
у використанні трансцендентних
методів для вирішення
загальних рівнянь п'ятого степеня.
Він розробив теорію автоморфних функцій, що
з'єднують алгебраїчні і геометричні результати,
це він опублікував у своїй книзі,
виданої
1884 р. Однак Пуанкаре
почав публікувати виклад його теорії автоморфних функцій, в 1881 році і, як
пояснюється це призвело до конкуренції між ними.
Повинні також
зазначити, пляшку Клейна,
односторонньо закритою поверхнею імені Клейна. Пляшка Клейна не може бути
побудована в евклідовому просторі. Краще за все, зображено у вигляді циліндра.
Однак це не є неперервною
поверхнею в тривимірному просторі.
Але можна
побудувати пляшку Клейна в
неевклідовому просторі.
У 1890 Клейн зацікавився математичною
фізикою, хоча протягом
всієї своєї кар'єри він показав, що він ніколи не був далекий від цієї області.
Виходячи з цього інтересу, він написав важливу роботу по гіроскопа з
Зоммерфельда.
Клейн
був обраний головою Міжнародної комісії з математичного Навчання в Римі
Міжнародний математичний конгрес 1908 року. Під його керівництвом німецького
відділення комісія опублікувала багато томів на викладання математики на всіх
рівнях в Німеччині.
Клейн
був обраний членом Королівського товариства в 1885 році і отримав медаль Коплі
Товариства в 1912 році. Лондонське математичне товариство нагородило його своєю
медолю
де Моргана у 1893 році. Помер Ф.Клейн в
1925році, 22травня.
Додоток2
Задача 1. Основою
піраміди
 є
рівнобедрений прямокутний трикутник
є
рівнобедрений прямокутний трикутник 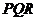 з гіпотенузою
з гіпотенузою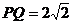 . Бічне ребро
. Бічне ребро 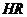 перпендикулярне
до площини основи і дорівнює 1. Знайти величину кута і відстань між мимобіжними
прямими, одна з яких проходить через точку
перпендикулярне
до площини основи і дорівнює 1. Знайти величину кута і відстань між мимобіжними
прямими, одна з яких проходить через точку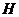 і середину ребра
і середину ребра  , а друга - через точку
, а друга - через точку  і середину
і середину .
.
Розв’язування.
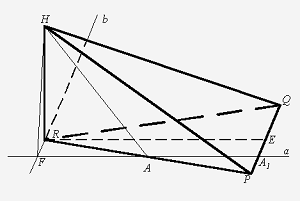
Рис.
Позначимо через 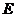 - середину
- середину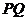 , через
, через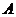 - середину
- середину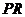 .
.
Тоді  та
та - мимобіжні
прямі, відстань і кут між якими і треба знайти за умов:
- мимобіжні
прямі, відстань і кут між якими і треба знайти за умов: 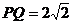 ,
, 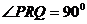 ,
, 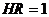 ,
, 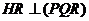
Проведемо через точку  пряму
пряму  ||
||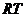 , а через
точку
, а через
точку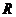 пряму b||
пряму b|| 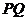 (у площині
основи).
(у площині
основи).
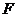 - точка перетину прямих а та b,
- точка перетину прямих а та b,  - точка
перетину прямих а та
- точка
перетину прямих а та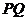 .
.
Згідно означення кута між
мимобіжними прямими, менший з кутів  та
та  і буде шуканим.
і буде шуканим.
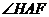 - кут ∆
- кут ∆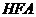 . За умовою
. За умовою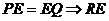 - медіана рівнобедреного трикутника
- медіана рівнобедреного трикутника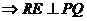 , але
, але 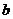 ||
||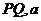 ||
|| 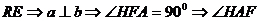 гострий кут
прямокутного ∆
гострий кут
прямокутного ∆
 - шуканий.
- шуканий.
З ∆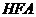 :
: 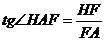 ,
, 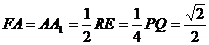 .
.
З ∆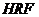 :
: 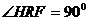 ,
, 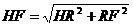 , де
, де 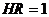 - за
умовою.
- за
умовою.
З ∆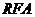 :
: 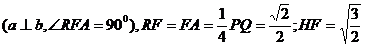 ,тоді
,тоді
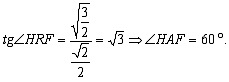
Тепер знайдемо відстань між
вказаними прямими. Очевидно, що в силу побудови, шукана відстань буде
дорівнювати відстані від точки до площини
до площини 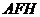 (адже
(адже 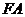 ||
|| 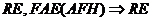 ||
|| 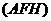 ). Для знаходження цієї відстані розглянемо
тетраедр
). Для знаходження цієї відстані розглянемо
тетраедр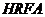 в якому
в якому 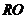 - шукана
відстань і висота.
- шукана
відстань і висота.
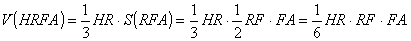
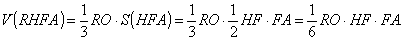
Враховуючи, що 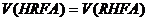 ,
,
маємо 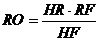 ,
,  .
.
Відповідь: 60о та 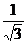 . Задача2.
В
правильній трикутній призмі
. Задача2.
В
правильній трикутній призмі 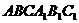
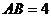 см,
см, 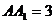 см. Знайти відстань між прямими
см. Знайти відстань між прямими 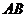 та
та  , де
, де  - середина
ребра
- середина
ребра  .
.
Рис.
Розв’язування
Оберемо систему координат
так, щоб початок співпав з вершиною  , вісь ординат містила ребро
, вісь ординат містила ребро 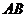 , вісь
аплікат - ребро
, вісь
аплікат - ребро 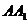 , а вісь
абсцис проведемо паралельно медіані
, а вісь
абсцис проведемо паралельно медіані 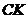 Δ
Δ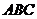 .
.
Визначимо координати точок у обраній
системі координат, враховуючи, що  - середина сторони
- середина сторони 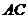 ,
, 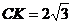 - медіана
правильного трикутника
- медіана
правильного трикутника 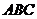
 ,
,  ,
,
 .
.
Проведемо  ||
||  , тоді
, тоді  ||
||  і
і .
.
Запишемо рівняння площини 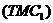 ,
користуючись схемою.
,
користуючись схемою.
За відповідною формулою маємо
Відповідь.