Прогнозирование в сельском хозяйстве
Задание1
По имеющимся исходным данным урожайности
зерновых культур в Западно-Сибирском районе требуется обосновать прогнозы
развития зернового производства. В качестве исходных данных используется
информация об урожайности зерновых культур за период 23 года с начальной точкой
динамического ряда 1947г. В качестве альтернатив применим линейную,
параболическую и синусоидальную форму зависимости.
Исходные данные имеют вид:
|
Год
|
1947
|
1948
|
1949
|
1950
|
1951
|
1952
|
1953
|
1954
|
1955
|
1956
|
1957
|
|
Урожайность,ц/га
|
10,7
|
10,2
|
4,0
|
8,6
|
7,5
|
4,4
|
5,0
|
5,9
|
2,8
|
22,7
|
13,6
|
|
1958
|
1959
|
1960
|
1961
|
1962
|
1963
|
1964
|
1965
|
1966
|
1967
|
1968
|
1969
|
|
18,9
|
13,7
|
11,5
|
11,7
|
7,2
|
4,2
|
17,9
|
8,6
|
27,2
|
15,7
|
25,2
|
21,5
|
Как видно из исходных данных, наименьшая
урожайность наблюдается в 1955 году, а наибольшая - в 1966 г. На фоне общей
динамики наблюдается довольно значительный упадок урожайности в 1949 г., а
также в 1951-55 гг., однако уже в 1956 г. заметен резкий рост показателя, такой
же скачок повторяется в 1966 году.
В качестве альтернатив применим линейную, параболическую
и синусоидальную форму зависимости.
Аналитическое выравнивание по прямой (линейная
зависимость):
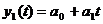 ,
,
где 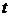 - условное обозначение времени, а
- условное обозначение времени, а 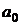 и
и 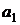 - параметры
искомой прямой.
- параметры
искомой прямой.
Параметры прямой находятся из
решения системы уравнений:
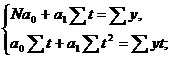
где 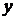 - фактические уровни, N - число
членов ряда динамики.
- фактические уровни, N - число
членов ряда динамики.
Выравнивание по многочлену высокой
степени - по параболе второго порядка:
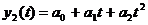 .
.
Система нормальных уравнений для
определения параметров параболы имеет вид:
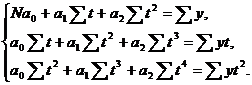
Синусоидальная функция
(комбинированная зависимость):
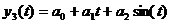 .
.
Система нормальных уравнений для
определения параметров принимает вид:
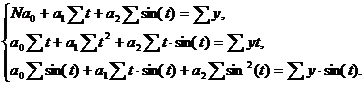
Для определения искомых параметров
прямой, параболы и гиперболы воспользуемся данными, взятыми из таблицы:
|
t
|
Y
|
t^2
|
t^3
|
t^4
|
Y*t
|
t*sin(t)
|
Y*t^2
|
sin(t)
|
(sin(t))^2
|
Y*sin(t)
|
|
1
|
10,7
|
1
|
1
|
1
|
10,7
|
0,84147
|
10,7
|
0,84147
|
0,70807
|
9,00374
|
|
2
|
10,2
|
4
|
8
|
16
|
20,4
|
1,81859
|
40,8
|
0,9093
|
0,82682
|
9,27483
|
|
3
|
4
|
9
|
27
|
81
|
12
|
0,42336
|
36
|
0,14112
|
0,01991
|
0,56448
|
|
4
|
8,6
|
16
|
64
|
256
|
34,4
|
-3,02721
|
137,6
|
-0,7568
|
0,57275
|
-6,5085
|
|
5
|
7,5
|
25
|
125
|
625
|
37,5
|
-4,79462
|
187,5
|
-0,95892
|
0,91954
|
-7,19193
|
|
6
|
4,4
|
36
|
216
|
1296
|
26,4
|
-1,67649
|
158,4
|
-0,27942
|
0,07807
|
-1,22943
|
|
7
|
5
|
49
|
343
|
2401
|
35
|
4,59891
|
245
|
0,65699
|
0,43163
|
3,28493
|
|
8
|
5,9
|
64
|
512
|
4096
|
47,2
|
7,91487
|
377,6
|
0,98936
|
0,97883
|
5,83721
|
|
9
|
2,8
|
81
|
729
|
6561
|
25,2
|
3,70907
|
226,8
|
0,41212
|
0,16984
|
1,15393
|
|
10
|
22,7
|
100
|
1000
|
10000
|
227
|
-5,44021
|
2270
|
-0,54402
|
0,29596
|
-12,3493
|
|
11
|
13,6
|
121
|
1331
|
14641
|
149,6
|
-10,9999
|
1645,6
|
-0,99999
|
0,99998
|
-13,5999
|
|
12
|
18,9
|
144
|
1728
|
20736
|
226,8
|
-6,43888
|
2721,6
|
-0,53657
|
0,28791
|
-10,1412
|
|
13
|
13,7
|
169
|
2197
|
28561
|
178,1
|
5,46217
|
2315,3
|
0,42017
|
0,17654
|
5,75629
|
|
14
|
11,5
|
196
|
2744
|
38416
|
161
|
13,8685
|
2254
|
0,99061
|
0,9813
|
11,392
|
|
15
|
11,7
|
225
|
3375
|
50625
|
175,5
|
9,75432
|
2632,5
|
0,65029
|
0,42287
|
7,60837
|
|
16
|
7,2
|
256
|
4096
|
65536
|
115,2
|
-4,60645
|
1843,2
|
-0,2879
|
0,08289
|
-2,0729
|
|
17
|
4,2
|
289
|
4913
|
83521
|
71,4
|
-16,3438
|
1213,8
|
-0,9614
|
0,92429
|
-4,03787
|
|
18
|
17,9
|
324
|
5832
|
104976
|
322,2
|
-13,5178
|
5799,6
|
-0,75099
|
0,56398
|
-13,4427
|
|
19
|
8,6
|
361
|
6859
|
130321
|
163,4
|
2,84767
|
3104,6
|
0,14988
|
0,02246
|
1,28894
|
|
20
|
27,2
|
400
|
8000
|
160000
|
544
|
18,2589
|
10880
|
0,91295
|
0,83347
|
24,8321
|
|
21
|
15,7
|
441
|
9261
|
194481
|
329,7
|
17,5698
|
6923,7
|
0,83666
|
0,69999
|
13,1355
|
|
22
|
25,2
|
484
|
10648
|
234256
|
554,4
|
-0,19473
|
12196,8
|
-0,00885
|
7,8E-05
|
-0,22305
|
|
23
|
21,5
|
529
|
12167
|
279841
|
494,5
|
-19,4631
|
11373,5
|
-0,84622
|
0,71609
|
-18,1937
|
|
276
|
278,7
|
4324
|
76176
|
1431244
|
3961,6
|
0,56452
|
68594,6
|
0,97981
|
11,7133
|
4,14185
|
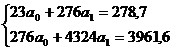
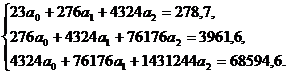
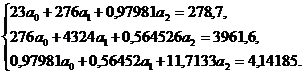
Для определения искомых параметров
прямой, параболы и синусоиды решим данные системы уравнений Методом Наименьших
Квадратов при помощи программы Mathcad 11 Enterprise Edition. Получим:
параметры прямой: 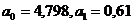 ;
;
уравнение имеет вид: 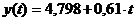 ;
;
параметры параболы: 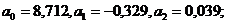
параметры синусоиды: 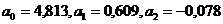 ;
;
уравнение имеет вид: 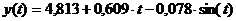 .
.
Получили выровненные значения для
трех случаев.
|
t
|
Y
|
Y1
|
Y2
|
Y3
|
|
1
|
10,7
|
5,408
|
8,422
|
5,356365
|
|
2
|
10,2
|
6,018
|
8,21
|
5,960075
|
|
3
|
4
|
6,628
|
8,076
|
6,628993
|
|
4
|
8,6
|
7,238
|
8,02
|
7,308031
|
|
5
|
7,5
|
7,848
|
8,042
|
7,932796
|
|
6
|
4,4
|
8,458
|
8,142
|
8,488794
|
|
7
|
5
|
9,068
|
8,32
|
9,024755
|
|
8
|
5,9
|
9,678
|
8,576
|
9,60783
|
|
9
|
2,8
|
10,288
|
8,91
|
10,26185
|
|
10
|
22,7
|
10,898
|
9,322
|
10,94543
|
|
11
|
13,6
|
11,508
|
9,812
|
11,59
|
|
12
|
18,9
|
12,118
|
10,38
|
12,16285
|
|
13
|
13,7
|
12,728
|
11,026
|
12,69723
|
|
14
|
11,5
|
13,338
|
11,75
|
13,26173
|
|
15
|
11,7
|
13,948
|
12,552
|
13,89728
|
|
16
|
7,2
|
14,558
|
13,432
|
14,57946
|
|
17
|
4,2
|
15,168
|
14,39
|
15,24099
|
|
18
|
17,9
|
15,778
|
15,426
|
15,83358
|
|
19
|
8,6
|
16,388
|
16,54
|
16,37231
|
|
20
|
27,2
|
16,998
|
17,732
|
16,92179
|
|
21
|
15,7
|
17,608
|
19,002
|
17,53674
|
|
22
|
25,2
|
18,218
|
20,35
|
18,21169
|
|
23
|
21,5
|
18,828
|
21,776
|
18,88601
|
Проиллюстрируем графически результаты
произведенного аналитического выравнивания ряда динамики.
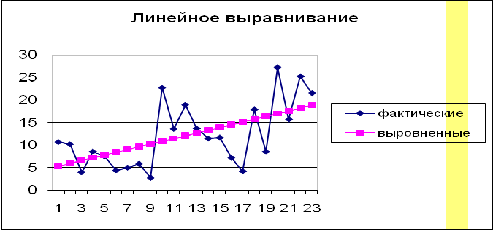
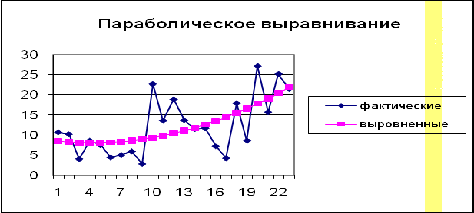
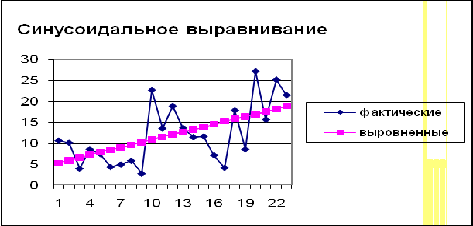
Из диаграмм видно, что все три графика примерно
одинаково аппроксимируют исходные данные, поэтому нельзя однозначно определить
подходящую зависимость, исходя из графиков. Выберем ее, найдя для полученных
регрессионных уравнений:
- дисперсию остатков регрессии 
общую дисперсию регрессии 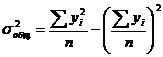
тесноту связи 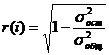
стандартное отклонение 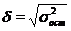
среднюю ошибку 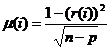
Рассчитанные данные отражены в
таблице:
|
Линейная
зависимость
|
Параболическая
зависимость
|
Синусоидальная
зависимость
|
|
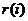 0,517250,534610,48062 0,517250,534610,48062
|
|
|
|
|
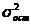 36,189335,287237,9952 36,189335,287237,9952
|
|
|
|
|
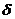 6,015755,94036,164022 6,015755,94036,164022
|
|
|
|
|
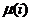 0,1598340,1596990,171954 0,1598340,1596990,171954
|
|
|
|
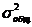 =49,4084
=49,4084
Как видно из представленной таблицы, дисперсии
остатков регрессии, уровни корреляции и стандартные отклонения всех трех
зависимостей отличаются незначительно (в десятых и сотых долях), что подтверждает
выводы, сделанные по графикам. Лучше всего из предложенных зависимостей к
исходным данным подогнано параболическое уравнение. Оно имеет сравнительно
большую тесноту связи, меньшие остаточную вариацию и среднюю ошибку. Хуже всего
подогнана синусоидальная зависимость. Параболическую связь можно признать
достоверной и ее оценочные результаты могут использоваться для прогнозирования.
Найдем значения 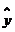 при t=24, 25, …,
31 и сведем полученные результаты в таблицу:
при t=24, 25, …,
31 и сведем полученные результаты в таблицу:
|
t
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
|
ŷ
|
23,28
|
24,862
|
26,522
|
28,26
|
30,076
|
31,97
|
33,942
|
35,992
|
Проиллюстрируем полученные значения прогноза:
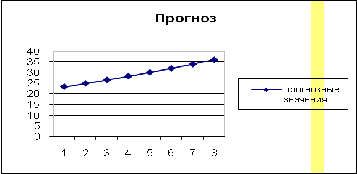
Из диаграммы видно, что в дальнейшем урожайность
будет значительно расти и почти достигнет своего пика в рассматриваемом периоде
(1966 г.). Среднее значение прогноза 29,363.
Задание 2
Прогнозирование рядов экономической динамики на
основе методологии скользящих средних.
Суть данного метода заключается в том, чтобы
нивелировать случайные отклонения в сильно колеблющихся динамических рядах
путем усреднения пиковых изменений, что дает возможность выявить закономерную
динамику, оценить ее и провести расчет значений прогноза на перспективу с
использованием пиковых амплитуд колебаний. Прогнозное значение при этом
приобретает ту же качественную природу изменений, что и исходные данные. Важным
моментом в использовании метода скользящих средних является выбор параметра
сглаживания. Этот параметр характеризует конечное число данных ряда, между
которыми рассчитывается среднее значение. Он может составлять колебания от 2 до
(N-2) значений. Для
проведения расчетов будем применять параметр скольжения не более 11.
Расчет скользящих средних осуществляется путем
вычислений величин осредненного ряда:
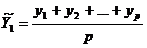 ;
; 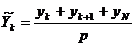 .
.
Выберем параметр сглаживания для нашего ряда,
для этого рассчитаем скользящие средние путем вычисления величин осредненного
ряда для p=9, 11, 13.
|
p=11
|
|
p=15
|
|
p=17
|
|
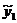 =8,67273 =8,67273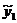 =10,08 =10,08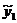 =9,564706 =9,564706
|
|
|
|
|
|
|
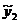 =9,41818 =9,41818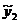 =9,846667 =9,846667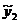 =9,988235 =9,988235
|
|
|
|
|
|
|
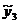 =9,73636 =9,73636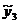 =9,446667 =9,446667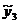 =9,894118 =9,894118
|
|
|
|
|
|
|
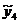 =10,4182 =10,4182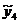 =10,37333 =10,37333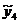 =11,25882 =11,25882
|
|
|
|
|
|
|
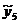 =10,7 =10,7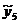 =10,37333 =10,37333 =11,67647 =11,67647
|
|
|
|
|
|
|
 =10,6727 =10,6727 =11,68667 =11,68667 =12,71765 =12,71765
|
|
|
|
|
|
|
 =10,6545 =10,6545 =12,44 =12,44 =13,72353 =13,72353
|
|
|
|
|
|
|
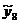 =11,8273 =11,8273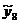 =13,78667 =13,78667
|
|
|
|
|
|
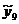 =12,0727 =12,0727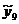 =14,82667 =14,82667
|
|
|
|
|
|
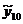 =14,2909 =14,2909
|
|
|
|
|
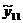 =13,6545 =13,6545
|
|
|
|
|
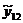 =14,7091 =14,7091
|
|
|
|
|
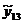 =14,9455 =14,9455
|
|
|
|
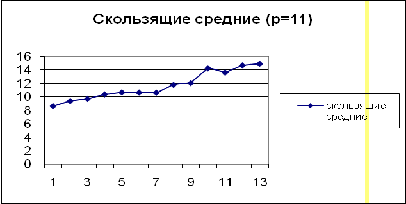
Наиболее приемлемыми для прогноза оказались
данные при параметре сглаживания p=11.
Следовательно, для p=11
аналитически сгладим ряд. Выберем в качестве функций регрессии - линейную и
параболическую:
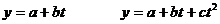
) 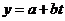
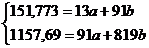
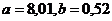
) 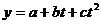
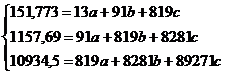
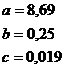
При помощи программы Mathcad
11 Enterprise
Edition получили уравнения
вида:
прямая: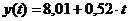
парабола: 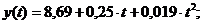
Произведем необходимые расчеты, где Y1,
Y2, - прогнозные
значения для двух функций соответственно. Все вычисления сведем в таблицу:
|
t
|
Y^
|
t^2
|
t^3
|
t^4
|
Y*t
|
Y*t^2
|
Y1
|
Y2
|
|
1
|
8,67273
|
1
|
1
|
1
|
8,67273
|
8,67273
|
8,53
|
8,959
|
|
2
|
9,41818
|
4
|
8
|
16
|
18,8364
|
37,6727
|
9,05
|
9,266
|
|
3
|
9,73636
|
9
|
27
|
81
|
29,2091
|
87,6273
|
9,57
|
9,611
|
|
4
|
10,4182
|
16
|
64
|
256
|
41,6727
|
166,691
|
10,09
|
9,994
|
|
5
|
10,7
|
25
|
125
|
625
|
53,5
|
267,5
|
10,61
|
10,415
|
|
6
|
10,6727
|
36
|
216
|
1296
|
64,0364
|
384,218
|
11,13
|
10,874
|
|
7
|
10,6545
|
49
|
343
|
2401
|
74,5818
|
522,073
|
11,65
|
11,371
|
|
8
|
11,8273
|
64
|
512
|
4096
|
94,6182
|
756,945
|
12,17
|
11,906
|
|
9
|
12,0727
|
81
|
729
|
6561
|
108,655
|
977,891
|
12,69
|
12,479
|
|
10
|
14,2909
|
100
|
1000
|
10000
|
142,909
|
1429,09
|
13,21
|
13,09
|
|
11
|
13,6545
|
121
|
1331
|
14641
|
150,2
|
1652,2
|
13,73
|
13,739
|
|
12
|
14,7091
|
144
|
1728
|
20736
|
176,509
|
2118,11
|
14,25
|
14,426
|
|
13
|
14,9455
|
169
|
2197
|
28561
|
194,291
|
2525,78
|
14,77
|
15,151
|
Составим график скользящих средних:
Найдем для полученных регрессионных уравнений
скользящих средних дисперсию остатков регрессии, общую дисперсию регрессии,
тесноту связи, стандартное отклонение и среднюю ошибку. Рассчитанные данные
отражены в таблице:
|
Линейная
зависимость
|
Параболическая
зависимость
|
|
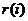 0,96140,96677 0,96140,96677
|
|
|
|
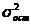 0,310320,26788 0,310320,26788
|
|
|
|
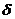 0,5570646610,517567444 0,5570646610,517567444
|
|
|
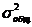 = 4,09891
= 4,09891
В обоих случаях коэффициенты корреляции высоки,
связи достоверны, поэтому для прогнозирования могут использоваться оценочные
результаты этих случаев. Однако, параболическая функция имеет большую тесноту
связи, меньшие остаточную вариацию и среднюю ошибку. Линейную связь можно
признать достоверной и ее оценочные результаты могут использоваться для прогнозирования:
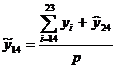 ;
;
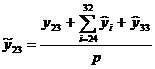 .
.
Получили следующие прогнозные
значения:
|
t
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
32
|
33
|
|
ŷ
|
20,31
|
20,93
|
16,85
|
14,27
|
28,38
|
19,5
|
38,52
|
27,44
|
37,36
|
Проиллюстрируем полученные прогнозные значения:
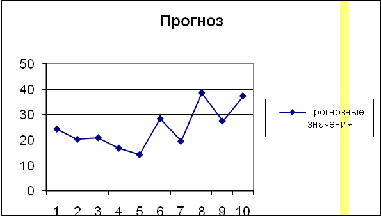
Из графика видно, что в среднем исходные данные
останутся в пределах своего изменения, колебания незначительны, график имеет
тенденцию к росту.
прогноз зерновой динамика
сглаживание
Задание 3
Исследовать исходный динамический ряд с помощью
метода экспоненциального сглаживания с использованием подхода Роберта Брауна.
1. В
качестве форм зависимости экспоненциального сглаживания выберем линейную и
параболическую.
Выберем параметр сглаживания a=0,15. При 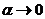 большее
влияние на прогноз оказывают ранние данные. Определим начальные условия:
большее
влияние на прогноз оказывают ранние данные. Определим начальные условия:
·
для
линейной формы зависимости:
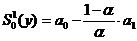 ;
;
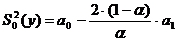 ;
;
·
для
параболической формы зависимости:
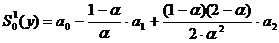 ;
;
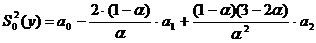 ;
;
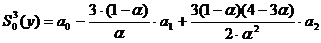 .
.
1. Определим
оценки коэффициентов и характеристики сглаживания динамического ряда:
оценки коэффициентов:
·
для
линейной формы зависимости:
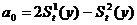 ;
;
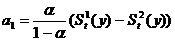 ;
;
·
для
параболической формы зависимости:
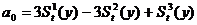 ;
;
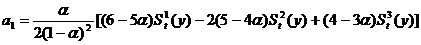 ;
;
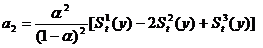 .
.
характеристики сглаживания:
·
для
линейной формы зависимости:
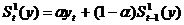 ;
;
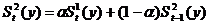 ;
;
·
для
параболической формы зависимости:
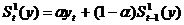 ;
;
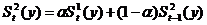 ;
;
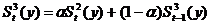 .
.
1. Определим
сглаженные значения и остаточные вариации.
Все расчеты сведем в таблицу.
·
для
линейной формы зависимости:
|
t
|
Yt
|
S1
|
S2
|
a0
|
a1
|
Yпр
|
(Y-Yпр)^2
|
|
0
|
|
1,341
|
-2,1153
|
4,798
|
0,61
|
|
|
|
1
|
10,7
|
2,745
|
-1,38626
|
6,87653
|
0,72907
|
7,6056
|
9,57531
|
|
2
|
10,2
|
3,863
|
-0,59882
|
8,32555
|
0,78744
|
9,90043
|
0,08974
|
|
3
|
4
|
3,884
|
0,07358
|
7,69414
|
0,6724
|
9,71134
|
32,6194
|
|
4
|
8,6
|
4,591
|
0,75124
|
8,43132
|
0,67765
|
11,1419
|
6,46147
|
|
5
|
7,5
|
5,028
|
1,39269
|
8,66249
|
0,64145
|
11,8697
|
19,0947
|
|
6
|
4,4
|
4,933
|
1,9238
|
7,9431
|
0,53111
|
11,1298
|
45,2899
|
|
7
|
5
|
4,943
|
2,37675
|
7,51012
|
0,45294
|
10,6807
|
32,2707
|
|
8
|
5,9
|
5,087
|
2,78327
|
7,39056
|
0,40653
|
10,6428
|
22,4938
|
|
9
|
2,8
|
4,744
|
3,07736
|
6,4104
|
0,29409
|
9,05721
|
39,1527
|
|
10
|
22,7
|
7,437
|
3,73135
|
11,1432
|
0,65399
|
17,6831
|
25,1689
|
|
11
|
13,6
|
8,362
|
4,42591
|
12,2975
|
0,69455
|
19,9376
|
40,1649
|
|
12
|
18,9
|
9,942
|
5,25339
|
14,6315
|
0,82748
|
24,5613
|
32,0501
|
|
13
|
13,7
|
10,51
|
6,04129
|
14,9709
|
0,7879
|
25,2136
|
132,563
|
|
14
|
11,5
|
10,66
|
6,73337
|
14,577
|
0,69208
|
24,2661
|
162,973
|
|
15
|
11,7
|
10,81
|
7,34515
|
14,2786
|
0,61178
|
23,4553
|
138,187
|
|
16
|
7,2
|
10,27
|
7,78389
|
12,7563
|
0,43874
|
19,7762
|
158,161
|
|
17
|
4,2
|
9,36
|
8,02025
|
10,6989
|
0,23635
|
14,717
|
110,607
|
|
18
|
17,9
|
10,64
|
8,41331
|
12,868
|
0,39306
|
19,9431
|
4,17421
|
|
19
|
8,6
|
10,33
|
8,7015
|
11,9676
|
0,28819
|
17,4432
|
78,2016
|
|
20
|
27,2
|
12,86
|
9,32593
|
16,4028
|
0,62443
|
28,8914
|
2,86098
|
|
21
|
15,7
|
13,29
|
9,9205
|
16,6589
|
0,59457
|
29,1449
|
180,765
|
|
22
|
25,2
|
15,08
|
10,6939
|
19,4587
|
0,77336
|
36,4727
|
127,073
|
|
23
|
21,5
|
16,04
|
11,4958
|
20,5839
|
0,80189
|
39,0274
|
307,211
|
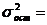 81,2957
81,2957
·
для
параболической формы зависимости:
|
t
|
Yt
|
S1
|
S2
|
S3
|
a0
|
a1
|
a2
|
Y2
|
(Y-Y2)^2
|
|
0
|
|
13,302
|
20,3967
|
29,996
|
8,712
|
-0,329
|
0,078
|
|
|
|
1
|
10,7
|
12,9117
|
19,2739
|
28,38769
|
9,301023
|
-0,10877
|
0,085688
|
9,27794
|
2,022242912
|
|
2
|
10,2
|
12,5049
|
18,2586
|
26,86832
|
9,607431
|
0,037167
|
0,088945
|
10,0375
|
0,02639209
|
|
3
|
4
|
11,2292
|
17,2042
|
25,4187
|
7,4938
|
-0,2291
|
0,069744
|
7,4342
|
11,79371999
|
|
4
|
8,6
|
10,8348
|
16,2488
|
24,04321
|
7,801375
|
-0,07816
|
0,074133
|
8,67486
|
0,005604698
|
|
5
|
7,5
|
10,3346
|
15,3616
|
22,74097
|
7,659845
|
-0,02028
|
0,073255
|
9,38982
|
3,571422029
|
|
6
|
4,4
|
9,44441
|
14,4741
|
21,50094
|
6,411993
|
-0,15158
|
0,062198
|
7,74162
|
11,16640634
|
|
7
|
5
|
8,77775
|
13,6196
|
20,31874
|
5,793149
|
-0,17002
|
0,057839
|
7,43709
|
5,939399069
|
|
8
|
5,9
|
8,34609
|
12,8286
|
19,19521
|
5,747725
|
-0,0967
|
0,058676
|
8,72934
|
8,005180113
|
|
9
|
2,8
|
7,51417
|
12,0314
|
18,12065
|
4,568902
|
-0,21787
|
0,048954
|
6,57338
|
14,23838782
|
22,7
|
9,79205
|
11,6955
|
17,15688
|
11,44647
|
0,975221
|
0,110799
|
32,2786
|
91,75003575
|
|
11
|
13,6
|
10,3632
|
11,4957
|
16,3077
|
12,91039
|
1,156132
|
0,114589
|
39,4931
|
670,4548368
|
|
12
|
18,9
|
11,6438
|
11,5179
|
15,58922
|
15,96683
|
1,568934
|
0,130709
|
53,6161
|
1205,208132
|
|
13
|
13,7
|
11,9522
|
11,583
|
14,98829
|
16,09577
|
1,456066
|
0,117543
|
54,8893
|
1696,561295
|
|
14
|
11,5
|
11,8844
|
11,6282
|
14,48429
|
15,25268
|
1,192078
|
0,096919
|
50,9379
|
1555,351546
|
|
15
|
11,7
|
11,8567
|
11,6625
|
14,06102
|
14,64363
|
0,989721
|
0,080742
|
47,6564
|
1292,86491
|
|
16
|
7,2
|
11,1582
|
11,5869
|
13,68989
|
12,40393
|
0,541384
|
0,052143
|
34,4148
|
740,6439767
|
|
17
|
4,2
|
10,1145
|
11,366
|
13,34131
|
9,586726
|
0,045865
|
0,02254
|
16,8805
|
160,7941429
|
|
18
|
17,9
|
11,2823
|
11,3534
|
13,04313
|
12,8297
|
0,583897
|
0,050404
|
39,6709
|
473,9709786
|
|
19
|
8,6
|
10,88
|
11,2824
|
12,77902
|
11,57163
|
0,332179
|
0,034073
|
30,1836
|
465,8496607
|
|
20
|
27,2
|
13,328
|
11,5893
|
12,60056
|
17,81669
|
1,320245
|
0,085641
|
78,4778
|
2629,416401
|
|
21
|
15,7
|
13,6838
|
11,9034
|
12,49599
|
17,837
|
1,188619
|
0,073896
|
75,3863
|
3562,457862
|
|
22
|
25,2
|
15,4112
|
12,4296
|
12,48603
|
21,43085
|
1,645721
|
0,09461
|
103,428
|
6119,633042
|
|
23
|
21,5
|
16,3245
|
13,0138
|
12,5652
|
22,49726
|
1,63894
|
0,08913
|
107,342
|
7368,934436
|
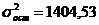 .
.
5. Составим уравнение прогноза:
для линейной формы зависимости: 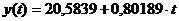 ;
;
·
для
параболической формы зависимости:
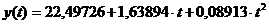 .
.
Приведем графическую иллюстрацию сглаживания:
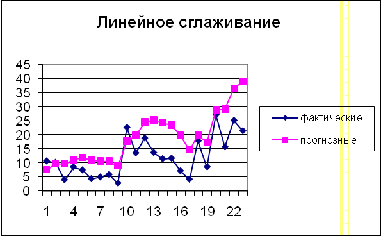
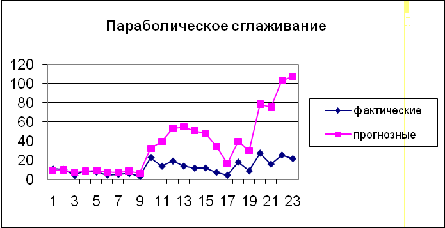
Как видно из таблиц, наименьшую остаточную
вариацию имеет функция линейного выравнивания, она лучше описывает исходные
данные. Значит, оценочные результаты этого случая могут использоваться для
прогнозирования.
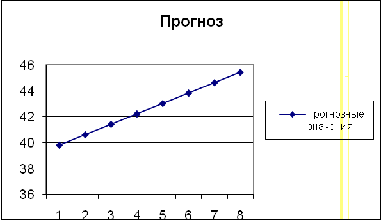
Получили следующие прогнозные значения:
|
t
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
|
ŷ
|
39,8293
|
40,6312
|
41,4331
|
42,23502
|
43,0369
|
43,8389
|
44,6407
|
45,44259
|
Проиллюстрируем результат:
Задание 4
Произвести выравнивание динамического ряда при
помощи рядов Фурье.
В качестве функций выравнивания возьмем первые
три гармоники ряда Фурье:
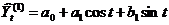 ;
;
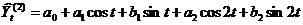 ;
;
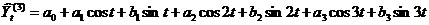 ,
,
где 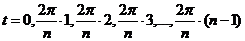 .
.
Коэффициенты функций выравниваний
найдем с помощью формул:
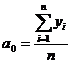 ;
; 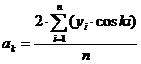 ;
; 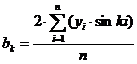 ;
;
Рассчитанные коэффициенты гармоник
ряда Фурье выглядят следующим образом:
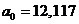 ;
; 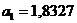 ;
; 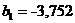 ;
; 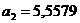 ;
; 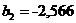 ;
; 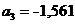 ;
; 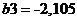 .
.
Получим динамический ряд выровненный
с помощью рядов Фурье:
|
t
|
Y
|
Y1
|
Y2
|
Y3
|
|
1
|
10,7
|
12,870
|
16,285
|
13,682
|
|
2
|
10,2
|
11,734
|
12,013
|
10,019
|
|
3
|
4
|
10,626
|
7,687
|
7,570
|
|
4
|
8,6
|
9,629
|
4,328
|
6,161
|
|
5
|
7,5
|
8,817
|
2,697
|
5,316
|
|
6
|
4,4
|
8,249
|
3,093
|
4,835
|
|
7
|
5
|
7,968
|
5,277
|
5,036
|
|
8
|
5,9
|
7,995
|
8,552
|
6,481
|
|
9
|
2,8
|
8,328
|
11,971
|
9,384
|
|
10
|
22,7
|
8,942
|
14,611
|
13,150
|
|
11
|
13,6
|
9,791
|
15,835
|
16,428
|
|
12
|
18,9
|
10,813
|
15,472
|
17,742
|
|
13
|
13,7
|
11,931
|
13,849
|
16,355
|
|
14
|
11,5
|
13,063
|
11,682
|
12,832
|
|
15
|
11,7
|
14,126
|
9,846
|
8,911
|
|
16
|
7,2
|
15,039
|
9,108
|
6,681
|
|
17
|
4,2
|
15,735
|
9,880
|
7,502
|
|
18
|
17,9
|
16,164
|
12,088
|
11,269
|
|
19
|
8,6
|
16,292
|
15,183
|
16,443
|
|
20
|
27,2
|
16,110
|
18,291
|
20,830
|
|
21
|
15,7
|
15,633
|
20,468
|
22,674
|
|
22
|
25,2
|
14,894
|
20,976
|
21,449
|
|
23
|
21,5
|
13,950
|
19,508
|
17,947
|
Проиллюстрируем выравнивание:
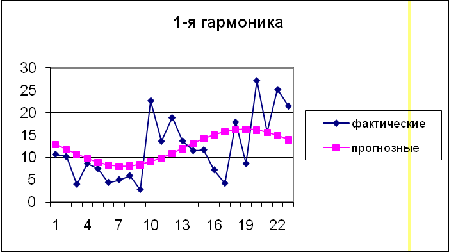
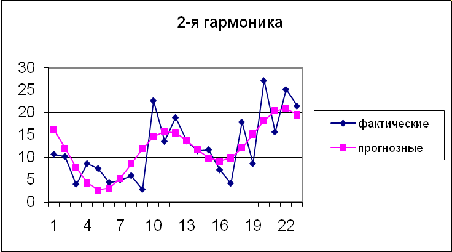
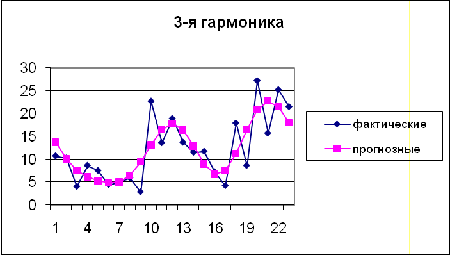
Исходя из диаграмм, видно, что наиболее
приближена к исходным данным гармоника 3-го порядка. Проверим это аналитически,
для чего найдем значения дисперсии ошибок, стандартного отклонения и уровня
корреляции. Рассчитанные данные сведены в таблицу:
|
1-я
гармоника
|
2-я
гармоника
|
3-я
гармоника
|
|
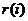 0,313060,69930,75428 0,313060,69930,75428
|
|
|
|
|
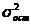 44,566225,246421,2983 44,566225,246421,2983
|
|
|
|
|
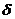 6,6757895,0245754,615009 6,6757895,0245754,615009
|
|
|
|
Как видно из представленной таблицы, лучше всего
из предложенных зависимостей к исходным данным подогнана гармоника 3-го
порядка. Она имеет довольно большую тесноту связи, меньшие остаточную вариацию
и стандартное отклонение. Хуже всего подогнана гармоника 1-го порядка. Выводы,
сделанные на основе графиков, подтвердились. Выравнивание на основе
использования ряда Фурье с использованием гармоники 3-го порядка можно признать
достоверным, его оценочные результаты будем использовать для прогнозирования.
Найдем значения 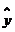 при t=24, 25, …,
31 и сведем полученные результаты в таблицу:
при t=24, 25, …,
31 и сведем полученные результаты в таблицу:
|
t
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
|
ŷ
|
13,681
|
10,0194
|
7,5697
|
6,16095
|
5,3164
|
4,8354
|
5,0362
|
6,48105
|
Проиллюстрируем полученные значения прогноза:
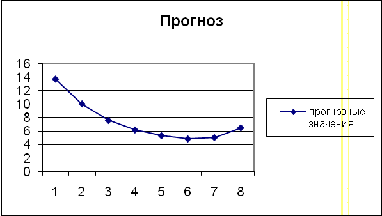
Вывод
Сравним функции, выбранные в качестве лучших по
результатам исследований в ходе выполнения четырех заданий. Это линейное
выравнивание исходного ряда, линейное выравнивание скользящих средних, линейное
сглаживание динамического ряда, ряд Фурье с гармоникой 3-го порядка. Лучшие
значения оценок (меньшая дисперсия и большая теснота связи) имеет ряд Фурье с
гармоникой 3-го порядка. Это же можно сказать, исходя из приведенных графиков.
Таким образом, будем считать наиболее приближенной функцией ряд Фурье, а
наиболее достоверным прогнозом - прогноз, выполненный по параметрам этой
функции.
Таким образом получили сравнительно
незначительно колеблющиеся данные для прогноза на будущие 8 лет, но в целом
урожайность озимой пшеницы возрастает с течением времени. А прогнозные данные
не сильно отличаются по своим значениям от исходных данных.