Изучение критерия Колмогорова–Смирнова и сравнение его с другими критериями согласия
Введение
Критерий согласия - это критерий проверки
гипотезы о предполагаемом законе распределения генеральной совокупности.
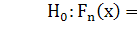
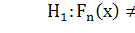
где - эмпирическая функция распределения вероятностей;
- эмпирическая функция распределения вероятностей;  -
гипотетическая функция распределения вероятностей [1].
-
гипотетическая функция распределения вероятностей [1].
В статистике критерий согласия Колмогорова -
Смирнова используется для того, чтобы определить, подчиняются ли два
эмпирических распределения одному закону, либо определить, подчиняется ли
полученное распределение предполагаемой модели [2].
Модифицированные статистики критерия
Колмогорова-Смирнова позволяют применять их в некоторых частных случаях и для
ситуации с неизвестными параметрами гипотетических распределений [3].
Критерий Колмогорова - Смирнова является одним
из основных и наиболее широко используемых непараметрических методов, так как
достаточно чувствителен к различиям в исследуемых выборках[4].
Целью данной курсовой работы является изучение
критерия согласия типа Колмогорова-Смирнова, сравнение с другими критериями
согласия: Пирсона и  ; и исследование
его асимптотических свойств.
; и исследование
его асимптотических свойств.
1. Критерии согласия
1.1 Критерий
Колмогорова-Смирнова
Пусть  -эмпирическая
функция распределения случайной величины
-эмпирическая
функция распределения случайной величины  , представленной
выборкой
, представленной
выборкой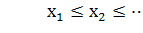 :
:
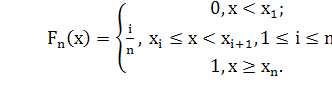
Для проверки нулевой гипотезы 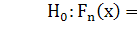 ,
где
,
где  -полностью
определенная (с точностью до параметров) теоретическая функция распределения,
рассматривается расстояние между эмпирической и теоретической функциями
распределения
-полностью
определенная (с точностью до параметров) теоретическая функция распределения,
рассматривается расстояние между эмпирической и теоретической функциями
распределения
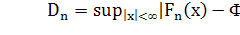
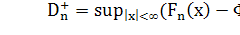
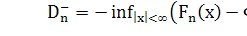
Здесь  -точные
верхняя и нижняя границы соответствующих разностей.
-точные
верхняя и нижняя границы соответствующих разностей.
Для практического применения используются формулы
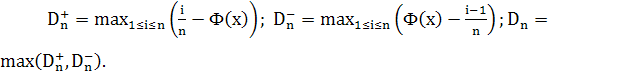
Колмогорованашел предельное распределение
статистики  (при
(при  )[3].
Если верна гипотеза
)[3].
Если верна гипотеза  , то независимо от
функции
, то независимо от
функции  ,
случайная величина
,
случайная величина  имеет
распределение Колмогорова [5]:
имеет
распределение Колмогорова [5]:
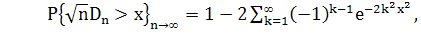
Смирнов развил результаты Колмогорова на случай
статистик  .
.
Между критическими значениями 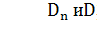 существует
соотношение
существует
соотношение 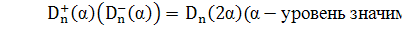 .
.
В качестве первого приближения можно
использовать соотношение
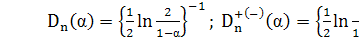
Если 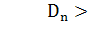 ,
гипотеза согласия (
,
гипотеза согласия ( ) отклоняется на
уровне значимости
) отклоняется на
уровне значимости  .
.
При  полезна
аппроксимация
полезна
аппроксимация
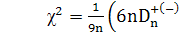
распределениекоторой удовлетворительно
описывается распределением хи-квадрат с  степенями
свободы.
степенями
свободы.
При  необходимо
использовать более точное приближение
необходимо
использовать более точное приближение
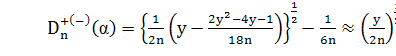
где 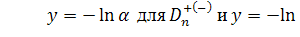 для
для
 ,
при
,
при 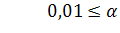 и
и
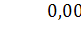 .
Наиболее просты в приложениях результаты Стефенса, который предложил
преобразования статистик
.
Наиболее просты в приложениях результаты Стефенса, который предложил
преобразования статистик 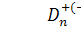 устанавливающие
зависимость их процентных точек
устанавливающие
зависимость их процентных точек 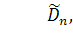 от объема выборки
от объема выборки  :
:
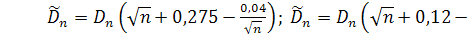
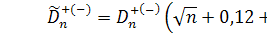
Первые две аппроксимации используются
соответственно для нижних и верхних процентных точек. Критические значения
статистик Стефенса приведены в таблице 1.1[3].
Таблица 1.1 - Процентные точки статистик 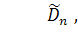
|
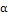
|
0,150
|
0,100
|
0,050
|
0,025
|
0,010
|
|
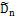
|
0,973
|
1,073
|
1,224
|
1,358
|
1,518
|
|
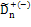
|
1,138
|
1,224
|
1,358
|
1,480
|
1,628
|
.2 Критерий Пирсона
Критерий основан на сравнении эмпирической
гистограммы распределения случайной величины с ее теоретической плотностью.
Диапазон изменения экспериментальных данных разбивается на интервалов,
и подсчитывается статистика
интервалов,
и подсчитывается статистика
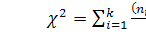
где  -
количество значений случайной величины, попавших в -й интервал;
-
количество значений случайной величины, попавших в -й интервал; 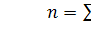 -
объем выборки;
-
объем выборки;  - гипотетический
теоретический закон распределения вероятностей случайной величины;
- гипотетический
теоретический закон распределения вероятностей случайной величины; 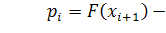 -
теоретическая вероятность попадания случайной величины в
-
теоретическая вероятность попадания случайной величины в  -й
интервал.
-й
интервал.
Дисперсия статистики критерия  равна
равна
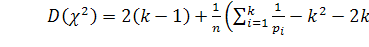
Если 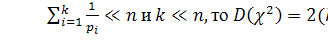 ,
т.е. совпадает с дисперсией случайной величины, имеющей
,
т.е. совпадает с дисперсией случайной величины, имеющей  -распределение.
На этом основании принято считать, что статистика
-распределение.
На этом основании принято считать, что статистика  имеет
распределение, близкое к распределению хи-квадрат.
имеет
распределение, близкое к распределению хи-квадрат.
На мощность статистического критерия  сильное
влияние оказывает число интервалов разбиения гистограммы
сильное
влияние оказывает число интервалов разбиения гистограммы и
порядок ее разбиения (т.е. выбор длин интервалов внутри диапазона изменения
значений случайной величины). На практике принято считать, что статистику
и
порядок ее разбиения (т.е. выбор длин интервалов внутри диапазона изменения
значений случайной величины). На практике принято считать, что статистику  можно
использовать, когда
можно
использовать, когда 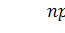
Так или иначе, статистика  имеет
распределение хи-квадрат с
имеет
распределение хи-квадрат с 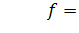 степенями свободы в
том случае, когда проверяется простая гипотеза
степенями свободы в
том случае, когда проверяется простая гипотеза  ,
т.е., когда гипотетическое распределение, на соответствие которому проверяется
эмпирический ряд данных, известно с точностью до значения своих параметров.
Если гипотеза сложная и параметры гипотетического распределения оцениваются по
самой выборке, то число степеней свободы уменьшается на число оцениваемых
параметров
,
т.е., когда гипотетическое распределение, на соответствие которому проверяется
эмпирический ряд данных, известно с точностью до значения своих параметров.
Если гипотеза сложная и параметры гипотетического распределения оцениваются по
самой выборке, то число степеней свободы уменьшается на число оцениваемых
параметров  .
.
Правило проверки гипотезы просто: если
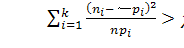
то на уровне значимости  ,
т.е. с достоверностью
,
т.е. с достоверностью  гипотеза
гипотеза  отклоняется
[3].
отклоняется
[3].
1.3 Критерий Смирнова-Крамера-фон
Мизеса
Статистика критерия имеет вид
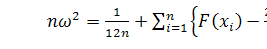
Необходимо помнить, что теоретическая функция
распределения должна быть известна с точностью до параметров. Распространенная
ошибка - использование в качестве  функции
распределения с параметрами, оцениваемыми по выборке - приводит к уменьшению
величины критического значения статистики, т.е. к увеличению количества ошибок
второго рода[6]. При объеме выборки
функции
распределения с параметрами, оцениваемыми по выборке - приводит к уменьшению
величины критического значения статистики, т.е. к увеличению количества ошибок
второго рода[6]. При объеме выборки  можно
использовать приведенные в таблице 1.2 квантили распределения
можно
использовать приведенные в таблице 1.2 квантили распределения  ,
которые следуют из его предельного распределения (
,
которые следуют из его предельного распределения ( - уровень значимости, принятый для проверки
- уровень значимости, принятый для проверки  ).
).
Таблица 1.2 - Квантили распределения 
|
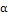
|
0,100
|
0,050
|
0,010
|
0,005
|
0,001
|
|
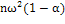
|
0,3473
|
0,4614
|
0,7435
|
0,8694
|
1,1679
|
При  таблицей
можно пользоваться с заменой
таблицей
можно пользоваться с заменой  на
на
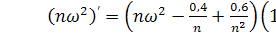
Небходимо отметить, что и критерий  и
критерий Колмогорова-Смирнова подсчитывается по негруппированным выборкам (в
отличие от критерия
и
критерий Колмогорова-Смирнова подсчитывается по негруппированным выборкам (в
отличие от критерия  ) [3].
) [3].
2. Проверка
гипотез о виде распределения
Для проверки гипотезы о виде распределения
смоделированы выборки из генеральных совокупностей, имеющих следующие законы
распределения: экспоненциальное, степенное и распределение Парето.
2.1 Экспоненциальное
распределение
Случайная величина  имеет
экспоненциальное (показательное) распределение с параметром
имеет
экспоненциальное (показательное) распределение с параметром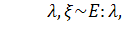 ,
если функция распределения имеет вид:
,
если функция распределения имеет вид:
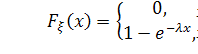
а плотность распределения:
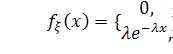
Математическое ожидание равно 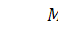 .
.
Дисперсия случайной величины равна  .
.
Плотность и функция показательного распределения
случайной величины с параметром  представлены на
рисунках 2.1 и 2.2 [7].
представлены на
рисунках 2.1 и 2.2 [7].
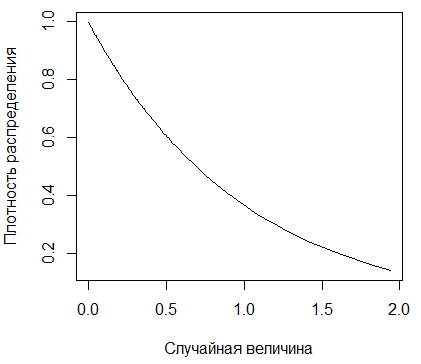
Рисунок 2.1 - График плотности экспоненциального
распределения с параметром 
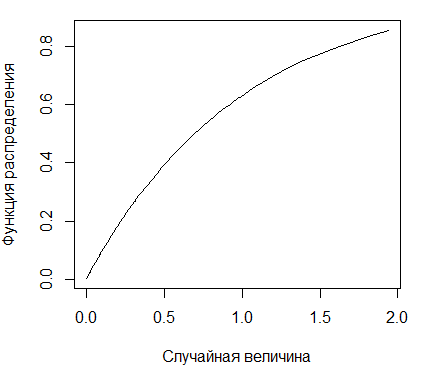
Рисунок 2.2 - График функции экспоненциального
распределения с параметром 
2.2 Степенное
распределение
Случайная величина  имеет
степенное распределение с параметром
имеет
степенное распределение с параметром 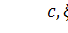 ,
если функция распределения имеет вид:
,
если функция распределения имеет вид:
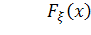
а плотность распределения[8]:
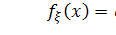
Область значения 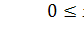
Математическое ожидание равно 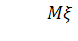
Дисперсия случайной величины равна 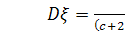 [9].
[9].
Плотность и функция степенного распределения
случайной величины с параметром  представлены на
рисунках 2.3 и 2.4.
представлены на
рисунках 2.3 и 2.4.
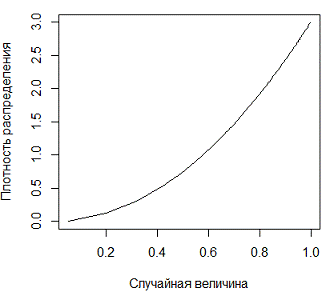
Рисунок 2.3 - График плотности степенного
распределения с параметром 
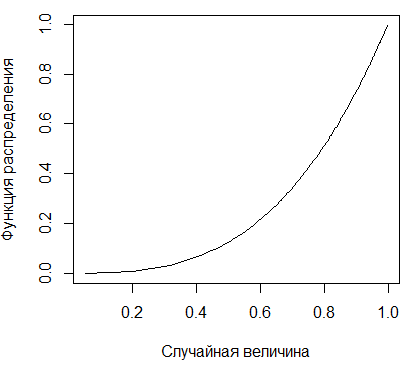
Рисунок 2.4 - График функции степенного
распределения с параметром 
2.3 Распределение Парето
Случайная величина  имеет
распределение Парето с параметром
имеет
распределение Парето с параметром 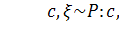 ,
если функция распределения имеет вид:
,
если функция распределения имеет вид:
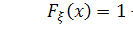
а плотность распределения
[8]:
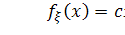
критерий согласие
колмогоров смирнов
Область значения 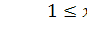
Математическое ожидание равно
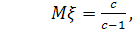
Дисперсия случайной величины равна
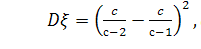 [10].
[10].
Плотность и функция степенного распределения
случайной величины с параметром  представлены на
рисунках 2.5 и 2.6.
представлены на
рисунках 2.5 и 2.6.
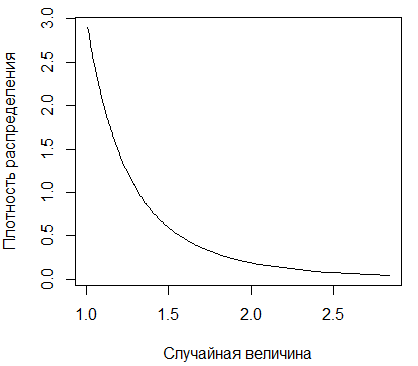
Рисунок 2.5 - График плотности распределения
Парето с параметром 
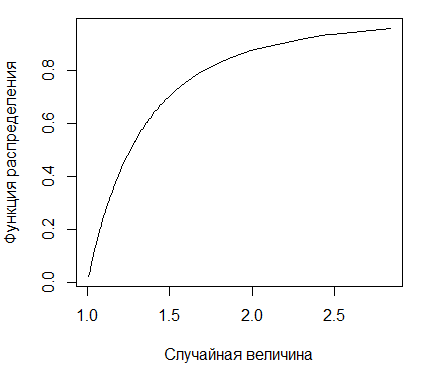
Рисунок 2.6 - График функции распределения
Парето с параметром 
2.4 Результаты проверки гипотезы
о виде распределения
Смоделировав выборки объемом 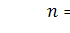 из
генеральных совокупностей, имеющих вышеуказанные законы распределения с
известными параметрами, проведена проверка гипотезы о виде распределения
методами типа Колмогорова-Смирнова и Пирсонанауровне значимости
из
генеральных совокупностей, имеющих вышеуказанные законы распределения с
известными параметрами, проведена проверка гипотезы о виде распределения
методами типа Колмогорова-Смирнова и Пирсонанауровне значимости 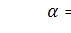 .
Результаты проверки представлены в виде таблицы 2.1.
.
Результаты проверки представлены в виде таблицы 2.1.
Таблица 2.1 - Результаты проверки гипотез о виде
распределения двумя методами
|
Критерии
согласии
|
законы
распределения
|
|
экспоненциальное
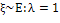
|
степенное
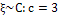
|
Парето
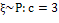
|
|
Колмогорова-Смирнова
|
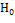
|
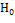
|
|
Пирсона
|
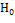
|
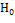
|
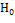
|
Из полученной таблицы следует, что критерии
согласия Колмогорова-Смирнова и Пирсона не противоречат друг другу.
Для сравнения критерий Колмогорова-Смирнова и  на
чувствительность к объему выборки и степени различия параметров распределения
рассмотрена выборка, имеющая экспоненциальное распределение.Графики зависимости
статистик критерий от объема выборки
на
чувствительность к объему выборки и степени различия параметров распределения
рассмотрена выборка, имеющая экспоненциальное распределение.Графики зависимости
статистик критерий от объема выборки  представлены
на рисунках 2.7-2.8.Графики изменения статистик критерий при изменении
параметра экспоненциального распределения
представлены
на рисунках 2.7-2.8.Графики изменения статистик критерий при изменении
параметра экспоненциального распределения  представлены
на рисунках 2.9-2.10.
представлены
на рисунках 2.9-2.10.
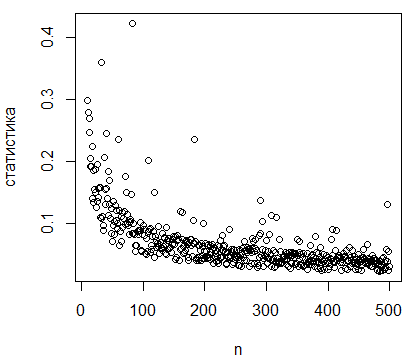
Рисунок 2.7 - График изменения статистики  при
различных объемах выборки
при
различных объемах выборки
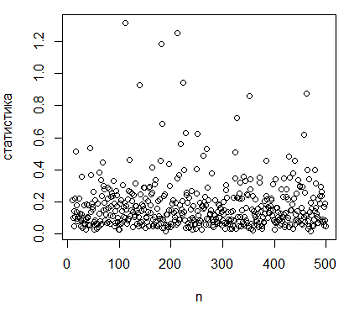
Рисунок 2.8 - График изменения статистики  при
различных объемах выборки
при
различных объемах выборки 
По полученным графикам видно, что статистика
критерия Колмогорова при увеличении объема выборки стремится к нулю, статистика
критерию  увеличивается
с увеличением объема выборки.
увеличивается
с увеличением объема выборки.
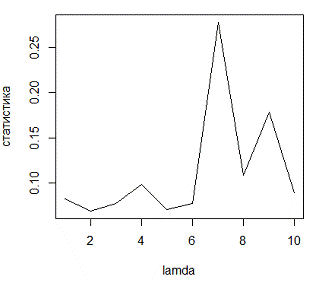
Рисунок 2.9 - График изменения статистики  при
различных значениях параметра
при
различных значениях параметра
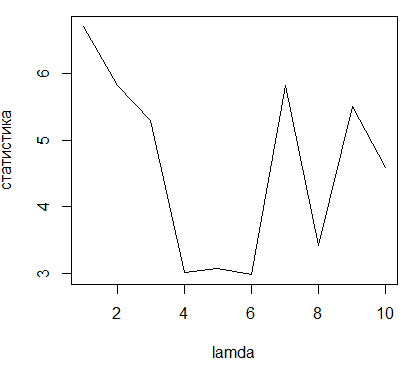
Рисунок 2.10 - График изменения статистики  при
различных значениях параметра
при
различных значениях параметра
Отсюда следует, что статистика критерия  и
статистика критерия Колмогорова-Смирнова не зависят от параметра распределения.
и
статистика критерия Колмогорова-Смирнова не зависят от параметра распределения.
3. Асимптотические
свойства критерия
Для проверки асимптотических свойств критерия
типа Колмогорова-Смирнова проведена кратную
проверку гипотезы о распределении,
кратную
проверку гипотезы о распределении, 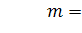 ,
при различных объемах выборки
,
при различных объемах выборки  . Графики
теоретической и эмпирической функций распределения Колмогорова представлены на
рисунках 3.1-3.3.
. Графики
теоретической и эмпирической функций распределения Колмогорова представлены на
рисунках 3.1-3.3.
По полученным графикам видно, что при увеличении
объема выборки  эмпирическая
функция распределения Колмогорова стремиться к теоретической функции
распределения.
эмпирическая
функция распределения Колмогорова стремиться к теоретической функции
распределения.
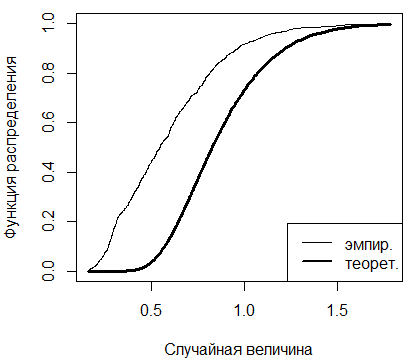
Рисунок 3.1 - Графики теоретической и
эмпирической функций распределения Колмогорова при 
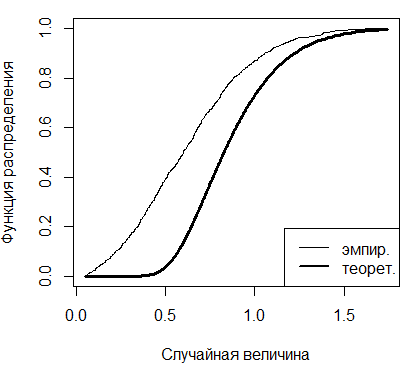
Рисунок 3.2 - Графики теоретической и
эмпирической функций распределения Колмогорова при 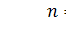
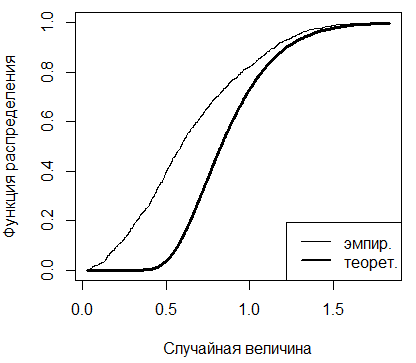
Рисунок 3.3 - Графики теоретической и
эмпирической функций распределения Колмогорова при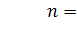
Заключение
В данной курсовой работе был изучен критерий
согласия типа Колмогорова-Смирнова. И также рассмотрены критерии согласия
Пирсона и  .
.
В ходе выполнения данной курсовой работы
былисмоделированы выборки из генеральных совокупностей, имеющих различные
законы распределения: экспоненциальное, Парето, степенное; и проверены гипотезы
о виде распределения методами типа Колмогорова-Смирнова и Пирсона.
Проведено сравнение критерия Колмогорова с
критерием  на чувствительность
к объему выборки и степени различия параметров распределения.
на чувствительность
к объему выборки и степени различия параметров распределения.
Исследованы асимптотические свойства критерия
согласия.
Полученные в ходе исследования выводы говорят о
том, что критерий согласия Колмогорова используется только в случае
непрерывного распределения, в отличие от критерия согласия Пирсона, и не
зависит от параметров распределения, но зависит от объема выборки.
В процессе исследования был использован пакет
статистического анализа данных R.