Решение задачи Неймана для уравнения Пуассона в прямоугольной области
Курсовая работа
«Решение задачи Неймана для уравнения Пуассона в прямоугольной
области»
Содержание
Введение
Аннотация
. Численная постановка задачи
. Решение заданного примера
. Листинг программы
. Результаты работы программы
Литература
Введение
Актуальность решения уравнения
Пуассона состоит в том что, при вычислении решения системы уравнений
Навье-Стокса, алгоритм решения этой системы происходит в несколько этапов одним
из сложных является решение уравнения Пуассона.
Аннотация
Разработать программу для решения
дифференциального уравнения Лапласа:
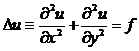
в прямоугольной области ABCD, с вершинами A(0;0),
B(0:1), C(1;1), D(1,0), шагом h=l/n, где n-количество узлов,
принимающее условия Дирихле на всех границах кроме правой (на правой поставлено
условие Неймана). Уравнение решается методом сеток, c
точностью ε= 0,0000001. Программа разработана на языке C++.
1. Численная постановка задачи
Уравнение Лапласа является модельным
для эллиптических уравнений в частных производных.
Некоторые важные задачи, часто
встречающиеся в приложениях, сводятся к решению одного эллиптического
уравнения. К ним относятся задачи расчета дозвукового безвихревого
(потенциального) течения газа и определения стационарного поля температуры в
твердом теле.
В данной работе требуется решить,
конечно - разностную задачу Дирихле или Неймана для уравнения Лапласа в
прямоугольной области т. е. найти непрерывную функцию u(х,у), удовлетворяющую внутри
многоугольной области
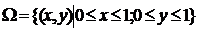уравнению Лапласа
(1)
и принимающую на границе
области W
заданные значения, т. е.
,
,
,
,
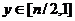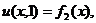
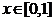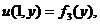
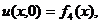
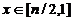где f1=0, f2=0,
f3=0, f4=0.
Будем считать, что u(х,у) непрерывна на границе области W,
т. е.
,
,
,
.
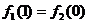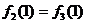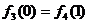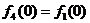Выбрав шаги h, l по x и y соответственно, строим
сетку:
, 
,
,
,
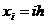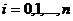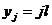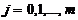где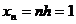 
,
.
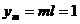Вводя обозначения
,
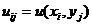аппроксимируем частные
производные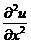 
и
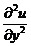в
каждом внутреннем узле сетки центральными разностными производными второго
порядка
,
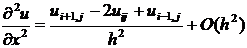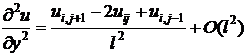
и заменим уравнение Лапласа
конечно-разностным уравнением
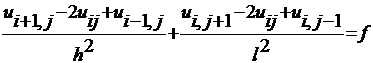, (2)
, 
.
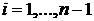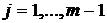Погрешность замены
дифференциального уравнения разностным, составляет величину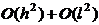 
.
Уравнения (2) вместе со
значениями 
в
граничных узлах образуют систему линейных алгебраических уравнений относительно
приближенных значений функции и(х, у) в узлах сетки 
.
Наиболее простой вид имеет эта система при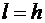 
:
, 
,
,
,
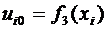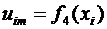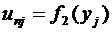(3)
, 
.
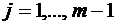При получении сеточных уравнений (3)
была использована схема узлов. Набор узлов,
используемых для аппроксимации уравнения в точке, называется шаблоном. В данной
работе используется шаблон типа «крест».
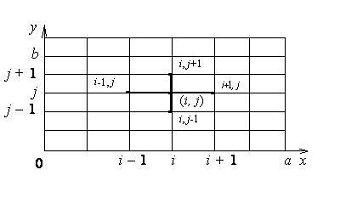
Численное решение задачи
Дирихле для уравнения Лапласа в многоугольнике состоит в нахождении
приближенных значений искомой
функции u(х,у) во внутренних узлах сетки. Для определения величин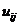 
требуется
решить систему линейных алгебраических уравнений (3).
В данной работе она решается методом минимальных невязок, который состоит в построении
последовательности итераций вида:
,
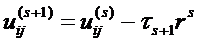где 
-
невязка
- итерационный параметр
(верхним индексом s обозначен номер итерации). При 
последовательность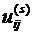 
сходится
к точному решению системы (3). В качестве условия окончания итерационного
процесса можно принять
.
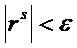Таким образом, погрешность
приближенного решения, полученного методом сеток, складывается из двух
погрешностей: погрешности аппроксимации дифференциального уравнения разностными
значениями; погрешности, возникающей в результате приближенного решения системы
разностных уравнений (3).
Известно, что описанная
здесь разностная схема обладает свойством устойчивости и сходимости.
Устойчивость схемы означает, что малые изменения в начальных данных приводят к
малым изменениям решения разностной задачи. Только такие схемы имеет смысл
применять в реальных вычислениях. Сходимость схемы означает, что при стремлении
шага сетки к нулю (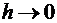
)
решение разностной задачи стремится к решению исходной задачи. Таким образом,
выбрав достаточно малый шаг h,
можно как угодно точно решить исходную задачу.
Пример решения такой
задачи Дирихле, приведен в решении заданного примера.
. Решение заданного
примера
программа уравнение
лаплас прямоугольный
Используя метод сеток,
составить приближенное решение задачи Дирихле для уравнения Лапласа (1).
Решение получить в
квадрате ABCD, с вершинами A(0;0),
B(0:1), C(1;1), D(1,0) шагом h=l/n, где n-количество узлов,
принимающее условия Дирихле на всех границах кроме правой (на правой границе
поставлено условие Неймана).
; 
;
;
.
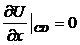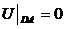Систему линейных
алгебраических уравнений решить по методом минимальных невязок, при ε=0,0000001.
1) Построим сетку с шагом h=l=0,2
2. Построим итерационный процесс
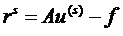
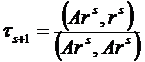
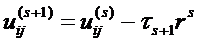
В виде начального
приближения возьмем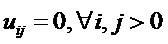 
,
условия окончания
итерационного процесса: .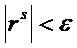
. Листинг программы
#define _USE_MATH_DEFINES
#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <iostream>
#include<windows.h>namespace
std;
//объявление типов точек области
начало
#define FictivePoint 0 //не
расчетная точка
#define ActualPoint 1 //расчетная
точка
#define TopPoint 2 //точка
на верхней границе
#define RightPoint 3 //точка
на правой границе
#define BottomPoint 4 //точка
на нижней границе
#define LeftPoint 5 //точка
на левой границе
#define LeftBottomPoint 6 //точка
на выпуклом угле
//объявление типов точек области
конец*file;
//проверка на симетричность
началоSimetric(int n,double **M)
{
int k=0;
for(int i=0;i<n;i++)
{
for(int
j=0;j<n;j++)
{
if(M[i][j]==M[j][i])
{
k++;
}
}
}
if(k==n*n)
{
for(int i=0;i<n;i++)
{
for(int
j=0;j<n;j++)
{
if(M[i][j]==M[j][i])
{
if(i!=j)
{
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 2 ) ;
}
if(i==j)
{
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
}
cout<<M[i][j]<<"
";
}
}
cout<<endl;
}
SetConsoleTextAttribute (
GetStdHandle ( STD_OUTPUT_HANDLE ) , 2 ) ;
cout<<"Матрица
симетрична!"<<endl;
SetConsoleTextAttribute (
GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
}
if(k!=n*n)
{
for(int
i=0;i<n;i++)
{
for(int
j=0;j<n;j++)
{
if(M[i][j]==M[j][i])
{
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
cout<<M[i][j]<<"
";
}
if(M[i][j]!=M[j][i])
{
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 4 ) ;
cout<<M[i][j]<<"
";
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
}
}
cout<<endl;
}
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 4 ) ;
cout<<"Матрица
не симетрична!"<<endl;
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
}
return 0;
}
//проверка на симетричность
конец
//проверка на
знакоопределенность началоMore_then_0(int n,double **M)
{
double d;
SetConsoleTextAttribute (
GetStdHandle ( STD_OUTPUT_HANDLE ) , 9 ) ;
cout<<"Приводим
матрицу к треугольному виду..."<<endl;
SetConsoleTextAttribute (
GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
for(int k=0;k<n-1;k++)
{
for(int
i=k+1;i<n;i++)
{
if(M[k][k]==0)
{
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 4 ) ;
printf("Произошло
деление на 0!\nДля выхода нажмите любую клавишу...\n");
_getch();
exit(0);
}
else
{
d
= M[i][k]/M[k][k];
for(int
j=0;j<n;j++)
{
M[i][j]=M[i][j]-M[k][j]*d;
}
}
}
}
int z=0,p=0;
double DetM=1;
double *detM;
detM=new double[n];
SetConsoleTextAttribute (
GetStdHandle ( STD_OUTPUT_HANDLE ) , 9 ) ;
cout<<"Находим
главные миноры..."<<endl;
SetConsoleTextAttribute (
GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
for(int i=0;i<n;i++)
{
DetM*=M[i][i];
detM[i]=DetM;
printf("минор[%d]
= %lf\n",i+1,detM[i]);
}
for(int i=0;i<n;i++)
{
if(detM[i]>0)
{
z++;
}
}
if(z==n)
{
cout<<"Так
как все главные миноры имеют положительный знак то: "<<endl;
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 2 ) ;
cout<<"Матрица
положительно определена!"<<endl;
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
}
else
{
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 4 ) ;
cout<<"Матрица
не знакоопределена!"<<endl;
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 7 ) ;
}
return 0;
}
//проверка на знакоопределенность
конец
//оператор Пуассона началоA(int
n,int **mask, double **u, double **res_A)
{
double h=1./n;
for(int i=0; i<=n; i++)
{
for(int j=0;
j<=n; j++)
{
if(mask[i][j]==ActualPoint)
{
res_A[i][j]=
- ( (u[i+1][j]-2*u[i][j]+u[i-1][j]+u[i][j+1]-2*u[i][j]+u[i][j-1])/(h*h) );
}
if(mask[i][j]==RightPoint)
{
res_A[i][j]=
(u[i][j]-u[i-1][j])/(h*h);
}
if(mask[i][j]==TopPoint)
{
res_A[i][j]=
(u[i][j]-u[i][j-1])/(h*h);
}
if(mask[i][j]==BottomPoint)
{
res_A[i][j]=
(u[i][j]-u[i][j+1])/(h*h);
}
if(mask[i][j]==LeftPoint)
{
res_A[i][j]=
(u[i][j]-u[i+1][j])/(h*h);
}
if(mask[i][j]==LeftBottomPoint)
{
res_A[i][j]=-(u[i+1][j]-4*u[i][j]+u[i][j+1])/(h*h); }
}
}
//оператор Пуассона конец
//разность векторов началоSubstruction(int
n,int **mask,double **a,double **b,double **res_S)
{
for(int i=0; i<=n; i++)
{
for(int j=0;
j<=n; j++)
{
if(
mask[i][j]!=FictivePoint )
{
res_S[i][j]=a[i][j]-b[i][j];
}
}
}
}
//разность векторов конец
//умножение вектора на скаляр
началоScalar(int n, int **mask,double **a, double **b)
{
double tmp=0;
for(int i=0;i<=n;i++)
{
for(int
j=0;j<=n;j++)
{
if( mask[i][j]!=FictivePoint )
{
tmp=tmp+a[i][j]*b[i][j];
}
}
}
return tmp;
}
//умножение вектора на скаляр конец
//вычисление нормы вектора
началоNorm(int n, int **mask, double **a)
{
double tmp=0;
for(int i=0;i<=n;i++)
{
for(int
j=0;j<=n;j++)
{
if(
mask[i][j]!=FictivePoint )
{
tmp=tmp+a[i][j]*a[i][j];
}
}
}
tmp=sqrt(tmp);
return tmp;
}
//вычисление нормы вектора конец
//вывод началоprint(int n,double
**a, double *f)
{
fprintf(file,"\n");
for(int i=0; i<=n-1;
i++)
{
for(int j=0;
j<=n-1; j++)
{
fprintf(file,"%5.0lf
",a[i][j]);
}
fprintf(file,"|
%5.0lf\n",f[i]);
}
fprintf(file,"\n");
}
//вывод конец
//копирование вектора в вектор
началоcopy(int n, double **a, double **b)
{
for (int i=0;i<=n;i++)
{
for (int
j=0;j<=n;j++)
{
b[i][j]=a[i][j];
}
}
return 0;
}
//копирование вектора в вектор конец
main()
{
int n=0,**mask,count_it=0;
double **u,**u_accur,**f,
**res_S,**res_A,
norm_r=0,h,tau,
eps=0.00000001,
**A_u,**A_u_accur,
**A_u_u_accur,**r,
**z,**z_1d,*f_1d;
char
fname[]="out.txt"; //имя выходного файла
setlocale(LC_CTYPE,"Russian"); //ставим
русский язык консоли
printf("Введите
количество узлов сетки: ");//
scanf_s("%d",&n); //
n--; //
h=1./n; //вычисляем
шаг сетки
printf("Вывод данных в
файл %s...\n",fname);
file = fopen(fname,
"w");
//инициализация переменных
начало
mask=new int *[n+1];
u=new double *[n+1];
f=new double *[n+1];
res_S=new double *[n+1];
res_A=new double *[n+1];
A_u=new double *[n+1];
A_u_accur=new double
*[n+1];
A_u_u_accur=new double
*[n+1];
r=new double *[n+1];
z=new double *[n+1];
for(int i=0; i<=n; i++)
{
mask[i]=new int
[n+1];
u[i]=new double
[n+1];
u_accur[i]=new
double [n+1];
f[i]=new double
[n+1];
res_S[i]=new
double [n+1];
res_A[i]=new
double [n+1];
A_u[i]=new double
[n+1];
A_u_accur[i]=new
double [n+1];
A_u_u_accur[i]=new
double [n+1];
r[i]=new double
[n+1];
z[i]=new double
[n+1];
}
for(int i=0; i<=n; i++)
{
for(int j=0;
j<=n; j++)
{
mask[i][j]=0;
u[i][j]=0;
u_accur[i][j]=0;
f[i][j]=0;
res_S[i][j]=0;
res_A[i][j]=0;
z[i][j]=0;
}
}
//инициализация переменных
конец
//создание маски квадратной
области с вырезом и условием Дирихле на границах начало
int iStep, jStep;
iStep=n/2;
jStep=n/2;
for(int i=0; i<=n; i++)
{
for(int j=0;
j<=n; j++)
{
if((i>iStep)
|| ((i<=iStep)&&(j>jStep)))
{
mask[i][j]=ActualPoint;
}
if
(i==0) mask[i][j]=FictivePoint; //левая граница
if
(i==n) mask[i][j]=FictivePoint; //правая граница
if
(j==0) mask[i][j]=FictivePoint; //нижняя граница
if
(j==n) mask[i][j]=FictivePoint; //верхняя граница
}
}
//создание маски квадратной
области с вырезом и условием Дирихле на границах конец
//вывод маски начало
fprintf(file,"МАСКА
ОБЛАСТИ!\n");
for(int j=n; j>=0; j--)
{
for(int i=0;
i<=n; i++)
{
fprintf(file,"%d
",mask[i][j]);
}
fprintf(file,"\n");
}
//вывод маски конец
//вычисление u_accur, f в
зависимости от маски начало
for(int i=0; i<=n; i++)
{
for(int j=0;
j<=n; j++)
{
if
(mask[i][j]==ActualPoint)
{
u_accur[i][j]=sin(M_PI*i*h)*sin(M_PI*j*h);
f[i][j]
= -( -2*M_PI*M_PI*sin(M_PI*i*h)*sin(M_PI*j*h) );
}
if
(mask[i][j]==TopPoint)
{
u_accur[i][j]
= sin(M_PI*i*h)*sin(M_PI*j*h);
f[i][j]=-(M_PI*sin(M_PI*i*h)*cos(M_PI*j*h)/h);
}
if
(mask[i][j]==RightPoint)
{
u_accur[i][j]
= sin(M_PI*i*h)*sin(M_PI*j*h);
f[i][j]=-(M_PI*cos(M_PI*i*h)*sin(M_PI*j*h)/h);
}
if
(mask[i][j]==BottomPoint)
{
u_accur[i][j]
= sin(M_PI*i*h)*sin(M_PI*j*h);
f[i][j]=(M_PI*sin(M_PI*i*h)*cos(M_PI*j*h)/h);
}
if
(mask[i][j]==LeftPoint)
{
u_accur[i][j]
= sin(M_PI*i*h)*sin(M_PI*j*h);
f[i][j]=(M_PI*cos(M_PI*i*h)*sin(M_PI*j*h)/h);
}
if
(mask[i][j]==LeftBottomPoint)
{
u_accur[i][j]
=
sin(M_PI*i*h)*sin(M_PI*j*h);[i][j]=((M_PI*cos(M_PI*i*h)*sin(M_PI*j*h)/h)+(M_PI*cos(M_PI*j*h)*sin(M_PI*i*h)/h));
}
}
}
//вычисление u_accur, f в
зависимости от маски конец
int matrixSize=0;
for(int i=0; i<=n; i++)
{
for(int j=0;
j<=n; j++)
{
if(mask[i][j]!=FictivePoint)
{
matrixSize++;
}
}
}
z_1d=new double
*[matrixSize];
for(int i=0;
i<=matrixSize; i++)
{
z_1d[i]=new
double[matrixSize];
}
//Проверка сопряженности -
начало
int p=0,k=0;
for(int i=0; i<=n; i++)
{
for(int j=0;
j<=n; j++)
{
if(i>0)
{
z[i-1][n]=0;
z[i-1][n-1]=0;
z[2][1]=0;
z[2][2]=0;
}
if(mask[i][j]!=FictivePoint)
{
z[i][j-1]=0;
z[i][j]=1;
A(n,mask,z,res_A);
for(int
l=0; l<=n; l++)
{
for(int
m=0; m<=n; m++)
{
if(mask[l][m]!=FictivePoint)
{
z_1d[p][k]=res_A[l][m];
p++;
}
}
}
k++;
p=0;
}
}
}
f_1d=new double
[matrixSize];
p=0;
for(int l=0; l<=n; l++)
{
for(int m=0;
m<=n; m++)
{
if(mask[l][m]!=FictivePoint)
{
f_1d[p]=f[l][m];
p++;
}
}
}
print(matrixSize,z_1d,f_1d);
//Проверка сопряженности -
конец
//Проверка семетричночти и
положительноопределенности оператора начало
Simetric(matrixSize,z_1d);
More_then_0(matrixSize,z_1d);
//Проверка семетричночти и
положительноопределенности оператора конец
//приведение к треуг виду с
правой частью начало
double d=0;
for(int k=0;k<n-1;k++)
{
for(int
i=k+1;i<n;i++)
{
if(z_1d[k][k]==0)
{
SetConsoleTextAttribute
( GetStdHandle ( STD_OUTPUT_HANDLE ) , 4 ) ;
printf("Произошло
деление на 0!\nДля выхода нажмите любую клавишу...\n");
_getch();
exit(0);
}
else
{
d
= z_1d[i][k]/z_1d[k][k];
for(int
j=0;j<n;j++)
{
z_1d[i][j]=z_1d[i][j]-z_1d[k][j]*d;
}
f_1d[i]=f_1d[i]-f_1d[k]*d;
}
}
}
print(matrixSize,z_1d,f_1d);
//приведение к треуг виду с
правой частью конец
do
{
A(n,mask,u,res_A);
Substruction(n,mask,res_A,f,res_S);
A(n,mask,res_S,res_A);
tau=Scalar(n,mask,res_A,res_S)/Scalar(n,mask,res_A,res_A);
for(int
i=0;i<=n;i++)
{
for(int
j=0;j<=n;j++)
{
if(mask[i][j]!=0)
{
u[i][j]=u[i][j]-tau*res_S[i][j];
}
}
}
norm_r=Norm(n,mask,res_S);
count_it++;
}
while(norm_r > eps);
fprintf(file,"Норма =
%.40lf \n",norm_r);
fprintf(file,"\n\n");
fprintf(file,"Количество
итераций: %d\n",count_it);
//проверка линейности
оператора начало
A(n,mask,u,res_A);
copy(n,res_A,A_u);
//print(n,A_u);
A(n,mask,u_accur,res_A);
copy(n,res_A,A_u_accur);
//print(n,A_u_accur);
Substruction(n,mask,A_u,A_u_accur,res_S);
copy(n,res_S,r);
//print(n,res_S);
Substruction(n,mask,u,u_accur,res_S);
A(n,mask,res_S,res_A);
copy(n,res_A,A_u_u_accur);
//print(n,A_u_u_accur);
Substruction(n,mask,A_u_u_accur,r,res_S);
double maxDiff = 0;
for (int i=0;i<=n;i++)
{
for (int j=0;j<=n;j++)
{
if
(abs(res_S[i][j])>maxDiff)
{
maxDiff
= abs(res_S[i][j]);
}
}
}
fprintf(file,"max(Lin)
= %.25f\n",maxDiff);
//проверка линейности
оператора конец
fclose(file);
system("pause");
return 0;
}
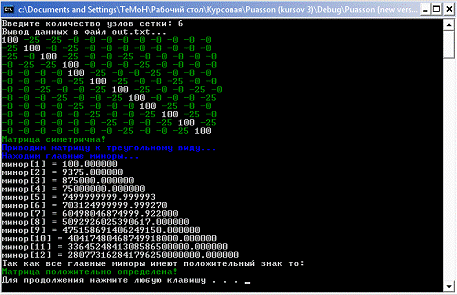
4. Результаты работы программы
При n=6:
) Внешний текстовый файл out.txt:
МАСКА ОБЛАСТИ!
0 0 0 0 0
1 1 1 1 0
1 1 1 1 0
0 0 1 1 0
0 0 1 1 0
0 0 0 0 0
100 -25 -25 -0 -0 -0 -0 -0 -0 -0 -0
-0 | 11
-25 100 -0 -25 -0 -0 -0 -0 -0 -0 -0
-0 | 7
-25 -0 100 -25 -0 -0 -25 -0 -0 -0 -0
-0 | 18
-0 -25 -25 100 -0 -0 -0 -25 -0 -0 -0
-0 | 11
-0 -0 -0 -0 100 -25 -0 -0 -25 -0 -0
-0 | 11
-0 -0 -0 -0 -25 100 -25 -0 -0 -25 -0
-0 | 18
-0 -0 -25 -0 -0 -25 100 -25 -0 -0
-25 -0 | 18
-0 -0 -0 -25 -0 -0 -25 100 -0 -0 -0
-25 | 11
-0 -0 -0 -0 -25 -0 -0 -0 100 -25 -0
-0 | 7
-0 -0 -0 -0 -0 -25 -0 -0 -25 100 -25
-0 | 11
-0 -0 -0 -0 -0 -0 -25 -0 -0 -25 100
-25 | 11
-0 -0 -0 -0 -0 -0 -0 -25 -0 -0 -25
100 | 7
100 -25 -25 -0 -0 -0 -0 -0 -0 -0 -0
-0 | 11
0 94 -6 -25 0 -0 -0 -0 -0 -0 -0 -0 |
7
0 0 93 -27 0 -0 -25 -0 -0 -0 -0 -0 |
18
0 0 0 86 0 -0 -7 -25 -0 -0 -0 -0 |
11
0 0 0 0 100 -25 -0 -0 -25 -0 -0 -0 |
11
0 0 0 0 0 94 -25 -0 -6 -25 -0 -0 |
18
0 0 -0 0 0 0 86 -27 -2 -7 -25 -0 |
18
0 0 -0 0 0 0 -0 84 -1 -2 -8 -25 | 11
0 0 -0 0 0 0 -0 0 93 -27 -1 -0 | 7
0 0 -0 0 0 0 -0 0 0 85 -27 -1 | 11
0 0 -0 0 0 0 -0 0 0 -0 83 -28 | 11
0 0 -0 0 0 0 -0 0 0 -0 0 83 | 7
Норма =
0.0000000081934754114870509000000000000000
Количество итераций: 65
max(Lin) =
0.0000000000000071054273576
2) Консоль
Литература
1. Демидович Б.П., Марон И.А., Шувалова Э.З. “ Численные методы
анализа. Приближение функций, дифференциальные и интегральные уравнения”, М.:
Наука, 1967. - 368 с.
. Вержбицкий В.М. “Численные методы. Математический анализ и
обыкновенные дифференциальные уравнения” , М.: Высшая школа, 2001. - 384 с.
3. Бундаев В.В., Дамбаев Ж.Г. “Методические указания и
контрольные задания по численным методам”, Улан-Удэ: РИО ВСГТУ, 2003. - 16 с.