Представление знаний в интеллектуальных системах
1. Синтаксис логики предикатов. Примеры. Преобразование унарных
предикатов в бинарные. Примеры
Синтаксис логики предикатов. Примеры
ПРЕДИКАТ - языковое выражение, обозначающее к.-л. свойство или отношение.
П., указывающий на свойство отдельного предмета (напр., «зеленый», «теплый»)
Предикатом называется функция, которая возвращает логическое значение. С
помощью предикатов часто определяют критерии сортировки или поиска.
Логика
предикатов - раздел математической логики
<#"551400.files/image001.gif">
2. Основные стратегии решения задач. Предварительные понятия и
примеры
Основные стратегии решения задач
Общая схема для представления задач называется пространством состояний.
Пространство состояний - это граф, вершины которого соответствуют ситуациям,
встречающимся в задаче ("проблемные ситуации"), а решение задачи
сводится к поиску пути в этом графе. Процесс решения задачи включает в себя
поиск в графе, при этом, как правило, возникает проблема, как обрабатывать
альтернативные пути поиска. Две основные стратегии перебора альтернатив, а
именно поиск в глубину и поиск в ширину.
Предварительные понятия и примеры
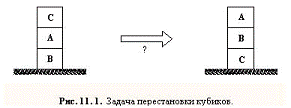
Задача состоит в выработке плана переупорядочивания кубиков, поставленных
друг на друга, как показано на рисунке. На каждом шагу разрешается переставлять
только один кубик. Кубик можно взять только тогда, когда его верхняя
поверхность свободна. Кубик можно поставить либо на стол, либо на другой кубик.
Для того, чтобы построить требуемый план, мы должны отыскать последовательность
ходов, реализующую заданную трансформацию.
Эту задачу можно представлять себе как задачу выбора среди множества
возможных альтернатив. В исходной ситуации альтернатива всего одна: поставить
кубик С на стол. После того как кубик С поставлен на стол, мы имеем три
альтернативы:
• поставить А на стол или
• поставить А на С, или
• поставить С на А. (Рис.)
Ясно, что альтернативу "поставить С на стол" не имело смысла
рассматривать всерьез, так как этот ход никак не влияет на ситуацию.
Как показывает рассмотренный пример, с задачами такого рода связано два
типа понятий:
(1) Проблемные ситуации.
(2) Разрешенные ходы или действия, преобразующие одни проблемные ситуации
в другие.
Проблемные ситуации вместе с возможными ходами образуют направленный
граф, называемый пространством состояний.
3. Преобразование унарных предикатов в бинарные. Примеры.
Преобразование m-арных предикатов
в произведение бинарных.
Преобразование унарных предикатов в бинарные
Унарный предикат проверяет некоторое свойство одного аргумента. Типичный
пример - функция, используемая в качестве критерия поиска первого простого
числа.
Бинарные предикаты обычно сравнивают некоторое свойство двух аргументов.
Например, чтобы отсортировать элементы по нестандартному критерию, программист
передает алгоритму простую предикатную функцию.
Унарный предикат состоит из предикатного имени и значения своего
единственного аргумента. Следовательно, его формат такой: Предикатное_имя
(значение_аргумента). Значение аргумента есть конкретизация предикатного имени
или переменной. Например, Человек (Сократ) указывает, что имя собственное
«Сократ» - конкретизация имени совокупности «человек», а Человек (х) указывает,
что х - человек (не что-либо иное). Фразу «Сократ - человек» можно представить
бинарным предикатом Конкр (Сократ, человек).
Преобразование m-арных
предикатов в произведение бинарных
Фразу «Жак посылает книгу Мари» нетрудно представить тернарным (т.е. с
тремя аргументами) предикатом:
Посылка (Жак_2, Мари_4, Книга_22).
Определив новые предикаты, можно представить эту фразу произведением
(конъюнкцией) бинарных предикатов:
Отправитель (Посылка, Жак_2)
Получатель (Посылка, Мари_4)
Объект (Посылка, Книга_22).
Данная логическая формула читается так: «отправитель посылки - Жак,
получатель посылки - Мари и объект посылки - книга».
Этот пример подсказывает правило преобразования m-арных предикатов (с m
аргументами) в эквивалентное произведение бинарных предикатов. Всякий m-арный
предикат состоит из предикатного имени и m значений аргументов:
Предикатное_имя(значение_1, значение_2, ..., значение_m).
Например, предикат для описания посылки некоторого объекта отправителем
получателю может иметь следующий формат:
Посылка (отправитель, получатель, объект).
Функция «отправитель посылки» учитывается первым аргументом, функция
«получатель посылки» - вторым, функция «объект посылки» - третьим.
Первоначально выбранный порядок аргументов для соответствия «функция -
аргумент» может быть произвольным, но должен сохраняться неизменным.
Функциональную организацию m-арного предиката можно представить так:
Предикатное_имя (функция_1, функция_2, ..., функция_т).
При записи m-арного предиката через бинарные предикаты используется
специальное соглашение, позволяющее сохранить и явно указать соответствующие
функциональные отношения. Каждая функция становится именем бинарного предиката,
первый аргумент которого является именем исходного m-арного предиката, а второй
- значением относящегося к этой функции аргумента. Функциональная организация
исходного m-арного предиката и значения его аргументов представляются
произведением бинарных предикатов:
Функция_1 (предикатное_имя, значение_1) Функция_m (предикатное_имя,
значение_m).
4. Основные стратегии решения задач. Поиск в ширину
Основные стратегии решения задач
Общая схема для представления задач называется пространством состояний.
Пространство состояний - это граф, вершины которого соответствуют ситуациям,
встречающимся в задаче ("проблемные ситуации"), а решение задачи
сводится к поиску пути в этом графе. Процесс решения задачи включает в себя
поиск в графе, при этом, как правило, возникает проблема, как обрабатывать
альтернативные пути поиска. Две основные стратегии перебора альтернатив, а
именно поиск в глубину и поиск в ширину.
Поиск в ширину
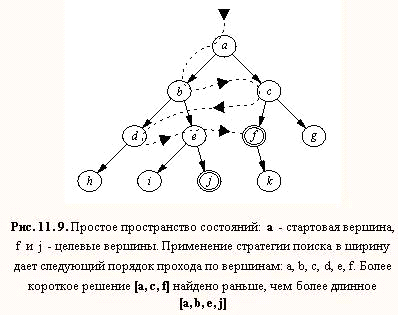
В противоположность поиску в глубину стратегия поиска в ширину
предусматривает переход в первую очередь к вершинам, ближайший к стартовой
вершине. В результате процесс поиска имеет тенденцию развиваться более в
ширину, чем в глубину, что иллюстрирует
Поиск в ширину программируется не так легко, как поиск в глубину. Причина
состоят в том, что нам приходится сохранять все множество альтернативных
вершин-кандидатов, а не только одну вершину, как при поиске в глубину. Более
того, если мы желаем получить при помощи процесса поиска решающий путь, то
одного множества вершин недостаточно. Поэтому мы будем хранить не множество
вершин-кандидатов, а множество путей-кандидатов. Таким образом, цель
в ширину (Пути, Решения)
истинна только тогда, когда существует путь из множества кандидатов Пути,
который может быть продолжен вплоть до целевой вершины. Этот продолженный путь
и есть Решение.
5.
Явное представление ссылок. Представление функциями. Примеры
Явное представление ссылок
Символы объектного языка, такие как Жак_2, Мари_4 и Книга_22, введены для
того, чтобы избежать двусмысленности ссылок на вполне определенных людей и
книгу. Фраза «Жак посылает книгу Мари» указывает определенное «почтовое
событие» (или «действие отправления»), на которое желательно иметь возможность
ссылаться в дальнейшем. Следовательно, придется дать ему имя индивидуума
Посылка_8 и указать, что оно - часть множества событий с именем совокупности
посылки. Перевод фразы на бинарные предикаты выглядит так:
Отправитель (Посылка_8, Жак_2)
Получатель (Посылка_8, Мари_4)
Объект (Посылка_8, Книга_22)
Элем(Посылка_8, посылки)
Предикатное имя Элем означает «есть элемент такого-то множества»
Представление функциями
Отношения между значением Посылка_8 и аргументами тернарного предиката
Посылка можно выразить также функциями на множестве почтовых посылок (одной
переменной). Функция называется также функциональной формой. Фраза «Жак
посылает книгу Мари» выражается в терминах функций следующей формой:
Равно (отправитель (Посылка_8), Жак_2)
Равно (получатель (Посылка_8), Мари_4)
Равно (объект (Посылка_8), Книга_22)
Элем (Посылка_8, посылки).
Предикат Равно представляет отношение равенства. Это выражение используют
определенные на множестве «посылок» функции, значения которых представляют
конкретизации, касающиеся Посылки_8.
Примеры
Рассмотрим фразы той же синтаксической формы, что и «Жак посылает книгу
Мари», но с кванторами
По-русски: Жак посылает что-то каждому (всем одно и то же),
Логически: Посылка (Жак_2, х, у).
По-русски: Жак посылает что-то каждому (но не обязательно всем одно и то
же)
Логически-1: Посылка (Жак_2, х, у),
Логически-2: Посылка (Отправитель (посылка, Жак_2) Получатель (посылка,х)
Объект (посылка,у)),
Логически-3: (Отправитель z(Жак_2) Получатель (z,x) Объект(z,y) Эм (z,
посылки)).
Три представления фразы «Жак посылает что-то каждому» соответствует трем
представлениям фразы «Жак посылает книгу Мари».
6. Основные стратегии решения задач. Стратегия поиска в глубину
Основные стратегии решения задач
Общая схема для представления задач называется пространством состояний.
Пространство состояний - это граф, вершины которого соответствуют ситуациям,
встречающимся в задаче ("проблемные ситуации"), а решение задачи
сводится к поиску пути в этом графе. Процесс решения задачи включает в себя
поиск в графе, при этом, как правило, возникает проблема, как обрабатывать
альтернативные пути поиска. Две основные стратегии перебора альтернатив, а
именно поиск в глубину и поиск в ширину.
Стратегия поиска в глубину
Для того, чтобы найти решающий путь Реш из заданной вершины В в некоторую
целевую вершину, необходимо:
если В - это целевая вершина, то положить Реш = [В], или
если для исходной вершины В существует вершина-преемник В1, такая, что
можно провести путь Реш1 из В1 в целевую вершину, то положить Реш = [В | Peш1].
Рис. 11.4
На Пролог это правило транслируется так:
решить( В, [В] ) :-
цель( В).
решить( В, [В | Реш1] ) :-
после( В, В1 ),
решить( В1, Реш1).
Эта программа и есть реализация поиска в глубину. Мы говорим "в
глубину", имея в виду тот порядок, в котором рассматриваются альтернативы
в пространстве состояний. Всегда, когда алгоритму поиска в глубину надлежит
выбрать из нескольких вершин ту, в которую следует перейти для продолжения
поиска, он предпочитает самую "глубокую" из них. Самая глубокая
вершина - это вершина, расположенная дальше других от стартовой вершины.
7. Семантика логики предикатов
Стратегия определения семантических значений компонент и формул логики
предикатов базируется на понятии интерпретации логической формулы. Напомним это
понятие.
Объектами изучения естественных и формальных языков являются в частности,
синтаксис (который позволяет распознавать фразы среди набора слов) и семантика
(которая придает определенное значение фразам). В равной мере это относится к
исчислению высказываний.
Уже отмечалось, что высказывание либо истинно, либо ложно. Поэтому введем
семантическую область {И, Л}. Интерпретировать формулу - значит приписать ей
одно из двух значений истинности И или Л.
Семантика
(то есть набор правил интерпретации формул) должна быть композиционной:
значение формулы должно быть функцией значений ее составляющих. Точнее, значение
истинности формулы зависит только от структуры этой формулы и от значений
истинности составляющих ее высказываний. Таким образом, связки исчисления
высказываний представляют функции истинности: например значение истинности
формулы 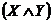 будет известно, если известны значения истинности Х и
Y. Следующие две таблицы описывают семантику отрицания
и бинарных связок.
будет известно, если известны значения истинности Х и
Y. Следующие две таблицы описывают семантику отрицания
и бинарных связок.
|
Х
|
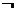 Х Х
|
|
И
|
Л
|
|
Л
|
И
|
|
Х
|
Y
|
X YX YX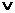 YX YX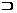 YX YX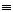 Y Y
|
|
|
|
|
И
|
И
|
И
|
И
|
И
|
И
|
|
И
|
Л
|
Л
|
И
|
Л
|
Л
|
|
Л
|
И
|
Л
|
И
|
И
|
Л
|
|
Л
|
Л
|
Л
|
Л
|
И
|
И
|
Интерпретация - это отображение i, сопоставляющее каждому элементарному высказыванию р некоторое значение
истинности. Интерпретацию i,
заданную на множестве элементарных высказываний, можно распространить
(продолжить) на множество формул (высказываний) посредством таблиц истинности.
Соответствующее продолжение (расширение) I тоже называется интерпретацией. Интерпретация, при которой
истинностное значение формулы есть И, называется моделью этой формулы.
Литера
- это элементарное высказывание или его отрицание. Литеры р и 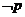 противоположны. Интерпретация определяет разбиение
множества L литер на два подмножества Lи и Lл,
каждое из которых содержит по одному элементу из каждой пары противоположных
литер.
противоположны. Интерпретация определяет разбиение
множества L литер на два подмножества Lи и Lл,
каждое из которых содержит по одному элементу из каждой пары противоположных
литер.
Формулы
исчисления предикатов, как и формулы исчисления высказываний, могут быть
интерпретированы, т.е. могут получить значение истинности. Однако формулы
исчисления предикатов состоят не только из подформул, но также из термов.
Следовательно, необходимо интерпретировать также термы. Терм интуитивно
означает объект. Таким образом, интерпретация должна специфицировать множество
объектов, называемое областью интерпретации.
Точнее,
интерпретация I - это тройка (D, Ic, Iv)
со следующими свойствами:
· D - непустое множество, область интерпретации.
· Ic - функция, которая сопоставляет каждой функциональной n-местной константе f некоторую функцию Ic(f) из Dn в D и которая сопоставляет каждой
предикатной m-местной константе Р некоторую
функцию Ic(Р) из Dm в {И, Л}.
· Iv - функция, сопоставляющая каждой переменной некоторый
элемент из D.
Теперь можно задать для интерпретации I = (D, Ic, Iv) такие правила, которые каждой формуле А ставят в
соответствие некоторое значение истинности I(A), а каждому
терму t сопоставляется элемент I(t) из D.
· Если х - свободная переменная, то I(x)=def Iv(x).
· Если f -
функциональная n-местная
константа, t1, ... ,tn - термы, то I(f(t1, ... ,tn)) =def= =(Ic(f))(I(t1), ... ,I(tn))
· Если Р - предикатная m-местная константа, t1, ... ,tm - термы, то I(P(t1, ... ,tm)) =def=
=(Ic(P))(I(t1), ... ,I(tm))
· Если s и t термы, то I(s=t) есть И при I(s)=I(t), а иначе Л.
· Если А и В -
формулы, то 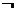 А, (А
А, (А В), (А
В), (А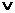 В), (А
В), (А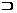 В) и (А
В) и (А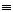 В) интерпретируются как в исчислении высказываний.
В) интерпретируются как в исчислении высказываний.
Осталось задать интерпретацию для двух типов квантифицированных формул.
Введем сначала одно понятие. Если I - интерпретация c
областью DI, x - переменная, d -
элемент из DI, то Ix/d означает такую
интерпретацию J, что DJ = DI, Jc = Ic, Jv(x) = d и Jv(y) = Iv(y) для всех
свободных переменных у отличных от х.
Правила интерпретации будут такими:
· Если А -
формула и х - переменная, то I( хА) есть И при условии, что Ix/d (А)
есть И для всех элементов d из D.
хА) есть И при условии, что Ix/d (А)
есть И для всех элементов d из D.
· Если А -
формула и х - переменная, то I(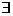 хА) есть И при условии, что Ix/d (А)
есть И хотя бы для одного элемента d из D
хА) есть И при условии, что Ix/d (А)
есть И хотя бы для одного элемента d из D
Формула А исчисления предикатов называется истинной при интерпретации I, если I(A)=И.
Теперь
видно, что запрещение перекрытия кванторов, действующих на одну и ту же
переменную, не является существенным ограничением. В частности, 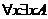 интерпретируется как
интерпретируется как 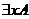 и
и 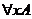 интерпретируется как
интерпретируется как 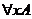 . Ясно
также, почему требуется условие D
. Ясно
также, почему требуется условие D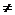 ø; без него естественные импликации
ø; без него естественные импликации
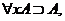
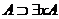

не
всегда были бы истинны.
Заметим
также, что эти правила интерпретации соответствует интуитивным представлениям.
В частности, формальное значение кванторов хорошо моделирует их естественное
значение.
Как
и формулы исчисления высказываний, формулы исчисления предикатов делятся на три
класса: общезначимые формулы, которые истинны при всех интерпретациях,
невыполнимые, которые ложны при всех интерпретациях, и нейтральные (или просто
выполнимые), которые истинны только при некоторых интерпретациях. В
противоположность тому, что имело место для исчисления высказываний, эти три
класса не являются рекурсивными: не существует детерминированного алгоритма,
который определял бы, к какому классу принадлежит произвольная формула
исчисления предикатов.
Теперь,
после того как мы вспомнили понятие интерпретации логической формулы, можно
вернуться к вопросу семантики логики предикатов.
Прежде
всего задаем семантическое значение для каждого базисного выражения. Затем
вводим семантические правила вычисления семантических значений сложных
логических формул по известным значениям семантических компонент. Иначе говоря,
приписываем семантическое значение все более и более крупным составляющим
логической формулы, так что в конце концов семантическое значение будет
приписано и всей формуле. Этот процесс называется композиционным методом.
Предположим
для определенности, что универсум рассуждения содержит лишь имена трех людей:
«Жак Дюпон», «Мари Дюран», «Джорж Буль» - и название одной книги: «Законы
мышления». С каждым именем индивидуума, используемым в логических формулах,
можно следующим образом связать одно из перечисленных имен, которое станет семантическим
значением:
|
Имена индивидуумов
|
Семантические значения
|
|
Жак_2
|
Жак Дюпон
|
|
Мари_4
|
Мари Дюран
|
|
Джордж_5
|
Джордж Буль
|
|
Книга_22
|
Законы мышления
|
Левый столбец составлен из лингвистических сущностей, т.е. из лексических
компонент особой синтаксической категории некоторого языка. Правый - из
сущностей реального мира.
Подчеркнем, что следует приписывать уникальное семантическое значение
каждому базисному выражению. Это устраняет лексические двусмысленности
реального мира. Напротив, некоторые объекты реального мира могут вообще не
получать индивидуального имени на языке или получать несколько имен. Итак, мы
хотим определить функцию (в математическом смысле), отображающую имена
объектного языка на сущности реального мира. Сами эти сущности выражены на так
называемом метаязыке, роль которого играет здесь русский язык.
Фундаментальным понятием семантики является понятие истины реального
мира. Более общее понятие - истина в модели. Здесь моделью является реальный
мир. Состояние реального мира позволяет приписывать семантические значения
«истинно» или «ложно» предикатам и функциям. Например:
|
Предикат
|
Семантическое значение
|
|
Посылка(Жак_2, Мари_4,
Книга_22)
|
истинно
|
|
Посылка (Мари_4, Жак_2,
Книга_22)
|
ложно
|
|
Написанное (Джордж_5,
Книга_22)
|
истинно
|
|
Написанное (Жак_2,
Книга_22)
|
ложно
|
Композиционный
метод гарантирует, что семантическое значение сложного выражения всегда
является функцией его семантических составляющих и способа их комбинирования.
Если семантическое значение формул F и G известны, то
можно определить семантическое значение формул 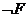 ,
, 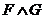 ,
, 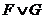 ,
, 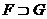 ,
,  с помощью
таблиц истинности логики высказываний. Например:
с помощью
таблиц истинности логики высказываний. Например:
|
Формула
|
Семантическое значение
|
Посылка(Жак_2,
Мари_4, Книга_22)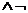 Написанное (Жак_2, Книга_22)
Написанное (Жак_2, Книга_22)
Посылка(Жак_2,
Мари_4, Книга_22) Написанное (Джордж_5, Книга_22)
Написанное (Джордж_5, Книга_22)
Основной задачей представления знаний является перевод неформальных
выражений или описаний метаязыка в фразы объектного языка.
8.
Функции, выполняемые экспертной системой
Экспертная система - это программа, которая ведет себя подобно эксперту в
некоторой проблемной области.
Типичные применения экспертных систем включают в себя такие задачи, как
медицинская диагностика, локализация неисправностей в оборудовании и
интерпретация результатов измерений. Экспертные системы должны решать задачи,
требующие для своего решения экспертных знаний в некоторой конкретной области.
В той или иной форме экспертные системы должны обладать этими знаниями. Поэтому
их также называют системами, основанными на знаниях. Однако не всякую систему,
основанную на знаниях, можно рассматривать как экспертную. Экспертная система
должна также уметь каким-то образом объяснять свое поведение и свои решения
пользователю, так же, как это делает эксперт-человек. Это особенно необходимо в
областях, для которых характерна неопределенность, неточность информации
(например, в медицинской диагностике). В этих случаях способность к объяснению
нужна для того, чтобы повысить степень доверия пользователя к советам системы,
а также для того, чтобы дать возможность пользователю обнаружить возможный
дефект в рассуждениях системы. В связи с этим в экспертных системах следует
предусматривать дружественное взаимодействие с пользователем, которое делает
для пользователя процесс рассуждения системы "прозрачным".
Часто к экспертным системам предъявляют дополнительное требование -
способность иметь дело с неопределенностью и неполнотой. Информация о
поставленной задаче может быть неполной или ненадежной; отношения между
объектами предметной области могут быть приближенными. Например, может не быть
полной уверенности в наличии у пациента некоторого симптома или в том, что
данные, полученные при измерении, верны; лекарство может стать причиной
осложнения, хотя обычно этого не происходит. Во всех этих случаях необходимы
рассуждения с использованием вероятностного подхода.
В самом общем случае для того, чтобы построить экспертную систему, мы
должны разработать механизмы выполнения следующих функций системы:
· решение задач с использованием знаний о конкретной предметной
области - возможно, при этом возникнет необходимость иметь дело с
неопределенностью
· взаимодействие с пользователем, включая объяснение намерений
и решений системы во время и после окончания процесса решения задачи.
Каждая из этих функций может оказаться очень сложной и зависит от
прикладной области, а также от различных практических требований. В процессе
разработки и реализации могут возникать разнообразные трудные проблемы.
9. (10)Структура экспертной системы
Грубая
структура экспертной системы
При разработке экспертной системы принято делить ее на 3 основных модуля,
показано на рис.14.1:
(1) база знаний,
(2) машина логического вывода,
(3) интерфейс с пользователем.
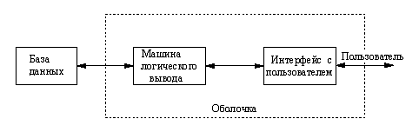
Рис. 14. 1. Структура экспертной системы.
База знаний содержит знания, относящиеся к конкретной прикладной области,
в том числе отдельные факты, правила, описывающие отношения или явления, а
также, возможно, методы, эвристики и различные идеи, относящиеся к решению
задач в этой прикладной области. Машина логического вывода умеет активно
использовать информацию, содержащуюся в базе знаний. Интерфейс с пользователем
отвечает за бесперебойный обмен информацией между пользователем и системой; он
также дает пользователю возможность наблюдать за процессом решения задач,
протекающим в машине логического вывода. Принято рассматривать машину вывода и
интерфейс как один крупный модуль, обычно называемый оболочкой экспертной
системы, или, для краткости, просто оболочкой.
В описанной выше структуре собственно знания отделены от алгоритмов,
использующих эти знания. Такое разделение удобно по следующим соображениям.
База знаний, очевидно, зависит от конкретного приложения. С другой стороны,
оболочка, по крайней мере в принципе, независима от приложений. Таким образом,
разумный способ разработки экспертной системы для нескольких приложений
сводится к созданию универсальной оболочки, после чего для каждого приложения
достаточно подключить к системе новую базу знаний. Разумеется, все эти базы
знаний должны удовлетворять одному и тому же формализму, который оболочка
"понимает". Практический опыт показывает, что для сложных экспертных
систем наш сценарий с одной оболочкой и многими базами знаний работает не так
гладко, как бы этого хотелось, за исключением тех случаев, когда прикладные
области очень близки. Тем не менее даже если переход от одной прикладной
области к другой требует модификации оболочки, то по крайней мере основные
принципы ее построения обычно удается сохранить.
В этой главе мы намерены разработать относительно простую оболочку, при
помощи которой, несмотря на ее простоту, мы сможем проиллюстрировать основные
идеи и методы в области экспертных систем. Мы будем придерживаться следующего
плана:
(1) Выбрать формальный аппарат для представления знаний.
(2) Разработать механизм логического вывода, соответствующий этому
формализму.
(3) Добавить средства взаимодействия с пользователем.
(4) Обеспечить возможность работы в условиях неопределенности.
10. (9)Модальная логика предикатов. Модальные операторы. Примеры
модальных операторов
В обыденном языке часто говорят о допустимости чего-либо, о
гипотетических событиях, целях, которые можно пытаться достигнуть, догадках о
будущем. Большая часть фраз языка может быть то истинной, то ложной в
зависимости от обстоятельств, текущего момента, точки зрения каждого из нас. В
естественных языках модальности «возможный», «необходимый» и допустимый
выражаются вспомогательными глаголами, такими как «должен» и «могу».
Возможность и необходимость называются алетическими модальностями или
модальностями возможности. Так же как кванторы «для всех» и «существует»
вводились в синтаксис логики первого порядка, можно построить формальный язык,
используя пару понятий «возможно»/ «необходимо» как кванторы, действующие на
формулы. Логическая система, базирующаяся на операторах «возможно, что» и
«необходимо чтобы», называется логикой возможного, или алетической логикой.
Для
обозначения модальности «необходимо» используется символ □. Формула □F
читается «необходимо, чтобы F» или «F необходимо». Двойственный □ оператор
обозначается через ◊. Формула ◊F читается
«возможно, что F» или «F возможно». Один из этих операторов принимается за
основной, а другой определяется через него и отрицание (эквивалентность □F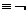 ◊
◊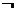 F можно установить, применяя доводы, подобные тем,
которые можно использовать при доказательстве соотношения
F можно установить, применяя доводы, подобные тем,
которые можно использовать при доказательстве соотношения 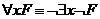 ).
).
В
обыденном языке употребляются и другие модальные формы, которые важно перевести
в логику. Деонтическая логика вводит модальности «разрешено» «обязательно»,
реализующая модальные языковые конструкции «разрешается» «надо, чтобы».
Эпистемическая логика, или логика знания, исследует модальности «знания» и
«веры», тогда как временная логика вводит модальности «иногда» и «всегда» (в
«будущем» и «прошлом») вместе с их отрицаниями «часто» и «никогда».
Ввиду
формального сходства между этими логическими системами их часто изучают все
вместе или хотя бы по группам. Часто используют термин модальная логика для
обозначения совокупности этих логик. Старейшая среди них - логика возможного.
Часто именно ее называют модальной.
Название
модальная логика происходит от того, что модальные логические системы вводят
такие операторы над логическими формулами, которые позволяют модифицировать их
интерпретацию. Например, в утверждениях «Возможно, что F», «Поль
думает, что F», «Часто правда, что F», «В будущем,
возможно, будет правда, что F», предшествующие логической формуле F
выражения являются модальными операторами. Они могут относиться к какой угодно
логической формуле F. Значение истинности зависит не только от значения
истинности формулы F, которую они содержат, но и от момента провозглашения
модальной формулы (временные логики), от человека, который думает, что F,
или верит, что F (логика веры), или от необходимого, возможного или
случайного характера некоторого факта (логики возможного).
Модальные
операторы
Имеется сходство между определениями каждой из пар операторов (вроде
«возможно»/ «определено», «иногда»/ «всегда» и т. д.) и определением пары
кванторов существования/ общности. Это подсказывает следующее определение модальных
операторов:
Модальный
оператор общности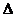 является:
является:
· либо именем модального оператора,
· либо выражением, состоящим из имени модального оператора, за
которым следует список (t1, t2, ... ,tn) термов ti (i=1,2, ... , n).
Модальный оператор существования ▼определяется через отрицание
модального оператора общности:
▼F =def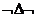 F.
F.
Примеры
модальных операторов
· Алетические операторы:
- □: необходимо;
□А истинно тогда и только тогда, когда
А необходимо истинно (а)
или А абсолютно истинно (b)
или А истинно во всех возможных мирах. (с)
- ◊: возможно;
◊А истинно,
если А может оказаться истинным, (а)
или если А условно истинно, (b)
или если А истинно в некотором из возможных миров. (с)
(Интерпретации (а), (b) и
(с) для □ и ◊ соответственны; в каждой из пар (а), (b) и (с) сгруппированы двойственные
интерпретации).
· Временные оператор:
- G: всегда (в будущем);
GА
истинно, если А остается истинным навсегда.
- H: всегда (в прошлом);
HА
истинно, если А всегда было истинным.
- F: иногда (в будущем);
FА
истинно, если А иногда будет истинным.
- Р: иногда (в прошлом);
РА истинно, если А иногда оказывалось истинным.
- U: до тех пор пока;
U(А,
В) истинно, если А истинно (начиная с текущего момента) до тех пор, пока В не
станет истинным в некоторый момент в будущем.
(G, F и
Н, Р двойственные операторы в смысле FA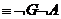 и РА
и РА 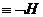
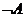 .
Некоторые временные логики учитывают только будущее. В этом случае часто употребляются
обозначения □ и ◊ соответственно для операторов G и F)
.
Некоторые временные логики учитывают только будущее. В этом случае часто употребляются
обозначения □ и ◊ соответственно для операторов G и F)
· Эпистемические операторы:
- верит (а)
верит (а)А истинно, если индивид а верит в формулу А
Очевидно, что модальные формулы бесчисленны. Философы предложили и
использовали их в огромном количестве. Все эти формулы представимы с помощью
модальных операторов.
11. Синтаксис модальной логики предикатов. Примеры
Пусть М1, М2, … , Мn -
модальные ораторы. Правила образования модальных формул таковы:
· Все правила построения из логики предикатов (первого порядка) являются
также правилами построения в модальной логике предикатов.
· Если F -
формула и Мi - модальный оператор, то MiF - формула.
И опять основной задачей представления знаний является перевод фраз и
описаний, относящихся к области экспертизы, в формулы модальной логики
предикатов. Семантические значения этих модальных формул должно соответствовать
истинам области экспертизы.
Примеры
· По-русски: Возможно, что Жак посылает книгу Мари,
Логически: ◊ Посылка (Жак_2, Мари_4, Книга_22).
· По-русски: Не было возможным, чтобы Жак посылал что-нибудь
каждому,
Логически
Р(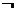 (◊ (
(◊ (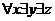 Отправитель
(z, Жак_2)
Отправитель
(z, Жак_2) Получатель(z,x)
Получатель(z,x) Объект (z,y)
Объект (z,y) Элем (z,
посылки))))
Элем (z,
посылки))))
(Словесное
прочтение этой формулы таково: в прошлом (Р) не является (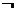 ) возможным (◊), чтобы Жак посылал что-нибудь
каждому).
) возможным (◊), чтобы Жак посылал что-нибудь
каждому).
· По-русски: Если Жак верит данному высказыванию, то он верит,
что верит ему (аксиома позитивной интроспексии)
Логически:
верит (Жак_2) р 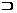 верит (Жак_2)(верит (Жак_2)р).
верит (Жак_2)(верит (Жак_2)р).
· По-русски: Если Жак не верит данному высказыванию, то он
верит, что не верит ему (аксиома негативной интроспексии)
Логически:
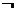 верит (Жак_2) р
верит (Жак_2) р 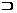 верит
(Жак_2)(
верит
(Жак_2)( 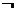 верит (Жак_2)р).
верит (Жак_2)р).
· По-русски: Если факт, что Жак верит данному высказыванию,
влечет , что оно истинно, то Жак знает это высказывание,
Логически:
(верит (Жак_2) р 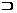 р)
р) 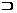 (знает
(Жак_2) р). (Во многих случаях желательно, чтобы убеждения людей были
истинными. Это приводит к понятию скорее знания, чем веры)
(знает
(Жак_2) р). (Во многих случаях желательно, чтобы убеждения людей были
истинными. Это приводит к понятию скорее знания, чем веры)
· По-русски: Жак верит, что он послал книгу (а не что-нибудь
иное) Мари,
Логически:
верит (Жак_2) (Р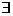 х[Посылка (Жак_2, Мари_4, х)
х[Посылка (Жак_2, Мари_4, х) Элем(х, книги)].
Элем(х, книги)].
· По-русски: Жак верит, что он послал книгу (вполне
определенную) Мари,
Логически:
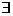 х [верит (Жак_2) (Р Посылка (Жак_2, Мари_4, х)
х [верит (Жак_2) (Р Посылка (Жак_2, Мари_4, х) Элем(х, книги)].
Элем(х, книги)].
(Последнее
выражение показывает, что в системе убеждений Жака имеется формула типа [Р
Посылка (Жак_2, Мари_4, х) Элем(х, книги)]. Но ее окончательный вид зависит от
конкретного объекта, к которому относится переменная х. Предпоследнее выражение
показывает, что в системе убеждений Жака содержится формула (Р
Элем(х, книги)]. Но ее окончательный вид зависит от
конкретного объекта, к которому относится переменная х. Предпоследнее выражение
показывает, что в системе убеждений Жака содержится формула (Р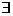 х[Посылка
х[Посылка Элем).)
Элем).)
12.
Правила «если-то» для представления знаний
В качестве кандидата на использование в экспертной системе можно
рассматривать, в принципе, любой непротиворечивый формализм, в рамках которого
можно описывать знания о некоторой проблемной области. Однако самым популярным формальным
языком представления знаний является язык правил типа "если-то",
называемых также продукциями. Вот примеры:
· если предварительное условие Р то заключение (вывод) С
· если ситуация S то действие А
· если выполнены условия С1 и С2 то не выполнено условие С
"Если-то"-правила обычно оказываются весьма естественным
выразительным средством представления знаний. Кроме того, они обладают
следующими привлекательными свойствами:
· Модульность: каждое правило описывает небольшой, относительно
независимый фрагмент знаний.
· Возможность инкрементного наращивания: добавление новых
правил в базу знаний происходит относительно независимо от других правил.
· Удобство модификации (как следствие модульности): старые
правила можно изменять и заменять на новые относительно независимо от других
правил.
· Применение правил способствует прозрачности системы.
Последнее свойство - это важное, отличительное свойство экспертных
систем. Под прозрачностью мы понимаем способность системы к объяснению принятых
решений и полученных результатов. Применение "если-то"-правил
облегчает получение ответов на следующие основные типы вопросов пользователя:
(1) Вопросы типа "как": Как вы пришли к этому выводу?
(2) Вопросы типа "почему": Почему вас интересует эта
информация?
Если
тип инфекции - это первичная бактериемия и
материал для посева был отобран стерильно, и
предполагаемые ворота инфекции - желудочно- кишечный тракт
То
имеются веские аргументы (0.7) за то,
что инфекционный агент является бактерией
Рис. 14. 2. "Если-то"-правило медицинской консультативной
системы MYCIN (Shortliffe, 1976). Параметр 0.7 показывает степень доверия этому
правилу.
"Если-то"-правила часто применяют для определения логических
отношений между понятиями предметной области. Про чисто логические отношения
можно сказать, что они принадлежат к "категорическим знаниям",
"категорическим" - потому, что соответствующие утверждения всегда,
абсолютно верны. Однако в некоторых предметных областях, таких, как медицинская
диагностика, преобладают "мягкие" или вероятностные знания. Эти
знания являются "мягкими"; в том смысле, что говорить об их
применимости к любым практическим ситуациям можно только до некоторой степени
("часто, но не всегда"). В таких случаях используют модифицированные
"если-то"-правила, дополняя их логическую интерпретацию вероятностной
оценкой. Например:
если условие А то заключение В с уверенностью F
Правила, содержащиеся в базе знаний, имеют вид
ИмяПравила : если Условие то Заключение
где Заключение - это простое утверждение, а Условие - это набор простых
утверждений, соединенных между собой операторами и и или. Мы также разрешим в
части условия использовать оператор не, хотя и с некоторыми оговорками.
Заметим, что оператор и связывает операнды сильнее, чем или, что соответствует
обычным соглашениям.
Рассмотрим еще одну небольшую базу знаний, которая может помочь
локализовать неисправности в простой электрической схеме, состоящей из
электрических приборов и предохранителей. Электрическая схема показана на рис.
14.6. Вот одно из возможных правил:
Если
лампа1 включена и
лампа1 не работает и
предохранитель1 заведомо цел
то
лампа1 заведомо неисправна.
Вот другой пример правила:
Если
радиатор работает
то
предохранитель1 заведомо цел.
Эти два правила опираются на некоторые факты (относящиеся к нашей
конкретной схеме), а именно что лампа1 соединена с предохранитель1 и что лампа1
и радиатор имеют общий предохранитель. Для другой схемы нам понадобится еще
один набор правил. Поэтому было бы лучше сформулировать правила в более общем
виде (используя прологовские переменные) так, чтобы они были применимы к любой
схеме, а затем уже дополнять их информацией о конкретной схеме. Например, вот
одно из полезных правил: если прибор включен, но не работает, а соответствующий
предохранитель цел, то прибор неисправен.
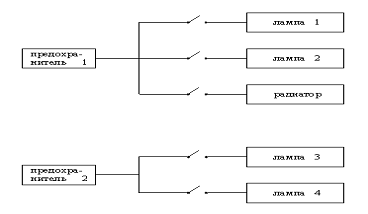
Рис. 14. 6. Соединения между предохранителями и приборами в простой
электрической схеме.
На наш формальный язык это транслируется так:
правило_поломки:
если
Прибор включен и
не (Прибор работает) и
Прибор соединен с Предохранитель и
Предохранитель заведомо цел
То
Прибор заведомо неисправен.
База знаний такого рода показана на рис. 14. 7.
13. Трехзначная семантика для модальной логики предикатов. Пример
Семантику для модальной логики предикатов можно определить, как для классической.
Проиллюстрируем модальную семантику, введя аппроксимацию (замена одних объектов
другими, в том или ином смысле близкими к исходным, но более простыми)
некоторых форм логики возможного с помощью трехзначной логики. Бинарная логика
с двумя значениями {Л или 0, и И или 1} самая элементарная. Истина и ложь - это
два множества высказываний, и законы (классической) логики утверждают, что
любое высказывание есть элемент хотя бы одного из этих множеств (закон
исключения третьего) и что никакое высказывание не является элементом сразу
двух этих множеств (закон противоречия).
Какие изменения надо внести в эту теорию, если вводятся модальности
«возможно» и «необходимо»? Надо рассмотреть несколько классов высказываний.
Обозначим через N класс
«необходимых» высказываний, через Р - «возможных», через I -«невозможных» (или «абсурдных») и
через С - «нейтральных» (или «возможно (случайно) ложных»). Никакое
высказывание не принадлежит одновременно N и С или I и Р.
Далее, класс N содержится в Р, а класс I - в С. Это отражено в законах
следования возможного из необходимого и нейтрального из абсурдного:
любое необходимое высказывание возможно;
любое абсурдное высказывание не является необходимым.
Существуют высказывания, которые являются возможными и нейтральными одновременно.
Их называют «проблематичными». Множество таких высказываний обозначим через U. Имеет место закон исключения
четвертого:
любое высказывание принадлежит либо N, либо U,
либо I.
Посмотрим, как эту теорию модальности можно перевести в алгебраическую
форму. Каждому из классов N, U, I соответствует своя интерпретация: «необходимо»,
«проблематично», «невозможно». Возьмем три символа 2, 1, 0. Эти логические
значения сопоставляем указанным интерпретациям. Каждому высказыванию можно
приписать логическое значение. Эта трехзначная логика предложена Лукасевичем.
В логике Лукасевича каждое высказывание обладает одним из значений 0, 1
или 2 (интерпретируемых как семантическое значение высказывания). Семантические
значения можно находить, используя таблицы, приведенные ниже. Они задают
семантику для аппроксимации модальной логики возможного с помощью трехзначной
логики. Иное описание этой семантики возможно, но мы не будем его
рассматривать.
|
F GF GF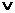 GF GF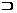 GF GF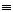 G G
|
|
|
|
|
|
|
|
F
|
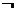 FF\G012012012012 FF\G012012012012
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
2
|
|
0
|
0
|
0
|
0
|
|
0
|
1
|
2
|
|
2
|
2
|
2
|
|
2
|
1
|
0
|
|
1
|
1
|
|
1
|
1
|
1
|
|
1
|
2
|
2
|
|
1
|
2
|
2
|
|
1
|
2
|
1
|
|
2
|
0
|
|
2
|
0
|
1
|
2
|
|
2
|
2
|
2
|
|
0
|
1
|
2
|
|
0
|
1
|
2
|
|
F
|
◊F
|
□F
|
|
0
|
0
|
0
|
|
1
|
2
|
0
|
|
2
|
2
|
2
|
14. Экспертные системы. Разработка оболочки
Если мы посмотрим на правила наших двух маленьких баз знаний рис. 14.5 и
14.7, мы сразу увидим, что они по своему смыслу эквивалентны правилам Пролога.
Однако, с точки зрения синтаксиса Пролога, эти правила в том виде, как они
написаны, соответствуют всего лишь фактам. Для того, чтобы заставить их
работать, самое простое, что может прийти в голову, это переписать их в виде
настоящих прологовских правил. Например:
Животное это млекопитающее :-
Животное имеет шерсть;
Животное 'кормит детенышей' молоком.
Животное это хищник :-
Животное это млекопитающее,
Животное ест мясо.
. . .
Теперь эта программа сможет подтвердить, что тигр по имени Питер - это
действительно тигр, если мы добавим в нее некоторые из свойств Питера (в виде
прологовских фактов):
питер имеет шерсть.
питер ленив.
питер большой.
питер имеет 'рыжевато-коричневый цвет'.
питер имеет 'черные полосы'.
питер ест мясо.
Тогда мы можем спросить:
?- питер это тигр.
?- питер это гепард.
Хотя пролог-система и отвечает на вопросы, используя для этого нашу базу
знаний, нельзя сказать, что ее поведение вполне соответствует поведению
эксперта. Это происходит по крайней мере по двум причинам:
(1) Мы не можем попросить систему объяснить свой ответ; например, как она
установила, что Питер это тигр, и почему Питер это не гепард.
(2) Прежде, чем задать вопрос, нужно ввести в систему всю необходимую
информацию (в виде прологовских фактов). Но тогда пользователь, возможно,
введет какую-нибудь лишнюю информацию (как в нашем примере) или же упустит
какую-нибудь информацию, имеющую решающее значение. В первом случае будет
проделана ненужная работа, а во втором - система будет давать неверные ответы.
Для того, чтобы исправить эти два недостатка, мы нуждаемся в более
совершенном способе взаимодействия между пользователем и системой во время и
после завершения процесса рассуждений. Поставим себе целью добиться того, чтобы
система взаимодействовала с пользователем так, как в следующем примере диалога
(ответы пользователя даются полужирным шрифтом, реплики пролог-системы -
курсивом):
Пожалуйста, спрашивайте:
питер это тигр.
Это правда: питер имеет шерсть?
да.
Это правда: питер ест мясо?
нет.
Это правда: питер имеет острые зубы?
да.
Это правда: питер имеет когти?
почему.
Чтобы проверить по прав3, что питер это хищник,
Чтобы проверить по прав5, что питер это тигр
Это был ваш вопрос
Это правда: питер имеет когти?
да.
Это правда: питер имеет глаза, направленные вперед?
да.
Это правда: питер имеет рыжевато-коричневый цвет?
да.
Это правда: питер имеет черные полосы?
да.
(питер это тигр) это правда
Хотите узнать, как?
да.
питер это тигр
было выведено по прав5 из
питер это хищник,
было выведено по прав3 из
питер это млекопитающее
было выведено по прав1 из
питер имеет шерсть
было сказано
и
питер имеет острые зубы
было сказано
и
питер имеет когти
было сказано
и
питер имеет глаза, направленные вперед
было сказано
и
питер имеет рыжевато-коричневый цвет
было сказано
и
питер имеет черные полосы
было сказано
Как видно из диалога, система задает пользователю вопросы, касающиеся
"примитивной" информации, например:
Это правда: питер ест мясо?
Эту информацию нельзя отыскать в базе знаний или вывести из другой
информации. На подобные вопросы пользователь может отвечать двумя способами:
(1) сообщив системе в качестве ответа на вопрос необходимую информацию
или
(2) спросив систему, почему эта информация необходима.
Последняя из двух возможностей полезна, поскольку она позволяет
пользователю заглянуть внутрь системы и увидеть ее текущие намерения.
Пользователь спросит "почему" в том случае, когда вопрос системы
покажется ему не относящимся к делу либо когда ответ на вопрос системы
потребует от него дополнительных усилий. Из объяснений системы пользователь
поймет, стоит ли информация, которую запрашивает система, тех дополнительных
усилий, которые необходимо приложить для ее приобретения. Предположим,
например, что система спрашивает: "Это животное ест мясо?"
Пользователь, не знающий ответа на этот вопрос, поскольку он никогда не видел,
как это животное ело что-либо, может решить, что не стоит ждать, пока он
застанет животное за едой и убедится, что оно действительно ест мясо.
Для того, чтобы заглянуть внутрь системы и до какой-то степени
представить себе протекающий в ней процесс рассуждений, можно воспользоваться
прологовскими средствами трассировки. Но эти средства в большинстве случаев
окажутся недостаточно гибкими для наших целей. Поэтому, вместо того, чтобы
воспользоваться собственным механизмом интерпретации Пролога, который не сможет
справиться с нужным нам способом взаимодействия с пользователем, мы создадим
свое средство интерпретации в виде специальной надстройки над пролог-системой.
Этот новый интерпретатор будет включать в себя средства для взаимодействия с
пользователем.
Процесс
рассуждений
Наш интерпретатор будет принимать вопрос и искать на него ответ. Язык
правил допускает, чтобы в условной части правила была И / ИЛИ-комбинация
условий. Вопрос на входе интерпретатора может быть такой же комбинацией
подвопросов. Поэтому процесс поиска ответов на эти вопросы будет аналогичен
процессу поиска в И / ИЛИ-графах, который мы обсуждали в гл. 13.
Ответ на заданный вопрос можно найти несколькими способами в соответствии
со следующими принципами:
Для того, чтобы найти ответ Отв на вопрос В, используйте одну из
следующих возможностей:
· если В найден в базе знаний в виде факта, то Отв - это
"В это правда"
· если в базе знаний существует правило вида
· "если Условие то В",
· то для получения ответа Отв рассмотрите Условие
· если вопрос В можно задавать пользователю, спросите пользователя
об истинности В
· если в имеет вид В1 и В2, то рассмотрите В1, а затем,
если В1 ложно, то положите Отв равным "В это ложь", в противном
случае рассмотрите В2 и получите Отв как соответствующую комбинацию ответов на
вопросы В1 и В2
· если В имеет вид В1 или В2, то рассмотрите В1, а затем,
если В1 истинно, то положите Отв равным "В1 это правда", в противном
случае рассмотрите В2 и получите Oтв как соответствующую комбинацию ответов на
вопросы В1 и В2.
Вопросы вида
не В
обрабатываются не так просто, и мы обсудим их позже.
Формирование
ответа на вопрос "почему"
Вопрос "почему" возникает в ситуации, когда система просит
пользователя сообщить ей некоторую информацию, а пользователь желает знать,
почему эта информация необходима. Допустим, что система спрашивает:
а - это правда?
В ответ пользователь может спросить:
почему?
Объяснение в этом случае выглядит примерно так:
Потому, что
Я могу использовать а,
чтобы проверить по правилу Па, что b, и
Я могу использовать b,
чтобы проверить по правилу Пb, что с, и
Я могу использовать с,
чтобы проверить по правилу Пc, что d, и
. . .
Я могу использовать y,
чтобы проверить по правилу Пy, что z, и- это ваш исходный вопрос.
Объяснение - это демонстрация того, как система намерена использовать
информацию, которую она хочет получить от пользователя. Намерения системы
демонстрируются в виде цепочки правил и целей, соединяющей эту информацию с
исходным вопросом.
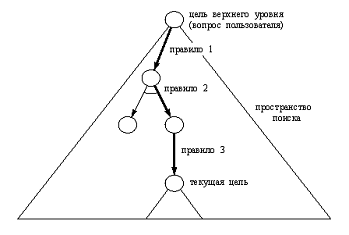
Рис. 14. 8. Объяснение типа "почему". На вопрос "Почему
вас интересует текущая цель?" дается объяснение в виде цепочки правил и
целей, соединяющей текущую цель с исходным вопросом пользователя, находящимся в
верхушке дерева. Эта цепочка называется трассой.
Будем называть такую цепочку трассой. Трассу можно себе представлять как
цепочку правил, соединяющую в И / ИЛИ-дереве вопросов текущую цель с целью
самого верхнего уровня так, как это показано на рис. 14.8. Таким образом, для
формирования ответа на вопрос "почему" нужно двигаться в пространстве
поиска от текущей цели вверх вплоть до самой верхней цели. Для того, чтобы
суметь это сделать, нам придется в процессе рассуждений сохранять трассу в
явном виде.
Формирование
ответа на вопрос "как"
Получив ответ на свой вопрос, пользователь возможно захочет увидеть, как
система пришла к такому заключению. Один из подходящих способов ответить на
вопрос "как" - это представить доказательство, т. е. те правила и
подцели, которые использовались для достижения полученного заключения. Это
доказательство в случае нашего языка записи правил имеет вид решающего И /
ИЛИ-дерева. Поэтому наша машина логического вывода будет не просто отвечать на
вопрос, соответствующий цели самого верхнего уровня - этого нам недостаточно, а
будет выдавать в качестве ответа решающее И / ИЛИ-дерево, составленное из имен
правил и подцелей. Затем это дерево можно будет отобразить на выходе системы в
качестве объяснения типа "как". Объяснению можно придать удобную для
восприятия форму, если каждое поддерево печатать с надлежащим отступом,
например:
питер это хищник
было выведено по прав3 из
питер это млекопитающее
было выведено по прав1 из
питер имеет шерсть
было сказано
и
питер ест мясо
было сказано
15. Рассуждения, использующие логические формулы. Рассуждения по
поводу знаний
Исчисление
предикатов содержит правила вывода, применимые к одним логическим формулам для
получения других. Особенно важны правила «modus
ponens» ( Если Х и (Х 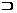 Y) - теоремы, то Y есть теорема)
и «обобщения» (Если х не связана в теореме Р, то
Y) - теоремы, то Y есть теорема)
и «обобщения» (Если х не связана в теореме Р, то  хР -
теорема). Правила вывода порождают некоторое множество формул из примитивных
(исходных, первоначальных) формул. В исчислении предикатов выведенные формулы
называются «теоремами», а последовательность примененных для их получения
правил вывода (с указанием используемых в них формул) - «доказательством
теоремы». Многочисленные приложения исчисления предикатов к ИИ можно толковать
как методы доказательства теорем.
хР -
теорема). Правила вывода порождают некоторое множество формул из примитивных
(исходных, первоначальных) формул. В исчислении предикатов выведенные формулы
называются «теоремами», а последовательность примененных для их получения
правил вывода (с указанием используемых в них формул) - «доказательством
теоремы». Многочисленные приложения исчисления предикатов к ИИ можно толковать
как методы доказательства теорем.
При
доказательстве теорем обычно используют процедуры опровержения. Множество
гипотез {Hj}, подходящих для доказательства теоремы, добавляют к
множеству присущих области экспертизы аксиом {Ai}. Затем
стремятся получить опровержение (или прийти к противоречию), присоединяя {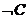 } - отрицание утверждения теоремы - к системе {Hj, Ai} и
пытаясь доказать формулу
} - отрицание утверждения теоремы - к системе {Hj, Ai} и
пытаясь доказать формулу
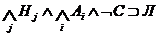 .
.
Эта
формула логически эквивалентна формуле
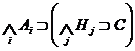 .
.
Процедуры,
позволяющие строить доказательства формул такого типа, называются «доказательствами
посредством опровержения». Они помогают избегать менее перспективных
направлений поиска. Системы доказательства теорем во многих приложениях
включают формулы логики предикатов с переменными, связанными кванторами
существования. В таких случаях доказательства позволяют находить конкретизации
этих переменных.
Например,
интересно выяснить, можно ли формулу 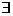 хС(х)
логически вывести из гипотез и аксиом. Если да, то хотелось бы знать конкретизацию
для х в терминах вывода. Попытка доказать
хС(х)
логически вывести из гипотез и аксиом. Если да, то хотелось бы знать конкретизацию
для х в терминах вывода. Попытка доказать 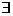 хС(х) из
{Hj, Ai} должна быть конструктивной. Проиллюстрируем подобное
доказательство следующим примером.
хС(х) из
{Hj, Ai} должна быть конструктивной. Проиллюстрируем подобное
доказательство следующим примером.
Рассуждения
по поводу знаний
В
большинстве встречающихся в ИИ систем относящихся к области экспертизы знания
делятся на две категории: «факты» и «правила» . Факты - это данные
(представленные предикатами), касающиеся области экспертизы. Например, данные о
персонале некоторого университета составляют множество фактов.
· Факт(1)
По-русски: Жак - профессор факультета информатики.
Логически: Проф(Инфо, Жак_2).
· Факт(2).
По-русски: Мари - студентка математического факультета,
Логически: Студ (Мат, Мари-4).
Правила - это данные, представленные с помощью импликации или в иной
эквивалентной логической форме. Они представляют собой обобщающие знания об
области экспертизы.
· Правило(1)
По-русски: Если y -
профессор факультета х и w
студент(ка) факультета z при x≠z, то y
может служить внешним экзаменатором для w.
Логически:
Проф (x,y)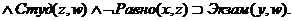
Задача
доказательства (обоснования) теоремы состоит в установлении выводимости из
фактов и правил некой формулы («предложения-цели», «заключения»), представляющий
некоторый вопрос.
· Предложение-цель (1).
По-русски: Может ли Жак служить внешним экзаменатором для Мари?
Логически: Экзам(Жак_2. Мари_4).
Можно применять различные приемы для выработки стратегий доказательства
теоремы.
16.
Язык Prolog. Термы и объекты. Факты и
элементарные вопросы
Термы и объекты
В Прологе объекты (т.е. элементы) универсума рассуждения представляются с
помощью термов так же, как в логике. В силу того, что язык эти термы не
интерпретирует, объекты сами являются термами - синтаксическими объектами одной
из следующих категорий:
· индивидные константы (атомы)
· переменные
· функции (функциональные термы), состоящие из имени функции и
списка аргументов-термов
Синтаксис различает атомы, переменные и функции. Используемые соглашения
сообразны конкретным применениям. Здесь мы используем синтаксис Си-Пролога.
Однако выбор конкретной версии языка Пролог не влияет на различие между
переменной (именем нарицательным) и константой (именем собственным).
· Атом записывается тремя способами:
- как идентификатор, начинающийся со строчной буквы жаклин генрих_4
(допускается использование подчёркивания)
как число 123 1.23
как произвольную последовательность символов, расположенную между
апострофами ‘Что Вы говорите’ ‘Больше нечего сказать’
· Переменная - это идентификатор, начинающийся с прописной
буквы Х Имя Король_Франции
· Функция - это имя функции, за которым следует список термов,
помещённых в скобки и разделённых запятыми. Имя функции - это нечисловой атом.
автор(книга, 1987) f(X) ‘Что ты говоришь?’(штука)
На практике прологовская программа представляет собой некую
действительность, а термы - реальные объекты. Например, при описании библиотеки
атомами будут имена авторов и/или издателей, годы издания, названия и т.д., а
функциями - издательства и/или книги:
издат(дюно, 1987) книга(жюль_верн, мишель_строгофф, издат(этцель, 1876))
Каждый атом - это отдельный объект, считающийся элементарным.
Предпочтительны мнемонические идентификаторы, а не анонимные (вроде х2 и bb). То же относится и к функциональным
термам: лучше взять издат(_,_), а не и(_,_). Отметим, что в программе на
Прологе функциональный терм является структурой данных, сложным объектом,
который можно эффективно построить или анализировать. Это не функция,
сопоставляющая результат набору аргументов.
Данные (константы) Пролога - это термы, не имеющие переменных. В логике
они называются индивидными термами (а также константными термами). Числовые
атомы - это константы для программирования численных расчётов.
Факты и элементарные вопросы
Простые предикаты (атомарные формулы и/или предикатные формы) формальной
логики, такие, как Автор(Эрнани,Гюго)принимают значения И или Л. Почти то же
самое имеет место для фактов и вопросов Пролога, не содержащих переменных.
Простой предикат Пролога записывается в виде функционального терма, например:
автор(эрнани.гюго) дифф(Х,Х,1) Предикат от функции отличают по контексту.
Простые предикаты являются составляющими базы фактов и вопросов. Приведём
пример небольшой программы, представляющей собой множество фактов:
/* библио*/
книга(грэм, ‘рассуждать, чтобы программировать’ ,издат(дюно,1986)).
книга(кондиляк, ‘пролог’, издат(дюно,1986)).
книга(дьедонне, ‘математика’, издат(эрман,1986)).
книга(гюго, ‘отверженные’, издат(пош,1984)).
книга(гюго, ‘эрнани’, издат(галлимар,1974)).
книга(хартман, ‘параллельный паскаль’, издат(шпрингер,1977)).
библиотекарь(эмиль).
начальник(эмиль, анри).
начальник(жозев, анри).
идёт_дождь.
Точка, стоящая после предиката, указывает на то, что рассматриваемое
выражение является фактом. Первая строка - это комментарий: любая
последовательность символов, записанная между парой ограничителей /* и */, при
выполнении игнорируется. Каждый факт, содержащийся в программе, имеет
соответствующее значение истинности и порождает (определяет) отношение между
термами. Например, двухместное отношение (предикат) начальник установлено между
термами эмиль и анри, а трёхместное отношение книга - для 6 троек термов и т.д.
Последний факт в приведённом примере - идёт дождь - является нульместным
отношением (не имеющим аргументов).
Множество фактов можно рассматривать как реляционную БД. Впрочем, мы
употребляем понятие базы данных для обозначения множества фактов и правил некой
программы.
Из простых предикатов строят также вопросы, например: ? -
начальник(эмиль, анри).
Это выражение нового факта не устанавливает, но «система запрашивает о
том, установлен или нет данный факт. Значение вопроса (т.е. ответ) зависит от
БД. В нашем примере вопрос простой, переменные и правила отсутствуют. Значение
есть И, если в БД содержится факт с предикатом вопроса. В противном случае
значение есть Л. Всё это интуитивно ясно. На практике задаётся
последовательность «вопрос - ответ»:
? - начальник(эмиль, анри).
- > да
Таким образом, простейшие программы на Прологе регистрируют элементарные
факты в БД и отвечают на вопросы, связанные с этими фактами. Сама же БД
определяет некие расширения содержащихся в ней отношений. Например: идёт_дождь,
начальник(_,_), библиотекарь(_) и книга(_,_,_). Простые вопросы, не содержащие
никаких переменных, называются да-нет-вопросами. Они допускают лишь два
возможных ответа в соответствии с тем, имеется или отсутствует подходящий факт
в БД. Семантика вопроса определяется состоянием БД при поиске ответа. Для БД
библио имеем:
? - книга(грэм, ‘рассуждать, чтобы программировать’ ,издат(дюно,1986)).
- - > да
? - книга( ‘рассуждать, чтобы программировать’ ,издат(дюно,1986)).
- - > нет
? - начальник(эмиль, генри).
- - > нет
? - идёт_дождь(сейчас)
- - > нет
Так как в Прологе нет объявления и контроля типов, то нет и ошибок программирования.
Неверно написанное пользователем имя для системы является новым атомом: анри и
генри - два атома, которые не имеют ничего общего. Бинарное отношение не
годится в качестве тернарного, зато тернарное отношение задаёт три бинарных
отношения с одинаковыми именами - для трёх пар из трёх аргументов: отношения
книга(_,_) и книга(_,_,_) для системы различны, чем и обусловлен ответ на
второй приведённый выше вопрос.
17. Системы прямой дедукции. Системы обратной дедукции
Системы прямой дедукции
В системах прямой дедукции новые знания получают, применяя выводы к
фактам и правилам. Алгоритм завершает работу при получении некоторого знания,
эквивалентного цели (или непосредственно влекущего ее). Для иллюстрации системы
прямой дедукции обратимся снова к предыдущему примеру. Докажем теорему
(Факт
(1)  Факт (2)
Факт (2)  Правило
(1))
Правило
(1)) 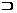 Цель (1).
Цель (1).
· Этап(1):
Преобразуем Факт(1) и Правило (1)) в дизъюнкты, чтобы применить затем
метод резолюций. С помощью резолюции выводим новое правило (2), используя
обозначение
Факт(1) Правило (1)
Правило (2)
Факт(1): Правило (1):
Проф(Инфо,
Жак_2) 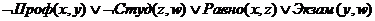
Правило
(2): 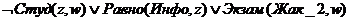
· Этап (2): из Факта (2) и Правила (2) резолюцией выводим новый
Факт(3):
Факт(2): Правило(2)
Студ(Мат,
Мари_4) 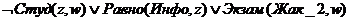
Факт(3):
Экзам(Жак_2, Мари_4)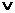 Равно(Инфо,Мат)=Л
Равно(Инфо,Мат)=Л
(Отношение
Равно(Инфо,Мат)=Л должно быть явно указано в БД)
· Этап (3):
Факт(3) соответствует Цели(1). Следовательно, она подтверждена.
Аналогично выведем утверждение Л из Факта(3) и отрицания Цели(1):
Факт(3):
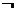 Цель(1):
Цель(1):
Экзам(Жак_2,
Мари_4) 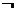 Экзам(Жак_2, Мари_4)
Экзам(Жак_2, Мари_4)
Систему
прямой дедукции можно трактовать как систему, в которой применяется теорема о
прямой дедукции: Если F1, F2, … , Fn, G - логические выражения, то G является
логическим следствием из F1, F2, … , Fn тогда и только тогда, когда логическое выражение(F1 …
…  Fn
Fn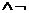 G) тождественно
ложно, т.е. невыполнимо. Правила вывода и стратегии, используемые в системах
прямой дедукции, графически представимы И/ИЛИ - деревьями.
G) тождественно
ложно, т.е. невыполнимо. Правила вывода и стратегии, используемые в системах
прямой дедукции, графически представимы И/ИЛИ - деревьями.
Системы
обратной дедукции
В
системах обратной дедукции выводы применяют к цели и к правилам, чтобы
построить новые частичные цели. Алгоритм завершает работу, когда все частичные
цели соответствуют фактам. Такую систему можно толковать с логической точки
зрения как систему, в которой применяется теорема об обратной дедукции, которая
гласит: Если F1, F2, … , Fn, G - логические выражения, то G является
логическим следствием из F1, F2, … , Fn тогда и только тогда, когда логическое выражение (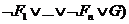 тождественно истинно, т.е. общезначимо.
тождественно истинно, т.е. общезначимо.
В
системах обратной дедукции правила и цели преобразуют в конъюнкты, чтобы
применить затем правило согласия
· Этап (1): из Цели (1) и отрицания Правила(1), используя
правило согласия, выводим новую Цель (2):
Цель(1)
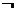 Правило(1)
Правило(1)
Экзам(Жак_2.
Мари_4) 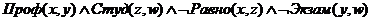
Цель(2):
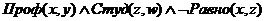
· Этап (2): из Цели (2) и отрицания Факта(1), с помощью правила
согласия, выводим Цель (3):
Цель(2):
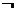 Факт(1):
Факт(1):
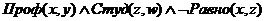
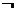 Проф(Инфо, Жак_2)
Проф(Инфо, Жак_2)
Цель
(3):
Студ(z,
Мари_4)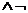 Равно(Инфо, z)
Равно(Инфо, z)
· Этап (3): из Цели (3) и отрицания Факта(2) выводим теорему:
Цель
(3): 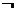 Факт(2):
Факт(2):
Студ(z,
Мари_4)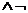 Равно(Инфо, z)
Равно(Инфо, z) 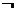 Студ(Мат,
Мари_4)
Студ(Мат,
Мари_4)
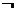 Равно(Инфо,Мат)=И
Равно(Инфо,Мат)=И
18.
Язык Prolog. Конъюнкция. Переменные
Конъюнкция
В логических формулах используют связки и простые предикаты. То же самое
имеет место и в Прологе. Самую ходовую связку - конъюнкцию - обозначают
запятой:
? - начальник(эмиль, анри), начальник(жозев, анри).
Это выражение соответствует такой логической формуле
Начальник(Эмиль,
Анри)  Начальник(Жозев, Анри).
Начальник(Жозев, Анри).
Конъюнкция
в Прологе, как и в логике, истинна только при истинности всех компонент. Однако
имеется важное отличие: в Прологе семантика учитывает порядок оценки компонент
(слева направо)
Переменные
Использование
переменных в Прологе аналогично, но не идентично использованию их в логике.
Вопросы, включающие переменные носят перечислительный характер (в отличие от
да-нет-вопросов): ответы в этом случае представляют собой списки термов.
Например, вопрос «Кто в подчинении у Анри?» является вопросом
«перечислительного» («списочного») типа. Ответ БД библио мог бы быть [эмиль,
жозеф].
Прологовским
эквивалентом местоимения «кто» является переменная:
?
- начальник(Х, анри).
Ответ
здесь хотелось бы получить посредством замены Х на такую константу, для которой
в БД найдётся подходящий факт. Взяв константу Эмиль получаем:
?
- начальник(Х, анри).
-
- > Х=эмиль
Система
ответила одним значением переменной, преобразовав вопрос в истинный предикат,
но почему не жозеф и не [эмиль, жозеф]? Для объяснения произвольности выбора
вникнем в алгоритм получения ответа. Факты и правила БД - это не множество, а
список. Обычно они текстуально упорядочены. Для получения ответа система
просматривает БД в соответствующем порядке и выбирает первое удовлетворяющее
предикату вопроса выражение.
Предикат
вопроса представляет собой цель. Здесь это начальник(Х, анри).
Цель
достигнута, если в БД удалось найти факт или правило, который (которое)
удовлетворяет этому предикату. Чтобы удовлетворить приведённому только что
простому предикату, нужно иметь факт вида начальник(_, анри), т.е. факт,
содержащий:
· такое же имя предиката (начальник),
· столько же аргументов (два),
· те же константы на тех же местах (анри на втором месте)
При выполнении этих условий факт соответствует (следовательно,
удовлетворяет) предикату. В нашем примере годится факт начальник(эмиль, анри).
Переменная Х принимает значение той константы, которая стоит на
соответствующем месте в найденном факте. Хотя объяснять несколько долго, но это
именно то, что подсказывает интуиция.
Ещё один способ выразить семантику рассмотренного выше вопроса состоит в
формулировании следующего запроса: «Можно ли сопоставить (присвоить, назначить)
переменной Х такой терм, чтобы результатом была формула из БД?» Утвердительный
ответ обеспечивает назначение Х=эмиль. Это лишь одно из возможных
назначений-ответов. Си-Пролог в интерактивном режиме даёт все ответы, если
после каждого ставить точку с запятой:
? - начальник(Х, анри).
- - > Х=эмиль;
- - > Х=жозеф;
- - > нет
Нет означает исчерпание возможностей.
Если вопрос ? - начальник(Х, анри). считать обращением к процедуре, то
константа анри будет входом, а переменная Х - результатом. Это взгляд
пользователя, но не Пролога. В выражениях, содержащихся в БД, различие между
аргументами не производится. Лишь в вопросах переменные «заказывают» значения
для ответов, например:
? - начальник(жозеф, Y).
- - > Y=анри;
- - > нет
? - начальник(Х, Y).
- - > Х=эмиль, Y=анри;
- - > Х=жозеф, Y=анри;
- - > нет
Переменные
можно также использовать в фактах: начальник(Х, адемар). Это выражение является
записью на Прологе фразы «Адемар - большой начальник» и логической формулы 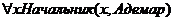 . Цель вида начальник(_, адемар) достигается в том
случае, если в БД содержится факт начальник(Х, адемар).
. Цель вида начальник(_, адемар) достигается в том
случае, если в БД содержится факт начальник(Х, адемар).
При
использовании переменной в конъюнкции переменная устанавливает связь между
сомножителями конъюнкции. Разумеется, все вхождения переменной принимают одно и
то же значение. Ответ на вопрос ? - начальник(Х, анри), библиотекарь(Х). («Над
каким библиотекарем Анри начальник?») получается путём последовательного
удовлетворения двух частей (достижения двух частичных целей, подцелей)
конъюнкции. Первая часть начальник(Х, анри), удовлетворяется фактом
начальник(эмиль, анри). реализующим присваивание (назначение) Х=эмиль. Если бы
первая подцель не достигалась, то ответ на весь вопрос был бы - нет.
Присваивание значения переменной Х преобразует вторую подцель библиотекарь(Х) в
библиотекарь(эмиль) которая достигается. Полный ответ
-
- > Х=эмиль.
Для
получения второго ответа система сперва ищет второе достижение второй подцели.
Это всегда библиотекарь(эмиль). при дальнейшем пробегании по БД в предписанном
порядке (Дублирование выражений запрещено). Подцель теперь не достигается
вновь. Система возвращается к предыдущей подцели начальник(Х, анри). т.е.
осуществляет возврат. Подцель вновь достигается при использовании факта
начальник(жозеф, анри). Отсюда получаем присваивание Х=жозеф и т.д. В
рассмотренном нами примере только один ответ, ибо недостижима цель
библиотекарь(жозеф), средствами (фактами) БД библио.
19. Концептуальные графы. Пример и терминология
Концептуальные графы содержат прямоугольники для представления аргументов
и круги для имен предикатов. Круг соединяется стрелкой с прямоугольником, если
они представляют соответственно имя и аргумент одного и того же предиката.
Предикаты могут иметь несколько аргументов. Следовательно, круги могут
иметь несколько входящих и/или выходящих стрелок. Большинство предикатов,
используемых для представления знаний, обладает двумя аргументами (бинарные
предикаты). Тогда круги соединены с прямоугольниками двумя стрелками: входящей
и выходящей.
Снова обратимся к примеру. На рисунке изображен концептуальный граф
предиката Посылка (Жак_2, Мари_4, Книга_22), формализующий фразу «Жак посылает
книгу Мари».

На следующем рисунке приведен концептуальный граф логического
представления той же фразы бинарными предикатами, т.е. граф, соответствующей
формуле
Отправитель(
Посылка_8, Жак_2)
Получатель(Посылка_8,
Мари_4) 
Объект(Посылка_8,
Книга_22) 
Элем(Посылка_8,
посылки).

При
графическом представлении бинарных предикатов круги иногда опускают, а имена
предикатов указывают на стрелках. Напомним, что в одной из прошлых лекций было
описано общее правило преобразования m-арного предиката (m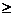 2) вида
2) вида
Предикатное_имя(знчение_1,
знчение_2, …, значение_ m) в произведение m бинарных
предикатов
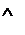 Функция_j(предикатное_имя,
значение_j).
Функция_j(предикатное_имя,
значение_j).
Свяжем
с каждым бинарным оператором концептуальный граф, как показано на следующем
рисунке.

Стрелки предикатов направлены от первого аргумента предиката (предикатное
имя) к имени предиката (Функция_j) и
от имени предиката ко второму аргументу (значение_j). В записи, называемой по-английски slot-assertion, имя предиката соответствует "имени слота", а значение -
"значению слота". Вообще в концептуальных графах "значение
слота" соответствует некоторому концепту.
Графическое представление m-арных
предикатов основано на следующем соглашении. Стрелка, соответствующая m-арному аргументу, направлена к
прямоугольнику, представляющему этот аргумент. Все остальные стрелки направлены
от прямоугольников к кругу, представляющему имя предиката. Стрелки помечены от
1 до m, чтобы явно показать соответствие
между стрелкой и аргументом (первый рисунок нашего примера).
Вообще имя бинарного предиката представляет некую функцию. Узел
концептуального графа, указывающий это имя, называется связывающим узлом, ибо
он связывает два концепта, представленных двумя аргументами бинарного
предиката. Функция, представленная этим связывающим узлом, носит по той же
причине название концептуального отношения. Термины "имя бинарного
предиката" и "аргумент", представляющие соответственно функцию и
концепт, часто заменяются на "связывающий узел" и
"узел-концепт" в графическом представлении.
20.
Язык Prolog. Переменные. Анонимные переменные
Использование переменных в Прологе аналогично, но не идентично
использованию их в логике. Вопросы, включающие переменные носят
перечислительный характер (в отличие от да-нет-вопросов): ответы в этом случае
представляют собой списки термов. Например, вопрос «Кто в подчинении у Анри?»
является вопросом «перечислительного» («списочного») типа. Ответ БД библио мог
бы быть [эмиль, жозеф].
Прологовским эквивалентом местоимения «кто» является переменная:
? - начальник(Х, анри).
Ответ здесь хотелось бы получить посредством замены Х на такую константу,
для которой в БД найдётся подходящий факт. Взяв константу Эмиль получаем:
? - начальник(Х, анри).
- - > Х=эмиль
Система ответила одним значением переменной, преобразовав вопрос в
истинный предикат, но почему не жозеф и не [эмиль, жозеф]? Для объяснения
произвольности выбора вникнем в алгоритм получения ответа. Факты и правила БД -
это не множество, а список. Обычно они текстуально упорядочены. Для получения
ответа система просматривает БД в соответствующем порядке и выбирает первое
удовлетворяющее предикату вопроса выражение.
Предикат вопроса представляет собой цель. Здесь это начальник(Х, анри).
Цель достигнута, если в БД удалось найти факт или правило, который
(которое) удовлетворяет этому предикату. Чтобы удовлетворить приведённому
только что простому предикату, нужно иметь факт вида начальник(_, анри), т.е.
факт, содержащий:
· такое же имя предиката (начальник),
· столько же аргументов (два),
· те же константы на тех же местах (анри на втором месте)
При выполнении этих условий факт соответствует (следовательно,
удовлетворяет) предикату. В нашем примере годится факт начальник(эмиль, анри).
Переменная Х принимает значение той константы, которая стоит на
соответствующем месте в найденном факте. Хотя объяснять несколько долго, но это
именно то, что подсказывает интуиция.
Анонимные переменные
Переменные, которые рассматривались выше, имели имена. Существуют и
анонимные переменные. Допустим, что мы интересуемся наличием в БД библио хотя
бы одной книги Виктора Гюго. Вопрос
? - книга(гюго, Х,Y).
вызовет последовательность ответов
- - > Х=отверженные, Y=издат(пош,1984);
- - > Х=эрнани, Y=издат(галлимар,1974);
- - > нет
Это не совсем то, что надо: - предполагалось получить «да» или «нет».
Однако, заменяя Х и Y анонимными
переменными (знак подчёркивания), получаем то, что хотели: на вопрос
? - книга(гюго, _,_). ответ будет
Для получения списка авторов, книги которых имеются в наличии, ставим
следующий вопрос:
? - книга(А, _,_). Это даёт нам такой список
- - > А=грэм;
- - > А=кондиляк;
- - > А=дьедоне;
- - > А=гюго;
- - > А=гюго;
- - > А=хартман;
- - > нет
Анонимные переменные не отличаются от обычных при поиске соответствий, но
не принимают значений и не появляются в ответах. Отметим, что различные вхождения
знака подчёркивания означают различные анонимные переменные.
21. Семантические сети. Правила конъюнкции и упрощения
Ранее указывалось, что каждый концептуальный граф представляет одну
логическую формулу. Семантическая сеть гораздо сложнее. Она представляет не
только набор (соединение) формул, но также описывает их взаимосвязи и
погружение их в контекст области рассуждений. Семантические сети получаются из
концептуальных графов по правилам соединения, которые будут введены посредством
примеров.
Правила конъюнкции и упрощения
Рассмотрим набор из трех фраз:
Фраза 1: Жак пишет книгу.
Фраза 2: Жак посылает эту книгу Мари.
Фраза 3: Мари читает эту книгу (которую Жак ей послал).
Каждую из этих фраз можно представить либо формулой исчисления
предикатов, либо концептуальным графом. Первый этап построения семантической
сети основан на использовании двух следующих формальных правил получения
концептуального графа g из
двух графов g1 и g2.
Правило конъюнкции. Если узел-концепт с1 в g1 идентичен узлу-концепту с2 в g2, то g
получается удалением с2 и соединением с с1 всех связывающих узлов, которые были
связаны с с2 в g2.
Правило упрощения. Если концептуальный граф g содержит два идентичных (соединенных с одними и теми же
узлами-концептами) связывающих узла, то можно удалить один из них вместе со
связанными с ним стрелками.
Применим правило конъюнкции к приведенному примеру. "Книга, которую
написал Жак, которую он послал Мари и которую Мари читала" представляется
конкретизацией Книга_22. Эта конкретизация книги появляется в концептуальных
графах, представляющих рассмотренные выше фразы 1), 2), 3). Группирование
конкретизаций Книга_22, Жак_2 и Мари_4 порождает концептуальный граф,
изображенный на следующем рисунке. На нем рамками выделены графы фраз 1, 2, 3 и
граф группы фраз.

22.
Язык Prolog. Правила. Рекурсивные правила
Последним и самым мощным видом выражений в Прологе являются правила
обобщающие понятие факта. Например, для построения семейной БД можно
перечислить родительские отношения при помощи списка фактов:
мать(каролина,юлия). мать(каролина, альбертина). Выражать фактами отношения
внуков с дедами необходимости нет, ибо они могут быть выведены из отношений
предшествования «Х является дедом Y, если существует субъект Z, отец
которого Х и который сам отец или мать Y». На Прологе это высказывание записывается в виде двух
правил: дед(Х,Y):-отец(Х,Z), мать(Z,Y). дед(Х,Y):-отец(Х,Z),
отец(Z,Y)., где символ «:-» читается «если» («при условии, что»).
Вообще правило выглядит так: Н:-Р1,Р2, … , Рn, где Н,Р1,Р2, … , Рn - простые предикаты. Это выражение читается следующим образом: «Н если
(Р1 и Р2 …и Рn)». Предикат Н называется заголовком
правила, а последовательность Р1,Р2, … , Рn - телом правила.
Приведённые
только что правила являются аналогом предложения Н, если (Р1  Р2 …
Р2 … Рn),
или выражения (Р1
Рn),
или выражения (Р1  Р2 …
Р2 … Рn)
Рn)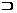 Н или формулы ¬Р1
Н или формулы ¬Р1 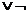 Р2 …
Р2 … Рn
Рn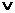 Н, которые суть различные записи хорновских
дизъюнктов. Приведённое правило похоже, кроме того, на объявление процедуры в
языке программирования.
Н, которые суть различные записи хорновских
дизъюнктов. Приведённое правило похоже, кроме того, на объявление процедуры в
языке программирования.
Заголовок
правила дед(Х,Y) объявлен как и тело правила отец(Х,Z),
мать(Z,Y). Это правило указывает на то, что вопрос, имеющий
форму ? - дед(андре,каролина). преобразуется в вопрос ? - отец(андре,Z),
мать(Z,каролина). Наличие правила (как и факта) в БД
означает общезначимость соответствующей формулы. Считается, что все переменные
в правиле связаны кванторами общности. Например, правило дед(Х,Y):-отец(Х,Z),
мать(Z,Y). толкуется как 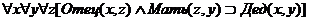 .
.
Правила
- самые общие выражения Пролога, факт представляет собой правило без правой
части, а вопрос - без левой:
Н
истинно, если Р1 и Р2 …и Рn истинны (правило),
Н
истинно (факт или правило без тела),
Р1
и Р2 …и Рn истинны? (вопрос или правило без заголовка).
Рассмотрим
следующую БД:
мать(каролина,юлия).
мать(каролина,
альбертина).
мать(мари,проспер).
мать(анна,каролина).
отец(проспер,юлия).
отец(проспер,альбертина).
отец(альфонс,проспер).
отец(андре,каролина).
дед(Х,Y):-отец(Х,Z),
мать(Z,Y).
дед(Х,Y):-отец(Х,Z),
отец(Z,Y).
бабка(Х,Y):-мать(Х,Z),
мать(Z,Y).
бабка(Х,Y):-мать(Х,Z),
отец(Z,Y).
Отношения
мать и отец заданы фактами, а отношение дед и бабка определяются с помощью
правил.
На
вопрос ? - дед(альфонс,юлия). ответов среди фактов нет (ни один факт не
соответствует предикату вопроса). Но заголовки некоторых правил соответствуют
этому предикату.
Цель
заголовка какого-либо правила считается достигнутой (как и для факта) при
совпадении имени предиката, числа аргументов в нём и констант стоящих на
соответствующих местах предиката. Так, например факт дед(альфонс,юлия) обеспечивает
реализуемость (удовлетворение, достижение) цели дед(Х,Y). Переменным
из заголовка правила присваиваются значения: Х=альфонс, Y=юлия.
Новой целью будет далее тело с новыми значениями переменных отец(альфонс,Z),отец(Z,юлия).
Эта последовательность предикатов обрабатывается как последовательность
подцелей. Их достижение обеспечивается присваиванием Z=проспер.
В
итоге получаем последовательность вопрос-ответ
?
- дед(альфонс,юлия).
-
- > да
Значение
внутренней (отсутствующей в вопросе) переменной не входит в ответ. Это вполне
естественно, ибо вопрос «да-нет» и переменные X, Y, Z
нужны только для вычисления (нахождения) ответа.
Рекурсивные
правила
База
данных семья должна отвечать на вопрос является ли Х предком Y.
Определение предиката «быть предком» рекурсивно. Для предков по женской линии
соответствующие правила на Прологе записываются так. предок(Х,Y):-мать(Х,Y).
предок(Х,Y):-мать(Х,Z),предок(Z,Y).
Такие рекурсии разрешается использовать, иначе язык был бы слишком примитивным.
Рекурсивное определение предиката обязательно должно содержать базис, т.е.
нерекурсивную часть, иначе оно будет логически некорректным и программа
зациклится. Чтобы избежать зацикливания, надлежит, кроме того, позаботиться о
порядке выполнения, а следовательно, и порядке написания соответствующих
выражений. Поэтому практически полезно, а порой и необходимо придерживаться
принципа: «сначала нерекурсивные выражения».
23. Представления контекста. Пример введения кванторов
Представление контекста
Сам по себе концептуальный граф несет немного информации, тогда как
включение в семантическую сеть позволяет связать его концепты и функциональные
связи с областью рассуждений (экспертизы). Например, Книга_22 - конкретизация
слова "книга", которое представляет абстрактное понятие (или, иначе,
тип). Отношение принадлежности типу представлено связывающим узлом (именем
предиката) Конкр (от слова "конкретизация"). Кроме факта, что
Книга_22 относится к типу "книга", мы хотим показать, что она
принадлежит некоторому "множеству книг" (например, из библиотеки
некоторого университета). Отношение принадлежности множеству представлено
связывающим узлом (именем предиката) Элем (от слова "элемент"). На
рисунке конкретизации Жак_2, Кни га_22 и Мари_4
связаны с различными типами и множествами, которым они принадлежат.
Отметим, что "тип" употребляется в абстрактном смысле (абстрактный
тип). Утверждения о типах аналитические, например: средний возраст студентов
университета двадцать лет.

Наоборот, свойства множеств - синтетические: число студентов университета
равно десяти тысячам.
Используем связывающий узел, представляющий имя предиката Подмн для
представления отношения между двумя множествами, из которых первое -
подмножество второго. Как Элем объявляет о принадлежности элемента множеству,
Подмн означает включение одного множества в другое. Элем и Подмн отражают
принадлежность множеству.
Связывающий узел Это используется для представления отношения между
первым типом и более общим вторым. Напомним, что предикат Конкр когда-то
использовался нами для представления принадлежности индивида типу. Это и Конкр
отражают принадлежность типу.
Концепты в семантических сетях обладают различными свойствами, делящимися
на аналитические (свойства "типа") и синтетические (свойства
"множества"). Важно учитывать это различие при построении сетей,
чтобы избежать некорректных выводов.
Представление «совокупность - ссылка»
Существует графическое представление (эквивалентное рассмотренным ранее)
с узлами, представляющими типы и называемыми «узлами-совокупностями» или
«родовыми узлами», представляющими конкретизации типов и называемыми
«узлами-индивидами» или «узлами-ссылками»
Семантическая сеть образуется последовательностями из трёх узлов,
соединённых так: за узлом -ссылкой (например, представляющей конкретизацию
Книга_22) следует связывающий узел Конкр, сопровождаемый узлом совокупностью
(например, представляющим тип «книга»).
Используя метод Совы, эти три узла можно сгруппировать и представить
одним «узлом-прямоугольником», состоящим из двух полей: из «поля-совокупности»,
содержащего некоторый тип, и следующего за этим полем «поля ссылки», например с
конкретизацией типа из первого поля (следующий рисунок). Здесь поле ссылки (справа
от двоеточия) представляет тип. Представление [книга: Книга_22] (или короче,
[книга:22]) означает вполне определённый объект типа «книга». Представление
[книга: х] означает просто какой-то объект типа «книга». Отметим, что наличие
переменной в правом поле необязательно. Например, можно заменить представление
[книга: х] эквивалентным ему представлением [книга] (рисунок).

Пример
Фразы
· Жак посылает (вполне определённую) книгу Мари,
· Жак посылает (какую-то) книгу Мари
представляются двумя графами, которые можно выделить на следующем
рисунке: первая фраза - графом без элементов с (2), вторая фраза - графом без
элементов с (1).

Пример введения кванторов
Введем графическое обозначение кванторов на примере трех фраз:
· (1): Жак посылает (какую-то) книгу каждой женщине,
· (2) :Жак посылает всякую книгу каждой женщине,
· (3): Жак посылает (одну и ту же) книгу каждой женщине.
Запишем эти фразы в логике предикатов
· (1): 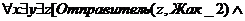
Получатель
(z,x) Объект(z,y)
Объект(z,y)
Конкр(z,
посылка) Конкр(y, книга)
Конкр(y, книга)
Конкр(
х, женщина)],
· (2): 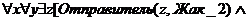
Получатель
(z,x) Объект(z,y)
Объект(z,y)
Конкр(z,
посылка) Конкр(y, книга)
Конкр(y, книга)
Конкр(
х, женщина)],
· (3): 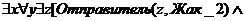
Получатель
(z,x) Объект(z,y)
Объект(z,y)
Конкр(z,
посылка) Конкр(y, книга)
Конкр(y, книга)
Конкр(
х, женщина)],
Перевод
с логического языка на графический осуществляется по следующим правилам.
Прежде
всего концептуальный граф делят на иерархическое множество зон, каждая из
которых соответствует области одного или нескольких кванторов. Например,
рассмотрим логическую форму фразы (1). Соответствующий граф изображён на
следующем рисунке (элементы с (2) удалить). Для графического изображения нужно
ввести обозначение области действия кванторов общности по переменной х. С этой
целью установим иерархию прямоугольников концептуального графа. На этом и
следующем за ним рисунках жирно выделены прямоугольники наивысшего порядка. Они
содержат конкретизацию (Конкр) концепта совокупности «формула под квантором
общности» (на последних рисунках, о которых идёт речь, этот концепт обозначен  Квант-форм). Каждая переменная под квантором общности
в этих формулах представлена связывающим узлом под знаком
Квант-форм). Каждая переменная под квантором общности
в этих формулах представлена связывающим узлом под знаком  .
.
Читатель
может проверить, что с учётом этих соглашений относительно записи предпоследний
рисунок, о котором идёт речь, без элементов (2), изображает формулу (1), что он
же, но вместе с элементами, помеченными знаком (2), изображает формулу (2) и
что последний рисунок, о котором идёт речь, представляет формулу (3).


24. Язык Prolog.
Дизъюнкция. Отрицание
Дизъюнкция
Чистый Пролог разрешает применять только конъюнкцию в вопросах и
правилах. Язык, используемый на практике, богаче: в нём допускаются дизъюнкция
и отрицание в телах правил и вопросах (т.е. целях, которые исследуются на
достижимость). Рассмотрим снова БД библио и следующие выражения со связкой
дизъюнкции, обозначаемой точкой с запятой: начальник(Х,анри);библиотекарь(Х)
Оно является аналогом логической формулы
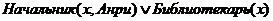 .
.
Для
достижения цели, содержащей дизъюнкцию, система сперва пытается удовлетворить
левую часть рассматриваемой дизъюнкции, а если это не удаётся, то переходит к
поиску удовлетворения для правой части той же дизъюнкции. Для нашего примера
имеем:
?
- начальник(Х,анри);библиотекарь(Х).
-
- > Х=эмиль;
-
- > Х=жозеф;
-
- > Х=эмиль;
-
- > нет.
В
этом простом примере дизъюнкция не включена ни в какой более сложный предикат и
поэтому всё дело свелось к двум последовательным вопросам. Первый предикат
удовлетворён дважды, второй - один раз (причём независимо от первого).
Отрицание
В
Прологе отрицание имеет имя not и для представления отрицания какого-либо выражения Р
используется запись not(P). Цель not(P) достижима тогда и только тогда, когда не
удовлетворяется предикат (цель) Р. При этом переменным значения не
присваиваются. В самом деле, если достигается Р, то не достигается not(P);
значит, надо стереть все присваивания, приводящие к этому результату, наоборот,
если Р не достигается, то переменные не принимают никаких значений. Рассмотрим
пример, связанный с БД библио:
?
- not(начальник(эмиль,арсен)).
-
- > да
?
- not(начальник(эмиль,Х)).
-
- > нет
Чтобы
обработать отрицание, Пролог рассматривает возможность проведения
доказательства как эквивалент значения Л. Следовательно not(P)
считается истинным тогда и только тогда, когда не удовлетворяется Р. Подход
этот в высшей степени прагматический, не имеющей эквивалента в логике.
25. Сетевое представление знаний. Временные и модальные операторы
Используемые в логике знания глаголы (например, «полагать» и «знать»)
относятся к объектам, которые могут быть целыми фразами. Эти глаголы
пронизывают иерархическую графическую структуру, в которой целые графы можно
интерпретировать как узлы графов высшего порядка.
Фразу «Жак посылает книгу Мари» изображают классическим концептуальным
графом в отличие от фразы «Поль полагает, что Жак посылает книгу Мари»,
отражённый (с пометкой (с)) в центральной части графа на следующем рисунке. Из
этого рисунка видно, что Мысль_8 принадлежит типу мысль. Объект Мысль_8 -
концепт типа (точнее, с «меткой типа») высказывание. Ссылка Мысль_8 - граф
фразы «Жак посылает книгу Мари». Полагающий это человек - Поль_6.
Любую форму модальной логики можно рассматривать в духе этого примера. В
модальной логике всегда можно отделить пропозициональную часть фразы (выразимую
в логике предикатов) от собственно модальности. При изображении концептуальных
графов пропозициональная часть поля ссылки концепта обозначена типом
высказывание. Такие модальности, как ◊,, полагает, знает суть
концептуального отношения графа. На рисунке фраза «Не может быть так, чтобы
Поль полагал, будто Жак посылает книгу Мари» представлена в виде
концептуального графа.

26. Язык Prolog. Области
действия имен
предикат логика знание логический
В Прологе программист свободен в выборе имён констант, переменных,
функций и предикатов. Исключение составляют резервированные имена и числовые
константы. Переменные не объявляются, отличаясь от констант первой буквой
(строчная или прописная). Разные обозначения представляют разные объекты. Есть
довольно очевидные исключения. Например, 133.1 и 133.10 - одно и то же число.
Область действия имени представляет собой часть программы, где это имя
имеет один и тот же смысл (как во всех языках программирования). В Прологе:
· для переменной областью действия является выражение (факт,
правило или вопрос), её содержащее,
· для остальных имён (констант, функций или предикатов) - вся
программа.
Многократно можно использовать в одной программе лишь имена переменных. В
приводимом ниже фрагменте из БД семья имеются: два вхождения имени каролина -
это одна и та же константа, четыре вхождения имени (предикатного) мать - один и
тот же предикат (всюду двухместный). Но переменные первого и вотрого правил
независимы (это интуитивно ясно).
мать(каролина,юлия).
мать(каролина, альбертина).
дед(Х,Y):-отец(Х,Z), отец(Z,Y).
бабка(Х,Y):-мать(Х,Z), мать(Z,Y).
27. Канонические графы. Правила построения. Унаследованные свойства
В концептуальном графе есть узлы-концепты и узлы-связи (связывающие
узлы). Каждая входящая в связывающий узел стрелка (или выходящая из него)
соединена с узлом концептом. Однако некоторые комбинации узлов бессмысленны.
Например, можно изобразить графом фразу «удалить последнее слово следующей
строки» (какого-то текста). С позиций грамматики эта фраза синтаксически и
семантически корректна. Напротив фраза «удалить последнюю строку следующего
слова» синтаксически корректна, но абсурдна (семантически некорректна). Чтобы
исключить графы нереальных (невозможных) ситуаций области рассуждений, Сова
определил канонические (семантически корректные) графы разрешённых комбинаций
слов. Каждый составляет представление о мире, выразимом каноническими графами,
исходя из личного опыта.
Таким образом, возможный путь построения таких графов следующий: мозг
вырабатывает систему концептов, базируясь на поступающих ощущениях, и так
расставляет сформированные концепты, чтобы они отражали реальную ситуацию.
Следовательно, можно считать, что мозг строит канонические графы,
представляющие, вообще говоря, очевидности (другими словами тавтологии
исчисления предикатов). Новые канонические графы строятся из имеющихся по
определённым правилам построения. Эти правила формируют порождающую грамматику
для концептуальных графов точно так же, как это делается посредством правил
переписывания Хомского в случае порождающих грамматик для синтаксических
структур естественных языков.
Правила построения
Сова предложил четыре правила построения для конструирования нового
канонического графа g из имеющихся
графов g1 и g2 (которые могут совпадать):
Правило конъюнкции: Если узел-концепт с1 в g1 идентичен узлу-концепту с2 в g2, то g
получается удалением с2 и соединением с с1 всех связывающих узлов, которые были
связаны с с2 в g2.
Правило упрощения. Если концептуальный граф g содержит два идентичных (соединенных с одними и теми же
узлами-концептами) связывающих узла, то можно удалить один из них вместе со
связанными с ним стрелками.
Правило копирования: граф g есть
копия графа g1.
Правило ограничения: Для любого концепта с концептуального графа g тип (с) можно заменить неким
подтипом. Если с - концепт совокупности, то её ссылку можно заменить
индивидуальным указателем (какой-то конкретизацией). Такие замены разрешены
лишь тогда, когда ссылка для с соответствует типу (с).
Проиллюстрируем эти правила на концептуальных графах представленных на
следующем рисунке. Граф без элементов с (2) - для фразы «Жак срочно посылает
книгу кому-то» Граф без элементов с (1) - для фразы «Жак посылает почтой книгу
Мари». Применение правила конъюнкции к этим двум графам даёт весь граф
изображённый на рисунке. Можно было бы далее применить к последнему графу
правило ограничения, заменяя обозначенную х совокупность «кому-то» меньше
совокупностью «женщина». Однако прежде надо убедиться в свойстве «Мари -
женщина». Предыдущие правила являются фактически правилами суждения:
ограничение сужает концепты, а конъюнкция добавляет условия на графах.
Аналогично можно определить правила расширения, которые представляют собой
правила, обратные к правилам суждения.

Унаследованные свойства
Форма различных концептов, типов и множеств во многих приложениях
иерархическая. Классификация животных по родам, видам, семействам, отрядам и
т.д. - классический пример иерархии. Другой пример - множество слов в словаре.
Книги, транспортные средства и постройки образуют иерархически упорядоченные
множества. Можно иерархически классифицировать и абстрактные концепты действий,
состояний, свойств, убеждений. Используемые в обыденных рассуждениях
классификации, как правило, сложнее биологических: индивид принадлежит, вообще
говоря, не одному типу и не одному множеству. Однако в большинстве случаев для
ИИ используются сравнительно простые иерархии.
Сначала проиллюстрируем иерархию типов на примере, а затем дадим
формальное определение. Если известно, что Жак (представленный конкретизацией
Жак_2) - профессор университета, то можно сделать заключение о наличии у него
докторской степени и о том, что он работает в университете. Информация «Жак -
профессор университета» предоставила нам целую цепочку сведений о Жаке.
Унаследованными называют такие свойств, которые можно вывести подобным образом.
Особых причин детально останавливаться на них нет. Ясно, что кое-какие
характеристики профессоров университета можно описать исходя из принадлежности
к профессуре; некоторые характеристики профессуры выносятся из того факта, что
они содержатся в совокупности работников умственного труда, и, в конечном
счёте, всех людей. Соображения эффективности побуждают нас не связывать с Жаком
все общие профессоров университета, вообще профессоров и, наконец, всех людей.
Весьма общее свойство, как например, «У Жака две руки и две ноги»,
сопоставляется узлу, характеризующему всех людей. Это даёт возможность не
провозглашать наличие указанного свойства отдельно, для каждого индивида.
28. Язык Prolog. Сложные
термы, или структуры
Структурные объекты (или просто структуры) - это объекты, которые состоят
из нескольких компонент. Эти компоненты в свою очередь могут быть структурами.
Например, дату можно рассматривать как структуру, состоящую из трех компонент:
день, месяц, год. Хотя они и составлены из нескольких компонент, структуры в
программе ведут себя как единые объекты. Для того, чтобы объединить компоненты
в структуру, требуется выбрать функтор. Для нашего примера подойдет функтор date. Тогда дату 1-е мая 1983 г. можно
записать так.
date
(1, may, 1983).
Все компоненты в данном примере являются константами (две компоненты-
целые числа и одна- атом). Компоненты могут быть также переменными или
структурами. Произвольный день в мае можно представить структурой
date (Day, may, 1983).
Заметим, что Day является
переменной и ей можно приписать произвольное значение на некотором более
позднем этапе вычислений.
Синтаксически все объекты данных в Прологе представляют собой термы.
Например,
May
и
date(1,
may, 1983)
суть термы.
Следующий пример показывает, как можно использовать структуры для представления
геометрических объектов.

Рис 7. Простые геометрические объекты.
Точка в двумерном пространстве определяется двумя координатами; отрезок
двумя точками, а треугольник можно задать тремя точками. Введем следующие функторы:
tochka
для точек
otrezok
для отрезков и
treugolnik для треугольников
Тогда объекты представленные на Рис. 7. можно представить следующими
прологовскими термами:
P1 = tochka (1, 1)= tochka (2, 3)= otrezok (P1, P2) =
otrezok (tochka (1, 1), tochka (2, 3))= treugolnik (tochka
(1, 1), tochka (7, 1), tochka (6, 4))
Если представить эти объекты в виде деревьев (Рис. 8) (как впрочем и
любые другие объекты), то функтор, служащий корнем дерева называется главным
функтором терма.

Рис. 8. Представление объектов с рис. 7 в виде деревьев
Если бы в такой же программе фигурировали точки трехмерного пространства,
то можно было бы для их представления использовать другой функтор, например:
Tochka3
(X, Y, Z)
Можно, однако, воспользоваться одним и тем же именем tochka одновременно и для точек двумерного
и для точек трехмерного пространств и написать, например, так
tochka
(X1, Y1) и tochka
(X, Y, Z)
Если одно и то же имя появляется в программе в двух различных смыслах,
как в вышеупомянутом примере с точкой, то поролог-система будет различать их по
числу аргументов и интерпретировать это имя как два функтора: один -
двухаргументный; второй - трех. Это возможно потому, что каждый функтор
определяется двумя параметрами:
1) именем, синтаксис которого совпадает с синтаксисом атомов;
2) арностью - т.е. числом аргументов.
Все структурные объекты в Прологе - это деревья, представленные в
программе термами. Рассмотрим еще два примера, чтобы понять насколько удобно
сложные объекты данных представляются с помощью прологовских термов. На рис. 9
показано древовидная структура, соответствующая арифметическому выражению
(а+в)*(с-5)

Этот, совершенно правильный прологовский терм, конечно не соответствует
той форме, которую нам хотелось бы иметь при записи арифметических выражений.
Хотелось бы применять обычную инфиксную запись принятую в математике.
29.
Решетки типов, иерархия типов. Определение типа посредством рода и различия
Пусть
t1 и t2 - метки типов, если t1 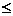 t2, то t1 - подтип типа t2, а t2 -
надтип типа t1. Типы «профессор» и «студент» имеют много общих
надтипов: «работник умственного труда», «человек», «высшее млекопитающее». В
графе «работник умственного труда» - наименьший общий надтип для «профессора» и
«студента». Типы « профессор» и «сотрудник университета» имеют общий подтип
«профессор университета». В графе «профессор» и «студент» не имеют общего подтипа.
t2, то t1 - подтип типа t2, а t2 -
надтип типа t1. Типы «профессор» и «студент» имеют много общих
надтипов: «работник умственного труда», «человек», «высшее млекопитающее». В
графе «работник умственного труда» - наименьший общий надтип для «профессора» и
«студента». Типы « профессор» и «сотрудник университета» имеют общий подтип
«профессор университета». В графе «профессор» и «студент» не имеют общего подтипа.
Для
преобразования иерархической формы в решётку надо ввести две особые метки
соответственно в высшей и низшей точках иерархии - универсальный тип U
(надтип всех типов) и абсурдный тип А (подтип всех типов). Иерархия типов даст
решётку типов со всеми свойствами решётки:
· любая пара меток t1 и t2 имеет наименьший общий надтип,
· любая пара меток t1 и t2 имеет наибольший общий подтип,
· для любого
типа t выполняется соотношение А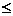 t
t 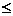 U.
U.
Данное отношение порядка представляется функциональным отношением Это.
Конкр означает принадлежность индивида типу.
Решётки множеств и решётки типов
Можно также ввести отношение порядка для множеств (подмножество
множества) с помощью предиката Подмн или связывающего узла с тем же именем. При
одноэлементном подмножестве Подмн заменяется на Элем. Иерархия типов позволила
упорядоченно классифицировать свойства типов, а иерархия множеств - свойства
множеств. Следующий рисунок иллюстрирует различие составных частей двух
иерархий. Введём на концептуальных графах (в духе классики) несколько функций и
операторов, действующих над множеством типов. Прежде всего - функция тип. Она
отображает множество концептов на множество Т, элементы которого называются
метками (ярлыками) типа. Концепты с1 и с2 имеют один общий тип, если тип(с1) =
тип(с2). Денотатом типа t
называется множество всех тех сущностей, которые являются конкретизациями
некоторого концепта типа t.
Оператор, сопоставляющий типу t его
денотат, обозначается через Денот. Тип профессор_университета есть подтип типа
профессор. Следовательно, денотат Денот(профессор_университета) является подмножеством
Денот(профессор).

Каждой конкретизации (например, Жак_2) сопоставимо два вида узлов: узел
описания типа конкретизации и узел описания множества, которому принадлежит эта
конкретизация. Таким образом, имеем три вида узлов: узел, представляющий
индивида (конкретизацию), который через промежуточные связывающие узлы соединён
с узлами типа (Конкр) и множества (Элем). Естественно ввести четвёртый вид: {x| тип} - для произвольного индивида
{х} определённого типа (тип).
Профессор х (о котором больше ничего не известно) обозначен {х| проф}.
Этот узел соединен с узлом, представляющим множество профессоров, через
связывающий узел Элем. С другой стороны, он соединён с узлом, представляющим
тип профессора, через связывающий узел Абст. Оператор Абст определяет тип
(абстрактный концепт) по описанию какого-либо элемента этого типа. Наконец,
можно определить оператор «прототип_для», который можно считать приблизительно
обратным оператору Абст. Оператор «прототип_для» (Протот) представляется
связывающим узлом, который соединяет тип с описанием этого типа, даваемым
«прототипом». Последний позволяет сжато описать мир, разделённый по типам
объектов. Описание, даваемое прототипом, можно рассматривать как описание
некоторого типичного представителя множества. Следовательно, прототип -
разновидность мифической константы. Узел прототипа отличается от узла {x| тип}, который доставляет множество
общих свойств объектов одного типа или одного множества. В этом смысле
операторы Абст и Протот не являются взаимно обратными.
С абстрактным концептом «профессора университета» связано свойство
обладания докторской степенью. С другой стороны, вполне вероятно, что каждый
индивид из множества «профессоров университета» имеет докторскую степень.
Следовательно, соответствующие иерархии типов и множеств, приведённые на этом
рисунке изоморфны (каждому элементу одной системы соответствует один элемент
другой системы, а каждой операции в одной системе - операция в другой).
Определение типа посредством рода и различия.
Фраза «Жак посылает книгу Мари». Соответствующая запись её логической
формулой такова:
Отправитель
(посылка: 8, мужчина: Жак_2)
Получатель(посылка:
8, женщина: Мари_4)  Объект(посылка: 8, книга: 22) (6)
Объект(посылка: 8, книга: 22) (6)
В
таком представлении каждое значение аргумента типизировано, т.е. ему приписана
некая метка типа. Определение типа должно задавать множество необходимых и
достаточных условий, характеризующих тот факт, что рассматриваемый объект
является объектом типа.
Можно
определить метки типов, используя так называемый Аристотелев подход, - через
род (genus) в различие (differentia).
Тип определяется исходным типом род и высказыванием, называемым различие и
отделяющим новый тип от исходного. Например, Посылка - «событие (род), которое
происходит, когда два человека, отправитель и получатель, обеспечивают
перемещение предмета по почте (различие)». Формально:
Тип
Посылка (х) есть (род)
Конкр(х,
событие) 
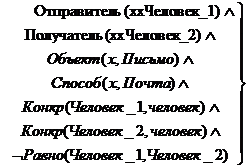 (различие)
(различие)
Определение
типов можно формализовать с помощью λ-выражений. Пусть t -метка типа, λxF - λ-выражение.
Тогда тип t(x) есть F, где тело F этого λ-выражения является различием метки t, а t(x) -
её родом. На следующем рисунке приведено определение типа ресторана с
использованием концептуального графа.

30. Язык Prolog. Операторы.
Синтаксис операторов
Напомним, что функциональный терм - это имя функции с аргументами в
скобках. Само имя функции представляет собой нечисловой атом. Вообще же
нечисловой атом - это функциональный терм без аргументов. Любой терм можно
представить в виде дерева, корню которого приписано имя внешней функции, а
ветвям соответствующие наборы аргументов. Например, терм f(x, g(y,z)) задаётся следующим деревом:

Такое представление является канонической формой: она не зависит от
способа записи термов. Каноническую форму полезно бывает использовать в тех
случаях, когда требуется уточнить представление термов (некоторые термы могут
быть записаны многими способами). В частности, для термов с одним или двумя
аргументами функциональное обозначение можно заменить именем операции, причём
имя функции-операции записывается как унарный префиксный (или постфикный)
оператор, либо как бинарный инфиксный оператор: ор1 с а ор2 b вместо ор1(с) ор2(а,b). При этом именам функций-операций
(ор1 и ор2) надо придать статус операторов с приоритетом. Очевидно, что
выражения а ор2 b и ор2(а,b) задают один и тот же объект:

Новые имена функций и предикатов можно записывать в виде операторов.
Например, a+b*c и +(a*(b,c)) один и тот же
терм; его дерево выглядит так:

Приоритет «+» ниже, чем у «*» (как обычно). Подчеркнём, что a + b * c -
терм Пролога, а не числовой оператор, описывающий процедуру вычисления.

31. Прототипы. Схемы и схематические кластеры
Определить какой-то тип можно ещё путём демонстрации нескольких примеров
индивидов «некоего типа» и утверждая, что всё, чем похожи индивиды, относится к
обсуждаемому типу. Прототип - это конкретизация типа или, иначе, типовая
конкретизация. Метод прототипов описывает скорее типичного индивида некоего
класса, чем произвольного представителя этого класса с набором характерных
свойств.
Прототип указывает свойства, истинные в типичном, но не обязательно в
каждом отдельном случае. Он позволяет гибко определять класс объектов. Прототип
содержит фиксированную часть (соответствующую тому общему, что есть у всех
конкретизаций этого класса) и переменную часть (обязательную или нет, свою для
каждой конкретизации).
Схемы и схематические кластеры
Концептуальный граф служит для представления знаний. Его можно также
использовать для рассуждений и вычислений. Для этого введём понятие схемы,
увязав его с правдоподобными и имеющими смысл рассуждениями. Схему можно
определить, вводя последовательно ограничения на концептуальный граф.
· В произвольном концептуальном графе не накладываются никакие
ограничения на расстановку узлов.
· Канонически графы имеют семантические ограничения,
представляя нечто «семантически корректное» или «понятное».
· Схемы включают «специфические знания» об области рассуждений
(экспертизы), представляя всё правдоподобное.
Понятие схемы подразумевает не только определение, но и способ
применения. Для иллюстрации этого аспекта сначала сравним определение схемы и
типа. Формальное определение схемы дадим потом. Каждый концепт имеет ровно одно
определение его типа, дающее необходимые и достаточные условия принадлежности
конкретизации определённому типу.
Каждому типу можно сопоставить несколько схем, каждая из которых будет
представлять один из способов применения концепта данного типа. Это приводит к
понятию «множества схем» как возможного источника информации, эквивалентной
определению типа. А сам концепт можно определить «множеством его формальных
применений».
Для формального описания концепта было введено понятие кластера или
набора схем. Каждая из них указывает способ применения данного концепта. Набор
всех возможностей применения типа называется его схематическим кластером.
Каждую схему можно формализовать с помощью λ-выражений действуя так как при
определении типа посредством рода и различия. Пусть λxF - представляющее схему λ
- выражение. Формальный
параметр х будет представлять концепт того типа, который требуется определить,
а тело F укажет один из способов применения
этого типа. Здесь F - логическая
формула или представляющий её канонический граф.
Определим схематические кластеры с помощью λ-выражений. Схематический кластер для
класса t есть множество {λx1F1, … , λxpFp}
λ-выражений, где
каждый формальный параметр xi
принадлежит типу t и каждое
выражение λxiFi -
схема для типа t.
В отличие от определений типа, выражающих необязательные условия, схема
не обязательно истинна при всяком применении. При заданном схематическом
кластере соответствующий концепт применим, если хотя бы одна схема из этого
кластера окажется истинной для этого применения.
Теперь сравним определение понятия схемы и прототипа. Схемы показывают
типичные способы использования концептов. Они не описывают типичных
конкретизаций для этих концептов. Напротив, прототип - это типичная
конкретизация. Понятия схемы и схематического кластера позволяют более
формализовано определить прототип.
Прототип р для типа t есть
λ-выражение λxF со следующими свойствами:
· Формальный параметр х принадлежит типу t.
· Прототип р получается сочетанием (по правилу конъюнкции)
одной или нескольких схем из схематических кластеров для t и ограничением (по правилу
ограничения) части или всех концептов этих схем только
концептами-совокупностями (без индивидов).
При подходящих реализациях схемы соответствуют созвездиям, фреймам
(кадрам) и сценариям (предписаниям).
32. Язык Prolog.
Арифметические действия
Пролог рассчитан главным образом на обработку символьной информации, при
которой потребность в арифметических вычислениях относительно мала. Поэтому и
средства для таких вычислений довольно просты. Для осуществления основных
арифметических действий можно пользоваться несколькими предопределенными операторами.
+ сложение
- вычитание
* умножение
/ деление
mod
модуль, остаток от целочисленного деления.
Следующий вопрос - наивная попытка произвести арифметическое действие:
?- Х =1+ 2
Пролог-система «спокойно» ответит
Х = 1+2
а не Х=3, как возможно ожидалось. Причина этого проста: выражение 1+2
обозначает лишь прологовский терм, в котором + является функтором, а 1 и 2 -
его аргументами. В вышеприведенной цели нет ничего, что могло бы заставить
систему выполнить операцию сложения. Для этого в Прологе существует специальный
оператор is (есть). Этот оператор заставит
систему выполнить вычисление. Таким образом, чтобы правильно активизировать
арифметическую операцию надо написать
?- Х is 1 + 2
Вот теперь ответ будет
Х=3
Сложение здесь выполняется специальной процедурой, связанной с оператором
+. Мы будем называть такие процедуры встроенными.
В Прологе не существует общепринятой нотации для записи арифметических
действий, поэтому в различных реализациях она может слегка различаться.
Например, оператор ‘/’ в одних реализациях означать целочисленное деление, а в
других вещественное. В нашей реализации ‘/’ означает вещественное деление, а
для целочисленного же будем использовать оператор ‘//’. В соответствии с этим
на вопрос
?- Х is 3 / 2,
Y is 3 // 2.
ответ должен быть такой
Х = 1.5
Y = 1.
Левым аргументом оператора is
является простой объект. Правый аргумент - арифметическое выражение,
составленное с помощью арифметических операторов, чисел и переменных. Поскольку
оператор is запускает арифметические вычисления,
к моменту начала вычисления этой цели все ее переменные должны быть
конкретизированы какими-либо числами. Приоритеты этих предопределенных
операторов выбраны с таким расчетом, чтобы операторы применялись к аргументам в
том порядке, который принят в математике. Чтобы изменить обычный порядок
вычислений, применяются скобки (тоже, как в математике). Заметьте, что +, -, *,
/, // определены как yfx,
что определяет порядок их выполнения слева направо. Например,
Х is 5 - 2 -1
понимается как
Х is (5 -2) - 1
Арифметические операции используются также и при сравнении числовых
величин. Мы можем, например, проверить, что больше 10000 или результат
умножения 277 на 37 с помощью цели
?- 277 * 37 > 10000
yes
Заметьте, что так же как и is,
оператор ‘>’ вызывает выполнение вычислений.
Предположим, у нас есть программа, в которую входят отношения рожд,
связывающее имя человека с годом его рождения. Тогда имена людей, родившихся
между 1950 и 1960 годами включительно, можно получить при помощи такого
вопроса:
?- рожд( Имя, Год),
Год >= 1950,
Год <= 1960.
Ниже перечислены операторы сравнения
X >
Y X больше Y
X <
Y X меньшеY
X
>= Y X больше или равенY
X
=< Y X меньше или равенY
X =:=Y величины X и Yсовпадают
(равны)
X =\=Y величины X иYне равны
Обратите внимание на разницу между операторами сравнения ‘=’ и ‘=:=’,
например в таких целях как X = Y и X =:= Y.
Первая цель вызовет сопоставление объектов X и Y, и
если X и Y сопоставимы, возможно приведет к конкретизации каких-либо
переменных в этих объектах. Никаких вычислений при этом производиться не будет.
С другой стороны X =:= Y вызовет арифметическое вычисление и
не может привести к конкретизации переменных. Это различие можно
проиллюстрировать следующими примерами
?- 1+2 =:= 2+1
yes
? - 1+2 =2+1
no
?- 1 + A = B + 2
A = 2
B =1.
Давайте рассмотрим использование арифметических операций на двух простых
примерах. В первом примере ищется наибольший общий делитель, во втором -
определяется количество элементов в некотором списке.
Если заданы два целых числа Х иY, то их наибольший общий делитель Д можно найти, руководствуясь
следующими тремя правилами:
1) Если Х иY
равны то Д равен Х.
2) Если Х >Y, то
Д равен наибольшему общему делителю Y и разности Х - Y.
) Если Y < Х, то
формулировка аналогична правилу 2), если Х иY поменять в нем местами.
На примере легко убедиться, что эти правила действительно позволяют найти
наибольший общий делитель. Выбрав, скажем, Х=20 и Y=25 мы руководствуясь приведенными правилами, после серии
вычитаний получим Д=5.
В нашем следующем примере требуется произвести некоторый подсчет, для
чего, как правило, необходимы арифметические действия. Примером такой задачи
может служить вычисление длины какого-либо списка; иначе говоря, подсчет его
элементов. Определим процедуру
длина( Список, N)
Которая будет подсчитывать элементы списка Список и конкретизировать N полученным числом. Как и раньше.
Когда речь шла о списках, полезно рассмотреть два случая:
1) Если список пуст, то его длина равна 0.
2) Если список не пуст, то Список = [Голова| Хвост] и его длина
равна 1 плюс длина хвоста Хвост.
Эти два случая соответствуют следующей программе:
длина([],0).
длина([_| Хвост], N):-
длина( Хвост, N1) ,
N is 1 + N1.
Применить процедуру длина можно так:
?- длина( [a,b, [c,d], e], N).
N=4
Заметим, что во втором предложении этой процедуры две цели его тела
нельзя поменять местами. Причина состоит в том, что переменная N1 должна быть конкретизирована до
того, как начнет вычисляться цель
N is 1+N1
Таким образом, мы видим, что введение встроенной процедуры is привело нас к примеру отношения,
чувствительного к порядку обработки предложений и целей. Очевидно, что
процедурные соображения для подобных отношений играют жизненно важную роль.
Итак
· Для выполнения арифметических действий используются
встроенные процедуры.
· Арифметические операции необходимо явно запускать при помощи
встроенной процедуры is.
Встроенные процедуры связаны также с предопределенными операторами +, -, *, /, // и mod.
· К моменту выполнения операций все их аргументы должны быть
конкретизированы числами.
· Значения арифметических выражений можно сравнивать с помощью
таких операторов, как <, =< и т.д. Эти операторы вычисляют значения своих
аргументов.
33. Рассуждения, использующие семантические сети
Одна из ключевых проблем организации памяти - эффективное управление данными
и запросами. При иерархической организации индивидуальные свойства связаны с
именами индивидов. Например, индивидуальные свойства Жака (возраст, адрес,
семейное положение и т.д.) связаны с именем Жак_2. Кроме того, наследственное
свойство связывает Жака с (абстрактным) концептом профессора университета.
Выходящие из узла Жак_2 стрелки представимы набором (конъюнкцией) бинарных
предикатов:
Возр(Жак_2,
45_лет) Адрес(Жак_2, ул_буля_7)
Адрес(Жак_2, ул_буля_7) 
Сем_пол(Жак_2,
холст)  Конкр(Жак_2, проф_унив).
Конкр(Жак_2, проф_унив).
Эти
предикаты указывают, что Жаку 45 лет, он проживает на улице Буля дом 7, холост
и принадлежит типу профессоров университета.
Различные
имена предикатов, связанные с узлами-индивидами образуют первое множество
гипотез (некой теоремы). Например, вопрос об адресе Жака выражается предикатом
Адрес(Жак_2, х). Этот предикат составит цель (заключение) теоремы, достоверные
гипотезы которой - названные выше свойства Жака. Доказательство сводится к
поиску конкретизации для х, позволяющей вывести заключение из гипотез. Проверка
показывает, что такой является ул_буля_7.
Иначе
обстоит дело с вопросом: «Какой диплом у Жака?», ибо мы не находим гипотезы
вида Диплом(Жак_2, …)
Но
если воспользоваться связью Конкр, можно получить подходящую гипотезу.
Связанная с узлом проф_унив часть графа представима логической формулой:
Конкр(х,
проф_унив) 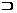 (Диплом(х, доктор)
(Диплом(х, доктор)  Место(х,
унив)
Место(х,
унив)  Это(х, проф)
Это(х, проф)  Это(х,
сотр_унив)).
Это(х,
сотр_унив)).
Если
добавить эту логическую формулу к множеству (индивидуальных) гипотез, то можно,
используя обычную технику доказательства теорем вывести, что Жак имеет
докторскую степень. Таким образом, новое множество гипотез и поставленный
вопрос составляют формулировку логической теоремы. Исходя из этой формулировки
и применяя обычный механизм доказательства, получаем ответ на вопрос.
Механизм
доказательства теорем в иерархической среде можно смоделировать следующим
образом. Вопрос (составляющий заключение или цель доказываемой теоремы) имеет
следующую общую форму.
По-русски:
Каково значение некоего индивида по отношению к некоторому свойству?
Логически:
Свойство_i(индивид_j, x)
Ожидаемый
ответ - конкретизация, представляющая некоторое значение для х. Сначала
попытаемся доказать эту теорему, пользуясь лишь гипотезами, прямо связанными с
узлом индивид_j в соответствующей графе. Эти гипотезы имеют следующую
форму.
По-русски:
Значение некоторого индивида по отношению к некоторому свойству есть …
Логически:
Свойство(индивид_j, значение_i).
Если
так доказать не удается, используем связь Конкр, исходящую из узла,
представляющего индивида и указывающего на новое множество гипотез, которое
имеет следующий вид.
По-русски:
Если индивид принадлежит типу t, то он имеет дополнительное множество значений по
отношению к дополнительному множеству свойств.
Логически:
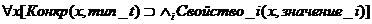
Из
этой логической формулы и предиката Конкр(индивид_j, тип_t)
выводим новое множество свойств относительно данного индивида. Если эти новые
гипотезы позволяют доказать нашу теорему, то доказательство закончено. Если же
нет, то связь Это укажет на тип повыше, который в свою очередь даст новое
множество гипотез. Эта процедура с последовательными множествами гипотез
заведомо эффективнее общего метода доказательства теорем, не использующего
иерархической структуры данных. Процедура вывода схематически изображена на
следующем рисунке.

34. Язык Prolog. Синтаксис
списков
Списки - это последовательности символьных элементов, которые сами могут
быть списками. Эти структуры данных очень полезны и популярны в символьном
программировании и в ИИ. В прологе для записи списков используют символьный
атом [] пустого списка и пары с точками - бинарные функциональные термы. Точка
- имя функции. Например, списками являются: [] .(a,X) .(a,.b[]))
Рекурсивное определение:
· атом [] является списком и представляет пустой список,
· если L -
список и Т - произвольный терм, то .(T,L) - список с головой Т и хвостом L.
Например, список, состоящий из элементов a,b и с есть терм
вида .(a,.(b,.(c,[])))
Однако для списков существует несколько лучший синтаксис:
· символьный атом [] представляет пустой список,
· непустой список - это последовательность термов, разделённых
запятыми и помещённых в квадратные скобки, причём термы любые, не обязательно
атомы или списки.
Например, [a,b,c], [эта, маленькая(шапка),[для, кюре]]
Непустой список допускает две эквивалентные записи «с точками» и «в
квадратных скобках». Например, [a]≡.(a,[]) [a,b,c]≡.(a,.(b,.(c,[])))

Представление деревьями - одно и то же для обоих обозначений (см. рис.
6.3). Обозначение [T|Q] представляет собой список с
заголовком Т и хвостом Q. [A,B,C|Q] представляет собой список с заголовком
А,В,С и хвостом Q. Эти
обозначения, использованные для удовлетворения целей, годны для анализа
списков:
? - [T|Q]=[a].
- - > T=a, Q=[]
? - [A1,A2,_,A4|Q]=[прекрасная, маркиза, ваши,
прекрасные, глаза]
- - > А1= прекрасная, А2 = маркиза, А4 = прекрасные, Q=[глаза]
35. Сцепки. Фреймы и слоты. Явные фреймы. Функциональные фреймы
Сцепки.
Предположим, что мы хотим представить фразы
: Жак пишет книгу.
: Жак посылает эту книгу Мари.
: Мари читает эту книгу (которую Жак ей послал).
В БД с этими фразами использовались конкретизации Жак_2, Мари_4,
Посылка_8 и Книга_22 для ссылок в объектном языке на имена концептов метаязыка,
упомянутые в этих фразах. Если расширить БД, то добавятся новые концепты и
дополнительная информация о них.
Жак_2
Пишет(Жак_2, Книга_22)
Посылает(Жак_2, Мари_4, Книга_22)
Мари_4
Посылает(Жак_2, Мари_4, Книга_22)
Читает(Мари_4, Кника_22)
Книга_22
Пишет(Жак_2, Книга_22)
Посылает(Жак_2, Мари_4, Книга_22)
Читает(Мари_4, Кника_22)
Фреймы и
слоты.
Если выразить эти фразы бинарными предикатами, то сцепки будут называться
фреймами. Нам известно, что тернарный предикат
Посылает(Жак_2, Мари_4, Книга_22)
Преобразуется в произведение бинарных предикатов
Отправитель
(Посылает, Жак_2)
Получатель(Посылает,
Мари_4) 
Объект(Посылает,
Книга_22).
Концепту
«посылает» соответствует следующий фрейм:
ФРЕЙМ
Посылает (объект)
Отправитель Жак_2 (слот_1)
Получатель Мари_4 (слот_2)
Объект Книга_22 (слот_3)
(атрибуты или (значения или
имена слотов) значения слотов)
Каждая пара (атрибут, значение) фрейма называется слотом или (имя_слота,
значение_слота). Сам фрейм по-английски - slot-and-filter notation. В этих обозначениях различные слоты
сгруппированы вокруг объекта, охарактеризованного фреймом.
Явные фреймы.
Мы знаем, что часто бывает полезно представление знаний с явным указанием
всех ссылок. Именно поэтому мы постулировали в нашем примере существование
вполне определенной Посылки_8. Фраза «Жак посылает книгу Мари» бинарными
предикатами представляется так:
Посылка_8
Элем посылки
Отправитель Жак_2
Получатель Мари_4
Объект
Книга_22
Следовательно, в процессе выявления ссылок можно не только дать явные
значения аргументов и имена предикатов, но также имена, представляющие
высказывания логических формул. Например, Посылка_8 - имя высказывания
Посылает(Жак_2, Мари_4, Книга_22). Такой формализм называется явным фреймом.
(по-английски case-frame).
Функциональны
фреймы.
Мы уже показывали, что представление бинарными предикатами легко можно
выразить в функциональной форме. Отношения между Посылка_8 и первоначальными
аргументами для посылает можно выразить функциями на множестве посылок. Введем следующие
функциональные обозначения для фреймов:
Посылка_8
элем : (элем_из посылок)
отправитель : Жак_2
получатель : Мари_4
объект : Книга_22
Форма «элемент_из» в слоте имеет имя «элем» для указания того, что
описанный фреймом объект является элементом некоторого множества (в нашем
примере это множество посылок). Определенный таким образом фрейм называется
функциональным.
36. Язык Prolog.
Представление списков
Список - это последовательность, составленная из произвольного числа
элементов, например, энн, теннис, том, лыжи. На Прологе это записывается так
[энн, теннис, том, лыжи ]
Однако таково лишь внешнее представление списка. Как мы уже видели, все
структурные объекты Пролога - это деревья. Списки не являются исключением из
этого правила.
Каким образом можно представить список в виде стандартного прологовского
объекта? Мы должны рассмотреть два случая: пустой список и не пустой список. В
первом случае список записывается как атом []. Во втором случае список следует
рассматривать как структуру, состоящую из двух частей:
1) первый элемент, называемый головой списка;
2) остальная часть списка, называемая хвостом.
Например, для списка
[энн, теннис, том, лыжи ]
энн - это голова, а хвостом является список
[теннис, том, лыжи ]
В общем случае, головой может быть что угодно (любой прологовский объект,
например, дерево или переменная); хвост же должен быть списком. Голова
соединяется с хвостом при помощи специального функтора. Выбор этого функтора
зависит от конкретной реализации Пролога; мы будем считать, что это точка:
.( Голова, Хвост)
Поскольку Хвост - это список, он либо пуст, либо имеет свои собственные
голову и хвост. Таким образом, выбранного способа представления списков
достаточно для представления списков любой длины. Наш список представляется
следующим образом:
.( энн, .( теннис, .(том, .( лыжи, [] ) ) ) )
На следующем рисунке изображена соответствующая древовидная структура.

Заметим, что показанный пример содержит пустой список []. Дело в том, что
самый последний хвост является одноэлементным списком:
[ лыжи ]
Хвост этого списка пуст
[ лыжи ] = .( лыжи, [] )
Рассмотренный пример показывает. Как общий принцип структуризации
объектов данных можно применить к спискам любой длины. Из нашего примера также
видно, что такой примитивный способ представления в случае большой глубины
вложенности подэлементов в хвостовой части списка может привести к довольно
запутанным выражениям. Вот почему в Прологе предусматривается более лаконичный
способ изображения списков, при котором они записываются как последовательности
элементов, заключенные в квадратные скобки. Программист может использовать оба
способа, но представление с квадратными скобками, конечно в большинстве случаев
пользуется предпочтением. Мы, однако, всегда будем помнить, что это всего лишь
косметическое улучшение и что во внутреннем представлении наши списки выглядят
как деревья. При выводе же они автоматически преобразуются в более лаконичную
форму представления. Так, например, возможен следующий диалог:
?- Список1 = [a, b, c],
Список2 = (а, .(b, .( c, []) ) )
Список1 = [a, b, c],
Список2 = [a, b, c]
?- Увлечения1 = .( теннис, .(музыка, [] ) ),
Увлечения2 =[ лыжи, еда ]
L =
[энн, Увлечения2, том, Увлечения2].
Увлечения1 =[теннис, музыка]
Увлечения2 = [лыжи, еда]
L
=[энн, [теннис, музыка], том, [лыжи, еда]]
Приведенный пример напоминает нам о том, что элементами списка могут быть
любые объекты, в частности тоже списки.
На практике часто бывает удобным трактовать хвост списка как
самостоятельный объект. Например, пусть
= [a, b, c]
Тогда можно написать:
Хвост =[ b, c] и L= .(a,
Хвост)
Для того, чтобы выразить это при помощи квадратных скобок, в Прологе
предусмотрено еще одно расширение нотации для представления СПиска, а именно
вертикальная черта, отделяющая голову от хвоста.
L = [a | Хвост]
На самом деле вертикальная черта имеет более общий смысл: мы можем
перечислить любое количество элементов списка, затем поставить символ «|», а
после этого - список остальных элементов. Так, только что рассмотренный пример
можно представить следующими различными способами:
[a, b, c] = [a, | [b, c]] = [a, b, | [ c]] = [a, b, c | [ ]]
Подытожим:
· Список - это структура данных, которая либо пуста, либо
состоит из двух частей: головы и хвоста. Хвост в свою очередь сам является
списком.
· Список рассматривается в Прологе как специальный частный
случай двоичного дерева. Для повышения наглядности программ в Прологе
предусматриваются специальные средства для списковой нотации, позволяющие
представлять списки в виде:
[Элемент1, Элемент2, …]
или
[Голова | Хвост]
или
[Элемент1, Элемент2, …| Остальные]
37. Рассуждения, использующие объектное представление. Паросочетание
Рассуждения, использующие объектное представление.
Объектные представления были введены фактически по прагматическим
причинам. Эти представления часто связаны с вполне определенными классами
проблем. Объектно-ориентированные языки (известнейший из них Смолток)
характеризуются взаимопроникновением структур данных и процедур. Связанные с
этими представлениями законы вывода, вообще говоря, лишены формальной строгости
правил вывода логики предикатов. Концепция объектных представлений больше
направлялась заботой об эффективности исчисления, чем стремлением к его
полноте. Очевидно, можно было бы развить для них системы выводов, эквивалентные
использованным в логике предикатов. Такой синтаксис был бы весьма громоздок, и
его применение лишило бы объектное представление его прагматических достоинств.
Вместо того. Чтобы покоиться на полном множестве законов дедукции, различные
используемые в ИИ системы используют сокращенные версии классических законов
вывода.
Паросочетание
Рассмотрим следующее определение.
Два объектных представления паросочетательны тогда и только тогда, когда
логическую формулу для первого можно унифицировать с логической формулой для
второго. Слово «унифицировать» означает здесь, что существуют подстановки для
переменных делающих логические формулы идентичными.
Если наша цель построить язык запросов(query language) для извлечения информации из БД, то
нужно более ограниченное определение паросочетания. Операция паросочетания
вообще не должна быть симметричной в том смысле, что она связывает заключение
(объект-цель) с гипотезами (объектами-фактами). Объект-цель «паросочетается» с
объектом-фактом, если влекущая объект-цель логическая формула унифицируется с
одним из сомножителей объекта-факта, представленного конъюнкцией гипотез и
аксиом.
В терминах доказательства теорем это означает, что операция паросочетания
может осуществляться тогда и только тогда, когда цель можно доказать из гипотез
и аксиом.
Рассмотрим фрейм-гипотезу
Посылка_8
элем : (элем_из посылок)
отправитель : Жак_2
получатель : Мари_4
объект : Книга_22
Можно установить паросочетание этого фрейма-факта с фреймом-целью
z(x)
элем : (элем_из посылок)
отправитель : Жак_2
получатель : х
объект : у(х)
Фрейм-цель интерпретируется как вопрос: Кому Жак послал книгу?
Паросочетание фрейма-цели и фрейма-факта приводит к подстановке {(z, Посылка_8) , (х, Мари_4), (у,
Книга_22)}, которую можно интерпретировать как ответ на вопрос.
38. Язык Prolog. Некоторые
операции над списками
Наиболее часто используемые операции над списками аналогичны операциям
над множествами.
· проверка, является ли некоторый объект элементом списка;
· конкатенация (сцепление) двух списков, что соответствует объединению
множеств;
· добавление некоторого объекта в список или удаление
некоторого объекта из него.
Принадлежность
к списку
Мы представим отношение принадлежности как
принадлежит ( Х, L)
где Х - объект, а L -
список. Цель принадлежит ( Х, L)
истинна, если элемент Х встречается в L. Например, верно что
принадлежит ( b, [a, b,c])
и наоборот, не верно, что
принадлежит ( b, [a, [b,c] ])
но
принадлежит ( [b,c], [a, [b,c] ])
истинно.
Составление программы для отношения принадлежности может быть основано на
следующих соображениях:
1) Х есть голова L,
либо
2) Х принадлежит хвосту L.
Это можно записать в виде двух предложений, первое из которых есть
простой факт, а второе правило:
принадлежит (Х, [Х | Хвост] ).
принадлежит (Х, [Голова | Хвост] ) :-
принадлежит (Х, Хвост).
Сцепление (конкатенация)
Для сцепления списков мы определим отношение
конк( L1, L2, L3)
Здесь L1 и L2 два списка, а L3 - список, получаемый при их сцеплении. Например,
конк( [a, b], [c, d], [a,b,c,d])
истинно, а
конк( [a, b], [c, d], [a,b, а. c,d])
ложно.
Определение отношения конк, как и раньше, содержит два случая в
зависимости от вида первого аргумента L1:
1) Если первый пуст, тогда второй и третий аргумент представляют
собой один и тот же список (назовем его L), что выражается в виде следующего прологовского факта:
конк ([], L, L)
2) Если первый аргумент отношения конк не пуст, то он имеет голову и
хвост и выглядит так
[X | L1]
Хотя программа для конк выглядит довольно просто, она обладает большой
гибкостью и ее можно использовать многими другими способами. Например, ее можно
применить как бы в обратном направлении для разбиения заданного списка на две
части:
? - конк (L1, L2, [a, b, c] )=
[]=[a, b, c];= [a]=[b, c];=[a,b]2=[c];
L1=[a,b,c]
L2=[];
no
Список [a, b, c] разбивается на
два списка четырьмя способами, и все они были обнаружены нашей программой при
помощи механизма автоматического перебора.
Нашу программу можно также применить для поиска в списке комбинации
элементов, отвечающей некоторому условию, задаваемому в виде шаблона или
образца. Например, можно найти все месяцы, предшествующие данному, и все
месяцы, следующие за ним, сформулировав такую цель:
? - конк ( До, [май | После], [янв, фев, март, апр, май, июнь, июль, авг,
сент, окт, ноябрь, дек]).
До=[янв, фев, март, апр]
После = [июнь, июль, авг, сент, окт, ноябрь, дек]
Далее мы сможем найти месяц, непосредственно предшествующий маю, и месяц,
непосредственно следующий за ним, задав вопрос
?- конк(_, [Мсяц1, май, Месяц2 | _],[янв, фев, март, апр, май, июнь,
июль, авг, сент, окт, ноябрь, дек])
Месяц1 = апр
Месяц2 = июнь
Более того, мы сможем, например, удалить из некоторого списка L1 все, что следует за тремя
последовательными вхождениями элемента z в L1
вместе с этими тремя z.
Например, это можно сделать так
? - L1 = [a, b, z,z, c,z, z, z, d, e],
конк (L2,
[z, z, z | _ ], L1).= [a, b, z,z, c,z, z, z, d, e],
L2 = [a, b, z,z, c]
Мы уже запрограммировали отношение принадлежности. Однако, используя
конк, можно было бы определить это отношение следующим эквивалентным способом:
принадлежит1( X, L) :-
конк(L1, [X |L2], L).
В этом предложении сказано: «Х принадлежит L, если список L
можно разбить на два списка таким образом, чтобы элемент Х являлся головой
второго из них. Разумеется принадлежит1 определяет то же самое отношение, что и
принадлежит. Мы использовали другое имя только для того, чтобы различать таким
образом реализации этого отношения. Заметим, что используя анонимную
переменную, можно записать вышеприведенное предложение так
принадлежит1( X, L) :-
конк(_, [X |_], L).
Добавление элемента.
Наиболее простой способ добавить элемент в список - это вставить его в
самое начало так, чтобы он стал его новой головой. Если Х - это новый элемент,
а список, в который Х добавляется - L, тогда результирующий список - это просто
[X | L]
Таким образом, для того чтобы добавить новый элемент в начало списка, не
надо использовать никакой процедуры. Тем не менее, если мы хотим определить
такую процедуру в явном виде, то ее можно представить в форме такого факта:
добавить(Х , L, [X | L] ).
Удаление
элемента
Удаление элемента Х из списка L можно запрограммировать в виде отношения
удалить (Х, L, L1)
где L1 совпадает со списком L, у которого удален элемент Х.
отношение удалить можно определить аналогично отношению принадлежности. Имеем
снова два случая:
1) Если Х является головой списка, тогда результатом удаления будет
хвост списка.
2) Если Х находится в конце списка, тогда его нужно удалить оттуда.
удалить (Х, [X | Хвост],
Хвост).
удалить (Х, [Y | Хвост], [Y | Хвост1]) :-
удалить (Х, Хвост, Хвост1).
Как и принадлежит, отношение удалить по природе своей недетерминировано.
Если в списке встречается несколько вхождений элемента Х, то удалить сможет
исключить их все при помощи возвратов. Конечно, вычисление по каждой
альтернативе будет удалять лишь одно вхождение Х, оставляя остальные в
неприкосновенности. Например:
? - удалить (a, [a, b, a, с,a], L).= [b, a, с,a];= [a, b, с,a];= [a, b, a,с];
no
При попытке исключить элемент, не содержащийся в списке, отношение
удалить потерпит неудачу.
Отношение удалить можно использовать в обратном направлении для того,
чтобы добавлять элементы в список, вставляя их в произвольные места. Например,
если мы хотим во всевозможные места списка [1, 2, 3] вставить атом а, то мы
можем это сделать задав вопрос: «Каким должен быть список L, чтобы после удаления из него
элемента а получился список [1, 2, 3]?»
?- удалить (a, L, [1, 2, 3] ).=[a,1,
2, 3];=[1,a, 2, 3];=[1,
2, a,3];
L=[1,
2, 3,a];
no
Вообще операция по внесению Х в произвольное месть некоторого списка
Список, дающее в результате БольшийСписок, может быть определена предложением:
внести( Х, Список, БольшийСписок):-
удалить(Х, БольшийСписок, Список).
В принадлежит1 мы изящно реализовали отношение принадлежности через конк.
Для проверки на принадлежность можно также использовать и удалить. Идея
простая: некоторый Х принадлежит списку Список, если Х можно из него удалить:
принадлежит2(Х,
Список) :-
удалить( Х, Список, _).
39. Функциональные атрибуты. Автоматические рассуждения, использующие
фреймы. Иерархические рассуждения, использующие фреймы. Рассуждения с
умолчаниями
Функциональные
атрибуты
Атрибуты описывают множество характеристик связанных с функциями
функционального фрейма. Атрибут не обязательно является конкретизацией
некоторых данных вроде Жак_2; с тем же успехом он может быть функциональным
выражением. Рассмотрим фразу «Жак посылает книгу Мари, а Поль получает письмо
от человека, которому Жак послал книгу». Ее первая часть выражается фреймом
Посылка_8
элем : (элем_из посылок)
отправитель : Жак_2
получатель : Мари_4
объект : Книга_22
Вторая часть представляется фреймом, для которого некое функциональное
выражение является атрибутом «отправителя»:
Посылка_9
элем : (элем_из посылок)
отправитель : получатель(Посылка_8)
получатель : Поль_6
объект : Письмо_3
Мари_4 и получатель(Посылка_8) - два разных способа представления одного
и того же лица.
Если пытаемся установить паросочетания между фреймами, содержащие
функциональные выражения в качестве атрибутов, то следует предположить, что эти
выражения получат значения сразу, как только это будет возможно. Присваивание
значений осуществляется посредством ссылки на объект, указанный аргументом этой
функции.
Предположим, что поставлен вопрос: «Посылала ли Мари что-нибудь
кому-нибудь?», представленный фреймом-целью
z(x)
элем : (элем_из посылок)
отправитель : Мари_4
получатель : х
объект : у
Множество фреймов-фактов содержат Посылку_8 и Посылку_9. Так как
получатель(Посылка_8) может получить значение Мари_4, то фрейм Посылка_9
получит Мари_4 в качестве значения функции отправитель. Ответ на вопрос даст
паросочетание фрейма Посылка_9 с фреймом z.
С помощью подстановки {(х, Поль_6), (у, Письмо_3)} можно получить ответ
«да, Мари отправила письмо Полю»
Автоматические рассуждения, использующие фреймы
Только что мы рассмотрели, что атрибуты функций во фреймах не обязательно
константы или конкретизации, но могут также быть функциональными выражениями.
Сделаем еще шаг и рассмотрим еще одну возможность для атрибутов (представляющих
множество связанных с объектами характеристик) - быть процедурами или подпрограммами.
Это приводит нас к понятию объектно-ориентированных языков, предназначенных для
автоматических рассуждений на основе объектного представления.
Язык KRL - объектно-ориентированный,
основанный на представлении знаний фреймами. В нем все знания описаны в
терминах UNITS-KRL. Ограничимся двумя примерами:
[Путешествие UNIT Абстрактное
<SELF (Событие)>
<способ (ИЛИ АВИА Авто Поезд)>
<назначение (Город)>]
[Путешествие UNIT Абстрактное
<SELF (Взаимодействие)>
<визитер (Человек)>
<визит (Множество из (Человек))>]
Первую часть можно интерпретировать следующим образом. «Путешествие -
абстрактное понятие, связанное с самолетом, машиной или поездом и имеющее некий
город пунктом назначения.» Вторую часть можно интерпретировать аналогично. KRL материализует некоторый процесс
рассуждений, управляемый правилом паросочетания.
Иерархические рассуждения, использующие фреймы.
Операция паросочетания аналогична унификации из логики предикатов. Можно
также связать объектное представление с более мощными правилами вывода, такими
как теорема дедукции.
Рассмотрим лишь частный случай одного нередко используемого закона
дедукции, в соответствии с которым с помощью импликации приписываются свойства
каждому элементу определенного множества. Речь идет о свойстве наследования,
который мы уже рассматривали. Займемся иерархией, где типы «профессор
университета» и «профессор» заменены соответствующими множествами.
Концептуальный граф, окружающий узел Жак_2, представляется объектно и логически
следующим образом:
Объектные
обозначения
Жак_2
элем : (элем_из проф_унив)
возр : 45_лет
адр : ул_буля_7
сем_пол : холост
Логические обозначения (Факт)
Элем
(Жак_2, проф_унив)
Возр
(Жак_2, 45_лет) 
Адр
(Жак_2, ул_буля_7) 
Сем_пол
(Жак_2, холост)
Мы
видели вопросы наподобие «Сколько лет Жаку?» или «Кто проживает по улице Буля
дом 7?» представимы фреймом целью или логическим заключением:
Объектные
обозначения Логические обозначения
(Цель)
· Жак_2
возр:х Возр(Жак_2,х)
· у
адр: ул_буля_7 Адр(у, ул_буля_7)
Мы уже знаем, как получить ответы на эти вопросы, используя операцию
паросочетания (для объектных обозначений) или унификацию (для логических).
Далее рассмотрим вопрос «Какой диплом у Жака?», формализованный следующим
образом:
Объектные обозначения Логические обозначения
(Цель)
Жак_2
дипл: у Дипл(Жак_2, у)
Нельзя получить немедленного ответа на этот вопрос. Придется обратиться к
объектным и логическим обозначениям, описывающим свойства индивида х из
множества преподавателей университета:
Объектные обозначения Логические обозначения
(Правило)
{х|
проф_унив} Элем(х, проф-унив)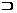
дипл:
доктор (Дипл (х, доктор)
место:
унив Место (х, унив))
Осуществим
паросочетание и унификацию целей с правилами для получения новой цели
Объектные
обозначения Логические обозначения
(Цель)
Жак_2
элем: Элем(Жак_2,
(элем_из проф_унив) проф_унив)
Эта новая фраза точно соответствует фразе «Жак - профессор университета»,
что является фактом. Ответ «Жак имеет степень доктора» также найден. Такой вид
доказательства отвечает системе прямой индукции.
Если нельзя ответить на вопрос, рассматривая свойства индивида (Жак_2)
или содержащего его множества (проф_унив), то обратимся к новому множеству
(проф), подмножеством которого является прежнее. Подмножество профессоров
университета связано с множеством профессоров следующим образом:
Объектные обозначения Логические обозначения
Проф_унив
элем: подмож в проф Подм (проф_унив, проф)
Рассуждения с
умолчаниями
Используемые экспертами в большинстве областей правила лишь приблизительно
точны и не всегда применимы. Многочисленные описания вида «все х имеют свойство
Р» надо считать лишь приблизительно истинными. Например, можно говорить, что
все птицы летают (за исключением страусов, пингвинов и т.д.).
Вообще интересно использовать знания, вроде «все птицы летают», и
подвергать рассуждения сомнению лишь в некоторых заранее известных
исключительных случаях. Это называется рассуждением с умолчаниями. Предложены
многочисленные формализации для выражения «все х имеют свойство Р, за исключением
тех случаев, когда явно указано противное для некоторых конкретизаций
переменной х»
Изложим формализм, основанный на объектном представлении и допускающий
построение рассуждения с умолчаниями. Рассматриваемый нами подход сохраняет
определенную простоту рассуждений. Он состоит в разрешении осуществлять
исключения в рассуждениях Утверждение вида «все преподаватели университета
имеют степень доктора» можно поначалу сделать без всяких исключений. Из него
выводим, что «Жак имеет степень доктора, если Жак преподает в университете».
Если в дальнейшем выяснится, что Жак не имеет степени доктора, то мы аннулируем
нашу дедукцию и так изменим универсальное утверждение о преподавателях
университета, чтобы Жак оказался исключенным.
Способ, которым операция паросочетания использует наследственное
свойство, может дать автоматический механизм обработки исключений такого рода.
Управляющий операцией паросочетания механизм может использовать наследственное
свойство для вывода некоторого свойства объекта, только если специфическая
информация об этом свойстве не появится в соответствующем этому объекте фрейме.
Например, мы интересуемся, какой диплом у Жака. Для ответа на вопрос сначала
попробуем установить паросочетание фрейма-цели с фреймом фактом. Если фрейм
факт по Жаку имеет вид
Жак_2
элем : (элем_из проф_унив)
дипл : магистр
то паросочетание вовлекает унификацию (у, магистр) и ответ таков: магистр
(Жак имеет диплом магистра). Наоборот, если фрейм-факт по Жаку говорит лишь,
что он профессор университета:
Жак_2
элем : (элем_из проф_унив)
то механизм паросочетания использует фрейм
{х| проф_унив}
дипл: доктор
и ответ - доктор.
40. Язык Prolog.
Декларативный и процедурный смысл пролог программ
Следует различать два уровня смысла программ на языке Пролог, а именно:
· декларативный
смысл и
· процедурный смысл
Декларативный смысл касается только отношений, определенных в программе.
Таким образом, декларативный смысл определяет, что должно быть результатом
работы программы. С другой стороны, процедурный смысл определяет еще и как этот
результат был получен, т.е. как отношения реально обрабатываются
Пролог-системой.
Способность пролог-системы прорабатывать многие процедурные детали
самостоятельно считается одним из специфических преимуществ Пролога. Это
свойство побуждает программиста рассматривать декларативный смысл программы
относительно независимо от ее процедурного смысла. Поскольку результаты работы
программы в принципе определяются ее декларативным смыслом, последнего (опять
же в принципе) достаточно для написания программ. Этот факт имеет практическое
значение, поскольку декларативные аспекты программы являются обычно более
легкими для понимания, нежели процедурные детали. Чтобы программисту извлечь из
этого обстоятельства наибольшую пользу, программисту следует сосредоточиться главным
образом на декларативном смысле и по возможности не отвлекаться на детали
процесса вычислений. Последние следует в возможно большой мере предоставить
самой Пролог-системе.
Такой декларативный подход и в самом деле часто делает программирование
на Прологе более легким, чем на таких типичных процедурно-ориентированных
языках, как Паскаль. К сожалению, однако, декларативного подхода не всегда
оказывается достаточно. Далее станет ясно, что особенно в больших программах,
программист не может полностью игнорировать процедурные аспекты по соображениям
эффективности вычислений. Тем не менее следует поощрять декларативный стиль при
написании пролог-программ, а процедурные аспекты игнорировать в тех пределах,
которые устанавливают практические ограничения.