Основные этапы разработки программы вычисления определенного интеграла функции по методу Симпсона
Введение
Одним из этапов изучения дисциплины
«Программирование на языке высокого уровня», на котором проверяется уровень
подготовки студентов по профилю изучаемой дисциплины, умение самостоятельно
работать с литературой, принимать обоснованные решения при разработке
программных средств прикладного характера, наличие соответствующих навыков
программирования при составлении, отладке и тестировании программ, является
курсовое проектирование.
Основная цель данной курсовой работы - это
углубление знаний, полученных в результате изучения теоретического курса
дисциплины, развитие у студентов практических навыков программирования и
использования полученных теоретических знаний на практике.
В данной курсовой работе приведена программа вычисления
приближённого значения определенного интеграла иррациональной логарифмической
функции f(x), общий вид которой: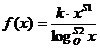 
, где k, s1, s2, O - коэффициенты (вводятся с клавиатуры),
от которых зависит вид интегрируемой функции.
Определенный интеграл от функции, имеющей неэлементарную
первообразную, можно вычислить с помощью той или иной приближенной формулы. Для
решения этой задачи на компьютере, среди прочих, можно воспользоваться
формулами прямоугольников, трапеций или формулой Симпсона. В данной работе
рассматривается именно последняя.
Поставленная задача решена на алгоритмическом языке Турбо Паскаль.
Основными источниками литературы являются: «Справочник по высшей
математике для инженеров и учащихся вузов», Бронштейн И.Н., Семендяев К.А.
«Турбо Паскаль 7.0; язык, среда программирования» Сергиевский М.В., Шалашов
А.В.
1. Постановка
задачи
.1 Задача
Заданием на курсовую работу является создание программы на языке
высокого уровня, которая должна осуществлять решение следующей задачи:
Вычислить приближённое значение интеграла функции f(x) на
интервале с точностью до 0.01 методами Симпсона и трапеции с целью сравнения.
Интегрируемая функция: 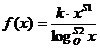, где k, s1, s2, O - коэффициенты (вводятся с клавиатуры),
от которых зависит вид интегрируемой функции.
Определить метод, который решает поставленную задачу за
минимальное число повторений.
Построить график функции f(x) на заданном интервале. Решить
поставленную задачу с использованием функций и процедур алгоритмического языка
Турбо Паскаль.
Для решения поставленной задачи необходимо выполнить следующие
действия:
) Ввести параметры, определяющие функцию:
коэффициент при x в числителе;
степень, в которую необходимо возвести x;
основание логарифма;
степень, в которую необходимо возвести логарифм;
) Ввести значения границ отрезков;
) Вывести график функции на экран с учётом масштаба;
) Вычислить интеграл методом Симпсона;
) Вычислить интеграл методом трапеций;
1.2 Математическое обоснование метода решения задачи
.2.1 Определенный интеграл
Для начала раскроем понятия дифференцирования и первообразной
функции.
Дифференцирование функции - это вычисление ее производной.
Задание.
Дана функция f(x)=2x. Найти функцию F(x),
для которой f(x) является производной.
То есть (F(x))' =2x.
Решение
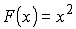, потому что 
,
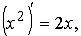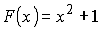, потому что 
,
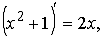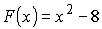, потому что 
,
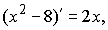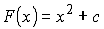, потому что 
,
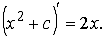Эта задача имеет бесконечно много решений.
Определение.
Функция y = F(x) называется первообразной функции y
= f(x) на интервале [a; b], если для всех x
из этого интервала верно (F(x))'=f(x).
Вывод: если y=F(x) - первообразная функции y=f(x),
то y=F(x)+c, где c - константа, тоже
первообразная функции y = f(x).
Функция y=f(x) имеет бесконечно много
первообразных.
Определение. Множество всех первообразных функции y=f(x)
на интервале [a; b] называется неопределенным интегралом функции y=f(x).
Обозначают:
.
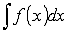
f(x) - это подынтегральная функция,
f(x) dx - это подынтегральное
выражение.
Пример: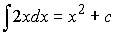 
.
Интегрирование - это вычисление первообразной для данной функции.
Интегрирование - это действие, обратное дифференцированию.
Задача.
Найти приращение функции, первообразной для функции f(x), при переходе
аргумента x от значения a к значению b.
Решение. Положим, что интегрированием найдено
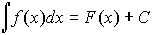
Тогда F(x)+C1, где С1 - любое
данное число, будет одной из первообразных функций для данной функции f(x).
Найдем её приращение при переходе аргумента от значения a к значению b.
Приращением функции называется величина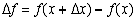 
. Получим:
[F(x)+C1]x=b -
[F(x)+C1]x=a=F(b) +C1 - F(a) - C1
=F(b) - F(a)
Как видим, в выражении приращения первообразной функции F(x)+C1
отсутствует постоянная величина C1. А так как под C1
подразумевалось любое данное число, то полученный результат приводит к
следующему заключению: при переходе аргумента x от значения x=a к
значению x=b все функции F(x)+C, первообразные для данной функции
f(x), имеют одно и то же приращение, равное F(b) - F(a).
Это приращение принято называть определенным интегралом и
обозначать символом
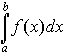
Определение.
Приращение первообразных функций F(x)+C при переходе аргумента x
от значения x=a к значению x=b, равное разности F(b) - F(a),
называется определенным интегралом и обозначается символом
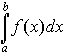
так, что если
,
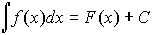то
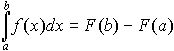
Данное равенство называется формулой Ньютона-Лейбница.
Предполагается при этом, что подинтегральная функция f(x) непрерывна при
всех значениях x, удовлетворяющих условиям
£ x £ b.
Формулы, позволяющие по известным значениям приближённо определить
значение интеграла, называются квадратурными формулами.
Для наглядности мы будем прибегать к геометрической интерпретации
смысла определённого интеграла, как площади некоторой поверхности, в случае
функции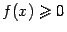 
. Следует, однако, иметь в виду, что
квадратурные формулы, которые мы будем получать, имеют смысл для функций,
принимающих значения произвольного знака.
При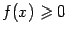 
вычислить интеграл, значит найти площадь
под графиком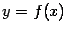 
, расположенную над отрезком 
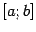. Естественной идеей является следующее
построение: разобьём отрезок на части точками деления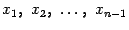 
и положим 
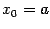и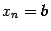 
. Тогда разбиение отрезка 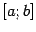состоит из отрезков 
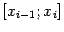при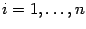 
. Вместо площади под графиком будем приближённо находить суммарную
площадь узких полосок, лежащих над отрезками разбиения .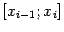
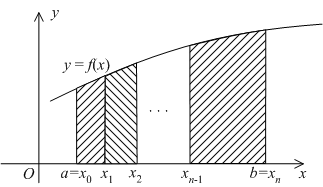
Рисунок 1 - График функции f(x) на отрезке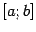
1.2.2
Квадратурная формула Симпсона (формула парабол)
Выберем приближение графика функции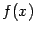 
в виде параболы - графика некоторого квадратного трёхчлена 
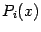. Его вид, конечно, будет зависеть от
отрезка 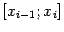, на котором мы выбираем приближение.
Выберем, например, такой квадратный трёхчлен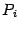 
, чтобы его значения в точках 
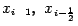и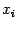 
совпадали со значениями функции 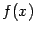в этих же точках:
Через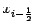 
мы обозначаем середину отрезка 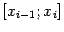, то есть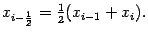 
Функцию можно записать в виде
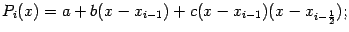
Действительно, раскрыв скобки, получим некоторый квадратный
трёхчлен. Подберём числа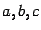 
так, чтобы выполнялись равенства (1).
Положим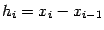 
, тогда 
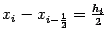и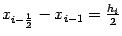 
. Подставим 
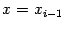в выражение для 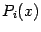и получим:
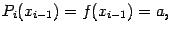
то есть
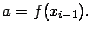
Подстановка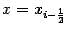 
даёт
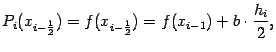
откуда
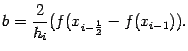
Наконец, подставим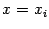 
и получим
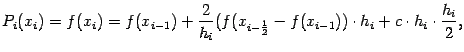
откуда
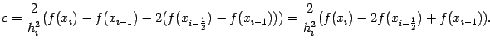
Вычислим теперь интеграл от интерполяционной функции 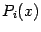, для чего сделаем в нём замену 
:
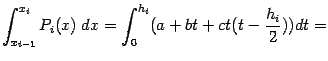
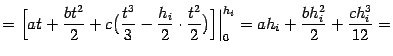
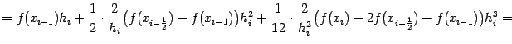
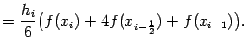
Осталось просуммировать эти величины по всем отрезкам разбиения.
При этом получаем квадратурную формулу, которая называется формулой Симпсона,
или формулой парабол:
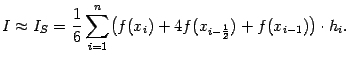
Таким образом, формула Симпсона - это квадратурная формула
четвёртого порядка точности. Это означает, что при уменьшении шага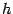 
вдвое ошибка 
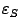уменьшится примерно в 
раз, а при уменьшении шага в 10 раз ошибка
уменьшится примерно в 
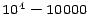раз.
Доказательство приведённой оценки для формулы Симпсона можно
найти, например, в книге «Численные методы», Самарский А.А, Гулин А.В.
2. Алгоритм
решения задачи
2.1 Словесное описание алгоритма
математический программирование алгоритм листинг
Алгоритм программы представлен в виде блок-схемы и включает в
себя, помимо основной программы, подпрограмму вычисления интеграла по методу
Симпсона. Также блок-схема содержит подпрограмму вычисления интеграла по методу
трапеций. В главной программе запускаются циклы вычислений интеграла методами
Симпсона и трапеций до достижения необходимой точности, для каждого метода
рассчитывается количество шагов, за которые они решаются.
В подпрограмме вычисления интеграла методом Симпсона
запускается цикл решения уравнений, согласно правилу нахождения интеграла по
методу Симпсона. Приведена подпрограмма вычисления интеграла методом трапеций,
реализованная согласно правилу нахождения интеграла по методу трапеций.
Подпрограмма вычисления интеграла методом Симпсона, как и
подпрограмма вычисления интеграла по методу трапеций, ссылается на
функциональный модуль, куда вводится функция, для которой рассчитывается
определенный интеграл.
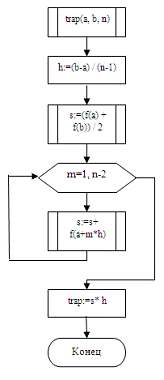
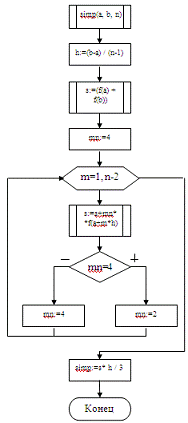
2.2 Блок-схема алгоритма решения задачи
В соответствии с приведённым словесным описанием алгоритма
решения поставленной задачи разработана блок схема решаемой задачи.
1. Блок-схема программы
2. Вычисление интеграла по методу трапеций
. Вычисление интеграла по методу Симпсона
4. Интегрируемая функция
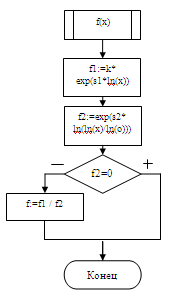
3. Выбор языка программирования
Существует множество языков программирования, различающихся
по предоставляемым возможностям. Выбор языка программирования для решения
конкретной задачи существенно влияет на качество программы, получаемой в
результате разработки, а также на скорость и удобство самого процесса
разработки. В результате использования данных языков получаются более объемные
и менее быстродействующие исполняемые программы, что, однако, компенсируется
скоростью их разработки и меньшим содержанием ошибок, хотя бы вследствие малых
объемов исходных данных. К таким языкам относится Turbo Pascal.
Язык Паскаль - это один из наиболее распространённых языков
программирования 80-90х годов, поддерживающий самые современные методологии
проектирования программ (нисходящее, модульное проектирование, структурное
программирование), которые имеют свою достаточно богатую историю развития.
Новую жизнь языку дала фирма Борланд, разработавшая на его
базе семейство Паскаль - систем, называемых Турбо Паскалем. Интегрированная
среда, обеспечивающая многооконную разработку программной системы, обширный
набор встроенных в неё средств компиляции и отладки, доступных для работы через
легко осваиваемое меню, - всё это обеспечивает высокую производительность труда
программиста, недостижимую при работе со старыми средами.
Выбор языка Pascal не случаен - это учебный язык, с легко
просматриваемой алгоритмикой программы; язык типизирован, что позволяет на его
основе изучать более сложные языки; язык позволяет научиться хорошему стилю
программирования.
4. Текст программы решения задачи
Program tr_s;
uses crt, graph;m, m1;:char;, b:real; {Границы отрезка}
r, r2:real; {Предыдущее и текущее приближенные значения
интеграла}:integer; {Счетчики}, f2:real; {Числитель и Знаменатель}
s1, s2, s3:real; {Степени}
k, o:real; {Некоторые коэффициенты}
{Интегрируемая функция}f (x:real):real;:=k*exp (s1*ln(x)); {k*(x в степени s1)}:=exp
(s2*ln (ln(x)/ln(o))); {log o x - это ln(x)/ln(o)}:=f1/f2;;
{Метод трапеций}trap (a,
b:real; n:integer):real;
var:real; {Полученная сумма}:real; {Шаг}:integer;
{Счетчик}:=(b-a)/(n-1); {Определяется шаг}:=(f(a)+f(b))/2; {Начальное значение
суммы}m:=1 to n-2 do s:=s+f (a+m*h); {Суммирование остальных элементов}:=s*h;
{Возвращается значение интеграла}
end;
{Метод Симпсона}simp (a,
b:real; n:integer):real;:real; {Сумма}:real; {Шаг}:integer; {Счетчик}:integer; {Очередной множитель}
begin:=(b-a)/(n-1); {Рассчитывается шаг}:=f(a)+f(b);
{Начальное значение шага}:=4; {Первый множитель - 4}
{Суммирование остальных элементов}
for m:=1 to n-2 do begin:=s+mn*f (a+h*m);(mn=4)
then mn:=2 else mn:=4; {Изменение множителя 2<>4}
end;:=s*h/3; {Возвращается вычисленное значение};
{Процедура вычисления порядка числа}
procedure norm (a:real);n:real;
begin
{Если число слишком мало - возвращается ноль}
if (a<0.00001) then n:=0begin
{Если число меньше единицы}(a<1) then begin
n:=1;:=a*10;:=n/10;(trunc(a)<>0);else begin
{Если число больше единицы}:=1;
repeat:=a/10;:=n*10;(trunc(a)=0);;;
a:=n;;
{Построение графика функции}
sx:real; {Шаг по оси X}, dlty:integer; {Приращение на графике
при смещении графика}:string; {Строка}
{Инициализация графики}
drv:=VGA;:=VGAHi;(drv, mode, '');
{Выяснение порядков минимумов и максимумов}
norm(xmax);(ymax);(ymin); ymin:=ymin/10;(xmin);
ymin:=ymin/10;(xmin/xmax)>0.01 then dltx:=20 else
dltx:=0;(ymin/ymax)>0.01 then dlty:=20 else dlty:=0;
{Расчет масштабов}:=500/(xmax-xmin);:=400/(ymax-ymin);
{Расчет приращения по X}:=(xmax-xmin)/550;
{Вывод системы координат}
settextjustify
(1,1);:=xmin;(1);(trunc(40+mx*(xx-xmin)+dltx), 20, trunc
(40+mx*(xx-xmin)+dltx), 469);(xx:4:2, s);(15);(trunc(40+mx*(xx-xmin)+dltx),
475, s);:=xx+50*sx;(xx>(xmax+50*sx));:=ymin+(ymax-ymin)/10;(1);(41, trunc
(470-my*(yy-ymin) - dlty), 630, trunc (470-my*(yy-ymin) - dlty));(yy:4:2,
s);(15);(20, trunc (470-my*(yy-ymin) - dlty),
s);:=yy+(ymax-ymin)/10;(yy>(ymax+(ymax-ymin)/10));(40,0,40,480);(0,470,640,470);(40,0,38,10);(40,0,42,10);(640,470,630,472);(640,470,630,468);
{Вывод графика}:=xmin;:=f(xx);(trunc(40+mx*(xx-xmin)+dltx),
trunc (470-my*(yy-ymin) - dlty), 7);:=xx+sx;(xx>xmax);(300,10,' Press ESC to
continue ');until (readkey=#27);;;
{Основная программа}
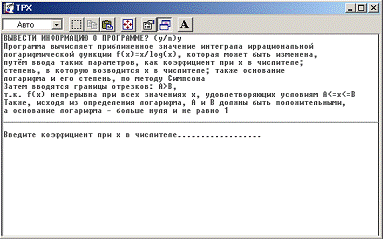
{Ввод границ отрезкa};('ВЫВЕСТИ ИНФОРМАЦИЮ О ПРОГРАММЕ? (y/n)');(I); I='y' then
begin('Программа вычисляет приближенное значение
интеграла иррациональной ');('логарифмической функции f(x)=x/log(x), которая
может быть изменена, ');('путём ввода таких параметров, как коэффициент при х в
числителе; ');('степень, в которую возводится х в числителе; также основание
');('логарифма и его степень, по методу Симпсона');('Затем вводятся границы
отрезков: А>B, ');('т.к. f(x) непрерывна при всех значениях x,
удовлетворяющих условиям A<=x<=B');('Также, исходя из определения
логарифма, А и В должны быть положительными, ');('а основание логарифма -
больше нуля и не равно
1');('________________________________________________________________________________');;:
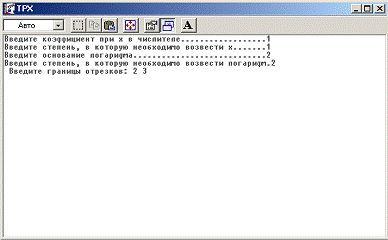
write ('Введите коэффициент при х в числителе………………');
{$I-}(k);ioresult<>0 do
begin('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ ЧИСЛЕННЫЕ
ЗНАЧЕНИЯ!!!');('Введите коэффициент при х в числителе………………');(k);;
{$I+}('Введите степень, в которую необходимо возвести x…….');
{$I-}(s1);ioresult<>0 do
begin('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ ЧИСЛЕННЫЕ
ЗНАЧЕНИЯ!!!');('Введите степень, в которую необходимо возвести x…….');(s1);
{$I+};('Введите основание логарифма……………………….');
{$I-}(o);(o<=0) or (o=1) do
begin('НЕВЕРНЫЙ ВВОД!!! ОСНОВАНИЕ ЛОГАРИФМА БОЛЬШЕ НУЛЯ И НЕ
РАВНО 1');('Введите основание логарифма……………………….');
readln(o);(ioresult<>0) do
begin
writeln ('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ ЧИСЛЕННЫЕ
ЗНАЧЕНИЯ!!!');('Введите основание логарифма……………………….');
readln(o);;
{$I+};
write ('Введите степень, в которую необходимо возвести
логарифм.');
{$I-}(s2);ioresult<>0 do
begin('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ ЧИСЛЕННЫЕ
ЗНАЧЕНИЯ!!!');('Введите степень, в которую необходимо возвести логарифм ');
readln(s1);;
{$I+}: write (' Введите границы отрезков: ');
{$I-}(a, b);ioresult<>0 do
begin('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ ЧИСЛЕННЫЕ ЗНАЧЕНИЯ!!!');('
Введите границы отрезка: ');
readln (a, b);;
{$I+}a=b then
writeln ('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ РАЗЛИЧНЫЕ ЗНАЧЕНИЯ!!!');
goto m;
end;a<=0 then
begin('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ A>0!!!');
goto m;;b<=0 then
begin('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ B>0!!!');
goto m;
end;a>b then
begin
writeln ('НЕВЕРНЫЙ ВВОД!!! ВВОДИТЕ A<B!!!');
goto m;;(ln(a)=0) or (ln(b)=0) then
begin('ДЕЛЕНИЕ НА НОЛЬ!!! НЕТ РЕШЕНИЙ!!!');('ЗАПУСТИТЬ
ПРОГРАММУ СНАЧАЛА? (y/n)');
readln(I);;I='y' then goto m1;;
{Выводится график функции}
out_grp (a, b, f(b),
f(a));
{Вычисляется интеграл по методу трапеций}:=3;:=trap (a, b,
n); {Начальное значение}:=r; {Запоминается предыдущее значение}:=n+2;
{Увеличивается количество шагов}:=trap (a, b, n); {Рассчитывается новое
значение}(abs (r-r2)<0.001); {Повторяется до достижения необходимой
точности}
{Вывод
результатов}('________________________________________________________________________________');('
Результат по методу трапеций равен: ', abs(r):6:3);(' для получения необходимой
точности интервал был разбит на ');(n, ' отрезков');
{Вычисляется интеграл по методу Симпсона}:=3;:=simp (a, b,
n); {Начальное значение}:=r; {Запоминается предыдущее значение}:=n+2;
{Увеличивается количество шагов}:=simp (a, b, n); {Рассчитывается новое
значение}(abs (r-r2)<0.001); {Повторяется до достижения необходимой
точности}
{Вывод результатов}(' Результат по методу Симпсона равен: ',
abs(r):6:3);(' для получения необходимой точности интервал был разбит на ');
writeln (n, ' отрезков');;
write ('ЗАПУСТИТЬ ПРОГРАММУ СНАЧАЛА? (y/n)');
readln(I);;I='y' then goto m1;
end.
5. Спецификация программы
Программа состоит из следующих функциональных модулей:
) Функция f - вычисляет значение интегрируемой функции;
) Функция simp - вычисляет интеграл методом Симпсона;
) Функция trap - вычисляет интеграл методом трапеций;
) Процедура norm - вычисляет порядок числа, необходимый для
построения графика функции с учётом масштаба;
) Процедура out_gr - строит график функции на экране в
графическом режиме с учётом масштаба.
Основная (главная) программа осуществляет ввод параметров,
определяющих функцию, ввод границ отрезков, вызов функциональных модулей
вычисления и вывод результатов на экран.
При запуске программы, пользователь, при желании, может
получить информацию о программе. При вводе неверных данных, программа
информирует об этом пользователя и дает возможность сразу ввести другие данные,
не прерывая процесс работы программы. Также, после ввода необходимых данных и
вывода результатов на экран, либо после вывода информации об исключительной
ситуации, есть возможность повторить процедуру вычисления.
Затем вводятся параметры и границы отрезков.
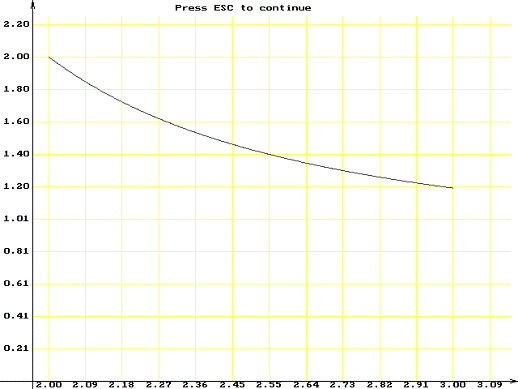
И, наконец, вывод результатов.
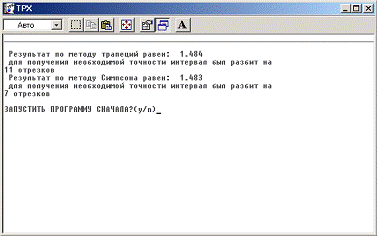
6. Контрольный пример
Тестирование программы численного интегрирования методом
Симпсона проводилось при помощи программы Mathcad 2000 Professional.
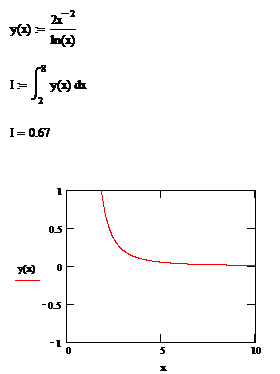
7. Результаты работы программы
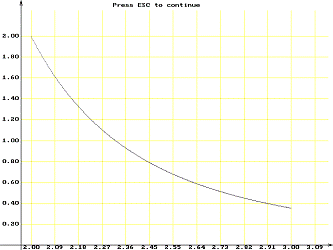
Пусть нужно вычислить интеграл от функции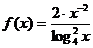 
на интервале [2; 3] методом Симпсона.
Запустим программу и введем данные, соответствующие примеру, проверим реакцию
программы на неверные данные.
Как уже было сказано, результаты решения интеграла функции методом
Симпсона сравнивались с результатами решения методом трапеций.
Результаты работы программы:
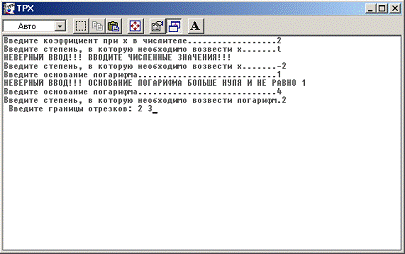
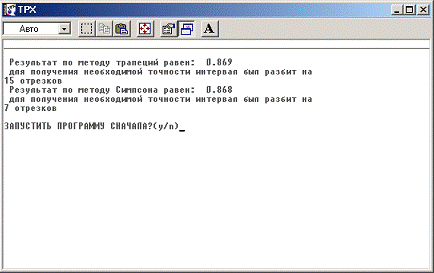
Проверим программу и на ввод значений, при которых возникают
исключительные ситуации.
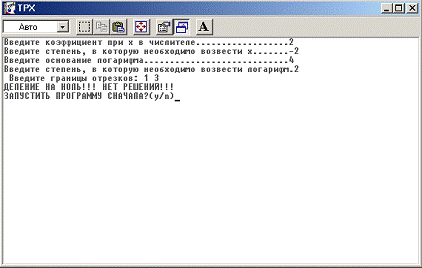
Анализ полученных в ходе работы программы результатов говорит
о том, что поставленная задача успешно решается.
Метод трапеции является наиболее простым методом
приближённого интегрирования, этот метод позволяет точно интегрировать
многочлен первой степени, а для интегрирования данной функции требуется
довольно много итераций. Более совершенным является метод Симпсона, который
позволяет точно интегрировать многочлен второй производной и даже некоторые
многочлены третьей степени, поэтому он требует в 2-3 раза меньше количества
интервалов для получения результата.
Заключение
В данной курсовой работе решена задача приближённого
интегрирования функции методом Симпсона.
В процессе создания курсовой работы разработан алгоритм
решения поставленной задачи. По этому алгоритму на языке Турбо Паскаль 7.0.
составлена и отлажена программа.
В ходе тестирования были получены результаты работы метода
трапеции и метода Симпсона, по которым видно, что результаты интегрирования
обоими методами совпадают с достаточной точностью. Заметна лишь разница в
качестве приближения интервалов.
Программа является полностью работоспособной, что подтверждается
результатами её тестированием.
Список литературы
1
Бронштейн И.Н., Семендяев К.А. Справочник по высшей математике для инженеров и
учащихся вузов. - М.: Наука. 1981. - 718 с.
2
Сергиевский М.В., Шалашов А.В. Турбо Паскаль 7.0; язык, среда программирования.
- М.: Машиностроение.1994. - 254 с.
3
Самарский А.А, Гулин А.В. Численные методы. - М.: Наука. 1989. - 430 с.