Осцилятор с неподвижным ограничителем

Осцилятор с неподвижным ограничителем

ОСЦИЛЯТОР С НЕПОДВИЖНЫМ ОГРАНИЧИТЕЛЕМ

Свободные колебания груза соударяющегося с препятствием

Груз массы М совершает колебания на пружине жёсткости С с ограничителем с одной стороны от центра колебаний (Рис. 13). Колебания происходят в среде без сопротивления. Амплитуда свободных колебаний превышает величину зазора 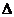, то есть при 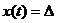 происходит ударное взаимодействие тела с препятствием. Полагаем что удар абсолютно упругий.

колебание груз вибрационный кратность

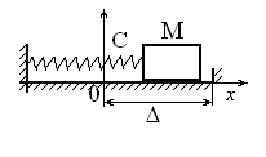
Рис. 1

Уравнение движения тела между соударениями имеет вид

,

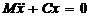или

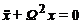, (2)

где 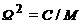. Будем полагать, что при ударе скорость тела меняется мгновенно, а координаты остаются неизменными.

Общее решение уравнения (2) имеет вид:

.

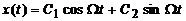Для определения констант интегрирования необходимо задать два условия. Будем искать периодические решения. Для этого будем полагать, что в начальный момент времени тело взаимодействовало с ограничителем

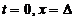
и совершив полный цикл движения в момент времени 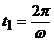 (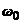− частота вибрационных колебаний) вновь соударяется с ограничителем

.

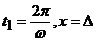Из этих условий получим

,

, , .

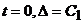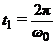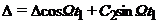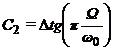Решение имеет вид

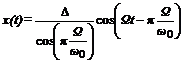. (3)

Полученное решение определено на интервале 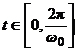. Для его продолжения на всю временную ось разложим решение (3) в ряд Фурье.

,

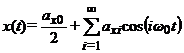где коэффициенты имеют вид

,

.

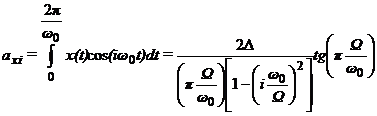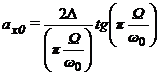Фазовые траектории решения показаны на рисунке Рис. 2

.

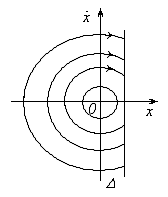
Рис. 2

Можно установить связь начального отклонения тела, величины зазора 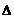 и частоты вибрационных колебаний.

На фазовой плоскости движение тела по дуге траектории происходит с постоянной скоростью 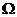. Длинна дуги 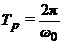. Радиус окружности 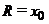, определяется начальным отклонением тела. Из рисунка (Рис. 3), можно видеть



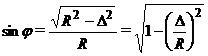
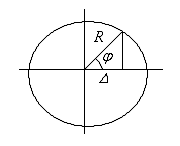
Рис. 3

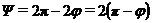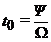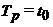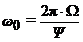Следовательно, дуга, которая проходится телом . Время прохождения этой дуги  и оно равно периоду вибрационных колебаний . Отсюда следует, что  или

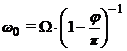
Заметим, что

,

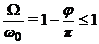поскольку 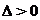, то .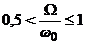

Обозначим координату максимального отклонения процесса 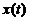 через .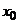

Амплитуда вибрационных колебаний будет равна

, .

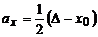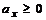Максимальное значение 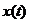 (3)

,

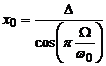то есть

.

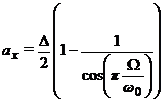Скелетная кривая показана на рисунке рис. 4

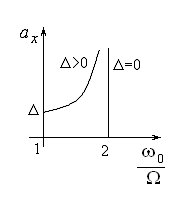
Рис. 4

Можно видеть, что при увеличении амплитуды колебаний их частота приближается к удвоенной частоте линейного осциллятора.

Поскольку разложение 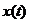 в ряд Фурье сходится 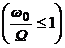, то амплитуда основного тона

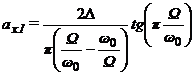
достаточно точно описывает колебания груза.

Рассмотрим вибрационные колебания в среде с сопротивлением и с учётом не идеальности удара.

В этом случае уравнение движения тела будут иметь вид

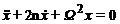, (4)

где 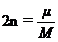,  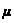− коэффициент сопротивления или демпфирования.

Решение уравнения (4) может быть записано в виде

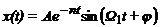, (5)

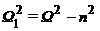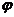где , А,  − амплитуда и фаза колебаний, определяемые начальными условиями.

Очевидно, что вибрационные колебания в среде с сопротивлением и неупругих ударах будут затухать (Рис. 5). Вибрационное затухание будет происходить до того момента времени, когда амплитуда вибрационных колебаний станет меньше зазора 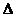. Дальнейший процесс затухания будет проходить как при затухании обычных колебаний.

Зададим следующие начальные условия

.

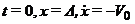В этом случае для амплитуды и фазы получим

, .

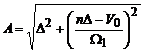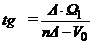Следующее соударение произойдёт в момент времени 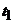, который определяется из условия 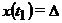. Скорость соударения будет равна

.

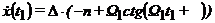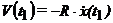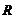Полагая удар неупругим, получим начальное значение скорости для следующего цикла , где  − коэффициент восстановления.

Рис. 5

Потери энергии за один цикл будут равны

.

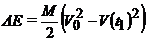Вынужденные вибрационные колебания

Установившиеся вынужденные вибрационные колебания носят периодический характер. Причем возможно существование многократных режимов соударения за один период воздействия внешней силы.

Уравнения вынужденных колебаний тела в среде без сопротивления имеют вид

,

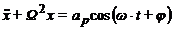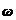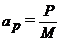где − частота вынуждающей силы, , Р − амплитуда вынуждающей силы, 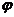 − начальная фаза возбуждения.

Решение ищется в виде

,

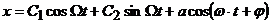где , .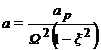

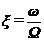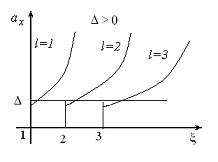
Рис. 6

Скелетные кривые различной кратности

Константы интегрирования определяются из условия существования периодических виброударных режимов

,

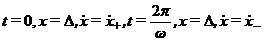где 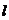− кратность режима соударения, 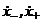− скорости тела до удара и после удара о преграду. Эти скорости связаны соотношение 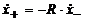, 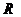− коэффициент восстановления.

Определяя константы интегрирования получим

,

, ,

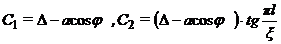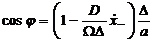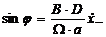где .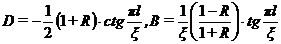

Из выражений для фазы колебаний выразим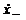

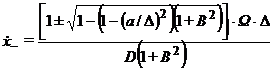. (5)

Условие существования действительного решения имеет вид

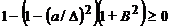 (6)

или

.

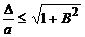Виброударный режим возможен при условии .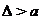

Потребуем, чтобы закон движения удовлетворял условиям 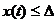 в любой момент времени. Для этого потребуем выполнения следующего неравенства .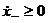

Если подкоренное выражение больше единицы, то условие положительности скорости после удара выполняется для одного корня. Оно реализуется при условии 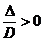 или с учётом значений D получим

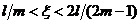. (7)

При абсолютно упругом ударе 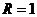. Решение имеет вид

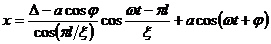, (8)

.

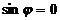Экстремум достигается в момент времени .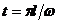

.

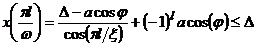Учитывая выражение для амплитуды вынужденных колебаний 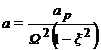, запишем

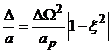. Область существования периодических режимов (6) показана на рисунке Рис. 19.

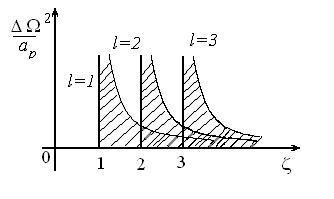
Рис. 7

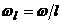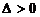Кратность режима определяется как отношение периода движения системы к периоду возбуждения, то есть . Заметим, что при частота 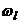 лежит в пределах

.

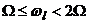Режимы различной кратности мало отличаются по амплитуде друг от друга и близки к свободным колебаниям.

.

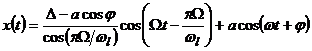Вид решения при разных режимах кратности показан на Рис. 7.

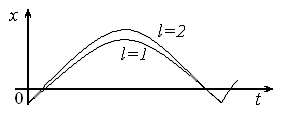
Рис. 7

В работе [2] показано, что режимы многократного соударения устойчивы в областях существования решения, то есть они реализуемы на практике.

Потери энергии при этом определяются коэффициентом ударного сопротивления, скоростью движения ротора, то есть частотой его колебаний.

Используемая литература

1. Болотин В.В. Неконсервативные задачи теории упругой устойчивости. М: ФИЗМАТГИЗ. 1961, 339 с.

2.      Бабицкий В.И. Теория виброударных систем М.: Наука 1978, 352 с.