Модернизация магнитоэлектрического милливольтметра
Московский
Авиационный Институт
(Национальный
Исследовательский Университет)
Кафедра 305
Дисциплина:
"Электротехника"
"Модернизация
магнитоэлектрического милливольтметра"
Выполнил
студент группы 03-211
Падерин Ф.Г.
Принял:
Мельников В.Е.
Содержание
Введение. 2
. Теоретическая часть. 3
.1 Вольтметр. 3
.2 Акселерометр. 5
.3 Схематичный набросок
исследуемого милливольтметра с размерами. 8
. Расчетная часть. 9
.1 Исходные данные. 9
.2 Расчет характеристик
милливольтметра. 10
.2.1 Расчет электрического
момента 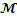 : 10
: 10
.2.2 Расчет коэффициента
жесткости пружины 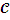 12
12
.2.3 Расчет суммарного
момента инерции 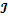 12
12
.2.4 Расчет коэффициента
демпфирования 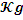 16
16
.2.5 Заключение расчетной
части, расчет 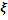 и
и 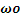 : 18
: 18
. Модификация милливольтметра
в маятниковый акселерометр. 20
Введение
милливольтметр акселерометр маятниковый модификация
Целью данной работы является функциональная модернизация
магнитоэлектрического милливольтметра от исходной функции измерения напряжения
на входных зажимах прибора к функции измерения ускорения. Такая модернизация
проводится последовательно два этапа:
· Расчет основных характеристик милливольтметра.
· Изменение компоновки и взаимодействия функционально и
конструктивно необходимых элементов измерительного прибора (и.п.), опираясь при
этом на предварительно рассчитанные основные характеристики и.п.
1. Теоретическая часть
.1
Вольтметр
Вольтметр - измерительный прибор определяющий, с заданной точностью,
разность электрических потенциалов на своих входных зажимах.
Вольтметры бывают:
· Электромеханические - магнитоэлектрические, электродинамические,
электростатические, выпрямительные, термоэлектрические;
· Электронные - аналоговые и цифровые;
Рассмотрим схематическое изображение аналогового (электромагнитного)
вольтметра.
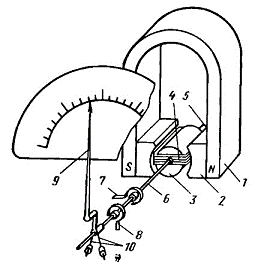
Рис. 1 «Аналоговый Вольтметр»
- Постоянный магнит.
- Магнитопровод.
- Неподвижный сердечник.
- Подвижная прямоугольная катушка (рамка). Намотанный медный или
алюминиевый провод на алюминиевом каркасе.
,6 - Полуоси удерживающие катушку.
,8 - Спиральные пружины, предназначенные для создания противодействующего
момента, также используемые для подачи измеряемого тока.
- Стрелка, жестко закрепленная с рамкой.
- Балансиры.
Электрокинематическая схема электромагнитного вольтметра.
- Подвес, ось вращения.
- Катушка, каркас.
- Спиральная пружина, токоотвод.
- Магнитная система.
- Корпус.
Структурная схема вольтметра.
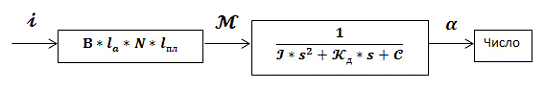
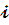
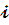 - Ток в
катушке.
- Ток в
катушке.
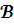
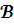 - Магнитная индукция в рабочем зазоре.
- Магнитная индукция в рабочем зазоре.
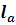
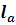 - Ширина магнитного потока через который проходит
катушка и каркас.
- Ширина магнитного потока через который проходит
катушка и каркас.
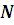
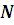 - Количество витков.
- Количество витков.
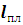
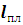 - Плечо
силы Ампера, действующей на обмотку, каркас.
- Плечо
силы Ампера, действующей на обмотку, каркас.
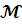
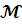 - Электрический момент.
- Электрический момент.
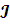
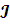 - Суммарный момент инерции.
- Суммарный момент инерции.
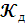
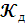 - Коэффициент демпфирования.
- Коэффициент демпфирования.
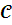
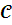 - Коэффициент жесткости пружины.
- Коэффициент жесткости пружины.
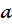
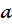 - Угол отклонения.
- Угол отклонения.
1.2
Акселерометр
Акселерометр - измерительный прибор определяющий проекцию кажущегося
ускорения (разность между абсолютным ускорением объекта и гравитационным
ускорением, точнее ускорением свободного падения).
Акселерометры бывают:
· Осевые
· Маятниковые
· Пьезоэлектрические
· Переменной емкости
Рассмотрим схематическое изображение маятникового компенсационного
акселерометра.
Принцип действия акселерометра изображенного на Рис. 2 во многом подобен
принципу действия вольтметра показанного на Рис. 1, а именно:
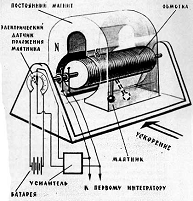
Рис. 1
При ускорении систему, с которой связан акселерометр, катушка, вследствие
смещенного, относительно оси подвеса, центра тяжести, совершает вращательные
движения. Датчик положения маятника регистрирует угол отклонения, и передает по
цепи соответствующее напряжение, источником эдс является батарея, также на
рисунке представлен усилитель(усиливающий до необходимого уровня напряжение).
При вращении катушки в ней индуцируется ток, Рис. 2 «Акселерометр маятникового
типа» создающий демпфирующий эффект.
Электрокинематическая схема маятникового компенсационного
акселерометра.

Рис. 2 «Акселерометр маятникового типа
ЧЭ - маятник совершает угловое движение относительно оси Y.
Угол поворота α маятника относительно оси Y контролируется датчиком угла.
m - центр
тяжести ЧЭ, на расстоянии l
от оси Y подвеса.
U1 - сигнал
с выхода преобразователя угла α, в электрический сигнал. Ду датчик
угла с коэффициентом преобразования Кду,
U1=Kдуα
ДМ - датчик момента - преобразователь электрического сигнала (тока) в
момент силы - Му.
- Му=Кдмi, момент обратной связи, уравновешивающий инерционный
момент Ми = maxl.
Выходной сигнал акселерометра определится:
Uвых = Rнi
Структурная схема компенсационного акселерометра.
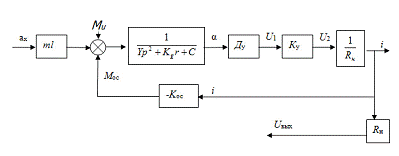
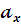
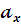 -
Проекция смещения подвеса на ось.
-
Проекция смещения подвеса на ось.
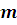
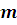 - Масса
подвеса.
- Масса
подвеса.

 -
Расстояние от центра тяжести подвеса до оси вращения.
-
Расстояние от центра тяжести подвеса до оси вращения.
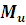
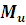 -
Инерциальный момент.
-
Инерциальный момент.
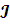
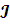 - Момент
инерции.
- Момент
инерции.
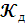
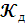 -
Коэффициент демпфирования.
-
Коэффициент демпфирования.
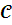
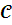 -
Собственная жесткость.
-
Собственная жесткость.
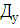
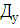 -
Коэффициент датчика угла.
-
Коэффициент датчика угла.
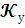
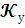 -
Коэффициент усилителя.
-
Коэффициент усилителя.
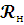
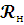 -
Нагрузка (сопротивление).
-
Нагрузка (сопротивление).
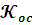
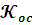 -
Коэффициент обратно связи.
-
Коэффициент обратно связи.
1.3
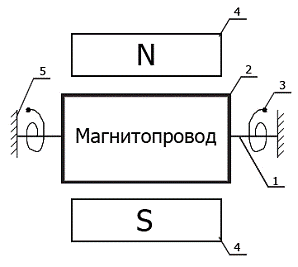
Схематичный набросок исследуемого милливольтметра с размерами
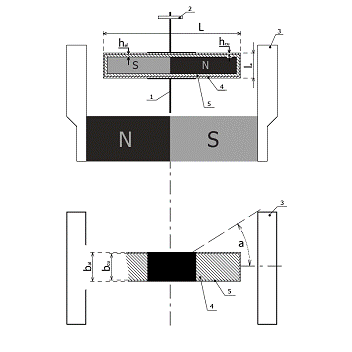
Рис. 3 а) - фронтальный вид; б) - вид сверху
- Ось подвеса, вращения.
- Спиральная пружина.
- Магнитопровод.
- Медная обмотка.
- Алюминиевый каркас.
2.
Расчетная часть
.1
Исходные данные
Измеренные значения (см. Рис.3(а, б)):
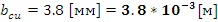
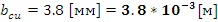 - Ширина
слоя меди.
- Ширина
слоя меди.
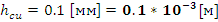
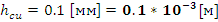 - Высота слоя меди.
- Высота слоя меди.
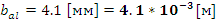
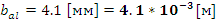 - Ширина
алюминиевого каркаса.
- Ширина
алюминиевого каркаса.
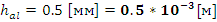
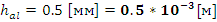 - Высота алюминиевого каркаса.
- Высота алюминиевого каркаса.
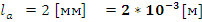
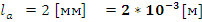 - Ширина рабочего зазора, также высота обмотки,
каркаса.
- Ширина рабочего зазора, также высота обмотки,
каркаса.
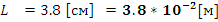
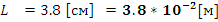 - Плечо силы Ампера, длинна горизонтальной части обмотки,
каркаса.
- Плечо силы Ампера, длинна горизонтальной части обмотки,
каркаса.
Выбранные
значения:
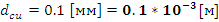
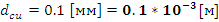 -
Диаметр медной проволоки.
-
Диаметр медной проволоки.
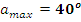
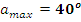 - Максимальный угол отклонения обмотки, каркаса.
- Максимальный угол отклонения обмотки, каркаса.
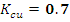
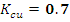 - Коэффициент заполнения медной проволоки.
- Коэффициент заполнения медной проволоки.
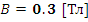
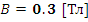 - Магнитная индукция.
- Магнитная индукция.
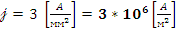
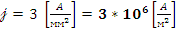 -
Максимальная плотность тока медной проволоки.
-
Максимальная плотность тока медной проволоки.
Табличные
значения:
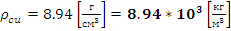
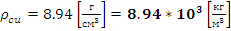 -
Плотность меди.
-
Плотность меди.
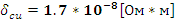
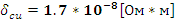 - Удельное электрическое сопротивление меди.
- Удельное электрическое сопротивление меди.
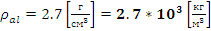
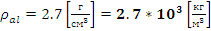 - Плотность алюминия.
- Плотность алюминия.
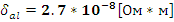
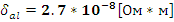 - Удельное электрическое сопротивление алюминия.
- Удельное электрическое сопротивление алюминия.
2.2
Расчет характеристик милливольтметра
Общее
уравнение состояние милливольтметра:

 ; (1)
; (1)
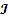
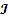 - Суммарный момент инерции каркаса и обмотки.
- Суммарный момент инерции каркаса и обмотки.
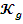
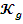 - Коэффициент демпфирования.
- Коэффициент демпфирования.
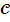
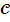 - Коэффициент жесткости.
- Коэффициент жесткости.
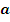
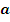 - Угол отклонения.
- Угол отклонения.
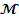
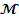 - Электрический момент.
- Электрический момент.
Вынося
суммарный момент инерции за скобку получим:
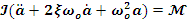
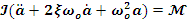 ; (2)
; (2)
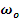
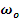 - Собственная круговая частота недемпфированных
колебаний.
- Собственная круговая частота недемпфированных
колебаний.
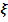
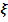 - Относительный коэффициент демпфирования.
- Относительный коэффициент демпфирования.
2.2.1
Расчет электрического момента 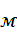
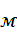
При пропускании электрического тока через рамку проводника в магнитном
поле, со стороны последнего на рамку действует сила Ампера:
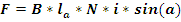
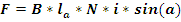
-
здесь 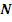
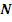 -
количество витков,
-
количество витков, 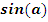
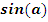 - синус угла между проводником и вектором магнитной
индукции.
- синус угла между проводником и вектором магнитной
индукции.
Соответственно
электрический момент будет равен:
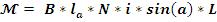
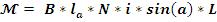 ; (3)
; (3)
Заметим
что из рисунка 3.а видно, что угол между проводником находящимся в магнитном
поле и вектором магнитной индукции равен 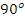
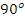 .
Неизвестными величинами в (3) являются
.
Неизвестными величинами в (3) являются 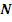
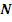 и
и 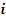
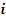 . Найдем
. Найдем 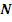
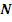 .
.
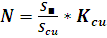
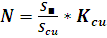 ; (4)
; (4)
Здесь
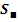
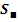 - площадь сечения слоя меди,
- площадь сечения слоя меди, 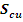
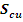 - площадь сечения медной проволоки.
- площадь сечения медной проволоки.
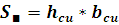
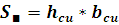 ; (5)
; (5)
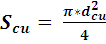
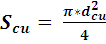 ; (6)
; (6)
Подставляя
формулы (5) и (6), а также значение коэффициента заполнения в уравнение (4)
получим:
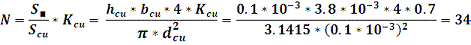
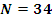
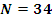 - количество витков медной проволоки, заметим, что это
значения является округлением значения 33.868.
- количество витков медной проволоки, заметим, что это
значения является округлением значения 33.868.
Найдем
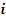
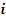 .
.
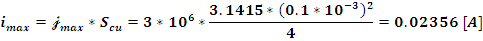
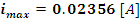
Подставив
найденные значения в формулу (3) найдем 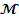
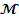 :
:
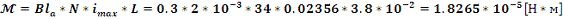
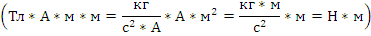
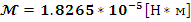
2.2.2
Расчет коэффициента жесткости пружины 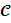
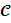
Найдем
коэффициент жесткости пружины из условия завершения всех колебательных
процессов в системе (т.к. колебания затухающие).
Соответственно,
подставляя некоторое постоянное, максимальное, значения угла отклонения в
уравнение (1) получим:
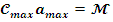
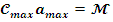 =>
=> 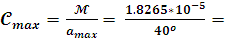
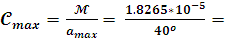
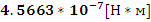
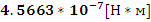
.2.3
Расчет суммарного момента инерции 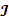
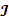

 ; (7)
; (7)
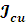
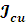 - Суммарный момент инерции медной обмотки.
- Суммарный момент инерции медной обмотки.
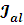
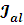 - Суммарный момент инерции алюминиевого каркаса.
- Суммарный момент инерции алюминиевого каркаса.
Найдем
суммарный момент инерции медной обмотки.
Заметим,
что геометрически и обмотка и каркас представляют собой прямоугольные формулы,
следовательно, их моменты инерции можно найти, посчитав по отдельности сначала
моменты инерции горизонтальных, а затем и вертикальных участков.
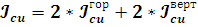
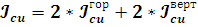 ; (8)
; (8)
Момент
инерции горизонтального участка обмотки:
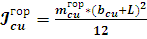
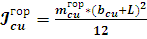 ; (9)
; (9)
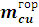
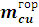 - масса отдельно горизонтального участка обмотки.
- масса отдельно горизонтального участка обмотки.
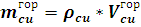
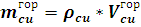 ; где
; где 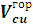
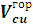 - объем горизонтального участка обмотки.
- объем горизонтального участка обмотки.
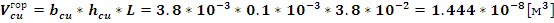
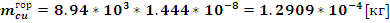
Подставляя
найденное значение массы горизонтального участка обмотки в (9) найдем:
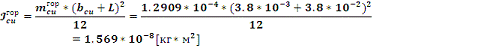
Момент
инерции вертикального участка обмотки:
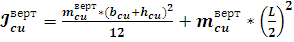
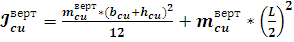 ; (10)
; (10)
Здесь
применена теорема Штейнера для расчета момента инерции относительно оси
отстоящей на 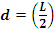
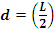 .
.
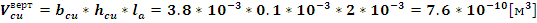
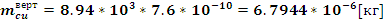
Подставляя
найденное значение массы вертикального участка обмотки в (10) найдем:
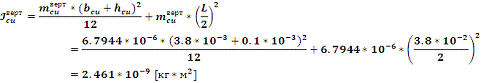
Подставим
найденные значения 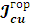
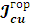 ,
, 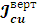
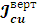 в (8) получим:
в (8) получим:
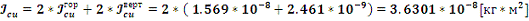
Найдем
суммарный момент инерции алюминиевого каркаса.
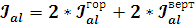
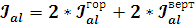 ; (11)
; (11)
Момент
инерции горизонтального участка каркаса:
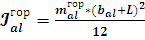
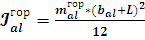 ; (12)
; (12)
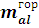
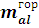 - масса отдельно горизонтального участка каркаса.
- масса отдельно горизонтального участка каркаса.
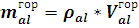
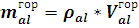 ; где
; где 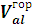
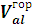 - объем горизонтального участка каркаса.
- объем горизонтального участка каркаса.
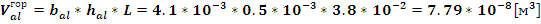
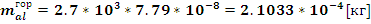
Подставляя
найденное значение массы горизонтального участка каркаса в (12) найдем:
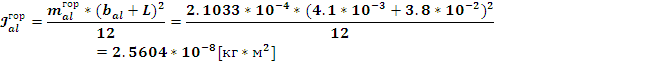
Момент
инерции вертикального участка каркаса:
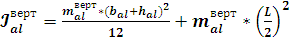
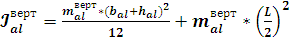 ; (13)
; (13)
Здесь
применена теорема Штейнера для расчета момента инерции относительно оси
отстоящей на 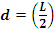
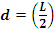 .
.
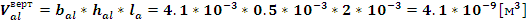
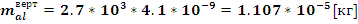
Подставляя
найденное значение массы вертикального участка каркаса в (13) найдем:
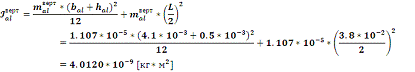
Найдем
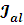
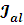 подставив найденные значения
подставив найденные значения 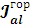
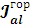 и
и 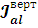
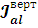 в (13):
в (13):
Для
суммарного момента инерции обмотки и каркаса получим, соответственно формуле
(7):
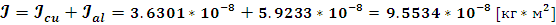
2.2.4
Расчет коэффициента демпфирования 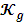
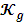
При
прохождении замкнутого токопроводящего контура через магнитный поток, в контуре
индуцируется ток, согласно Рис.3 видим, что в подвижной части милливольтметра
присутствует такой замкнутый токопроводящий контур, а именно алюминиевый каркас.
Медную обмотку не рассматриваем, т.к. предполагается, что она подключена к
внешнему источнику тока.
Следовательно,
при вращении каркаса в нем будет самоиндуцируваться ток, который будет
создавать момент силы препятствующий изменению магнитного потока через каркас,
а следовательно играющий роль демпфера.
Запишем
выражение для такого демпфирующего момента:
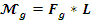
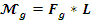 ; (14)
; (14)
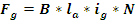
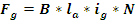 ; (15)
; (15)
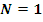
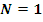 для каркаса.
для каркаса.
Демпфирующий
ток определим из выражения:
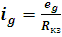
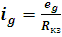 ,где
,где 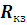
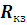 - это сопротивление короткого замыкания алюминиевого
каркаса, а
- это сопротивление короткого замыкания алюминиевого
каркаса, а 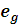
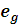 -ЭДС в алюминиевом каркасе.
-ЭДС в алюминиевом каркасе.
Запишем
выражение для 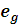
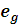 :
: 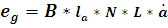
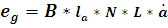 ,
, 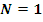
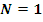 ;
;
Подставив
выражение для ЭДС в формулу для тока получим:
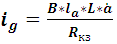
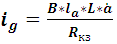 ; (16)
; (16)
Подставляя
(16) и (15) в (14) получим финальное выражение для демпфирующего момента:
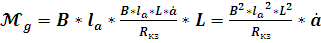
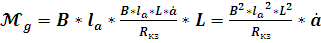 ; (17)
; (17)
Сравнивая
полученное выражение с изначальной формулой общего состояния (1) видим, что
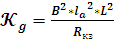
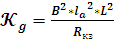 ; (18)
; (18)
В
формуле (18) неизвестно только сопротивление короткого замыкания 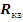
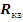 , найдем
его:
, найдем
его:
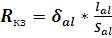
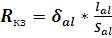 ; (19)
; (19)
Общая
длина алюминиевого каркаса: 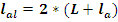
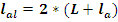 ;
;
Площадь
сечения алюминиевого каркаса: 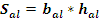
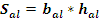 ;
;
Подставляя
эти два выражения в (19) получим:
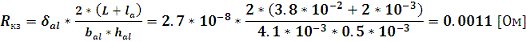
Найдем
коэффициент демпфирования, подставив найденное значение 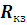
 и известные значения других параметров в формулу (18):
и известные значения других параметров в формулу (18):
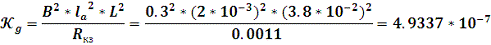
Определим
размерность 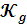
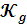 :
:
Заметим
что в уравнении (1) справа после знака равенства стоит размерность 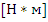
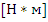 , следовательно,
для выполнения равенства, слева тоже должна быть размерность
, следовательно,
для выполнения равенства, слева тоже должна быть размерность 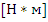
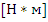 , т.е.
, т.е.
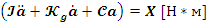
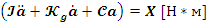 ,где Х - это какое-то число. следовательно
,где Х - это какое-то число. следовательно 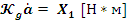
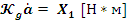 , т.к.
, т.к. 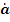
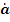 имеет размерность
имеет размерность 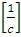
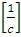 , то
, то 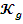
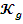 должен иметь размерность
должен иметь размерность 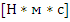
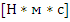 , чтобы
равенство (1) выполнялось.
, чтобы
равенство (1) выполнялось.
Проверим
размерность формулы (18) учитывая 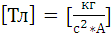
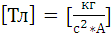 , и
, и 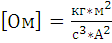
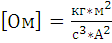 получаем:
получаем:
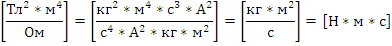
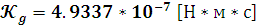
2.2.5
Заключение расчетной части, расчет 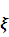
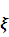 и
и 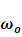
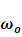
Итого нашли все четыре коэффициента из уравнения (1):

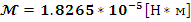
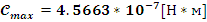
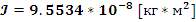
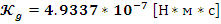
Найдем
собственную круговую частоту недемпфированных колебаний 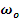
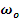 и относительный коэффициент демпфирования
и относительный коэффициент демпфирования 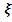
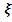 .
.
Из
уравнения (2) 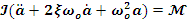
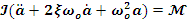 видим, что
видим, что

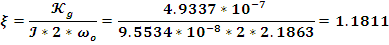
Относительный
коэффициент демпфирования величина безразмерная (
 ).
).
3.
Модификация милливольтметра в маятниковый акселерометр
Сравнивая
рисунки 1 и 2 видим, что для измерения кажущегося ускорения с помощью
аналогового милливольтметра, необходимо:
-
Сместить центр тяжести вращающейся части (ротора) относительно оси вращения.
-
Замкнуть обмотку на себя, для усиления демпфирующего эффекта.
-
Добавить элемент регистрирующий значение и направление тока, индуцированного в
катушке и каркасе, а, следовательно, и отклонение центра тяжести ротора от
положения покоя.
-
Добавить внутренний источник питания, или сделать подключение к внешнему
источнику.
-
Опционально можно добавить усилитель сигнала на выходе регистрирующего
элемента.