Коэффициент лобового сопротивления корпуса бескрылого ЛА при сверхзвуковых скоростях и вариации одного из его геометрических параметров

Содержание

Введение

Цель, порядок выполнения задания

Теоретическая часть

Исходные данные

Расчет лобового сопротивления бескрылого ЛА

Выводы

Введение

лобовое сопротивление бескрылый летательный аппарат

Фюзеляжи самолетов, беспилотных летательных аппаратов, корпуса снарядов и ракет представляют собой длинные тонкие тела вращения, обычно состоящие из конических (параболических) и цилиндрических отсеков.

В отличие от крыла, фюзеляж при малых углах атаки почти не создает подъемной силы. Основной составляющей аэродинамической силы для тел вращения является сила лобового сопротивления. В условиях установившегося полета она определяет тягу двигателей, необходимую для поддержания движения летательного аппарата (ЛА). Следовательно, формы фюзеляжей и корпусов ЛА должны обеспечивать минимальное, при данных размерах, лобовое сопротивление.

Сопротивление тел вращения при дозвуковых скоростях складывается примерно на 75% из сопротивления трения, а оставшиеся 25% приходятся на долю вихревого сопротивления давления. При около- и сверхзвуковых скоростях кроме этих видов сопротивлений появляется волновое сопротивление, которое может составлять до 2/3 и даже более от общей величины сопротивления.

Сверхзвуковое тело вращения, исходя из конструктивных и аэродинамических соображений, обычно представляют как совокупность трех частей: головной, цилиндрической и кормовой. Головная и кормовая части играют основную роль в образовании сопротивления давления (волнового и донного), а средняя - цилиндрическая часть создает основную долю сопротивления трения. Сила лобового сопротивления определяется по общей формуле аэродинамической силы

,

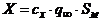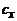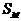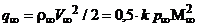где  - коэффициент лобового сопротивления корпуса ЛА, отнесенный к площади миделя ; - скоростной напор набегающего потока.

Составляющие аэродинамической силы определяют либо расчетным путем по полуэмпирическим зависимостям, либо экспериментальным путем, при исследовании моделей или натурных образцов ЛА в аэродинамических трубах или в полетных условиях. Теоретическое исследование проводят для нахождения распределений давлений и касательных напряжений с последующим вычислением нужных силовых характеристик или для непосредственного их расчета. Исследования и расчеты подобного рода удобно проводить с помощью ЭВМ, используя аналитические решения и экспериментальные зависимости. Использование ЭВМ позволяет, в конечном счете, значительно сократить время для принятия основного решения при проектировании перспективных ЛА.

Цель, порядок выполнения задания

Цель задания: провести численный расчет коэффициента лобового сопротивления при осесиметричном (угол атаки a=0) обтекании корпуса бескрылого ЛА, совершающего полет в атмосфере на высотах до 80 км со скоростями, соответствующими числам Маха от 1,5 до 5, при вариации размеров некоторых элементов форм головной или кормовой частей ЛА, сделать анализ полученных результатов.

Корпус ЛА простейшей формы имеет головную часть в виде заостренного конуса или параболоида, среднюю - цилиндрическую часть и кормовую - расширяющуюся оконечность параболической формы.

В данном задание следует принимать значения геометрических параметров ЛА, не изменяемых в процессе исследований, исходя из следующих рекомендаций:

длину конической головной части - ;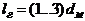

длину цилиндрической части - ;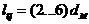

длину кормовой части - ;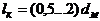

диаметр цилиндра (миделя) - ;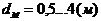

диаметр кормового среза 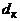 - (не нарушая условия - 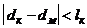): для расширяющейся .

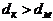На значение переменного геометрического параметра эти рекомендации не распространяются. Числовые значения указанных переменных выбирались самостоятельно и согласовывались с преподавателем.

Расчетным путем устанавливаем влияние переменного геометрического параметра и числа М_¥ (и высоты полета, если она переменна) на величину коэффициента лобового сопротивления ЛА и его отдельных составляющих.

По результатам расчета строят следующие графики:

1. зависимость каждой из составляющих коэффициента сопротивления, на которую влияет переменный геометрический параметр, от величины этого параметра для нескольких чисел 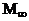. Для приведенного примера это график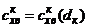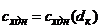и ,  и ;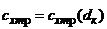

. для одного из значений переменного геометрического параметра зависимость каждой из составляющих коэффициента сопротивления от числа 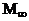 на одном графике;

. для каждого значения переменной геометрической величины зависимость .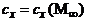

Теоретическая часть

Методика расчета коэффициента лобового сопротивления

Коэффициент лобового сопротивления тела вращения (бескрылого ЛА) в диапазоне сверхзвуковых скоростей можно представить в виде суммы трех составляющих:

,

где 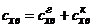 - коэффициент волнового сопротивления корпуса ЛА;

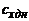- коэффициент донного сопротивления;

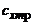- коэффициент сопротивления трения.

1. Волновое сопротивление

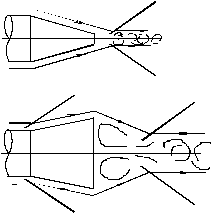
Рис. 2. Скачки уплотнения у кормовых частей

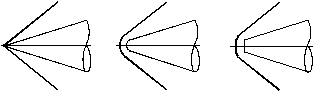
Рис. 1. Скачки уплотнения у головных частей

Волновое сопротивление обусловлено необратимыми потерями механической энергии в скачках уплотнения, возникающих около головной (рис.1) и кормовой (рис.2) частей рассматриваемой упрощенной конфигурации ЛА. Поэтому, полный коэффициент волнового сопротивления тела вращения представляем в виде суммы коэффициентов волнового сопротивления головн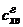ой  и кормовой 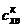 частей, каждый из которых рассчитываем по отдельной формуле.

Коэффициенты волнового сопротивления для рассматриваемых форм головной и кормовой частей рассчитываются по следующим полуэмпирическим формулам:

а) головная часть - параболическая заостренная:

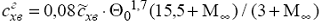
где: 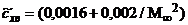 - коэффициент волнового сопротивления конуса с углом полураствора равным 1 градусу;

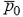 - коэффициент давления в передней критической точке за прямым скачком уплотнения.

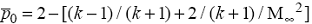
б) кормовая часть - параболическая расширяющаяся:

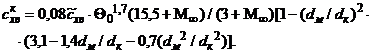
Q_к - угол полураствора конуса (головного или кормового), а Q₀ - полуугол при вершине параболы, которые рассчитываем по следующим формулам:

а) головная часть - параболическая заостренная:

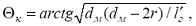
б) кормовая часть - параболическая расширяющаяся:

;

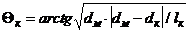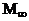 - число Маха невозмущенного набегающего потока;

d_м - диаметр миделя ЛА (диаметр цилиндрической части);

d_к - диаметр кормового среза;

r - радиус притупления головной части;

Следует еще раз заметить, что волновое сопротивление для большинства конструкций вносит наибольший вклад в суммарную величину 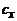, особенно при малых и умеренных сверхзвуковых скоростях полета.

2. Донное сопротивление

Рис. 3. Течение в донной области при сверхзвуковых скоростях

Донное сопротивление обусловлено разрежением в донной области тела. Коэффициент донного сопротивления численно равен коэффициенту донного давления, взятому с противоположным знаком. Донное разрежение зависит от скорости полета, состояния поверхности тела, его длины, т.е. от состояния пограничного слоя в области донного среза, и сужения кормовой части. Чем толще пограничный слой у донного среза (длинное тело или большая шероховатость), тем больше донное давление и меньше донное сопротивление. При сверхзвуковых скоростях с ростом числа 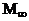 разрежение в донной области тела увеличивается и при достаточно больших числах 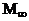 за дном возникает абсолютный вакуум.

Донное сопротивление для некоторых тел вращения может достигать 30% полного сопротивления. У тел вращения большого удлинения увеличение угла атаки до a»5^° практически не влияет на величину донного давления.

Расчет коэффициента донного сопротивления производим по формуле:

,

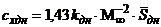где .

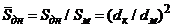Поправочный коэффициент 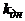, учитывающий отличие донного давления от абсолютного вакуума, зависит от числа 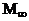 и геометрических характеристик тела вращения и равен

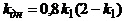 при k₁£ 1

или 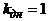при k₁> 1,

В формуле для расчета

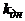
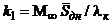  (здесь  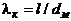- удлинение ЛА).

При определенных сочетаниях параметров входящих в 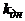 (изменение скорости полета или величины переменного геометрического размера) расчетная схема автоматически переходит от расчета величины 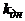 по приведенной формуле, к постоянному значению 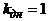. Этому случаю отвечает скачкообразное изменение величины донного сопротивления в зависимостях 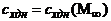 или .

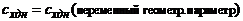3. Сопротивление трения

Проекцию главного вектора приложенных к ЛА касательных сил на направление невозмущенного потока называют сопротивлением трения. Наибольший вклад в сопротивление трения тел вращения дает его средняя (обычно цилиндрическая) часть. Коэффициент сопротивления трения 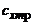 зависит от состояния пограничного слоя; при сверхзвуковых скоростях полета с ростом числа М_¥ коэффициент сопротивления трения убывает в связи с уменьшением толщины пограничного слоя.

При сверхзвуковых скоростях полета длинного тела, ламинарный пограничный слой имеет место только в небольшой области, примыкающей к носовой оконечности тела, т.е. практически на всей поверхности ЛА реализуется турбулентный режим течения. Место перехода пограничного слоя из одного состояния в другое может быть приближенно определено через отношение критического числа Рейнольдса к числу Рейнольдса в данной точке траектории ЛА. В настоящей расчетной схеме за критическое число Рейнольдса принято значение .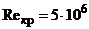

Используя распространенный в аэродинамике прием, когда криволинейная внешняя поверхность реального ЛА заменяется плоской пластиной, эквивалентной по площади и той же протяженности по потоку, что и рассматриваемая поверхность тела вращения, расчетную формулу для определения сопротивления трения запишем в виде:

,

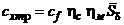где 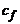- коэффициент сопротивления трения плоской пластины в пограничном слое несжимаемой жидкости;

 - коэффициент, учитывающий отличие тела вращения от плоской пластины;

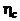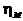 - коэффициент, учитывающий сжимаемость среды;

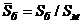 - относительная площадь боковой поверхности ЛА; 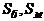- полная площадь боковой поверхности и площадь миделевого сечения ().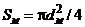

). При 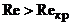 на поверхности ЛА существует смешанный пограничный слой. Поэтому среднее для ЛА значение местного коэффициента трения рассчитываем по следующей формуле:

,

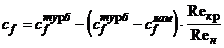в которой коэффициенты трения для ламинарного и турбулентного пограничных слоев рассчитываем по формулам:

,;

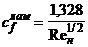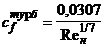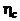Значение коэффициента  зависит от удлинения тела вращения. Приведенная в книге [2] графическая зависимость аппроксимирована несколькими простейшими аналитическими формулами и использована в программе расчета. При расчете коэффициента 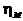 также учтен смешанный характер течения на поверхности ЛА:

,

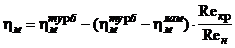где  .

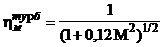
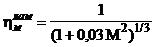) При 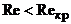 имеет место чисто ламинарное обтекание всей поверхности ЛА, поэтому , .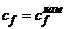

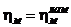В формулах для расчета коэффициента трения 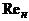 - число Рейнольдса, рассчитанное по параметрам атмосферы на заданной высоте

,

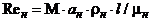где 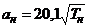 - скорость звука на данной высоте;

m_н, Т_н, r_н - динамический коэффициент вязкости, температура и плотность воздуха на заданной высоте (по таблице стандартной атмосферы,; в программе расчета параметры стандартной атмосферы заданы в виде аналитических выражений);

l - общая длина ЛА;

С увеличением высоты полета коэффициент кинематической вязкости n непрерывно возрастает ввиду опережающего влияния уменьшения плотности атмосферы. Это приводит к росту толщины пограничного слоя и к увеличению .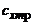

Число 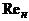 при увеличении H уменьшается и может стать даже меньше 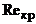, то есть доля поверхности обтекаемой турбулентным пограничным слоем уменьшается и на некоторой высоте полета пограничный слой на всей поверхности ЛА становится ламинарным. Характер влияния высоты полета на коэффициент сопротивления трения довольно сложный и необходимо быть особенно внимательным при анализе графиков для 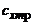 в условиях переменной высоты полета при одновременном увеличении скорости движения ЛА. Высота и скорость полета оказывают противоположное влияние на величины 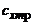 и скоростного напора 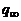. Поэтому при анализе их влияния на силу сопротивления трения следует, исходя из выражения 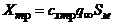, учитывать скорость и направление изменения как 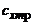, так и 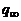. Изменение геометрических размеров ЛА (длин или углов раствора головной и кормовой частей, диаметра кормового среза, радиуса притупления головной части) может привести к изменению, как общей длины ЛА, так и площади боковой поверхности 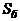. Эти изменения в обязательном порядке скажутся на величине .

Исходные данные

Задание № 210

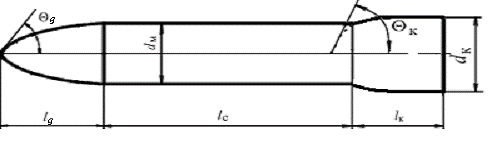
Схематический чертеж ЛА

Расчет лобового сопротивления бескрылого ЛА

Носовая часть: Параболическая заостренная

Кормовая часть: Параболическая расширяющаяся

Носовая часть: Параболическая заостренная

Кормовая часть: Параболическая расширяющаяся

Носовая часть: Параболическая заостренная

Кормовая часть: Параболическая расширяющаяся

Носовая часть: Параболическая заостренная

Кормовая часть: Параболическая расширяющаяся

Носовая часть: Параболическая заостренная

Кормовая часть: Параболическая расширяющаяся

Носовая часть: Параболическая заостренная

Кормовая часть: Параболическая расширяющаяся

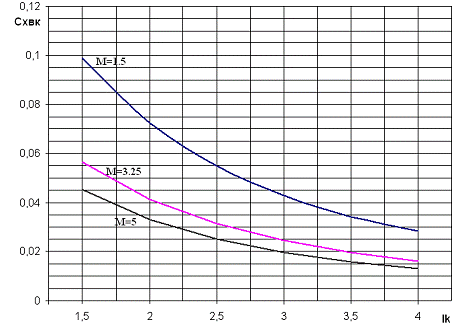
Зависимость коэффициента волнового сопротивления кормовой части от ее длины

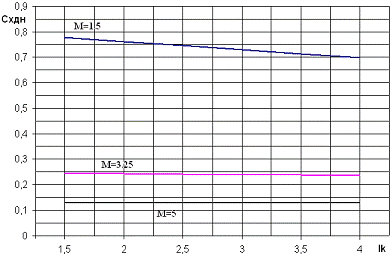
Зависимость коэффициента донного сопротивления от длины кормы

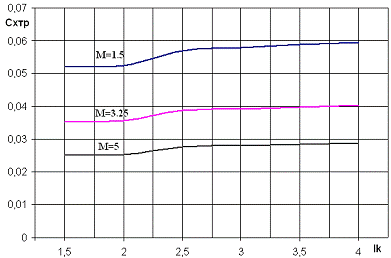
Зависимость коэффициента сопротивления трения от длины кормы

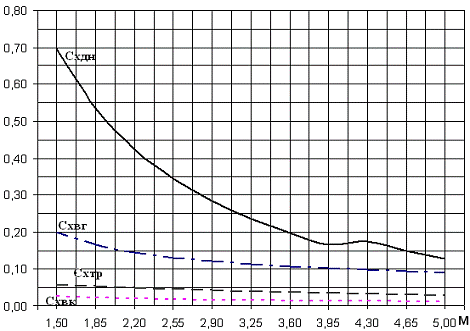
Зависимость составляющих коэффициента лобового сопротивления от числа Маха (l_k =4)

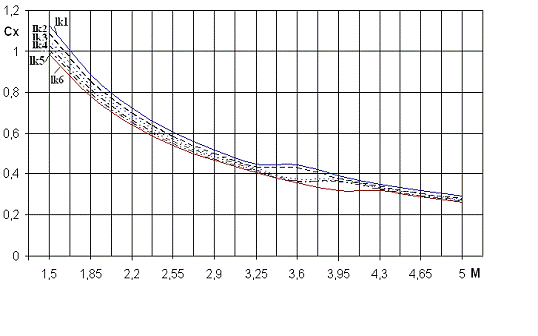
Зависимость коэффициента лобового сопротивления ЛА от числа Маха при различной длине кормовой части

l_k1 = 1.5 м

l_k2 = 2 м

l_k3 = 2.5 м

l_k4 = 3 м

l_k5 = 3.5 м

l_k6 = 4 м

Выводы

. Коэффициент волнового сопротивления в кормовой части с увеличением длины кормовой части падает, потому что уменьшается угол полураствора кормовой части. Следовательно, и интенсивность скачка уплотнения тоже будет уменьшаться, а это обуславливает снижение потерь механической энергии.

С увеличением числа Маха, коэффициент волнового сопротивления в кормовой части так же будет уменьшаться, так как уменьшается интенсивность и угол наклона косого скачка уплотнения.

. Коэффициент донного сопротивления с увеличением длины кормовой части ЛА незначительно уменьшается, так как увеличивается длина ЛА, а следовательно, увеличивается толщина пограничного слоя в области донного среза.

С ростом числа Маха увеличивается перепад давлений, но скоростной напор растет значительно быстрее, поэтому С_хдн уменьшается.

. С увеличением длины кормовой части, увеличивается площадь боковой поверхности ЛА, что ведет к росту С_хтр. В то же время, с ростом числа Маха коэффициент С_хтр будет уменьшаться в связи с уменьшением толщины пограничного слоя. Этим объясняется положение кривых на графике.

. С_хвг уменьшается, т.к. с ростом числа Маха угол наклона скачка уплотнения уменьшается и потери механической энергии становятся меньше.

Изменение С_хвк ведет себя таким же образом.

С_хтр уменьшается из-за уменьшения пограничного слоя.

С ростом числа Маха возрастает скоростной напор, вследствие этого С_хдн уменьшается. Но с ростом числа Маха увеличивается разрежение в донной области, и при достаточно больших числах Маха за дном возникает абсолютный вакуум. Поэтому, при числе Маха приближенно равном 4, поправочный коэффициент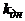 заменяется с расчетной величины  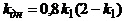на постоянную - 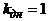. Этим объясняется скачкообразное изменение величины С_хдн.

. Наибольшее влияние на коэффициент лобового сопротивления оказывают коэффициент донного сопротивления и коэффициент волнового сопротивления головной части ЛА.

По полученным данным и построенным графикам наибольшее лобовое сопротивление наблюдается при длине кормы равной 1.5 м. Наименьшее С_х будет при длине кормы равной 4м.

Оптимальным является вариант с длиной кормовой части 4 метра.