Динамика микромеханического гироскопа камертонного типа на подвижном основании
Аннотация
В данной работе рассматривается динамика
микромеханического гироскопа камертонного типа на подвижном основании,
чувствительным элементом которого являются два полукольца, закреплённые на
рамке с помощью шарниров.
Целью работы был анализ режимов работы гироскопа
при малой угловой скорости основания. Двумя способами (с использованием
принципа Гамильтона-Остроградского и с помощью вариационных уравнений Эйлера)
были построены уравнения движения для различных случаев - без учета трения и
при его наличии. При этом отдельно рассматривались случаи одночастотной системы
на неподвижном и подвижном основании и разночастотной системы на подвижном
основании. Для одночастотной системы без учета влияния трения найдено точное
решение, построены фазовые траектории системы, сделан вывод о том, что гироскоп
является датчиком угла поворота. Для разночастотной системы рассмотрено два
случая: в первом проводился анализ гироскопа на неподвижном основании. Найдено
точное решение, получена угловая скорость прецессии гироскопа. Приведен
численный пример, исходя из материалов которого, построена угловая скорость
прецессии волновой картины колебаний, иллюстрирующая биение резонатора. Во
втором случае рассматривался гироскоп на подвижном основании. Для него получено
точное решение, численное решение, приведены графики, иллюстрирующие изменение
амплитуды колебаний в результате частотной расстройки. В работе изучены
свободные колебания гироскопа на подвижном основании при учете трения. Подробно
рассмотрен случай одночастотной системы, найдено точное решение, построены
фазовые траектории системы, сделан вывод о том, что гироскоп является датчиком
угла поворота. Для случая разночастотной системы с учетом трения получено
численное решение, приведены графики, иллюстрирующие изменение амплитуды
колебаний в результате частотной расстройки. Поиск решений во всех случаях
велся в переменных Ван-Дер-Поля методом Страбла.
Введение
Гироскоп (от др.-греч.
<#"550902.files/image001.gif"> (1.1)
Запишем удельную, отнесенную к единице длины
осевой линии резонатора кинетическую энергию гироскопа. Она складывается из
кинетической энергии полукольца и рамки:
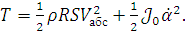 (1.2)
(1.2)
Здесь:
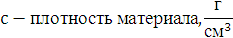
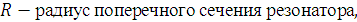
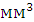
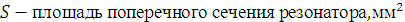
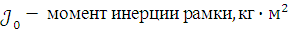
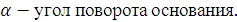
Для того, чтобы найти абсолютную скорость
движения точки полукольца в скалярном виде, нужно сначала перейти к её
векторному представлению. В векторном пространстве абсолютная скорость состоит
из суммы переносной и относительной скоростей.
 (1.3)
(1.3)
Переносную скорость найдем по формуле Эйлера:
 (1.4)
(1.4)

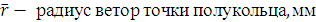
Зададимся декартовой системой координат так,
чтобы начало координат располагалось посередине рамки, ось y
была соосна рамке, ось x
- направлена перпендикулярно, а ось z, являющаяся осью чувствительности
гироскопа, - направлена на нас. Зададимся базисом 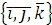 .
Операцию дифференцирования по координате
.
Операцию дифференцирования по координате 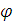 будем
обозначать штрихом, а операцию дифференцирования по времени t будем обозначать
точкой.
будем
обозначать штрихом, а операцию дифференцирования по времени t будем обозначать
точкой.
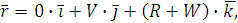 (1.5)
(1.5)
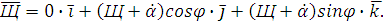 (1.6)
(1.6)
Здесь V
и W - упругие смещения
элемента кольцевого резонатора в окружном и радиальном направлениях.
Итак, переносная скорость движения в разложении
по данному базису есть:
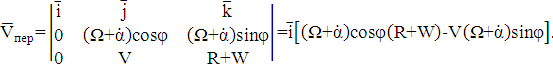 (1.7)
(1.7)
Разложим относительную скорость движения по
данному базису:
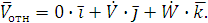 (1.8)
(1.8)
Теперь можем записать абсолютную скорость:
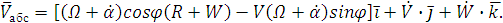 (1.9)
(1.9)
Мы нашли все неизвестные, запишем удельную
кинетическую энергию:
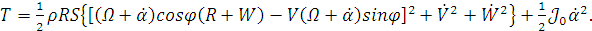 (1.10)
(1.10)
Найдем удельную потенциальную энергию гироскопа.
Она состоит из потенциально энергии полукольца и потенциальной энергии балки:
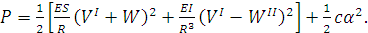 (1.11)
(1.11)
Здесь с - жесткость балки, 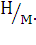
Далее проинтегрируем удельную кинетическую и
удельную потенциальную энергию от 0 до 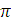 ,
чтобы получить кинетическую и потенциальную энергию для полукольца и построим
Лагранжиан (1.1) системы:
,
чтобы получить кинетическую и потенциальную энергию для полукольца и построим
Лагранжиан (1.1) системы:
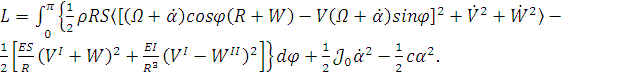 (1.12)
(1.12)
1.1 Составление уравнений движения с
помощью принципа Гамильтона
Получим уравнения движения гироскопа, используя
принцип наименьшего действия Гамильтона-Остроградского.
Действие по Гамильтону имеет вид:
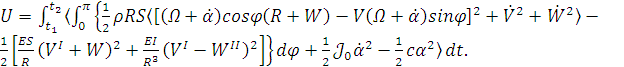 (1.13)
(1.13)
Воспользуемся гипотезой о нерастяжимости
срединной линии резонатора:
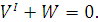 (1.14)
(1.14)
Проведем соответствующую замену переменных:
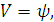 (1.15)
(1.15)
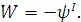 (1.16)
(1.16)
Таким образом (1.13):
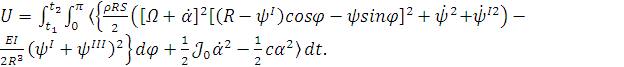 (1.17)
(1.17)
На истинном пути действие по Гамильтону
принимает стационарное значение, то есть 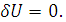 Следовательно,
Следовательно,
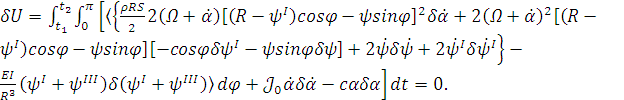 (1.18)
(1.18)
Выполним некоторые преобразования над
варьируемыми переменными:
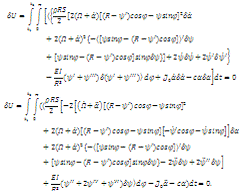
Выпишем интегро-дифференциальные уравнения
гироскопа:
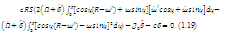
1.2 Составление
уравнений движения с помощью уравнений Эйлера
гироскоп колебание трение скорость
Проведём проверку полученных уравнений движения
гироскопа с помощью уравнений Эйлера
Действие по Гамильтону имеет вид
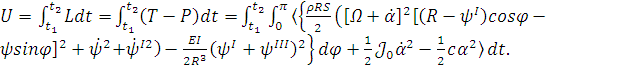 (1.20)
(1.20)
Подынтегральное выражение есть функция 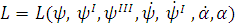
Оба уравнения вариационной задачи будут
выглядеть:
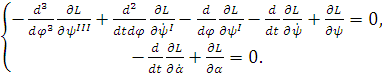 (1.21)
(1.21)
Выведем первое интегро-дифференциально уравнение
гироскопа:
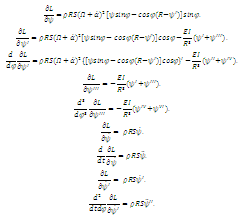
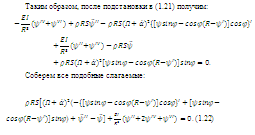
Выведем второе интегро-дифференциально уравнение
гироскопа:
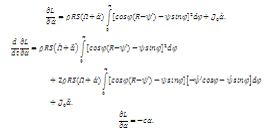
Таким образом, после подстановки в (1.21)
получим:
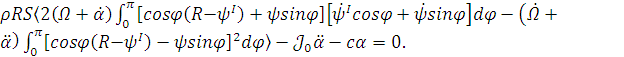 (1.23)
(1.23)
Получили интегро-дифференциальные уравнения
движения гироскопа с помощью уравнений Эйлера. Они совпадают с уравнениями
(1.19), полученными с использованием принципа наименьшего действия
Гамильтона-Остроградского.
1.3 Решение уравнений движения
методом Бубнова-Галеркина
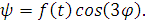 (1.24)
(1.24)
Чтобы подставить функцию в уравнения, найдем все
остальные ее производные:
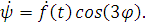
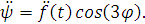
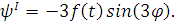
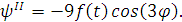
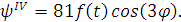
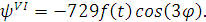
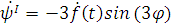
Интегро-дифференциальные уравнения после
подстановки примут вид:

Для первого уравнения проведем непосредственно
процедуру Бубнова-Галеркина:
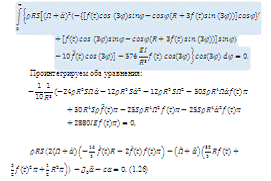
.4 Линеаризация уравнений движения
Раскроем скобки в уравнениях (1.26),
получившихся после проведения процедуры Бубнова-Галеркина:

1.5 Нормализация уравнений движения
Обезразмерим переменную 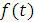 ,
для этого введем новую переменную
,
для этого введем новую переменную 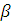
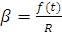 (1.29)
(1.29)
Уравнения движения примут следующий вид:
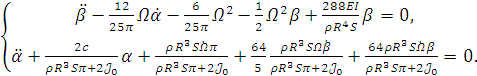 (1.30)
(1.30)
Обозначим частоту колебаний решения в первом
уравнении как:
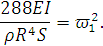
Коэффициент при гироскопическом слагаемом в
первом уравнении как:
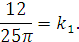
Обозначим частоту колебаний решения во втором
уравнении как:
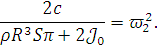
Коэффициент при гироскопическом слагаемом во
втором уравнении как:
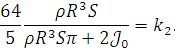
В итоге получили уравнения:
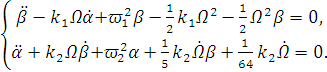 (1.31)
(1.31)
Т.к. 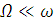 :
:
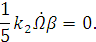
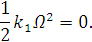
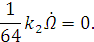
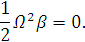
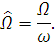
Уравнения примут вид:
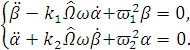 (1.31)
(1.31)
2. Свободные колебания гироскопа без
учета трения
.1 Случай одночастотной системы:
Имеем следующую систему:
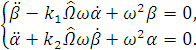 (1.31)
(1.31)
Найдем решение системы (1.31) в переменных
Ван-Дер-Поля. Применим к нашей системе метод Страбла и приведем ее к
стандартному виду посредством перехода от переменных 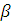 и
и
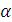 к
медленным переменным
к
медленным переменным 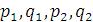 по формулам:
по формулам:
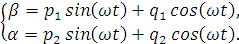 (1.32)
(1.32)
Найдем производные первого и второго порядков
переменных 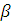 и
и 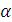 по
времени t:
по
времени t:

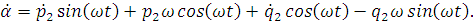
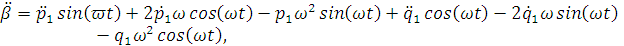
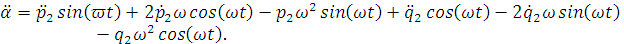
Подставим полученные уравнения в нашу систему
(1.32):
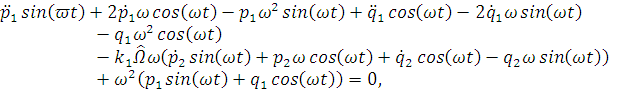
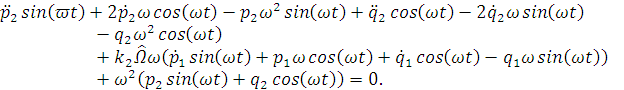
После линеаризации система примет вид:
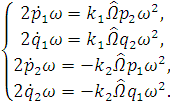
Разделим на коэффициенты при старшей
производной, т. о. получим уравнения для медленных переменных:
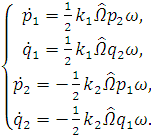 (1.33)
(1.33)
Найдем решение системы (1.33), для этого запишем
второе и четвертое уравнение следующим образом:
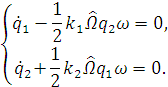
Введем замену переменных:
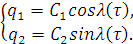 (1.34)
(1.34)
Продифференцируем уравнения замены:
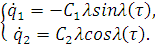 (1.35)
(1.35)
Запишем уравнения для 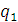 и
и
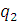 с
учетом замены (1.34), (1.35):
с
учетом замены (1.34), (1.35):
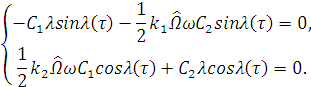
Упрощая выражения, получим:
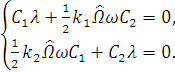 (1.36)
(1.36)
Запишем определитель 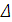 полученной
системы (1.36):
полученной
системы (1.36):
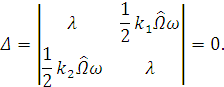
Найдем значение 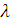 и
подставим его в 1 уравнение системы:
и
подставим его в 1 уравнение системы:
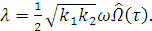 (1.37)
(1.37)
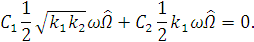
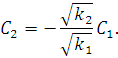
Теперь введем обратную замену:
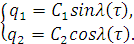 (1.38)
(1.38)
Запишем выражения для 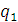 и
и
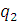 с
учетом замены (1.38):
с
учетом замены (1.38):
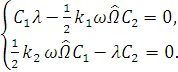 (1.39)
(1.39)
Запишем определитель 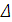 полученной
системы:
полученной
системы:
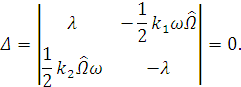
Найдем 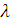 и
подставим его в первое уравнение системы:
и
подставим его в первое уравнение системы:
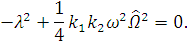
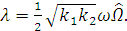 (1.40)
(1.40)
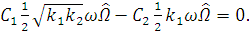
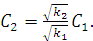
Производя аналогичные построения для переменных 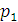 и
и
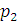 ,
мы получим полный набор коэффициентов для записи решения системы:
,
мы получим полный набор коэффициентов для записи решения системы:
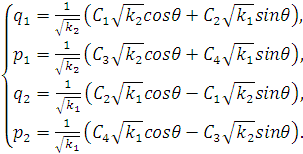 (1.41)
(1.41)
Где 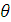 -
угол, пропорциональный интегралу от угловой скорости основания гироскопа:
-
угол, пропорциональный интегралу от угловой скорости основания гироскопа:
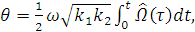 (1.42)
(1.42)
Эти формулы являются решением с точностью до
порядка 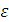 .
.
Найдем произвольные постоянные 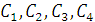 из
следующих начальных условий:
из
следующих начальных условий:

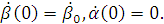 (1.44)
(1.44)
Производные по переменным 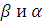 определим
из выражений:
определим
из выражений:
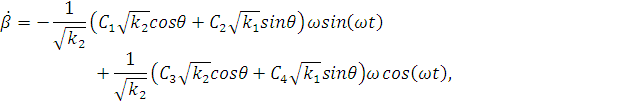
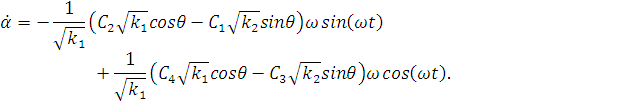
Здесь мы пренебрегли производными по переменным 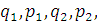 т.к.
они имеют порядок бесконечно малой величины
т.к.
они имеют порядок бесконечно малой величины 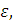 в
то время как на практике величины
в
то время как на практике величины 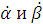 всегда
конечны.
всегда
конечны.
Тогда, подставляя начальные условия в выражения,
получим:
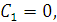
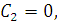
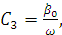
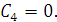
Учитывая условия, запишем 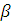 и
и
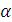 :
:
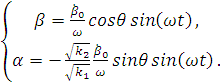 (1.45)
(1.45)
Рассмотрим соотношение 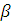 и
и
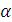 в
уравнениях:
в
уравнениях:
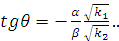 (1.46)
(1.46)
В плоскости 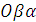 фазовая
точка описывает прямую, которая со временем будет поворачиваться в зависимости
от угловой скорости основания:
фазовая
точка описывает прямую, которая со временем будет поворачиваться в зависимости
от угловой скорости основания:
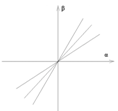
Рис.1. Фазовые траектории системы.
Таким образом гироскоп является датчиком угла
поворота.
2.2 Случай разночастотной системы
.2.1 Рассмотрим свободные колебания
гироскопа на неподвижном основании
Уравнения преобразуются следующим образом:
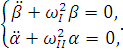 (2.1)
(2.1)
где 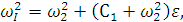
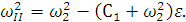
Ищем решение системы в виде:
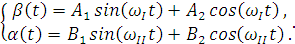 (2.2)
(2.2)
Где 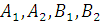 -
произвольные постоянные.
-
произвольные постоянные.
Обозначим для кратности 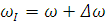 ,
,
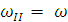 , где
, где 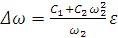 .
.
В этом случае уравнения примут вид:
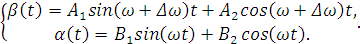 (2.3)
(2.3)
Собственная форма колебаний резонатора:
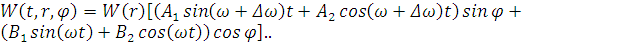 (2.4)
(2.4)
Таково решение исходной задачи по основной форме
колебаний. Далее установим связь между каноническим представлением волновой
картины колебаний и медленно изменяющимися переменными, которые измеряются
емкостными датчиками прибора.
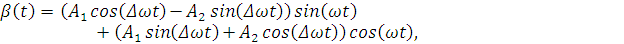
(2.5)
что дает возможность получить формулы перехода
от переменных 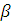 и
и 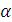 и
медленных переменных
и
медленных переменных 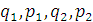 Ван-Дер-Поля,
непосредственно измеряемых в гироскопе.
Ван-Дер-Поля,
непосредственно измеряемых в гироскопе.
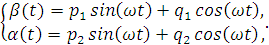 (2.6)
(2.6)
где 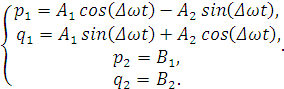 (2.7)
(2.7)
Установим связь с каноническим представлением
волновой картины колебаний в тороидальных координатах:
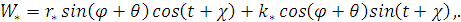 (2.8)
(2.8)
где 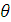 -
угол ориентации волновой картины,
-
угол ориентации волновой картины, 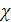 -
фаза, характеризующая изменение частоты колебаний.
-
фаза, характеризующая изменение частоты колебаний.
Определим связь между переменными 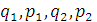 и
и
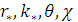 из
уравнений путем тригонометрических преобразований
из
уравнений путем тригонометрических преобразований
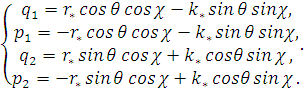 (2.9)
(2.9)
Из этих соотношений получаем:
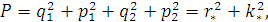
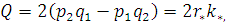
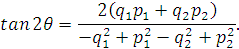
Величина P
характеризует сумму квадратов амплитуд нормальной и основной квадратурной волн
колебаний резонатора, значение Q=0
является условием существования стоячей волны колебаний резонатора.
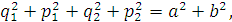
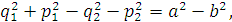
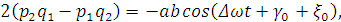
(2.10)
здесь a,
b,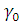 ,
,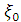 - медленные переменные амплитуда-фаза.
- медленные переменные амплитуда-фаза.
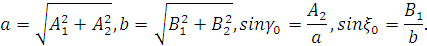
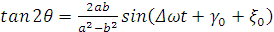 .
. (2.11)
(2.11)
Отсюда получим угол прецессии:
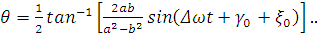 (2.12)
(2.12)
Угловая скорость прецессии:
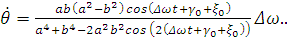 (2.13)
(2.13)
Рассмотрим интересный с точки зрения практики
случай возбуждения стоячей волны колебаний. Пусть 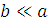 тогда
получим угловую скорость в виде:
тогда
получим угловую скорость в виде:
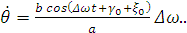 (2.14)
(2.14)
Числовой пример.
Таблица 1. Массово-упругие характеристики
|
Материал
|
Плотность
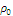 , , 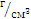
|
Модуль
упругости 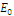 , ГПа , ГПа
|
|
Плавленый
кварц
|
2.201
|
73
|
Таблица 2. Геометрические характеристики
|
Радиус
полукольца R, мм
|
Толщина
полукольца
h,
мм
|
Ширина
полукольца
b,
мм
|
Площадь
поперечного сечения, 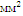
|
Момент
инерции сечения I, 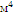
|
|
3
|
0.15
|
0.3
|
0.045
|
1125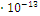
|
Собственная частота колебательного контура 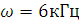 .
.
Частотная расстройка 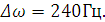
Коэффициент трения 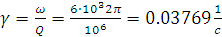 ,
,
Здесь 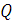 -
добротность.
-
добротность.
В дополнение к данным предыдущего числового
примера положим, что имеется малая инструментальная погрешность изготовления
резонатора по толщине диска 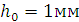 , максимальная
погрешность составляет 1мкм
, максимальная
погрешность составляет 1мкм 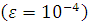 . В этом случае
имеем расщепление частот
. В этом случае
имеем расщепление частот 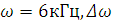 = 240Гц = 0.004%
= 240Гц = 0.004%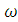 .
.
Связанное с этим биение резонатора
иллюстрируется:
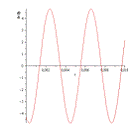
Рис.2 Скорость прецессии волновой картины
колебаний.
Анализ показывает, что инструментальная
погрешность изготовления резонатора вызывает переодическое изменение ориентации
волновой картины колебаний резонатора, являющихся систематической погрешностью
гироскопа.
2.2.2 Рассмотрим свободные колебания
гироскопа на подвижном основании
Предположим теперь, что имеем разночастотную
систему:
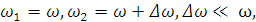
При этом 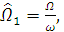 а
а
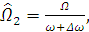 но
т.к.
но
т.к. 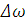 мало,
значит
мало,
значит 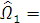
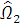 ,
тогда система уравнений гироскопа примет вид:
,
тогда система уравнений гироскопа примет вид:
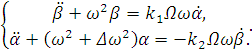 (2.15)
(2.15)
Используя замену переменных, найдем производные
первого и второго порядка переменных 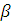 и
и
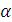 по
времени.
по
времени.
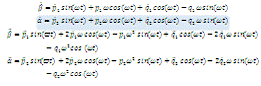

Получим уравнения для медленных переменных:
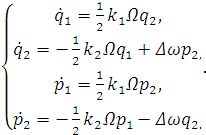 (2.16)
(2.16)
Введем следующую замену:
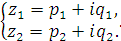 (2.17)
(2.17)
Выделим первое и третье уравнения системы.
Умножим первое уравнение на мнимую единицу и сложим со вторым.
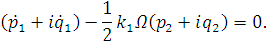
С учетом замены получаем:
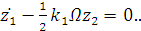 (2.18)
(2.18)
Выделим второе и четвертое уравнения системы.
Умножим второе уравнение на мнимую единицу и сложим с четвертым.
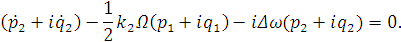
C учетом замены
получим:
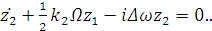 (2.19)
(2.19)
Решение будем искать в виде:
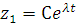 ,
, 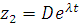 .
. (2.20)
(2.20)
Запишем определитель для данной системы:
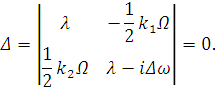
Найдем 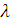 и
подставим его в первое уравнение системы:
и
подставим его в первое уравнение системы:
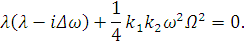
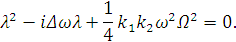
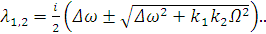 (2.21)
(2.21)
Обозначим для простоты
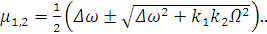 (2.22)
(2.22)
Выразим константы 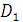 и
и
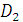 через
через
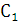 и
и
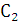 ,
для этого запишем:
,
для этого запишем:
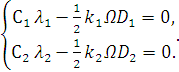 (2.23)
(2.23)
При этом 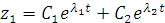 ,
,
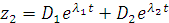 ,
,
Подставим 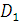 и
и
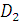 ,
получим:
,
получим:
 (2.25)
(2.25)
При этом по формуле Эйлера:
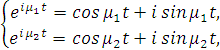
 (2.26)
(2.26)
Константы 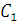 и
и
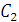 представим
как:
представим
как:
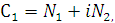
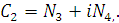 (2.27)
(2.27)
Т.о.:
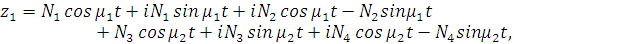
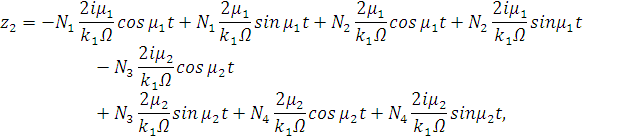
Мы получили решение для медленных переменных
Ван-Дер-Поля:
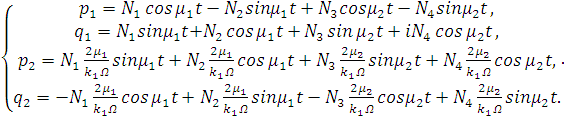
(2.28)
Произвольные постоянные найдем исходя из
начальных условий :
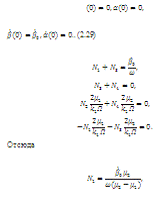

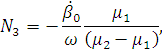
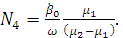 (2.30)
(2.30)
После подстановки получаем:
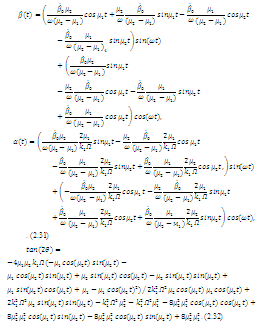
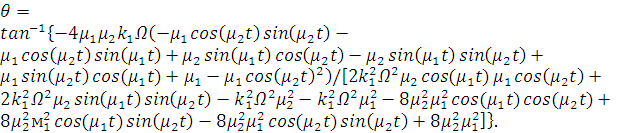 (2.33)
(2.33)
Мы получили
точное
решение
системы.
Теперь
найдем
численное.
Вернемся
к
системе.
Приведем
ее к виду:
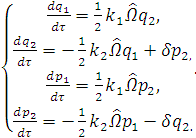 (2.34)
(2.34)
где 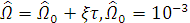 ,
,
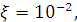
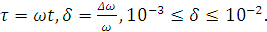
Решение представим в виде переменных 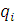 и
и
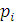 от
безразмерного времени в зависимости от различных
от
безразмерного времени в зависимости от различных :
:
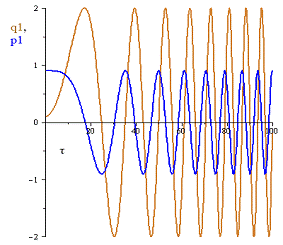
Рис.3 График переменных 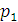 и
и
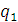 при
при
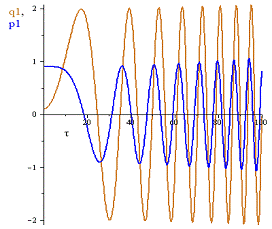
Рис.4 График переменных 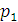 и
и
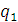 при
при
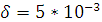 .
.
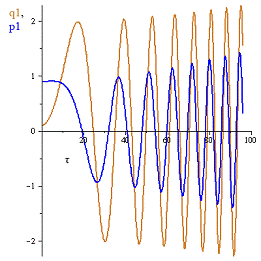
Рис.5 График переменных 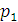 и
и
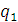 при
при
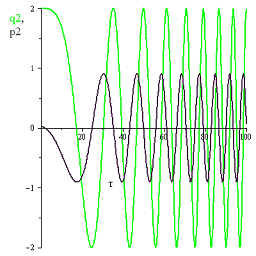
Рис.6 График переменных 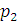 и
и
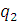 при
при
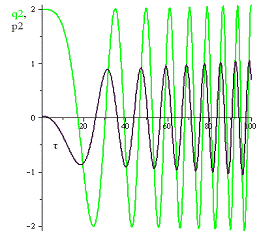
Рис.7 График переменных 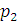 и
и
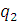 при
при
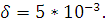
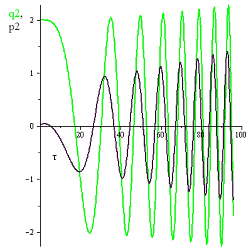
Рис.8 График переменных 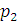 и
и
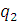 при
при
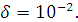
Амплитуды колебаний гироскопа будем искать в
виде:
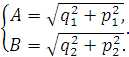 (2.35)
(2.35)
где А - амплитуда колебаний по переменной 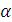 ,
а B - по переменной
,
а B - по переменной 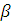 .
.
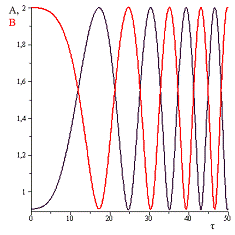
Рис.9 Амплитуда собственных колебаний при 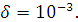
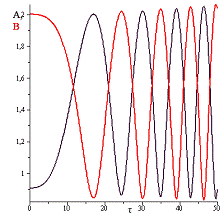
Рис.10 Амплитуда собственных колебаний при 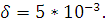
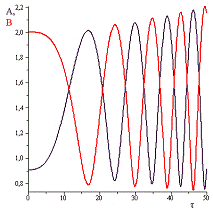
Рис.11 Амплитуда собственных колебаний при 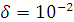 .
.
Полученные графики дают нам представление об
изменении амплитуды колебаний гироскопа.
Проиллюстрируем более наглядно изменение
амплитуды А от величины разночастотности. Для этого выведем все три графика
амплитуды А в зависимости от времени 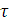 :
:
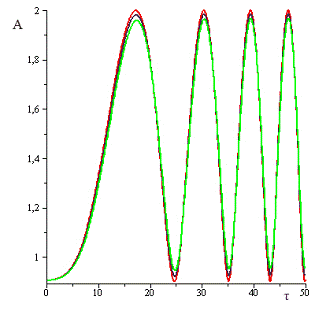
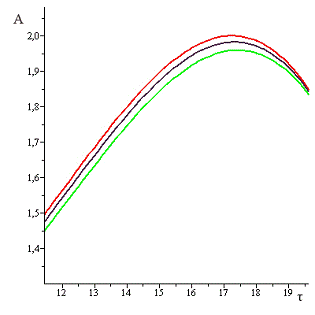
Рис.12 Численное моделирование амплитуды А при 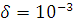 ,
,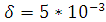 ,
,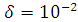 (красным цветом представлена А при
(красным цветом представлена А при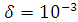 ,
серым, - А при ,
,
серым, - А при ,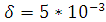 , зеленым, А - при
, зеленым, А - при 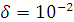 ).
).
3. Свободные колебания гироскопа на
подвижном основании с учетом трения
.1 Случай одночастотной системы
Имеем следующую систему уравнений движения
гироскопа:
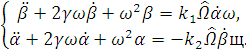 (3.1)
(3.1)
Найдем решение в переменных Ван-Дер-Поля.
Применим к нашей системе метод Страбла и приведем ее к стандартному виду
посредством перехода от переменных 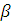 и
и
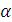 к
медленным переменным
к
медленным переменным 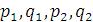 по формулам:
по формулам:
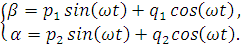 (3.2)
(3.2)
Найдем производные первого и второго порядков
переменных 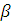 и
и 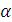 по
времени t:
по
времени t:

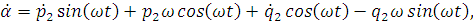
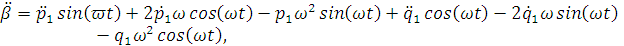
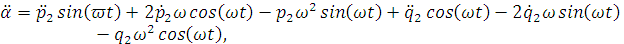
Подставим полученные уравнения в нашу систему:
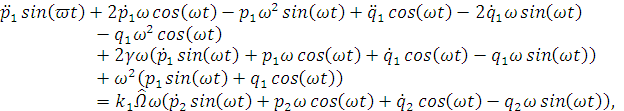
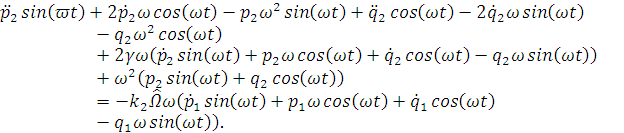
Запишем дифференциальные уравнения гироскопа
пренебрегая слагаемыми второго порядка малости:
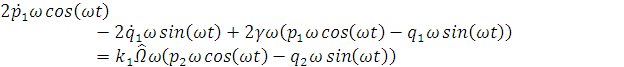
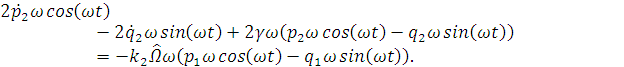
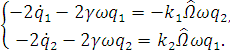
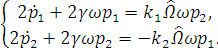
Получим уравнения для медленных переменных:
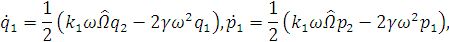
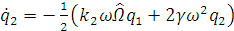 ,
, 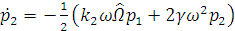 .
. (3.3)
(3.3)
Найдем решение системы, для этого введем замену
переменных:
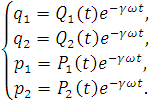
 (3.4)
(3.4)
Запишем систему с учетом переменных:
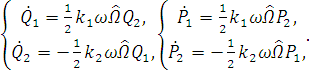 (3.5)
(3.5)
Заметим, что структура системы идентична
структуре системы без трения, поэтому можно записать решение в аналогичном
виде:
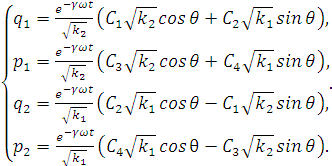 (3.6)
(3.6)
Где 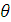 -
угол, пропорциональный интегралу от угловой скорости основания гироскопа:
-
угол, пропорциональный интегралу от угловой скорости основания гироскопа:
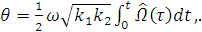 (3.7)
(3.7)
Перейдем, используя замену 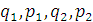 к
переменным
к
переменным 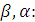
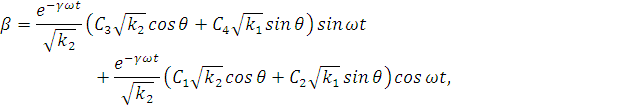
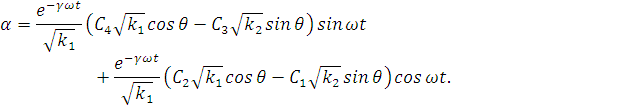
 (3.8)
(3.8)
Эти формулы являются решением с точностью до
порядка 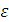 .
.
Найдем произвольные постоянные 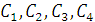 из
следующих начальных условий:
из
следующих начальных условий:

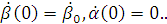 (3.9)
(3.9)
Производные по переменным 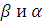 определим
из выражений:
определим
из выражений:
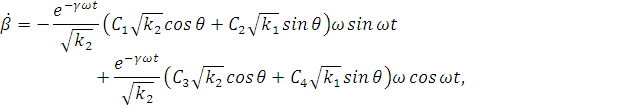
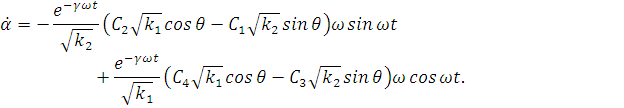
Здесь мы пренебрегли производными по переменным 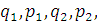 т.к.
они имеют порядок бесконечно малой величины
т.к.
они имеют порядок бесконечно малой величины 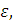 в
то время как на практике величины
в
то время как на практике величины 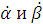 всегда
конечны.
всегда
конечны.
Тогда, подставляя начальные условия в выражения,
получим:
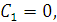
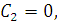
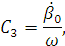
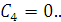 (3.10)
(3.10)
Учитывая условия, запишем 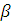 и
и
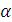 :
:
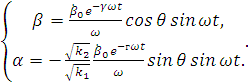 (3.11)
(3.11)
Рассмотрим соотношение 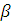 и
и
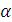 в
уравнениях:
в
уравнениях:
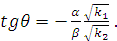 (3.12)
(3.12)
В плоскости 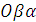 фазовая
точка описывает прямую, которая со временем будет поворачиваться в зависимости
от угловой скорости основания:
фазовая
точка описывает прямую, которая со временем будет поворачиваться в зависимости
от угловой скорости основания:
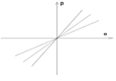
Рис.13. Фазовые траектории системы.
Таким образом гироскоп является датчиком угла
поворота.
.2 Случай разночастотной системы:
Предположим теперь, что имеем разночастотную
систему:
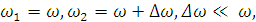
При этом 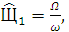 а
а
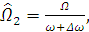 но
т.к.
но
т.к. 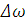 мало,
значит
мало,
значит 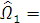
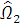 ,
тогда система уравнений гироскопа примет вид:
,
тогда система уравнений гироскопа примет вид:
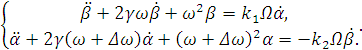 (3.13)
(3.13)
Используя замену переменных, найдем производные
первого и второго порядка переменных 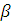 и
и
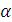 по
времени.
по
времени.

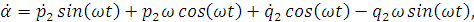
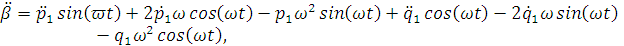
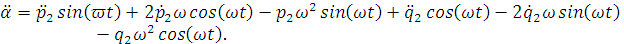
Подставим полученные уравнения в нашу систему:
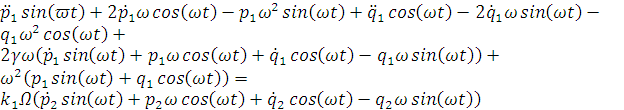 ,
,
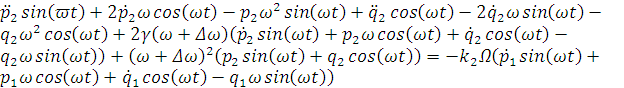 .
.
Запишем дифференциальные уравнения гироскопа
пренебрегая слагаемыми второго порядка малости:
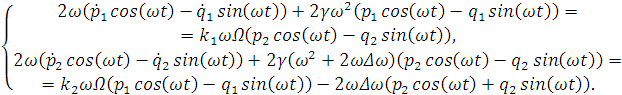
В силу ортогональности можем записать выражения
для 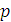 и
и
 :
:
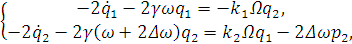
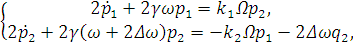
Получим уравнения для медленных переменных:
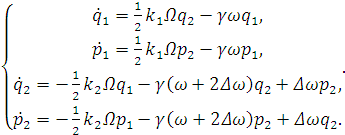 (3.14)
(3.14)
Найдем численное решение системы, для этого
приведем ее к виду:
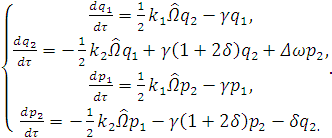 (3.15)
(3.15)
где 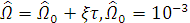 ,
,
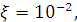
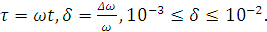
Решение представим в виде переменных 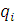 и
и
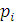 от
безразмерного времени в зависимости от различных
от
безразмерного времени в зависимости от различных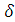 :
:
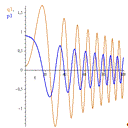
Рис.14 График переменных 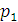 и
и
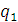 при
при
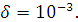
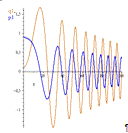
Рис.15 График переменных 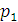 и
и
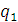 при
при
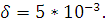
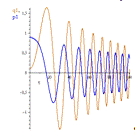
Рис.16 График переменных 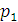 и
и
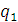 при
при
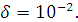
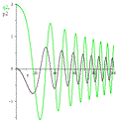
Рис.17 График переменных 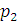 и
и
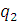 при
при
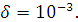
Рис.18 График переменных 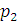 и
и
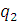 при
при
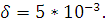
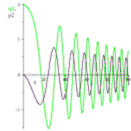
Рис.19 График переменных 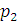 и
и
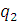 при
при
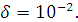
Амплитуды колебаний гироскопа будем искать в
виде:
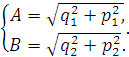 (3.16)
(3.16)
где А - амплитуда колебаний по переменной 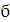 ,
а B - по переменной
,
а B - по переменной 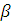 .
.
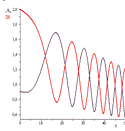
Рис.20 Амплитуда собственных колебаний при 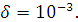
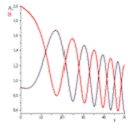
Рис.21 Амплитуда собственных колебаний при 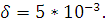
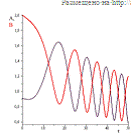
Рис.22 Амплитуда собственных колебаний при 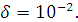
Полученные графики дают нам представление об
изменении амплитуды колебаний гироскопа.
Проиллюстрируем более наглядно изменение
амплитуды А от величины разночастотности. Для этого выведем все три графика
амплитуды А в зависимости от времени 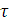 :
:
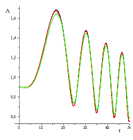
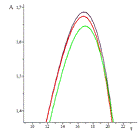
Рис.23 Численное моделирование амплитуды А при 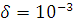 ,
,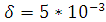 ,
,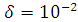 (красным цветом представлена А при
(красным цветом представлена А при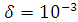 ,
серым, - А при
,
серым, - А при 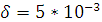 , зеленым, А - при
, зеленым, А - при 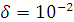 ).
).
Заключение
Была разработана новая математическая модель
микромеханического гироскопа камертонного типа на подвижном основании. Были
получены и проанализированы уравнения движения данного гироскопа. В ходе
исследования было установлено, что в случае равных собственных частот гироскоп
может работать как датчик угла поворота основания. В случае же различных
собственных частот изучение поведения гироскопа сильно усложняется, что
позволяет сделать вывод о необходимости поисков методов частотной настройки.
Список литературы
1. Журавлев
В. Ф., Климов Д.М. Волновой твердотельный гироскоп. - М.: Наука, 1985. 125 с.
. Меркурьев
И. В., Подалков В. В. Динамика микромеханического и волнового твердотельного
гироскопов. - М.: ФИЗМАТЛИТ, 2009. - 228 с.