Волны плоского оптического волновода
Российский
Университет Дружбы Народов
Факультет
физико-математических и естественных наук
Курсовая
работа
На
тему
Волны
плоского оптического волновода
Исполнитель:
Баляева О.Н.
Москва
Введение
В основе интегральной оптики лежит главным
образом тот факт, что световые волны могут распространяться по очень тонким
слоям (пленкам) прозрачных материалов. Объединяя такие слои вместе и, придавая
им необходимую конфигурацию, с помощью методов интегральной оптики можно
создавать разные компоненты, позволяющие осуществить ряд операций над
оптическими волнами. Так, свет в тонкопленочных структурах можно
канализировать, отклонять, излучать в пространство и т.д. Эти компоненты малы и
компактны. Они должны способствовать решению многих задач, из которых наиболее
перспективной является обработка оптических сигналов в оптических линиях связи.
Для решения этой задачи необходимо оборудование, обладающее миниатюрными
размерами и прочной, долговечной и надежной конструкцией с низким потреблением
энергии. Интегральная оптика рассматривает разнообразные явления, связанные с
волноводным распространением света и управлением им с помощью тонких
электрических пленок и полосок. Изучение свойств плоского оптического волновода
является необходимым условием для понимания физических процессов, лежащих в
основе работы устройств интегральной оптики.
В своей работе я хочу проанализировать
распространение волн в плоском оптическом волноводе, как с геометрической точки
зрения, так и с точки зрения электромагнитной теории. Также рассмотреть
распределения электромагнитного поля в волноводе и зависимости свойств
волновода от его параметров.
1. Теория диэлектрических волноводов
диэлектрический волновод плоский
оптический
Диэлектрические волноводы
Диэлектрические волноводы представляют собой
структуры, которые используются для ограничения и направления света в
волноводных устройствах и схемах интегральной оптики.
Простейшим диэлектрическим волноводом является
волновод на рис.1.1, у которого пленка с показателем преломления nf
помещена между подложкой и покровным материалом с более низкими показателями
преломления ns
и nc
(nf>ns≥nc).
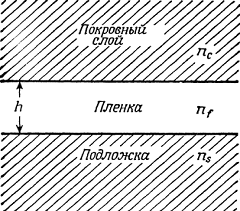
Рис.1.1 Поперечное сечение плоского волновода,
состоящего из тонкой пленки толщиной (или высотой) h
с показателем преломления nf,
заключенной между подложкой и покровным материалом с показателями преломления ns
и nc.
Часто покровным материалом служит воздух, в этом
случае nc=1.
Типичные значения разности между показателями преломления пленки и подложки
лежат в диапазоне от 10-3 до 10-1, а типичная толщина
пленки 1 мкм. Область распространения света ограничивается в результате полного
внутреннего отражения на поверхностях раздела пленка - подложка и пленка -
покровный слой. Оптическая волна, введенная в волновод, распространяется вдоль
волновода, при этом энергия волны сосредоточена в центральном слое и в
некоторой близости от него. Таким образом, в плоском волноводе происходит
распространение волны не в трех, а в двух измерениях вдоль поверхности
волновода.
. Геометрическая оптика плоских волноводов
ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ
Представим себе границу двух изотропных,
однородных диэлектрических сред без потерь, с показателями преломления n1
и n2 (рис.1.2).
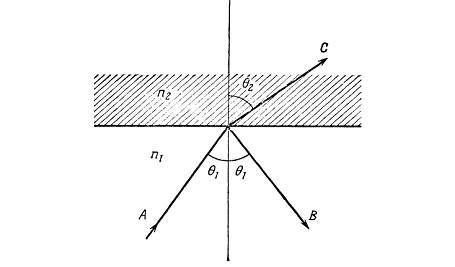
Рис.1.2 Направление нормалей к волновым
поверхностям преломленного и отраженного света на плоской границе раздела двух
сред с показателями преломления n1
и
n2.
Угол падения - ө1
На эту границу падает когерентная световая
волна, нормаль к волновой поверхности которой образует с нормалью к границе
раздела угол ө1. В общем случае волна с комплексной амплитудой
A на границе раздела
частично отражается и частично преломляется. Угол ө2 для
преломленной волны С можно определить из закона Снеллиуса:
 (1)
(1)
На границе комплексная амплитуда
отраженной волны В линейно связана через комплексный коэффициент отражения R с
комплексной амплитудой А:
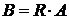 (2)
(2)
Коэффициент отражения зависит от
угла падения и поляризации света и определяется из формул Френеля. Для ТЕ -
поляризации мы можем записать ([5], гл. 5, § 65):
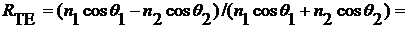

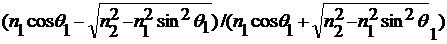 (3)
(3)
Так называемый критический угол өc
определяется выражением
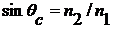 (4)
(4)
До тех пор, пока выполняется
неравенство ө1<өс, мы имеем только
частичное отражение света, и величина R принимает
действительные значения. Как только угол падения ө1 превзойдет
критическое значение өс (ө1>өс),
модуль коэффициента отражения |R|=1, и мы можем говорить о полном
отражении света. В данном случае величина R является
комплексной, и отраженный свет испытывает сдвиг по фазе относительно падающего
света. Мы можем записать
R=exp(2jφ) (5)
И получить с помощью формул Френеля
выражение для фазового сдвига φTE для
состояния поляризации:
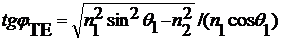 (6)
(6)
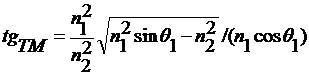
На рис.1.3 показана зависимость
фазового сдвига φTE от угла
падения ө1 при различных значениях отношения показателей
преломления n2/n1.
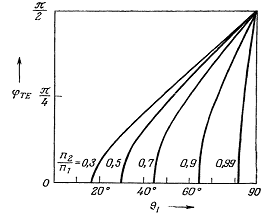
Рис.1.3 Зависимость фазового сдвига φTE для ТЕ-моды
от угла падения ө1.
Значения 0,3, 0,5 и 0,7
приблизительно соответствуют границам раздела воздух - GaAs, LiNbO3 и SiO2
соответственно. Заметим, что фазовый сдвиг возрастает от нуля при критическом
угле падения до π/2
при
скользящем угле падения (ө1=90°). Характер поведения фазового
сдвига φTM аналогичен.
Теперь рассмотрим плоскую
волноводную структуру (рис.1.4), состоящую из пленки, подложки и покровного
материала с показателями преломления nf, ns и nc
соответственно. В общем случае справедливо неравенство nf >ns>nc и
существуют два критических угла: угол полного внутреннего отражения өs на границе
раздела пленка - подложка и угол полного внутреннего отражения өс<өs на границе
раздела пленка - покровный слой. Если мы начнем увеличивать угол падения света ө,
то обнаружим, что существуют три различных случая, которые схематически
изображены на рис.1.4. При малых углах падения ө<өs, өс
свет, который распространяется со стороны подложки, преломляется согласно
закону Снеллиуса и выходит из волновода через покровный слой (а). В этом
случае, по существу, волноводное распространение света отсутствует. Если
увеличить угол падения ө, так чтобы выполнялось условие өс<ө<өs, то
распространяющийся по подложке свет преломляется на границе раздела пленка -
подложка, испытывает полное внутреннее отражение на границе пленка - покровный
слой, преломляется обратно в подложку и, пройдя через нее, также покидает
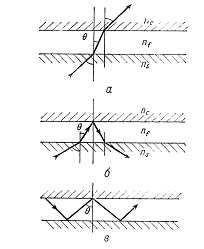
Рис.1.4 Распространение
зигзагообразных волн в плоском волноводе данную структуру (б).
В этом случае волноводное
распространение света снова не имеет места. Наконец, когда угол ө
достаточно велик (в), так что выполняется условие өs, өс<ө,
то наблюдается полное внутренне отражения на обеих границах раздела. Теперь
свет, который однажды попал в пленку, будет распространяться в ней волноводным
образом по зигзагообразному пути.
ВОЛНОВОДНЫЕ МОДЫ
На рис.1.5 показан вид сбоку на
плоский волновод. Это картина двух наложенных друг на друга однородных плоских
волн, нормали, к волновым фронтам которых движутся по зигзагообразному пути.
Данные волны монохроматичны и когерентны, их угловая частота равна ω, длина волны
в вакууме λ,
а
волновой вектор в направлении нормали к волновой

Рис.1.5 Вид сбоку на плоский
волновод и направление нормалей к волновым поверхностям зигзагообразных волн,
соответствующих волновой моде поверхности равен knf, причем
абсолютная величина вектора k равна
k=2π/λ=ω/c (7)
где с-скорость света в вакууме. Поля
таких волн изменяются по следующему закону:
exp[-jknf (±xcosө+zsinө)]
(8)
Согласно представлению о
зигзагообразных волнах, постоянная распространения β для
волноводной моды в плоском волноводе (и связанная с ней фазовая скорость υp)
определяется следующим выражением:
β=ω/υp=knfsinө (9)
и является z-составляющей
волнового вектора knf. Однако угол ө не
может принимать любые значения, так как только дискретный набор углов приводит
к появлению самосогласованной картины распределения поля, которая соответствует
тому, что мы называем волноводной модой. Рассмотрим поперечное сечение
волновода плоскостью z=const и
просуммируем сдвиги фаз, которые появляются при движении некоторой волны от
нижней границы пленки (x=0) к верхней границе (x=h) и затем
при движении отраженной волны к исходной границе пленки. В случае
самосогласования сумма всех этих фазовых сдвигов должна быть кратна 2π. В частности
для пленки толщиной h сдвиг фазы за первый проход поперек
пленки равен knfhcosө.
Сдвиг фазы в результате полного внутреннего отражения на границе раздела пленка
- покровный слой равен (-2φc). Сдвиг за
следующий проход вниз поперек пленки равен knfhcosө и
сдвиг из-за полного внутреннего отражения на границе раздела пленка - подложка
равен (-2φs). Таким
образом, мы получили условие самосогласованности (условие поперечного
резонанса):
knfhcosө-2φs-2φc=2νπ, (10)
где ν - целое число,
которое определяет порядок моды. Соотношение (10) , по существу, является
дисперсионным уравнением волновода, которое определяет постоянную
распространения β
как
функцию частоты ω
и
толщины пленки h. Согласно выражениям (4) и (9),
диапазон изменения постоянной распространения β для
волноводной моды ограничен значениями постоянных распространения плоских волн в
подложке и пленке:
kns<β<knf (11)
Во многих случаях удобно
воспользоваться понятием «эффективный волноводный показатель преломления»,
который определяется следующим образом:
N=β/k=nfsinө (12)
и изменяется в пределах
ns<N<nf. (13)
На рис.1.6 представлено графическое
решение дисперсионного уравнения (10) для основной моды (ν=0). На ней
изображены зависимости от угла ө фазового сдвига за проход поперек пленки
knfhcosө
(пунктирная линия) и суммы фазовых сдвигов (φs+φc) при
отражениях от границ пленки. Последняя зависимость для симметричного волновода
(φs=φc)представлена
сплошной линией, для асимметричного штриховой линией.
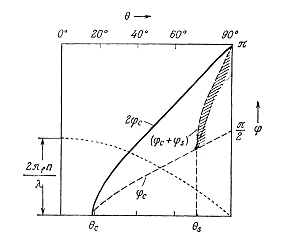
Рис.1.6 Графическое решение
дисперсионного уравнения для основных мод
3. Электромагнитная теория волноводов
УРАВНЕНИЯ, ОПИСЫВАЮЩИЕ РАСПРОСТРАНЕНИЕ
ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ОПТИЧЕСКОМ ВОЛНОВОДЕ
Считая, что электромагнитное поле изменяется во
времени по гармоническому закону, т.е.
уравнения Максвелла для комплексных
амплитуд можно записать:
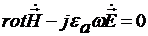 , (1)
, (1)
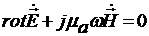 (2)
(2)
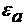 ,
, 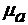 - абсолютные диэлектрическая и
магнитная проницаемости среды или в развернутом виде:
- абсолютные диэлектрическая и
магнитная проницаемости среды или в развернутом виде:
 a
a
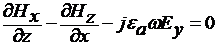 б (3)
б (3)
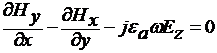 в
в
 а
а
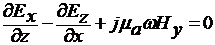 б (4)
б (4)
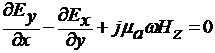 в
в
Рассмотрим плоский волновод
(рис.2.1), образованный диэлектрической пленкой, однородной в плоскости пленки
(в направлениях x и z). Структура
волновода неоднородна в направлении y. Положим,
что волны распространяются вдоль оси 0z. Тогда 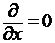 , т.к. в
направлении x структура
однородна, а волноводная мода распространяется по z (т.е.
представляющие ее плоские волны распространяются в плоскости yz).
, т.к. в
направлении x структура
однородна, а волноводная мода распространяется по z (т.е.
представляющие ее плоские волны распространяются в плоскости yz).
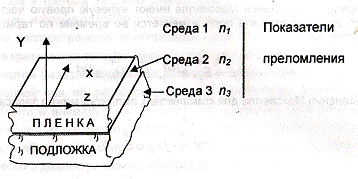
Рис.2.1 Схема плоского оптического
волновода
Запишем уравнения Максвелла с учетом
сказанного:
 a
a
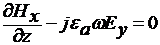 б (5)
б (5)
 в
в
 а
а
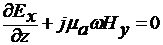 б (6)
б (6)
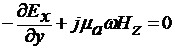 в
в
Подставим (6б) и (6в) в (5а).
Получаем уравнение
 (7)
(7)
Относительно Ex. Имеют
место соотношения
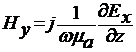 (8)
(8)
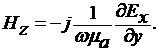
Уравнения (7) и (8) полностью
определяют электромагнитную волну с компонентами поля Ex, Hy и Hz. Остальные
компоненты поля никак не связаны с Ex и их можно
положить равными нулю. Такую волну называют ТЕ-волной. Действуя аналогичным
образом и подставляя (5б) и (5в) в (6а), получим волновое уравнение
относительно Hx, которое с
учетом (5б) и (5в) полностью определяет волну с компонентами поля Hx, Ey, Ez, т.е.
ТМ-волну. Т.о. система уравнений Максвелла (5), (6) имеет два независимых вида
решений - ТЕ и ТМ-волны. Ограничимся в дальнейшем только волнами ТЕ-типа.
В результате подстановки (8) в (5)
можно получить волновое уравнение для электрической компоненты поля:

Можно записать соотношения 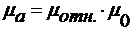 и
и  , где
, где 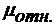 ,
, 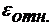 -
относительная магнитная и диэлектрическая проницаемость;
-
относительная магнитная и диэлектрическая проницаемость; 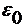 ,
, 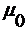 -
абсолютная диэлектрическая и магнитная проницаемость вакуума, и ввести
обозначения:
-
абсолютная диэлектрическая и магнитная проницаемость вакуума, и ввести
обозначения:
 и при
и при 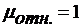 ,
, 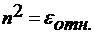 , (9)
, (9)
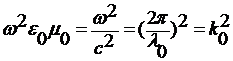 (10)
(10)
С учетом этих соотношений имеем
 (11)
(11)
Это уравнение описывает
распространение волн в оптической среде с показателем преломления n. Поскольку
в данной задаче границы пленки являются плоскостями y=0 и y=-h, т.е.
плоскостями, параллельными координатной плоскости y=0,
переменные в уравнении (11) разделяются и его решение следует искать в виде
произведения двух функций, одна из которых зависит только от y, а вторая
только от z.
Распределение амплитуды поля по координате x
предполагается равномерным. Таким образом
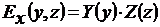 (12)
(12)
После подстановки в (11) получим:
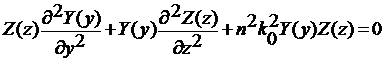 (13)
(13)
Или
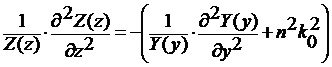 . (14)
. (14)
Поскольку левая и правая часть
выражения (14) зависят от различных переменных, то равенство может соблюдаться
только в том случае, когда каждая из частей равенства является константой.
Пусть эта константа обозначена 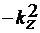 .
.
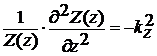 (15)
(15)
Уравнение (15) имеет решение вида
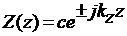 (16)
(16)
Приравнивая правую часть уравнения
(14) 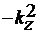 , получим
, получим
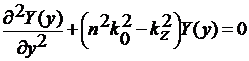 (17)
(17)
Конкретный вид функции Y(y)
определяется из уравнения (17) с учетом граничных условий и описывает
распределение амплитуд и фаз в поперечном сечении волноводного слоя и
прилегающих сред. Полный же вид решения определяется как произведение Y(y)Z(z) и с учетом
временной зависимости ejωt имеет вид
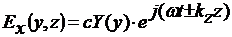 .
.
Таким образом, решение имеет вид
гармонической волны, распространяющейся вдоль оси 0z в
положительном (знак - ) или в отрицательном (знак +) направлении и имеющей
амплитудное распределение Y(y) в
направлении y.
Итак, после разделения переменных мы
можем искать распределение комплексных амплитуд поля ТЕ-волны в зависимости от
координаты y исходя из
уравнений:
для области 1:
 (18)
(18)
для области 2:
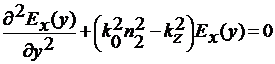 (19)
(19)
для области 3:
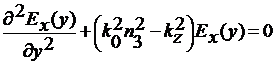 (20)
(20)
Необходимо найти коэффициенты ci (i-номер
области), которые удовлетворяют граничным условиям. Граничные условия
представляют собой уравнения непрерывности касательных E и H
составляющих компонент электромагнитного поля и для ТЕ-волн имеют вид:
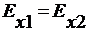 ,
, 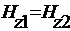 при y=0 (21)
при y=0 (21)
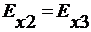 ,
, 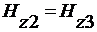 при y=-h (22)
при y=-h (22)
Условия непрерывности H-составляющих
на границах раздела эквивалентны условиям непрерывности производных от
распределения E-составляющих
поля на границах раздела слоев 1 и 2 и слоев 2 и 3. Рассматривая уравнения
(16-18), можно заметить, что вид решения существенно зависит от соотношения
между величиной коэффициента 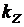 и величинами
и величинами 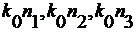 . Рассмотрим
свойства решений, соответствующих разным областям значений
. Рассмотрим
свойства решений, соответствующих разным областям значений 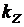 . Характер
возможных решений при различных
. Характер
возможных решений при различных 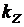 иллюстрируется графиком на рис.2.2.
иллюстрируется графиком на рис.2.2.
А. kz > k0n2.
При этом условии заведомо
выполняются условия kz > k0n3 и kz > k0n1. Решение,
соответствующее области А, физически неосуществимо.
B. k0n2 > kz > k0n3, k0n1.
Такой режим называется волноводным,
а центральный слой 2 называют несущим слоем волновода.
С. K0n3 > kz > k0n1 и, очевидно,
k0n2 > kz.
Такие моды называются излучательными
модами подложки. Причем излучение происходит в среду с показателем n3, т.е. в
подложку.
D. k0n1 > kz.
Такие моды также называются
излучательными модами волновода. Излучение происходит в подложку и в среду над
волноводом.
Основные результаты: в системе,
состоящей из трех диэлектрических слоев с показателями преломления n1, n2, n3 при условии
n2>n1, n2>n3 возможно распространение
волны вдоль слоя 2, при этом распределение электромагнитного поля в поперечном
сечении имеет максимальное значение внутри центрального слоя 2 и
экспоненциально спадает при удалении от границ слоя 2 в направлении оси 0y (или - 0y). Волна с
неоднородным распределением по координате y
распространяется вдоль плоскости волновода и характеризуется постоянной
распространения 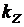 , при этом k0n3 < kz < k0n2.
, при этом k0n3 < kz < k0n2.
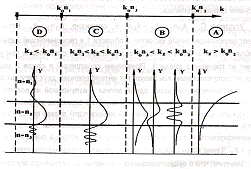
Условие B
соответствует волноводному режиму распространения волны. Три кривых показывают
вид распределения поля в поперечном сечении для разных поперечных мод.
ДИСПЕРСИОННЫЕ УРАВНЕНИЯ ТРЕХСЛОЙНОГО
ДИЭЛЕКТРИЧЕСКОГО ВОЛНОВОДА
Дисперсионное уравнение для
ТЕ-волны:
Из граничных условий (21), (22)
вытекает, что они выполняются лишь в том случае, когда выполняется соотношение
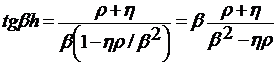 , (23)
, (23)
которое можно преобразовать к виду
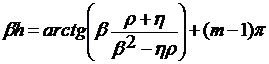 . (24)
. (24)
Где
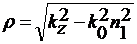 (25)
(25)
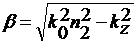 (26)
(26)
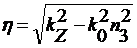 (27)
(27)
Полученное уравнение можно
представить в другой форме. Используем тождество 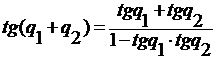 . Обозначим
. Обозначим 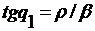 ,
, 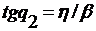 , тогда из
(23) получим тождество
, тогда из
(23) получим тождество 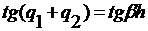 , т.е.
, т.е. 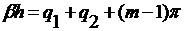 и формулу
для дисперсионного уравнения:
и формулу
для дисперсионного уравнения:
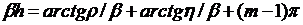 (28)
(28)
Здесь m=1,2,3…
Если подставить (25-27) в (23), то
получим уравнение относительно неизвестной 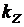 .
.
Величину 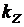 обычно
представляют в виде
обычно
представляют в виде 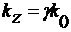 , где
, где 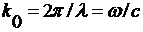 - волновое
число электромагнитной волны в свободном пространстве. Если выразить
- волновое
число электромагнитной волны в свободном пространстве. Если выразить 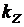 через
фазовую скорость волны в волноводе,
через
фазовую скорость волны в волноводе, 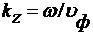 , то коэффициент
, то коэффициент 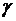 равен
отношению скорости волны в свободном пространстве к фазовой скорости волны в
волноводе
равен
отношению скорости волны в свободном пространстве к фазовой скорости волны в
волноводе
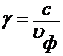 .
.
Уравнение (24), выраженное через 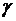 имеет вид
имеет вид
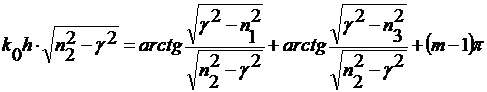 (29)
(29)
Корни этого уравнения 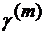 определяют
собственные значения постоянной распространения
определяют
собственные значения постоянной распространения 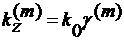 . При заданной толщине пленки h различные
значения
. При заданной толщине пленки h различные
значения 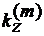 соответствуют
различным модам, т.е. различным типам волн, распространяющимся в волноводе.
Уравнение типа (24) носит название дисперсионного уравнения, так как оно, по
существу, связывает скорость волны с длиной волны, а также с параметрами
волновода: толщиной волноводного слоя, показателями преломления слоев.
соответствуют
различным модам, т.е. различным типам волн, распространяющимся в волноводе.
Уравнение типа (24) носит название дисперсионного уравнения, так как оно, по
существу, связывает скорость волны с длиной волны, а также с параметрами
волновода: толщиной волноводного слоя, показателями преломления слоев.
ДИСПЕРСИОННЫЕ ЗАВИСИМОСТИ
Для наглядности удобно представить
решение дисперсионного уравнения в виде графиков зависимостей 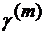 от толщины
волноводного слоя h. Для их построения необходимо
задать значения n1, n2, n3, и длину
волны
от толщины
волноводного слоя h. Для их построения необходимо
задать значения n1, n2, n3, и длину
волны 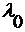 . После
этого по формуле (29) легко рассчитать и построить зависимости
. После
этого по формуле (29) легко рассчитать и построить зависимости 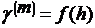 для каждого
числа m=1,2… Эти
семейства кривых для двух типов волноводов, различающихся параметрами n1, n2, n3, приведены
на рис.2.3.
для каждого
числа m=1,2… Эти
семейства кривых для двух типов волноводов, различающихся параметрами n1, n2, n3, приведены
на рис.2.3.
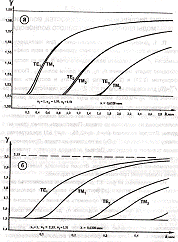
Рис.2.3 Зависимости замедления от
толщины слоя оптического волновода для двух характерных типов волноводов:
а) Волновод из пленки полистирола на
стеклянной подложке (n1=1, n2=1,59, n3=1,51;
λ=0,6328 мкм);
б) Волновод из пленки Ta2O5 на
стеклянной подложке (n1=1, n2=2,15, n3=1,51;
λ=0,6328 мкм)
КРИТИЧЕСКАЯ ТОЛЩИНА
Найти значение критической толщины
можно, приравняв 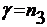 . При этом
начинается излучение волн в подложку и волновод теряет свои направляющие
свойства. Из выражения (29) имеем
. При этом
начинается излучение волн в подложку и волновод теряет свои направляющие
свойства. Из выражения (29) имеем
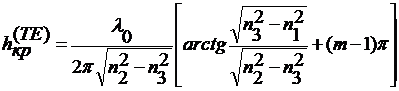 . (30)
. (30)
Когда в волноводе может
распространяться только одна мода, его называют одномодовым. При увеличении
толщины волноводного слоя 2 будут последовательно удовлетворяться условия
высших мод (TE2, TE3 и т.д.).
Волновод, в котором существуют высшие моды, называют многомодовым. Значение
критической толщины будет уменьшаться с увеличением разности показателей
преломления (n2-n3)
волноводного слоя и подложки.
РАСПРЕДЕЛЕНИЕ ПОЛЯ
Распределение компонент поля в
сечении волновода для различных мод задается выражениями
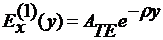 0 <
y < ∞,
0 <
y < ∞,
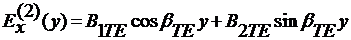 -h < y < 0,
-h < y < 0,
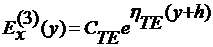 , -∞ < y < -h.
, -∞ < y < -h.
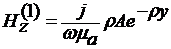 ,
,
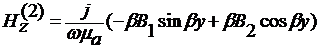 ,
,
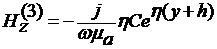
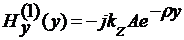
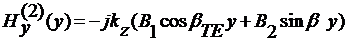


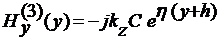
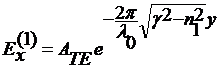 , 0 < y < +∞,
(31)
, 0 < y < +∞,
(31)
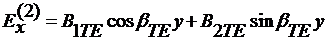 , -h < y < 0,
(32)
, -h < y < 0,
(32)
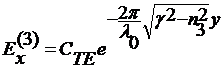 , -∞ < y < -h (33)
, -∞ < y < -h (33)
Характер распределения поля,
описываемого выражениями (31-33), изображен на рис.2.4.
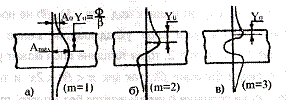
Рис.2.4 Вид распределения поля в
поперечном сечении волновода для различных волноводных мод
В волноводном режиме величина γ изменяется
от n3 до n2, (n3 > n1, причем n2 > n3). Отсюда
видно, что распределение поля в 1 среде довольно резко затухает на расстояниях
порядка длины волны, если разница между n3 и n1 не слишком
мала. Распределение поля в подложке также экспоненциально затухает, однако при γ → n3, т.е. когда
режим волновода приближается к критическому, показатель экспоненты стремится к
нулю. Распределение поля при этом вытягивается в подложку. Эффективную глубину
проникновения пол в подложку можно определить из выражения (34) как глубину, на
которой амплитуда напряженности поля уменьшается в e=2,7 раз по
сравнению с амплитудой поля на границе слоев 2 и 3.
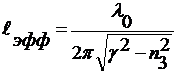 (34)
(34)
При 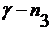 порядка 10-4 эта
величина составляет более десятка длин волн, что намного превышает саму толщину
центрального волноводного слоя. При удалении от критического режима поле в
подложке становится быстро затухающим. Так при
порядка 10-4 эта
величина составляет более десятка длин волн, что намного превышает саму толщину
центрального волноводного слоя. При удалении от критического режима поле в
подложке становится быстро затухающим. Так при 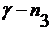 =0,1 эффективная глубина
проникновения составит уже долю длины волны.
=0,1 эффективная глубина
проникновения составит уже долю длины волны.
Распределение поля в центральном
слое - гармоническое, вида 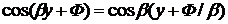 . Максимум этого распределения
сдвинут в область отрицательных значений y (в область
центрального слоя) на величину
. Максимум этого распределения
сдвинут в область отрицательных значений y (в область
центрального слоя) на величину 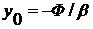 . Область значений y
простирается от 0 до -h, величина
. Область значений y
простирается от 0 до -h, величина  изменяется
от 0 до
изменяется
от 0 до 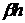 . Величину
. Величину 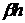 можно
определить из дисперсионного уравнения как
можно
определить из дисперсионного уравнения как
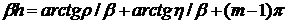 .
.
Отсюда видно, что в случае низших
мод (m=1), 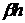 не превышает
π
и,
следовательно, на толщине слоя укладывается менее полупериода функции
не превышает
π
и,
следовательно, на толщине слоя укладывается менее полупериода функции 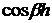 . Если же m=2, то на
толщине слоя может укладываться от 0,5 до 1 периода функции
. Если же m=2, то на
толщине слоя может укладываться от 0,5 до 1 периода функции 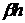 , так как π <
βh < 2π и так далее
при произвольном m на толщине h
укладывается без малого m пространственных полупериодов
функции
, так как π <
βh < 2π и так далее
при произвольном m на толщине h
укладывается без малого m пространственных полупериодов
функции 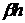 .
Распределение поля высших мод в центральном слое оказывается знакопеременным и
имеет m-1 переходов
через 0 в пределах толщины слоя, как это показано на рис. 4.
.
Распределение поля высших мод в центральном слое оказывается знакопеременным и
имеет m-1 переходов
через 0 в пределах толщины слоя, как это показано на рис. 4.
4. Расчет электромагнитных полей
Построим зависимость коэффициента замедления от
толщины волноводного слоя для трех низших ТЕ мод для заданных показателей
преломления и длины волны
n1=1,
n2=1.55,
n3=1.5,
λ0=1.3
мкм
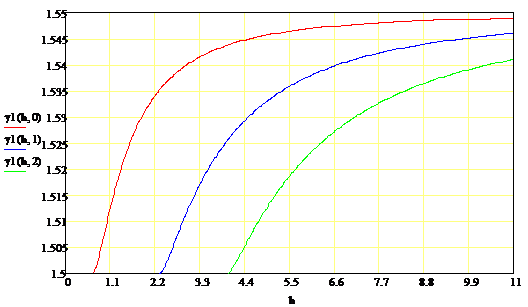
а также распределения поля для различных
волноводных мод
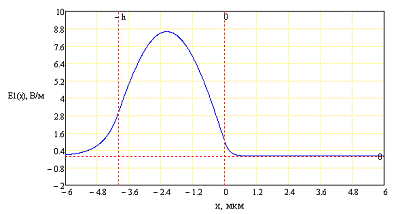
Для второй моды
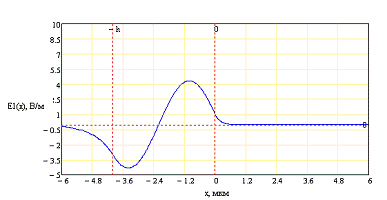
Для третьей моды
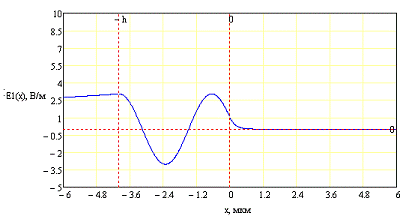
Также для компоненты Hz
Для первой моды
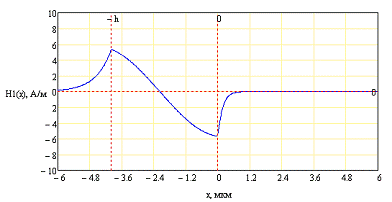
Для второй моды
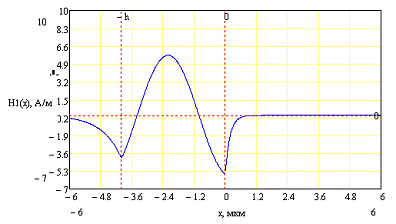
Для третьей моды
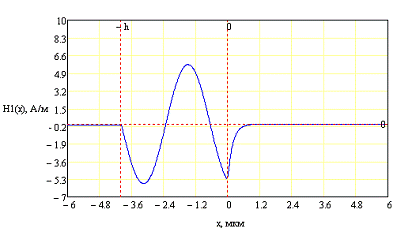
Для первой моды
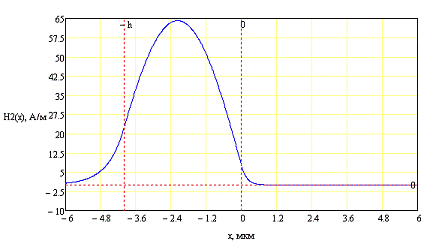
Для второй моды
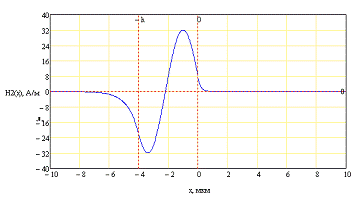
Для третьей моды
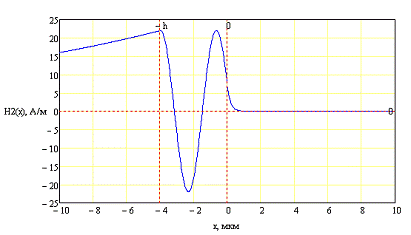
Заключение
Из последних приведенных мною графиков видно,
что распределение волны в волноводе зависит от его толщины, т.е. в зависимости
от того, как должна распределяться волна, выбирается та или иная толщина. Чем
шире волновод, тем большая часть волны будет распространяться внутри него. Если
требуется, чтобы волна распространялась большей частью в подложке, то
необходимо сделать волновод уже.
Итак, в своей работе я ознакомилась с
физическими процессами в волноводах. Рассмотрела характер волн в волноводе и их
распространение, также уравнения, описывающие эти волны. Познакомилась с таким
понятием как критическая толщина. Во второй части своей работы я привела
график, показывающий зависимость коэффициента замедления от толщины
волноводного слоя, а также графики, показывающие распределения поля волны для
различных волноводных мод.
Бурное развитие интегральной оптики вызвано
высокой практической эффективностью интегрально-оптических устройств.
Потребности современной техники передач и обработки информации оптическими
методами привели к разработке и созданию быстродействующих
интегрально-оптических устройств. Постоянно создаются новые типы волноводов и
волноводных устройств, позволяющих повысить информационную емкость волоконных
линий связи и быстродействие обработки информации в системах телекоммуникаций.
Список литературы
1. Под
ред. Тамира. Интегральная оптика, Москва, “Мир”, 1978
2. Комоцкий
В.А. Плоский оптический волновод: Учебно-методическое пособие. Москва, РУДН, 2001
. Никольский
В.В. Электродинамика и распространение радиоволн, Москва, “Наука”, 1978.
. Д.
Маркузе. Оптические волноводы, Москва, “Мир”, 1974.
. Сивухин
Д.В. Общий курс физики: оптика, Москва, “Наука”, 1980.