Криптографические протоколы на эллиптических кривых

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

САРАТОВСКИЙ         ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г.ЧЕРНЫШЕВСКОГО

Кафедра теоретических основ компьютерной безопасности и криптографии

КУРСОВАЯ РАБОТА

Криптографические протоколы на эллиптических кривых

студента 4 курса факультета компьютерных наук

и информационных технологий

Платонова Артема Сергеевича

Научный руководитель

доцент, канд. физ.-мат. наук

А.Н. Гамова

Зав. кафедрой

профессор, канд. физ.-мат. наук

В.Н. Салий

Саратов 2012

Содержание

Введение

Эллиптические кривые

Алгебраические кривые

Группа точек эллиптической кривой

Эллиптические кривые над конечными полями      

Алгоритмы на эллиптических кривых

Сложение точек эллиптической кривой

Алгоритм скалярного умножения

Алгоритм генерации случайных кривых

Генерация криптографически надежных параметров кривых

Использование различных систем координат

Проективные координаты

Стандартная проективная система координат (P)

Система координат Якоби (J)

Система координат Чудновского-Якоби (Jc)

Модифицированная система координат Якоби (Jm)

Смешанные координаты

Эллиптическая криптография

Криптосистема с открытым ключом

Шифр Эль-Гамаля на основе эллиптических кривых

Алгоритм цифровой подписи на основе эллиптических кривых

Преимущества использования схем эллиптической криптографии

Заключение

Список использованных источников

Введение

Средства и системы криптографической защиты информации играют важную роль в современных компьютерных информационных системах, используемых в сфере финансовой и коммерческой деятельности. Интерес к ним обусловлен не только возрастающими общественными потребностями в переводе экономических и государственно-правовых отношений на «электронную основу», но и сильно расширившимися возможностями передачи, обработки и хранения информации в распределенных вычислительных системах. Применение специальных криптографических протоколов и криптосистем позволяет осуществлять многообразные экономические отношения «дистанционно», исключая необходимость личной встречи участников этих отношений, а также поддерживать при этом должную финансовую и правовую дисциплину. К криптографическим протоколам относят протоколы шифрования, электронной цифровой подписи (ЭЦП), идентификации и протоколы аутентифицированного распределения ключей.

В 1985 году Нил Коблиц и Виктор Миллер независимо предложили использовать в криптографии некоторые алгебраические свойства эллиптических кривых. С этого момента началось бурное развитие нового направления в криптографии, для которого используется термин криптография на эллиптических кривых (Elliptic Curve Cryptography, сокращенно ECC). Криптосистемы с открытым ключом на эллиптических кривых обеспечивают такую же функциональность, как и алгоритм RSA. Однако их криптостойкость основана на другой проблеме, а именно на проблеме дискретного логарифма в группе точек эллиптической кривой (Elliptic Curve Discrete Logarithm Problem, сокращенно ECDLP). В настоящее время лучшие алгоритмы для решения ECDLP имеют экспоненциальное время работы, в отличие от алгоритмов для решения проблемы простого дискретного логарифма и проблемы факторизации целого числа, которые имеют субэкспоненциальное время работы. Это означает, что в системах на эллиптических кривых желаемый уровень безопасности может быть достигнут при значительно меньшей длине ключа, чем, например, в схеме RSA. Например, 160-битный ключ в ECC обеспечивает тот же уровень безопасности, что и 1024-битный ключ в RSA. В этой работе подробно рассматриваются способы и преимущества реализации криптографических протоколов с использованием теории эллиптических кривых и в качестве примера реализован алгоритм цифровой подписи на эллиптических кривых (Elliptic Curve Digital Signature Algorithm, сокращенно ECDSA) на языке Java.

алгоритм точка эллиптическая кривая протокол

Эллиптические кривые

В этом разделе будут изложены основы теории эллиптических кривых, даны основные определения, которые понадобятся в дальнейшем при описании алгоритмов арифметики эллиптических кривых.

Алгебраические кривые

Алгебраической кривой порядка n над полем F называется множество точек (x,y): x,y ÎF, удовлетворяющих уравнению F(X,Y) = 0, где F(X,Y) -многочлен степени n с коэффициентами из F. Пары (x,y) ÎF², удовлетворяющие уравнению кривой, называются ее точками.

Точка (x,y) кривой F(X,Y) = 0 называется неособой, если в ней не равны нулю обе частные производные многочлена F(X,Y). Кривая называется неособой, или гладкой, если все ее точки - неособые.

Эллиптической кривой E над полем F называется гладкая кривая, задаваемая уравнением вида

Y² + a₁ XY + a₃ Y = X³ + a₂ X² + a₄ X + a_{6 ,} a_i Î F.(1)

Будем обозначать E(F) множество точек (x,y) Î F², удовлетворяющих этому уравнению и содержащее кроме того бесконечно удаленную точку, обозначаемую.

Две кривые E и E’ над полем F называются изоморфными, если они переходят друг в друга при допустимой замене координат

X := u²x + r, Y := u³Y + u²sX + t.

В зависимости от характеристики поля F общее уравнение эллиптической кривой может быть упрощено. Далее рассмотрены стандартные формы записи эллиптических кривых для полей характеристики 2, 3 и для полей больших характеристик.

Поля больших характеристик. Если поле F не является полем характеристики 2 или 3, то заменив координаты

(x, y) ® ( ,  ),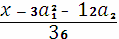

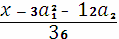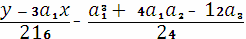
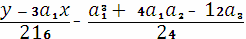можно привести кривую к виду

Y² = X³ + aX + b, a,b Î F, char F ≠ 2, 3(2)

C уравнением (2) эллиптической кривой E можно связать дискриминант

D(E) = −16(4a3 +27b2).          (3)

Понятие дискриминанта в общем случае кривой (1) выглядит более громоздко. А именно,

D(E) = - b₂² b₈ - 8b₄³ - 27b₆² + 9b₂b₄b ,

где

b₂ = a₁² + 4a₂ , ₄ = 2a₄ + a₁a₃ , ₆ = a₃² + 4a₆ ,

b₈ = a₁²a₆ + 4a₂a₆ - a₁a₃a₄ + a₂a₃² - a₄²;

Если D(E) = 0, то указанный многочлен имеет кратные корни и в точке (x, 0) нарушается условие гладкости кривой. Кривая Е является гладкой тогда и только тогда, когда ее дискриминант ненулевой.

Поля характеристики 2. Для полей характеристики 2 следует рассмотреть два случая. Если a₁ ≠ 0, то заменой

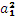
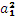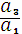
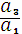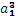
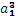(x, y) ® (x +  , y + ),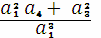

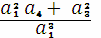эллиптическая кривая сводится к виду

Y² + XY = X³ + a₂X² +а₆, a_i Î F(4)

Кривые вида (4) называются несуперсингулярными. Дискриминант несуперсингулярной кривой равен D(E) = a₆ .

Если a₁ = 0, то можно провести замену (x, y) ® (x + a₂, y) и кривая будет иметь вид

Y² + a₃ X = X³ + a₄ X +a₆ , a_i Î F(5)

Кривые такого вида называются суперсингулярными, и их дискриминант имеет вид D(E) = a₃⁴.

Поля характеристики 3. Для полей характеристики 3 также возможны две замены. Если a₁² ≠ -a₂ , то заменой

(x, y) ® (x + 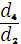 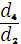, y + a₁ x + a₁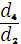 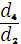 + a₃ ),

где d₂ = a₁² + a₂ , d₄ = a₄ - a₁ a₃ кривая преобразуется к виду

Y² = X³ + aX² + b(6)

Такие кривые называются несуперсингулярными и имеют дискриминант, равный D(E) = -а³ b.

Если a₁² = -a₂ , то заменой (x, y) ® (x, y + a₁ x +a₃) кривая преобразуется к виду

Y² = X³ + aX + b(7)

Такие кривые называются суперсингулярными и имеют дискриминант, равный D(E) = -а³.

Группа точек эллиптической кривой

На множестве E(F), состоящем из точек эллиптической кривой (1) и еще одного элемента - бесконечно удаленной точки кривой O (формально пока не являющейся точкой кривой), можно определить операцию, обладающую свойствами операции абелевой группы.

Принято получающуюся при этом группу рассматривать как аддитивную группу, а операцию называть операцией сложения и обозначать, как обычно, знаком плюс.

Упомянутая дополнительная точка O играет роль нейтрального элемента (в аддитивной записи нуля) этой группы.

По определению, полагаем для любой точки (x,y) Î E(F)

(x,y) + O = O + (x,y) = (x,y);+ O = O;

Чтобы определить в общем случае операцию сложения абелевой группы, сначала покажем, что каждой точке (x,y) эллиптической кривой можно сопоставить в определенном смысле симметричную точку (далее будет ясно, что такая точка и будет точкой -(x,y), противоположной к (x,y) точкой в группе данной кривой). Заметим, что вместе с точкой (x,y) кривая имеет и точку

(x,y’) = (x, -a₁x - a₃ - y);

Убедиться в этом можно, подставив X = x и Y = -a₁x - a₃ - y, и учитывая, что при X = x и Y = y имеет место равенство. Симметричность проявляется в том, что по тому же правилу точке (x, y’) соответствует исходная точка (x, y), так как имеет место инволютивный закон:

(x, y) = (x, y’’).

Если кривая E имеет вид (2), то

(x, y’) = (x, -y)

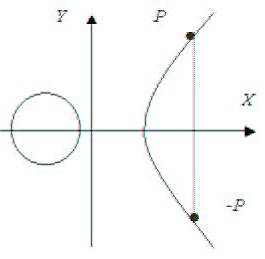
В частности, для эллиптических кривых над полем действительных чисел, точки (x, y) и (x, -y) располагаются на прямой Y = x симметрично относительно оси абсцисс, как показано на рисунке.

Для суперсингулярных и несуперсингулярных кривых характеристики 2 симметричная точка (x, y’) определяется соответственно уравнениями (x, y’) = (x, y+1) и (x, y’) = (x, x+y).

Полагается, что (x, y) + (x, y’) = O и (x, y’) обозначается -(x, y). Таким образом, множество E(F) удовлетворяет двум аксиомам группы (существует нулевой элемент и каждому элементу соответствует противоположный элемент).

Таким образом, операция сложения определена, когда одна из точек равна O или когда складываются противоположные точки.

Для двух точек (x₁, y₁), (x₂, y₂), таких, что x₁ ≠ x₂ или x₁ = x₂, y₁ = y₂ суммой двух этих точек объявляется точка

P + Q = -R = -(x₃, y₃) (в случае x₁ ≠ x₂)

P + P = 2P = -R = -(x₃, y₃) (в случае x₁ = x₂, y₁ = y₂)

Конкретные формулы для вычисления координат точки R в обоих случаях рассмотрены в разделе «Алгоритмы на эллиптических кривых». На рисунках изображено положение точки R для обоих случаев при рассмотрении эллиптической кривой над полем действительных чисел.

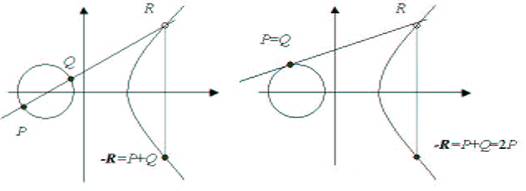
Логично было бы назвать результатом операции сложения саму точку R, но тогда не будет выполняться тождество

P + Q = R ó P = R - Q.

Операция сложения на множестве E(F) коммутативна и ассоциативна (это можно доказать, используя прямые формулы для вычисления R). Таким образом, множество E(F) (множество точек эллиптической кривой вместе с точкой О) с операцией сложения, описанной выше, является абелевой группой.

Порядком точки P эллиптической кривой E называется минимальное натуральное число n, такое, что nP = O. Если такого числа не существует, то точка имеет бесконечный порядок.

Эллиптические кривые над конечными полями

Эллиптические кривые над конечными полями имеют конечные группы точек. Порядок этой группы называется порядком эллиптической кривой. По теореме Лагранжа порядок точки делит порядок эллиптической кривой. Изоморфные кривые имеют одинаковые группы, а, следовательно, и порядки. Поэтому далее всегда можно ограничиться рассмотрением кривых с уравнениями специального вида (2), (4), (5), (6), (7).

Пользуясь символом Лежандра, легко указать формулу для числа точек на кривой Y² = f(X) над полем GF(p), p > 2 (поля больших характеристик). Действительно, сравнение Y² = f(X) (mod p) относительно Y при фиксированном X имеет (при p > 2) 1 + 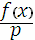 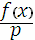решений (это верно и при f(x) = 0). Учитывая бесконечно удаленную точку, получаем формулу для порядка кривой над полем GF(p), p > 2 в виде

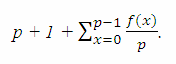
При малых простых p, пользуясь этой формулой и теорией квадратичных вычетов порядок кривой над полем GF(p) находится довольно легко. Но вычисление порядка эллиптической кривой не всегда просто и даже возможно. Общая формула для вычисления порядка произвольной кривой неизвестна. Неизвестно даже, можно ли за полиномиальное время найти кривую данного порядка. Тем не менее, известны способы выбора эллиптических кривых над конечными полями, допускающих простое определение порядка. Эти способы важны, потому что в криптографическом отношении полезными являются эллиптические кривые, порядок которых содержит большие простые множители. Для кривых, у которых порядок является гладким числом (т.е. разлагающимся только на малые простые) проблема дискретного логарифмирования может быть решена сравнительно быстро алгоритмом Полига-Хеллмана-Зильбера.

Алгоритмы на эллиптических кривых

В этом разделе представлены алгоритмы, необходимые для реализации криптографических приложений на эллиптических кривых.

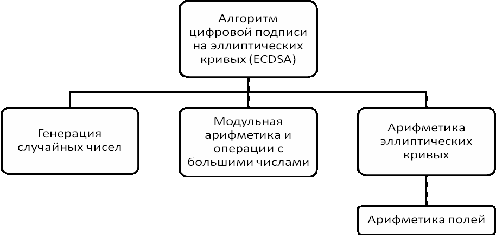
Диаграмма, приведенная ниже, показывает, какие модули необходимо создать при реализации алгоритма цифровой подписи на эллиптических кривых (ECDSA). В приложении данной работы генерация случайных чисел, модульная арифметика и операции над большими числами осуществляются стандартными средствами языка Java. Арифметика эллиптических кривых основана на алгоритмах, приведенных в этой главе.

Сложение точек эллиптической кривой

В соответствии с определением операции сложения в группе точек эллиптической кривой общая схема алгоритма сложения точек P₁ = (x₁ , y₁ ) и P₂ = (x₂ , y₂ ) выглядит следующим образом:

Вход: коэффициенты эллиптической кривой, точки P₁ и P₂.

Выход: R = P₁ + P₂.

Алгоритм: если P₁ = O, то R = P₂ ,

если P₂ = O, то R = P₁ ,

если P₂ = - P₁, то R = O ,

если x₂ ≠ x₁, то R = P₁ + P₂ = -(x₃ , y₃ ) ,

иначе R = 2P₁ = -(x₃ , y₃ ).

Вернуть: R.

Координаты x₃ , y₃ вычисляются по разным формулам в зависимости от вида эллиптической кривой и условия различия или совпадения точек.

Для эллиптических кривых над полем характеристики, большей 3 (т.е. для кривых, имеющих вид Y² = X³ + aX + b) противоположной точкой для точки P (x, y) будет являться -P = P (x , -y). Если P₁ ≠ P_2, то формулы для вычисления координат R выглядят так:

x₃ = l² -x₁ - x₂ ,

y₃ = y₁ + l(x₃ - x₁) , где l =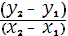

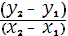
В случае P₁ = P₂ = (x, y) формулы имеют следующий вид:

x₃ = (l’)² - 2x,

 y₃ = y + l’(x₃ - x) , где l’ =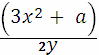

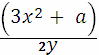
Для полей характеристики три (в общем виде Y² = X³ + a₂X² + a₄X + a₆) при P₁ ≠ P₂ формулы имеют вид:

x₃ = (l² -a₂ ) -x₁ - x₂ ,

y₃ = y₁ + l(x₃ -x₁ ), где l =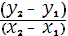

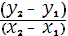
А при P₁ = P₂

x₃ = ((l’)² -a₂ ) - 2x ,

y₃ = y + l’(x₃ -x ), где l’ =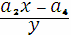

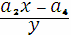
Для полей характеристики два случаи суперсингулярных и несуперсингулярных кривых рассматриваются отдельно. Точка кривой, противоположная точке (x,y) имеет координаты (x,x+y). Для несуперсингулярных кривых (в общем виде Y² + XY = X³ + a₂X² +а₆) при P₁ ≠ P₂ координаты R вычисляются по формулам:

x₃ = l² + l + a₂ + x₁ + x₂ ,

y₃ = x₃ + y₁ + l(x₃ + x₁ ), где l =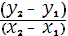

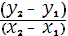
А при P₁ = P₂

x₃ = (l’)² + (l’) + a₂,

y₃ = x² + (l’ + 1)x₃, где l’ =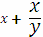

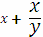
Для суперсингулярных кривых (в общем виде Y² + a₃ X = X³ + a₄ X +a₆) противоположной точкой для (x,y) будет (x,y + a₃). При P₁ ≠ P₂

x₃ = l + x₁ + x₂

y₃ = a₃ + y₁ + l(x₃ + x₁ ), где l =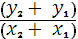

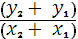
А при P₁ = P₂

x₃ = (l’)²

y₃ =l’(x + x₃) + y + a₃ , где l’ =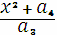

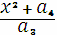
Следует отметить, что при вычислении суммы двух точек описанными выше формулами, самая трудоемкая операция в арифметике конечного поля - мультипликативное обращение, выполняется однократно.

Реализация этого алгоритма для кривых характеристики, большей 3, находится в приложении 1 данной работы (метод pointAdd класса eCurve).

Алгоритм скалярного умножения

Алгоритмы умножения точки P эллиптической кривой на числовую константу k (кратко - алгоритмы вычисления kP), они же алгоритмы скалярного умножения точки, являются основными в арифметике эллиптических кривых. Существует большое число алгоритмов, разработанных для кривых специального вида (в том числе для конкретных кривых, рекомендованных стандартами шифрования и цифровой подписи), а также существуют алгоритмы вычисления kP при известном P (например, P может быть известно заранее в алгоритме цифровой подписи).

В приложении данной работы для вычисления скалярного произведения был использован аналог алгоритма быстрого возведения в степень для эллиптических кривых.

Вход: k = (kt−1, . . ., k1, k0 )2, P ∈ E(Fq).

Выход: kP.

Алгоритм: 1. Q←O.

. Для всех i от 0 до t −1:

.1 Если k_i = 1 то Q←Q + P.

.2 P←2P.

Вернуть: Q.

Число k представляется в двоичной форме записи. Точка Q на первом шаге равняется O, т.е. является нейтральным элементом сложения. Далее запускается цикл с количеством шагов, равным длине k в двоичной форме записи. На каждом шаге если k_i = 1, то Q складывается с точкой P. В конце каждого шага P удваивается. Алгоритм состоит только из операций сложения двух точек и операций удвоения точки. Поэтому вычислительное время алгоритма зависит только от времени вычисления суммы двух точек и от времени удвоения точки.

Если точка P известна заранее, то можно произвести некоторые предварительные вычисления для повышения эффективности алгоритма. Например, вычислив все точки 2P, 2²P … 2^t-1P можно значительно ускорить вычисление скалярного произведения. Вычислительное время алгоритма будет зависеть только от времени вычисления суммы двух точек.

Алгоритм генерации случайных кривых

Алгоритм цифровой подписи с использованием эллиптических кривых (ECDSA) принят и описан в различных стандартах. Среди них ANSI X9.62, FIPS 186-2 (NIST), IEEE 1363-2000, ISO/IEC 14888-3, ISO/IEC 15946-3, SEC-1, SEC-2 и др.

Далее мы опишем основные рекомендации стандарта ANSI X9.62 ECDSA. К эллиптическим кривым предъявляются следующие требования:

. Кривые рассматриваются или над простыми полями (порядок q которых равен простому числу p), или над полями характеристики два (у которых q = 2m).

. Для представления элементов поля используется либо стандартный базис, порождаемый трехчленом или пятичленом, либо гауссов нормальный базис (GNB).

3. Кривая E задается выбором двух элементов a, b поля GF(q). В случае p > 2 она имеет вид y² = x³+ ax + b, а в случае p = 2 вид y²+ xy = x³+ ax²+ b. Таким образом, стандарт рекомендует только несуперсингулярные кривые.

. На кривой выбирается точка (xG, yG), xG, yG ∈ GF(q) простого порядка n > 2¹⁶⁰, n > 4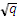 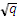и вычисляется кофактор h = |E(GF (q))|/n.  В качестве кривых можно и удобно выбирать в случае p = 2 кривые, у которых a, b равны 0, 1, но стандарт рекомендует все же случайные кривые, т.е. кривые со случайно выбранными a, b.

При этом рекомендуется использовать следующие алгоритмы генерации случайных кривых:

1) Случай q = p. Положим

t = log₂ p , s = (t − 1)/160, v = t − 160s.

1. Выбираем произвольную строчку битов seedE длиной g ≥ 160 бит, и полагаем z равным числу, двоичная запись которого совпадает с seedE.

. Применяя к seedE стандартную хеш-функцию SHА₁, вычисляем g-битовую строку H = SHA₁(seedE). Выбирая в H v самых правых битов, получаем строку c₀ длиной v битов.

. Заменяя в c₀ самый левый бит на 0, получаем строку W₀.

. Для i от 1 до s делаем следующее:

.1 полагаем s_i равной g−битной строке, являющейся двоичной записью числа z + i mod 2^g

4.2 вычисляем g-битовую строку W_i= SHА₁(s_i).

5. Полагаем битовую строку W равной конкатенации (произведению) битовых строк W_i , i = 0, . . . , s, т.е. W = W₀. . . W_s.

. Полагаем r равным целому числу с двоичной записью  W. Выполнение пункта 3 гарантирует, что r < p.

. Если r = 0 или 4r + 27 ≡ 0(mod p), то возвращаемся к шагу 1.

8. Выбираем ненулевые a, b ∈ GF (p) так, чтобы rb2    ≡ a3(mod p). Например, можно взять a = b = r.

9. Полученная кривая есть E : y2 = x3 + ax + b.

Заметим, что условие невырожденности кривой 4a3 + 27b2      6 ≠ 0 (mod p) гарантировано выполняется, так как при       b ≠ 0, r = a³/b²mod p удовлетворяет условиям r ≠ 0, 4r + 27 ≠ 0 (mod p). Имеется только две попарно неизоморфные кривые с одним и тем же r. Эти кривые являются скрученными и сумма их порядков равна 2 + 2p. Кривые с разными r неизоморфны друг другу. На шаге 8 поэтому есть по существу только еще одна возможность выбора a и b,  кроме явно указанной.

2) Случай q = 2^m. Положим, как и выше, s = (t − 1)/160, v = t − 160s.

1. Выбираем произвольную строчку битов seedE длиной        g ≥ 160 бит, и полагаем z, равным числу, двоичная запись которого совпадает с seedE.

. Вычисляем g-битовую строку H          = SHA₁(seedE). Выбирая в H v самых правых битов, получаем строку b₀ длиной v битов.

. Заменяя в b₀ самый левый бит на 0, получаем строку W₀.

. Для i от 1 до s делаем следующее:

.1 полагаем s_i равной g−битной строке, являющейся двоичной записью числа z + i mod 2_g

4.2 вычисляем g-битовую строку bi = SHA1(si ).

. Вычисляем битовую строку b = b0. . . bs и полагаем b равным соответствующему элементу поля GF (q).

. Если b = 0, то возвращаемся к шагу 1.

. Выбираем произвольный a ∈ GF (q).

. Полученная кривая есть E: y2 + xy = x3 + ax2       + b.

Генерация криптографически надежных параметров кривых.

Стандартом рекомендуется определенный алгоритм генерации надежных параметров кривых.

. Выбираем случайную кривую E(GF(q)) алгоритмом, указанным выше.

2. Вычисляем ее порядок N = |E(GF (q))|.

. Проверяем, делится ли N на ранее выбранное простое           n (n > 2160, n > 4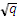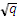). Если нет, то переходим к шагу 1.

. Проверяем, что n не делит ни одно из чисел qk − 1, k = 1, . . . 20. Если нет, то переходим к шагу 1.

. Проверяем, что n ≠ q. Если нет, то переходим к шагу 1.

. Выбираем произвольную точку G0 ∈ E(GF(q)) и полагаем G = (N/n) G0. Повторяем, пока не получим G ≠ O.

Генерация случайных кривых с подходящими криптографическими свойствами - чрезвычайно ресурсоемкий процесс. Кривую над полем GF(2^m) при m примерно равным 200 можно сгенерировать за несколько часов. В некоторые стандарты ECDSA включен набор сгенерированных эллиптических кривых со специальными параметрами, повышающими эффективность операций с точками этих кривых. Стандартом NIST к использованию рекомендуются кривые P-192, P-224, P-256, P-384, P-521 над полями больших характеристик (рассматриваются кривые вида y² =x³-3x+b, то есть a=-3). Для полей характеристики два для каждого поля рекомендованы две эллиптических кривых - несуперсингулярная кривая (вида y² + xy = x³ + x² + b) и кривая Коблица (кривые вида y² + xy = x³ + x² + 1, где a = 0,1). Вот, к примеру, рекомендованная стандартом NIST кривая для поля большой характеристики P-192.

Curve P-192

p = 6277101735386680763835789423207666416083908700390324961279

r = 6277101735386680763835789423176059013767194773182842284081

s = 3045ae6f c8422f64 ed579528 d38120ea e12196d5

c = 3099d2bb bfcb2538 542dcd5f b078b6ef 5f3d6fe2 c745de65

b = 64210519 e59c80e7 0fa7e9ab 72243049 feb8deec c146b9b1

Gx = 188da80e b03090f6 7cbf20eb 43a18800 f4ff0afd 82ff1012

Gy = 07192b95 ffc8da78 631011ed 6b24cdd5 73f977a1 1e794811

Для кривой заданы:

Простое целое p - характеристика поля.

Порядок кривой r

Входное значение для хэш-функции SHA₁ s = seedE

Выходное значение хэш-функции SHA₁ c.

Коэффициент b

Координаты порождающей точки G (Gx, Gy)

Использование различных систем координат

Как видно из раздела «Сложение точек эллиптической кривой», при сложении двух точек эллиптической кривой над полем характеристики, большей 3 (т.е. для кривой, имеющих вид y² = x³ + ax + b) требуется произвести два умножения, одно возведение в квадрат и одно обращение. Переход к другой системе координат позволяет полностью исключить операцию обращения за счет увеличения числа других операций. Поэтому если для данного поля операция обращения занимает значительно больше времени, чем операция умножения, то использование другой системы координат может значительно ускорить вычисления. В этом разделе будут рассмотрены наиболее часто используемые системы координат для кривых над полями больших характеристик (y² = x³ + ax + b):

· стандартная проективная система координат

·        система координат Якоби

·        система координат Чудновского-Якоби

·        модифицированная система координат Якоби

Для каждой системы координат будет получен алгоритм вычисления суммы двух точек эллиптической кривой. Это позволит определить, сколько в точности операций нужно затратить на сложение двух точек в каждой из рассмотренных систем.

Также будет рассмотрен метод, позволяющий использовать в одном алгоритме несколько различных систем координат. Будет приведен пример алгоритма, использующего преимущества данного подхода.

Проективные координаты

Рассмотрим эллиптическую кривую над полем K, и положим c и d положительными числами. Определим отношение эквивалентности на ненулевых тройках из K³ следующим образом:

(X₁, Y₁, Z₁) ~ (X₂, Y₂, Z₂) если X₁ = l^c X₂ , Y₁= l^d Y₂ , Z₁ = lZ₂ для некоторого ненулевого l Î K.

Класс эквивалентности, содержащий тройку (X, Y, Z) Î K³ \ {(0, 0, 0)}, обозначим следующим образом:

(X : Y : Z) = {(l^c X, l^d Y, lZ): l Î K }.

Класс эквивалентности (X : Y : Z) называется проективной точкой, а (X, Y, Z) - ее представителем. Множество всех проективных точек обозначается P(K) . Следует отметить, что если (X’, Y’, Z’) Î (X : Y : Z), то (X’ : Y’ : Z’) = (X : Y : Z). Таким образом, каждый элемент класса эквивалентности может служить его представителем. В частности, если положить Z ≠ 0, то (X / Z^c , Y / Z^d , 1) является представителем проективной точки (X : Y : Z), причем единственным представителем с координатой Z = 1. Таким образом, мы получаем однозначное соответствие между набором проективных точек

P(K) = {(X : Y : Z) : X, Y, Z Î K, Z ≠ 0}

и набором аффинных точек (K) = {(x, y) : x, y Î K}.

Набор проективных точек(K)0 = {(X : Y : Z) : X, Y, Z ∈ K, Z = 0}

называется прямой в бесконечности, так как точки из этого набора не соответствуют никаким аффинным точкам.

Проективная форма уравнения эллиптической кривой E над полем K получается путем подстановки x = X / Z^c , y = Y / Z^d и избавления от знаменателей (то есть путем домножения на Z в некоторой степени). Если некоторый представитель класса (X, Y, Z) Î K³ \ {(0, 0, 0)} удовлетворяет полученному проективному уравнению, то ему удовлетворяет любой представитель класса (X:Y:Z). Таким образом можно сказать, что проективная точка (X : Y : Z) лежит на кривой E. Проективные точки из P(K)⁰, лежащие на кривой E, будут являться бесконечно удаленными точками.

Для удобства изложения дальнейшего материала, введем некоторые обозначения. Будем обозначать рассматриваемые системы координат прописными буквами латинского алфавита, с возможным добавлением верхнего индекса (например, аффинную систему координат будем обозначать A). Дадим также обозначение основным операциям, производящимся при сложении двух точек эллиптической кривой:

M - умножение двух чисел,

S - возведение числа в квадрат,

I - обращение числа.

Далее, число операций, требуемых для сложения двух точек (удвоения точки) в заданной системе координат будем обозначать следующим образом:

t(X₁ + X₂ = X₃) = nM + kS + lI, где n - число требуемых умножений, k - число требуемых возведений в квадрат, l - число требуемы обращений, X₁ и X₂ - используемые системы координат для первой и второй точки соответственно, X₃ - система координат результирующей точки (если X₁ = X₂ = X₃ , то сократим запись до t(X + X)).

Например, в описанных обозначениях для аффинных координат можно записать:

t(A + A) = 2M + S + I, t(2A) = 2M + 2S + I.

Стандартная проективная система координат (P)

В стандартной проективной системе координат c = d = 1. В этом случае уравнение кривой y² = x³ + ax + b преобразуется к виду:

Y ²Z = X ³ + aXZ ² + bZ ³

Бесконечно удаленная точка имеет координаты (0, 1, 0). Обратной точкой для (X, Y, Z) будет точка (X, -Y, Z).

Возьмем две проективные точки P₁ = (X₁, Y₁, Z₁), P₂ = (X₂, Y₂, Z₂), принадлежащие нашей кривой. Тогда координаты точки P₃:

P₃ = P₁ + P₂ = (X₃, Y₃, Z₃)

вычисляются по следующим формулам (эти формулы легко получаются при подстановке замен x, y в стандартные формулы сложения двух точек):

Если P₁ ≠ ±P₂ ,

u = Y₂Z₁ − Y₁Z₂,

v = X₂Z₁ − X₁Z₂,

w = u²Z₁Z₂ − v³ − 2v²X₁Z₂,

X₃ = vw,

Y₃ = u(v²X₁Z₂ − w) − v³Y₁Z₂,

Z₃ = v³Z₁Z₂.

Введем несколько дополнительных переменных с целью уменьшения числа операций:

t₁= Y₁Z₂ ; t₂ = X₁Z₂ ;

t₃ = Z₁Z₂ ;  v₂ = v² ;

v₃ = v³ = v₂v ; t₄ = v₂t₂ ;

Подставляя эти переменные в формулы для сложения, получим, что t(P+P) = 12M + 2S.

Рассмотрим теперь случай P₁ = P₂ (удвоение точки):

t = aZ₁² + 3X₁² ,

u = Y₁Z₁ ,

v = uX₁Y₁ ,

w = t² − 8v,

X₃ = 2uw,

Y₃ = t(4v − w) − 8Y₁²u² ,

Z₃ = 8u³.

Получаем, что t(2P) = 7M + 5S.

При P₁ = −P₂ получаем P₃ = O.

Теперь рассмотрим, какой выигрыш в производительности мы получим при использовании стандартных проективных координат. В последующих рассуждениях учитываются только операции умножения, возведения в квадрат и обращения. Операции сложения и вычитания производятся намного быстрее и при оценке скорости алгоритма их можно не учитывать.

Напомним, что при использовании обычного метода сложения двух точек нам требуется произвести 2 умножения, одно возведение в квадрат и одно обращение. Таким образом, при использовании стандартных проективных координат мы производим на 10 умножений и на 1 возведение в квадрат больше, но нам не требуется операция обращения элемента.

При удвоении точки в проективных координатах нам требуется провести на 5 умножений и на 3 возведения в квадрат больше. Обращение из алгоритма также исключается.

Таким образом, для того, чтобы использование проективных координат давало прирост производительности, необходимо, чтобы операция обращения была хотя бы в 11 раз медленнее операции умножениях в случае сложения двух точек и в 8 раз медленнее в случае удвоения точки. Для сравнения скорости работы этих операций была написана отдельная программа (test.java в приложении данной работы, метод compMultInv). Эта программа использует реализации операций умножения и обращения из библиотеки BigInteger языка java (именно эта библиотека используется в данной работе при реализации ECDSA). В результате работы данной программы было установлено, что обращение элемента поля K в среднем занимает приблизительно в 14-16 раз больше времени, чем умножение двух элементов данного поля (характеристика поля K выбиралась случайным образом, ее длина полагалось равной 200 битам). Из этих результатов можно сделать следующий вывод: в заданных условиях при использовании стандартных проективных координат сложение двух точек происходит в среднем в ~1.28 раз быстрее, а удвоение точки - в ~1.58 раз быстрее.

Следует отметить, что при использовании стандартных проективных координат на суперсингулярных кривых можно получить еще больший прирост производительности, так как для сложения двух точек там требуется лишь 9 операций умножения, а для удвоения точки - только 6 возведений в квадрат. Таким образом, переходя к проективным координатам, можно полностью избавиться от операции обращения, увеличив число умножений всего в 4.5 раза.

В результате получаем, что в реализации криптографических протоколов все операции над точками эллиптической кривой можно проводить в проективных координатах. Когда нужно будет совершить переход обратно к аффинным координатам, достаточно разделить координаты X, Y проективной точки на Z.

Система координат Якоби (J)

Рассмотрим теперь систему координат Якоби. В этой системе координат c = 2, d = 3, то есть (X : Y : Z) отображает аффинную точку (X / Z², Y / Z³). Эллиптическая кривая y² = x³ + ax + b преобразуется к виду:

Y ² = X ³ + aXZ ⁴ + bZ ⁶.

Бесконечно удаленная точка имеет координаты (1 : 1 : 0). Обратной точкой для (X, Y, Z) будет точка (X, -Y, Z).

Возьмем две проективные точки P₁ = (X₁, Y₁, Z₁), P₂ = (X₂, Y₂, Z₂), принадлежащие нашей кривой. Тогда координаты точки P₃:

P₃ = P₁ + P₂ = (X₃, Y₃, Z₃)

вычисляются по следующим формулам:

Если P₁ ≠ ±P₂ ,

r = X₁Z₂², s = X₂Z₁²,

t = Y₁Z₂³, u = Y₂Z₁³,

v = s - r, w = u - t,

X₃ = -v³ - 2rv² + w²,

Y₃ = -tv³ + (rv² - X₃)w,

Z₃ = vZ₁Z₂.

Если P₁ = P₂ (удвоение точки):

v = 4X₁Y₁²,  w = 3X₁² + aZ₁⁴,

X₃ = -2v + w²,

Y₃ = -8Y₁⁴ + (v - X₃)w,

Z₃ = 2Y₁Z₁.

При P₁ = −P₂ получаем P₃ = O.

В этой системе координат t(J + J) = 12M + 4S. Удвоение точки требует t(2J) = 3M + 6S. Операция обращения, как и в случае стандартных проективных координат, не задействована. Следовательно, сложение точек в системе координат Якоби происходит чуть медленнее, чем в стандартной проективной системе координат. Однако в сравнении со стандартной проективной системой координат, удвоение точки требует на 4 умножения меньше и только на одно возведение в квадрат больше.

При использовании эллиптических кривых особого вида можно дополнительно ускорить процесс удвоения точки. Если в уравнении кривой a = -3, то

w = 3X₁² + aZ₁⁴ = 3(X₁² - Z₁⁴) = 3(X₁ - Z₁²)( X₁ + Z₁²).

В этом случае t(2J) = 4M + 4S. Именно по этой причине стандартом NIST над полями больших характеристик все рекомендуемые кривые имеют вид y² = x³ - 3x + b.

Полный алгоритм удвоения точки в системе координат Якоби для случая a = -3 выглядит следующим образом:

Вход: точка P = (X₁ : Y₁ : Z₁) в системе координат Якоби лежащая на кривой y² = x³ - 3x + b.

Выход: 2P = (X3 : Y3 : Z3) в системе координат Якоби.

Алгоритм: 1. Если P = O то вернуть (P).

. T1 ← Z₁²  

3. T2 ← X1 - T1.

. T1 ← X1 +T1.

. T2←T2 · T1.

. T2←3T2.

. Y3←2Y1.

. Z3←Y3 · Z1.

. Y3←Y3²

10. T3←Y3 · X1.

. Y3←Y3²

12. Y3←Y3/2.

. X3←T₂²

14. T1←2T3.

. X3←X3 − T1.

. T1←T3 − X3.

. T1←T1 · T2.

. Y3←T1−Y3.

Вернуть: (X3 : Y3 : Z3).       

Если требуется удвоить одну точку несколько раз подряд, то можно использовать следующий алгоритм, который работает немного быстрее, чем простое последовательное применение операции удвоения:

Выход: 2^m P в системе координат Якоби.

Алгоритм: 1. Если P = O то вернуть (P).

2. Y←2Y, W←Z⁴.

. Пока m > 0 выполнять:

.1 A←3(X² −W), B←XY ².

.2 X←A² −2B, Z←ZY.

.3 m←m −1. Если m > 0 то W←WY ⁴.

.4 Y←2A(B − X)−Y ⁴.

Вернуть: (X : Y/2 : Z).

Система координат Чудновского-Якоби ( J^c )

В системе координат Якоби удвоение точки происходит быстрее, чем в стандартной системе координат, однако сложение двух точек требует чуть больше операций. Для того, чтобы избавиться от этого недостатка, можно представлять точки в системе координат Якоби в виде пятерок (X, Y, Z, Z ², Z ³). Эта система координат называется системой Чудновского-Якоби. В этой системе координат:

t(J^c + J^c) = 10M + 4S, (2J^c) = 2M + 8S.

Модифицированная система координат Якоби ( J^m )

Использование системы координат Чудновского-Якоби позволяет «сбалансировать» операции удвоения точки и сложения двух точек. Мы получаем небольшой выигрыш в скорости сложения и платим за это проигрышем в скорости удвоения. Однако схожий подход может быть использован и для того, чтобы дополнительно ускорить операцию удвоения за счет еще большего замедления операции сложения. Для этого в системе координат Якоби добавим четвертую координату (X, Y, Z, aZ⁴). Возьмем две проективные точки P₁ = (X₁, Y₁, Z₁, aZ₁⁴), P₂ = (X₂, Y₂, Z₂, aZ₂⁴), принадлежащие нашей кривой. Тогда координаты точки P₃:

P₃ = P₁ + P₂ = (X₃, Y₃, Z₃, aZ₃⁴)

вычисляются по следующим формулам:

Если P₁ ≠ ±P₂ ,

u₁ = X₁Z₂², u₂ = X₂Z₁²,

s₁ = Y₁Z₂³, s₂ = Y₂Z₁³,

h = u₂ - u₁, r = s₂ - s₁,

X₃ = -h³ - 2u₁h² + r²,

Y₃ = -s₁h³ + r(u₁h² - X₃),

Z₃ = Z₁Z₂h,

aZ₃⁴ = aZ₃⁴.

Если P₁ = P₂ (удвоение точки):

s = 4X₁Y₁², u = 8Y₁⁴,

m = 3X₁² + (aZ₁⁴),

X₃ = -2s + m²,

Y₃ = m(s - X₃) - u,

Z₃ = 2Y₁Z₁,

aZ₃⁴ = 2u(aZ₁⁴).

При P₁ = −P₂ получаем P₃ = O.

Для этой системы координат получаем:

t(J^m + J^m) = 13M + 6S, (2J^m) = 4M + 4S.

Таким образом, мы получили систему координат, в которой очень выгодно производить операцию удвоения точки (при этом на кривую не накладывается никаких ограничений). Однако операция сложения в данной системе координат требует еще больше времени, чем в обычной системе координат Якоби. Рассмотрим далее метод, который позволит нам использовать преимущества различных систем координат.

Смешанные координаты

Из изложенной выше теории можно сделать вывод, что на данный момент не обнаружено «универсальной» системы координат. Некоторые системы координат позволяют быстро производить удвоение точки, другие - сложение двух точек. Однако при реализации алгоритмов на эллиптических кривых вовсе не обязательно использовать только одну систему координат. Если нам требуется складывать различные точки, можно использовать одну систему координат, а если нужно производить удвоения точки - другую. При этом в некоторых случаях мы можем даже складывать точки, которые представлены в разных системах координат. Рассмотрим пример использования этого метода.

Будем строить алгоритм умножения точки эллиптической кривой P на число k. Возьмем в качестве базы алгоритм, в котором k представляется в NAF (Non-adjacent form), и читается справа налево. На каждом шаге алгоритма происходит удвоение точки P и, возможно, сложение точки P с результирующей точкой P*.

Добавим теперь в этот алгоритм использование смешанных координат. Удвоение точки P каждый раз будем производить в модифицированной системе координат Якоби, то есть в самой выгодной для этого системе координат. Теперь нам нужно подобрать такую систему координат X, которая бы позволяла производить сложение вида J^m + X = X и при этом затраты на эту операцию были бы минимальными. На роль такой системы подходит обычная система координат Якоби. При этом для сложения вида J^m + J = J не требуется выполнять никаких преобразований координат (четвертая координата J^m просто игнорируется). Затрачивать это сложение будет столько же операций, сколько и сложение вида J + J = J. Таким образом, мы можем использовать преимущество модифицированной системы координат Якоби (минимальные затраты операций на удвоение точки) и не расплачиваться за это существенным замедлением операции сложения двух точек. Подробное описание алгоритма:

Вход: точка P = (X₁ : Y₁ : Z₁) в системе координат Якоби, лежащая на кривой y² = x³ + ax + b и целое число k > 0.

Выход: kP = (X_k : Y_k : Z_k) в системе координат Якоби.

Алгоритм: 1. P* ← (1, 1, 0); T ← (X1 : Y1 : Z1 : aZ₁⁴)

2. Пока k > 1 выполнять:

.1 Если k mod 2 = 1 то P* = P* + T.

иначе P* = P* - T.

.2 k = k/2

.3 T = 2T

3. P* = P* + T

Вернуть: P*

В данной работе реализованы операции сложения и удвоения точек в системе координат Якоби (метод pointAddJacobi класса eCurve), операция удвоения точки в модифицированной системе координат Якоби (метод pointDoubleJacobiM класса eCurve) и алгоритм умножения точки на число, описанный выше (метод pointMultiplyModifie класса eCurve). Также написана программа, позволяющая увидеть, какое преимущество в скорости дает использование в этом алгоритме проективных координат (test.java, метод compModStd).

Сравнение алгоритмов производилось для эллиптических кривых над полями характеристик p длины 192, 224, 256, 384, 521 бит (то есть те значения длины p, которые используются в стандарте NIST). Все параметры кривой, точка P и большое число k генерировались случайным образом. В результате сравнения были получены следующие результаты:

где t(A) - время работы алгоритма, который не использует проективные координаты;

t(A^m) - время работы алгоритма, который использует смешанные координаты (J и J^m).

Таким образом, использование смешанных координат увеличивает скорость основных операций эллиптических кривых в ~1.7-1.8 раз. При этом не накладывается никаких ограничений на параметры кривой и не требуется проводить предвычислений.

Эллиптическая криптография

В этом разделе будут рассмотрены реализации криптосистем с открытым ключом на основе эллиптических кривых.

Криптосистема с открытым ключом

Криптографическая система с открытым ключом (или асимметричный шифр) - система шифрования или электронной цифровой подписи (ЭЦП), при которой открытый ключ передаётся по открытому (незащищённому) каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для шифрования или генерации подписи сообщения используется секретный (private) ключ, который известен только пользователю. А для проверки подписи и для дешифровки используется открытый (public) ключ, который генерируется на основе секретного ключа при помощи некоторой односторонней функции. То есть по значению открытого ключа вычислить секретный практически невозможно (используя современные вычислительные средства, за обозримый интервал времени), чем сгенерировать открытый ключ из секретного. Таким образом, открытый ключ можно сообщать кому угодно и даже публиковать его.

Рассмотрим общую схему работы системы шифрования с открытым ключом. Пусть сторона А хочет послать конфиденциальное сообщение m стороне B. А получает копию открытого ключа В - e_B, и использует функцию шифрования Enc некоторого алгоритма шифрования для вычисления криптограммы c = Enc _eB (m). Затем А передает криптограмму с стороне В, которая использует функцию дешифровки Dec со своим секретным ключом d_b для получения исходного сообщения m = Dec _dB (c). Предполагается, что злоумышленник, зная только e_b , не сможет расшифровать криптограмму c, т.е. e_b может передаваться по незащищенному каналу. Важно лишь, чтобы сторона А получила неиспорченную копию ключа e_В, иначе сообщение будет зашифровано на неверном ключе и расшифровать его будет уже невозможно.

Теперь рассмотрим общую схему работы алгоритма цифровой подписи с открытым ключом. Пусть сторона А использует алгоритм генерации цифровой подписи Sign и ее секретный ключ d_A для вычисления подписи сообщения s = Sing _dA (m). При получении m и s, сторона В, которая имеет копию публичного ключа e_A использует алгоритм заверения подписи для подтверждения того, что подпись s была действительно получена из сообщения m и секретного ключа d_A. Так как d_A - секретный ключ, который известен только стороне А, сторона В может быть уверена в том, что сообщение действительно получено от А. Более того, так как заверение требует только не подлежащих засекречиванию данных m и e_A, то подпись s для сообщения m также может быть заверена третьей стороной для разрешения спора в том случае, если А отрицает акт подписи сообщения m. В отличие от обычной подписи документа, цифровая подпись s зависит от сообщения m, а значит, злоумышленник не сможет подделать подпись, просто приложив ее к другому сообщению m’. Несмотря на то, что на открытый ключ e_A не накладывается никаких ограничений секретности, необходимо чтобы заверяющая сторона В получила подлинную копию e_A при заверении сообщения, предположительно подписанного стороной А.

Таким образом, криптография с открытым ключом решает три проблемы симметричной криптографии, а точнее проблемы распределения ключей, работы с ключами и проблему безотказности. Однако следует отметить, что реализация систем с открытым ключом несколько сложнее реализации систем симметричной криптографии. Также, операции с открытыми ключами занимают больше времени, чем операции в симметричном шифровании.

Шифр Эль-Гамаля на основе эллиптических кривых

Генерация ключа. Пусть P - точка эллиптической кривой E над полем G(p), имеющая порядок n. Тогда циклическая подгруппа E порожденная точкой P будет состоять из точек {O, P,2P,3P, . . .,(n−1)P}. Характеристика поля p, уравнение эллиптической кривой E, точка P и ее порядок n являются параметрами кривой. Секретным ключом является число d, которое выбирается случайно из интервала [1, n-1], а открытым ключом является точка Q = dP. Задача вычисления d по известным параметрам кривой и точке Q называется проблемой дискретного логарифма в группе точек эллиптической кривой (ECDLP). Ниже предоставлен алгоритм генерации ключевой пары ECC.

Вход: Параметры кривой (p, E, P, n).

Выход: Открытый ключ Q и секретный ключ d.

Алгоритм: 1. Выбрать d ∈ R [1,n−1].

. Вычислить Q = dP.

Вернуть: (Q,d)

Шифрование.

Открытый текст m представляется в виде точки M, а затем шифруется путем сложения с точкой kQ. Отправитель передает точку C1 = kP и C2 = M + kQ получателю, который использует свой секретный ключ d для вычисления dC1 = d(kP) = kQ и затем восстанавливает M = C2 - kq. Злоумышленник, желающий восстановить M, должен вычислить kQ. Проблема вычисления kQ при знании параметров кривой, Q и C1 = kP, является аналогом проблемы Диффи-Хеллмана для эллиптических кривых. Ниже предоставлен алгоритм шифрования.

Вход: Параметры кривой (p, E, P,n), открытый ключ Q, текст m.

Вывод: Криптограмма (C1,C2).

Алгоритм: 1. Представить сообщение m в виде точки M кривой E(Fp).

. Выбрать k ∈ R [1,n−1].

. Вычислить C1 = kP.

. Вычислить C2 = M +kQ.

Вернуть: (C1,C2).

А алгоритм дешифрования выглядит следующим образом:

Вход: Параметры кривой (p, E, P,n), секретный ключ d, криптограмма (C1,C2).

Выход: Исходный текст m.

Алгоритм: 1. Вычислить M = C2 − dC1, и вычислить m из M.

Вернуть: (m).

Данные, которые размещаются в некоторой точке эллиптической кривой, должны состоять из несколько меньшего числа бит, чем элемент конечного поля, над которым строится кривая. Несколько бит должны оставаться неопределенными, чтобы обеспечить возможность попадания на кривую.

Алгоритм цифровой подписи на основе эллиптических кривых

Схема цифровой подписи ECDSA состоит из четырех алгоритмов:

. Алгоритм генерации параметров эллиптической кривой.

. Алгоритм генерации пары ключей.

. Алгоритм генерации цифровой подписи, на вход которого подаются параметры эллиптической кривой, секретный ключ и сообщение для подписи.

. Алгоритм заверения подписи, на вход которого подаются параметры кривой, открытый ключ, сообщение и подпись.

Алгоритм генерации пары ключей аналогичен генерации пары ключей в шифре Эль-Гамаля. Однако для повышения криптостойкости схемы в нее следует добавить алгоритм заверения открытого ключа. Данный алгоритм проверяет, обладает ли открытый ключ некоторыми арифметическими свойствами, которые может использовать злоумышленник. Успешное выполнение этого алгоритма доказывает, что на его вход подан действительно публичный ключ данной схемы шифрования.

Заверение открытого ключа особенно важно в алгоритмах, основанных на алгоритме Диффи-Хеллмана, в которых сторона A создает общий секрет k, складывая свой секретный ключ d с открытым ключом стороны B, и затем использует k в некотором протоколе с симметричном ключом. Если B окажется злоумышленником, то он может выбрать открытый ключ таим образом, что использование этого ключ стороной А может помочь ему узнать некоторую информацию о секретном ключу A.

Вход: Параметры кривой D, открытый ключ Q.

Выход: Принятие или отвержение ключа Q.

Алгоритм: 1. Установить, что Q 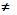 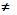O.

. Убедиться, что x₀ и y₀ являются элементами поля GF(q) (то есть являются целыми числами из интервала [0,q −1] если кривая задана над полем большой характеристики или последовательностями битов длины m, если кривая задана над расширением полем характеристики два GF(q=2^m)).

. Убедиться, что подстановка координат Q в уравнение эллиптической кривой обращает его в верное равенство.

. Убедиться, что nQ  O.

. Если хотя бы одна из проверок прошла неудачно, то вернуть (“Invalid”); иначе вернуть (“Valid”).

Алгоритм цифровой подписи на эллиптических кривых является аналогом алгоритма цифровой подписи DSA. Он является самым стандартизированным алгоритмом, использующим эллиптические кривые, и занесен в такие стандарты, как ANSI X9.62, FIPS 186-2, IEEE 1363-2000 и ISO/IEC 15946-2. В последующем описании алгоритма через H обозначается криптографическая хэш-функция, выходное значение которой не превышает числа n (если это условие не выполняется, то значения хэш-функции могут быть усечены).

Алгоритм генерации цифровой подписи:

Вход: Параметры эллиптической кривой D = (a, b, p), секретный ключ d, сообщение m, порождающая точка G и ее порядок q.

Выход: Подпись (r, s).

Алгоритм: 1. Выбрать k ∈ R [1,q−1].

. Вычислить kG = (x1, y1).

. Вычислить r = x1 mod q. Если r = 0 вернуться к шагу 1.

. Вычислить h = H(m).

. Вычислить s = k−1(h+d*r) mod q. Если s = 0 вернуться к шагу 1.

Вернуть: (r, s).

Алгоритм заверения цифровой подписи:

Вход: Параметры кривой D = (a, b, p), открытый ключ Q, сообщение m, подпись (r, s), порождающая точка G и ее порядок q.

Выход: Заверение или отвержение подписи.

Алгоритм: 1. Вычислить h = H(m).

. Вычислить w = s⁻¹ mod q.

. Вычислить u1 = hw mod q и u2 = rw mod q.

. Вычислить Pver = (x1, y1) = u1*G +u2*Q.

5. Если Pver =О то вернуть (“Reject the signature”);

6. Вычислить v= x1 mod q.

7. Если v = r то вернуть (“Accept the signature”);

Иначе вернуть (“Reject the signature”).

Можно легко показать, что данный алгоритм действительно успешно заверяет цифровую подпись. Если подпись (r, s) сообщения m была действительно сгенерирована с использованием секретного ключа, то s ≡ k⁻¹(h+dr) (mod q). Раскрывая скобки получим:

k ≡ s⁻¹(h + dr) ≡ s⁻¹h + s⁻¹rd ≡ wh + wrd ≡ u1 + u2d (mod q).

Тогда Pver = u1*G +u2*Q = (u1 +u2d)*G = kG и значит v = r, что и требуется для заверения подписи.

Преимущества использования схем эллиптической криптографии

При сравнении асимметричных схем шифрования наиболее существенными являются следующие критерии:

. Функциональность. Предоставляет ли данная схема шифрования все необходимые возможности?

. Безопасность. Какие гарантии того, что данная схема шифрования является безопасной?

. Производительность. Работает ли данная схема шифрования за допустимое время?

Все три основных схемы шифрования RSA, DL и EC предоставляют базовый набор функций криптографии с открытым ключом - шифрование, ЭЦП и использование общего ключа. Безопасность данных алгоритмов в основном определяется трудностью математической проблемы, лежащей в их основе. Для алгоритма RSA это проблема факторизации целых чисел, для DL - проблема дискретного логарифмирования, а для EC - проблема дискретного логарифмирования для эллиптических кривых. Сложность этих задач непосредственно сказывается на производительности, так как она определяет необходимый размер параметров шифрования и ключа, что в свою очередь сказывается на производительности всего алгоритма в целом.

Алгоритмы решения задачи факторизации целых чисел. Частным случаем проблемы факторизации целых чисел является задача разложения целого числа n на два простых числа размера l/2 бит. Размер входных данных - O(l) бит. Быстрейший известный алгоритм факторизации n - Number Field Sieve (NFS) имеет субэкспотенциальное ожидаемое время работы.

L_n [1/3, 1.923], где L_n[a ,c] = O()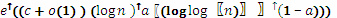

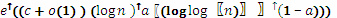Алгоритмы решения задачи дискретного логарифмирования. В задаче дискретного логарифмирования параметрами являются числа p и q, где p - простое число размером l бит и q - простой делитель числа p-1 размера t. Размер входных данных равен O(l) бит. Быстрейшими алгоритмами решения такой задачи являются Number Field Sieve (NFS) с ожидаемым временем работы L_n [1/3, 1.923] и Pollard’s rho algorithm с ожидаемым временем работы

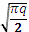
Выбор наиболее эффективного алгоритма зависит от размера входных данных.

Алгоритмы для решения задачи дискретного логарифмирования эллиптических кривых. Целью задачи является целое число d ∈ [1,n−1], такое, что Q = dP, где n - простое число размером t бит, P - точка порядка n эллиптической кривой над полем GF(p), и Q принадлежит циклической подгруппе, порожденной точкой P. Если положить n ≈ p, как обычно и бывает на практике, то размер входных данных составляет O(t) бит. Быстрейший алгоритм решения данной проблемы - Pollard’s rho algorithm, который имеет ожидаемое время работы

Как видно, сложность математической проблемы для всех трех алгоритмов сравнима. Самым важным преимуществом ECDSA является возможность его работы на значительно меньших полях GF(p). Предполагается, что битовый размер открытого ключа, который будет необходим для ECDSA, равен двойному размеру секретного ключа в битах. Ниже приведена таблица сравнения размера параметров ECDSA, RSA и DL для стандартных ключей длины 80 (SKPJACK), 112 (Triple-DES), 128 (AES-small), 192 (AES-medium), 256 (AES-large).

Таблица демонстрирует что в алгоритмах ECC могут быть использованы параметры намного меньше размера, чем в RSA и DL при достижении того же уровня безопасности. При этом разница в размере параметров растет с увеличением уровня безопасности. Соответственно, операции в алгоритмах ECC протекают намного быстрее, чем в RSA и DL.

Заключение

В данной работе изложены базовые понятия теории эллиптических кривых, необходимые для реализации криптографических протоколов. Рассмотрены основные алгоритмы арифметики точек эллиптической кривой, а также способы генерации кривых, пригодных для использования в криптографических алгоритмах. Даны алгоритмы шифрования Эль-Гамаля и ЭЦП с использование эллиптических кривых, а в приложение вынесен пример реализации схемы цифровой подписи ECDSA на языке Java с подробными комментариями.

Как следует из последнего раздела данной работы, основным преимуществом эллиптической криптографии является малый размер ключа относительно других схем асимметричного шифрования. Это свойство особенно важно при реализации криптографических протоколов в условиях ограниченности ресурсов памяти и производительности, например при программировании смарт-карт. Также ясно, что с улучшением производительности компьютеров шифры постепенно будут становиться все более уязвимыми при малых длинах ключа. А с увеличение длины ключа преимущества схем на эллиптических кривых над другими схемами шифрования возрастает многократно. За счет меньшей длины ключа возрастает и эффективность вычислительных процессов. Также следует отметить, что помимо общих алгоритмов арифметики эллиптических кривых, существует много специфических алгоритмов, разработанных для кривых специального вида (например, кривых Коблица), которые позволяют добиться еще большего преимущества в эффективности.

Список использованных источников

1. Элементарное введение в эллиптическую криптографию: Алгебраические и алгоритмические основы. А. А. Болотов [и др.]. - М.: КомКнига, 2006. - 328 с.

. Элементарное введение в эллиптическую криптографию: Протоколы криптографии на эллиптических кривых. А. А. Болотов [и др.]. - М.: КомКнига, 2006. - 280 с.

. Hankerson D. Guide to Elliptic Curve Cryptography. Darrel Hankerson, Alfred J. Menezes, Scott Vanstone. - New York:Springer, 2004. - 332 с.

. Anoop Deoras K. Implementation of elliptic curve cryptography. Anoop K. Deoras. - Pune: Electronics and Telecommunication, Government College of Engineering, 2008 - 77 с.

. Peters С. Counting points on elliptic curves over Fq / Christiane Peters. - New York:DIAMANT, 2008 - 30 с.

. Turki F. Al-Somani. Performance Evaluation of Elliptic Curve Projective Coordinates with Parallel GF(p) Field Operations and Side-Channel Atomicity / Turki F. Al-Somani // JOURNAL OF COMPUTERS, VOL. 5 - Saudi Arabia., 2010 - 99-109 c.

. Amoop M.S. Elliptic Curve Crypthography - An Implementation Tutorial. Anoop M.S. - Thiruvananthapuram.: Tata Elxsi Ltd, 2011. - 11 c.

. Washington, Lawrence C. Elliptic Curves: Number Theory and Cryptography / Lawrence C. Washington. - 2-е изд. - Maryland: University of Maryland, 2008. - 524 c.