Исследование математической модели маятника

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ВОСТОЧНО-УКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

имени ВЛАДИМИРА ДАЛЯ

КАФЕДРА СИСТЕМНОЙ ИНЖЕНЕРИИ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине «Математические методы в РТС»

на тему: «Исследование математической модели маятника»

Ст. гр. КТ-291

Руководители

доц. Василенко И.А.

асс. Пономаренко С.С.

Андросова С.И.

Луганск 2012

Реферат

Курсовая работа содержит пояснительную записку на 40 листах формата А4, которая включает 6 иллюстраций, 8 литературных источников.

Ключевые слова:

Дифференциальные уравнения, интегрирование, метод Рунге-Кутта, метод Эйлера, задача Коши, аппроксимация, функция, система, численные методы решения, моделирование, математическая модель.

Цель выполнения курсовой работы по дисциплине «Математические методы в РТС» - систематизация, закрепление и расширение теоретических знаний и практических навыков.

Основными задачами курсовой работы стали численные методы интегрирования и решения дифференциальных уравнений различных порядков, задачи компьютеризации и автоматизации в сфере промышленного производства, в проектно-конструкторских и научно-исследовательских разработках.

Объектом исследования данной курсовой работы является математический маятник.

Содержание

Введение

. Постановка задачи

. Обыкновенное дифференциальное уравнение высших порядков

.1 Линейные дифференциальные уравнения n-го порядка

. Численные методы решения дифференциальных уравнений

.1 Выбор метода для решения задачи

.2 Решение системы дифференциальных уравнений

.3 Метод Рунге-Кутта 4-го порядка для решения систем дифференциальных уравнений

. Программная реализация метода Рунге-Кутта 4-го порядка

.1 Блок-схема программы

.2 Описание интерфейса программы

.3 Исходный код программы

. Анализ результатов

Заключение

Литература

Введение

Применение новых технологий проектирования, основанных на использовании методов математического моделировании и вычислительной техники, позволяет обеспечить высокое качество и быстрые сроки выполнения проектно-конструкторских работ.

Моделирование представляет собой процесс замещения объекта исследования некоторой его моделью и проведение исследований на модели с целью получения необходимой информации об объекте.

Применение математического моделирования при проектировании в большинстве случаев позволяет отказаться от физического моделирования, значительно сократить объемы испытаний и доводочных работ, обеспечить создание технических объектов с высокими показателями эффективности и качества. Одним из основных компонентов системы проектирования в этом случае становится математическая модель.

Модель - это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта. Удобство проведения исследований может определяться различными факторами: легкостью и доступностью получения информации, сокращением сроков и уменьшением материальных затрат на исследование и др.

Различают моделирование предметное и абстрактное. При предметном моделировании строят физическую модель, которая соответствующим образом отображает основные физические свойства и характеристики моделируемого объекта. При этом модель может иметь иную физическую природу в сравнении с моделируемым объектом (например, электронная модель электродвигателя). Если модель и объект одной и той же физической природы, то моделирование называют физическим.

Физическое моделирование широко применялось до недавнего времени при создании сложных технических объектов. Однако данный вид моделирования сопряжен с большими временными и материальными затратами.

Абстрактное моделирование связано с построением абстрактной модели. Такая модель представляет собой математические соотношения, графы, схемы, диаграммы и т.п. Наиболее мощным и универсальным методом абстрактного моделирования является математическое моделирование. Оно широко используется как в научных исследованиях, так и при проектировании.

Математическое моделирование позволяет посредством математических символов и зависимостей составить описание функционирования технического объекта в окружающей внешней среде, определить выходные параметры и характеристики, получить оценку показателей эффективности и качества, осуществить поиск оптимальной структуры и параметров объекта. Применение математического моделирования при проектировании в большинстве случаев позволяет отказаться от физического моделирования, значительно сократить объемы испытаний и доводочных работ, обеспечить создание технических объектов с высокими показателями эффективности и качества. Одним из основных компонентов системы проектирования в этом случае становится математическая модель.

Математическая модель - это совокупность математических объектов и отношений между ними, адекватно отображающая физические свойства создаваемого технического объекта. В качестве математических объектов выступают числа, переменные, множества, векторы, матрицы и т.п. Процесс формирования математической модели и использования ее для анализа и синтеза называется математическим моделированием. В конструкторской практике под математическим моделированием обычно понимается процесс построения математической модели, а проведение исследований на модели в процессе проектирования называют вычислительным экспериментом.

Для осуществления вычислительного эксперимента на ЭВМ необходимо разработать алгоритм реализации математической модели.

Моделирование широко используется при создании машин, технических комплексов и других объектов. Как средство познания и преобразования материального мира моделирование применяется в экспериментальных и теоретических научных исследованиях.

Численные методы дают приближенное решение задачи. Это значит, что вместо точного решения и (функции или функционала) некоторой задачи мы находим решение у другой задачи, близкое в некотором смысле (например, по норме) к искомому. Основная идея всех методов - дискретизация или аппроксимация (замена, приближение) исходной задачи другой задачей, более удобной для решения на ЭВМ, причем решение аппроксимирующей задачи зависит от некоторых параметров, управляя которыми, можно определить решение с требуемой точностью.

Численные методы предоставляют широкие возможности для проведения трудоемких математических расчетов (построении математической модели), моделирования реально протекающих физических процессов и их анализа.

Численные методы получили широкое распространение в решении дифференциальных уравнений.

Дифференциа́льное уравне́ние - уравнение <#"550598.files/image001.gif">

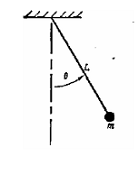
Если угол отклонения θ мал, то дифференциальное уравнение можно линеаризовать, приняв sin θ=θ. Сравнить полученные результаты с результатами для линейного случая. Построить графики.

Для решения поставленной задачи необходимо осуществить ряд действий:

1.  Проанализировать дифференциальные уравнения.

2.      Привести дифференциальные уравнения к нормальной форме.

.        Выбрать наиболее подходящий метод для решения дифференциальных уравнений.

.        Разработать подпрограмму, реализующую физическое и математическое поведение тела.

.        Сравнить полученные результаты.

2. Обыкновенное дифференциальное уравнение высших порядков

Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида:

F(x, y, y', y'',..., y⁽ⁿ⁾) = 0,

где F - известная функция (n+2) переменных,, x - независимая переменная, y - неизвестная функция, n - порядок уравнения.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной - уравнения, записанные в нормальной форме:

y⁽ⁿ⁾) = f(x, y, y', y'',..., y^(n-1)).

Функция y(x) называется решением дифференциального уравнения n-го порядка, если она n раз непрерывно дифференцируема на промежутке (a, b) и удовлетворяет уравнению для всех x из (a, b).

у = а(х, С₁,...,С_n),

содержащая n произвольных постоянных и обращающая уравнение в тождество.

Соотношение Ф(х, у, С₁,...,С_n) = 0 определяющее общее решение как неявную функцию независимой переменной, называется общим интегралом уравнения.

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

Дифференциальное уравнение n-го порядка имеет, вообще говоря, бесконечное множество решений. Чтобы выделить единственное решение уравнения, т. е. решить задачу Коши, достаточно определить начальные условия:

y(x₀) = y₀ ; y'(x₀) = y_0,1 ; y''(x₀) = y_0,2 ;...; y^(n-1)(x₀) = y_0,n-1.

При определенных ограничениях на правую часть уравнения эта задача имеет единственное решение.

.1 Линейные дифференциальные уравнения n-го порядка

Линейным дифференциальным уравнением n -го порядка называется уравнение вида

y⁽ⁿ⁾ + a₁(x) y^(n-1) +... + a_n-1 (x) y' + a_n(x) y = f(x),

где y = y(x) - неизвестная функция, a₁(x), a₂(x),..., a_n-1(x), a_n(x), f(x) - известные непрерывные функции.

Выражение в левой части уравнения называется линейным дифференциальным оператором n -го порядка:

L(y) = y⁽ⁿ⁾ + a₁(x) y^(n-1) +... + a_n-1 (x) y' + a_n(x) y.

Уравнения (2.12) и (2.13) называются соответственно однородным и неоднородным линейным дифференциальными уравнениями n - го порядка.

y⁽ⁿ⁾ + a₁(x) y^(n-1) +... + a_n-1 (x) y' + a_n(x) y = 0,⁽ⁿ⁾ + a₁(x) y^(n-1) +... + a_n-1 (x) y' + a_n(x) y = f(x),

где f(x) ≠ 0

Часто однородные и неоднородные линейные дифференциальные уравнения записывают в виде: L(y) = 0 и L(y) = f(x) соответственно.

Если y₁, y₂,... y_k - частные решения однородного линейного уравнения L(y)=0, то их линейная комбинация y = c₁ y₁ + c₂ y₂ +... + c_k y_k при произвольных постоянных c₁, c₂,..., c_k так же является решением того же уравнения.

Система функций

₁ = y₁(x) + y₂ (x) +... + y_n(x)

называется линейно независимой, если их линейная комбинация c₁ y₁ + c₂ y₂ +... + c_n y_n ни при каких значениях c₁, c₂,..., c_n, кроме c₁ = c₂ =... = c_k = 0, не обращается тождественно в нуль.

Если функции y₁, y₂,..., y_k - линейно независимые частные решения однородного линейного уравнения, то их называют фундаментальной системой решений.

Общее решение однородного уравнения имеет вид y = c₁ y₁ +... + c_n y_n, где y₁,..., y_n - фундаментальная система решений, c_j - произвольные постоянные. Последние можно определить так, чтобы частное решение удовлетворяло начальным условиям у = у₀,..., у^{(n - 1)} = у₀^{(n - 1)} при х = х₀.

Если известен частный интеграл y₁(x) однородного уравнения, то подстановкой z = y/y₁, а затем z′ = u получим линейное уравнение порядка n-1.

Общее решение неоднородного уравнения есть сумма какого-нибудь частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения.

Если известно общее решение c₁ y₁ +... + c_n y_n соответствующего однородного уравнения, то решение неоднородного уравнения можно найти методом вариации произвольных постоянных.

Решение имеет вид:

у = с₁(х)у₁ + с₂(х)у₂ +... + с_n(х)у_n,

где неизвестные функции с_j(х) находятся из системы уравнений относительно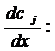

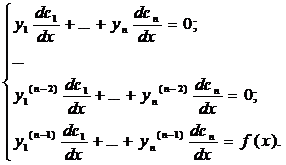
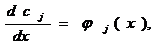
Решив систему и получив, находим

с_j = ∫ц_ј(х)dx + Аj,

где Аj - постоянные интегрирования.

3. Численные методы решения дифференциальных уравнений

При решении научных и инженерно-технических задач часто бывает необходимо математически описать какую-либо динамическую систему. Лучше всего это делать в виде дифференциальных уравнений (ДУ) или системы дифференциальных уравнений. Наиболее часто они такая задача возникает при решении проблем, связанных с моделированием кинетики химических реакций и различных явлений переноса (тепла, массы, импульса) - теплообмена, перемешивания, сушки, адсорбции, при описании движения макро- и микрочастиц.

3.1 Выбор метода для решения задачи

Наибольшее распространение из всех численных методов решения дифференциальных уравнений получили методы Рунге-Кутта различных порядков. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методами Рунге-Кутта являются модифицированные и исправленные методы Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями. Методы седьмого порядка должны иметь по меньшей мере девять стадий, в схему восьмого порядка входит 11 стадий. Хотя схемы девятого порядка не имеют большой практической значимости, неизвестно, сколько стадий необходимо для достижения этого порядка точности. Аналогичная задача существует для схем десятого и более высоких порядков

В методе Рунге-Кутта 4-го порядка на каждом шаге интегрирования дифференциального уравнения искомая функция 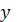 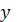аппроксимируется рядом Тейлора, содержащим член ряда с :

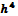
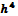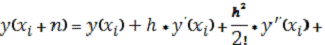
В результате ошибка на каждом шаге приблизительно равна .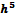

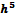.2 Решение системы дифференциальных уравнений

Для решения дифференциальных уравнений высоких порядков вида

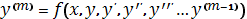
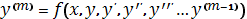
необходимо представить данное уравнение в виде системы при помощи замен:

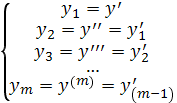
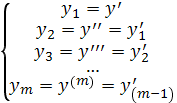
В результате дифференциальное уравнение m-го порядка сводится к системе, состоящей из m дифференциальных уравнений первого порядка:

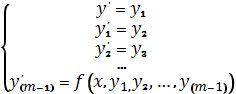
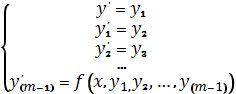
Численным решением системы, а значит и дифференциального уравнения m-го порядка, является m табличных функций

,

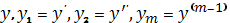
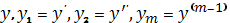т.е. функция 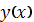 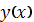и все ее производные, включая производную (m-1)-го порядка.

При этом каждая из табличных функций определяется на промежутке [a, b] с шагом h и включает n узловых точек. Таким образом, численным решением уравнения или системы является матрица порядка (n x m) (табл. 3.1).

Таблица 3.1

Здесь:

m - порядок дифференциального уравнения, равен количеству столбцов матрицы;

n = (b-a)/h - количество шагов интегрирования, равно количеству строк матрицы;

каждый j-й столбец матрицы - это массив решений одной j-й табличной функции по всем n шагам интегрирования;

каждая i-ая строка матрицы - это массив решений m табличных функций на одном i-ом шаге интегрирования.

На графике решением дифференциального уравнения m-го порядка является совокупность (n x m) узловых точек. При этом каждому шагу интегрирования, т.е. каждому значение 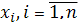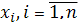, соответствуют m узловых точек с координатами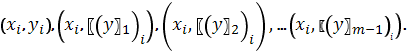

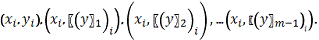
Рассмотрим заданное дифференциальное уравнение в нормальной форме:

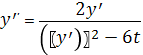
С учетом системы имеем:

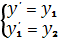
Следовательно, заданное дифференциальное уравнение сводится к системе:

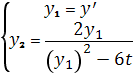
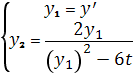
3.3 Метод Рунге-Кутта 4-го порядка для решения систем дифференциальных уравнений

Как говорилось ранее, в методе Рунге-Кутта 4-го порядка на каждом шаге интегрирования дифференциального уравнения искомая функция 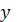 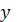аппроксимируется рядом Тейлора, содержащим член ряда с 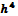 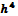(2.1).

В результате ошибка на каждом шаге приблизительно равна .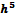

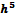Для решения системы дифференциальных уравнений вида (2.4) методом Рунге-Кутта 4-го порядка применяются формулы Рунге-Кутта:

Где Y - массив решений длиной m,

Y1 - рабочий массив длиной m,

T - рабочая матрица порядка (4 x m).

4. Программная реализация метода Рунге-Кутта 4-го порядка

.1 Блок-схема программы

Программная часть курсового проекта реализована на языке высокого уровня ObjectPascal в среде Delphi и представляет собой оконное приложение Windows.

Был проанализирован метод Рунге-Кутта 4-го порядка. Были составлены схемы алгоритмов, представленных на рис. 3.1 и рис. 3.2 соответственно

Рис. 4.1

Обозначения в схеме алгоритма:

m - порядок системы,

h - шаг интегрирования,

n - количество шагов интегрирования,

t - начальное и далее - текущее значение t,

Y - массив длинной m, куда заносим

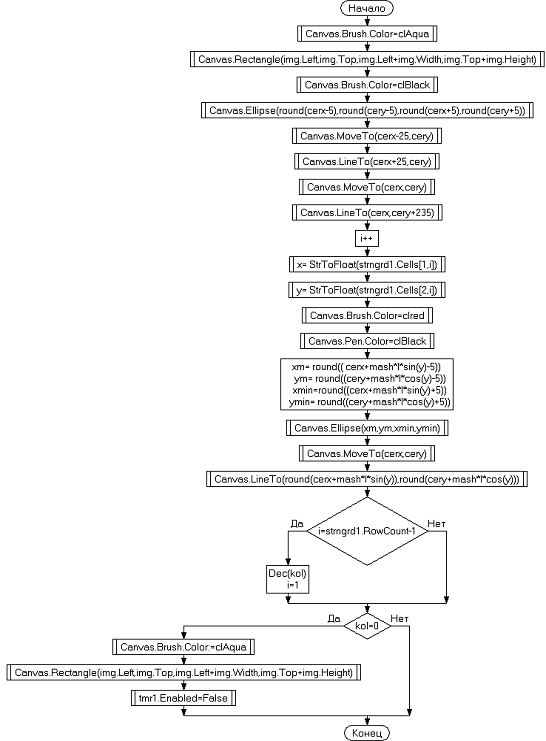
Рис. 4.2 Схема моделирования движения системы

4.2 Описание интерфейса программы

Пользоваться программой очень легко. Программ имеет интуитивно понятный интерфейс пользователя. Главное окно программы представлено на Рис. 4.3. Назначение элементов управления описаны далее.

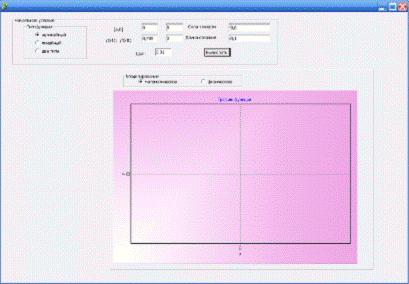
Рис. 4.3 Главное окно программы расчета курсового задания

Окно программы содержит следующие управляющие элементы:

.        Поля ввода данных:

·        «Интервал» - поле, в которое мы вносим начальную и конечную точки отрезка рассматриваемой функции.

·        «y(x1), y’(x1)» - поле для ввода начального значения в точке х₀ и значение производной функции в точке х₀.

·        «Шаг» - поле, в котором мы указываем с каким шагом будем рассчитывать функцию.

·        «Сила тяжести» - поле для ввода коэффициентов силы тяжести.

·        «Длина стержня» - для ввода заданной длины стержня.

.        Поля вывода данных:

·        График. На него выводится функция, построенная на основе полученной таблицы.

.        Область модуляции поведения системы.

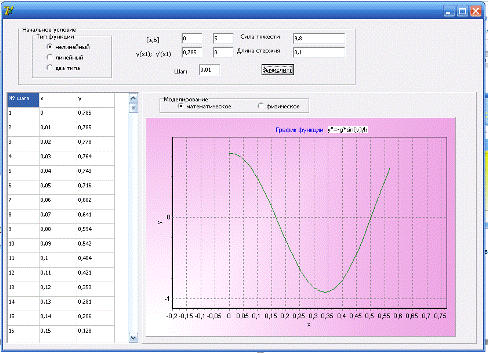
а)

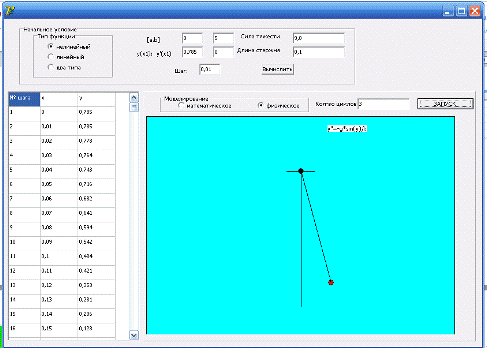
б)

Рис 4.4 а), б) Вид диалогового окна программы во время расчета

4.3 Исходный код программы

Unit1;

uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, ExtCtrls, TeeProcs, TeEngine, Chart, Grids, StdCtrls, Series,, ComCtrls;mash=2000 ;= class(TForm): TGroupBox;: TButton;: TRadioGroup;: TRadioButton;: TRadioButton;: TRadioButton;: TEdit;: TEdit;: TEdit;: TEdit;: TEdit;: TLabel;: TLabel;: TStringGrid;: TEdit;: TEdit;: TPanel;: TChart;: TLineSeries;: TLineSeries;: TBubbleSeries;: TRadioGroup;: TRadioButton;: TRadioButton;: TButton;: TLabel;: TEdit;: TImage;: TTimer;: TLabel;

lbl5: TLabel;: TLabel;: TLabel;

procedure poisk(x1,b1,z,z1,h1:real;tip:integer);btn1Click(Sender: TObject);cht1DblClick(Sender: TObject);dra(tip:integer);dra1(tip:integer);rb4Click(Sender: TObject);rb5Click(Sender: TObject);btn2Click(Sender: TObject);tmr1Timer(Sender: TObject);FormCreate(Sender: TObject);

{ Private declarations }

{ Public declarations };: TForm1;,b,y,y1,h,g,l:real; i,j,rb,kol,top,left,cerx,cery,inputdata:Integer;

{$R *.dfm}TForm1.poisk(x1,b1,z,z1,h1:real;tip:integer);f1,f2,t,fl1,fl2,ZL,ZL1:real; n,i1,p:integer;(tip=0) or (tip=1) then strngrd1.ColCount:=3strngrd1.ColCount:=4;:=z;tip=2 then:=z;:=z1;;:=round ((b1-x1)/h1);i1:=1 to n do:=z1;(tip=0)or (tip=2) then:=-(g/l)*sin(z) ;.Caption:='y"=-g*sin(y)/l;';.Caption:='y"=-g*y/l;';:=-(g/l)*(z);;tip=2 then:=zl1;:=-(g/l)*(zl);.Cells[3,i1]:=floatToStr(Round(1000*zl)/1000);.Cells[0,i1]:=IntToStr(i1);.Cells[1,i1]:=floatToStr(x1);.Cells[2,i1]:=floatToStr(Round(1000*z)/1000);((zl+h1*fl1)>t) or((z+h1*f1)>t) then;:=zl+h1*fl1;:=zl1+h1*fl2;.Cells[3,0]:='yl';.Caption:='y"=-g*y/l;';;.Cells[0,i1]:=IntToStr(i1);.Cells[1,i1]:=floatToStr(x1);.Cells[2,i1]:=floatToStr(Round(1000*z)/1000);(z+h1*f1)>t then Break;:=z+h1*f1;:=z1+h1*f2;:=x1+h1;;(strngrd1.Cells[1,i1-1]<>'') then.RowCount:=i1-1(strngrd1.Cells[1,i1+1]<>'') then.RowCount:=i1.RowCount:=i1+1;.Cells[0,0]:='№шага';.Cells[1,0]:='x';.Cells[2,0]:='y';;TForm1.btn1Click(Sender: TObject);(edt1.Text='') or (edt2.Text='') or (edt3.Text='')(edt4.Text='') or (edt5.Text='') or (edt6.Text='') or (edt7.Text='') then('Введите данные!');;;.Visible:=True;.Visible:=True;:=1;.Enabled:=False;i:=1 to strngrd1.ColCount-1 doj:=1 to strngrd1.RowCount-1 do strngrd1.Cells[i,j]:='';.RowCount:=1;.ColCount:=3 ;:=StrToFloat(edt1.Text);:=StrToFloat(edt2.Text);:=StrToFloat(edt3.Text);:=StrToFloat(edt4.Text);:=StrToFloat(edt5.Text);:=StrToFloat(edt6.Text);:=StrToFloat(edt7.Text);(rb1.Checked=true) then rb:=0(rb2.Checked=true) then rb:=1rb:=2;(x,b,y,y1,h,rb);.Checked:=True;(rb);:=1;;TForm1.cht1DblClick(Sender: TObject);Cht1.UndoZoom; end;TForm1.rb4Click(Sender: TObject);inputdata=0 then('Не введены данные-ошибка.');.Checked:=False;.Checked:=true;;;.Enabled:=False;(rb);.Visible:=false;.Visible:=false;.Visible:=false;.Visible:=false;;TForm1.dra(tip:integer);xm,xmin,ym,ymin,x,y:Real;.Clear; lnsrsSeries2.Clear; blsrsSeries1.Clear;:=StrToFloat(strngrd1.Cells[1,1]);:=StrToFloat(strngrd1.Cells[1,1]);:=StrToFloat(strngrd1.Cells[2,1]);:=StrToFloat(strngrd1.Cells[2,1]) ;i:=1 to strngrd1.RowCount-1 do:= StrToFloat(strngrd1.Cells[1,i]) ;:= StrToFloat(strngrd1.Cells[2,i]);x>xm then xm:=x;x<xmin then xmin:=x;y>ym then ym:=y;y<ymin then ymin:=y;.addxy (x,y,'',clGreen);tip=2 then:= StrToFloat(strngrd1.Cells[3,i]);y>ym then ym:=y;y<ymin then ymin:=y;.addxy (StrToFloat(strngrd1.Cells[1,i]),StrToFloat(strngrd1.Cells[3,i]),'',clRed);;;.AddBubble(xmin-0.2,ymin-0.2,0.001,'',clGray) ;.AddBubble(xm+0.2,ym+0.2,0.001,'',clGray);;TForm1.dra1(tip:integer);x,y:Real; xm,xmin,ym,ymin,zad:Integer;.Canvas.Brush.Color:=clWhite;.Canvas.Rectangle(img1.Left,img1.Top,img1.Left+img1.Width,img1.Top+img1.Height);.Canvas.Brush.Color:=clBlack;.Canvas.Ellipse(round(cerx-5),round(cery-5),round(cerx+5),round(cery+5));.Canvas.MoveTo(cerx-25,cery);.Canvas.LineTo(cerx+25,cery);.Canvas.MoveTo(cerx,cery);.Canvas.LineTo(cerx,cery+235);(i);:= StrToFloat(strngrd1.Cells[1,i]) ;:= StrToFloat(strngrd1.Cells[2,i]);.Canvas.Brush.Color:=clred;.Canvas.Pen.Color:=clBlack;:= round((cerx+mash*l*sin(y)-5));:= round((cery+mash*l*cos(y)-5));:=round((cerx+mash*l*sin(y)+5));:= round((cery+mash*l*cos(y)+5));.Canvas.Ellipse(xm,ym,xmin,ymin);.Canvas.MoveTo(cerx,cery);.Canvas.LineTo(round(cerx+mash*l*sin(y)),round(cery+mash*l*cos(y)));i=strngrd1.RowCount-1 then(kol);:=1;;kol=0 then.Canvas.Brush.Color:=clWhite;.Canvas.Rectangle(img1.Left,img1.Top,img1.Left+img1.Width,img1.Top+img1.Height);.Enabled:=False;;;TForm1.rb5Click(Sender: TObject);.Visible:=true;.Visible:=true;.Visible:=true;.Visible:=true;:= img1.Left+(Round(img1.Width/2)) ;:= img1.top+(Round(-img1.height/4+img1.height/2)) ;.Canvas.Brush.Color:=clWhite;.Canvas.Rectangle(img1.Left,img1.Top,img1.Left+img1.Width,img1.Top+img1.Height);;TForm1.btn2Click(Sender: TObject);(edt8.Text='')or (inputdata=0) then('Введите данные!');;;:=strtoint(edt8.Text);.Canvas.Brush.Color:=clBlack;.Canvas.Ellipse(round(cerx-5),round(cery-5),round(cerx+5),round(cery+5));.Canvas.MoveTo(cerx-25,cery);.Canvas.LineTo(cerx+25,cery);.Canvas.MoveTo(cerx,cery);.Canvas.LineTo(cerx,cery+235);:=1;.Canvas.Brush.Color:=clred;.Canvas.Pen.Color:=clBlack;:= StrToFloat(strngrd1.Cells[1,i]);:= StrToFloat(strngrd1.Cells[2,i]);.Canvas.Ellipse(round(cerx+mash*l*sin(y)-5),round(cery+mash*l*cos(y)-5),round(cerx+mash*l*sin(y)+5),round(cery+mash*l*cos(y)+5));.Enabled:=True;;TForm1.tmr1Timer(Sender: TObject);(0);;TForm1.FormCreate(Sender: TObject);: TImage;: TForm;.Interval := 50;:=0;:= TForm.create(nil);SplashForm do:= bsNone;:= poScreenCenter;:= 610;:= 378;;:= TImage.Create(SplashForm);SplashImage do.Picture.LoadFromFile('splash.bmp');:= true;:= alClient;:= SplashForm;;SplashForm do;I := 1 to 1 do;(1000);;;;;

end;;.

5. Анализ результатов

дифференциальный уравнение математический маятник

Целью данной курсовой работы было подготовить программу, которая моделировала бы движение заданной системы, и выполнить расчет для полного цикла колебаний. Была написана программа и в ней реализован алгоритм метода Эйлера. Было получено решение ДУ 2-го порядка, которое моделирует поведение системы. Таблица 5.1 содержит вычисления программы.

Таблица 5.1

Просмотреть функцию для линейного случая можно на Рис. 5.1., а для нелинейного - на Рис. 5.2.

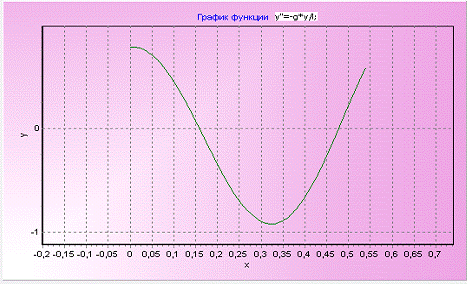
Рис. 5.1

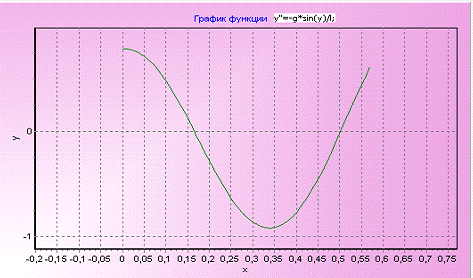
Рис. 5.2

Графики показывают, что отличия в ДУ для линейного и нелинейного случая имеет нарастающее смещение, которое можно проследить на Рис. 5.3.

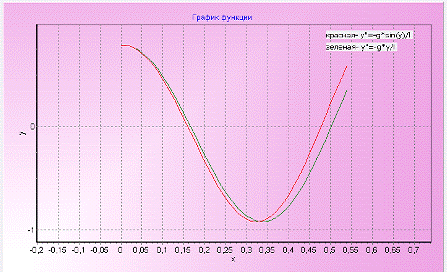
Рис. 5.3

При малых значениях угла можно заменить нелинейную функцию линейной. Расхождения результатов были незначительны, хоть и накапливались со временем.

Заключение

В данной работе была решена поставленная задача, в которой необходимо было подготовить программу, которая моделировала бы движение заданной системы, и выполнить расчет для полного цикла колебаний. В курсовой работе нужно было сравнить полученные результаты решения ДУ 2-го порядка для нелинейного и линейного случаев, а также построить графики.

Для решения поставленной задачи был осуществлен ряд действий:

1.  Проанализированы дифференциальные уравнения.

2.      Приведены к нормальной форме.

.        Выбран наиболее подходящий метод для решения дифференциальных уравнений.

.        Была разработана программа, реализующая физическое и математическое поведение тела.

.        Сравнили полученные результаты.

Основными задачами курсовой работы стали численные методы интегрирования и решения дифференциальных уравнений различных порядков, задачи компьютеризации и автоматизации в сфере промышленного производства, в проектно-конструкторских и научно-исследовательских разработках.

В данной курсовой работе были рассмотрены методы решения ДУ 2-го порядка. Показаны их преимущества и недостатки. На основе анализа для данной задачи был выбран метод Рунге-Кутта 4-го порядка.

Также была выведена формула для моделирования движения системы, которое выполняется систематически заданное количество раз.

Программа очень удобна в использовании. Интерфейс программы позволяет осуществлять все необходимые действия: строит таблицу вычисления угла поворота системы в зависимости от времени, интерпретирует полученные результаты не только в виде геометрической (графика), но и в виде физической (моделирует поведение системы) модели.

Также достоинством данной программы является то, что можно сравнить линейный и нелинейный случай отклонения угла в виде двух функций, изображенных на одном графике, что позволяет пользователю сделать вывод о допустимости линеаризации при малом угле отклонения θ.

Из полученных данных, можно сделать вывод, что отличия в ДУ для линейного и нелинейного случая имеет нарастающее смещение.

При малых значениях угла можно заменить нелинейную функцию линейной. И расхождения результатов были незначительны, хоть и накапливались со временем.

Литература

1.   Вычислительная техника в инженерных и экономических расчётах. Учебник для вузов / Петров А.В., Алексеев В.Е. и др. Под ред. А.В. Петрова. - М.: Высш. шк. 1984. - 320с.

2.      Л.Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.

.        А.Н. Тихонов, Васильева А.Б., А.Г. Свешников. Дифференциальные уравнения, 4е изд., Физматлит, 2005.

.        Волков Е.А. Численные методы. - М.: Наука, 1987. - 248с.

5.   Лапчик М.П. Вычисления. Алгоритмизация. Программирование: Пособие для учителя. - М.: Просвещение, 1988.

.     Шуп Т. Решение инженерных задач на ЭВМ. - М.: Радио и связь, 1985.

7.      Козин А.С., Лященко Н.Я. Вычислительная математика. - К.: Рад. школа, 1983. - 191с.

.        Маликов В.Т., Квотный Р.Н. Вычислительные методы и применение ЭВМ. - К.: Вища школа. 1989. - 213с.