Линейные уравнения и матрицы, их расчет
Контрольная
работа
По
дисциплине: Высшая математика
Задание
1.
Даны матрицы А и В.
Найти: А × В, В ×
А, 2Ат + В, А - 3Вт.
А = 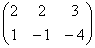 , В =
, В = 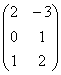
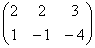 ×
×  =
= 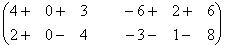 =
= 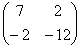 ;
;
 ×
× 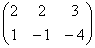 =
=  =
= 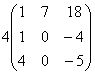 ;
;
А = 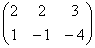 , Ат =
, Ат = 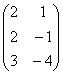 , 2Ат =
, 2Ат =
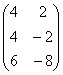
 +
+  =
= 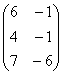 ;
;
В =  , Вт =
, Вт = 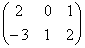 , 3Вт =
, 3Вт =
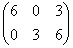
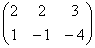 -
- 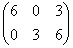 =
= 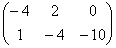
Задание
2.
Вычислить
определитель матрицы А:
а) по первой
строке;
б) по третьему
столбцу
А = 
а) 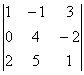 = 1×
= 1× 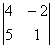 + (-1) ×
+ (-1) × 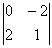 + 3 ×
+ 3 × 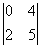 = 1(4 -
(-10)) - 1(0 - (-4)) + 3(0 - 8) = 14 - 4 - 24 = -14. D = -14.
= 1(4 -
(-10)) - 1(0 - (-4)) + 3(0 - 8) = 14 - 4 - 24 = -14. D = -14.
б) 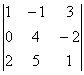 = 3 ×
= 3 ×  + (-2) ×
+ (-2) × 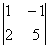 + 1 ×
+ 1 × 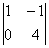 = 3(0 - 8)
- 2(5 - (-2)) + 1(4 - 0) = -24 - 14 + 4 = -34. D = -34.
= 3(0 - 8)
- 2(5 - (-2)) + 1(4 - 0) = -24 - 14 + 4 = -34. D = -34.
Задание
3.
Решить систему
линейных уравнений АХ=В:
а) Методом Гаусса;
б) по формулам Крамера; в) с помощью обратной матрицы.
А = 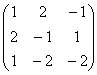 , В =
, В = 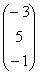
а) x1 +
2x2
- x3 =
-3
2x1
-
x2 +
x3 =
5
x1
-
2x2 -
2x3 =
-1
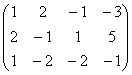 ~
~ 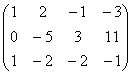 ~
~ 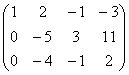 ~
~
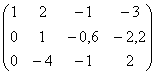 ~
~ 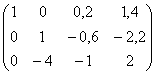 ~
~ 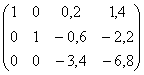 ~
~
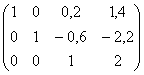 ~
~ 
x1
=
1
x2
=
-1
x3
=
2
б) x1 +
2x2
- x3 =
-3
2x1
-
x2 +
x3 =
5
x1
-
2x2 -
2x3 =
-1
D
= 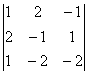 = 1× (-1) × (-2) + 2 × 1 × 1 + 2 × (-2) × (-1) - 1× (-1) × (-1) - 2 × 2 × (-2) - (-2)
× 1 × 1 = 17;
= 1× (-1) × (-2) + 2 × 1 × 1 + 2 × (-2) × (-1) - 1× (-1) × (-1) - 2 × 2 × (-2) - (-2)
× 1 × 1 = 17;
D1 = 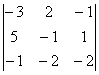 = 17; D2 =
= 17; D2 = 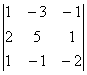 = -17; D3 =
= -17; D3 = 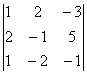 = 34.
= 34.
х1 = 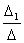 =
= 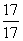 = 1; х2
=
= 1; х2
= 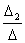 = -
= -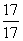 = -1; х3
=
= -1; х3
= 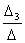 =
= 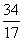 = 2.
= 2.
x1 = 1
x2 = -1
x3 = 2
в) А-1 = 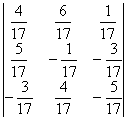 ;
;
Х = А-1 × В =  ×
×  =
= 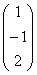 ;
;
x1 = 1
x2 = -1
x3 = 2
Задание
4.
Вычислить предел,
не используя правило Лопиталя.

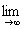
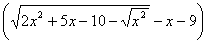 ;
;
L =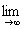
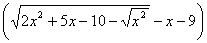 ;
;
неопределенность типа 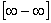 .
.
Умножим и разделим данное выражение
на сопряженное:
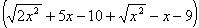 ;
;
L = 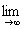
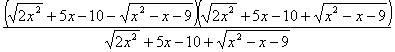 =
=
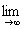
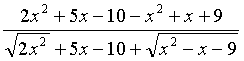 =
= 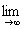
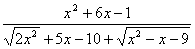 ;
;
Делим числитель и знаменатель на x:
L=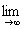
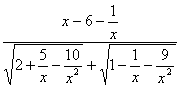 =
= 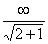 = ¥.
= ¥.
Задание
5.
Вычислить
производные функций:
а) y =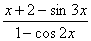 ;
;
y' = 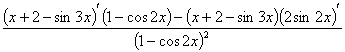 =
=
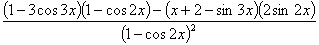 =
=
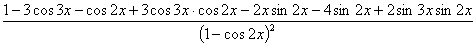 .
.
б) y = ln(1-x+e2-3x);
y' = 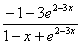 .
.
Задание
6.
Исследовать функцию
и построить ее график.
y = 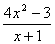 ;
;
) при x = 0, y =-3; y = 0,
при 4x2 = 3, т.е. x1,2 = ± 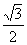
) знаменатель x + 1 = 0, при
x
= -1.
x1 = -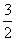 , x2
= -
, x2
= -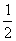 .
.
Исследуем y(x) на монотонность,
составим таблицу:
|
x
|
(-¥; -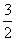 )- )-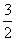 (- (-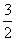 ; - ; -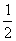 )- )-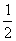 (- (-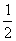 ; ¥) ; ¥)
|
|
|
|
|
|
y'
|
+
|
0
|
-
|
0
|
+
|
|
y
|
|
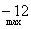 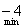
|
|
|
|
4) наклонная ya
= xb;
k = 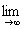
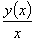 =
= 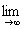
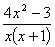 =
= 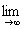
 = 4=
= 4= 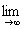 (y(x) - kx) =
(y(x) - kx) = 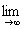
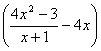 = 0, a = 4x.
= 0, a = 4x.
5) Построим
график
y" = 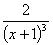 ¹ 0;
перегибов нет, знак меняется в точке x = -1
¹ 0;
перегибов нет, знак меняется в точке x = -1
выпуклость -1 вогнутость
Задание
7
матрица
уравнение функция предел
Найти частные
производные второго порядка функции многих переменных
u
= ln(x2
+ y - 2z);
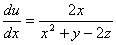 ;
; 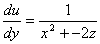 ;
; 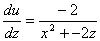 ;
;
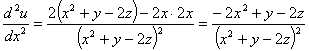
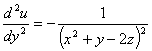
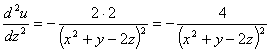
Задание
8
Вычислить
неопределенные интегралы
1) 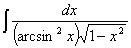 =
= 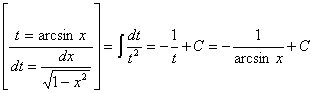 .
.
) 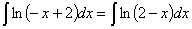 ;
;
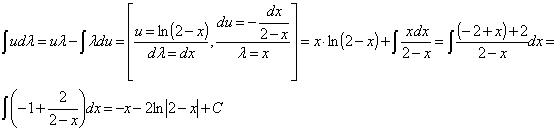
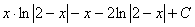 или
или 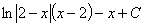
) 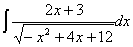 ; выделить в числителе группу
; выделить в числителе группу 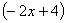
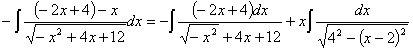 ,
,
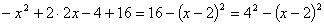 ,
,
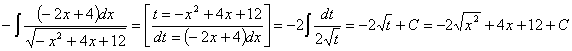
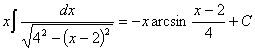 и
и 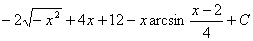
) 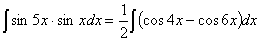 по формуле
по формуле
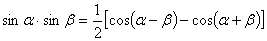 , тогда
, тогда
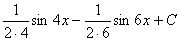 , т.е.
, т.е. 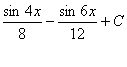
Задание
9.
Вычислить
определенные интегралы
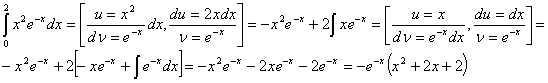
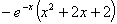
 =
= 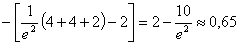
Задание
10.
Вычислить площадь
фигуры, ограниченной линиями
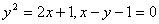 или
или 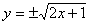 и
и 
Точки пересечения линий найдем из
решения уравнения:
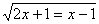
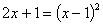
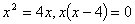 1 = 0, x2 = 4
1 = 0, x2 = 4
Построим график
 S =
S = 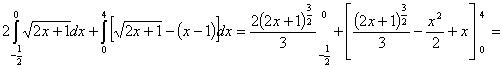
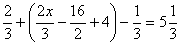 ;
;
S = 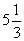 .
.