Обобщения полиномов Бернштейна в задачах устойчивости нелинейных динамических систем
ДИПЛОМНАЯ РАБОТА
на
тему:
"Обобщения
полиномов Бернштейна в задачах устойчивости нелинейных динамических
систем"
Введение
Теория динамических систем широко
востребована большим спектром наук - физикой, биологией, механикой, экономикой
и т.д. Она позволяет не только определить возможное направление развития
исследуемого объекта, но и разработать комплекс адаптивных воздействий на
систему для корректировки этого направления.
Исследованием динамических систем
занимались такие отечественные и зарубежные ученые, как Ляпунов, Понтрякин,
Четаев, Красовский, Аносов, Пуанкаре, Хайрер.
Одной из важных научных проблем
естествознания является решение задачи предсказания поведения изучаемого
объекта во времени и пространстве на основе определенных знаний о его начальном
состоянии. Эта задача сводится к нахождению некоторого закона, который
позволяет по имеющейся информации об объекте в начальный момент времени в точке
пространства определить его будущее в любой момент времени.
На практике часты случаи, когда
нельзя ограничиться рассмотрением только линейных математических моделей. Более
того, ряд других особенностей природных процессов таких, как наличие конечной
памяти, не может быть оставлен без внимания для более адекватного описания этих
процессов. К сожалению, на сегодняшний день арсенал методов исследования
динамических свойств процессов, описываемых нелинейными математическими
моделями с отклоняющимся аргументом в условиях параметрической
неопределенности, представлен в современных научных работах крайне скупо. В
этой связи особую актуальность приобретают задачи разработки новых и развитие
существующих методов исследования свойств нелинейных динамических моделей
процессов в условиях параметрической неопределенности.
Новые перспективы в исследовании
нелинейных систем открылись в связи с появлением компьютерного моделирования,
что фактически позволяет ставить вычислительный эксперимент, дающий
теоретическое решение в случае, когда аналитические методы исследования
невозможно применить.
В данной работе рассматриваются
нелинейные динамические системы, т.к. большинство практических задач механики,
термодинамики, аэродинамики и т.д. описываются именно ими. Если система
описывается алгебраическими уравнениями, то это описание состояния равновесия
(статические системы).
Устойчивость характеризует одну из
важнейших черт поведения систем и является фундаментальным понятием,
используемым в физике, биологии, технике, экономике, а также кибернетике.
Понятие устойчивости применяется для описания постоянства какой-либо черты
поведения системы, понимаемого в весьма широком смысле.
Точная и строгая формулировка
понятия устойчивости применительно к состоянию равновесия динамической системы
была дана выдающимся русским ученым A.M. Ляпуновым.
Предметом нашего анализа будут не
объекты вообще, а динамические системы в математическом понимании этого
термина.
В дипломной работе рассматривается
задача исследования устойчивости нелинейной динамической системы. Анализ носит
приближенный характер. Аппроксимации функций проводятся с использованием
обобщений полиномов Бернштейна. Основываясь на аппроксимационных многочленах
Бернштейна. Для созданной итерационной формулы сделан анализ ее скорости
сходимости и эффективности, приводится сравнение с классическими численными
методами (метод Ньютона и его модификации, метод секущих и т.д.).
Оценка устойчивости нелинейных
систем приводит к задаче решения нелинейных уравнений и систем нелинейных
уравнений. В работе предлагается вариант итерационного процесса для решения
этих задач.
Для оценки локальной устойчивости
нелинейных динамических систем в работе предлагается использовать метод функций
Ляпунова, в котором исследуется равномерное приближение функции Ляпунова,
основанное на обобщенных полиномах Бернштейна.
1. Основные понятия
теории динамических систем
1.1 Описание
динамических систем с помощью дифференциальных уравнений
Под динамической
системой понимают любой объект или процесс, для которого однозначно определено
понятие состояния как совокупности некоторых величин в данный момент времени и
задан закон, который описывает изменение (эволюцию) начального состояния с
течением времени. Этот закон позволяет по начальному состоянию прогнозировать
будущее состояние динамической системы, его называют законом эволюции. Описания
динамических систем для задания закона эволюции также разнообразны: с помощью
дифференциальных уравнений, дискретных отображений и т.д. Выбор одного из
способов описания задает конкретный вид математической модели соответствующей
динамической системы.
Математическая модель
динамической системы считается заданной, если введены параметры (координаты)
системы, определяющие однозначно ее состояние, и указан закон эволюции. В
зависимости от степени приближения одной и той же системе могут быть поставлены
в соответствие различные математические модели [5].
Исследование реальных
систем сводится к изучению математических моделей, совершенствование и развитие
которых определяются анализом экспериментальных и теоретических результатов при
их сопоставлении.
Динамические системы можно
классифицировать в зависимости от вида оператора отображения и структуры
фазового пространства. Если оператор предусматривает исключительно линейные
преобразования начального состояния, то он называется линейным. Линейный
оператор обладает свойством суперпозиции. Если оператор нелинейный, то и
соответствующая динамическая система называется нелинейной.
Различают непрерывные и
дискретные операторы и соответственно системы с непрерывным и дискретным
временем. Системы, для которых отображение с помощью оператора может быть
определено для любых (непрерывно во времени), называют также потоками по
аналогии со стационарным течением жидкости. Если оператор отображения определен
на дискретном множестве значений времени, то соответствующие динамические
системы называют каскадами или системами с дискретным временем.
Динамические системы
называются автономными, если они не подвержены действию внешних сил, переменных
во времени [1].
Рассмотрим динамические
системы, моделируемые конечным числом обыкновенных дифференциальных уравнений.
Применительно к таким системам сохранились представления и терминология,
первоначально возникшие в механике. В рассматриваемом случае для определения
динамической системы необходимо указать объект, допускающий описание состояния
заданием величин 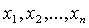 в
некоторый момент времени t = t0. Величины xi могут
принимать произвольные значения, причем двум различным наборам величин xi
отвечают два разных состояния. Закон эволюции динамической системы во времени
записывается системой обыкновенных дифференциальных уравнений.
в
некоторый момент времени t = t0. Величины xi могут
принимать произвольные значения, причем двум различным наборам величин xi
отвечают два разных состояния. Закон эволюции динамической системы во времени
записывается системой обыкновенных дифференциальных уравнений.
Если рассматривать
величины 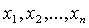 как
координаты точки x в n - мерном пространстве, то получается наглядное
геометрическое представление состояния динамической системы в виде этой точки,
которую называют изображающей, а чаще фазовой точкой, а пространство состояний
- фазовым пространством динамической системы. Изменению состояния системы во
времени отвечает движение фазовой точки вдоль некоторой линии, называемой
фазовой траекторией.
как
координаты точки x в n - мерном пространстве, то получается наглядное
геометрическое представление состояния динамической системы в виде этой точки,
которую называют изображающей, а чаще фазовой точкой, а пространство состояний
- фазовым пространством динамической системы. Изменению состояния системы во
времени отвечает движение фазовой точки вдоль некоторой линии, называемой
фазовой траекторией.
Необходимо уточнить
взаимосвязь понятий числа степеней свободы и размерности фазового пространства
динамической системы. Под числом степеней свободы понимается наименьшее число
независимых координат, необходимых для однозначного определения состояния
системы. Под координатами первоначально понимались именно пространственные
переменные, характеризующие взаимное расположение тел и объектов. В то же время
для однозначного решения соответствующих уравнений движения необходимо помимо
координат задать соответствующие начальные значения импульсов или скоростей. В
связи с этим система с m степенями свободы характеризуется фазовым
пространством в два раза большей размерности (n = 2m).
Теория динамических систем, основана
на дифференциальных уравнениях вида
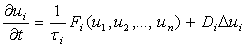 ,
, 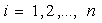 ,
(1.1)
,
(1.1)
где 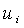 -
динамические переменные;
-
динамические переменные;
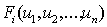 - функции (в общем
случае нелинейные), описывающие их (в смысле динамических переменных)
взаимодействие в данной точке пространства;
- функции (в общем
случае нелинейные), описывающие их (в смысле динамических переменных)
взаимодействие в данной точке пространства;
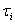 - характерные времена
изменения переменных
- характерные времена
изменения переменных 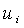 ;
;
член 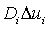 описывает
распространение динамических переменных
описывает
распространение динамических переменных 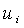 в пространстве.
в пространстве.
В частном случае, когда
все динамические переменные распределены в пространстве равномерно, мы имеем
систему обыкновенных дифференциальных уравнений:
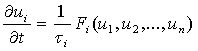 ,
, 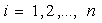 ,
(1.2)
,
(1.2)
Уравнения (1.1) или
(1.2) являются динамическими, т.е. их решения, вообще говоря, однозначно
определяются начальными и граничными условиями и, разумеется, свойствами и
параметрами самих уравнений [9].
Интуитивное
представление об устойчивости (или неустойчивости) есть у каждого. Неустойчиво,
например, состояние карандаша, поставленного на острие; неустойчиво движение
шарика по гребню. В то же время движение его по ложбине устойчиво. Более точное
представление дает анализ уравнений движения (и / или стационарных состояний).
Этот анализ основан на исследовании поведения малых отклонений от
соответствующего решения. Продемонстрируем это на примере стационарных
состояний точечной системы. Стационарными являются состояния, соответствующие
таким значениям переменных 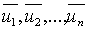 , при которых все
функции
, при которых все
функции 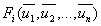 равны
нулю. При этом значения не меняются со временем, поскольку все производные
равны
нулю. При этом значения не меняются со временем, поскольку все производные 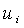 также
равны нулю. Однако малые отклонения от стационарных значений
также
равны нулю. Однако малые отклонения от стационарных значений 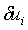 меняются
со временем, и их изменение можно описать системой линейных дифференциальных
уравнений
меняются
со временем, и их изменение можно описать системой линейных дифференциальных
уравнений
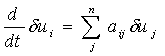 , (1.3)
, (1.3)
где 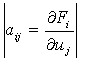 .
.
Решения имеют вид:
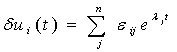 (1.4)
(1.4)
Здесь 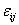 -
коэффициенты, пропорциональные начальным отклонениям
-
коэффициенты, пропорциональные начальным отклонениям 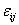 ;
они малы в меру малости последних. Величины
;
они малы в меру малости последних. Величины 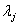 - числа, которые
являются решениями алгебраического уравнения:
- числа, которые
являются решениями алгебраического уравнения:
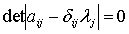 , (1.5)
, (1.5)
где 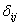 -
символ Кронекера
-
символ Кронекера 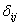 =1,
i=j;
=1,
i=j; 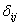 =0,
i≠j.
=0,
i≠j.
Величины 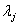 называются
также числами Ляпунова и играют главную роль в анализе устойчивости. Если все
числа Ляпунова отрицательны, то состояние устойчиво. Действительно, в этом
случае все отклонения со временем уменьшаются, т.е. система стремится обратно к
стационарному состоянию, даже если ее немного отклонить от него. Если хотя бы одно
из чисел Ляпунова положительно, то состояние неустойчиво. Действительно, тогда
отклонения
называются
также числами Ляпунова и играют главную роль в анализе устойчивости. Если все
числа Ляпунова отрицательны, то состояние устойчиво. Действительно, в этом
случае все отклонения со временем уменьшаются, т.е. система стремится обратно к
стационарному состоянию, даже если ее немного отклонить от него. Если хотя бы одно
из чисел Ляпунова положительно, то состояние неустойчиво. Действительно, тогда
отклонения 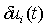 возрастают
со временем, причем достаточно быстро. В общем случае числа Ляпунова могут быть
комплексными. Устойчивость определяется тогда знаком реальной части. Если среди
чисел Ляпунова имеются равные нулю или чисто мнимые, то стационарное состояние
называется нейтральным; при отклонении от него не появляются ни возвращающие,
ни отклоняющие силы.
возрастают
со временем, причем достаточно быстро. В общем случае числа Ляпунова могут быть
комплексными. Устойчивость определяется тогда знаком реальной части. Если среди
чисел Ляпунова имеются равные нулю или чисто мнимые, то стационарное состояние
называется нейтральным; при отклонении от него не появляются ни возвращающие,
ни отклоняющие силы.
Анализ неустойчивых
движений основан на том же принципе: определяется временная зависимость малых
отклонений от заданной траектории. Используются линейные по отклонениям
уравнения (высшими степенями 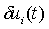 пренебрегают), решения
которых имеют вид:
пренебрегают), решения
которых имеют вид:
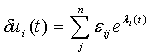 (1.6)
(1.6)
Числа Ляпунова при этом
уже не постоянны, а зависят от времени. Траектория является неустойчивой, если
среди чисел 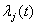 имеются
такие, вещественные части которых положительны при
имеются
такие, вещественные части которых положительны при 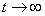 .
.
Подчеркнем важное
свойство: числа Ляпунова являются характеристическими (или собственными)
числами системы; они не зависят от начальных условий. Таким образом,
устойчивость (или неустойчивость) - внутреннее свойство исследуемой системы, а
не результат внешнего воздействия. Особенность его в том, что проявляется оно
только при наличии малых внешних воздействий. Эта особенность привела к важным
методологическим последствиям. Сейчас приходится пересматривать и подвергать
ревизии некоторые, казалось бы, установившиеся в физике понятия [12].
1.2 Методы решения
нелинейных уравнений и систем нелинейных уравнений
Очень часто в различных областях
физики, техники, экономики и т.д. приходится встречаться с математическими
задачами, для которых не удается найти решение классическими методами или
решения выражены громоздкими формулами, которые не приемлемы для практического
использования. Поэтому большое значение приобрели итерационные методы. В
большинстве случаев итерационные методы являются приближенными, так как с их
помощью обычно решаются задачи, аппроксимирующие исходные. В ряде случаев
итерационный метод строится на базе бесконечного процесса, который в пределе
сводится к искомому решению. Однако реально предельный переход не удается осуществить,
и процесс, прерванный на некотором шаге, дает приближенное решение. Кроме того,
источниками погрешности являются несоответствие математической модели
изучаемому реальному явлению и погрешность исходных данных [2].
Как известно, многие скалярные
уравнения не всегда имеют аналитическое решение, в этом случае используются
итерационные методы с заданной степенью точности: задача приближенного
вычисления нуля функции f(x), или что, то же самое, задача приближенного
вычисления корня уравнения f(x)=0. Термины нуль функции f, корень уравнения
f(x)=0 и решение уравнения f(x)=0 будут использоваться как эквивалентные.
По-видимому, у рассматриваемой задачи нет общепризнанного точного названия. В
самом деле, термин решение уравнения охватывает и решение дифференциальных
уравнений. Прилагательные алгебраическое и трансцендентное обычно используются
для различения случаев, когда f соответственно является или не является
многочленом. Представляется, что наиболее подходящим термином для данной задачи
является термин поиск корней.
Независимая переменная указывается
или не указывается явно в зависимости от того, идет ли речь о функции или о
значении функции в некоторой точке из области определения. Учитываются и
соображения удобства чтения формул. Таким образом, обозначения f и f(x) будут
использоваться как равноправные.
Производные функции f будут
обозначаться либо через f(l), либо через f΄΄f˝…, причем f(0)= f. Если f΄΄ не обращается в
нуль в окрестности точки α и производная f(l) непрерывна в этой окрестности, то у
f существует обратная функция F, производная F(l) которой непрерывна
в некоторой окрестности нуля.
Нуль α
имеет кратность m, если f(x)=(x-α)mg(x), причем функция
g(x) ограничена в окрестности точки α и g(α)≠ 0.
Будем предполагать, что m - целое
положительное число. Если m=1, то α называется простым нулем; если же m > 1, то α называется кратным
нулем.
Пусть xi, xi-1, …xi-n
- набор из n+1 точек, являющихся приближениями к решению α, а выбор xi+1
полностью определяется информацией, полученной в точках xi, xi-1,
…xi-n. Обозначим через φ функцию, задающую соответствие между набором xi, xi-1,
…xi-n и точкой очередного приближения xi+1, т.е.
xi+1= φ(xi, xi-1,
…xi-n) (1.7)
Определенную таким образом функцию φ будем называть
итерационной функцией. В дальнейшем вместо термина «итерационная функция» как в
единственном, так и во множественном числе будет использоваться аббревиатура
ИФ.
Даже простейший итерационный
алгоритм включает начальное приближение (приближения), ИФ и численный критерий,
позволяющий установить, что сходимость достигнута.
В основу классификации ИФ положим
характер использования ими информации.
Информацию о значениях функции f и
ее производных в точке xi, вычисляемую в ходе выполнения очередной
i-й итерации, будем называть новой в отличии от информации, вычисленной в ходе
предшествовавших итераций и уже использовавшейся при выборе соответствующих
приближений.
Последнюю будем называть старой, или
ранее вычисленной информацией. Предположим, что выбор xi+1 определяется
только новой информацией в точке xi, а ранее вычисленная информация
не используется. Тогда
i+1 = φ (xi), (1.8)
а φ
называется одноточечной ИФ.
Наиболее известным примером ИФ этого
рода является ИФ Ньютона.
Пусть теперь выбор xi+1 определяется
новой информацией в точке xi и ранее вычисленной информацией в
точках xi+1,…, xi-n. Тогда
xi+1 = φ(xi; xi-1, …xi-n) (1.9)
а φ
называется одноточечной ИФ с памятью.
Символ «;» в (1.9) отделяет точку xi,
в которой вычисляется новая информация, от точек, информация в которых уже
использовалась. Наиболее известным примером одноточечной ИФ с памятью является
ИФ метода секущих.
Пусть выбор xi+1
определяется на основе новой информации в точках xi,ω1(xi), …, ωk(xi), где k ≥
1, а ранее вычисленная информация не используется.
Тогда
i+1 = φ(xi; ω1(xi), …, ωk(xi)), (1.10)
а φ
называется многоточечной ИФ. Среди многоточечных ИФ нет широко
известных.
Наконец, обозначим zj,
набор из k+1 чисел xj; ω1(xj), …, ωk(xj), где k ≥ 1. Если
xi+1 = φ(zi; zi-1, …, zi-n), (1.11)
то φ
называется многоточечной ИФ с памятью. Как и в (1.9), символ «;» в
(1.11) отделяет точки, в которых определяется новая информация, от точек,
информация в которых уже использовалась [16].
Широко известных примеров
многоточечных функций с памятью не существует.
Мы подошли к важному понятию порядка
ИФ. Пусть последовательность x0, x1,…, xi, …
сходится к α.
Положим ei = xi - α. Если существует действительное число p и ненулевая константа C,
такие, что
| ei+1| / | ei
| → C (1.12)
то p называется порядком
последовательности, а C - константой асимптотики погрешности.
Установим связь между порядком
последовательности {xi} и порождающей ее ИФ.
Для этого представим (1.12) в виде
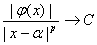 (1.13)
(1.13)
Если существуют
вещественное p и ненулевая константа С, удовлетворяющие (1.13), то приписываем
ИФ φ порядок p независимо от того, сходится порождаемая ею
последовательность или нет.
Ясно, что если
последовательность сходится, то порядок итерационной функции и порядок
порожденной ею последовательности совпадают. Единственность порядка будет
установлена ниже.
Принадлежность φ
классу ИФ, имеющих порядок p, будет обозначаться
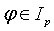 (1.14)
(1.14)
В приведенных
определениях порядок связан с кратностью. Будем называть порядок независимым от
кратности, если порядок одинаков для нулей любой кратности. В противном случае
будем называть порядок зависимым от кратности. В частности, порядок, равный
единице для всех кратных нулей, а для простых нулей превышающих единицу, будем
называть линейным для всех кратных нулей [7].
Прилагательные линейный
и квадратичный будут иногда использоваться вместо первый и второй.
Заметим, что если
порядок существует, то он единствен. В самом деле, пусть сходящаяся
последовательность имеет два порядка: 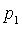 и
и 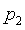 ,
причем
,
причем 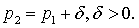 Тогда
Тогда
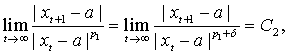
откуда следует, что
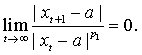
Но последнее
противоречит предположению о том, что порядок равен 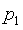 .
.
Ниже будет показано, что
ИФ с памятью не могут быть целого порядка.
Если производная 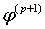 непрерывна
и
непрерывна
и
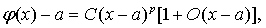 (1.15)
(1.15)
то φ
имеет порядок 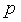 и
и 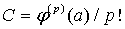 .
.
Уравнение (1.15) можно
переписать в виде: 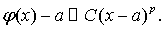
В классической работе E.
Schroder, относящейся к 1870 г., дано следующее определение порядка: φ
имеет порядок 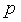 , если
, если
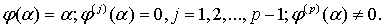 (1.16)
(1.16)
Это определение имеет смысл
только для ИФ одной переменной, имеющих 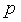 непрерывных производных
[18].
непрерывных производных
[18].
В отличие от многих
авторов, основывающихся на этом определении, мы предпочтем представить его в
виде утверждения теоремы 1.
Для достижения поставленных
целей нам потребуется мера информации, используемой ИФ, и эффективности ИФ.
В качестве измерителя
информации естественно принять объем информационного запроса d (informational
usage), выражаемый количеством элементов новой информации, используемой в
каждой итерации.
Поскольку информация
используется в форме значений 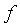 и ее производных, объем
информационного запроса равен количеству значений производных, вычисляемых в
ходе итерации (считается, что сама функция является производной нулевого
порядка).
и ее производных, объем
информационного запроса равен количеству значений производных, вычисляемых в
ходе итерации (считается, что сама функция является производной нулевого
порядка).
Принадлежность φ
классу ИФ порядка 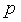 с
объемом информационного запроса d будем обозначать посредством
с
объемом информационного запроса d будем обозначать посредством
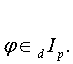 (1.17)
(1.17)
Меру эффективности
определим следующим образом: эффективность использования информации EFF равна
частному от деления порядка на объем информационного запроса, т.е.
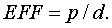 (1.18)
(1.18)
Другое определение
эффективности выглядит так:
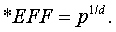 (1.19)
(1.19)
Величина (1.19) названа
индексом эффективности.
Одноточечные ИФ и
одноточечные ИФ с памятью вычисляют только одно новое значение каждой
производной или вычисляются первые 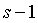 производных, то объем
информационного запроса равен s, а
производных, то объем
информационного запроса равен s, а
устойчивость
динамический берштейн аппроксимация
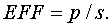 (1.20)
(1.20)
Предположим, что
одноточечная ИФ использует старую информацию в n точках. Положим
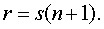 (1.21)
(1.21)
Таким образом, r равно
произведению числа элементов новой информации на общее число точек, в которых
используется информация. Величины 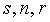 являются
характеристиками определенных семейств ИФ. Там, где невозможно двоякое
толкование, эти буквы будут использоваться и для иных целей. Оптимальными
назовем такие одноточечные ИФ, для которых
являются
характеристиками определенных семейств ИФ. Там, где невозможно двоякое
толкование, эти буквы будут использоваться и для иных целей. Оптимальными
назовем такие одноточечные ИФ, для которых 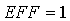 . Очевидно, что для
оптимальных одноточечных ИФ
. Очевидно, что для
оптимальных одноточечных ИФ 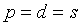 . Базовой
последовательностью ИФ назовем бесконечную последовательность ИФ
. Базовой
последовательностью ИФ назовем бесконечную последовательность ИФ 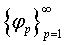 ,
,
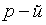 член
которой имеет порядок p. Оптимальной базовой последовательностью называется
базовая последовательность, все члены которой оптимальны.
член
которой имеет порядок p. Оптимальной базовой последовательностью называется
базовая последовательность, все члены которой оптимальны.
Иногда
последовательность и отдельные ее члены будут обозначаться одним и тем же
символом; при этом смысл обозначения будет ясен из контекста.
Рассмотрим решение
уравнения
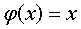 (1.22)
(1.22)
при помощи итерации
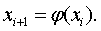 (1.23)
(1.23)
Число
α, удовлетворяющее уравнению (1.22), называется неподвижной точкой
функции 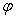 .
Проблема нахождения неподвижных точек функций возникает во многих областях
математики. Рассмотрим связь между решением задачи о неподвижной точке и
решением уравнения
.
Проблема нахождения неподвижных точек функций возникает во многих областях
математики. Рассмотрим связь между решением задачи о неподвижной точке и
решением уравнения 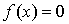 .
Пусть
.
Пусть 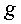 -
произвольная функция, значение
-
произвольная функция, значение  которой отлично от нуля
и конечно. Положим
которой отлично от нуля
и конечно. Положим
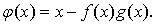 (1.24)
(1.24)
Очевидно, 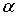 есть
решение уравнения
есть
решение уравнения 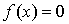 тогда
и только тогда, когда
тогда
и только тогда, когда 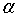 -
неподвижная точка функции
-
неподвижная точка функции 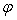 .
.
Мы покажем, что при
определенных условиях задача о неподвижной точке имеет единственное решение и
итерационная последовательность (1.23) сходится к этому решению. Вследствие
специального вида этих условий доказательство будет простым. Существует много
других доказательств подобных утверждений как для вещественных функций, так и
для абстрактных пространств, использующих различные предположения [26].
Предположим, что функция
φ определена на некотором замкнутом ограниченном интервале 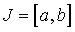 и
принимает значения из этого интервала. Тогда, если
и
принимает значения из этого интервала. Тогда, если 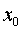 принадлежит
принадлежит
 ,
то и все
,
то и все 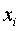 принадлежат
принадлежат
 .
Для существования решения уравнения (1.22) нужно предполагать непрерывность
φ. А именно, справедлива
.
Для существования решения уравнения (1.22) нужно предполагать непрерывность
φ. А именно, справедлива
Лемма 1. Пусть
φ - непрерывная функция, действующая из 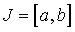 в
в
 .
Тогда существует такое
.
Тогда существует такое 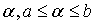 ,
что
,
что 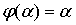 .
.
Доказательство.
Поскольку φ действует из  в
в  ,
то
,
то 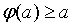 ,
,
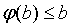 .
Положим
.
Положим 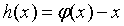 .
Тогда
.
Тогда 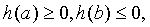 и,
согласно теореме о промежуточных значениях, существует такое число
α, что
и,
согласно теореме о промежуточных значениях, существует такое число
α, что  .
Последнее равнозначно соотношению
.
Последнее равнозначно соотношению 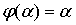 .
.
Для получения дальнейших
результатов наложим дополнительные ограничения на φ.
Пусть
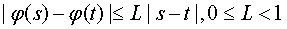 (1.25)
(1.25)
для производных точек  и
и
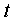 из
из
 .
Заметим, что это сжимающее условие Липшица обусловливает непрерывность.
Покажем, что при этом условии решение уравнения
.
Заметим, что это сжимающее условие Липшица обусловливает непрерывность.
Покажем, что при этом условии решение уравнения 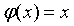 единственно.
единственно.
Лемма 2. Пусть 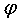 -
функция, действующая из
-
функция, действующая из  в
в
 и
удовлетворяющая сжимающему условию Липшица (1.25). Тогда уравнение
и
удовлетворяющая сжимающему условию Липшица (1.25). Тогда уравнение 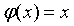 имеет
не более одного решения.
имеет
не более одного решения.
Доказательство.
Предположим, что существуют два различных решения 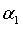 и
и
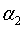 .
Следовательно,
.
Следовательно, 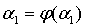 ,
,
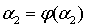 и
и
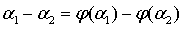 .
Используя (1.25), получаем
.
Используя (1.25), получаем
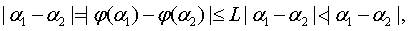
что невозможно.
Таким образом,
установлены условия, гарантирующие существование и единственность решения α
уравнения 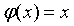 .
Покажем теперь, что последовательность, задаваемая соотношением
.
Покажем теперь, что последовательность, задаваемая соотношением 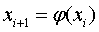 ,
сходится к этому решению.
,
сходится к этому решению.
Теорема 1. Пусть  -
замкнутый ограниченный интервал, φ -
функция, действующая из
-
замкнутый ограниченный интервал, φ -
функция, действующая из  в
в
 и
удовлетворяющая условию
и
удовлетворяющая условию
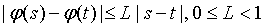
для произвольных точек  и
и
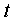 из
из
 .
Пусть
.
Пусть 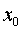 -
произвольная точка из
-
произвольная точка из  и
и
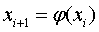 .
Тогда последовательность
.
Тогда последовательность 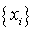 сходится
к единственному решению уравнения
сходится
к единственному решению уравнения 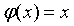 , лежащему в
, лежащему в .
.
Доказательство. Лемма 1
и 2 гарантируют существование и единственность решения α
уравнения 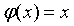 .
Это решение и претендует на роль предела последовательности, определяемой
соотношением
.
Это решение и претендует на роль предела последовательности, определяемой
соотношением 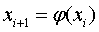 .
Очевидно,
.
Очевидно,
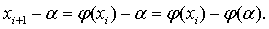
Из условия Липшица
следует, что
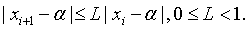
Таким образом, 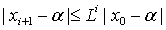 и
и
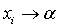 .
.
Если бы мы не знали, что
уравнение 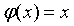 имеет
единственное решение, то пришлось бы показать, что последовательность
имеет
единственное решение, то пришлось бы показать, что последовательность 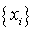 удовлетворяет
критерию Коши.
удовлетворяет
критерию Коши.
Оценка погрешности 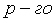 приближения,
зависящая только от первых двух приближений и константы Липшица, выводится так.
Из условия Липшица следует, что для всех
приближения,
зависящая только от первых двух приближений и константы Липшица, выводится так.
Из условия Липшица следует, что для всех 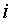
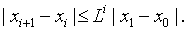 (1.26)
(1.26)
Пусть 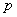 и
и
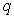 -
произвольные положительные целые числа. Тогда
-
произвольные положительные целые числа. Тогда
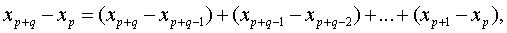
поэтому
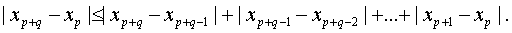
Учитывая (1.26),
получаем, что
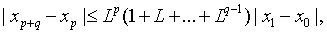
Или
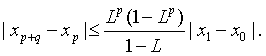 (1.27)
(1.27)
Пусть 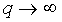 .
Тогда
.
Тогда
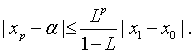
Это соотношение дает
верхнюю границу погрешности 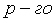 приближения. Отметим,
что если
приближения. Отметим,
что если 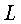 близко
к единице, то сходимость может быть очень медленной.
близко
к единице, то сходимость может быть очень медленной.
Выше для решения
уравнения 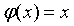 использовалась
итерационная процедура
использовалась
итерационная процедура 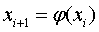 .
Для задач, которые мы будем рассматривать в дальнейшем, это нетипично. В общем
случае нам предстоит иметь дело с итерационным_уравнением вида
.
Для задач, которые мы будем рассматривать в дальнейшем, это нетипично. В общем
случае нам предстоит иметь дело с итерационным_уравнением вида 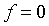 и
для него строить функционал, выполняющий роль ИФ. Показано, что если φ
удовлетворяет сжимающему условию Липшица, то итерационная последовательность
сходится к единственному решению задачи о неподвижной точке. В дальнейшем будем
уделять больше внимания не поиску слабых достаточных условий, обеспечивающих
сходимость итерационной последовательности, а построению таких ИФ, для которых
эта последовательность сходится быстро [22].
и
для него строить функционал, выполняющий роль ИФ. Показано, что если φ
удовлетворяет сжимающему условию Липшица, то итерационная последовательность
сходится к единственному решению задачи о неподвижной точке. В дальнейшем будем
уделять больше внимания не поиску слабых достаточных условий, обеспечивающих
сходимость итерационной последовательности, а построению таких ИФ, для которых
эта последовательность сходится быстро [22].
При этом мы будем готовы
потребовать выполнения гораздо более сильных условий, чем условие Липшица. В
частности, будем предполагать, что в рассматриваемом интервале 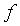 имеет
нуль.
имеет
нуль.
Предположим, что
производная 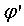 непрерывна
в окрестности точки α. Если
непрерывна
в окрестности точки α. Если 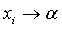 и
функция φ непрерывна, то
и
функция φ непрерывна, то
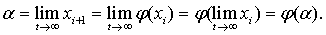
Поэтому потребуем, чтобы
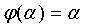 (1.28)
(1.28)
Отметим, что
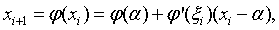
где 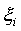 расположено
в промежутке между
расположено
в промежутке между 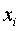 и
α. Используя (1.28), получаем
и
α. Используя (1.28), получаем
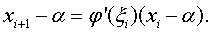 (1.29)
(1.29)
Потребуем, чтобы в
некоторой окрестности точки α выполнялось
условие 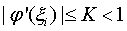 .
.
Ввиду непрерывности 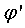 для
этого достаточно потребовать, чтобы
для
этого достаточно потребовать, чтобы 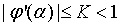 . Тогда существует такая
окрестность точки α, что
. Тогда существует такая
окрестность точки α, что 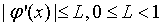 ,
для всех
,
для всех 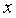 из
этой окрестности и
из
этой окрестности и 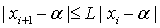 .
Тогда
.
Тогда 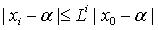 ,
и
,
и 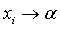 .
.
Точку
α, для которой при любой начальной точке 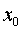 ,
взятой из достаточно малой окрестности точки α,
последовательность
,
взятой из достаточно малой окрестности точки α,
последовательность 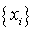 сходится
к α, называют точкой притяжения.
сходится
к α, называют точкой притяжения.
Только что доказанный
результат можно сформулировать так: если производная 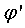 непрерывна
в окрестности точки α, для которой
непрерывна
в окрестности точки α, для которой 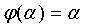 и
и 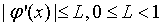 ,
то
,
то 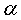 является
точкой притяжения.
является
точкой притяжения.
Далее, пусть 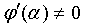 .
Тогда
.
Тогда 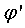 не
обращается в нуль в некоторой окрестности точки α.
Положим
не
обращается в нуль в некоторой окрестности точки α.
Положим 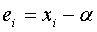 ;
при этом (1.29) примет вид
;
при этом (1.29) примет вид 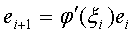 , ясно, что если
, ясно, что если 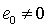 и
и
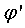 не
обращается в нуль, то и
не
обращается в нуль, то и 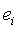 отлично
от нуля для любого конечного номера
отлично
от нуля для любого конечного номера 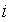 .
.
Иными словами,
итерационная последовательность не может сойтись к решению за конечное число
шагов, если ее члены лежат в окрестности точки α,
в которой 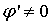 .
.
Следовательно, 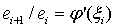 и
и
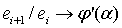 .
Это - случай сходимости первого порядка, или линейной сходимости.
.
Это - случай сходимости первого порядка, или линейной сходимости.
В случае же
сверхлинейной сходимости можно отказаться от требования 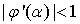 ;
итерационная последовательность всегда сходится в некоторой окрестности точки
α.
;
итерационная последовательность всегда сходится в некоторой окрестности точки
α.
В дополнение к условию 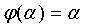 предположим
теперь, что производная
предположим
теперь, что производная 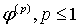 ,
непрерывна.
,
непрерывна.
Тогда
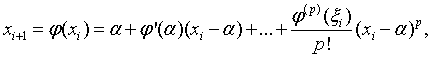
где точка 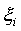 расположена
в промежутке между
расположена
в промежутке между 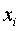 и
α. Ясно, что
и
α. Ясно, что 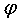 имеет
порядок
имеет
порядок 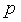 только
в том случае, если
только
в том случае, если  ,
а
,
а 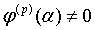 .
.
В этом случае 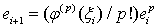 ,
где
,
где 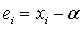 .
.
Поскольку  ,
производная
,
производная 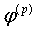 также
не обращается в нуль в некоторой окрестности точки
α. Но тогда алгоритм не может сойтись за конечное число шагов, если
также
не обращается в нуль в некоторой окрестности точки
α. Но тогда алгоритм не может сойтись за конечное число шагов, если
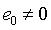 и
все члены итерационной последовательности лежат в окрестности точки
α, где
и
все члены итерационной последовательности лежат в окрестности точки
α, где 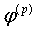 не
обращается в нуль.
не
обращается в нуль.
Теорема 2. Предположим,
что 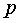 -я
производная
-я
производная 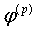 итерационной
функции непрерывна в некоторой окрестности точки α.
Положим
итерационной
функции непрерывна в некоторой окрестности точки α.
Положим 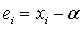 .
.
Тогда 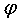 имеет
порядок
имеет
порядок 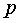 в
том и только том случае, если
в
том и только том случае, если
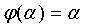 ;
; 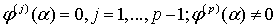 .
.
Кроме того, 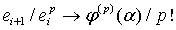 .
.
Напомним, что наличие у
итерационной функции некоторого положительного порядка еще не гарантирует
сходимости порождаемой ею последовательности.
Достаточные условия
сходимости этой последовательности будут установлены ниже.
Выше было показано, что
последовательность, порожденная ИФ линейного порядка, может не сходиться ни в
какой окрестности точки α. Теперь мы увидим, что порожденная сверхлинейной ИФ
последовательность всегда сходится в некоторой окрестности точки
α.
Проводимые ниже
рассуждения охватывают случаи как сверхлинейной, так и линейной сходимости
[14].
Исходным моментом наших
рассуждений является соотношение
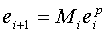 ,
, 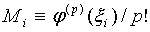 (1.30)
(1.30)
Положим 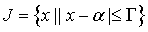 .
Предположим, что производная
.
Предположим, что производная 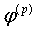 непрерывна на
непрерывна на 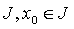 и
соотношение
и
соотношение 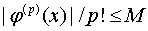 выполнено
для всех
выполнено
для всех 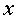 из
из
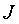 .
Из условия
.
Из условия 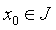 следует,
что
следует,
что 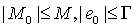 .
Поэтому
.
Поэтому 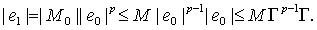
Предположим, что
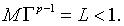 (1.31)
(1.31)
Тогда 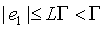 .
Следовательно,
.
Следовательно,  .
Докажем по индукции, что при выполнении (1.31) для всех
.
Докажем по индукции, что при выполнении (1.31) для всех 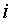 справедливо
справедливо
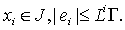 (1.32)
(1.32)
В самом деле, пусть
(1.32) выполнено для некоторого номера 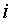 . Тогда
. Тогда
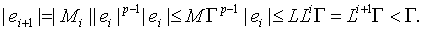
Следовательно, (1.32)
выполнено и для 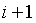 ,
что завершает индукцию. Поскольку
,
что завершает индукцию. Поскольку 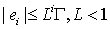 , то
, то  .
Таким образом, теорема доказана.
.
Таким образом, теорема доказана.
Теорема 3. Предположим,
что производная 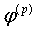 непрерывна
на интервале
непрерывна
на интервале 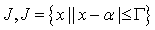 .
.
Пусть, кроме того, 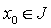 и
соотношение
и
соотношение
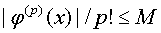
выполняется для всех 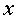 из
из
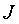 ,
причем
,
причем 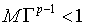 .
Тогда
.
Тогда 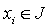 для
любого
для
любого 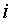 и
и
 .
.
Пусть производная 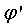 непрерывна
в окрестности точки α и
непрерывна
в окрестности точки α и 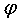 имеет
первый порядок.
имеет
первый порядок.
Сходимость к α
последовательности, порожденной 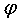 , эквивалентна условию
, эквивалентна условию 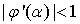 ,
за исключением случая, когда какой-то из элементов
,
за исключением случая, когда какой-то из элементов 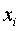 оказывается
в точности равным α.
оказывается
в точности равным α.
Существенность
последнего условия иллюстрирует пример

В рассматриваемом случае
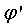 непрерывна
в окрестности нуля и
непрерывна
в окрестности нуля и  ,
тем не менее итерационная последовательность сходится для любого
,
тем не менее итерационная последовательность сходится для любого 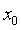 из
единичного интервала.
из
единичного интервала.
За исключением подобных
случаев, для сходимости необходимо, чтобы 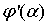 по модулю не превышало
единицу. В то же время, если производная
по модулю не превышало
единицу. В то же время, если производная 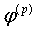 непрерывна в некоторой
окрестности точки α при
непрерывна в некоторой
окрестности точки α при 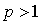 ,
то всегда существует такая окрестность точки α,
в которой итерация обязательно сходится.
,
то всегда существует такая окрестность точки α,
в которой итерация обязательно сходится.
Это только одно из
целого ряда преимуществ сверхлинейной сходимости над линейной [28].
Пожалуй, наиболее важное
преимущество можно нестрого сформулировать так: приближение 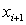 к
α имеет в
к
α имеет в 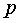 раз
больше верных цифр по сравнению с
раз
больше верных цифр по сравнению с 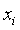 .
.
ИФ более высокого
порядка во многих случаях требует меньшего суммарного количества вычислений
значений функции 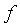 и
ее производных.
и
ее производных.
Основные недостатки,
проявляющиеся при использовании ИФ высокого порядка, состоят в росте сложности
формул и стоимости вычислений высших производных функции 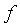 .
.
Задачу нахождения
решений скалярных уравнений можно сформулировать различными способами.
Например, как задачу на
нахождение корней: f(x)=0, или как задачу на нахождение неподвижной точки:
F(x)=x.
При этом, в зависимости
от формулировки задачи, удобно применять те или иные итерационные способы
решения: метод простых итераций, метод деления пополам, метод Ньютона и т.д.
Итак, задача отыскивания корней
нелинейного уравнения с одним неизвестным вида
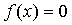 (1.33)
(1.33)
имеет многовековую
историю, но не потеряла свою актуальность и в наши дни. Она часто возникает как
элементарный шаг при решении различных научных и технических проблем. Корнем
(или решением) уравнения (1.33) называется значение 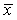 ,
при котором
,
при котором  .
Предположим, что в окрестности каждого из искомых корней функция
.
Предположим, что в окрестности каждого из искомых корней функция 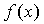 дважды
непрерывно дифференцируема.
дважды
непрерывно дифференцируема.
Корень 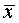 уравнения
(1.33) называется простым, если
уравнения
(1.33) называется простым, если 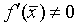 . В противном случае
(т.е. в случае
. В противном случае
(т.е. в случае 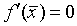 )
корень
)
корень 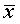 называется
кратным. Целое число
называется
кратным. Целое число 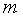 назовем
кратностью корня
назовем
кратностью корня 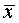 ,
если
,
если  для
для
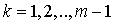 и
и
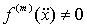 .
Геометрический корень
.
Геометрический корень 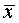 соответствует
точке пересечения графика функции
соответствует
точке пересечения графика функции 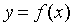 с осью
с осью 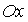 .
Корень
.
Корень 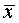 является
простым, если график пересекает ось
является
простым, если график пересекает ось 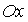 под ненулевым углом, и
кратным, если пересечение происходит под нулевым углом.
под ненулевым углом, и
кратным, если пересечение происходит под нулевым углом.
Уточним постановку
задачи. В конкретной задаче часто интерес представляют не все корни уравнения,
а лишь некоторые из них. Тогда постановку задачи уточняют, указывая на то,
какие из корней подлежат определению (положительные корни, корни из заданного
интервала, максимальный из корней и т.д.).
В подавляющем
большинстве случаев представить решение уравнения (1.27) в виде конечной
формулы оказывается невозможным. Невозможность найти точное решение нелинейного
уравнения кажется огорчительной. Однако нужно признать, что желание найти
точное числовое значение решения вряд ли следует считать разумным. Во-первых, в
реальных исследованиях зависимость 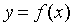 является лишь
приближенным описанием, моделирующим истинную связь между параметрами
является лишь
приближенным описанием, моделирующим истинную связь между параметрами 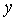 и
и
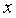 .
Поэтому точное решение
.
Поэтому точное решение 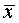 уравнения
(1.33) все равно является лишь приближенным значением того параметра x, который
в действительности соответствует значению
уравнения
(1.33) все равно является лишь приближенным значением того параметра x, который
в действительности соответствует значению 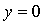 . Во-вторых, даже если
уравнение (1.33) допускает возможность нахождения решения в виде конечной
формулы, то результат вычислений по этой формуле почти с неизбежностью содержит
вычислительную погрешность и поэтому является приближенным.
. Во-вторых, даже если
уравнение (1.33) допускает возможность нахождения решения в виде конечной
формулы, то результат вычислений по этой формуле почти с неизбежностью содержит
вычислительную погрешность и поэтому является приближенным.
В дальнейшем мы
откажемся от попыток найти точные значения корней уравнения (1.33) и
сосредоточим внимание на методах решения более реалистичной задачи
приближенного вычисления корней с заданной точностью 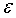 .
Под задачей отыскивания решений уравнения (1.33) будем понимать задачу
вычисления с заданной точностью
.
Под задачей отыскивания решений уравнения (1.33) будем понимать задачу
вычисления с заданной точностью 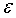 конечного числа
подлежащих определению корней этого уравнения [21].
конечного числа
подлежащих определению корней этого уравнения [21].
Решение задачи отыскания
корней нелинейного уравнения осуществляют в два этапа. Первый этап называется
этапом локализации (или отделения) корней, второй - этапом итерационного
уточнения корней. Отрезок  ,
содержащий только один корень
,
содержащий только один корень 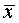 уравнения (1.33),
называют отрезком локализации корня
уравнения (1.33),
называют отрезком локализации корня 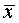 .
.
Цель этапа локализации
считают достигнутой, если для каждого из подлежащих определению корней удалось
указать отрезок локализации (его длину стараются по возможности сделать
минимальной).
Способы локализации
корней многообразны, и указать универсальный метод не представляется возможным.
Иногда отрезок локализации известен либо он определяется из физических
соображений. В простых ситуациях хороший результат может давать графический
метод. Широко применяют построение таблиц значений функций 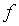 вида
вида
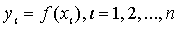 .
При этом способе локализации о наличии на отрезке
.
При этом способе локализации о наличии на отрезке 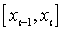 корня
судят по перемене знака функции на концах отрезка.
корня
судят по перемене знака функции на концах отрезка.
Основанием для
применения указанного способа служит следующая хорошо известная теорема
математического анализа.
Теорема 1. Пусть функция
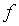 непрерывна
на отрезке
непрерывна
на отрезке  и
принимает на его концах значения разных знаков, т.е.
и
принимает на его концах значения разных знаков, т.е. 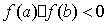 .
Тогда отрезок
.
Тогда отрезок  содержит
по крайней мере один корень уравнения
содержит
по крайней мере один корень уравнения  .
.
К сожалению, корень
четной кратности не удается локализовать на основании перемены знака с помощью
даже очень подробной таблицы. Дело в том, что в малой окрестности такого корня
функция 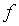 имеет
постоянный знак. Важно подчеркнуть, что далеко не всегда для успешного
отыскания корня
имеет
постоянный знак. Важно подчеркнуть, что далеко не всегда для успешного
отыскания корня 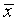 уравнения
(1) необходимо полное решение задачи локализации. Часто вместо отрезка
локализации достаточно найти хорошее начальное приближение
уравнения
(1) необходимо полное решение задачи локализации. Часто вместо отрезка
локализации достаточно найти хорошее начальное приближение 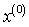 к
корню
к
корню 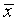 .
.
Очень важно рассмотрение
обусловленности задачи вычисления корня уравнения.
Пусть 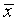 -
корень уравнения (1.33), подлежащий определению. Будем считать, что входными
данными для задачи вычисления корня
-
корень уравнения (1.33), подлежащий определению. Будем считать, что входными
данными для задачи вычисления корня 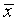 являются значения
являются значения 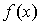 функции
функции
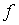 в
малой окрестности корня.
в
малой окрестности корня.
Так как значения 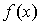 будут
вычисляться на ЭВМ по некоторой программе, то в действительности задаваемые
значения являются приближенными и их следует обозначать через
будут
вычисляться на ЭВМ по некоторой программе, то в действительности задаваемые
значения являются приближенными и их следует обозначать через  .
.
Ошибки в 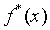 могут быть связаны не только с
неизбежными ошибками округления, но и с использованием для вычисления значений
функции
могут быть связаны не только с
неизбежными ошибками округления, но и с использованием для вычисления значений
функции 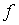 приближенных
методов. К сожалению, нельзя ожидать, что в окрестности корня относительная
погрешность
приближенных
методов. К сожалению, нельзя ожидать, что в окрестности корня относительная
погрешность 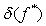 окажется
малой.
окажется
малой.
Реально рассчитывать
можно лишь на то, что малой окажется абсолютная погрешность вычисления значений
функции.
Будем предполагать, что
в достаточно малой окрестности корня выполняется неравенство 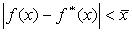 ,
где
,
где
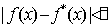 , где
, где 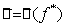 -
граница абсолютной погрешности.
-
граница абсолютной погрешности.
Сама погрешность корня
ведет себя крайне нерегулярно и в первом приближении может восприниматься
пользователем как некоторая случайная величина [18].
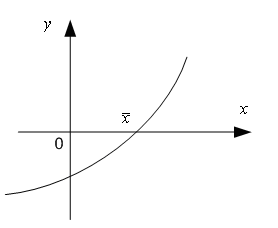
На рисунке 1, а
представлена идеальная ситуация, отвечающая исходной математической постановке
задачи, а на рисунке 1, б - реальная ситуация, соответствующая вычислениям
значений функции 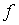 на
ЭВМ.
на
ЭВМ.
|
 а) а)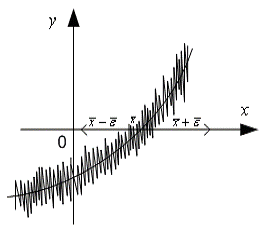 б)
б)
|
|
Рисунок 1 - а) график функции; б)
график зашумленной функции
Если функция 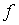 непрерывна,
то найдется такая малая окрестность
непрерывна,
то найдется такая малая окрестность 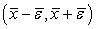 корня
корня 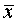 ,
имеющая радиус
,
имеющая радиус 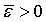 ,
в которой выполняется неравенство
,
в которой выполняется неравенство 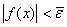 .
.
Для 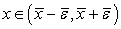 знак
вычисленного значения
знак
вычисленного значения  ,
вообще говоря, не обязан совпадать со знаком
,
вообще говоря, не обязан совпадать со знаком 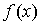 и, следовательно,
становится невозможным определить, какое именно значение
и, следовательно,
становится невозможным определить, какое именно значение 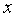 из
интервала
из
интервала 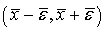 обращает
функцию
обращает
функцию 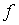 в
нуль (рисунок 1, б).
в
нуль (рисунок 1, б).
Будем называть этот
интервал интервалом неопределенности корня 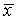 . Найдем оценку величины
. Найдем оценку величины
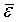 .
.
Пусть корень 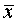 -
простой. Для близких к
-
простой. Для близких к 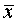 значений
значений
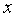 справедливо
приближенное равенство
справедливо
приближенное равенство
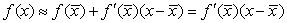
Поэтому равенство (2)
примет вид 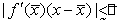 ,
откуда получаем
,
откуда получаем
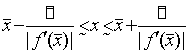 .
.
Следовательно,
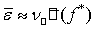 . (1.34)
. (1.34)
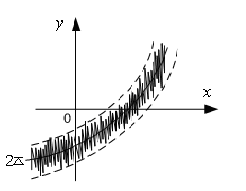 а)
а)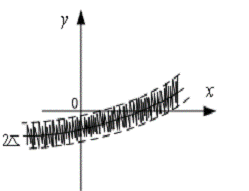 б)
б)
Рисунок 2 - График функции при
различных отклонениях
Здесь 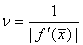 -
число, которое в рассматриваемой задаче играет роль абсолютного числа
обусловленности.
-
число, которое в рассматриваемой задаче играет роль абсолютного числа
обусловленности.
Действительно, если 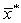 -
корень уравнения
-
корень уравнения 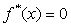 ,
то
,
то 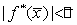 и
тогда выполнено неравенство
и
тогда выполнено неравенство
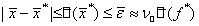 . (1.35)
. (1.35)
Заметим, что радиус
интервала неопределенности прямо пропорционален погрешности 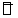 вычисления
значения
вычисления
значения 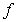 .
Кроме того,
.
Кроме того, 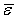 возрастает
(обусловленность задачи ухудшается) с уменьшением
возрастает
(обусловленность задачи ухудшается) с уменьшением 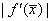 ,
т.е. с уменьшением модуля тангенса угла наклона, под которым график функции
пересекает ось
,
т.е. с уменьшением модуля тангенса угла наклона, под которым график функции
пересекает ось 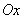 (рисунок
2, а, б).
(рисунок
2, а, б).
Если же 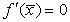 (т.е.
корень
(т.е.
корень 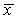 -
кратный), то формула (1.35) уже не верна. Пусть кратность корня равна
-
кратный), то формула (1.35) уже не верна. Пусть кратность корня равна 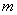 .
Тогда в силу формулы Тейлора справедливо приближенное равенство
.
Тогда в силу формулы Тейлора справедливо приближенное равенство 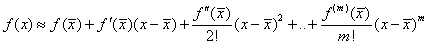 ,
в правой части которого все слагаемые, кроме последнего, равны нулю.
Следовательно, неравенство (1.34) имеет вид
,
в правой части которого все слагаемые, кроме последнего, равны нулю.
Следовательно, неравенство (1.34) имеет вид
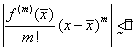 .
.
Решая его, получаем
аналогично (1.35) оценку радиуса интервала неопределенности:
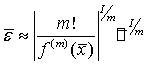 .
.
Эта оценка означает, что
для корня кратности 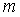 радиус
интервала неопределенности пропорционален
радиус
интервала неопределенности пропорционален 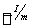 , что свидетельствует о
плохой обусловленности задачи вычисления кратных корней.
, что свидетельствует о
плохой обусловленности задачи вычисления кратных корней.
Отметим, что 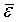 не
может быть меньше величины
не
может быть меньше величины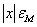 - погрешности представления корня
- погрешности представления корня 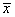 в ЭВМ.
в ЭВМ.
В реальной ситуации
оценить величину и даже порядок радиуса интервала неопределенности довольно
сложно. Однако, знать о его существовании нужно по крайней мере по двум
причинам.
Во-первых, не имеет
смысла ставить задачу о вычислении корня 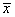 с точностью
с точностью 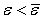 .
.
В условиях
неопределенности, вызванных приближенным заданием функции, любое значение 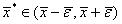 может
быть с одной и той же степенью достоверности принято за решение уравнения.
может
быть с одной и той же степенью достоверности принято за решение уравнения.
Во-вторых, нельзя требовать
от алгоритмов отыскания корня получения достоверных результатов после того, как
очередное приближение попало в интервал неопределенности или оказалось очень
близко от него; в этой ситуации вычисления следует прекратить и считать, что
получен максимум действительно возможного.
Для большинства
итерационных методов определить этот момент можно, поскольку начиная с него
поведение приближений 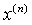 становится
крайне нерегулярным [24].
становится
крайне нерегулярным [24].
Если вдали от интервала
неопределенности величина
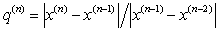 (1.36)
(1.36)
обычно бывает меньше
единицы 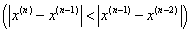 ,
то появление при некотором
,
то появление при некотором 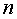 значения
значения 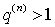 свидетельствует,
скорее всего, о начале «разболтки» - хаотического поведения итерационной
последовательности. В этой ситуации вычисления имеет смысл прервать, чтобы
выяснить причину явления и принять правильное решение.
свидетельствует,
скорее всего, о начале «разболтки» - хаотического поведения итерационной
последовательности. В этой ситуации вычисления имеет смысл прервать, чтобы
выяснить причину явления и принять правильное решение.
Лучшим из полученных
приближений к решению следует считать, конечно, 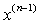 . Использование для
контроля вычислений величины (1.36) называют часто правилом Гарвика.
. Использование для
контроля вычислений величины (1.36) называют часто правилом Гарвика.
Задача отыскания решения
системы нелинейных уравнений с 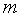 неизвестными вида
неизвестными вида
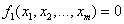 ,
,
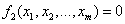 , (1.37)
, (1.37)
…………………
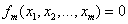 ,
,
является существенно более сложной,
чем задача отыскания решения уравнения с одним неизвестным.
Однако на практике она встречается
значительно чаще, так как в реальных исследованиях интерес представляет, как
правило, определение не одного, а нескольких параметров (нередко их число
доходит до сотен и тысяч).
Найти точное решение
системы, т.е. вектор 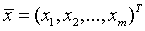 ,
удовлетворяющий уравнениям (1.37), практически невозможно.
,
удовлетворяющий уравнениям (1.37), практически невозможно.
Для дальнейшего удобно
использовать сокращенную векторную форму записи систем. Наряду с вектором
неизвестных 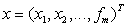 рассмотрим
вектор-функцию
рассмотрим
вектор-функцию 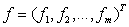 .
В этих обозначениях система (1.37) примет вид
.
В этих обозначениях система (1.37) примет вид 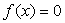 .
.
Будем считать функции 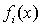 непрерывно
дифференцируемыми в некоторой окрестности решения
непрерывно
дифференцируемыми в некоторой окрестности решения 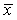 .
Введем для системы функций
.
Введем для системы функций 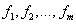 матрицу Якоби которая
будет использована в дальнейшем.
матрицу Якоби которая
будет использована в дальнейшем.
 , (1.38)
, (1.38)
Основные этапы решения. Как и в
случае уравнения с одним неизвестным, отыскание решений начинаются с этапа
локализации. Для каждого из искомых решений 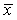 указывают множество, которое
содержит только одно это решение и расположено в достаточно малой его
окрестности. Часто в качестве такого множества выступает параллелепипед или шар
в m-мерном пространстве.
указывают множество, которое
содержит только одно это решение и расположено в достаточно малой его
окрестности. Часто в качестве такого множества выступает параллелепипед или шар
в m-мерном пространстве.
Иногда этап локализации
не вызывает затруднений; соответствующие множества могут быть заданными,
определяться из физических соображений, из смысла параметров 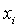 либо
быть известными из опыта решений подобных задач. Однако чаще всего задача
локализации (в особенности при больших m) представляет собой сложную проблему,
от успешного решения которой в основном и зависит возможность вычисления
решений системы (1.37). На этапе локализации особое значение приобретают
квалификация исследователя, понимание им существа решаемой научной или
инженерной проблемы, опыт решения этой или близких задач на ЭВМ.
либо
быть известными из опыта решений подобных задач. Однако чаще всего задача
локализации (в особенности при больших m) представляет собой сложную проблему,
от успешного решения которой в основном и зависит возможность вычисления
решений системы (1.37). На этапе локализации особое значение приобретают
квалификация исследователя, понимание им существа решаемой научной или
инженерной проблемы, опыт решения этой или близких задач на ЭВМ.
Во многих случаях полное
решение задачи локализации невозможно и ее можно считать решенной
удовлетворительно, если 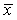 удается
найти хорошее начальное приближение
удается
найти хорошее начальное приближение 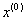 . В простейших случаях
(например, для системы двух уравнений с двумя неизвестными) могут быть
использованы графические методы.
. В простейших случаях
(например, для системы двух уравнений с двумя неизвестными) могут быть
использованы графические методы.
На втором этапе для
вычисления решения с заданной точностью 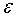 используют один из
итерационных методов решения нелинейных систем.
используют один из
итерационных методов решения нелинейных систем.
Будем считать, что
определения, связанные с характеризацией сходимости итерационных методов,
остаются в силе, причем в неравенствах знак модуля заменен на знак нормы, а 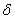 -окрестность
решения
-окрестность
решения 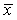 понимается
как множество точек
понимается
как множество точек 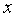 ,
удовлетворяющих условию
,
удовлетворяющих условию  .
.
Корректность и
обусловленность задачи. Будем считать, что система (1.37) имеет решение 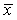 ,
причем в некоторой окрестности этого решения матрица Якоби
,
причем в некоторой окрестности этого решения матрица Якоби 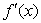 невырождена.
Выполнение последнего условия гарантирует, что в указанной окрестности нет
других решений системы (1.37).
невырождена.
Выполнение последнего условия гарантирует, что в указанной окрестности нет
других решений системы (1.37).
Случай, когда в точке 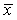 матрица
матрица
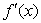 вырождена,
является существенно более трудным и нами рассматриваться не будет.
вырождена,
является существенно более трудным и нами рассматриваться не будет.
В одномерном случае
первая ситуации отвечает наличию простого корня уравнения 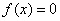 интервала
неопределенности, внутри которого невозможно определить, какая из точек
является решением уравнения.
интервала
неопределенности, внутри которого невозможно определить, какая из точек
является решением уравнения.
Аналогично, погрешности
в вычислении вектора-функции  приводят к появлению
области неопределенности D, содержащей решение
приводят к появлению
области неопределенности D, содержащей решение 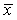 системы (1.37) такой,
что для всех
системы (1.37) такой,
что для всех 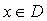 векторное
уравнение
векторное
уравнение 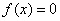 удовлетворяется
с точностью до погрешности. Область D может иметь довольно сложную
геометрическую структуру [19].
удовлетворяется
с точностью до погрешности. Область D может иметь довольно сложную
геометрическую структуру [19].
Мы удовлетворимся только
лишь оценкой радиуса 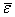 этой
области.
этой
области.
Предположим, что для
близких к 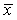 значений
значений
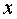 вычисляемые
значения
вычисляемые
значения 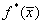 удовлетворяют
неравенству
удовлетворяют
неравенству 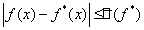 .
.
Тогда 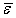 можно
приближенно оценить с помощью неравенства
можно
приближенно оценить с помощью неравенства 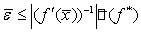 .
.
Таким образом, в
рассматриваемой задаче роль абсолютного числа обусловленности играет норма
матрицы, обратной матрице Якоби 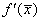 .
.
1.3 Численные алгоритмы
решения нелинейных уравнений
Многочлены в форме Бернштейна были
описаны Сергеем Натановичем Бернштейном в 1912 году и использованы им в
конструктивном доказательстве аппроксимационной теоремы Вейерштрасса.
С развитием компьютерной
графики, полиномы Бернштейна, заключённые в промежуток x 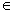 [0,
1], стали играть важную роль при построении кривых Безье.
[0,
1], стали играть важную роль при построении кривых Безье.
При натуральном n
алгебраический полином
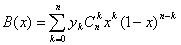 (1.39)
(1.39)
называется полиномом в форме
Бернштейна или просто полиномом Бернштейна [1]. Очевидно, что
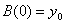 ,
,  .
(1.40)
.
(1.40)
Базисными полиномами Бернштейна от
одной переменной называются полиномы:
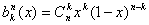 ,
, 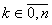 ,
n = 0, 1, …
,
n = 0, 1, …
Базисные полиномы 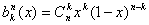 обладают
следующими свойствами:
обладают
следующими свойствами:
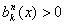 при x
при x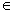 (0, 1) и всех k = 0, 1,…, n; (1.41)
(0, 1) и всех k = 0, 1,…, n; (1.41)
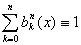 (1.42)
(1.42)
Лемма 1. При всех
вещественных x справедливо равенство:
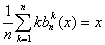 (1.43)
(1.43)
Доказательство.
Равенство (1.37) достаточно проверить при x є (0, 1). Имеем
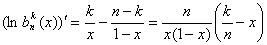 .
.
Вместе с тем,  .
Значит,
.
Значит, 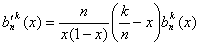 .
.
Теперь продифференцируем
тождество (1.43). Получим
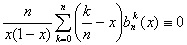 .
.
Отсюда и из (1.42)
следует (1.43).
Теорема 1. Справедлива
формула
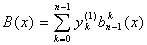 , (1.44)
, (1.44)
где 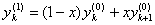 .
.
Доказательство. Имеем
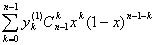 =
=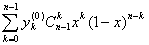 +
+ =
=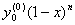 +
+
+ +
+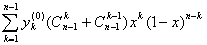 =
=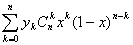 .
.
Мы воспользовались тем,
что 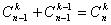 при
k(1, n-1).
при
k(1, n-1).
Преобразование (1.44)
можно продолжить:
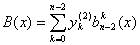 ,
,
где 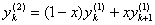 и
т.д. В результате получим
и
т.д. В результате получим
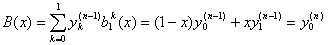 .
.
Таким образом, выведено
рекуррентное соотношение
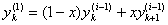 , i=1, …, n, k=0,1,…,
n-i;
, i=1, …, n, k=0,1,…,
n-i; 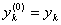 ,
k = 0, 1,…, n,
,
k = 0, 1,…, n,
которое позволяет
вычислить значение 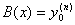 в
фиксированной точке x (0, 1).
в
фиксированной точке x (0, 1).
Перепишем формулу (1.39) в виде
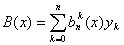 .
.
С учетом свойств (1.41)
и (1.42) коэффициентов 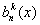 заключаем,
что число B(x) при фиксированном x ∈
(0, 1) есть выпуклая комбинация чисел y0, y1,…, yn.
Рекуррентное соотношение (1.44) представляет собой быстрый способ вычисления
этой выпуклой комбинации.
заключаем,
что число B(x) при фиксированном x ∈
(0, 1) есть выпуклая комбинация чисел y0, y1,…, yn.
Рекуррентное соотношение (1.44) представляет собой быстрый способ вычисления
этой выпуклой комбинации.
Рассмотрим двумерный случай.
Базисные полиномы Бернштейна от двух
переменных определяются следующим образом:
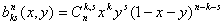 ,
, 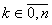 ,
,
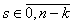 ,
n = 0, 1, …,
,
n = 0, 1, …,
где 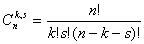 -
так называемые триномиальные коэффициенты.
-
так называемые триномиальные коэффициенты.
В частности,
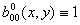 ,
, 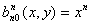 ,
,
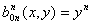 ,
,
 ;
;
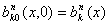 ,
, 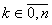 ;
;
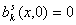 ,
,
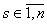 ,
,
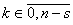 ;
;
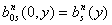 ,
, 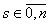 ;
;
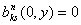 ,
,
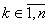 ,
,
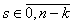 .
.
При 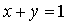
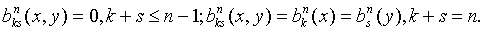
Отметим также, что 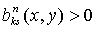 при
при
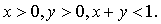
Справедливо тождество
 (1.45)
(1.45)
Оно следует из общей
формулы
(Здесь мы
воспользовались тем фактом, что  .)
.)
Подставив в (1.45) 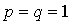 ,
получим
,
получим
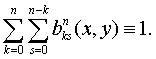
1. Рассмотрим полином от двух
переменных в форме Бернштейна
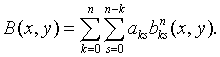
Введём конечные разности
на треугольном массиве коэффициентов
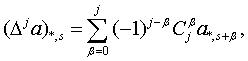
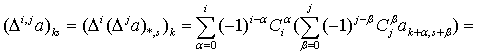
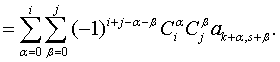
Предложение 1. Полином 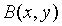 допускает
представление
допускает
представление
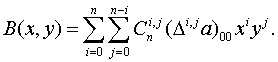 (1.46)
(1.46)
Доказательство. Имеем
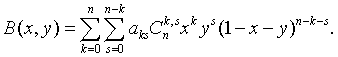
Применив формулу (1.46)
к 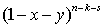 ,
получим
,
получим
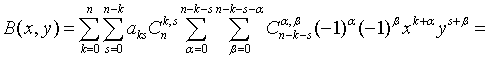
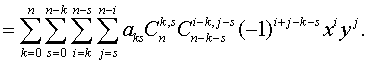
Поменяем порядок
суммирования по 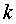 и
по
и
по 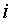 (через
(через
 ).
Поскольку
).
Поскольку
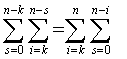 и
и 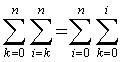 ,
,
то
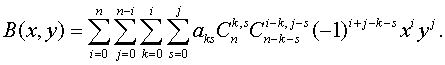
Воспользуемся равенством
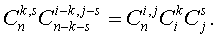
Придем к требуемому
представлению
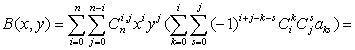
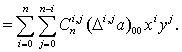
Предложение доказано.
. Зафиксируем два
целых неотрицательных числа 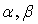 и положим
и положим 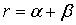 .
.
Предложение 2. Для
частной производной 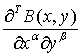 полинома
в форме Бернштейна при
полинома
в форме Бернштейна при 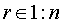 справедлива
формула
справедлива
формула
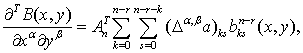 (1.47)
(1.47)
где 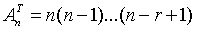 .
.
Доказательство.
Продифференцируем
тождество (1.46) по 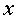 .
Учитывая, что
.
Учитывая, что 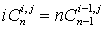 ,
получаем
,
получаем
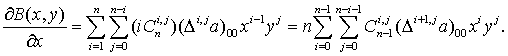
Но 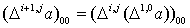 ,
так что
,
так что
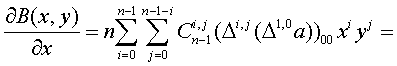
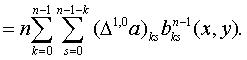
Это соответствует
формуле (1.47) при 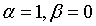 .
.
Далее
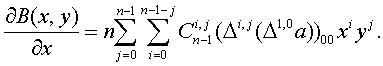
Продифференцируем данное
тождество по 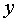 .
Учитывая, что
.
Учитывая, что 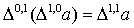 ,
аналогично предыдущему получаем
,
аналогично предыдущему получаем
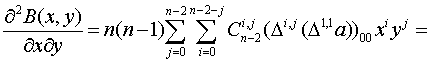
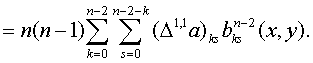
Продолжив
дифференцирование, придём к (1.47).
. Рассмотрим 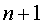 треугольных
массивов базисных полиномов Бернштейна
треугольных
массивов базисных полиномов Бернштейна 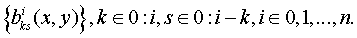
Положим для удобства 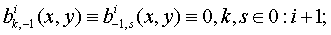
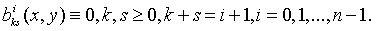
Например, при 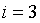 получим
15 искусственно добавленных полиномов.
получим
15 искусственно добавленных полиномов.
Предложение 3. При любых
вещественных  справедливы
рекуррентные соотношения
справедливы
рекуррентные соотношения
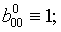
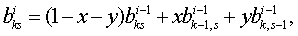 (1.47)
(1.47)
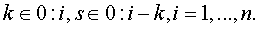
Доказательство.
Перепишем тождества (1.46), заменив в них 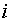 на
на 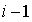 :
:
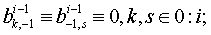
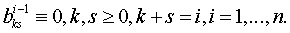 (1.48)
(1.48)
Зафиксируем 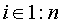 .
При
.
При 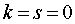 обе
части
обе
части 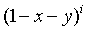 .
Пусть
.
Пусть 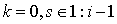 .
Тогда
.
Тогда
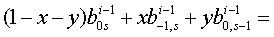
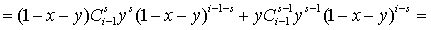
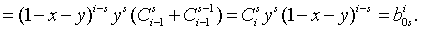
При 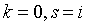 обе
части (1.45) равны
обе
части (1.45) равны 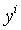 .
.
Аналогично проверяется
случай 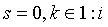 .
.
Если 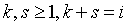 ,
то, согласно (1.44),
,
то, согласно (1.44), 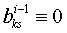 ,
так что
,
так что
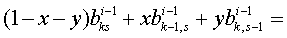
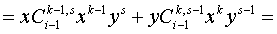
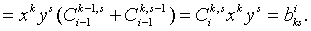
Осталось рассмотреть
случай 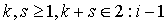 .
Имеем
.
Имеем

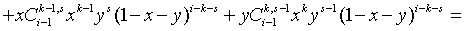
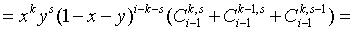
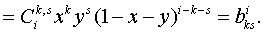
Мы воспользовались легко
проверяемой формулой
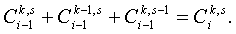
Предложение доказано.
. Зафиксируем
произвольные вещественные 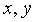 .
Для вычисления значения
.
Для вычисления значения 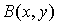 введем
введем
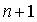 треугольных
массивов
треугольных
массивов 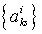 с
помощью рекуррентных соотношений
с
помощью рекуррентных соотношений
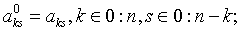
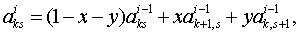 (1.49)
(1.49)
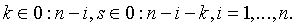
Предложение 4.
Справедливо равенство 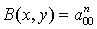 .
.
Доказательство. При 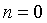 утверждение
тривиально. При
утверждение
тривиально. При 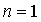 оно
проверяется так:
оно
проверяется так:

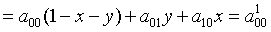
Пусть 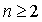 .
Согласно (1.47), (1.48) и (1.49) имеем
.
Согласно (1.47), (1.48) и (1.49) имеем
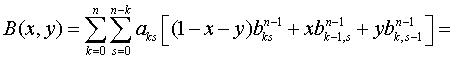
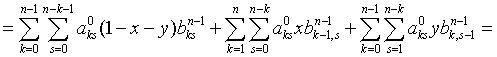
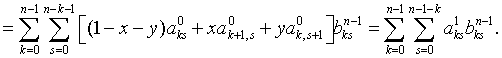
Продолжив аналогично,
получим
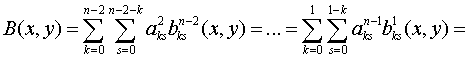
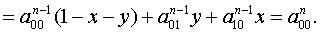
Предложение доказано.
. Обратимся к
вопросу о вычислении производных полинома 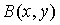 . Нам потребуется
соотношение
. Нам потребуется
соотношение
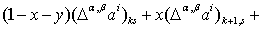
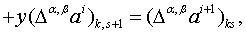 (1.50)
(1.50)
которое непосредственно
следует из (1.49). Действительно,
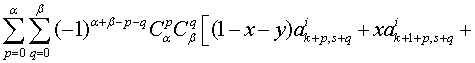
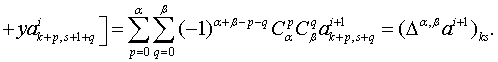
Предложение 5. При
фиксированных 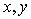 частные
производные от полинома в форме Бернштейна можно вычислить по формуле
частные
производные от полинома в форме Бернштейна можно вычислить по формуле
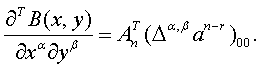
Здесь 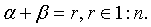
Доказательство. Согласно
(1.45)
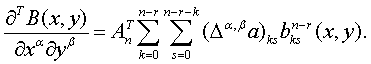
Воспользуемся приёмом из
доказательства и соотношением (1.50).
Запишем
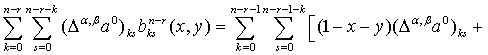
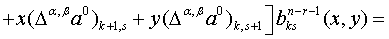
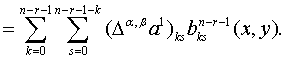
Продолжив данное
преобразование, получим
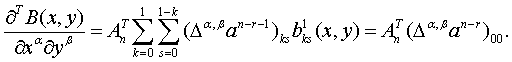
Предложение доказано.
Таким образом, 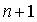 треугольных
массивов
треугольных
массивов 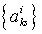 ,
построенных по формуле (8), дают возможность вычислить как значение полинома
,
построенных по формуле (8), дают возможность вычислить как значение полинома 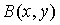 ,
таки значения всех его частных производных в фиксированной точке
,
таки значения всех его частных производных в фиксированной точке 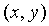 [17].
[17].
1.5 Применение полиномов
Бернштейна для решения нелинейных уравнений
Существуют различные способы
построения итерационных формул для решения скалярных уравнений [1, 54 с.].
Применение итерационными методов интерполяционного типа может быть затруднено способом
измерения или вычисления данных.
В данной работе предлагается способ
построения итерационной формулы основанный на аппроксимации с помощью полинома
Бернштейна [2]. Считается, что функция f(x) определена на отрезке [0,1] и её
значения заданы в ряде равноотстоящих точек xi = i/n, i = 0, 1, 2,
…, n.
Полином Бернштейна имеет вид
n(x) = å f
(k/n) Cnk xk(1-x)n-k
Замена в исходном уравнении функции,
её аппроксимацией, позволяет упростить задачу.
Уточнение значения корня
осуществляется за счет увеличения количества узлов или степени полинома.
На основе вычислительного
эксперимента выявлено влияние точности задания значений функции, количества
узлов степени полинома на качество решения.
Проведен сравнительный анализ
свойств предложенных итерационных формул, построенной на основе
аппроксимационного полинома Бернштейна, с известной итерационной формулой.
Теоретическая оценка погрешности для
трех равноотстоящих узлов:
n+1 ~C(en2-h2)
Рассмотрим тестовую
задачу: решим с помощью итерационно формулы на основе аппроксимационных
полиномов Бернштейна уравнение 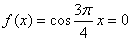 .
.
Построим функцию 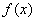 и
ее приближение полиномом
и
ее приближение полиномом 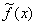 на
одном графике:
на
одном графике:
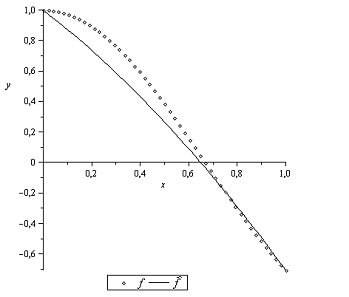
Рисунок 3 - Графики
функций 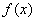 и
и
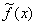
Точное решение уравнения
находим с помощью оператора solve среды Maple 11. Т.о. точное решение уравнения
выглядит так: 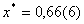 .
.
Запишем базисные
многочлены Бернштейна второй степени:
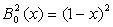 ,
,
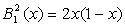 ,
,
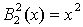 .
.
 ,
,
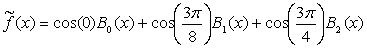 ,
,
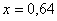 ,
, 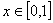 .
.
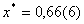 ,
, 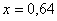
Погрешность вычислений
равна 0,02.
Теперь к исходному
уравнению добавим случайную величину (погрешность) ε,
например шум: 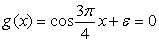 .
.
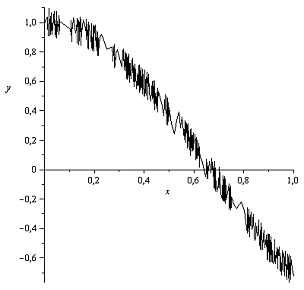
Рисунок 4 - График
функции g(x) при ε=0,1
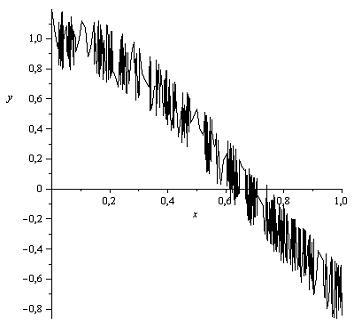
Рисунок 5 - График
функции g(x) при ε=0,2
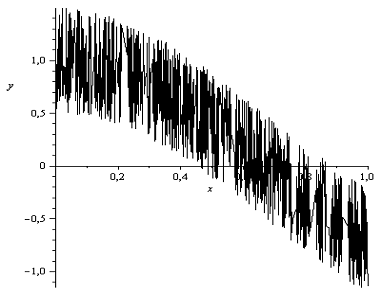
Рисунок 6 - График
функции g(x) при ε=0,5
С помощью Maple были
проведены вычисления для всех трех случаев.
Получены следующие
результаты (таблица 1, таблица 2, таблица 3):
Таблица 1 - Приближения
к корню уравнения при ε=10%
|
Номер итерации
|
Приближения
|
|
1
|
0.66396806
|
|
2
|
0.66442429
|
|
3
|
0.66426951
|
|
4
|
0.66435759
|
Таблица 2 - Приближения к корню
уравнения при ε=20%
|
Номер итерации
|
Приближения
|
|
1
|
0.5613358-0.025925I
|
|
2
|
0.561576-0.0269788I
|
|
3
|
0.561194-0.0257785I
|
|
4
|
0.560631-0.0244705I
|
Можно сделать вывод, что добавление
погрешности не влияет на качество решения.
Это выгодно отличает итерационную
формулу, построенную на основе апроксимационного полинома Бернштейна от ряда
классических итерационных методов: метод Ньютона, метод секущих и т.д.
Таблица 3 - Приближения к корню
уравнения при ε=30%
|
Номер итерации
|
Приближения
|
|
1
|
0.6539
|
|
2
|
0.6923
|
|
3
|
0.6812
|
|
4
|
0.6622
|
Также на качество решения не влияет
количество узлов полинома.
1.7
Обобщенные полиномы Бернштейна в задаче оценки параметров системы
Если область, в которой находится
корень системы является многогранником, обобщенные функции Бернштейна вводятся
так:
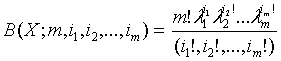 ;
;
Формулы для выпуклых комбинаций
вершин выпуклого n-угольника:
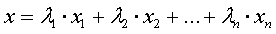
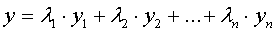
Существует два способа
для вычисления λi.
Первый способ: 1)
Разбиение области n - угольника с вершинами Ai(xi, yi),
i=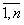 на треугольники. 2) В имеющейся n-угольной тонкой пластине выделим точку,
являющуюся геометрическим центром фигуры, и найдем ее координаты по формуле:
на треугольники. 2) В имеющейся n-угольной тонкой пластине выделим точку,
являющуюся геометрическим центром фигуры, и найдем ее координаты по формуле:
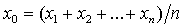

Соединив вершины
исходной фигуры с ее геометрическим центром, получим n треугольников.
Для каждого из которых,
коэффициенты выпуклой комбинации определены однозначно.
Второй способ основан на
решении оптимизационной задачи:
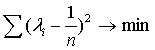
при ограничениях:
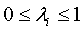
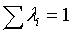
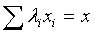 .
.
В данной работе было
рассмотрено решение систем нелинейных уравнений с применением формул для
обобщенных полиномов Бернштейна, что помогло избежать локализации корней.
1.8 Алгоритм оценки
параметров системы (корней нелинейной системы уравнений) с помощью обобщенных
полиномов Бернштейна
. Строим область:
выпуклый многогранник, в которой предположительно находится корень данной
системы нелинейных уравнений.
. Записываем
формулы для выпуклой комбинации вершин данного многогранника и условие
нормировки: 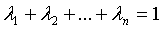 .
Затем выражаем все вершины многогранника через коэффициенты λ1,
λ2, …, λn.
.
Затем выражаем все вершины многогранника через коэффициенты λ1,
λ2, …, λn.
. В исходную
систему нелинейных уравнений подставляем выражения для вершин, т. о. получаем
преобразование систем:
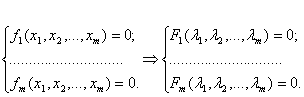
4. Полученную
(преобразованную) систему нелинейных уравнений решаем любым итерационным
методом.
В данной работе
рассмотрен итерационный метод Ньютона. При решении заранее необходимо задать
точность решения ε (ε=0.001).
5. После того как
получено приближенное решение нелинейной системы уравнений, λ1,
λ2, …, λn. необходимо
подставить в выражения для вершин многогранника и т. о. найти приближенной
решение исходной нелинейной системы уравнений.
Для компьютерной
реализации итерационного метода Ньютона, на Maple 11 была построена процедура,
высчитывающая корни системы нелинейных уравнений с заданной точностью и
затраченное на вычисление решения количество итераций (Приложение Б).
Для проверки
вышеприведенного алгоритма оценки параметров системы с помощью обобщенных
полиномов Бернштейна, рассмотрены числовые примеры, первый из которых, является
достаточно простым и имеет точное решение.
Второй пример
показывает, что алгоритм работает и в более сложных случаях.
Рассмотрим тестовый пример.
. Решим нелинейную систему уравнений
(1.51):
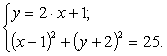 (1.51)
(1.51)
Данную систему уравнений
можно решить аналитически или графически и получить точное решение (найти
точный корень).
) Для решения системы
уравнений (1.51) воспользуемся методом подстановки, получим:
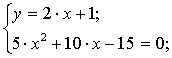
Получаем два решения
этой системы уравнений (1, 3) и (-3, 5).
Решим систему нелинейных
уравнений (1.51) на области треугольника с вершинами I - (0, 4); II - (8, 0);
III - (0, - 4).
Построим этот
треугольник в декартовой системе координат и отметим на ней корень (1, 3), т.
к. он лежит в области треугольника.
Рисунок 7 - Решение
системы уравнений в области треугольника
Т.к. любая точка
выпуклого многогранника является выпуклой комбинацией его вершин, для данного
треугольника получим систему уравнений, добавляя к вышесказанному условие
нормировки:
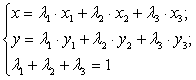 (1.52)
(1.52)
Подставляя вершины
треугольника в систему уравнений (1.52), получим:
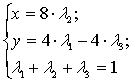 (1.53)
(1.53)
Подставим выраженные
через λ1, λ2,
λ3 переменные x и y в систему уравнений (1.51), добавляя к ней
условие нормировки, получим систему нелинейных уравнений относительно трех
неизвестных λ1, λ2,
λ3:
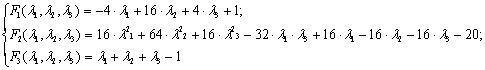 (1.54)
(1.54)
Решим систему нелинейных
уравнений (1.54) итерационным методом Ньютона (Приложение Б).
В Таблице 4 приведены
последовательные приближения корней.
Решение системы
нелинейных уравнений (1.54) найдено с точностью ε =0.001 и
имеет вид (0.813, 0.125, 0.062).
Подставим найденные λ1,
λ2, λ3 в
систему уравнений (1.52) получим:
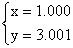
Итак, приближенный
корень для нелинейной системы уравнений (1.51) имеет вид (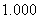 ,
,
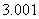 )
и практически совпадает с ее точным корнем (1, 3).
)
и практически совпадает с ее точным корнем (1, 3).
Таблица 4 - Приближения
корней методом Ньютона
|
i
|
λ1
|
λ2
|
λ3
|
|
0
|
0
|
0
|
0
|
|
1
|
1.125
|
0.333
|
−0.458
|
|
2
|
0.884
|
0.172
|
−0.056
|
|
3
|
0.818
|
0.129
|
0.053
|
|
4
|
0.813
|
0.125
|
0.062
|
2. Решим систему нелинейных
уравнений:
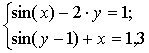 (1.55)
(1.55)
Данную систему уравнений
можно решить графически (рисунок 8).
Приблизительно корень
равен (2.25, -0.1).
Решим систему нелинейных
уравнений (1.51) на области треугольника с вершинами I - (0, 4); II - (8, 0);
III - (0, - 4).
Построим этот
треугольник в декартовой системе координат и отметим на ней корень (1, 3), т.
к. он лежит в области треугольника.
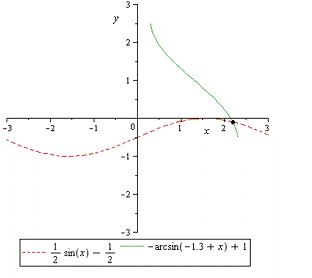
Рисунок 8 - Графическое
решение системы
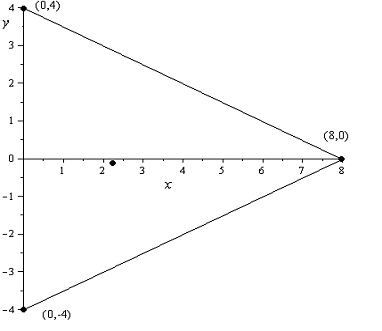
Рисунок 9 - Решение
системы уравнений в области треугольника
Используя выражения для
переменных x и y и условие нормировки из системы уравнений (1.52), получим
систему нелинейных уравнений относительно трех неизвестных λ1,
λ2, λ3:
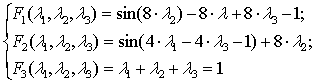 (1.56)
(1.56)
Решим систему нелинейных
уравнений (1.56) итерационным методом Ньютона.
Таблица 5 - Приближения корней
методом Ньютона
|
i
|
λ1
|
λ2
|
λ3
|
|
0
|
0
|
0
|
0
|
|
1
|
0.438
|
0.376
|
0.410
|
|
2
|
0.346
|
0.285
|
0.368
|
|
3
|
0.352
|
0.273
|
0.375
|
Итак, решение системы (1.56)
итерационным методом Ньютона с заданной точностью ε =0.001 имеет вид (0.352,
0.273, 0.375).
Подставим найденные значения λ1, λ2, λ3 в выражения для x и y и получим приближенный корень (2.187, −0.09)
для нелинейной системы уравнений (1.54).
.9 Решение систем нелинейных
уравнений на основе аппроксимации обобщениями полиномов Бернштейна
Рассмотрим
обобщения полиномов Бернштейна для полигональных областей на плоскости, которые
представляются следующим образом:
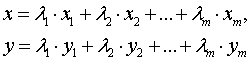
где
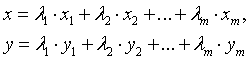
выпуклые комбинации
вершин m-угольника.
Рассмотрим тестовый пример:
Пусть задана система нелинейных
уравнений следующего вида:
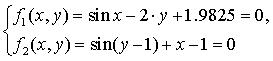
Исходная система уравнений в
выпуклой области локализации корня приближается обобщениями полиномов
Бернштейна.
Решение полученной системы
нелинейных алгебраических уравнений специального вида может быть записано в
виде цепной дроби.
Замена в исходной системе уравнений
функций их аппроксимантами, позволяет упростить задачу.
Уточнение значения корня
осуществляется за счет увеличения количества узлов или степени
аппроксимационного полинома.
Данную систему можно решить
несколькими способами. Ниже, на рисунке представлено графическое решение.
Нелинейная система уравнений:
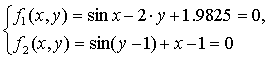 (1.57)
(1.57)
В данной главе была рассмотрена
задача оценки параметров системы (оценка корня нелинейной системы уравнений с
помощью задания точности вычислений) и алгоритм оценки параметров.
Использование обобщенных полиномов
Бернштейна помогло избежать локализации корней, благодаря заданию области и,
таким образом, к быстрому переходу к итерационному методу. Таким образом,
алгоритм оценки параметров системы упрощается, благодаря обобщенным полиномам
Бернштейна.
Уменьшение погрешности, с которой
вычислялся корень системы, привело к нахождению более точного решения [25].
2. Анализ устойчивости
нелинейных динамических систем
2.1 Основные понятия и
обозначения
Рассмотрим решение 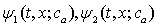 ,…
системы n уравнений, определенной в пространстве RN с координатами
,…
системы n уравнений, определенной в пространстве RN с координатами 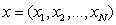 ,
,
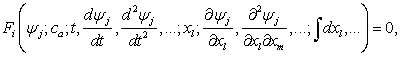 (2.1)
(2.1)
где 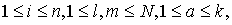 причем
переменные
причем
переменные 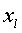 и
и
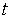 можно
считать соответственно пространственными и временными координатами. Решения
можно
считать соответственно пространственными и временными координатами. Решения 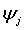 описывают
состояния некоторой системы, поэтому будем называть их переменными состояния.
Предполагается, что уравнения
описывают
состояния некоторой системы, поэтому будем называть их переменными состояния.
Предполагается, что уравнения 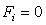 зависят от
зависят от 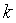 параметров
параметров
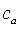 (числа
Рейнольдса, структурной константы, напряженности магнитного поля и т.д.), т.е.
последние могут качественно влиять на свойства решения
(числа
Рейнольдса, структурной константы, напряженности магнитного поля и т.д.), т.е.
последние могут качественно влиять на свойства решения 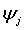 ,
и естественно назвать их управляющими параметрами.
,
и естественно назвать их управляющими параметрами.
Проблема исследования
решений системы уравнений (2.1), даже если речь идет о том, как зависят эти
решения от управляющих параметров 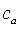 , является исключительно
сложной.
, является исключительно
сложной.
Однако, ее можно
упростить, сделав ряд последовательных предположений.
1. Предположим, что выражение (2.1),
которое в самом общем виде будет интегро-дифференциальным уравнением (или
значительно хуже), в действительности не содержит интегралов. Фактически это
означает, что система уравнений (2.1) есть не что иное, как множество
(нелинейных) уравнений в частных производных.
2. В целях дальнейшего
упрощения предположим, что система уравнений (2.1) не содержит пространственных
производных любого порядка, т.е.
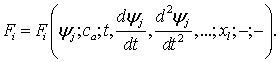 (2.2)
(2.2)
. Поскольку
решение данной системы уравнений вызывает существенные затруднения,
предположим, что она полностью не зависит от пространственных координат 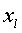 :
:
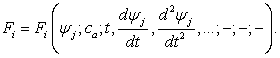 (2.3)
(2.3)
. Следующее
предположение сводится к тому, сто система уравнений (2.3) содержит производные
по времени не выше первого порядка и, кроме того, эти производные входят в
упрощенную функцию 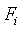 специальным
(«каноническим») образом:
специальным
(«каноническим») образом:
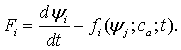 (2.4)
(2.4)
Систему уравнений
данного типа 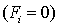 называют
динамической системой.
называют
динамической системой.
И опять же она слишком
трудна для исследования.
. Для упрощения
динамической системы предположим, что функции 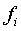 [выражение (2.4)]
полностью не зависит от времени.
[выражение (2.4)]
полностью не зависит от времени.
Тогда получим динамическую систему
уравнений:
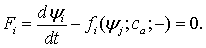 (2.5)
(2.5)
Относительно автономных
динамических систем, зависящих от малого числа управляющих параметров  ,
уже может быть высказано несколько полезных и сильных утверждений.
,
уже может быть высказано несколько полезных и сильных утверждений.
. Наконец,
заметим, что функции 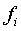 во
многом аналогичны компонентам силы в классической механике. В последней
существенное упрощение возможно тогда, когда сила является консервативной. Если
все функции
во
многом аналогичны компонентам силы в классической механике. В последней
существенное упрощение возможно тогда, когда сила является консервативной. Если
все функции 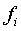 могут
быть заданы антиградиентом (по отношению к
могут
быть заданы антиградиентом (по отношению к 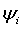 ) некоторой
потенциальной функции, то получаем систему уравнений
) некоторой
потенциальной функции, то получаем систему уравнений
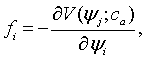
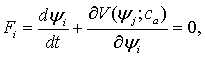 (2.6)
(2.6)
которую называют
градиентной системой 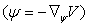 .
О свойствах таких систем может быть доказано довольно много глубоких теорем.
.
О свойствах таких систем может быть доказано довольно много глубоких теорем.
Особый интерес
представляет изучение состояния равновесия 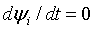 градиентных динамических
систем, которое может быть описано с помощью следующей системы уравнений:
градиентных динамических
систем, которое может быть описано с помощью следующей системы уравнений:
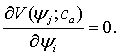 (2.7)
(2.7)
(Эти уравнения могут не
иметь решений 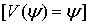 ,
иметь одно
,
иметь одно  или
более чем одно решение
или
более чем одно решение 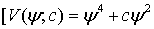 ,
одно решение, если
,
одно решение, если  ,
и три решения, если
,
и три решения, если 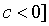 .)
В этом случае может быть доказано большое число полезных и сильных утверждений,
как о состоянии равновесия градиентных систем, так и о том, как эти состояния
зависят от управляющих параметров
.)
В этом случае может быть доказано большое число полезных и сильных утверждений,
как о состоянии равновесия градиентных систем, так и о том, как эти состояния
зависят от управляющих параметров 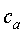 . Таким образом, можно
сделать вывод, согласно которому элементарная теория катастроф - это наука о
том, каким образом состояния равновесия
. Таким образом, можно
сделать вывод, согласно которому элементарная теория катастроф - это наука о
том, каким образом состояния равновесия 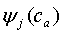 потенциальной функции
потенциальной функции  изменяются
при изменении управляющих параметров
изменяются
при изменении управляющих параметров 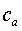 . Устойчивость
равновесия системы исследуется с помощью вспомогательной системы [13].
. Устойчивость
равновесия системы исследуется с помощью вспомогательной системы [13].
Рассмотрим систему дифференциальных
уравнений:
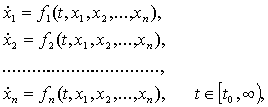 (2.8)
(2.8)
решение которой 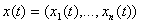 удовлетворяет
начальным условиям:
удовлетворяет
начальным условиям:
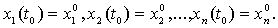 (2.9)
(2.9)
Обозначим
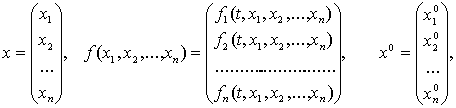 (2.10)
(2.10)
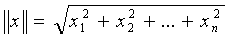 (2.11)
(2.11)
Согласно этим
обозначениям, задачу (2.8), (2.9) можно записать в виде:
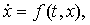 (2.12)
(2.12)
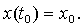 (2.13)
(2.13)
Пусть начальные данные х0
подвержены воздействию некоторых возмущений и вместо них имеем в (2.13)
начальные данные (значения) z0.
Тогда и решение задачи
(2.12), (2.13), вообще говоря, будут другими, отличными от х(t), которые
обозначим через z(t).
Определение 1
(устойчивость по Ляпунову)
Решение х=х(t) системы
дифференциальных уравнений (2.12), определенное при всех 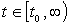 и
удовлетворяющее начальным условиям (2.13), называется устойчивым (по Ляпунову,
в смысле Ляпунова), если для любого действительного числа
и
удовлетворяющее начальным условиям (2.13), называется устойчивым (по Ляпунову,
в смысле Ляпунова), если для любого действительного числа 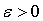 существует
такое действительное число
существует
такое действительное число 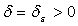 , что для всякого
решения z(t0)=z0, которое удовлетворяет неравенству
, что для всякого
решения z(t0)=z0, которое удовлетворяет неравенству
при всех 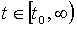 выполняется
неравенство
выполняется
неравенство
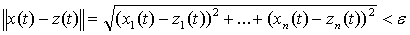 (2.15)
(2.15)
Таким образом,
устойчивость по Ляпунову решения x(t) системы (2.12), удовлетворяющей начальным
данным (2.13), означает, что малым изменениям в начальных данных x(t0)=x0
соответствуют малые изменения в самом решении x(t).
Определение 2
(неустойчивости по Ляпунову).
Решение x=x(t) системы
дифференциальных уравнений (2.12), определенное при всех 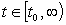 и
удовлетворяющее начальным условиям (2.13), называется неустойчивым по Ляпунову,
если для некоторого действительного числа
и
удовлетворяющее начальным условиям (2.13), называется неустойчивым по Ляпунову,
если для некоторого действительного числа 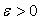 и любого
действительного
и любого
действительного 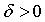 найдется
решение z(t) этой системы (2.12), отвечающее начальным данным z(t0)=z0
и момент времени t1>t0,
найдется
решение z(t) этой системы (2.12), отвечающее начальным данным z(t0)=z0
и момент времени t1>t0, 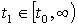 ,
такие, что
,
такие, что
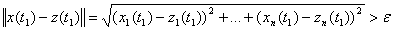 , (2.16)
, (2.16)
хотя
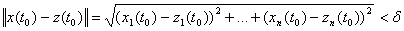 (2.17)
(2.17)
Следовательно,
неустойчивость по Ляпунову решения x(t) системы (2.12), удовлетворяющее
начальным данным (2.13), означает, что малым изменениям в начальных данных  x(t0)=x0
соответствуют большие изменения решения x(t).
x(t0)=x0
соответствуют большие изменения решения x(t).
Определение 3
(асимптотической устойчивости).
Решение x=x(t) системы
дифференциальных уравнений (2.12), определенное при всех  и
удовлетворяющее начальным условиям (2.13), называется асимптотически
устойчивым, если:
и
удовлетворяющее начальным условиям (2.13), называется асимптотически
устойчивым, если:
1. оно устойчиво по Ляпунову;
2. для всякого t1>t0
существует действительное число 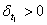 такое, что
такое, что
 (2.18)
(2.18)
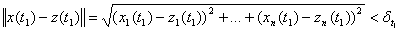 (2.19)
(2.19)
Асимптотическая
устойчивость решения x(t) системы (2.12) означает, что x(t) получает не только
малые изменения при малых изменениях начальных данных x(t0), но,
кроме того, эти изменения решения x(t) затухают с ростом t, начиная с момента
времени t1>t0.
Пусть найдено решение
x(t)=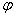 (t)
системы (2.12), удовлетворяющее начальным данным (2.13):
(t)
системы (2.12), удовлетворяющее начальным данным (2.13): 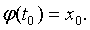
Тогда с помощью замены
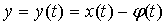 (2.20)
(2.20)
система (2.13)
преобразуется в эквивалентную систему
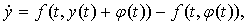 (2.21)
(2.21)
а начальные условия
примут вид
(t0)=0 (2.22)
Если задача (2.21),
(2.22) удовлетворяет условиям теоремы о единственности решения, то единственным
решением (2.21), (2.22) будет 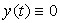 ,
, 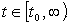 .
.
Нулевое решение y(t)=0, 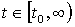 ,
принято называть тривиальным решением уравнения (2.22).
,
принято называть тривиальным решением уравнения (2.22).
Из сказанного следует,
что исследование на устойчивость решения задачи (2.12), (2.13) эквивалентно
исследованию на устойчивость тривиального решения y(t)=0 задачи (2.21), (2.22).
Второй метод Ляпунова.
Определение 5. Шаром
(радиуса 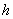 ,
,
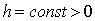 ,
и с центром в начале координат
,
и с центром в начале координат  ) в
) в 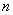 -
мерном пространстве называется множество точек
-
мерном пространстве называется множество точек 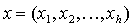 , удовлетворяющих
условию:
, удовлетворяющих
условию: 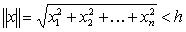 .
.
Обозначим  -
мерный шар радиуса
-
мерный шар радиуса 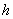 с
центром в точке
с
центром в точке  через
через
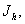 т.е.
т.е.
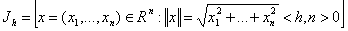 .
.
Определение 6. Скалярная
функция n переменных  непрерывная
в шаре
непрерывная
в шаре 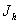 ,
называется:
,
называется:
. положительно -
определенной в шаре 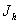 ,
если для всех
,
если для всех 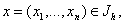 исключая
точку (0,0,…, 0), имеет место неравенство
исключая
точку (0,0,…, 0), имеет место неравенство 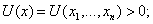
. отрицательно -
определенной в шаре 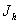 ,
если для всех
,
если для всех 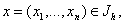 исключая
точку (0,0,…, 0), имеет место неравенство
исключая
точку (0,0,…, 0), имеет место неравенство 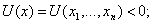
. знакоопределенной
в 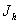 ,
если она является в
,
если она является в 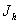 либо
только положительно - определенной, либо только отрицательно - определенной;
либо
только положительно - определенной, либо только отрицательно - определенной;
. положительно -
постоянной в 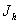 ,
если для всех
,
если для всех 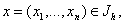 исключая
точку (0,0,…, 0), имеет место неравенство
исключая
точку (0,0,…, 0), имеет место неравенство 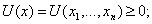
. отрицательно в 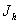 ,
если для всех
,
если для всех 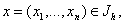 исключая
точку (0,0,…, 0), выполняется неравенство
исключая
точку (0,0,…, 0), выполняется неравенство 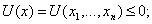
. знакопостоянной
в 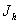 ,
если она является в
,
если она является в 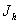 либо
только положительно - постоянной, либо только отрицательно - постоянной;
либо
только положительно - постоянной, либо только отрицательно - постоянной;
. знакопеременной
в 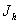 ,
если она является в
,
если она является в 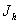 как
положительные, так и отрицательные значения.
как
положительные, так и отрицательные значения.
Пусть система
дифференциальных уравнений (2.12) (т.е. (2.8)) является автономной, т.е. функции
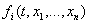 ,
не зависят явно от времени t:
,
не зависят явно от времени t:
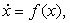 (2.23)
(2.23)
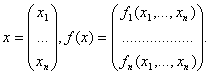
Будем предполагать, что
функции 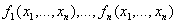 в
(2.23) при некотором h>0 удовлетворяют в шаре
в
(2.23) при некотором h>0 удовлетворяют в шаре 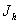 условиям:
условиям:
. они непрерывны
в 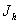 ;
;
. удовлетворяют
условиям Липшица:
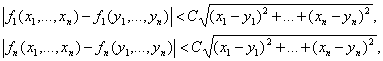
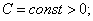
. 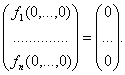 (2.24)
(2.24)
Выполнение условий 1) -
3) гарантирует, что при нулевом начальном условии 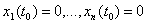 система
(2.23) имеет единственное тривиальное решение
система
(2.23) имеет единственное тривиальное решение 
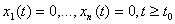 в шаре
в шаре 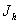 .
.
Теорема 4 (теорема
Ляпунова об устойчивости). Пусть существует (задана) функция 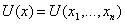 ,
которая в шаре
,
которая в шаре 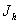 удовлетворяет
условиям:
удовлетворяет
условиям:
. 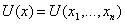 является
знакоопределенной функцией,
является
знакоопределенной функцией,
. 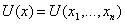 непрерывно
дифференцируема по переменным
непрерывно
дифференцируема по переменным 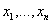 ,
,
. при 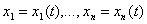 производная
производная
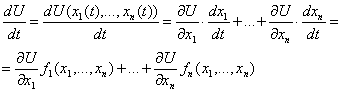
является знакопостоянной
и имеет знак, противоположный знаку 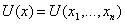 или тождественно равна
нулю.
или тождественно равна
нулю.
Тогда тривиальное
решение 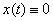 системы
дифференциальных уравнений (2.23) устойчиво.
системы
дифференциальных уравнений (2.23) устойчиво.
Теорема 5 (теорема
Ляпунова об асимптотической устойчивости).
Пусть существует
(задана) функция 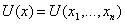 ,
которая в шаре
,
которая в шаре 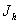 удовлетворяет
условиям:
удовлетворяет
условиям:
.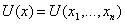 является знакоопределенной функцией.
является знакоопределенной функцией.
. 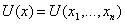 непрерывно
дифференцируема по переменным
непрерывно
дифференцируема по переменным 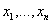 ,
,
. При 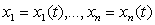 производная
производная
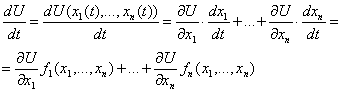 является
знакоопределенной и имеет знак, противоположный знаку
является
знакоопределенной и имеет знак, противоположный знаку 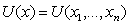 .
.
Тогда тривиальное
решение 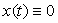 системы
дифференциальных уравнений (2.23) асимптотически устойчиво.
системы
дифференциальных уравнений (2.23) асимптотически устойчиво.
Теорема 6 (теорема
Ляпунова о неустойчивости).
Пусть существует
(задана) функция 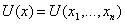 ,
которая в шаре
,
которая в шаре 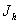 удовлетворяет
условиям:
удовлетворяет
условиям:
. 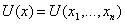 непрерывно
дифференцируема по переменным
непрерывно
дифференцируема по переменным 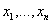 ,
,
. При 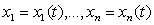 производная
производная
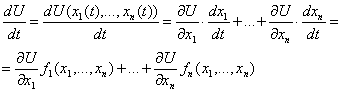 (2.25)
(2.25)
является
знакоопределенной. Пусть в любой окрестности точки (0,0,…, 0) найдется точка 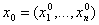 ,
для которой знак функции U(t) совпадает со знаком производной (2.25), т.е. либо
,
для которой знак функции U(t) совпадает со знаком производной (2.25), т.е. либо
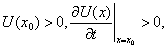 (2.26)
(2.26)
либо
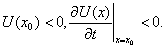 (2.27)
(2.27)
Тогда тривиальное
решение 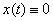 системы
дифференциальных уравнений (2.23) неустойчиво.
системы
дифференциальных уравнений (2.23) неустойчиво.
Замечание 1. Обратим
внимания, что условия (2.26), (2.27) можно записать следующим образом:
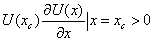 (2.28)
(2.28)
Замечание 2. В теореме 6
отсутствует требование о знакопостоянстве функции 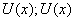 в
данном случае может как быть знакоопределенной функцией так и не быть ею.
в
данном случае может как быть знакоопределенной функцией так и не быть ею.
Замечание 3. Производную
вида (2.27) принято называть производной по 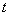 функции
функции 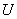 в
силу системы дифференциальных уравнений (2.23).
в
силу системы дифференциальных уравнений (2.23).
Замечание 4. функцию 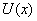 принято
называть функцией Ляпунова.
принято
называть функцией Ляпунова.
Замечание 5.
Исследование на устойчивость решения системы дифференциальных уравнений с
помощью теорем 1-3 требует определенных знаний о свойствах решения 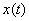 этой
системы. Совокупность теорем типа 1-3 называют первым методом Ляпунова
(исследования на устойчивость системы (2.23)). Совокупность теорем 4-6
позволяет обходиться при исследовании на устойчивость решения
этой
системы. Совокупность теорем типа 1-3 называют первым методом Ляпунова
(исследования на устойчивость системы (2.23)). Совокупность теорем 4-6
позволяет обходиться при исследовании на устойчивость решения 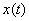 без
такого рода знаний: исследования производятся путем построения и изучения
свойств функции Ляпунова
без
такого рода знаний: исследования производятся путем построения и изучения
свойств функции Ляпунова 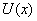 .
Поэтому совокупность теорем типа 4-6 принято называть вторым методом Ляпунова
[19].
.
Поэтому совокупность теорем типа 4-6 принято называть вторым методом Ляпунова
[19].
2.2 Анализ поведения
динамических систем на фазовой плоскости
Одним из основных методов
качественной теории дифференциальных уравнений является метод фазовой
плоскости.
Алгоритм построения фазового
портрета.
1. Выписать
характеристическое уравнение 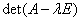 и найти его решения -
собственные значения
и найти его решения -
собственные значения  ,
,
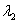 .
.
. По таблице
определить тип точки покоя и сделать вывод об устойчивости тривиального
решения.
. Начертить
фазовый портрет:
а) если точка покоя
является узлом или седлом, то следует найти собственные векторы 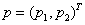 и
и
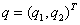 матрицы
матрицы
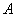 (в
случае
(в
случае 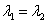 найти
только вектор
найти
только вектор 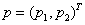 )
и начертить определяемые этими векторами прямые на фазовой плоскости. Далее
вычерчивается фазовый портрет. При этом учитывается, что в случае узла фазовые
траектории касаются той прямой, которая отвечает меньшему по модулю
собственному значению;
)
и начертить определяемые этими векторами прямые на фазовой плоскости. Далее
вычерчивается фазовый портрет. При этом учитывается, что в случае узла фазовые
траектории касаются той прямой, которая отвечает меньшему по модулю
собственному значению;
б) если точек покоя
является центром или фокусом, то семейство фазовых траекторий можно получить,
применив метод изоклин или, если это удобнее, решив уравнение аналитически;
в) если множество точек
покоя - прямая, то необходимо выписать уравнение этой прямой, которое является
решением одного из уравнений: 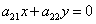 или
или 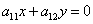 .
.
Уравнение семейства
фазовых траекторий, которые являются прямыми, в данном случае легко решаются
аналитически. По полученным уравнения множество точек покоя и фазовые
траектории вычерчиваются на фазовой плоскости;
г) в оставшихся случаях
(дикритический узел и фазовая плоскость) фазовый портрет вычерчивается
непосредственно.
. Определить направление
движения по фазовым траекториям и изобразить его стрелками на фазовом портрете.
Построим фазовый портрет
динамической системы
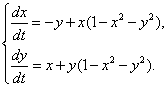
Решение. Можно сразу
выписать уравнение фазовых траекторий, разделив второе уравнение системы на
первое. Однако, для того чтобы получить аналитическое выражение для семейства
фазовых траекторий, удобнее сначала перейти к полярным координатам: 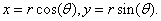
Отсюда 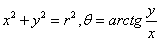 .
Продифференцируем последние два равенства по
.
Продифференцируем последние два равенства по 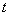 :
:
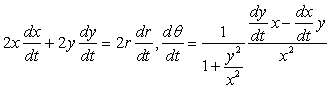
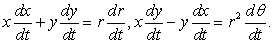 (2.29)
(2.29)
Теперь вернемся к
решаемой системе: умножим первое уравнение этой системы на 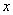 ,
а второе на
,
а второе на  и
сложим полученные уравнения:
и
сложим полученные уравнения:
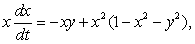
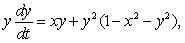
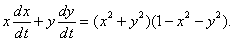
С учетом первого
уравнения системы (2.29) получаем
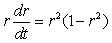 или
или 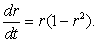 (2.30)
(2.30)
Далее умножим второе
уравнение исходной системы на 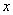 , а первое на
, а первое на  вычтем
из второго уравнения первое:
вычтем
из второго уравнения первое:
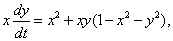
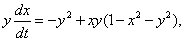
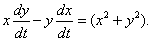
С учетом второго
уравнения системы (2.29) получаем
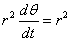 или
или 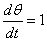 .
(2.31)
.
(2.31)
Интегрируем уравнение
(2.30):
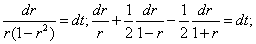
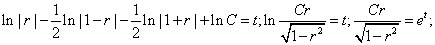
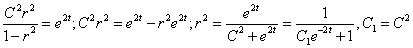
В результате получаем
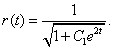 (2.32)
(2.32)
Решая уравнение (2.31),
находим 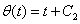 .
Таким образом, получаем общее решение поставленной задачи:
.
Таким образом, получаем общее решение поставленной задачи:
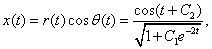
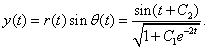
Полагая в (2.31) 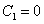 ,
получаем
,
получаем

Эти равенства определяют
замкнутую траекторию - окружность 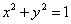 . Если
. Если 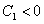 ,
то
,
то 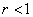 и
и
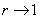 при
при
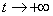 .
Это означает, что существует единственная замкнутая траектория
.
Это означает, что существует единственная замкнутая траектория 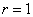 ,
к которой с течением времени приближаются все остальные траектории (рисунок
13).
,
к которой с течением времени приближаются все остальные траектории (рисунок
13).
Таким образом,
окружность 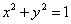 является
устойчивым предельным циклом системы.
является
устойчивым предельным циклом системы.
Заметим, что в данном
примере уравнение предельного цикла удалось найти явно [21].
В общем случае этого
сделать нельзя, поэтому обычно для построения фазового портрета используются
приближенные методы, например, метод изоклин.
2.3
Оценка локальной устойчивости нелинейных динамических систем
В работе рассматривается оценка
устойчивости равновесия системы с помощью метода функции Ляпунова, в котором
исследуется равномерное приближение функции Ляпунова, основанное на обобщенных
полиномах Бернштейна.
Исследуются автономные системы
дифференциальных уравнений. Задается система обыкновенных нелинейных
дифференциальных уравнений, имеющая следующий вид:
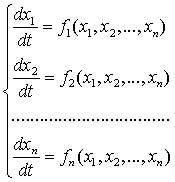 (2.33)
(2.33)
Рассмотрим алгоритм оценки
параметров нелинейной динамической системы с помощью обобщений полиномов
Бернштейна:
1. Область, в которой исследуется
решение выбранной системы, имеет вид выпуклого многогранника.
2. Функция
Ляпунова нелинейной системы (2.33) строится как сумма произведений
коэффициентов 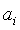 на
базисные полиномы Бернштейна:
на
базисные полиномы Бернштейна:
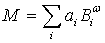 . (2.34)
. (2.34)
3. Записываются формулы для выпуклой
комбинации вершин данного многогранника:
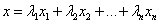
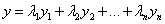 ,
,
где 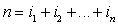 ,
,
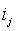 - номер вершины
треугольника.
- номер вершины
треугольника.
Добавляется условие
нормировки: 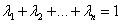 и
формулы для расчета узлов:
и
формулы для расчета узлов:
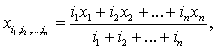 (2.35)
(2.35)
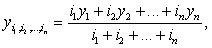 (2.36)
(2.36)
В формулу для обобщений
полиномов Бернштейна подставив выражения (2.35), (2.36), получим:
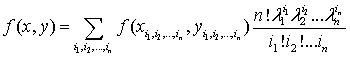 (2.37)
(2.37)
В формулу (2.34)
подставим выражение (2.37). Зададим условие для вспомогательной функции 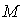 :
:
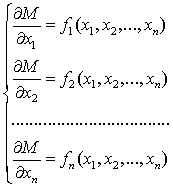 . (2.38)
. (2.38)
Решение системы (2.38)
методом наименьших квадратов (МНК) приводит к системе линейных алгебраических
уравнений, из которой находятся коэффициенты 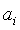 .
.
. Подставив
определенные коэффициенты 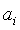 в
формулу (2.34), анализируется поведение функции
в
формулу (2.34), анализируется поведение функции 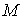 вблизи неподвижной
точки на основе теоремы Ляпунова об устойчивости.
вблизи неподвижной
точки на основе теоремы Ляпунова об устойчивости.
Иллюстрация метода на примере
исследования на устойчивость нелинейных динамических систем 2-го порядка.
. Задается автономная система нелинейных
дифференциальных уравнений 2-го порядка:
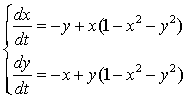 (2.39)
(2.39)
2. Строиться область: квадрат, в
которой предположительно находится неподвижная точка системы (2.39).
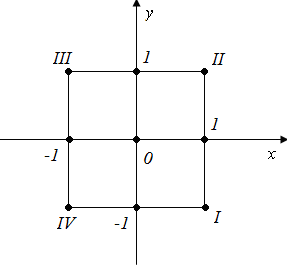
Рисунок 14 - Область нахождения
неподвижной точки
.
Записываются формулы для выпуклой комбинации вершин квадрата и условие
нормировки:

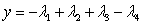
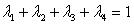
Выразим переменные 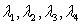 через
x и y:
через
x и y:
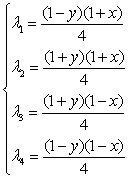 . (2.40)
. (2.40)
Выразив функцию 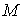 ,
подставив в (2.34) выражение (2.37). Приравнивая частные производные
,
подставив в (2.34) выражение (2.37). Приравнивая частные производные 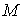 к
правым частям системы (2.39) (необходимо, чтобы степени левой и правой части
уравнения были равны), получается система линейных алгебраических уравнений, из
которой МНК находятся коэффициенты:
к
правым частям системы (2.39) (необходимо, чтобы степени левой и правой части
уравнения были равны), получается система линейных алгебраических уравнений, из
которой МНК находятся коэффициенты: 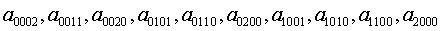 . Возвращаясь к
переменным x и y в выражении (2.34) получается функция, исследуя которую с
помощью теоремы Ляпунова (об устойчивости) можно сделать вывод, что система
нелинейных дифференциальных уравнений (2.37) устойчива.
. Возвращаясь к
переменным x и y в выражении (2.34) получается функция, исследуя которую с
помощью теоремы Ляпунова (об устойчивости) можно сделать вывод, что система
нелинейных дифференциальных уравнений (2.37) устойчива.
Заключение
В работе построены итерационные
алгоритмы решения нелинейных уравнений и систем нелинейных уравнений,
обеспечивающие высокую скорость сходимости и устойчивые к погрешностям в
исходных данных.
В ходе компьютерных экспериментов
было установлено, что итерационная формула на основе аппроксимационного
полинома Бернштейна, не зависит от изменения количества узлов, степени полинома
и точности задания функции в сравнении с классическими итерационными методами
(метод Ньютона, метод секущих).
В данной работе предлагается способ
исследования локальной устойчивости нелинейных систем обыкновенных
дифференциальных уравнений, основанный на аппроксимации функции Ляпунова
обобщениями полиномов Бернштейна.
На основе произведенного в работе
анализа получены следующие результаты:
1. Итерационная формула
аппроксимационного типа для решения нелинейных уравнений и систем нелинейных
уравнений.
2. Алгоритм анализа
устойчивости нелинейных динамических систем на основе теории Ляпунова.
Список источников
1. Сухно И.В. Численные методы и программирование / И.В.
Сухно, В.А. Волынкин, В.Ю. Бузько Краснодар: Парабеллум, 2002, 225 с.
2. Самарский А.А. Численные методы / А.В. Гулин, А.А.
Самарский М.: Мир, 1989. 215 с.
. Ракитин В.И. Практическое руководство по методам
вычисления / В.И. Ракитин, В.Е. Первушин, М. 1998. 269 с.
4. Бахвалов Н.С. Численные методы / Н.С. Бахвалов М.: Высш. шк.,
1975. 357 с.
. Губарь Ю.В. Введение в математическое моделирование, курс
лекций / Ю.В. Губарь, М.: Высш. шк., 2007. 316 с.
6. Джонсон К. Численные методы в химии / К. Джонсон, М.:
Мир, 1983. 362 c.
. Демидович Б.П. Численные методы анализа. Приближение
функций, дифференциальные и интегральные уравнения / Б.П. Демидович, И.А.
Марон, Э.З. Шувалова, М.: Наука, 1967. 386 с.
. Банди Б. Методы оптимизации. Вводный курс / Б. Банди, М.:
Радио и связь, 1988. 267 с.
. Данилина Н.И. Вычислительная математика. / Н.И. Данилина,
Н.С. Дубровская, О.П. Кваша, Г.Л. Смирнов, М.: Высшая школа, 1985. 435 с.
. Турчак Л.И. Основы численных методов / Л.И. Турчак, М.: Наука,
1987. 335 с.
. Тарасевич Ю.Ю. Информационные технологии в математике /
Ю.Ю. Тарасевич, М.: Солон-Пресс, 2003. 412 с.
. Дьяконов В.А. Maple 7: учебный курс / В.А. Дьяконов,
СПб.: Питер, 2002. 632 с.
. Дьяконов В.А. Mathcad 2000: учебный курс / В.А. Дьяконов
СПб.: Питер, 2000. 513 с.
. Трауб Дж. Итерационные методы решения уравнений / Дж.
Трауб, М.: Мир, 1985. 264 с.
. Амосов А.А. Вычислительные методы для инженеров / А.А.
Амосов, Ю.А. Дубинский, Н.В. Колченова, М.: Высшая школа, 1994. 554 с.
. Пантелеев А.В. Обыкновенные дифференциальные уравнения в
примерах и задачах / А.В. Пантелеев, А.С. Якимова, А.В. Босов, М.: Высшая
школа, 2001. 376 с.
. Барбанин Е.А Введение в теорию устойчивости / Е.А.
Барбанин, М.: Наука, 1967. 345 с.
. Арнольд В.И. Обыкновенные дифференциальные уравнения /
В.И. Арнольд, М.: Наука, 2000. 367 с.
. Крылов В.И. Вычислительные методы / В.И. Крылов, В.В.
Бабков, П.Н. Манастырный, М.: Наука, 1998. 264 с.
. Хейгман Л.Я. Прикладные итерационные методы / Пер. с
англ. А.Ю. Еремена и Е.И. Капорина; Под ред. Ю.А. Кузнецова, М.: Мир, 1986. 446
с.
. Бахвалов Н.С. Численные методы / Н.С. Бахвалов, М.:
Наука, 1975. 347 с.
. Боглаев Ю.П. Вычислительная математика и программирование
/ Ю.П. Боглаев, М.: Высшая школа, 1990. 208 с.
. Воробьева С.Н. Практикум по вычислительной математике /
С.Н. Воробьева, А.Н, Данилова, М.: Высшая школа, 1990. 208 с.
. И.В. Алферова Итерационные формулы аппроксимационного
типа для решения скалярного уравнения / И.В. Алферова, А.М. Кравцов, Материалы
VIII региональной научно-технической конференции «Вузовская
наука-Северо-Кавказскому региону». Том первый. Естественные и точные науки.
СевКавГТУ, 2009.