Исследование систем управления манипулятором MR-999Е
Міністерство
освіти і науки України
Харківський
національний університет радіоелектроніки
Факультет
Комп’ютерної інженерії та управління
Кафедра
Технології та автоматизація виробництва РЕЗ та ЕОЗ
МАГІСТЕРСЬКА
АТЕСТАЦІЙНА РОБОТА
ПОЯСНЮВАЛЬНА
ЗАПИСКА
Дослідження
систем керування маніпулятором MR-999E
Студент Козирєв Є.А.
Керівник проекту проф.Омаров М.А.
РЕФЕРАТ
Мета роботи - дослідження методів ідентифікації об’єктів у робочій зоні
робота.
Об’єкт дослідження - система технічного зору промислового робота.
Розглянуто методи розпізнавання та ідентифікації об’єктів роботизованого
виробництва, проаналізовано методи обробки інформації у системах технічного
зору роботів, побудована теоретико-множинна модель розпізнавання та
ідентифікації, розглянута практична реалізація методів обробки інформації в
робототехнічних системах, розроблено програмне забезпечення, що реалізує методи
розпізнавання та ідентифікації об’єктів роботизованого виробництва.
Основними методами обробки інформації є сегментація (процес розділу сцени
на складові частини або об'єкти), визначення порогового рівня,
обласними-орієнтована сегментація, дескриптори країв і областей зображень, опис
тривимірних сцен і структур, обробка візуальної інформації.
До числа перспективних напрямків досліджень слід віднести подальший
розвиток методів розпізнавання та ідентифікації, їх програмну реалізацію для
промислових операційних систем реального часу. У комбінації з системою
прийняття рішень такі розробки істотно прискорять реалізацію систем управління
інтелектуальними роботами.
СОДЕРЖАНИЕ
Перечень
условных обозначений, символов, единиц, сокращений и терминов
ВВЕДЕНИЕ
.
МЕТОДЫ ОБРАБОТКИ ИНФОРМАЦИИ В СИСТЕМАХ ТЕХНИЧЕСКОГО ЗРЕНИЯ РОБОТОВ
1.1 Классификация методов
обработки информации в СТЗ
.2 Методы предварительной
обработки изображений
.3 Сегментация объектов
.3.1 Проведение контуров и
определение границ
.3.2 Локальный анализ
.3.3 Глобальный анализ с
помощью преобразования Хоуга
.4 Определение порогового
уровня изображений
.5 Областно-ориентированная
сегментация
.5.1 Основные определения
.5.2 Расширение области за
счет объединения пикселей
.5.3 Разбиение и объединение
области
.5.4 Анализ движения объектов
.6 Проблема описания объектов
.7 Дескрипторы границы
.8 Дескрипторы областей
изображений
.8.1 Некоторые простые
дескрипторы
.8.2 Текстура
.8.3 Схема области
.9 Сегментация и описание
трехмерных структур
.10 Описание трехмерной сцены
плоскими участками
.11 Техника обработки
визуальной информации
. МЕТОДЫ ИДЕНТИФИКАЦИИ
ОБЪЕКТОВ В РОБОТИЗИРОВАННЫХ СИСТЕМАХ
.1 Метод сравнения с эталоном
.2 Методы теории графов и
распознавание
.3 Корреляционный метод
.4 Распознавание через связь
шаблонов
.4.1 Поиск объектов указанием
связей между шаблонами
.4.2 Описание фрагментов
изображения
.4.3 Указание признаков и
простая порождающая модель
.4.4 Вероятностные модели для
указания
.4.5 Доработка порождающей
модели
.4.6 Указание связей
.4.7 Указание на трехмерные
объекты
.5 Искусственные нейронные
сети и их использование при идентификации изображений
.6 Распознавание объектов и
их интерпретация
.7 Теоретико-множественная
модель распознавания и идентификации
3.
ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ МЕТОДОВ ОБРАБОТКИ ИНФОРМАЦИИ В СИСТЕМАХ ТЕХНИЧЕСКОГО
ЗРЕНИЯ
3.1 Основные подходы к
практической реализации методов обработки информации
.1.1 Методы пространственной
области
.1.2 Методы частотной области
.2 Библиотека Integrated
Performance Primitives (IPP)
.3 Библиотека AviCap
.4 Библиотека OpenCV
.4.1Операторы для определения
изображений при помощи библиотеки OpenCV
4.
РАЗРАБОТКА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОБЪЕКТОВ
РОБОТИЗИРОВАННОГО ПРОИЗВОДСТВА С ПОМОЩЬЮ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ
4.1 Основные особенности
разработанного программного обеспечения
.2Реализация функции
обработки изображений
.3 Реализация функций распознавания
и идентификации
5.
БЕЗОПАСНОСТЬ ЖИЗНИ И ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА
5.1 Анализ условий труда в
помещении лаборатории исследовательского бюро кафедры ТАПР
.2 Техника безопасности в
лаборатории исследовательского бюро
.3 Производственная санитария
и гигиена труда в лаборатории исследовательского бюро
.4 Пожарная профилактика
лаборатории исследовательского бюро
ВЫВОДЫ
ПЕРЕЧЕНЬ
ССЫЛОК
Приложение
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ, СИМВОЛОВ, ЕДИНИЦ, СОКРАЩЕНИЙ И
ТЕРМИНОВ
СТЗ- Система
технического зренияOpen Source Computer Vision Library, библиотека
компьютерного зрения с открытым исходным кодом
IPP-
Integrated Performance Primitives, библиотека компьютерного зренияMachine Learning LibraryAvi Capture
ЭВМ-
Электронно-вычислительная машина
ПСО-
Преобразование средних осей
ИНС-
Искусственные нейронные сетиMachine Learning Library
ВВЕДЕНИЕ
Зрительные возможности робота, как и людей, обеспечиваются сложным
чувствительным механизмом, который позволяет гибко реагировать на изменения
внешней среды. Использование технического зрения и других методов очувствления
диктуется постоянной необходимостью повышать гибкость и расширять области
применения робототехнических систем. Хотя датчики расстояния, тактильные
датчики и датчики силы играют большую роль в совершенствовании функционирования
робота, техническое зрение является наиболее мощным источником информации для
робота. В силу сказанного, исследования в области систем технического зрения
роботов продолжают оставаться одним из наиболее перспективных направлений
современной робототехники, что и подтверждает актуальность данной работы.
Зрение робота можно определить как процесс выделения, идентификации и
преобразования информации, полученной из трехмерных изображений. Этот процесс,
называемый также техническим или машинным зрением, разделяется на шесть
основных этапов: а) снятие информации, б) предварительная обработка информации,
в) сегментация, г) описание, д) распознавание, е) интерпретация. Снятие
информации представляет собой, процесс получения визуального изображения.
Предварительная обработка информации заключается в использовании таких методов
как понижение шума или улучшение изображения отдельных деталей. Сегментация -
процесс выделения на изображении интересующих объектов. При описании
определяются характерные параметры (например, размеры или форма), необходимые
для выделения требуемого объекта на фоне других. Распознавание представляет
собой процесс идентификации объектов (например, гаечного ключа, болта, блока
двигателя). Наконец, интерпретация выявляет принадлежность к группе
распознаваемых объектов.
Названные этапы удобно сгруппировать в соответствии со сложностью их
реализации. Выделим три уровня технического зрения: низкий, средний и высокий.
Хотя четких границ между этими уровнями не существует, их выделение целесообразно
для классификации различных процессов, характерных для систем технического
зрения.
Под низким уровнем технического зрения понимаются такие процессы, которые
являются простыми с точки зрения осуществления автоматических действий, не
требующих наличия искусственного интеллекта. К низкому уровню технического
зрения мы будем также относить снятие и предварительную обработку информации.
Под средним уровнем технического зрения понимаются процессы выделения,
идентификации и разметки элементов изображения, полученного на нижнем уровне. С
учетом принятого подразделения технического зрения к среднему уровню относятся
сегментация, описание и распознавание отдельных объектов.
Под высоким уровнем технического зрения понимаются процессы, относящиеся
к искусственному интеллекту. В то время как алгоритмы, используемые на нижнем и
среднем уровнях технического зрения, разработаны достаточно хорошо, знание и
понимание процессов высокого уровня пока еще недостаточны.
Целью данной магистерской аттестационной работы является исследование
методов идентификации объектов в рабочей зоне робота.
Объектом исследования является система технического зрения робота.
1. МЕТОДЫ ОБРАБОТКИ ИНФОРМАЦИИ В СИСТЕМАХ ТЕХНИЧЕСКОГО ЗРЕНИЯ РОБОТОВ
1.1 Классификация методов обработки информации в СТЗ
Одним из важнейших направлений развития робототехнических систем всегда
была организация взаимодействия манипулятора и сенсорных анализаторов.
Использование сенсоров придает системе гибкость, расширяет ее функциональные
возможности и увеличивает круг решаемых ею задач. Большинство ныне существующих
систем, использующих взаимодействие манипулятора и сенсоров, построены путем
связывания автономных сенсорной и робототехнической подсистем. Эти системы
продемонстрировали состоятельность концепции взаимодействия системы управления
роботом с сенсорной подсистемой, на основе которой разработана концепция
визуального управления роботами [1]. Схема обработки информации в СТЗ робота
показана на рис. 1.1.

Рисунок 1.1 - Обработка информации в СТЗ робота
С целью классификации методов и подходов, используемых в системах
технического зрения, зрение разбито на три основных подкласса: зрение низкого,
среднего и высокого уровней. Системы технического зрения низкого уровня предназначены
для обработки информации с датчиков очувствления [1].
Эти системы можно отнести к классу «интеллектуальных» машин, если они
обладают следующими признаками (признаками интеллектуального поведения):
а)возможностью
выделения существенной информации из множества независимых признаков;
б)способностью к
обучению на примерах и обобщению этих знаний с целью их применения в новых
ситуациях;
в)возможностью
восстановления событий по неполной информации;
г)способностью
определять цели и формулировать планы для достижения этих целей.
Создание систем технического зрения с такими свойствами для ограниченных
видов рабочего пространства в принципе возможно, но характеристики таких систем
далеки от возможностей человеческого зрения. В основе технического зрения лежит
аналитическая формализация, направленная на решение конкретных задач. Машины с
сенсорными характеристиками, близкими к возможностям человека, по-видимому,
появятся еще не скоро. Однако отметим, что копирование природы не является
единственным решением этой проблемы [1]. Современное решение задачи о полете в
пространстве в корне отличается от решений, подсказанных природой. По скорости
и достижимой высоте самолеты намного превосходят возможности птиц.
Системы технического зрения среднего уровня связаны с задачами
сегментации, описания и распознавания отдельных объектов. Эти задачи охватывают
множество подходов, основанных на аналитических представлениях. Системы
технического зрения высокого уровня решают проблемы, рассмотренные выше. Для
более ясного понимания проблем технического зрения высокого уровня и его связи
с техническим зрением низкого и среднего уровней обычно вводят ряд ограничений
и упрощают решаемую задачу.
1.2 Методы предварительной обработки изображений
Процесс идентификации объектов, находящихся в рабочей зоне робота, обычно
включает два этапа: выделение характерных признаков объектов; собственно
распознавание объектов по найденной совокупности характерных признаков. В
соответствии с такой структурой процесса идентификации алгоритмы обработки
информации в СТЗ принято делить на алгоритмы предварительной обработки и
алгоритмы распознавания, что носит в известной степени условный характер, так
как в некоторых практических приложениях одни и те же по математической сути
алгоритмы могут быть использованы на обоих этапах рассматриваемого процесса.
В соответствии со спектральным диапазоном преобразователей свет - сигнал
и принципом действия СТЗ датчик формирует изображение рабочей зоны робота.
Формально получение изображения заключается в определении функциональной
зависимости интенсивности излучений рабочей зоны от координат точек изображения
х и у:
= f (x, y). (1.1)
В дальнейшем под «изображением» будем понимать именно функциональную
зависимость f(x, у). С учетом принятой терминологии задачей предварительной
обработки является поиск каких-либо особенностей функции f(x, у), которые могли
бы указать на тип объекта, находящегося в рабочего зоне [2].
1.3 Сегментация объектов
1.3.1 Проведение
контуров и определение границ
Сегментацией называется процесс подразделения сцены на составляющие части
или объекты. Сегментация является одним из основных элементов работы
автоматизированной системы технического зрения, так как именно на этой стадии
обработки объекты выделяются из сцены для дальнейшего распознавания и анализа.
Алгоритмы сегментации, как правило, основываются на двух фундаментальных
принципах: разрывности и подобии. В первом случае основной подход основывается
на определении контуров, а во втором - на определении порогового уровня и
расширении области. Эти понятия применимы как к статическим, так и к
динамическим (зависящим от времени) сценам. В последнем случае движение может
служить мощным средством для улучшения работы алгоритмов сегментации.
Методы - вычисление градиента, пороговое разделение - определяют разрывы
в интенсивности представления образа объекта. В идеальном случае эти методы
определяют пиксели, лежащие на границе между объектом и фоном. На практике
данный ряд пикселов редко полностью характеризует границу из-за шума, разрывов
на границе вследствие неравномерной освещенности и других эффектов, приводящих
к размытию изображения. Таким образом, алгоритмы обнаружения контуров
сопровождаются процедурами построения границ объектов из соответствующих
последовательностей пикселов [3]. Ниже рассмотрено несколько методик, пригодных
для этой цели.
1.3.2 Локальный анализ
Одним из наиболее простых подходов соединения точек контура является
анализ характеристик пикселов в небольшой окрестности (например, в окрестности
размером 3 X 3 или 5 X 5) каждой точки (х, у) образа, который уже подвергся
процедуре обнаружения контура. Все точки, являющиеся подобными (определение
критерия подобия дано ниже), соединяются, образуя границу из пикселов,
обладающих некоторыми общими свойствами.
При таком анализе для установления подобия пикселов контура необходимо
определить:
а) величину
градиента, требуемого для построения контурного пикселя; б) направление
градиента.
Первая характеристика обозначается величиной G{f(x, у)}.
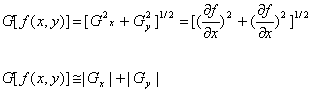 (1.2)
(1.2)
Таким образом, пиксель контура с координатами (х', у') подобен по
величине в определенной ранее окрестности (х, у) пикселя с координатами (х, у),
если справедливо неравенство
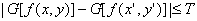 (1.3)
(1.3)
где Т-пороговое значение.
Направление градиента устанавливается по углу вектора градиента,
определенного в уравнении
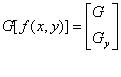 (1.4)
(1.4)
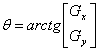 (1.5)
(1.5)
где q-угол (относительно оси х), вдоль
которого скорость изменения имеет наибольшее значение. Тогда можно сказать, что
угол пикселя контура с координатами {х', у') в некоторой окрестности (х, у)
подобен углу пикселя с координатами {х, у) при выполнении следующего
неравенства:
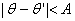 (1.6)
(1.6)
где
А-пороговое значение угла. Необходимо отметить, что направление контура в точке
{х, у) в действительности перпендикулярно направлению вектора градиента в этой
точке. Однако для сравнения направлений неравенство дает эквивалентные
результаты.
Основываясь
на этих предположениях, мы соединяем точку в некоторой окрестности (х, у) с
пикселем, имеющим координаты (х, у), если удовлетворяются критерии по величине
и направлению. Двигаясь от пикселя к пикселю и представляя каждую
присоединяемую точку как центр окрестности, процесс повторяется для каждой
точки образа. Для установления соответствия между уровнями интенсивности
освещения и последовательностями пикселов контура применяется стандартная
библиотечная процедура.
Цель
состоит в определении размеров прямоугольников, с помощью которых можно
построить качественное изображение. Построение таких прямоугольников
осуществляется в результате определения строго горизонтальных и вертикальных
контуров. Дальнейший процесс состоял в соединении сегментов контура,
разделенных небольшими промежутками, и в объединении отдельных коротких
сегментов.
1.3.3 Глобальный анализ с помощью преобразования Хоуга
Рассмотрим метод соединения граничных точек путем определения их
расположения на кривой специального вида. Первоначально предполагая, что на
плоскости ху образа дано п точек, требуется найти подпоследовательности точек,
лежащих на прямых линиях. Одно из возможных решений состоит в построении всех
линий, проходящих через каждую пару точек, а затем в нахождении всех
подпоследовательностей точек, близких к определенным линиям. Задача, связанная
с этой процедурой, заключается в нахождении п(п- 1)/2 ~ п2 линий и
затем в осуществлении п[п(п-1)]/2 ~ п3 сравнений каждой точки со
всеми линиями. Этот процесс трудоемок с вычислительной точки зрения за
исключением самых простых приложений [4].
Данную задачу можно решить по-другому, применяя подход, предложенный
Хоугом и называемый преобразованием Хоуга. Вычислительная привлекательность
преобразования Хоуга заключается в разделении пространства параметров на так
называемые собирающие элементы , где (aмакс, амин) и (bмакс,
bмин)-допустимые величины параметров линий. Собирающий элемент A (i,
j) соответствует площади, связанной с координатами пространства параметров (аi,
bj). Вначале эти элементы считаются равными нулю. Тогда для каждой
точки (xk, уk) в плоскости образа мы полагаем параметр а
равным каждому из допустимых значений на оси а и вычисляем соответствующее b,
используя уравнение b = -хk + yk Полученное значение b
затем округляется до ближайшего допустимого значения на оси b. Если выбор aр
приводит к вычислению bq, мы полагаем А(р, q) ==А(р, q) + 1. После
завершения этой процедуры значение М в элементе A (i, j) соответствует М точкам
в плоскости xy, лежащим на линии y=aix+b. Точность расположения этих
точек на одной прямой зависит от числа разбиений плоскости аb. Если мы
разбиваем ось а на К частей, тогда для каждой точки (xk, уk)
мы получаем К значений b, соответствующих К возможным значениям а. Поскольку
имеется п точек образа, процесс состоит из пК вычислительных операций.
робот
технический нейронный изображение
1.4 Определение порогового уровня изображений
Понятие порогового уровня (порога) тест вида
Т = Т [х, у, р (х, у), f (х, у)], (1.7)
где f(x, у) -интенсивность в точке (х, у), р(х, у)-некоторое локальное
свойство, определяемое в окрестности этой точки. Пороговое изображение дается
следующим выражением:
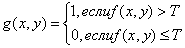 , (1.8)
, (1.8)
так что пиксели в g(x, у), имеющие значение 1, соответствуют объектам, а
пиксели, имеющие значение 0, соответствуют фону. В уравнении предполагается,
что интенсивность объектов больше интенсивности фона. Противоположное условие
получается путем изменения знаков в неравенствах.
1.5 Областно-ориентированная сегментация
1.5.1 Основные определения
Целью сегментации является разделение образа на области. Рассмотрим
методы сегментации, основанные на прямом нахождении областей [4].
Пусть R - область образа. Рассмотрим сегментацию как процесс разбиения R
на n подобластей R1, R2, ..., Rn, так что:
a)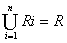 ;
;
б)Pi-связная
область, i= 1, 2, ..., п;
в)Ri =
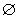 для всех i и j, i
для всех i и j, i 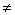 j;
j;
г)P(Ri) есть ИСТИНА для i= 1, 2, ..., n;
д)P(Ri U Ri) есть ЛОЖЬ для i 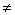 j, где P(Ri)- логический предикат,
определенный на точках из множества Ri, и
j, где P(Ri)- логический предикат,
определенный на точках из множества Ri, и 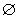 - пустое множество.
- пустое множество.
Условие
1 означает, что сегментация должна быть полной, т. е. каждый пиксель должен
находиться в образе. Второе условие требует, чтобы точки в области были
связными. Условие 3 указывает на то, что области не должны пересекаться.
Условие 4 определяет свойства, которым должны удовлетворять пиксели в
сегментированной области. Простой пример: Р(Ri) = ИСТИНА, если все
пиксели в Ri имеют одинаковую интенсивность. Условие 5 означает, что
области Ri и Ri различаются по предикату Р.
1.5.2 Расширение области за счет объединения пикселей
Расширение области сводится к процедуре группирования пикселов или
подобластей в большие объединения. Простейшей из них является агрегирование
пикселов. Процесс начинается с выбора множества узловых точек, с которых
происходит расширение области в результате присоединения к узловым точкам
соседних пикселов с похожими характеристиками (интенсивность, текстура или
цвет). Двумя очевидными проблемами являются: выбор начальных узлов для
правильного представления областей, представляющих интерес, и определение
подходящих свойств для включения точек в различные области в процессе
расширения. Выбор множества, состоящего из одной или нескольких начальных
точек, следует из постановки задачи. Например, в военных приложениях объекты,
представляющие интерес, имеют более высокую температуру, чем фон, и поэтому
проявляются более ярко. Выбор наиболее ярких пикселов является естественным
начальным шагом в алгоритме процесса расширения области. При отсутствии
априорной информации можно начать с вычисления для каждого пикселя набора
свойств, который наверняка будет использован при установлении соответствия
пикселя той или иной области в процессе расширения. Если результатом вычислений
являются группы точек (кластеры), тогда в качестве узловых берутся те пиксели,
свойства которых близки к свойствам центроидов этих групп. Так, в примере,
приведенном выше, гистограмма интенсивностей показала бы, что точки с
интенсивностью от одного до семи являются доминирующими. Выбор критерия подобия
зависит не только от задачи, но также от вида имеющихся данных об образе.
Например, анализ информации, полученной со спутников, существенно зависит от
использования цвета. Задача анализа значительно усложнится при использовании
только монохроматических образов. К сожалению, в промышленном техническом
зрении возможность получения мультиспектральных и других дополнительных данных
об образе является скорее исключением, чем правилом [5]. Обычно анализ области должен
осуществляться с помощью набора дескрипторов, включающих интенсивность и
пространственные характеристики (моменты, текстуру) одного источника
изображения. Отметим, что применение только одних дескрипторов может приводить
к неправильным результатам, если не используется информация об условиях связи в
процессе расширения области. Это легко продемонстрировать при рассмотрении
случайного расположения пикселов с тремя различными значениями интенсивности.
Объединение пикселов в «область» на основе признака одинаковой интенсивности
без учета условий связи приведет к бессмысленному результату при сегментации.
Другой важной проблемой при расширении области является формулировка
условия окончания процесса. Обычно процесс расширения области заканчивается,
если больше не существует пикселов, удовлетворяющих критерию принадлежности к
той или иной области. Выше упоминались такие критерии, как интенсивность,
текстура и цвет, которые являются локальными по своей природе и не учитывают
«историю» процесса расширения области. Дополнительный критерий, повышающий
мощность алгоритма расширения области, включает понятие размера, схожести между
пикселем-кандидатом и только что созданными пикселями (сравнение интенсивности
кандидата и средней интенсивности области), а также формы области, подлежащей
расширению. Использование этих типов дескрипторов основано на предположении,
что имеется неполная информация об ожидаемых результатах.
1.5.3 Разбиение и объединение области
Изложенная выше процедура расширения области начинает работу с заданного
множества узловых точек. Однако можно сначала разбить образ на ряд произвольных
непересекающихся областей и затем объединять и/или разбивать эти области с
целью удовлетворения условий. Итеративные алгоритмы разбиения и объединения,
работа которых направлена на выполнение этих ограничений, могут быть изложены
следующим образом [6].
На каждом шаге выполняются следующие операции:
а)разбиение
области Ri, для которой Р {Ri) = ЛОЖЬ, на четыре непересекающихся квадранта;
б)объединение
соседних областей Ri и Rk, для которых Р (Ri U Rk) = ИСТИНА;
в)выход на
останов, когда дальнейшее объединение или разбиение невозможно.
1.5.4 Анализ движения объектов
Движение представляет собой мощное средство, которое используется
человеком и животными для выделения интересующих их объектов из фона. В
системах технического зрения роботов движение используется при выполне1нии
различных операций на конвейере, при перемещении руки, оснащенной датчиком,
более редко при перемещении всей робототехнической системы.
Один из наиболее простых подходов для определения изменений между двумя
кадрами изображения (образами) f(x, у, ti) и f(x, у, tj),
взятыми соответственно в моменты времени ti и tj,
основывается на сравнении соответствующих пикселов этих двух образов. Для этого
применяется процедура, заключающаяся в формировании так называемой разности
образов.
Предположим, что мы имеем эталонный образ, имеющий только стационарные
компоненты. Если сравним этот образ с таким же образом, имеющим движущиеся
объекты, то разность двух образов получается в результате вычеркивания
стационарных компонент (т. е. оставляются только ненулевые записи, которые
соответствуют нестационарным компонентам изображения) [7].
1.6 Проблема описания объектов
В системах технического зрения проблемой описания называется выделение
свойств (деталей) объекта с целью распознавания. В идеальном случае дескрипторы
не должны зависеть от размеров, расположения и ориентации объекта, но должны
содержать достаточное количество информации для надежной идентификации объектов.
Описание является основным результатом при конструировании систем технического
зрения в том смысле, что дескрипторы должны влиять не только на сложность
алгоритмов распознавания, но также и на их работу. Рассмотрим три основные
категории дескрипторов: дескрипторы границы, дескрипторы области и дескрипторы
для описания трехмерных структур.
1.7 Дескрипторы границы
Цепные коды применяются для представления границы в виде
последовательности отрезков прямых линий определенной длины и направления.
Обычно в основе этого представления лежит 4- или 8-связная прямоугольная
решетка. Длина каждого отрезка определяется разрешением решетки, а направления
задаются выбранным кодом. Отметим что для представления всех направлений в
4-направленном цепном коде достаточно 2 бит, а для 8-направленного цепного кода
требуется 3 бит. Для порождения цепного кода заданной границы сначала
выбирается решетка. Тогда, если площадь ячейки, расположенной внутри границы,
больше определенного числа (обычно 50%), ей присваивается значение 1; в
противном случае этой ячейке присваивается значение 0. Окончательно мы кодируем
границу между двумя областями, используя направления. Результат кодирования в
направлении по часовой стрелке с началом в месте, помеченном точкой.
Альтернативная процедура состоит в разбиении границы на участки равной длины
(каждый участок имеет одно и то же число пикселов) и соединении граничных точек
каждого участка прямой линией, а затем присваивания каждой линии направления,
ближайшего к одному из допустимых направлений цепного кода. Важно отметить, что
цепной код данной границы зависит от начальной точки. Однако можно нормировать
код с помощью простой процедуры. Для создания цепного кода начальная точка на
решетке выбирается произвольным образом. Рассматривая цепной код как замкнутую
последовательность индексов направлений, мы вновь выбираем начальную точку
таким образом, чтобы результирующая последовательность индексов была целым
числом, имеющим минимальную величину. Также можно нормировать повороты, если
вместо цепного кода рассматривать его первую разность. Первая разность
вычисляется в результате отсчитывания (в направлении против часовой стрелки)'
числа направлений, разделяющих два соседних элемента кода. Нормирование можно
осуществить путем разбиения всех границ объекта на одинаковое число равных
сегментов и последующей подгонкой длин сегментов кода с целью их соответствия
этому разбиению.
Сигнатурой называется одномерное функциональное представление границы
[8]. Известно несколько способов создания сигнатур. Одним из наиболее простых
является построение отрезка из центра к границе как функции угла. Очевидно, что
такие сигнатуры зависят от периметра области и начальной точки. Нормирование
периметра можно осуществить, пронормировав кривую r(q) максимальным значением. Проблему
выбора начальной точки можно решить, определив сначала цепной код границы, а
затем применив метод, изложенный в предыдущем разделе. Конечно, расстояние,
зависящее от угла, не является единственным способом определения сигнатуры.
Например, можно провести через границу прямую линию и определить угол между
касательной к границе и этой линией как функцию положения вдоль границы.
Полученная сигнатура, хотя и отличается от кривой r(q), несет информацию об основных
характеристиках формы границы. Например, горизонтальные участки кривой
соответствовали бы прямым линиям вдоль границы, поскольку угол касательной
здесь постоянен. Один из вариантов этого метода в качестве сигнатуры использует
так называемую функцию плотности наклона. Эта функция представляет собой
гистограмму значений угла касательной. Поскольку гистограмма является мерой
концентрации величин, функция плотности наклона строго соответствует участкам
границы с постоянными углами касательной (прямые или почти прямые участки и
имеет глубокие провалы для участков, соответствующих быстрому изменению углов
(выступы или другие виды изгибов).
В задаче аппроксимации многоугольниками применяются методы объединения,
основанные на ошибке или других критериях. Один из подходов состоит в
соединении точек границы линией по методу наименьших квадратов. Линия
проводится до тех пор, пока ошибка аппроксимации не превысит ранее заданный
порог. Когда порог превышается, параметры линии заносятся в память, ошибка
полагается равной нулю и процедура повторяется; новые точки границы соединяются
до тех пор, пока ошибка снова не превысит порог. В конце процедуры образуются
вершины многоугольника в результате пересечения соседних линий. Одна из
основных трудностей, связанная с этим подходом, состоит в том, что эти вершины
обычно не соответствуют изгибам границы (таким, как углы), поскольку новая
линия начинается только тогда, когда ошибка превысит порог. Если, например,
длинная прямая линия пересекает угол, то числом (зависящим от порога) точек,
построенных после пересечения, можно пренебречь ранее, чем будет превышено
значение порогового уровня. Однако для устранения этой трудности наряду с
методами объединения можно использовать методы разбиения.
Один из методов разбиения сегментов границы состоит в последовательном
делении сегмента на две части до тех пор, пока удовлетворяется заданный
критерий.
.8 Дескрипторы областей изображений
1.8.1
Некоторые простые дескрипторы
Существующие системы технического зрения основываются на довольно простых
дескрипторах области, что делает их более привлекательными с вычислительной
точки зрения. Как следует ожидать, применение этих дескрипторов ограничено
ситуациями, в которых представляющие интерес объекты различаются настолько, что
для их идентификации достаточно несколько основных дескрипторов.
Площадь области определяется как число пикселов, содержащихся в пределах
ее границы. Этот дескриптор полезен при сборе информации о взаимном
расположении и форме объектов, от которых камера располагается приблизительно
на одном и том же расстоянии. Типичным примером может служить распознавание
системой технического зрения объектов, движущихся по конвейеру.
Большая и малая оси области полезны для определения ориентации объекта.
Отношение длин этих осей, называемое эксцентриситетом области, также является
важным дескриптором для описания формы области.
Периметром области называется длина ее границы. Хотя иногда периметр
применяется как дескриптор, чаще он используется для определения меры
компактности области, равной квадрату периметра, деленному на площадь. Отметим,
что компактность является безразмерной величиной (и поэтому инвариантна к
изменению масштаба) и минимальной для поверхности, имеющей форму диска.
Связной называется область, в которой любая пара точек может быть
соединена кривой, полностью лежащей в этой области. Для множества связных
областей (некоторые из них имеют отверстия) в качестве дескриптора полезно
использовать число Эйлера, которое определяется как разность между числом
связных областей и числом отверстий. Например, числа Эйлера для букв А и В
соответственно равны 0 и -1. Другие дескрипторы области рассматриваются ниже.
1.8.2
Текстура
Во многих случаях идентификацию объектов или областей образа можно
осуществить, используя дескрипторы текстуры. Хотя не существует формального
определения текстуры, интуитивно этот дескриптор можно рассматривать как
описание свойств поверхности (однородность, шероховатость, регулярность). Двумя
основными подходами для описания текстуры являются статистический и
структурный. Статистические методы дают такие характеристики текстуры, как
однородность, шероховатость, зернистость и т. д. Структурные методы
устанавливают взаимное расположение элементарных частей образа, как, например,
описание текстуры, основанной на регулярном расположении параллельных линий
[10].
1.8.3 Схема
области
Важным подходом для описания вида структуры плоской области является ее
представление в виде графа. Во многих случаях для этого определяется схема
(скелет) области с помощью так называемых прореживающих (или же сокращающих)
алгоритмов. Прореживающие процедуры играют основную роль в широком диапазоне
задач компьютерного зрения - от автоматической проверки печатных плат до
подсчета асбестовых волокон в воздушных фильтрах. Скелет области можно
определить через преобразование средних осей (ПСО), предложенное в работе. Хотя
ПСО дает довольно удовлетворительный скелет области, его прямое применение
затруднительно с вычислительной точки зрения, поскольку требуется определение
расстояния между каждой точкой области и границы. Был предложен ряд алгоритмов
построения средних осей, обладающих большей вычислительной эффективностью.
Обычно это алгоритмы прореживания, которые итеративно устраняют из рассмотрения
точки контура области так, чтобы выполнялись следующие ограничения:
а)не устранять
крайние точки;
б)не приводить к
нарушению связности;
в)не вызывать чрезмерного размывания области.
1.9 Сегментация
и описание трехмерных структур
По существу зрение является трехмерной проблемой, поэтому в основе
разработки многофункциональных систем технического зрения, пригодных для работы
в различных средах, лежит процесс обработки информации о трехмерных сценах.
Хотя исследования в этой области имеют более чем 10-летнюю историю, такие
факторы, как стоимость, скорость и сложность, тормозят внедрение обработки трехмерной
зрительной информации в промышленных приложениях.
Возможны три основные формы представления информации о трехмерной сцене.
Если применяются датчики, измеряющие расстояние, то мы получаем координаты (х,
у, z) точек поверхностей объектов [11]. Применение устройств, создающих
стереоизображение, дает трехмерные координаты, а также информацию об
освещенности в каждой точке. В этом случае каждая точка представляется функцией
f (х, у, z), где значения последней в точке с координатами (х, у, z) дают значения
интенсивности в этой точке (для обозначения точки в трехмерном пространстве и
ее интенсивности часто применяется термин воксель). Наконец, можно установить
трехмерные связи на основе одного двумерного образа сцены, т. е. можно выводить
связи между объектами, такие, как «над», «за», «перед». Поскольку точное
трехмерное расположение точек сцены обычно не может быть вычислено на основе
одного изображения, связи, полученные с помощью этого вида анализа, иногда
относятся к так называемой 2,5-мерной информации.
1.10 Описание трехмерной сцены плоскими участками
Один из наиболее простых подходов для сегментации и описания трехмерных
структур с помощью координат точек (х, у, z) состоит в разбиении сцены на
небольшие плоские «участки» с последующим их объединением в более крупные
элементы поверхности в соответствии с некоторым критерием. Этот метод особенно
удобен для идентификации многогранных объектов, поверхности которых достаточно
гладкие относительно разрешающей способности.
Когда сцена задана вокселями, ее можно описать плоскими участками с
помощью трехмерного градиента. В этом случае дескрипторы поверхности также
получаются в результате объединения этих плоских участков. Вектор градиента
указывает направление максимальной скорости изменения функции, а его величина
соответствует величине этого изменения. Эти понятия применимы для трехмерного
случая и также могут быть использованы для разбиения на сегменты трехмерных
структур тем же способом, который применялся для двумерных данных.
1.11 Техника обработки визуальной информации
Форма и размер. Будем считать все объекты, представленные в системе
автоматической сборки, точными проекциями соответствующих реальных объектов.
Объекты могут быть любой формы, число различных объектов неограниченно. Любое
обнаруженное анализирующей системой отклонение от формы или размера, которое
может повлечь за собой ошибки сборки, служит основанием для отбраковки детали
(это не означает, что предполагается проверка 100 % деталей). Поэтому
полученное в результате анализа описание объекта должно содержать всю
присутствовавшую в образе информацию о размерах и форме этого объекта.
Напротив, система распознавания символов в общем случае должна допускать
значительные отклонения (различное начертание) в распознаваемых символах [12].
В наиболее сложном случае распознаются рукописные символы. Однако число типов
распознаваемых символов всегда ограничено. Наибольшая достоверность
распознавания достигается при использовании шаблона при анализе печатных
шрифтов, специально предназначенных для оптического считывания, например ОКР-А
и ОКР-Б (OCR-A и OCR-B).
Параметры положения. Детали, с которыми работает робот-сборщик, могут
располагаться в любой точке в пределах поля зрения и иметь произвольную
ориентацию. Хотя для распознавания детали требуется ее описание, инвариантное к
параметрам положения, определение значений этих параметров также является
важной функцией анализатора визуальной информации. Значения параметров
положения используются при выполнении последующих операций. Задача
распознавания символов упрощается тем, что, хотя строчки символов могут быть
наклонными, отдельные символы обычно попадают в поле зрения распознающей
системы в довольно жестко фиксированном положении, измерять параметры которого
нет необходимости.
Число объектов. Естественно требовать от визуального анализатора
робота-сборщика умения работать с несколькими одновременно находящимися в поле
зрения и расположенными случайным образом деталями. Решение задачи разделения
объектов при распознавании символов облегчается тем, что заранее известны
размеры и курсив символа (в случае распознавания печатных символов). Такая
информация позволила создать приемы разделения соприкасающихся символов [1]. В
настоящей работе не ставится задача различить соприкасающиеся объекты. Их
совокупный силуэт будет восприниматься как единый, предположительно неизвестный
объект.
Отсутствие ограничения на количество типоразмеров объектов, с которыми
приходится работать распознающей системе, приводит к необходимости создавать
полное описание формы для каждого образа. Впрочем, существует несколько
основных параметров, которые однозначно определяются для контура любой
конфигурации. Используя их, можно получить ценную информацию о типе и положении
объекта.
В число этих параметров входят: площадь, периметр, минимальный
охватывающий прямоугольник (размеры), центр площади (центроид), радиус-вектор
минимальной длины (длина и направление), радиус-вектор максимальной длины
(длина и направление), характеристики отверстий (количество, размер,
расположение).
Значения площади и периметра - простейшие инвариантные к ориентации и
расположению характеристики. При решении задачи распознавания объекта
использовался безразмерный "коэффициент формы" -
(площадь)/(периметр). Координаты вершин минимального охватывающего прямоугольника
дают некоторую информацию о форме и величине объекта, но их значение зависит от
его ориентации. Центр площади это точка, которая легко определяется для любого
объекта независимо от его ориентации, вследствие чего центр площади играет
важную роль при обнаружении и распознавании объекта. Он же задает начало
радиус-вектора, соединяющего центр площади с точкой, лежащей на границе
объекта. В принципе, радиус-векторы максимальной и минимальной длины могут быть
полезны при распознавании и определении параметров положения объекта.
Обычно в промышленных деталях имеются отверстия. Их количество - тоже
полезная характеристика. Отверстия могут распознаваться как объекты некоторой
формы и размера, определенным образом ориентированные относительно основного
объекта, в котором они обнаружены.
Наиболее удобный способ получения подробного описания произвольного
геометрического объекта и установления связности образа - это прослеживание
границы. Прослеживание начинается с выбора произвольной точки, лежащей на
черно-белой границе проекции объекта. Затем выполняется алгоритм,
последовательно определяющий смежные точки, лежащие на границе, до тех пор,
пока не будет совершен полный обход контура. Последовательно записывая
направления движения вдоль границы от каждой текущей точки к последующей,
получаем одномерное описание проекции объекта, содержащее информацию о его
форме. Такие цепочки направлений всесторонне изучались Фрименом [13]. Когда
граница прослежена, легко определить площадь, периметр, центр площади и
охватывающий прямоугольник. Описание границы также удобно и для определения
радиус-векторов.
Прослеживание границы устанавливает связность анализируемого объекта.
Продолжая просмотр в поисках следующих объектов, можно повторно обнаружить уже
отслеженную границу.
Чтобы избежать этого, Розенфельд предлагает во всех точках, просмотренных
программой отслеживания границы, заменять единицы на двойки для первого
обрабатываемого объекта, на тройки - для второго объекта и т.д. (единица
соответствует объекту или "черному" элементу растра в исходном
образе, а ноль соответствует фону или "белому" элементу). Но такой
подход требует более одного бита для представления каждой точки исходного
образа, и из-за этого не годится для систем с малым размером памяти.
Авторы предлагают для решения этой задачи использовать оператор
поточечного дифференцирования или выделения границы, применяя его сразу же
после считывания образа телекамерой. Этот оператор заменяет все единицы в
образе на нули, за исключением точек, лежащих на границе черного и белого полей.
Полученные с помощью ЭВМ контуры квадрата и круга, расположенных в поле зрения
камеры, приведены на рис. 1.2 показан результат применения к этому изображению
оператора выделения границы. Процедура прослеживания границы EDGETRACE может
работать с промежуточным изображением точно так же, как с исходными объектами.
Она построена так, что просматриваемые ею элементы растра
"обнуляются", т.е. прослеживание границы объекта удаляет его из
изображения, делая невозможным повторное обнаружение.
Сглаживание. Метод обработки изображений объектов, основанный на
прослеживании границ, может оказаться неработоспособным, если на границе
объекта будут обнаружены резкие скачки контрастности. В системах распознавания
символов прослеживание границ обычно предваряется операцией сглаживания
(локального усреднения), которая пытается уничтожить просветы (белые точки,
которые должны были быть черными) и ложные черные точки, а также соединить
небольшие разрывы. В операции сглаживания по Дайнину на каждый элемент растра
по очереди накладывается окно размером пХп элементов и подсчитывается
количество черных элементов, попавших в окно. Создается новое растровое
представление, в котором каждый элемент соответствует отдельной позиции окна. В
этом растровом представлении элемент будет черным только в том случае, когда
количество черных элементов, попавших в соответствующее ему окно, превышает
некоторое заранее заданное число. Наименьший применяемый на практике размер
окна 3X3 элемента. Унгер предложил процедуру сглаживания, в которой вместо
усреднения содержимого окна размером 3X3 элемента к нему применяются некоторые
логические операции, определяющие значение элемента нового образа. Недостаток
обоих методов - довольно большой объем операций с памятью: и в том и в другом
случае все определения значения элемента нового образа приходится выполнить
около 100 машинных операций.
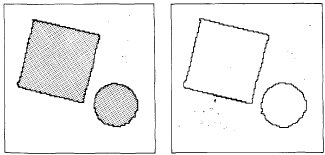
Рисунок 1.2 - Содержимое растра после процедуры INPUT-FRAME и содержимое
растра после выделения границ [8]
Объекты, с которыми имеет дело робот-сборщик, отличаются от печатных
символов тем, что любые просветы в соответствующих им образах означают наличие
дефектов и служат достаточным основанием для отбраковывания такого объекта
[14]. Изредка возникающие изолированные шумовые точки в общем случае не
оказывают влияния на работу алгоритма прослеживания границы. Поэтому
специальные сглаживающие операции не используются, хотя в процедуре
прослеживания предпринимаются меры для уменьшения влияния шумовых точек.
Выделение границы - процедура OUTLINEFRAME. Оператор выделения границы
должен создавать непрерывную последовательность граничных точек, обеспечивая
возможность прослеживания границы. Для минимизации времени вычисления при
создании каждого элемента нового образа следует использовать доступ к
минимально возможному количеству элементов исходного образа.
Варианты определения контура объекта: Розенфельд различает понятия
"край" и "граница". Край - это совокупность внешних
элементов растрового представления объекта, граница же проходит посередине
между горизонтально или вертикально смежными точками, одна из которых
принадлежит объекту, а другая - фону. Для наших целей будем использовать
концепцию границы, так как она более точно представляет линию, реально
разделяющую черные и белые области растра.
Эта концепция обеспечивает однозначность решения в случае линии толщиной
в одну точку. Использование концепции края приведет к получению результата,
непригодного для последующей работы алгоритма прослеживания, так как два края
линии будут совпадать.
Недостаток определения границы по Розенфельду заключается в том, что
итоговый массив имеет вдвое большую точечную плотность, чем исходный, при
сохранении взаимно однозначного соответствия двух массивов. Новый массив
граничных точек создается с таким же расстоянием между точками, как исходный,
но при этом каждая точка сдвигается по координатам х и у наполовину этого
расстояния. Каждая точка нового массива лежит в центре квадрата, в вершинах
которого находятся точки исходного массива, а ее состояние (черное или белое,
граница или не граница) определяется по состоянию этих четырех точек.
Шесть основных (из числа шестнадцати возможных) сочетаний состояний
четырех смежных элементов исходного образа показаны на рис. 4. Там же приведены
интуитивные определенные значения соответствующих элементов массива,
содержащего описание границы. Значение для конфигурации d выбрано нулевым для
обеспечения однозначности в случае линии толщиной в одну точку [15].
Прослеживание границы - процедура EDGETRACE. Параметры. EDGETRACE -
процедура, определяющая, принадлежит ли границе объекта точка, обнаруженная в
дифференцированном образе. Координаты начальной точки вводятся в глобальные
переменные целого типа STARTX, STARTY. Процедура EDGETRACE вызывается как
логическая процедура - функция, например, в оператореEDGETRACE THEN ... ELSE
Значение "истина" вырабатывается процедурой тогда, когда
найдена замкнутая граница, включающая в себя больше заранее определенного числа
точек.
Процедура EDGETRACE определяет значения совокупности параметров,
относящихся к контуру, а также создает описание самого контура в форме списка
векторов, представленных глобальными переменными.
Определение значений ХМ АХ, XMIN, YMAX, YMIN сделано необязательным. Если
оно желательно, следует установить признак слова EDGEF-LAG (т.е. сделать
значение соответствующего слова ненулевым). Точно так же с помощью признака
CHAINFLAG можно включать и выключать запись значений в счетчик CHAINCOUNT и
массив CHAIN.
Цепная запись и основной алгоритм. В настоящей работе точка матрицы,
соответствующей образу, считается связанной с другой точкой, если последняя
находится в одной из восьми позиций, непосредственно смежных с первой точкой.
Таблица 1.1 - Параметры, определяемые процедурой EDGETRACE
|
Переменная
|
Значение
|
|
PERIMETER
|
Длина прослеженного
контура, положительное целое число
|
|
AREA
|
Площадь, ограниченная
контуром, положительное целое число
|
|
ХМАХ XMIN YMAX YMIN
|
Максимальное и минимальное
значения координат точек, принадлежащих контуру, отрицательные целые числа
|
|
XCENTROID YCENTROID
|
Координаты центра площади,
ограниченной контуром, отрицательные целые числа
|
|
CHA1NCOUNT
|
Количество элементарных
векторов, составляющих контур, совпадающее с количеством просмотренных
граничных точек, отрицательное целое число
|
|
CHAIN
|
Упорядоченный массив значений,
задающих направления элементарных векторов, составляющих контур. Массив
состоит из элементов CHA1NCOUNT
|
Соединение любой пары связанных точек может быть представлено одним из
восьми элементарных векторов (рис 1.3), направления которых помечены значениями
от -8 до -1 (отрицательные значения взяты для совмещения со схемой индексации
ЭВМ PL-516).
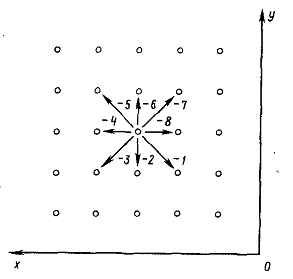
Рисунок 1.3 - Определение элементарных векторов [8]
Алгоритм прослеживания границы "обнуляет" значение найденной
точки, принадлежащей контуру, до перехода к следующей точке. Таким образом, из
матрицы FRAME удаляются прослеженные очерки. Базовая точка поиска перемещается
по контуру против часовой стрелки, что при поиске контуров с помощью развертки
обеспечивает первое вхождение в контур извне. Войти в контур изнутри можно
только в том случае, если он пересекает границу матрицы. При этом процедура
EDGETRACE выдаст сообщение об ошибке.
Нет необходимости проверять в каждой точке контура объекта все восемь
соседних точек - некоторые из них уже были проверены на предыдущем шаге, когда
базовой точкой поиска была предыдущая. До начала локального поиска в
зависимости от направления предыдущего вектора устанавливаются переменные
SEARCHDIRN (первое проверяемое направление) и ENDDIRN (последнее проверяемое
направление).
На каждом шаге поиска просматривается до шести точек, но обычно их число
меньше. На прямолинейных участках контура до нахождения следующей его точки
чаще всего достаточно просмотреть одну-две точки.
Полное описание очеркового контура формируется в виде списка направлений
векторов, соединяющих каждую точку контура с последующей в том порядке, в
котором они были найдены (массив CHAIN). Результат применения процедуры
прослеживания границы к простому контуру и полученное "цепное"
описание показаны на рис. 1.4.
Параллельно с определением точек контура проводятся вычисления периметра,
площади и моментов площади первого порядка [16].
Вычисление периметра. Параметр представляет собой сумму длин элементарных
векторов, составляющих контур. Эти векторы имеют длину 1 (направления с четными
номерами) или единицы растра (направления с нечетными номерами).
Предполагается, что расстояние между точками в матрице равно размеру элемента
растра.

Рисунок 1.4 - Описание контура простой формы
Таблица 1.2 - Номера и значения цепочки
|
Номер элемента цепочки
|
Значение элемента цепочки
|
|
-1
|
-2
|
|
-2
|
-2
|
|
-3
|
-2
|
|
-4
|
-8
|
|
-5
|
-1
|
|
-6
|
-2
|
|
-7
|
-8
|
|
-8
|
-8
|
|
-9
|
-8
|
|
-10
|
-8
|
|
-11
|
-6
|
|
-12
|
-6
|
|
-13
|
-6
|
|
-14
|
-6
|
|
-15
|
-5
|
|
-16
|
-5
|
|
-17
|
-4
|
|
-18
|
-4
|
|
-19
|
-3
|
|
-20
|
-4
|
По мере нахождения новой точки контура в зависимости от того, каким было
направление последнего вектора, увеличивается на единицу значение одной из
переменных - EVENPERIM или ODDPERIM. В конце процедуры вычисляется и
округляется до ближайшего целого значение периметра:
PERIMETER = EVENPERIM + ODDPERIM
Вычисление площади. Площадь, ограниченная контуром, вычисляется как сумма
площадей, ограниченных элементарным вектором, вертикалями, проведенными через
его концы, и подходящей горизонтальной линией (ей приписывают значение Y = 0).
С учетом нумерации направлений векторов получается, что элементарные векторы с
уменьшающейся компонентной х (-5, -4, -3) вносят в общую сумму положительные
значения, а векторы с увеличивающейся компонентой х (-7, -8, -1) -
отрицательные (из рис. 1.4 видно, что Y имеет отрицательные значения). При
таких условиях площадь, ограниченная контуром, прослеживаемым против часовой
стрелки, будет иметь положительное значение.
На рис. 1.6 показан простой пример. Во избежание лишних манипуляций с
коэффициентом 1/2 процедура EDGETRACE накапливает удвоенное значение площади
(AREA2) и в конце вычислений делит его пополам.
Определение первых моментов площади и центроидов. Аналогичный метод
используется для вычисления моментов ограниченной площади первого порядка
относительно осей х и у. На рис. 1.7 показаны восемь элементарных векторов и
первые моменты для площадей, заключенных между векторами и осью х (AWX).
Сумма всех компонент ДЛ/Х для контура даст отрицательное целое
число, которое после деления на значение ограниченной площади даст координату
ее центра по оси у.
Выражение для АМХ в случае векторов с направлениями, имеющими
нечетные номера, содержит постоянный член 1/6 или -1/6. В замкнутом контуре,
состоящем из большого числа элементарных векторов, можно считать количества
векторов всех направлений приблизительно одинаковым. Это приводит к взаимному
уничтожению постоянных членов. Кроме того, постоянный член достаточно мал по
сравнению с Y2 и с площадью, особенно в том случае, когда объект
рассматривается вблизи и его образ занимает большую часть поля зрения [17].
Поэтому можно упростить вычисления, пренебрегая постоянным членом.
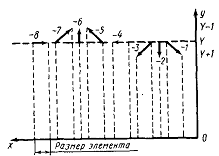
Рисунок 1.5 - Приращения, вносимые элементарными векторами в значение
площади, ограниченной контуром [8]
Таблица 1.3 - Значение площадей и приращений
|
Направление вектора
|
Приращение площади
|
Удвоенное приращение
|
|
-8
|
Y
|
2Y
|
|
-7
|
Y-1/2
|
2Y-1
|
|
-6
|
0
|
0
|
|
-5
|
(Y-1/2)(-1)
|
-2Y+1
|
|
-4
|
Y(-1)
|
-2Y
|
|
-3
|
(Y+1/2)(-1)
|
-2Y-1
|
|
-2
|
0
|
0
|
|
-1
|
Y+1/2
|
2Y+1
|

Рисунок 1.6 - Вычисление площади, ограниченной контуром
Таблица 1.4 - Нахождение суммарной площади
|
Номер элемента цепочки
|
Значение элемента цепочки
|
Удвоенное приращение
|
Удвоенная площадь
|
|
-1
|
-2
|
0
|
0
|
|
-2
|
-2
|
0
|
0
|
|
-3
|
-2
|
0
|
0
|
|
-4
|
-8
|
-8
|
-8
|
|
-5
|
-1
|
-7
|
-15
|
|
-6
|
-2
|
0
|
-15
|
|
-7
|
-8
|
-4
|
-19
|
|
-8
|
-8
|
-4
|
-23
|
|
-9
|
-8
|
-4
|
-31
|
|
-10
|
-8
|
0
|
-31
|
|
-11
|
-6
|
0
|
|
-12
|
-6
|
0
|
-31
|
|
-13
|
-6
|
0
|
-31
|
|
-14
|
-6
|
+13
|
-31
|
|
-15
|
-5
|
+15
|
-18
|
|
-16
|
-5
|
+15
|
-3
|
|
-17
|
-4
|
+16
|
+13
|
|
-18
|
-4
|
+16
|
+29
|
|
-19
|
-3
|
+15
|
+44
|
|
-20
|
-4
|
+14
|
+58
|
|
Суммарная площадь = 29
|
Операций с коэффициентом 1/2 избегают так же, как при вычислении площади,
- вычисляя значение 2 ДМХ. Это значение вычисляется удвоенной длины
XMOMENT процедурой SUMXMOMENT.
При завершении процедуры EDGETRACE XMOMENT делится на значение AREA2.
Округляя результат до ближайшего целого, получаем координату Y центра площади -
YCENTROID.
Точно так же, суммируя моменты площади относительно оси у получаем
значение XCENTROID. На рис. 1.8 показаны значения, вносимые векторами различных
направлений в суммарный момент.
Одна или небольшое число смежных "шумовых" точек,
соответствующих, например, случайно попавшему в поле зрения обломку стружки,
образуют контуры, состоящие из малого числа элементарных векторов. Подходящим
значением для переменной MINCHAIN оказалось -10, т.е. любой замкнутый контур,
длина которого не превышает 10 векторов, попросту не рассматривается.
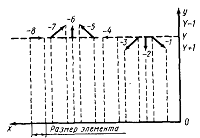
Рисунок 1.7 - Моменты первого порядка относительно оси Х [8]
Таблица 1.5 - Значение моментов относительно оси Х
|
Направление вектора
|
Приращение площади
|
Удвоенное приращение
|
|
-8
|
Y2/2
|
Y2
|
|
-7
|
Y2/2- Y/2+1/6
|
Y(Y-1)
|
|
-6
|
0
|
0
|
|
-5
|
-Y2/2+
Y/2-1/6
|
Y(-Y+1)
|
|
-4
|
-Y2/2
|
Y2
|
|
-3
|
-Y2/2+
Y/2-1/6
|
Y(-Y+1)
|
|
-2
|
0
|
0
|
|
-1
|
Y2/2- Y/2+1/6
|
Y(Y-1)
|
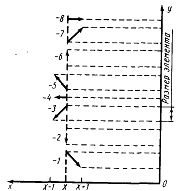
Рисунок 1.8 - Моменты первого порядка относительно оси Y [8]
Таблица 1.6 - Значение моментов относительно оси Y
|
Направление вектора
|
Приращение площади
|
Удвоенное приращение
|
|
-8
|
0
|
0
|
|
-7
|
X2/2+X/2+1/6
|
X(X+1)
|
|
-6
|
X2/2
|
X2
|
|
-5
|
X2/2- X/2+1/6
|
X(X-1)
|
|
-4
|
0
|
0
|
|
-3
|
-X2/2+
X/2-1/6
|
X(-X+1)
|
|
-2
|
-X2/2
|
-X2
|
|
-1
|
-X2/2+
X/2-1/6
|
X(-X-1)
|
Матрица образа после процедуры EDGETRACE. Описанный алгоритм
прослеживания границ, обрабатывая дифференцированную матрицу, обнуляет все
просмотренные точки, но это не означает, что будут просмотрены и обнулены все
точки контура. Оставшиеся в матрице единичные точки обычно не составляют
полного контура и при последующих операциях выступают как "шумовые".
Для минимизации их влияния должны предприниматься специальные меры. На рис. 1.9
показан вид матрицы образа FRAME после того, как процедура EDGETRACE обработала
оба контура. Видны оставшиеся шумовые точки.
Идентификация отверстий - процедура INSIDE. Процедура INSIDE определяет,
внутри или снаружи определенного контура лежит некоторая точка, принадлежащая
матрице образа FRAME [18].
Предполагается, что контур, выделенный процедурой EDGETRACE, хранится в
виде массива CHAIN и переменная CHAINCOUNT определяет его длину. Начальная
точка цепочки задается целыми переменными PARTXSTART и PARTYSTART.
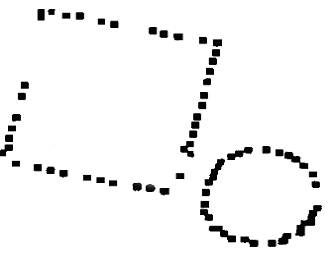
Рисунок 1.9 - Матрица изображения после прослеживания обоих границ [8]
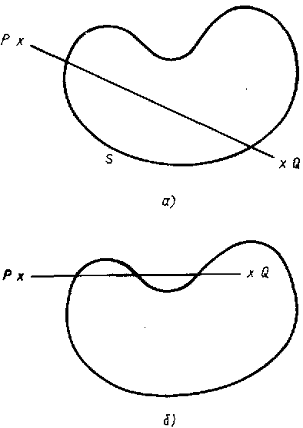
Рисунок 1.10 - К теореме о пересечении прямой и замкнутой линии [8]
Координаты проверяемой точки вводятся в переменные STARTX и STARTY и
вызывается логическая процедура-функция INSIDE. Она вырабатывает значение
"истина", если проверяемая точка лежит внутри контура. При этом
никакие значения в памяти не меняются.
Используемый алгоритм основан на следующей справедливой для плоскости
теореме: если точка Р, лежащая вне замкнутой кривой S, соединена отрезком
прямой с точкой Q, то точка Q тоже лежит вне кривой S тогда и только тогда,
когда отрезок PQ пересекает кривую S четное число раз. Если PQ пересекает
кривую S нечетное число раз, точка Q лежит внутри замкнутой кривой S (рис.
1.10). Доказательство приводится Курантом и Роббинсом.
В процедуре INSIDE упомянутый отрезок прямой проводится из проверяемой
точки до края матрицы FRAME параллельно оси х, т.е. представляет собой часть
луча Y = STARTY, X > STARTX. Пара локальных переменных (XCOORD и YCOORD)
первоначально устанавливаются равными координатам начала хранимого контура. Из
массива CHAIN последовательно считываются элементарные векторы. В зависимости
от их значения модифицируются XCOORD и YCOORD (процедура UNCHAIN). Таким
образом, XCOORD и YCOORD последовательно принимают значения координат всех
точек, прослеженных в исходном контуре [19].
На каждом шаге проверяется, не лежит ли точка контура на луче У = STARTY,
х > STARTX. Количество пересечений контура с этим лучом подсчитывается в
целой переменной CROSSCOUNT. Множественные пересечения, когда линия контура
совпадает с тестовым лучом в нескольких смежных точках, не учитываются. В
момент вхождения линии контура в тестовый луч в переменной STRIKEDIRN
записывается индекс направления вектора, входящего в луч. Для последующих
точек, лежащих на луче, никаких действий не предпринимается. Когда очередной
вектор контура выходит из тестового луча, текущее направление сравнивается со
значением, записанным в STRIKEDIRN для проверки: был ли пересечен контуром
тестовый луч (CROSSCOUNT увеличивается на единицу) или контур прошел касательно
к лучу (CROSSCOUNT не меняется).
Когда все точки хранимого контура будут восстановлены, и проверены,
проверяется значение CROSSCOUNT и процедура завершается с соответствующим
результатом. Неоднозначные предельные случаи, когда проверяемые точки лежат на
самом контуре, исключаются, т.к. в процессе прослеживания границы все такие
точки обнулены.
После того, как выявлены контуры объекта, должны быть определены его
ориентация и положение. Эта информация необходима для правильной работы с
деталью в процессе сборки.
Задача определения ориентации. Основные процедуры обработки визуального
образа анализируют содержащиеся в нем контуры (объекта и отверстий в нем) в
параметрах площади, периметра, положения центра площади, охватывающего
прямоугольника, описания контура цепочкой векторов. Эти параметры полезны для
выполнения начальной обработки, но для распознавания образа и определения его
ориентации требуется более полное использование информации об отверстиях и
контуре.
Модель объекта, использующая отверстия. Рисунок, образованный
отверстиями, имеющимися в объекте, можно анализировать, используя расстояния
центров площадей отверстий от центра площади объекта и их относительные угловые
координаты. Кроме того, могут использоваться уже измеренные площади и периметры
отверстий.
Эта модель инвариантна к ориентации основного объекта и может
непосредственно сравниваться с моделью-образцом. Когда будет установлено
соответствие между отдельными отверстиями рассматриваемого объекта и модели,
значения ее абсолютных угловых координат могут использоваться для определения
ориентации объекта.
Выделение особенностей контура. Модель контура представляет собой список
- цепочку векторов. Но сравнивать представленную такой моделью входную
информацию с образцом, как это делает, например, Фримен, сложно и долго.
Основная трудность заключается в том, что начальная точка цепочки, представляющей
контур объекта, расположена на нем случайным образом. Ее конкретное положение
зависит от ориентации объекта и направления сканирования при просмотре.
Сравниваемые цепочки приходится циклически смещать относительно друг друга до
совпадения. К сожалению, описание контура цепочкой векторов не слишком удобно
для выполнения операции поворота на угол, не кратный 45 . Установление
соответствия еще более затрудняется тем, что эталон и входная цепочка в общем
случае состоят из различного числа элементарных векторов.
Разработан ряд методов сглаживания цепных списков и нормализации их длин,
обеспечивающих возможность сравнения. Зах и Монтанари описали методы получения
аппроксимаций с помощью прямых минимальной длины, снижающие объем данных,
подлежащих обработке. Но эти методы слишком сложны для использования в системе
автоматической сборки. В такой системе основное требование - не обеспечить
100%-ное совпадение, при сравнении модели контуров, выделенных из входного
изображения, с эталонами, а подтвердить результаты пробных проверок и
определить ориентацию объекта.
Требуется модель, которая позволит наиболее быстро и легко определять
ориентацию объекта. Наиболее подходящим для такой модели может оказаться
подход, основанный на выделении особенностей очеркового контура. Многие методы
распознавания символов, например по Хоскингу, используют повторяющиеся
особенности структуры штрихов, составляющих символ. Такими особенностями
являются концы штрихов, точки их соединения или излома, петли. Аналогичными
особенностями, характерными для материальных объектов, могут служить резкие
изменения направления контура (углы) и точки, максимально и минимально
удаленные от центра площади фигуры. К сожалению, отсутствие ограничений на
форму деталей, с которыми приходится иметь дело роботу-сборщику, ограничивает
ценность методов, использующих заранее составленный набор стандартных
особенностей.
Модель с использованием окружностей. Угловые координаты радиус-векторов
максимальной и минимальной длины могут служить удобным критерием распознавания
объекта и средством определения его ориентации. Их значение выводится
непосредственно из информации, генерируемой процедурой EDGETRACE. Но если в
окрестности точки, экстремально удаленной от центра площади, длина
радиус-вектора меняется мало (рис. 18), координаты RMAX и RMIN
будут ненадежны. Из этого вытекает, что более целесообразно во время настройки
системы задавать такие значения длины радиус-вектора R, для которых
соответствующая позиция конечной точки может быть четко определена. По сути
дела, это сводится к наложению на образ окружности заданного радиуса, центр
которой совпадает с центром площади объекта. Точки пересечения этой окружности
с контуром объекта используются как его особенности. На рис. 19 особые точки
определяются параметрами R, 0,, в2, в3, в4.
Разности углов составляют инвариантный к ориентации набор параметров для
распознавания, а их абсолютные значения могут использоваться для определения
ориентации объекта.
Точки пересечения определяются на основе информации, сгенерированной
процедурой EDGETRACE: для каждой точки контура, представленного цепным списком
векторов, вычисляется ее расстояние от центра площади. Отмечаются точки, для
которых это расстояние равно заданному радиусу, и вычисляются их угловые
координаты относительно центра площади. Таким образом, точки пересечения
оформляются в виде упорядоченного списка. Которая из точек находится в начале
этого списка -зависит от того, с какого места контура начиналась процедура
EDGETRACE.
Критериями выбора значения радиуса окружности могут служить следующие
положения:
- точки пересечения должны однозначно определять ориентацию
объекта;
- количество точек пересечения не должно быть слишком большим
(например, не больше восьми);
- для повышения точности измерений радиус должен быть по
возможности большим;
- малые изменения длины радиуса не должны сильно влиять на
угловые координаты точек пересечения;
- малые изменения длины радиуса не должны приводить к
исчезновению или появлению новых точек пересечения.
Последние два пункта необходимы для снижения влияния малых искажений во
входном представлении образа.
Чтобы однозначно определить ориентацию детали или отличить ее от другой
такой же детали, может оказаться необходимым задать более одной окружности.
Тогда точки пересечения, найденные при обходе контура, будут представлены в
виде упорядоченного списка пар значений радиус - угол.
Сравнение значений измеренных углов необходимо выполнять только в случае
полного совпадения списков обозначений радиусов. Это упрощает процедуру
сравнения. Когда установлено соответствие обоих списков, могут быть вычислены
разности абсолютных угловых координат для каждой пары смежных точек
пересечения. Эти шесть значений предназначены для определения ориентации одного
объекта относительно другого. Еще одним свойством модели, использующей
окружности, является возможность фиксировать случай, когда деталь лежит
обратной стороной вверх. Таким образом, модель с использованием окружностей
представляет собой мощное средство определения особых точек на очерковом
контуре объекта произвольной формы. Эти точки могут использоваться при
распознавании и определении ориентации. Размер памяти, используемой для
хранения модели-эталона составляет всего два слова на каждую точку пересечения,
а необходимые данные о сканируемой детали могут быть получены из информации,
генерируемой процедурой EDGETRACE. В сочетании с моделью, использующей
отверстия, она использовалась на низшем уровне распознавания и определения
ориентации деталей в управляющей системе робота-сборщика.
Таким образом, в первой части магистерской аттестационной работы
проанализированы методы обработки информации в системах технического зрения
роботов. Процесс идентификации объектов, находящихся в рабочей зоне робота,
включает два этапа, такие как выделение характерных признаков объектов и
распознавание объектов по найденной совокупности характерных признаков.
Основными методами обработки информации являются сегментация (процесс
подразделения сцены на составляющие части или объекты), определение порогового
уровня, областно-ориентированная сегментация, дескрипторы границ и областей
изображений, описание трехмерных сцен и структур, обработка визуальной
информации
2. МЕТОДЫ ИДЕНТИФИКАЦИИ ОБЪЕКТОВ В РОБОТИЗИРОВАННЫХ СИСТЕМАХ
2.1 Метод сравнения с эталоном
Идентификация объектов в СТЗ чаще всего производится методами сравнения с
эталоном. При этом, как правило, СТЗ решают одну из двух задач. Первая задача
заключается в получении изображения одного объекта и сравнении со всеми
эталонами заданного класса. По совпадению выбирается наилучший эталон и
осуществляется идентификация объекта, а затем при необходимости находятся
параметры его положения и ориентации [20].
Вторая задача заключается в получении изображения нескольких объектов и
поочередном их сравнении с эталоном того объекта, который необходимо выделить.
После этого вычисляются его положение и ориентация в рабочей зоне робота.
Метод состоит в установлении совпадения двух точечных изображений. Если
совпадение имеет место, считается, что предмет опознан. Преимущество метода
наложения эталона заключается в независимости от конкретного вида и сложности
объекта. В случае двумерных систем распознать ключ не сложнее, чем круг или
любую другую фигуру. С другой стороны, этот метод распознавания может отнять
много времени при использовании вычислительной машины. Покажем возникающие
затруднения на примере. На рисунке изображены контуры, соответствующие кубу и
пирамиде. Пусть ставится задача методом совпадения изображений определить,
содержит ли эта фигура где-нибудь квадрат. Изготовим эталон из ряда черных
клеток, образующих квадрат, окруженный снаружи и внутри белыми клетками.
Наложим его на фигуру и будем перемещать до установления совпадения. Могут
возникнуть затруднения по многим причинам:
- эталон должен иметь правильный размер, иначе необходимо изготовить
множество эталонов, отличающихся друг от друга лишь масштабным увеличением;
- неизвестно, в каком месте фигуры находится предполагаемый
квадрат. Поэтому поиск необходимо проводить двояко - по сдвигу и вращению;
- сказывается пространственное квантование. Даже при правильном
наложении эталона совпадение не идеальное, а лучшее из возможных. По этим
причинам метод сравнения с эталоном для роботов представляет интерес лишь при
наличии информации, позволяющей заранее вычислить размер эталона и привести
число сравнений к реально осуществимому.
Метод сравнения с эталоном оказывается интересным в отдельных случаях.
Благодаря тому, что способы изготовления оптических корреляторов (и даже
электронных корреляторов, например диссектора изображений) известны, до сих пор
этот метод применялся в оптических устройствах, которые на роботах не
устанавливались. Однако при этом всегда заранее известны размеры используемых
эталонов, а предметы расположены и ориентированы надлежащим образом. Речь идет
лишь о том, чтобы опознать объект из заданного множества объектов. Робот должен
решать более сложные задачи. Полное совпадение объекта с эталоном в
пространстве выбранных признаков, как правило, не достигается, поэтому задается
допустимое различие между эталоном и изображением, в пределах этого различия и
проверяется их совпадение.
Брагин и Войлов [17] дают такую трактовку этого метода. Если обозначить
исходное изображение объекта F(i, j), эталон Е (j, i), а вычисленное различие
T, то процедуру сравнения можно формально записать как
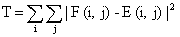 ; (2.1)
; (2.1)
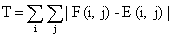 . (2.2)
. (2.2)
Здесь
индексы i и j характеризуют положение элементов в дискретном цифровом
изображении.
Совпадение
эталона с объектом проверяется по правилу
≥T,
(2.3)
где
D - заданное пороговое различие.
Если
условие не выполняется, то необходимо заменить эталон или перейти к другому
изображению.
Покажем
особенности метода сравнения с эталонами при использовании некоторых систем
признаков. Если в качестве признаков выбраны площадь и периметр изображения,
размеры вписанных и описанных фигур, момент инерции и подобные геометрические
свойства, то следует учесть масштабирование и на этапе предварительной
обработки нормировать изображения по какому-либо параметру. Например, площадь
описанного прямоугольника или окружности нормируется квадратом периметра
изображения, а периметр - значением корня квадратного из площади изображения
[21].
Изображение аккумулятивной разности формируется в результате сравнения
эталонного образа с каждым образом в данной последовательности. В процедуре
построения изображения аккумулятивной разности имеется счетчик, предназначенный
для учета расположения пикселов. Его значение увеличивается каждый раз, когда
возникает различие в расположении соответствующих пикселов эталонного образа и
образа из рассматриваемой последовательности. Таким образом, когда k-й кадр
сравнивается с эталонным, запись в данном пикселе аккумулятивной разности
означает, во сколько раз интенсивность пикселя k-го кадра отличается от
интенсивности пикселя эталонного образа. Различия устанавливаются, например, с
помощью уравнения.
Нередко полезно рассматривать три типа изображений аккумулятивной
разности: абсолютное, положительное и отрицательное.
Успех применения методов зависит от эталонного образа, относительно
которого проводятся дальнейшие сравнения. Как уже говорилось выше, различие
между двумя образами в задаче распознавания движущихся объектов определяется
путем исключения стационарных компонент при сохранении элементов,
соответствующих шуму и движущимся объектам. Проблема выделения образа из шума
решается методом фильтрации или с помощью формирования изображения
аккумулятивной разности.
На практике не всегда можно получить эталонный образ, имеющий только
стационарные элементы, и это приводит к необходимости построения эталона из
набора образов, содержащих один или более движущихся объектов. Это особенно
характерно для ситуаций, описывающих сцены со многими быстроменяющимися объектами
или в случаях, когда возникают частые изменения сцен. Рассмотрим следующую
процедуру генерации эталонного образа. Предположим, что мы рассматриваем первый
образ последовательности в качестве эталонного. Когда нестационарная компонента
полностью вышла из своего положения в эталонном кадре, соответствующий фон в
данном кадре может быть перенесен в положение, первоначально занимаемое
объектом в эталонном кадре. Когда все движущиеся объекты полностью покинули
свои первоначальные положения, в результате этой операции воссоздается
эталонный образ, содержащий только стационарные компоненты.
2.2 Методы теории графов и распознавание
При определении краев и контуров изображений применяют методы графов.
Рассмотрим глобальный подход, основанный на представлении сегментов контура в
виде графа и поиске на графе пути наименьшей стоимости, который соответствует
значимым контурам, описанный в книге Брагина и Войлова [20] . Этот подход
представляет приближенный метод, эффективный при наличии шума. Как и следует ожидать,
эта процедура значительно сложнее и требует больше времени обработки, чем
методы, изложенные выше.
Сначала дадим несколько простых определений. Граф G = (N, А) представляет
собой конечное, непустое множество вершин N вместе с множеством А неупорядоченных
пар различных элементов из N. Каждая пара из А называется дугой.
Граф, в котором дуги являются направленными, называется направленным
графом. Если дуга выходит из вершины ni, к вершине nj,
тогда nj называется преемником вершины ni. В этом случае
вершина ni называется предшественником вершины nj.
Процесс идентификации преемников каждой вершины называется расширением этой
вершины. В каждом графе определяются уровни таким образом, чтобы нулевой
уровень состоял из единственной вершины, называемой начальной, а последний
уровень-из вершин, называемых целевыми. Каждой дуге (ni nj)
приписывается стоимость c(ni nj). Последовательность
вершин n1, n2, ..., nk, где каждая вершина ni
является преемником вершины ri-1, называется путем от ni
к nk, а стоимость пути определяется формулой
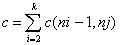 . (2.4)
. (2.4)
Элемент контура мы определим как границу между двумя пикселями р и q. В
данном контексте под контуром понимается последовательность элементов контура.
Важным методом идентификации изображений по геометрическим или другим
признакам служит метод построения графов решений. Его успешно применяют в тех
случаях, когда в заданном классе изображений имеются объекты, которые
невозможно различить по одному признаку изображения, и для правильного
распознавания необходимо использовать несколько признаков. От метода сравнения
изображения и эталона по векторам признаков метод графов отличается тем, что в
нем на каждом этапе сравнения происходит отбор возможных решений. Таким образом,
число возможных решений задачи распознавания уменьшается на каждом этапе
сравнения.
Граф (или дерево) распознавания по геометрическим признакам представлен
на рис….. Цифрами I, II, …, X обозначены возможные решения - номера
распознаваемых объектов. Буквы A, B, …, Q в вершинах графа обозначают
операторы, выделяющие определенные признаки изображения. Например, оператор А
проводит классификацию изображения по длине и высоте описанного прямоугольника,
операторы В и С - по площади, DEFG могут быть операторами, проводящими
классификацию по числу углов, H и Q - по отстоянию углов друг от друга. Граф
может иметь больше или меньше уровней, и содержание операторов может быть
различным.
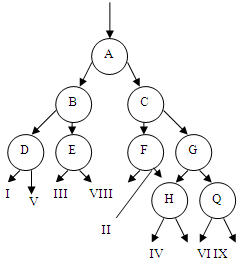
Рисунок 2.1 - Дерево распознавания
2.3 Корреляционный метод
Модификацией метода сравнения с эталоном является корреляционный метод,
основанный на вычислении взаимокорреляционной функции между эталоном и
изображением.
Корреляция - статистическая взаимосвязь двух или нескольких случайных
величин (либо величин, которые можно с некоторой допустимой степенью точности
считать таковыми). При этом, изменения одной или нескольких из этих величин
приводят к систематическому изменению другой или других величин. Математической
мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляционный анализ - метод обработки статистических данных,
заключающийся в изучении коэффициентов корреляции между переменными. При этом
сравниваются коэффициенты корреляции между одной парой или множеством пар
признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа - обеспечить получение некоторой информации
об одной переменной с помощью другой переменной. В случаях, когда возможно
достижение цели, говорят, что переменные коррелируют. В самом общем виде
принятие гипотезы о наличии корреляции означает что изменение значения
переменной А, произойдет одновременно с пропорциональным изменением значения Б.
Классификация изображений проводится по результату: чем больше значение
функции взаимной корреляции, тем с большей вероятностью эталон совпадает с
изображением. Используя обозначения, принятые в выражении, формулу для
вычисления взаимокорреляционной функции К
можно представить в виде

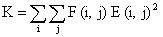 . (2.5)
. (2.5)
Максимальное
значение взаимокорреляционной функции равно,
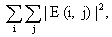 (2.6)
(2.6)
и
достигается при полном совпадении изображения с эталоном. Нормированная
взаимокорреляционная функция
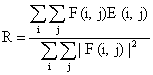 , (2.7)
, (2.7)
при
совпадении эталона с изображением достигает максимального значения, равного
единице.
Использование
корреляционного метода и метода прямого сравнения с эталоном предъявляет к
процессу предварительной обработки изображений общие требования. Они
заключаются в том, что изображение и эталон должны быть одинаково
ориентированы, иметь равный масштаб и не быть сдвинутыми друг относительно
друга в поле изображения. Другим свойством этих методов, которое следует
учитывать, является необходимость использования большого количества эталонов.
Это особенно важно в тех случаях, когда решаются задачи распознавания объектов
изменением их проекции.
2.4 Распознавание через связь шаблонов
2.4.1 Поиск объектов указанием связей между шаблонами
Часто наблюдаемый объект обладает внутренними степенями свободы, а это
означает, что его внешний вид может сильно варьироваться (например, люди могут
двигать руками и ногами, рыбы деформируются при плавании, змеи извиваются и
т.д.). Данное явление может чрезвычайно затруднить сравнение с шаблоном,
поскольку потребуется либо классификатор с гибкими границами (и множество
образцов), либо много различных шаблонов.
Многие объекты названного типа содержат небольшое число компонентов,
довольно строго упорядоченных. Можно попытаться согласовать данные компоненты
как шаблоны, а затем определить, какие объекты присутствуют, изучив
предложенные связи между найденными шаблонами. Например, вместо поиска лица по
одному полному шаблону лица, можно искать глаза, нос и рот с приемлемым
взаимным расположением.
Данный подход имеет несколько потенциальных преимуществ. Во-первых,
узнать шаблон глаза может быть легче, чем узнать шаблон лица, поскольку первая
структура очевидно проще. Во-вторых, можно получить и использовать относительно
простые вероятностные модели, поскольку могут существовать некоторые свойства
независимости, которые можно будет использовать. В-третьих, возможно, удастся
согласовать большое число объектов с относительно небольшим числом шаблонов.
Хороший пример этого явления - морды животных; почти все животные с
характерными мордами имеют глаза, нос и рот, отличается лишь пространственное
расположение этих элементов. Наконец, из сказанного следует, что для построения
сложных объектов можно использовать простые отдельные шаблоны. Например, люди
могут двигать руками и ногами, и похоже, что обучить цельный явный шаблон
обнаруживать людей целиком значительно сложнее, чем получить отдельные шаблоны
для частей тела и вероятностную модель, описывающую их степени свободы.
Рассматриваемая тема не настолько хорошо изучена, чтобы к ней выработался
какой-либо стандартный подход. В то же время основной вопрос достаточно
очевиден - как закодировать набор связей между шаблонами в форму, с которой
легко работать. В данной главе изучается ряд различных подходов к данной
задаче. Во-первых, каждый шаблон может указывать на объекты, которые он может
представлять, а затем каким-то образом считается число указателей. Если
построить некоторую явную вероятностную модель, для описания деталей
пространственных отношений можно использовать больше весовых коэффициентов.
Данную модель можно получить из функций правдоподобия; по сути, нужна функция
распределения вероятностей, дающая большое значение, когда конфигурация
компонентов подобна объекту, и малое - в противном случае. Тогда поиск объектов
превращается в поиск шаблонов, которые при подстановке в вероятностную модель
дают большие значения. Нужно отметить, что следует внимательно относиться к
сокращению поиска. Сложность этого подхода заключается в том, что даже при
сокращении поиск может быть дорогим. Как утверждают Форсайт и Понс, в то же
время при определенном классе вероятностных моделей можно провести эффективный
поиск [21].
Простые модели объектов могут обеспечивать достаточно эффективное
распознавание. Простейшая модель - это рассматривать объект как набор
фрагментов изображения (небольших окрестностей элементов характерного вида)
нескольких различных типов, формирующих образ (pattern). Чтобы определить,
какой образ наблюдается, находятся все фрагменты, каждый из которых указывает
на все образы, в которые он входит. То изображение, на которое было указано
наибольшее число, и считается присутствующим. Хотя данная стратегия проста, она
довольно эффективна. Ниже описываются методы поиска фрагментов, а затем
представляется ряд последовательно усложняющихся реализаций данной стратегии.
2.4.2 Описание фрагментов изображения
Небольшие фрагменты изображения могут иметь достаточно характерный вид,
если имеют много ненулевых производных (например, в углах). Авторы [16] искали
углы на изображении, часто именуемые точками интереса. Далее оценивался набор
производных функции яркости в этих углах и набор производных, инвариантных
относительно вращения, трансляции, определенного изменения масштаба и изменения
освещения. Данные признаки назывались инвариантными локальными особенностями
(invariant local jets).
Далее будем предполагать, что фрагменты изображения можно разбить на
несколько классов. Представители каждого класса могут быть получены
использованием нескольких изображений каждого объекта - как правило,
соответствующие фрагменты будут относиться к одному классу, но, возможно,
вследствие шума иметь несколько отличающиеся инвариантные локальные потоки.
Подходящий набор классов можно определить либо посредством ручной классификации
фрагментов, либо посредством кластеризации фрагментов-образцов (несколько
лучший метод). Теперь требуется определить, когда два набора инвариантных
локальных потоков представляют один класс фрагментов изображения. Шмид (Schmid)
и Mop (Mohr) для проверки использовали расстояние Махаланобиса (Mahalanobis
distance) между векторами признаков тестируемого фрагмента и фрагмента-образца;
если замер был меньше некоторого порога, тестируемый фрагмент считался
идентичным образцу.
Обратим внимание на то, что по сути описан классификатор (он распределяет
фрагменты по классам, представленным образцами, или отказывается от
классификации), а фрагменты представляют шаблоны. Программу согласования
шаблонов можно построить с помощью любой техники, не используя признаки,
инвариантные относительно вращения, как говорили Форсайт и Понс [21]. Для этого
можно использовать набор настроек, содержащий версии каждого фрагмента-образца,
которые отличаются вращением и изменением масштаба, при варьирующихся условиях
освещения, так чтобы классификатор мог определить, что вращение, изменение
масштаба и освещения не влияет на идентификацию фрагмента. Преимущество
использования инвариантных признаков заключается в том, что классификатору не
нужно узнавать об инвариантности из набора настроек.
2.4.3 Указание признаков и простая порождающая модель
Пусть дано изображение, в котором находяться интересующие нас точки и в
каждой точке изображения классифицируется фрагмент изображения. Возникает
следующий вопрос: какие образы находятся в изображении? Для ответа на этот
вопрос можно построить соответствие между фрагментами изображения и образами.
Предположим, что всего на изображении имеется Ni фрагментов. Более
того, предположим, что на изображении либо присутствует один образ из данной
коллекции, либо ни одного. Отдельный фрагмент может порождаться либо
единственным присутствующим образом, либо шумом. Впрочем, образы, как правило,
содержат фрагменты не всех классов. Это означает, что утверждение о присутствии
определенного образа равнозначно утверждению о том, что некоторые фрагменты
изображения порождены шумом (поскольку может присутствовать только один образ,
а имеются фрагменты изображения, которые принадлежат классам, не содержащимся в
текущем образе).
Окончательно приходим к простой порождающей модели изображения. Когда
образ присутствует, возникнуть могут только фрагменты некоторых определенных
классов. Разрабатывая данную модель, получаем ряд алгоритмов сопоставления
образов с наблюдаемыми картинами.
Простейшая версия данной модели получается в предположении, что образ
порождает все фрагменты классов, которые он может породить, а значит требуется,
чтобы шумом порождалось минимальное число фрагментов. Данное предположение
сводится к простой схеме указания. Берется каждый фрагмент изображения и
указывается каждый образ, который может породить фрагменты этого класса.
Выбирается образ, получивший наибольшее число указаний, он же считается
присутствующим на изображении. Данная стратегия может быть эффективной, хотя ее
использование приводит к некоторым проблемам.
2.4.4 Вероятностные модели для указания
Полученный простой процесс голосования можно интерпретировать через
вероятностную модель, поскольку при этом проявляются сильные и слабые стороны
описанного подхода. Фосайт и Понс [16] пишут, что используемую порождающую
модель можно превратить в вероятностную, предположив, что фрагменты генерируются
независимо и случайным образом, причем также предполагается, что объект
присутствует. Запишем
Р{фрагмент i-гo типа есть на изображении | присутствует j-й образ} = pij
Р{фрагмент i-го типа | нет образа} = рix.
В простейшей модели предполагается, что для каждого образа j, pij
= µ, если образ может породить данный фрагмент, и 0 - в противном случае. Более
того, предполагается, что рix = λ < µ для всех i. Наконец, предполагается,
что каждый наблюдаемый фрагмент на изображении может порождаться либо отдельным
образом, либо шумом. Всего на изображении ni фрагментов. При таких
допущениях для вычисления функции правдоподобия нужно знать только, какие
фрагменты порождены образом, а какие - шумом. В частности, если взять функцию
правдоподобия изображения при данном образе и предположить, что np фрагментов
порождены данным образом, а np - ni фрагментов порождены
шумом, можно записать:
Р(интерпретация
| образ) = 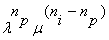 , (2.8)
, (2.8)
причем
данная величина больше для больших значений np. В то же время,
поскольку не каждый образ может породить любой фрагмент, максимальный доступный
выбор np зависит от выбранного образа. Принятый метод указания
равнозначен выбору образа с максимальным возможным правдоподобием при данной
(простой) порождающей модели.
Отсюда
видится источник определенных сложностей: если образ мало правдоподобен,
следует учесть дополнительную (априорную) информацию. Более того, вследствие
шума некоторые фрагменты могут порождаться легче, чем другие - если не учесть
этот факт, при подсчете голосов некоторые образы будут в более выгодном
положении. Наконец, при данном объекте некоторые фрагменты могут быть более
вероятными, чем другие. Например, углы значительно чаще будут встречаться на
образе шахматной доски, чем на изображении полос зебры.
2.4.5 Доработка порождающей модели
Относительно просто учитывать все вышесказанное и соответствующим образом
усовершенствовать простейшую модель (фрагменты появляются независимо при
условии наличия образа). Предположим, что имеется N различных типов фрагментов.
Форсайт и Понс [16] пишут, что фрагменты каждого типа генерируются со своей
вероятностью всеми изображениями и шумом. Теперь предположим, что на
изображении присутствует nil экземпляров
фрагментов l-го типа. Более того, nk из них генерируется образом, а
остальные - шумом. Теперь поскольку фрагменты возникают независимо при данном
образе и шум не зависит от образа, правдоподобие равно
Р(фрагменты порождены образом | j-й образ)
Р(фрагментов порождено шумом). (2.9)
Первый член равен
Р(тип 1 | j-й образ)"1 Р(тип 2 | j-й образ)"2
… (2.10)
Р(тип N | j-й образ)nN,Р(шум), (2.11)
что можно оценить как
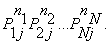 (2.12)
(2.12)
Теперь
предположим, что фрагменты порождаются шумом независимо друг от друга. Это
означает, что шумовую составляющую можно записать следующим образом:
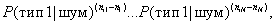 (2.13)
(2.13)
что
можно оценить как
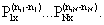 (2.14)
(2.14)
Это
означает, что правдоподобие можно записать как
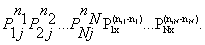 (2.15)
(2.15)
Для
каждого типа фрагментов k возможны два случая: если pkj > pkx
, то максимум достигается при nk = nik; в противном
случае максимум достигается при nk = 0. Обозначим через πi
априорную вероятность того, что содержит j-й образ, а через π0 -
априорную вероятность того, что оно не содержит ни одного объекта. Это
означает, что для каждого типа образов j максимальное значение апостериорной
вероятности запишется следующим образом:
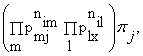 (2.16)
(2.16)
где
индекс m служит для подсчета значений признаков, для которых pmj
> рmх, а l - для подсчета значений признаков, для которых рlj
< plx. Данная величина формируется для каждого объекта, а затем
выбирается та из них, которая имеет наибольшее апостериорное значение. Обратите
внимание, что данная модель является реляционной, хотя в действительности мы не
вычисляем геометрические признаки, связывающие образы. Это объясняется тем, что
фрагменты связываются условными вероятностями их появления при данном образе,
которые отличаются для разных образов.
2.4.6 Указание связей
Для улучшения простой стратегии указания можно использовать
геометрические связи. Фрагмент сопоставляется с объектом, только когда с
объектом сопоставлены соседние фрагменты и все эти фрагменты образуют
подходящую конфигурацию. Термин "подходящая конфигурация" может быть
источником сложностей, но предположим пока, что объекты сопоставлены с
точностью до плоского вращения, трансляции и масштаба (это предположение
разумно, например, для лиц анфас). Предположим теперь, что дан фрагмент,
соответствующий некоторому объекту. Далее берем р ближайших фрагментов и
проверяем, согласуется ли более 50% их с тем же объектом и совпадают ли углы
между тройками согласованных фрагментов с соответствующими углами объекта - все
это называется полулокальными условиями. Если эти две проверки пройдены,
указатель на объект, поданный этим фрагментом, регистрируется. Отметим, что
вероятностную интерпретацию данного подхода построить довольно трудно -
вероятности появления фрагментов теперь зависят от того, где они расположены в
образе, а также от того, какой образ их генерирует.
2.4.7 Указание на трехмерные объекты
Хотя подход Шмида и Мора был описан с позиции двумерных образов, его
относительно просто расширить на распознавание трехмерных объектов. Для этого
каждый набор проекций объекта Форсайт и Понс [16] рассматривают как иной
двумерный образ. При наличии достаточного числа проекций этот подход работает,
поскольку небольшие изменения в двумерном изображении, вызванные малыми
изменениями угла наблюдения, будут компенсироваться разрешенным уровнем ошибок
процесса согласования инвариантных локальных потоков и углов.
Данная стратегия сведения трехмерного распознавания к двумерному
применяется довольно широко, но имеет и свои сложности. Основная проблема - это
большое число моделей, что может привести к затруднению процедуры указания.
Неизвестно также, каково минимальное число проекций, требуемых для согласования
в подобной схеме.
2.5 Искусственные нейронные сети и их использование при идентификации
изображений
Искусственные нейронные сети (ИНС) - математические модели, а также их
программные или аппаратные реализации, построенные по принципу организации и
функционирования биологических нейронных сетей - сетей нервных клеток живого
организма. Это понятие возникло при изучении процессов, протекающих в мозге, и
при попытке смоделировать эти процессы.
ИНС представляют собой систему соединённых и взаимодействующих между
собой простых процессоров (искусственных нейронов). Такие процессоры обычно
довольно просты, особенно в сравнении с процессорами, используемыми в
персональных компьютерах. Каждый процессор подобной сети имеет дело только с
сигналами, которые он периодически получает, и сигналами, которые он
периодически посылает другим процессорам. И тем не менее, будучи соединёнными в
достаточно большую сеть с управляемым взаимодействием, такие локально простые
процессоры вместе способны выполнять довольно сложные задачи. Простая
искусственная нейронная сеть представлена на рис. 2.2.
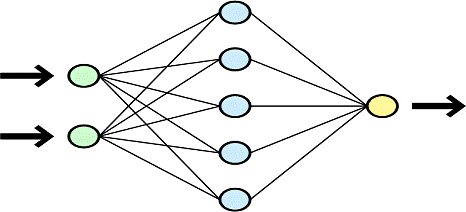
Рисунок 2.2 - Простая нейронная сеть
С точки зрения машинного обучения, нейронная сеть представляет собой
частный случай методов распознавания образов, дискриминантного анализа, методов
кластеризации и т. п. С математической точки зрения, обучение нейронных сетей -
это многопараметрическая задача нелинейной оптимизации. С точки зрения
кибернетики, нейронная сеть используется в задачах адаптивного управления и как
алгоритмы для робототехники. С точки зрения развития вычислительной техники и
программирования, нейронная сеть - способ решения проблемы эффективного
параллелизма. А с точки зрения искусственного интеллекта, ИНС является основой
философского течения коннективизма и основным направлением в структурном
подходе по изучению возможности построения (моделирования) естественного интеллекта
с помощью компьютерных алгоритмов.
Нейронные сети не программируются в привычном смысле этого слова, они
обучаются. Возможность обучения - одно из главных преимуществ нейронных сетей
перед традиционными алгоритмами. Технически обучение заключается в нахождении
коэффициентов связей между нейронами. В процессе обучения нейронная сеть
способна выявлять сложные зависимости между входными данными и выходными, а
также выполнять обобщение. Это значит, что в случае успешного обучения сеть
сможет вернуть верный результат на основании данных, которые отсутствовали в
обучающей выборке, а также неполных и/или «зашумленных», частично искаженных
данных.
В качестве образов могут выступать различные по своей природе объекты:
символы текста, изображения, образцы звуков и т. д. При обучении сети
предлагаются различные образцы образов с указанием того, к какому классу они
относятся. Образец, как правило, представляется как вектор значений признаков.
При этом совокупность всех признаков должна однозначно определять класс, к
которому относится образец. В случае если признаков недостаточно, сеть может
соотнести один и тот же образец с несколькими классами, что неверно. По
окончании обучения сети ей можно предъявлять неизвестные ранее образы и
получать ответ о принадлежности к определённому классу.
Топология такой сети характеризуется тем, что количество нейронов в
выходном слое, как правило, равно количеству определяемых классов. При этом
устанавливается соответствие между выходом нейронной сети и классом, который он
представляет. Когда сети предъявляется некий образ, на одном из её выходов
должен появиться признак того, что образ принадлежит этому классу. В то же
время на других выходах должен быть признак того, что образ данному классу не
принадлежит. Если на двух или более выходах есть признак принадлежности к
классу, считается что сеть «не уверена» в своём ответе [22].
2.6 Распознавание объектов и их интерпретация
Распознаванием называется процесс разметки, т.е. алгоритмы распознавания
идентифицируют каждый объект сцены и присваивают ему метки (гаечный ключ,
перемычка). Обычно в большинстве промышленных систем технического зрения
предполагается, что объекты сцены сегментированы как отдельные элементы. Другое
общее ограничение относится к расположению устройств сбора информации
относительно исследуемой сцены (обычно они располагаются перпендикулярно
рабочей поверхности). Это приводит к уменьшению отклонений в характеристиках
формы, а также упрощает процесс сегментации и описания в результате уменьшения
вероятности загораживания одних объектов другими. Управление отклонениями в
ориентации объекта производится путем выбора дескрипторов, инвариантных к
вращению, или путем использования главных осей объекта для ориентирования его в
предварительно определенном направлении.
Современные методы распознавания делятся на две основные категории:
теоретические и структурные методы. Теоретические методы основываются на
количественном описании (статическая структура), а в основе структурных методов
лежат символические описания и их связи (последовательности направлений в
границе, закодированной с помощью цепного кода).
Интерпретацию - процесс, который позволяет системе технического зрения
приобрести более глубокие знания об окружающей среде по сравнению со знаниями,
полученными с помощью методов, изложенных выше. Рассматриваемая с этой точки
зрения интерпретация охватывает данные методы как неотъемлемую часть процесса
понимания зрительной сцены. Хотя в области технического зрения она и является
объектом активных исследований, достижения пока весьма незначительны. Ниже мы
кратко рассмотрим проблемы, представляющие современные исследования в этой
области технического зрения .
Мощность системы технического зрения определяется ее способностью
выделять из сцены значимую информацию при различных условиях наблюдения и
использовании минимальных знаний об объектах сцены. По ряду причин
(неравномерное освещение, наличие тел, загораживающих объекты, геометрии
наблюдения) этот тип обработки представляет трудную задачу. Много внимания
уделено методам уменьшения разброса в интенсивности. Способы обратного и
структурированного освещения позволяют устранить трудности, связанные с
произвольным освещением рабочего пространства. К этим трудностям относятся
теневые аффекты, усложняющие процесс определения контуров, и неоднородности на
гладких поверхностях. Это часто приводит к тому, что они распознаются как
отдельные объекты. Очевидно, многие из этих проблем обусловлены тем, что
относительно мало известно о моделировании свойств освещения и отражения
трехмерных сцен. Методы разметки линий и соединений представляют собой
некоторые попытки в этом направлении, но они не в состоянии количественно
объяснить эффекты взаимодействия освещения и отражения. Более перспективный
подход основан на математических моделях, описывающих наиболее важные связи
между освещением, отражением и характеристиками поверхности, такими, как
ориентация.
2.7 Теоретико-множественная модель распознавания и
идентификации
Рассмотрим теоретико-множественную модель процесса распознавания и
идентификации объектов роботизированного производства.
Пусть задано пространство S в котором существует множество объектов X ={x1…
xn}, также в нем находится робот R, оснащенный системой технического
зрения SR. Пусть каждому объекту хі соответствует набор
признаков {f1і…fkі}.
Тогда множество объектов X = {x1, x2… xn}
можно охарактеризовать матрицей признаков:
F
= 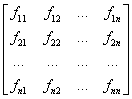 .
.
Процесс
идентификации будет заключаться в том, что объект хі может быть
распознан по подмножеству признаков 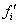 из
множества признаков F. Для всего множества объектов Х набор подмножеств
из
множества признаков F. Для всего множества объектов Х набор подмножеств 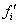 формирует множество
формирует множество 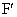 :
:
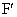 =
= 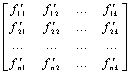 .
.
Общий
вид процедуры распознавания объектов формально представляется в виде:
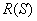
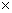 Х
Х 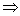
 ,
,
где
R(S) - робот, оснащенный системой датчиков S; 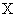 -
множество объектов;
-
множество объектов; 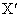 - множество распознанных объектов.
- множество распознанных объектов.
Процедура
распознавания и идентификации объектов представлена в виде
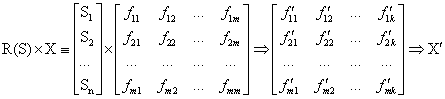 ,
,
где
 - множество сенсоров;
- множество сенсоров; 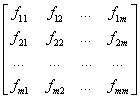 -
множество признаков;
-
множество признаков;
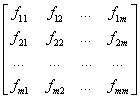 -
-
множество
распознанных признаков; 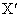 - множество распознанных объектов.Таким образом,
процедура идентификации будет состоять в определении в матрице распознанных
признаков тех из них, которые являются достаточными для идентификации объектов:
- множество распознанных объектов.Таким образом,
процедура идентификации будет состоять в определении в матрице распознанных
признаков тех из них, которые являются достаточными для идентификации объектов:
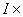
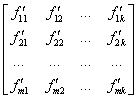
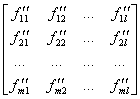 =
=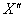 ,
,
где
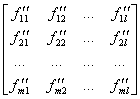 - матрица идентифицированных признаков, характеризующее
множество идентифицированных объектов
- матрица идентифицированных признаков, характеризующее
множество идентифицированных объектов 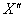 .
.
Данная
модель может быть использована при разработке подсистем распознавания и
идентификации в составе систем технического зрения. Ее применение позволит
обеспечить решение задач распознавания и идентификации объектов в рабочей зоне
манипуляционных и мобильных роботов.
Во
второй части работы проанализированы методы идентификации объектов в
робототехнических системах и построена теоретико-множественная модель
распознавания и идентификации.
Основными
методами являются:
- метод сравнения с эталоном (установление совпадения двух
точечных изображений);
- методы теории графов и распознавание (представление сегментов
контура в виде графа и поиске на графе пути наименьшей стоимости, который
соответствует значимым контурам);
- корреляционный метод (вычисление взаимокорреляционной функции
между эталоном и изображением);
- распознавание через связи шаблонов (согласование компонентов
изображения как шаблон и определение, какие объекты присутствуют, изучив
предложенные связи между найденными шаблонами);
- искусственные нейронные сети (обучение сети по различным
образцам образов с указанием того, к какому классу они относятся).
. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ МЕТОДОВ ОБРАБОТКИ ИНФОРМАЦИИ В СИСТЕМАХ
ТЕХНИЧЕСКОГО ЗРЕНИЯ
3.1 Основные подходы к практической реализации методов
обработки информации
3.1.1 Методы пространственной области
Рассмотрим два основных подхода к предварительной обработке информации.
Первый подход основан на методах пространственной области, а второй - на
методах частотной области с использованием преобразования Фурье. Вместе эти
подходы охватывают большинство из существующих алгоритмов предварительной
обработки информации, применяемых в системах технического зрения роботов [24].
К пространственной области относится совокупность пикселов, составляющих
изображение. Методы пространственной области являются процедурами, оперирующими
непосредственно с этими пикселями. Функции предварительной обработки в
пространственной области записываются в виде
(x, y) = h[f(x, у)], (3.1)
где f{x, у)-входное изображение, g(xy у)-выходное
(обработанное) изображение, a h - оператор функции /, определенный в некоторой
области (х, у). Оператор h можно применять также к ряду входных изображений для
формирования, например, суммы пикселов К изображений при уменьшении шума
Основным подходом при определении окрестности точки (х, у) является
использование квадратной или прямоугольной области части изображения с центром
в точке (х, у). Центр этой части изображения перемещается от пикселя к пикселю,
начиная, например, от левого верхнего угла; при этом для получения g(xy
у) оператор применяется для каждого положения (х, у). Хотя иногда используются
и другие формы окрестности (например, круг), квадратные формы более
предпочтительны из-за простоты их реализации.
Один из наиболее часто встречающихся методов пространственной области
основан на использовании так называемых масок свертки (или шаблонов, окон или
фильтров). Обычно маска представляет собой небольшую (например, размерность
3X3) двумерную систему, коэффициенты которой выбираются таким образом, чтобы
обнаружить заданное свойство изображения.
Предположим для начала, что дано изображение с постоянной интенсивностью,
которое содержит отдельные удаленные друг от друга пиксели с отличной от фона
интенсивностью. Процесс заключается в следующем. Центр маски перемещается по
изображению определенным образом. При совпадении центра маски с положением
каждого пикселя производится умножение значений всех пикселов, находящихся под
маской, на соответствующий коэффициент на маске. Затем результаты этих девяти
умножений суммируются. Если все пиксели под маской имеют одинаковые значения
(постоянный фон), то сумма будет равна нулю. Если же центр маски разместится
над точкой с другой интенсивностью, сумма будет отлична от нуля. В случае
размещения указанной точки вне центра сумма также будет отлична от нуля, но на
меньшую величину. Это различие может быть устранено путем сравнения значения
суммы с пороговым значением.
Отметим, что использование окрестности не ограничивается областями
размерностью 3X3 и случаями, которые будут приведены в дальнейшем, например
снижение шума, получение переменных порогов изображения, подсчет измерений
параметров изображения и формирование структуры объекта.
3.1.2 Методы частотной области
К частотной области относится совокупность комплексных пикселов в виде
преобразования Фурье от изображения. Понятие «частота» используется при
интерпретации преобразования Фурье и вытекает из того факта, что результат
этого преобразования представляет собой сумму синусоид. Из-за повышения
требований к обработке результатов методы частотной области не так широко
используются в техническом зрении роботов, как методы пространственной области
[25].
Однако преобразование Фурье играет важную роль при анализе движения
объекта и при описании объекта. Кроме того, многие пространственные методы для
улучшения качества и восстановления изображения базируются на концепциях
преобразования Фурье.
Позволяется проводить прямую процедуру вычисления двумерного
преобразования Фурье, используя только одноразмерный БПФ-алгоритм.
Преобразование Фурье можно использовать при решении многих задач систем
технического зрения. Например, с помощью представления границы объекта в виде
одномерного массива точек и вычисления их преобразования Фурье полученные
значения могут быть использованы в качестве описания формы границы. Одномерное
преобразование Фурье является также эффективным при обнаружении движения
объекта.
Использование дискретного двумерного преобразования Фурье возможно при
изменении, увеличении и восстановлении изображений, хотя, как уже отмечалось,
применение этого метода в промышленных системах технического зрения до сих пор
ограничено сложностью требуемых вычислений. Этот подход, требующий
использования прецизионного оптического оборудования, применяется в
промышленных условиях для решения таких задач, как проверка качества
поверхности металла после финишной обработки.
3.2 Библиотека Integrated Performance
Primitives (IPP)
Возможностями Intel IPP являются следующие функции:
- кодирование и декодирование видео;
- кодирование и декодирование аудио;
- JPEG/JPEG2000;
- машинное зрение;
- криптография;
- сжатие данных;
- преобразование цвета;
- обработка изображения;
- трассировка луча/визуализация;
- обработка сигналов;
- кодирование речи;
- распознавание речи;
- обработка строк;
- векторная/матричная математика.
Библиотека использует расширенные наборы инструкций процессора MMX, SSE,
SSE2, SSE3, SSSE3, SSE4 и многоядерные процессоры.IPP разделен на три основные
группы: сигналы (линейный массив данных или вектор), изображения и матрицы.
Половина функций для матричных операций, треть для обработки сигналов и
оставшиеся для изображений. Функции Intel IPP разделены на 4 типа данных: 8u
(8-битные беззнаковые), 8s (8-битые со знаком), 16s, 32f (32-битые с плавающей
точкой), 64f и т.д. Как правило, разработчики приложений работает только с
одним доминирующим типом данных для большинства функций обработки, и только в
конце обработки производят преобразование в выходной формат [26].
3.3 Библиотека AviCap
Приложения, предназначенные для записи звуковых данных и видеоданных,
могут воспользоваться удобным высокоуровневым интерфейсом, предоставляемым
библиотекой avicap.dll. Создавая приложения для записи видео, вам не придется
заботиться о внутренней структуре avi-файлов, о компрессии (сжатии) данных при
записи, об интерфейсе с драйверами устройства (или устройств) записи. При
необходимости, вы, тем не менее, можете воспользоваться интерфейсом более низкого
уровня, который обеспечивается библиотекой avifile.dll.
Для создания приложений, записывающих видео, лучше всего воспользоваться
классом окна AVICap, определенном в библиотеке avicap.dll . Создав окно на базе
класса AVICap, приложение получит в свое распоряжение простой интерфейс для
записи видео и звуковых данных в avi-файл, для предварительного просмотра видео
и выполнения других операций.
В классе AVICap предусмотрены средства динамического переключения
устройств записи видео и звука, что удобно в тех случаях, когда возможно
поочередное использование нескольких таких устройств, установленных в
компьютере. Приложение может создать avi-файл, предназначенный для записи,
скопировать содержимое одного avi-файла в другой, установить частоту кадров,
вывести на экран диалоговую панель, с помощью которой пользователь сможет
задать формат записи. Есть средства для работы с палитрами и универсальным
буфером обмена Clipboard.
Для записи звука класс окна AVICap пользуется срествами библиотеки
mmsystem.dll.
3.4 Библиотека OpenCV
.4.1Операторы для определения изображений при помощи
библиотеки OpenCV
OpenCV (англ. Open Source Computer Vision Library, библиотека
компьютерного зрения с открытым исходным кодом) - библиотека алгоритмов
компьютерного зрения, обработки изображений и численных алгоритмов общего
назначения с открытым кодом. Реализована на C/C++, так же разрабатывается для
Python, Ruby, Matlab и других языков.предназначена для повышения вычислительной
эффективности процедур обработки видеоизображения с особым упором на применение
в задачах реального времени.написана на C хорошо оптимизирована и может
использовать преимущества многоядерных процессоров. Для более полного
использования возможностей библиотеки рекомендуется установить Intel
Performance Primitives (IPP). Это позволит повысить производительность процедур
библиотеки (где взять и как ставить смотреть здесь ).
Позволяет достаточно быстро и эффективно реализовывать сложные алгоритмы
машинного зрения. Библиотека содержит более 500 функций, которые позволяют
реализовывать приложения работающие во многих областях, в том числе:
- контроль качества выпускаемой продукции;
- обработке изображений в медицине;
- обеспечении безопасности;
- интерфейсе пользователя;
- робототехнике.содержит библиотеку общих функций
искусственного интеллекта «Machine Learning Library» (MLL). Она служит, в
основном, для распознавания фрагментов изображения и кластеризации.
Данную библиотеку применяют:
- для утверждения общего стандартного интерфейса компьютерного
зрения для приложений в этой области;
- для способствования росту числа таких приложений и создания
новых моделей использования PC;
- сделать платформы Intel привлекательными для разработчиков
таких приложений за счёт дополнительного ускорения OpenCV с помощью Intel®
Performance Libraries (Сейчас включают IPP (низко-уровневые библиотеки для
обработки сигналов, изображений, а также медиа-кодеки) и MKL (специальная
версия LAPACK и FFTPack));
- OpenCV способна автоматически обнаруживать присутствие IPP и
MKL и использовать их для ускорения обработки.
Основными модулями являются следующие модули.
Ядро cxcore производит:
- базовые операции над многомерными числовыми массивами;
- матричная алгебра, математические функции, генераторы
случайных чисел DFT, DCT;
- запись/восстановление структур данных в/из XML/YAML;
- базовые функции 2D графики;
- поддержка более сложных структур данных: разреженные массивы,
динамически растущие последовательности, графы;- является модулем обработки
изображений и компьютерного зрения. Его функциями являются:
- базовые операции над изображениями (фильтрация,
геометрические преобразования, преобразование цветовых пространств и т. д.)
- анализ изображений (выбор отличительных признаков,
морфология, поиск контуров, гистограммы);
- структурный анализ (описание форм, плоские разбиения);
- анализ движения, слежение за объектами;
- обнаружение объектов, в частности лиц;
- калибровка камер, элементы восстановления пространственной
структуры;- Модуль для ввода/вывода изображений и видео, создания
пользовательского интерфейса
Необходим для выполнения следующих операций:
- захват видео с камер и из видео файлов, чтение/запись
статических изображений;
- функции для организации простого UI (сейчас все демо
приложения используют HighGUI).- Экспериментальные и устаревшие функции
Данный модуль выполняет:
- пространственное зрение: стерео калибрация, само калибрация;
- поиск стерео-соответствия, клики в графах;
- нахождение и описание черт лица;
- сравнение форм, построение скелетонов;
- скрытые Марковские цепи;
- описание текстур.
Оператор Собеля вычисляет первые, вторые, третьи или смешанные
производные изображения, используя расширенный оператор.
Функция вычисляет производную изображения, скручивая изображение с
соответствующим ядром.
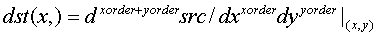 (3.2)
(3.2)
Операторы
Собеля комбинируют Гауссово сглаживание и дифференцирование, таким образом
результат более или менее устойчив к искажению. Чаще всего, функция вызвана,
чтобы вычислить сначала x-или y-производную изображения. Первый случай
(Х-оператор) соответствует
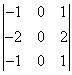 ,
,
второй
случай (У-оператор)
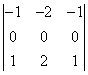
или
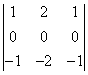
в
зависимости от начала координат изображения. Так как масштабирование не
сделано, изображение адресата обычно имеет больший размер абсолютной величины,
чем исходное изображение.
Ядра
применяются к каждому пикселю изображения: он помещается в центр ядра, и
значения интенсивности в соседних точках умножаются на соответствующие
коэффициенты ядра, после чего полученные значения суммируются. Х-оператор
Собеля, примененный к 3х3 матрице исходного изображения, дает величину
горизонтальной составляющей градиента интенсивности в центральной точке этой
матрицы, а Y-оператор Собеля дает величину вертикальной составляющей градиента
[1]. Коэффициенты ядра выбраны так, чтобы при его применении одновременно
выполнялось сглаживание в одном направлении и вычисление пространственной
производной - в другом. Величина градиента определяется как квадратный корень
из суммы квадратов значений горизонтальной и вертикальной составляющих
градиента.
В
результате образуется массив чисел, характеризующих изменения яркости в
различных точках изображения. Затем выполняется операция сравнения с порогом и
определяется положение элементов изображения с наиболее сильными перепадами
яркости. Выбор порога является одним из ключевых вопросов выделения перепадов
[27].
В
результате обработки получается бинарная матрица, где единицам соответствуют
точки со значительным перепадом яркости, нулям - все остальные. В качестве
дополнительной меры в борьбе с шумом и ликвидации возможных разрывов в контурах
применяются морфологические операции.
В
библиотеке компьютерного зрения OpenCV этот оператор представлен функцией void
cvSobel( const CvArr* src, CvArr* dst, int xorder, int yorder, int
aperture_size=3 ), где src - исходное изображение; dst - получаемое
изображение; xorder - производная по координате х; yorder - производная по
координате у; aperture_size - размер апертуры изображения (Апертура в оптике -
действующее отверстие оптического прибора, определяемое размерами линз или
диафрагмами).
Оператор
Лапласа. Найдем вероятность попадания случайной величины, распределенной по
нормальному закону, в заданный интервал.
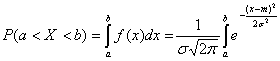 (3.3)
(3.3)
обозначим
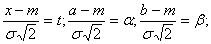 ; (3.4)
; (3.4)
тогда
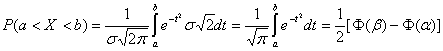 (3.5)
(3.5)
Т.к.
интеграл 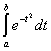 не выражается через элементарные функции, то вводится
в рассмотрение функция
не выражается через элементарные функции, то вводится
в рассмотрение функция
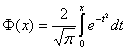 (3.6)
(3.6)
которая
называется функцией Лапласа или интегралом вероятностей.
Значения
этой функции при различных значениях х посчитаны и приводятся в специальных
таблицах.
Ниже
показан график функции Лапласа.
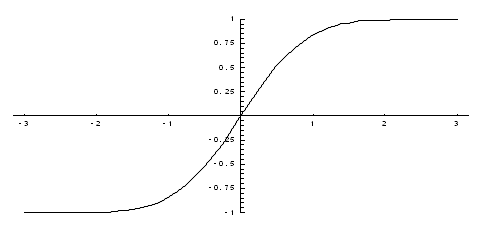
Рисунок
3.1 - график функции Лапласа
Функция
Лапласа обладает следующими свойствами:
)
Ф(0) = 0;
)
Ф(¥)
= 1.
Функцию
Лапласа также называют функцией ошибок и обозначают erf x.
Еще
используется нормированная функция Лапласа, которая связана с функцией Лапласа
соотношением:
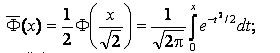 (3.7)
(3.7)
Ниже
показан график нормированной функции Лапласа:
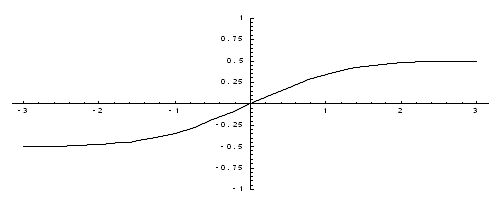
Рисунок
3.2 - график нормированной функции Лапласа
В
библиотеке компьютерного зрения OpenCV этот оператор представлен функцией
void cvLaplace( const CvArr* src, CvArr* dst, int
aperture_size=3 ),
где
src - исходное изображение; dst - получаемое изображение; aperture_size -
размер апертуры изображения (аналогично функции cvSobel).
Отличие
функции Лапласа от функции Собеля заключается в том, что в функции Лапласа
находится вторая производная, а в функции Собеля первая.
Алгоритм
Кэнни. Углы характеризуют контуры объектов на изображении и потому являются
очень важной проблемой в обработке изображений.
Углы на изображении - это области с резкими скачками интенсивности цвета
при переходе от одного пикселя к другому. Выделение углов на изображении
используется для значительного сокращения объёма данных при обработке, сохраняя
при этом основные структурные свойства исходного изображения.
Алгоритм Кэнни выделения углов на изображении известен многим как
оптимальный детектор угловых точек. Целью Кэнни было улучшить детекторы,
созданные до него на момент разработки. И он успешно добился своей цели,
изложив свои идеи и методы.
Этот алгоритм актуален и на сегодняшний день и лежит в основе многих
современных алгоритмов выделения углов.
В своей работе Кэнни следовал некоторому списку критериев с тем, чтобы
улучшить современные методы выделения углов.
Первым и наиболее очевидным критерием был низкий уровень погрешности.
Очень важно, чтобы точность угловых точек изображения не была потеряна и,
следовательно, чтобы не возникало ссылок на не угловые точки. Вторым критерием
выступал хороший уровень локализации угловых точек. Иными словами, чтобы
расстояние между найденными угловыми точками и действительными углами сводилось
к минимуму. Третьим критерием было, чтобы каждому углу соответствовало не более
одной точки. Этот критерий был поставлен, поскольку первых двух было
недостаточно для полного исключения возможности множественного соответствования
различных точек одному и тому же углу.
Основываясь на этих критериях, детектор углов Кэнни сначала сглаживает
изображение для уменьшения шума. Потом находит градиент изображения в каждой
точке для выделения областей с наибольшей величиной пространственной
производной. Далее алгоритм проходит по этим областям и глушит пиксели с не
максимальным значением градиента (процедура nonmaximum suppression). Массив
градиентов далее сокращается процедурой гистерезиса (лат. - hysteresis),
которая используется для обработки оставшихся пикселей, которые не были
приглушены. Процедура гистерезиса использует два порога. Если величина
градиента меньше первого, то пиксель устанавливается в ноль (не угол). Если
величина градиента больше второго порога, пиксель устанавливается в
максимальное значение (делается углом). И если величина лежит между двумя
порогами, то пиксель не устанавливается в ноль, пока не найден путь от данного
пикселя к пикселю с величиной градиента больше второго порога.
В библиотеке компьютерного зрения OpenCV этот оператор представлен
функцией
void cvCanny( const CvArr* image, CvArr* edges, double
threshold1, double threshold2, int aperture_size=3 ),
где image - входное изображение; edges - изображение для выделения краев
с помощью функции ; threshold1 - первый порог изображения; threshold2 - второй
порог изображения; aperture_size - размер апертуры изображения.
Детектор Харриса. За последние двадцать лет было создано довольно много
различных детекторов точечных особенностей изображений. Чаще всего используются
детектор Харриса и детектор по минимальным собственным значениям. В данной
работе реализованы оба.
Рассмотрим
детектор по минимальным собственным значениям. Берем первое изображение
последовательности. Для каждого пикселя 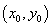
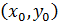 рассчитываем
следующую матрицу:
рассчитываем
следующую матрицу:

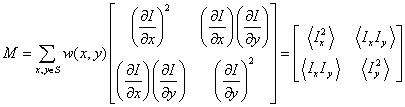 (3.8)
(3.8)
где
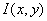 - яркость в точке
- яркость в точке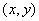 ,
, 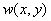 - весовая функция по окрестности
- весовая функция по окрестности 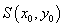 , в качестве которой обычно берут распределение
Гаусса. У точки, окрестность которой похожа на угол, матрица
, в качестве которой обычно берут распределение
Гаусса. У точки, окрестность которой похожа на угол, матрица 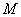 будет иметь два больших положительных собственных
значения. Таким образом, условие похожести точки на угол запишется следующим
образом:
будет иметь два больших положительных собственных
значения. Таким образом, условие похожести точки на угол запишется следующим
образом:
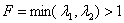 (3.9)
(3.9)
Теперь
остается найти локальные максимумы функции отклика угла 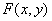 , которые и будут соответствовать особым точкам.
, которые и будут соответствовать особым точкам.
Чтобы
упростить вычисления, Харрис предложил отказаться от подсчета собственных
значений матрицы, и вместо них ввел следующую функцию отклика угла:
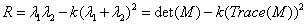 (3.10)
(3.10)
В библиотеке компьютерного зрения OpenCV этот оператор представлен
функцией
void cvCornerHarris( const CvArr* image, CvArr*
harris_responce,block_size, int aperture_size=3, double k=0.04 ),
где
image - входное изображение; harris_responce - изображение для вывода функции,
которое должно иметь такой же размер как и входное изображение; block_size -
размер блоков; aperture_size - размер апертуры изображения; k - свободный
параметр детектора Харриса; 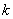
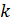 - параметр Харриса, его величина обычно лежит в
пределах
- параметр Харриса, его величина обычно лежит в
пределах 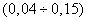 и определяется эмпирически.
и определяется эмпирически.
Далее
с ней проводятся аналогичные действия, поиск локальных максимумов, и введение
порогового значения.
На
втором этапе - этапе слежения (Tracking) - определяются смещения для каждой
особой точки между соседними кадрами и рассчитывается средний по всем точкам
вектор сдвига для каждой пары кадров.
Основная
идея задачи слежения состоит в поиске окрестности в текущем кадре, максимально
похожей на окрестность точки в предыдущем кадре. Следующий ключевой момент
состоит в том, что этот поиск окрестности производится не по всему изображению,
а в некотором радиусе от исходного положения особой точки. Здесь мы вводим
предположение, что за время между двумя кадрами в сцене не происходит больших
изменений, поэтому нет смысла искать точку далеко от текущего её положения.
Таким
образом, если в предыдущем кадре координаты особой точки обозначить 
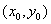 , то в
области поиска
, то в
области поиска 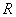
 ищется
такой вектор
ищется
такой вектор 
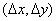 , что
сумма по окрестности
, что
сумма по окрестности 
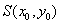 будет
минимальна:
будет
минимальна:
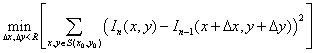 (3.11)
(3.11)
где
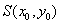 - окрестность сравнения,
- окрестность сравнения, 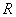
 -
область поиска особенности,
-
область поиска особенности, 
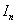 и
и 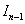
 -
яркость точки в текущем и предыдущем кадрах.
-
яркость точки в текущем и предыдущем кадрах.
Функцией поиска контуров является функция cvFindContours:
int cvFindContours( CvArr* image, CvMemStorage* storage,
CvSeq** first_contour, int header_size=sizeof(CvContour), int
mode=CV_RETR_LIST, int method=CV_CHAIN_APPROX_SIMPLE, CvPoint
offset=cvPoint(0,0) ) ,
где image - исходное 8-битное одноканальное изображение. Ненулевые
пиксели считаются 1, нулевые остаются 0 - рассматривается как двоичный файл.
Для получения такого бинарного изображения с оттенками серого, можно
использовать функции cvThreshold, cvAdaptiveThreshold или cvCanny. Функция
изменяет содержимое исходного изображения; Storage - ячейка памяти, содержащая
полученные контура; first_contour - выходной параметр, содержащий указатель на
первый найденный контур; header_size - размер последовательности заголовка
>=sizeof(CvChain).
Таблица 3.1 - Параметры функции выделения контуров
|
CV_RETR_EXTERNAL
|
если необходимы только
крайние внешние контуры
|
|
CV_RETR_LIST
|
выделение всех контуров и
помещение их в список
|
|
CV_RETR_CCOMP
|
выделение всех контуров и
помещение их в двойную иерархию
|
|
CV_RETR_TREE
|
получить все контура и
реконструировать полную иерархию вложенных контуров
|
- метод аппроксимации (для всех модов, кроме CV_RETR_RUNS,который
использует встроенную аппроксимацию);
И offset - каждый контур точки сдвинулся. Используется если контуры
извлекаются из изображений, затем они должны быть проанализированы в контексте
целого изображения.
Таблица 3.2 - Методы аппроксимации для функции определения контуров
|
CV_CHAIN_APPROX_NONE
|
преобразует все точки из
цепочки в точки
|
|
CV_CHAIN_APPROX_SIMPLE
|
сжимает горизонтальных,
вертикальных и диагональных сегментах, то есть функция остается только
прекращение их центры
|
|
CV_CHAIN_CODE
|
выходные контура в
цепочечном коде Фримена
|
|
CV_CHAIN_APPROX_TC89_L1,
CV_CHAIN_APPROX_TC89_KCOS
|
применение одного из
аппроксимационных цепочечных кодов Тех-Чина
|
|
CV_LINK_RUNS
|
использовать другой алгоритм
поиска контура с помощью горизонтальных связей сегментов в один. Только
CV_RETR_LIST может быть использован с этим методом
|
Функция Приближения полигональных кривой (кривых) с заданной точностью
CvSeq* cvApproxPoly( const void* src_seq, int header_size,
CvMemStorage* storage, int method, double parameter, int parameter2=0 );
_seq - последовательность ряда точек; header_size - размер заголовка
кривой; storage- Контейнер с аппроксимируемыми контурами. Если NULL, то
используется ячейка с входными последовательностями; мethod - метод
аппроксимации; только CV_POLY_APPROX_DP, который описывает метод
Дугласа-Пеукера; parameter - параметр специального метода; CV_POLY_APPROX_DP
для точной аппроксимации; parameter2 - если src_seq является единичной последовательностью,
то он должен быть приближен для всех последовательностей на том же уровне или
ниже src_seq. Если src_seq является массив (CvMat *) точек, параметр
определяет, будет ли кривая замкнута.
Функции уменьшения и увеличения размера изображений:
void cvPyrDown( const CvArr* src, CvArr* dst, int
filter=CV_GAUSSIAN_5x5 );
где src - исходное изображение; dst - входящее изображение (должно
содержать длину и ширину); filter - тип фильтра ; только CV_GAUSSIAN_5x5
поддерживается.
void cvPyrUp( const CvArr* src, CvArr* dst, int
filter=CV_GAUSSIAN_5x5 );
где src - исходное изображение; dst - входящее изображение (должно
содержать длину и ширину); filter - тип фильтра ; только CV_GAUSSIAN_5x5
поддерживается.
Пороговая функция в библиотеке компьютерного зрения OpenCV определяется
как
void cvThreshold( const CvArr* src, CvArr* dst, double
threshold, double max_value, int threshold_type );
где src - входной массив (8-битный, 32-битный); dst - выходной массив
(такого же типа как и входной); threshold - пороговое значение; max_value -
максимальное значение, которое используется с CV_THRESH_BINARY и
CV_THRESH_BINARY_INV; threshold_type - тип пороговой функции.
Нахождение кругов в оттенках серого изображения, используя преобразование
Хафа;
CvSeq* cvHoughCircles( CvArr* image, void* circle_storage,
int method, double dp, double min_dist, double param1=100, double param2=100,
int min_radius=0, int max_radius=0 );
- входящее 8-битное изображение; circle_storage - Ячейка, хранящая
обнаруженные круги. Это может быть хранилищем (в данном случае
последовательность кругов создается при хранении и возвращается функцией), или
одну строку / один столбец матрицы (CvMat *) типа CV_32FC3, к которому пишутся
параметры кругов. Если circle_storage - матрица и фактическое число линий
превышает размер матрицы, максимально возможное количество кругов возвращается.
Каждый круг кодируется 3 числа с плавающей точкой: центр координатами (х, у) и
радиуса; Method - реализована только метод CV_HOUGH_GRADIENT; Dp - Установка
аккумулятора, который используется для обнаружения центров окружностей.
Например, если он равен 1, аккумулятор будет иметь то же разрешение, как у
исходного изображения, если это 2 - аккумулятор будет в два раза меньше ширины
и высоты и т.д.; min_dist - Минимальное расстояние между центрами обнаруженных
кругов. Если параметр слишком мал, несколько соседних кругов может быть ложно
обнаружено в дополнение к истинным. Если он слишком большой, некоторые круги
могут быть упущены; param1 - Первый метод конкретных параметров. В случае
CV_HOUGH_GRADIENT это высший порог, край детектора (ниже 1 будет в два раза
меньше); param2 - Второй метод конкретных параметров. В случае
CV_HOUGH_GRADIENT - аккумулятор. Чем меньше параметр, тем больше ложных кругов
могут быть обнаружены; min_radius - минимальный радиус искомых кругов;
max_radius - максимальный радиус.
В третьей части работы рассмотрена практическая реализация методов
обработки информации в робототехнических системах. Существуют два основных
подхода к предварительной обработке информации. Первый подход основан на
методах пространственной области, а второй - на методах частотной области с
использованием преобразования Фурье. Вместе эти подходы охватывают большинство
из существующих алгоритмов предварительной обработки информации, применяемых в
системах технического зрения роботов. Основными библиотеками, работающими с
методами распознавания и идентификации являются библиотека Integrated
Performance Primitives (IPP), библиотека AviCap, библиотека компьютерного
зрения с открытым кодом OpenCV. Рассмотрены основные функции и их реализация в
библиотеке OpenCV.
4. РАЗРАБОТКА ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ
ОБЪЕКТОВ РОБОТИЗИРОВАННОГО ПРОИЗВОДСТВА С ПОМОЩЬЮ СИСТЕМЫ ТЕХНИЧЕСКОГО ЗРЕНИЯ
4.1 Основные особенности разработанного программного
обеспечения
Целью разработки данного программного обеспечения является исследование
программных методов распознавания и идентификации простых объектов с помощью
библиотеки компьютерного зрения OpenCV.
С точки зрения MFC проект будет состоять из двух классов: CApp (класс
приложения) и CMainWin (главное окно) с соответствующей первому функцией
InitInstance(); конструктором и картой сообщений для класса окна.
В программе указывается глобальное объявление функции обработки кадра -
void mycallback (IplImage *img).
Указателями на изображение будут являться: IplImage
*image1,*src2,*dst,*dst2,*dst3,*dst4,*gray,*dst5,*dst6,*dst7,*dst8.
Далее выделяются переменные для сохранения памяти. В данном случае это
CvMemStorage *storage,*storage2;
Конструктор главного окна программы необходимо описать следующим образом:
CMainWin::CMainWin()
{ Create (NULL, "OpenCV");
Далее в конструкторе указывается дескриптор главного окна программы:
w= this->GetSafeHwnd();
Также в конструкторе определяется количество камер с помощью команды
ncams=cvcamGetCamerasCount();
Далее идет проверка наличия камер, если их количество ненулевое,
выполняется ряд функций, связанных с инициализацией камеры, основных окон
программы и свойств изображений:
if (ncams) {bCreate=true;vidFmt={800,600,20.0};(0,CVCAM_PROP_ENABLE,CVCAMTRUE);(0,CVCAM_PROP_CALLBACK,mycallback);(0,CVCAM_PROP_WINDOW,&w);(0,CVCAM_PROP_SETFORMAT,&vidFmt);(cvGetWindowName(w),CV_WINDOW_AUTOSIZE);
}
На рис 4.1 указано главное окно программы, которое содержит пример исходного
изображения, полученного камерой СТЗ робота.
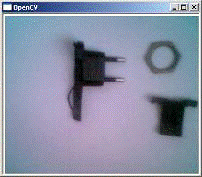
Рисунок 4.1 - Пример изображения в главном окне программы
Для организации вывода результатов обработки визуальной информации
используется функция cvNamedWindow( "Canny", 1 ), где 1 -
идентификатор окна. Результат каждого преобразования исходного изображения
выводится при помощи команды cvShowImage().
На рис. 4.2 приведен пример применения функции Canny, обеспечивающей
выделение границ изображений.
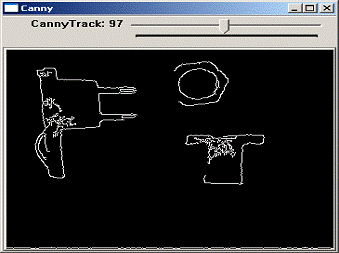
Рисунок 4.2 - Окно программы с функцией Canny
С помощью функции cvCreateTrackbar создается полоса прокрутки
cvCreateTrackbar("CannyTrack","Canny",&cannyt,200,NULL)
и задается размер окна для функции cvResizeWindow("Canny",320,200).
Аналогичным образом создается окно для вывода функции определения
контуров. На рисунке 4.3 приведено выполнение функции.
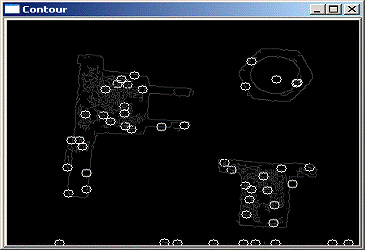
Рисунок 4.3 - Определение контуров изображений
Затем производится инициализация камеры, либо выводится сообщение об
ошибке:
(!cvcamInit()) MessageBox("Error");
в противном случае производится запуск камеры:
();}
либо выдается сообщение о том, что она не найдена.
Закрытие главного окна программы должно обеспечивать закрытие всех
программных окон (в противном случае они могут остаться в памяти). Для этого
необходимо использовать функцию void CMainWin::OnClose(), в которой
производится остановка камеры (cvcamStop()),закрытие всех окон
(cvDestroyAllWindows()), выход из режима камеры (cvcamExit()) и закрытие
главного окна:
if(!bCreate) cvReleaseImage(&dst);(); }.
4.2 Реализация функции обработки изображений
Обработка изображений в OpenCV производится кадр за кадром, а функции
обратного вызова (mycallback), которая в разработанном программном обеспечении
выглядит так: void mycallback(IplImage *src)
Изображение, полученное с камеры в тексте программы обозначено переменной
src и выводится в основное окно программы (рис. 4.4).
В приложении используются различные типы моделей памяти, соответствующие
различным типам изображений, например:
src2=cvCreateImage(cvSize(src->width,src->height),IPL_DEPTH_8U,3);=cvCreateImage(cvSize(src->width,src->height),IPL_DEPTH_32F,3);=cvCreateImage(cvSize(src->width,src->height),IPL_DEPTH_8U,1);
Для поворота изображения использовалась функция cvFlip(src, src2).

Рисунок 4.4 - Основное окно программы (уменьшенный вид)
Для нормальной работы функции Кенни, необходимо преобразовать исходное
изображение в черно-белое (используется функция
cvCvtColor(src2,gray,CV_RGB2GRAY)), после чего выполнить само преобразование
функцией cvCanny(gray,dst3,25,100+cannyt,3).
Далее производится вывод этого изображения в окно dst3 при помощи функции
cvShowImage("Canny",dst3). На рис. 4.5 представлен пример выполнения
функции Кенни к исходному изображению.
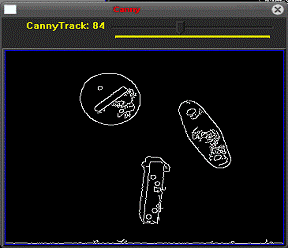
Рисунок 4.5 - Пример преобразования Кенни
Одной из простейших функций обработки изображений является пороговая
функция. В библиотеке OpenCV она представленав виде:
cvThreshold( tgray, gray, 100, 255, CV_THRESH_BINARY ).
Здесь tgray - входной массив (8- или 32-битный); gray - выходной массив
такого же типа как и tgray; 100 и 255 - минимальное и максимально значение,
используемое пороговой функцией; CV_THRESH_BINARY - показывает тип пороговой
функции. Пример использования пороговой функции представлен на рис. 4.6.
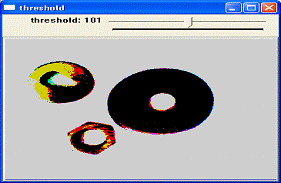
Рисунок 4.6 - Применение пороговой функции
Более улучшенной разновидностью пороговой функции является функция
сvAdaptiveThreshold (dst3, dst4, 5+thresh2, CV_ADAPTIVE_THRESH_MEAN_C,
CV_THRESH_BINARY,3,5). Пример использования функции приведен на рис. 4.7.
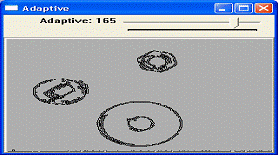
Рисунок 4.7 - Применение адаптивной пороговой функции
.3 Реализация функций распознавания и идентификации
Результатом выполнения функции Кенни является изображение, содержащее
края объектов в исходном кадре, и являющиеся основой для последующих
преобразований, в частности для выделения контуров.
Рассмотрим функцию cvFindContours, которая находит контура объектов,
находящихся в поле зрения камеры:
cvFindContours(gray, storage, &contours,
sizeof(CvContour), CV_RETR_LIST, CV_CHAIN_APPROX_SIMPLE, cvPoint(0,0) ).
Здесь gray является исходным изображением в 8-битном формате, в области
памяти storage хранятся полученные контура; в массиве contours содержится
информация о первом найденном контуре; CvContour показывает размер структуры
данных контура; параметр CV_RETR_LIST означает, что все выделенные контура
помещаются в список; параметр CV_CHAIN_APPROX_SIMPLE означает, что функция
выделяет центры контуров; cvPoint(0,0) показывает, что контуры извлекаются из
изображений и затем должны быть проанализированы в контексте целого
изображения.
Для нахождения нескольких контуров используется цикл, представленный
ниже:
while(contours)
{ result = cvApproxPoly( contours, sizeof( CvContour),
storage, CV_POLY_APPROX_DP, cvContourPerimeter( contours)*0.02, 0 );(
result->total == 4 && fabs( cvContourArea( result, CV_WHOLE_SEQ))
> 1000 && fabs( cvContourArea( result, CV_WHOLE_SEQ)) <(
img->height * img->width/2 ) && cvCheckContourConvexity( result)
)
{ s = 0; for( int i = 0; i < 5; i++ )
{if( i >= 2) { t = fabs( angle( ( CvPoint*)cvGetSeqElem(
result, i ), ( CvPoint*)cvGetSeqElem( result, i-2 ),
( CvPoint*)cvGetSeqElem( result, i-1 ))); s = s > t ? s :
t; } } if( s < 0.5 )for( int i = 0; i < 4; i++ )cvSeqPush( squares, (
CvPoint*)cvGetSeqElem( result, i )); }
contours = contours->h_next; }.
На рис. 4.8 представлен результат применения функции выделения контуров.
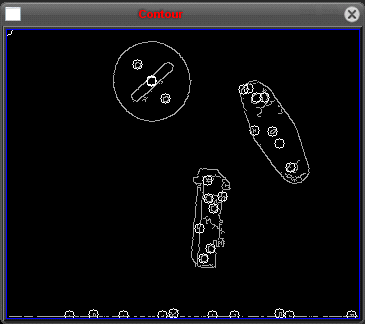
Рисунок 4.8 - Пример выделения контуров изображений
Функция cvHoughCircles находит окружности на сером изображении, используя
преобразование Хью:
cvHoughCircles( gray, cstorage, CV_HOUGH_GRADIENT, 1,
gray->height/16, 8, 10, 4, 50 ).
В данной функции, использованной в программном обеспечении параметр gray
является 8-битым изображением; cstorage - область памяти, в которой хранятся
окружности, обнаруженные функцией; CV_HOUGH_GRADIENT - метод реализации
функции; 1 - стек, который используется для обнаружения центров окружностей с
тем же разрешением, что и исходное изображение; gray->height/16 -
вычисляется минимальное расстояние между центрами обнаруженных окружностей;
следующие 2 параметра отвечают за накопление порогов в обнаруженных
окружностях; последние 2 параметра отвечают за минимальный и максимальный
радиус находимых окружностей.
Для отображения окружностей используется цикл, который выглядит так:
for( int i = 0; i < circles-> total; i++ )
{ float* p = ( float*)cvGetSeqElem( circles, i );( out,
cvPoint( cvRound( p[0]), cvRound( p[1])),
, CV_RGB( 200, 0, 0), -1, 8, 0 );( out, cvPoint( cvRound(
p[0]), cvRound( p[1])), cvRound( p[2]), CV_RGB( 200, 0, 0), 1, 8, 0 ); }
Пример выполнения функции представлен на рис. 4.9.

Рисунок 4.9 - Применение функции выделения кругов
Отображение прямоугольных изображений осуществляется командой
void drawSquares(IplImage *img, CvSeq* squares);
Прямоугольные объекты определяются при помощи функции полилиний
cvPolyLine( img, &rect, &count, 1, 1,
CV_RGB(200,0,0), 1, CV_AA, 0 );
Далее читается последовательность 4 линий
CV_READ_SEQ_ELEM( pt[0], reader );_READ_SEQ_ELEM( pt[1],
reader );_READ_SEQ_ELEM( pt[2], reader );_READ_SEQ_ELEM( pt[3], reader ).
Угол поворота линий полилинии задан при помощи функции :
double angle = abs(pt[1].y-pt[2].y)/sqrt((pt[1].x-pt[2].x)*
(pt[1].x-pt[2].x)+(pt[1].y-pt[2].y)*(pt[1].y-pt[2].y)+0.00001);
Сами линии полилинии прорисовываются с помощью функций:
cvLine( img, cvPoint(0,img->height/2),
cvPoint(img->width,img->height/2), CV_RGB(200,200,200),1, 8, 0 );( img,
cvPoint(img->width/3,0), cvPoint(img->width/3,img->height),
CV_RGB(200,200,200),1, 8, 0 );( img, cvPoint(img->width/3*2,0), cvPoint(img->width/3*2,img->height),
CV_RGB(200,200,200),1, 8, 0 );cvPutText( img, st, pt[1], &font,
CV_RGB(200,0,0).
Вывод прямоугольных объектов производится функцией
drawSquares(out,findSquares4(gray, mainStorage)), где out - изображение,
содержащее прямоугольные фигуры. Пример выполнения выделения прямоугольных
объектов показан на рис. 4.10.
Таким образом разработанное программное обеспечение выполняет съем и
обработку информации, поступающую с WEB-камеры (СТЗ робота), обеспечивает
выполнение границ, контуров, идентификацию простых объектов.
Полный текст программы приведен в приложениях А и Б.

Рисунок 4.10 - Выполнение выделения прямоугольных объектов
В четвертой части исследованы и программно реализованы методы
распознавания и идентификации простых объектов. Базовой библиотекой
распознавания выбрана библиотека компьютерного зрения OpenCV. Полученные
результаты обеспечивают выделение границ и контуров объектов, определение
центров масс. Для простых объектов реализованы функции распознавания и идентификации.
5. БЕЗОПАСНОСТЬ ЖИЗНИ И ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА
5.1 Анализ условий труда в помещении лаборатории
исследовательского бюро кафедры ТАПР
Анализ условий труда производится для помещения лаборатории
исследовательского бюро. Помещение лаборатории находится на 1 этаже 4-этажного
кирпичного здания.
Помещение лаборатории, в котором размещены рабочие места операторов ЭВМ,
обладает следующими параметрами: высота 3 м, ширина 10 м, длина 12 м, площадь 120 м2, объем
360 м3, площадь окон 12 м2, потребляемая мощность 3 кВт,
персонал - 3 человека.
В помещении находится 3 рабочих места, одновременно в помещении работает
3 человека.
На каждое рабочее место приходится по одному ПК, общая потребляемая
мощность оборудования составляет 3 кВт.
Электропитание
лаборатории осуществляется от трёхфазной четырехпроводной сети переменного тока
с напряжением 380/220 В, частотой 50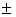 1 Гц, с
глухозаземленной нейтралью.
1 Гц, с
глухозаземленной нейтралью.
Рассмотрим
систему Ч-М-С, ограниченную размерами помещения (элемент «среда»), в составе
всего рабочего коллектива (элемент «человек») и всего комплекса технических
средств, прямо или косвенно участвующих в технологическом процессе (элемент
«машина»).
Разделим
элемент «человек» на три функциональные части: Ч1 - «человек - управление
машиной»; Ч2- человек, рассматриваемый с точки зрения непосредственного влияния
на окружающую среду; Ч3- человек рассматриваемый с точки зрения его
физиологического состояния под влиянием факторов, воздействующих на него в
производственном процессе.
В данном случае элементом «человек» является коллектив из 3-х человек,
находящихся в помещении лаборатории №Лаборатория исследовательского бюро.
Элемент «машина» (3 персональных ЭВМ) выполняет основную технологическую
функцию - влияние на предмет труда, дополнительную - формирование параметров
окружающей среды. Таким образом, элемент «машина» можно разделить на три
элемента: М1 - выполняет основную технологическую функцию; М2 - функция
аварийной защиты;
М3 - как источник ОВПФ;
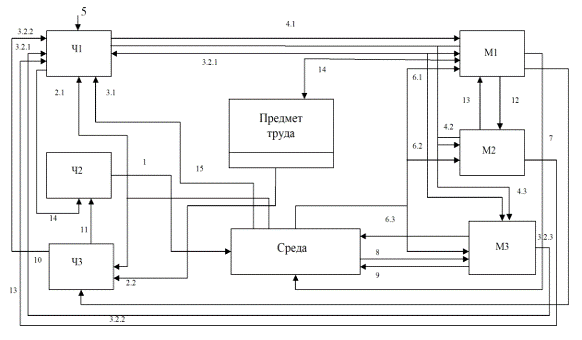
Рисунок 5.1 - Модель системы «человек - машина - среда» (ЧМС)
Элементом «среда» является окружающая среда (воздух, температура,
влажность, шум, освещенность, электромагнитное поле и др.). Модель
разработанной системы Ч-М-С для лаборатории представлена на рисунке 5.1.
Используя ГОСТ 12.0.003-74, выделим опасные и вредные производственные
факторы, которые действуют в системе Ч-М-С. В таблице Д.1 приведены результаты
анализа связей системы Ч-М-С.
В результате анализа системы Ч-М-С в лаборатории были выявлены следующие
ОВПФ: повышенная температура воздуха рабочей зоны; превышение продолжительности
сосредоточения; повышенная напряженность анализаторов.
Таблица 5.1 - Результаты анализа связей системы Ч-М-С
|
Номер связи на схеме
|
Наим-ние связи
|
Действия, влияния
|
Опасные и вредные
производственные факторы по ГОСТ 12.0.003-074
|
|
1
|
2
|
3
|
4
|
|
1
|
Ч2 - С
|
Влияние человека как
биологического объекта на среду
|
- выделение углекислого
газа; - тепловыделение;
|
|
2.1
|
С-Ч1
|
Влияние окружающей среды на
качество работы оператора (изменение работоспособности при изменении
температуры, влажности, атмосферного состава, освещенности, уровня
электромагнитного поля)
|
- повышенная или пониженная
температура воздуха на рабочем месте; - повышенная или пониженная влажность
воздуха рабочей зоны; - повышенная или пониженная подвижность воздуха в
рабочей зоне;
|
|
2.2
|
С-Ч3
|
Влияние среды на состояние
организма человека (изменение функциональных возможностей организма при
изменении температуры, влажности, атмосферного состава, освещенности, уровня
электромагнитного поля)
|
- повышенная или пониженная
температура воздуха на рабочем месте; - повышенная или пониженная влажность
воздуха рабочей зоны; - повышенная или пониженная подвижность воздуха в
рабочей зоне; - недостаточная освещенность рабочей зоны; - перенапряжение
анализаторов;
|
|
3.1
|
С-Ч1
|
Информация о состоянии
среды, которая обрабатывается человеком
|
- умственное
перенапряжение; - повышенная или пониженная ионизация воздуха;
|
|
3.2.1 3.2.2 3.2.3
|
М1-Ч1 М2-Ч1 М3-Ч1
|
Информация о состоянии
машины, которая обрабатывается человеком, информация про предмет труда и
среду, получаемая от машины
|
- повышенный уровень шума
на рабочем месте; - пониженная контрастность;
|
|
4.1 4.2 4.3
|
Ч1-М1 Ч1-М2 Ч1-М3
|
Влияние человека на
управление техникой и ее настройкой (включение/выключение, настройка и
обслуживание ПЭВМ, монитора и принтера)
|
- повышенная напряженность
электрического поля; - повышенная напряженность магнитного поля;
|
|
5
|
Внешняя система управления
|
Управляющая информация про
технологический процесс с внешней системы управления
|
- монотонность труда -
умственное перенапряжение;
|
|
6.1 6.2 6.3
|
С1-М1 С1-М2 С1-М3
|
Влияние среды на работу
машины (изменение температуры, влажности, напряжения сети)
|
- повышенное значение
статического электричества;
|
|
7
|
М1-С1
|
Влияние машины на среду
(повышение температуры, повышение электромагнитного поля)
|
- повышенная или пониженная
температура воздуха; - повышенная или пониженная влажность воздуха;
|
|
8
|
С-М3
|
Информация об окружающей
среде, которая обрабатывается машиной
|
- повышенная запыленность и
загазованность воздуха в рабочей зоне;
|
|
9
|
М3-С
|
Целенаправленное влияние
машины на среду
|
- повышенная яркость света;
- повышенная пульсация светового потока;
|
|
10
|
Ч3-Ч1
|
Влияние состояния организма
человека на качество его работы (усталость, ослепление, невнимательность)
|
- эмоциональные перегрузки;
- перенапряжение анализаторов;
|
|
11
|
Ч3-Ч2
|
Влияние
психо-физиологического состояния на степень интенсивности обмена веществ
между организмом и средой и энерговыделения человека
|
- физические перегрузки; -
нервно-психические перегрузки;
|
|
12
|
М2-М1
|
Аварийные управляющие
влияния
|
- повышенное значение
напряжения в электрической цепи, замыкание которого может произойти через
тело человека;
|
|
13
|
М1-М2
|
Информация, необходимая для
выработки аварийных управляющих влияний
|
- повышенный уровень
ионизирующих излучений в рабочей зоне; - повышенное значение статического
электричества;
|
|
14
|
М1-ПТ
|
Влияние машины на предмет
труда
|
- повышенная напряженность
электрического поля; - повышенная напряженность магнитного поля;
|
|
15
|
ПТ-Ч3
|
Влияние предмета труда на
физиологическое состояние человека
|
- умственное
перенапряжение; - перенапряжение анализаторов.
|
5.2 Техника безопасности в лаборатории исследовательского
бюро
При
эксплуатации вычислительных машин главная опасность - поражение электрическим
током. Опасность поражения может возникнуть при случайном прикосновении к
нетоковедущим частям. Электропитание осуществляется от трёхфазной
четырехпроводной сети переменного тока с напряжением 380/220 В, частотой 50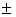 1 Гц, с глухозаземленной нейтралью.
1 Гц, с глухозаземленной нейтралью.
По
степени опасности поражении электрическим током согласно ПУЭ, помещение
лаборатории относится к классу помещений без повышенной опасности.
В
соответствии с ПТЭ и ПТБ потребителям и обслуживающему персоналу
электроустановок предъявляются следующие требования: лица, не достигшие
18-летнего возраста, не могут быть допущены к работам в электроустановках; лица
не должны иметь увечий и болезней, мешающих производственной работе; лица
должны после соответствующей теоретической и практической подготовки пройти
проверку знаний и иметь удостоверение на доступ к работам в электроустановках.
При
эксплуатации ПК должны выполняться следующие требования:
· не подключать и не отключать разъемы и кабели электрического
питания при поданном напряжении сети;
· не оставлять ПК включенным без наблюдения, также во время
грозы;
· по окончании работы отключить ПК от сети;
· устройства должны быть расположены на расстоянии 1 м от
нагревательных приборов;
· устройства не должны подвергаться воздействию прямых
солнечных лучей;
Обучение работников проводят в соответствии с ДНАОП 0.00-4.12-94.
В соответствии с требованиями ГОСТ 12.1.030-81 для электроустановок
переменного тока напряжением питания до 1000 В применяется зануление,
преднамеренное электрическое соединение с нулевым защитным проводом
металлических нетоковедущих частей, которые могут оказаться под напряжением. По
контуру помещения лаборатории проложена шина повторного заземления, которая
соединена с заземлителем сопротивлением 10 Ом.
5.3 Производственная санитария и гигиена труда в лаборатории
исследовательского бюро
Согласно ГОСТ 12.2.032 - 78 «Рабочее место при выполнении работ сидя.
Общие эргономические сведения» конструкцией рабочего места должно быть
обеспечено выполнение трудовых операций в пределах зоны досягаемости моторного
поля.
В лаборатории исследовательского бюро установлены столы прямоугольной
формы. Таким образом, рабочие места в лаборатории соответствуют ГОСТ 12.2.032 -
78.
В лаборатории располагаются 3 рабочих места. Площадь лаборатории - 120 м2,
объем - 360 м3. Соответственно, площадь, выделенная на 1 рабочее
место составляет не менее 6 м2 и объем составляет не менее 20 м3.
Согласно ГОСТ 12.1.005-88, ДСН 3.3.6-042-99 работа в зале с ПК по
категории работ относится к легким (категория Iа - легкие физические работы с
энергозатратами до 139 Вт или 120 ккал/ч). Работа производятся сидя, не требует
систематического физического напряжения и перемещения тяжестей.
Анализируя выявленные в лаборатории ОВПФ можно сказать, что рабочее место
относится к III классу 1 степени вредности. Доминирующим вредным фактором
является повышенная температура воздуха рабочей зоны (на 3˚С больше, чем
норма, установленная ГОСТ 12.1.005-88 «Система стандартов безопасности труда.
Общие санитарно-гигиенические требования к воздуху рабочей зоны», равная 22-28˚С).
В рабочей зоне помещения согласно ГОСТ 12.1.005-88 могут быть установлены
оптимальные (сочетание параметров микроклимата) или допустимые
микроклиматические условия.
В санитарных нормах ДСП 173-96 установлены величины параметров
микроклимата, создающие комфортные условия (таблица 5.3). Параметры
устанавливаются в зависимости от времени года, характера трудового процесса и
характера производственного помещения. Нормы подачи свежего воздуха в
помещения, где расположены компьютеры, приведены в таблице 5.4.
Таблица 5.3 - Параметры микроклимата для помещений, где установлены
компьютеры
|
Период года
|
Параметры микроклимата
|
Величина
|
|
Теплый
|
Температура воздуха в помещении
Относительная влажность Скорость движения воздуха
|
22-24 ˚С 40-60 % До
0.1 м\с
|
|
Холодный
|
Температура воздуха в
помещении Относительная влажность Скорость движения воздуха
|
23-25 ˚С 40-60 %
0.1-0.2 м\с
|
Таблица 5.4 - Нормы подачи свежего воздуха в помещения, где расположены
компьютеры
|
Характеристика помещения
|
Объемный расход подаваемого
в помещение свежего воздуха м3 на человека в час
|
|
Объём до 20 м3
на человека
|
Не менее 30
|
|
20-40 м3 на
человека
|
Не менее 20
|
Таким образом, необходимо разработать систему кондиционирования.
Согласно СНиП 2.0Д.05-91 (таблица Д.4), если объем помещения,
приходящийся на одного человека, меньше 20 м3, то количество
приточного воздуха, необходимого для проветривания, должно быть не менее G1
= 30 м3/час на каждого работающего; при объеме помещения более
20 м3 на одного работающего количество приточного воздуха для
проветривания должно быть не менее G1 = 20 м3/час на
каждого работающего. Найдем объем помещения, приходящийся на одного
человека:=360 м3; n = 3 человек
=360 ∕ 3 = 120 м3 (5.1)
Поскольку V1> 20 м3/чел, то тогда норма подачи
приточного воздуха на 1 человека G1 = 20 м3/час.
Количество приточного воздуха с учетом того, что в помещении работает 3
человека (м3/час) рассчитывается по формуле:
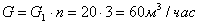 (5.2)
(5.2)
Произведем
расчет воздухообмена по избыткам тепла. Для этого определим поступления тепла в
помещение по формуле:
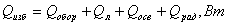 (5.3)
(5.3)
где
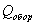 - выделение тепла от оборудования;
- выделение тепла от оборудования;
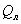 -
выделение тепла от людей;
-
выделение тепла от людей;
 - выделение
тепла от приборов освещения;
- выделение
тепла от приборов освещения;
 -
поступление тепла через наружные ограждения конструкций от солнечной радиации;
-
поступление тепла через наружные ограждения конструкций от солнечной радиации;
Найдем
выделение тепла при работе оборудования:
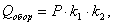 (5.4)
(5.4)
где
P = 3 кВт - суммарная мощность оборудования;
к1
= 0.8 - коэффициент использования установленной мощности;
к2
= 1 - коэффициент одновременности работы оборудования.
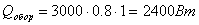
Найдем
выделение тепла от людей по формуле:
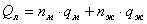 ,(5.5)
,(5.5)
где
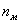 - количество работающих мужчин в помещении;
- количество работающих мужчин в помещении;
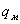 -
количество тепла, выделяемого одним мужчиной;
-
количество тепла, выделяемого одним мужчиной;
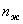 -
количество работающих женщин в помещении;
-
количество работающих женщин в помещении;
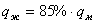 -
количество тепла, выделяемого одной женщин;
-
количество тепла, выделяемого одной женщин;
Используя
табл. 9 пособия 2.91 к СНиП 2.0Д.05-91 находим количество тепла, выделяемого
одним мужчиной при 30˚С при выполнении легкой физической работы - qм
= 146 Вт. Т.о. получаем:
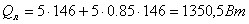
В
помещении имеются 8 осветительных прибора по 100 Вт каждый. Найдем выделение
тепла от освещения. Таким образом:
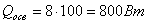
Величина
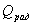 рассчитаем по формуле:
рассчитаем по формуле:
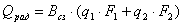 (5.6)
(5.6)
где
Всз - коэффициент теплопропускания солнцезащитных устройств;1,
F2 - площади световых проемов, освещаемых солнцем и находящихся в
тени, м2; q1, q2 - количество тепла,
поступающего в помещение в июле, через остекление светового проема, Вт/м2,
в расчетный час суток для освещенной части и части, находящейся в тени;
Считаем,
что световые проемы не затенены, значение F2 принимаем равным нулю.
Значения
q1 и q2 (СНиП II-33-75):
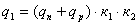 (5.7)
(5.7)
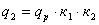 (5.8)
(5.8)
1 - коэффициент,
учитывающий затенение остекления и загрязнения атмосферы;2 -
коэффициент, учитывающий загрязнение стекла;п - количество тепла от
прямой солнечной радиации;р - количество тепла от рассеянной
солнечной радиации.
Значения
прямой и рассеянной солнечной радиации qвп, qвр из
таблицы 5.5.
Таблица
5.5 - Значения прямой и рассеянной солнечной радиации
|
Географическая широта
|
qп
|
qр
|
|
48
|
427
|
112
|
|
52
|
448
|
114
|
п
= (427+ 448)/2 = 437.5 Втр = (112+ 114)/2 = 113 Вт
Всз = 0.15 для штор из светлой ткани (СНиП II-3-79);1
= 12 м2;1 = 0.45 для остекления в двойных деревянных
переплетах, с учетом загрязнения атмосферы, промышленного района и
географической широты (СНиП 2.0Д.05-86);2 = 0.95 для незначительного
загрязнения вертикального остекления (СНиП 2.0Д.05-86).
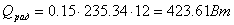
Определим
поступление тепла в помещение по формуле Д.3:
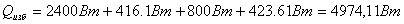
Произведем
расчет воздухообмена по избыткам тепла в лаборатории по формуле:
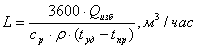 (5.9)
(5.9)
где
3600 - коэффициент для перевода м3/с в м3/час;
ρ=1.2 кг/м3 - плотность воздуха;уд -
температура удаляемого воздуха;пр - температура приточного воздуха;
Разница
температур приточного и удаляемого воздуха находится в пределах 5-8˚С.
Рассчитаем
воздухообмен по избыткам тепла в лаборатории:
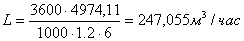
Таким
образом, для поддержания установочных параметров микроклимата лаборатории
достаточно подавать 247,055м3/час воздуха.
Раздача
обработанного воздуха в помещении осуществляется по воздуховодам через
потолочные диффузоры (рисунок Д.3.). Количество воздуха распределяется по
помещению, пропорционально выделяемому теплу.
Рабочее
место организовано в соответствии с требованиями ГОСТ 12.2.032-78 и ДСанПиН
3.3.2.007-98. Конструкция рабочего места и взаимное расположение всех его
элементов соответствуют антропометрическим, физиологическим и психологическим
требованиям, а также характеру работы. Учитывая вредность работы и нагрузку,
установлен восьми часовой рабочий день. Рабочая неделя состоит из 5 дней.
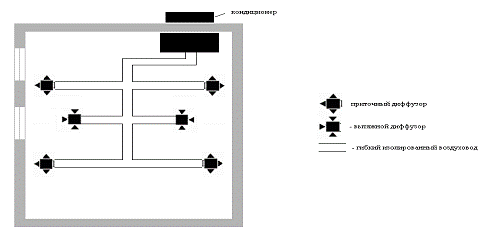
Рисунок 5.3 - Схема системы кондиционирования
На рисунке 5.4 показано размещение рабочих мест и оборудования в данной
лаборатории.
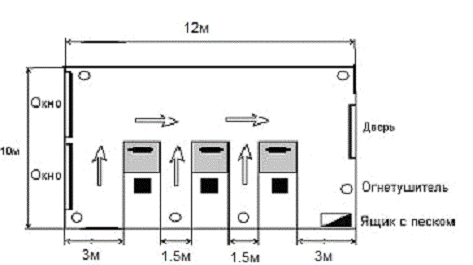
Рисунок 5.4 - Схема размещения рабочих мест и маршрут эвакуации при
пожаре
5.4 Пожарная профилактика лаборатории исследовательского бюро
Согласно СНиП 2.09.02-85 помещение лаборатории, в котором расположен
персонал, имеет категорию пожарной опасности. Оно, согласно СНиП 2.01.02-85
имеет II степень огнестойкости. По пожароопасности данное помещение
классифицируется как помещение класса П-IIа по ПУЭ, так как это помещение в
котором имеется мебель из дерева и ДВП. Горючими компонентами в лаборатории
являются: строительные материалы для акустической и эстетической отделки
помещений, перегородки, двери, полы, изоляция кабелей и др.
В соответствии с ГОСТ 12.1.004-91 пожарная безопасность объекта
обеспечивается: система предотвращения пожара, системы противопожарной защиты.
Предотвращение пожара обеспечивается: максимально возможным применением
негорючих и трудно-горючих веществ в помещении; применением в
электрооборудовании быстродействующих средств защитного отключения возможных
источников зажигания; устройством молниезащиты здания.
Противопожарная защита обеспечивается: 1) применением средств
пожаротушения и соответствующих видов пожарной техники; углекислотные
огнетушители ОУ-2-7 шт (из расчета 2 огнетушителя на 20 м2); эти
огнетушители предназначены для тушения электроустановок находящегося под
напряжением; 2) применение автоматической установки пожарной сигнализации, а
именно использование 7-ми автоматических дымовых пожарных извещателя ИП-105.01
(1 извещатель располагается на 20м2). Они располагаются под потолком
в помещения и собраны на основе магнитоуправляемого герметизированного контакта
(геркона), что позволяет быстро реагировать на появления дыма; 3) телефон
установленный в легкодоступном месте; 4)ящик с песком V = 0,15 м3;
5) организации эвакуации людей (эвакуация организовывается согласно СНиП
2.01.02-85); схема эвакуации представлена на рисунке 5.4.
ВЫВОДЫ
В данной магистерской аттестационной работе основное внимание уделено
рассмотрению методов распознавания и идентификации объектов в системах
технического зрения роботов.
В первой части магистерской аттестационной работы были проанализированы
методы обработки информации в системах технического зрения роботов. Процесс
идентификации объектов, находящихся в рабочей зоне робота, включает два этапа,
такие как выделение характерных признаков объектов и распознавание объектов по
найденной совокупности характерных признаков. Основными методами обработки
информации являются сегментация (процесс подразделения сцены на составляющие
части или объекты), определение порогового уровня, областно-ориентированная сегментация,
дескрипторы границ и областей изображений, описание трехмерных сцен и структур,
обработка визуальной информации
Во второй части проанализированы методы идентификации объектов в
робототехнических системах и построена теоретико-множественная модель распознавания
и идентификации.
Основными методами являются:
- метод сравнения с эталоном (установление совпадения двух
точечных изображений);
- методы теории графов и распознавание (представление сегментов
контура в виде графа и поиске на графе пути наименьшей стоимости, который
соответствует значимым контурам);
- корреляционный метод (вычисление взаимокорреляционной функции
между эталоном и изображением);
- распознавание через связи шаблонов (согласование компонентов
изображения как шаблон и определение, какие объекты присутствуют, изучив
предложенные связи между найденными шаблонами);
- искусственные нейронные сети (обучение сети по различным
образцам образов с указанием того, к какому классу они относятся).
В третьей части работы была рассмотрена практическая реализация методов
обработки информации в робототехнических системах. Существуют два основных
подхода к предварительной обработке информации. Первый подход основан на
методах пространственной области, а второй - на методах частотной области с
использованием преобразования Фурье. Вместе эти подходы охватывают большинство
из существующих алгоритмов предварительной обработки информации, применяемых в
системах технического зрения роботов. Основными библиотеками, работающими с
методами распознавания и идентификации являются библиотека Integrated
Performance Primitives (IPP), библиотека AviCap, библиотека компьютерного
зрения с открытым кодом OpenCV. Рассмотрены основные функции и их реализация в
библиотеке OpenCV.
В четвертой части исследованы и программно реализованы методы
распознавания и идентификации простых объектов. Базовой библиотекой
распознавания выбрана библиотека компьютерного зрения OpenCV. Полученные
результаты обеспечивают выделение границ и контуров объектов, определение
центров масс. Для простых объектов реализованы функции распознавания и
идентификации.
К числу перспективных направлений исследований следует отнести дальнейшее
развитие методов распознавания и идентификации, их программную реализацию для
промышленных операционных систем реального времени. В комбинации с системой
принятия решений такие разработки существенно ускорят реализацию систем
управления интеллектуальными роботами.
ПЕРЕЧЕНЬ ССЫЛОК
1.Анисимов
Б.В. Распознавание и цифровая обработка изображений [Текст] / Б.В. Анисимов,
В.Д. Курганов - М.: Мир, 2007. - 295с.
.Фу К.
Робототехника [Текст] / К.Фу, Р.Гонсалес, К. ЛИ, : пер. с англ. - М.: Мир,
2009. - 624 с.
.Катыс Г.П.
Техническое зрение роботов [Текст] / Г.П. Катыс. - 2006. - 176 с.
.Хорн Б.К.П.
Зрение роботов [Текст] / Б.К.П. Хорн. - М: Мир, 2009. - 488 с.
5.Sung
K. K. Learning Human Face Detection in Cluttered Scene [Текст] / K. K. Sung, T. Poggio // Lecture
Notes in Computer Science - Computer Analysis of Images and Patterns, 2005. P.
432-439.
.Rosenblum
M. Human Emotion Recognition from Motion Using a Radial Basis Function Network
Architecture [Текст] M. Rosenblum, Y.Yacoob,
L.Davis // IEEE Workshop on Motion of Non-Rigid and Articulated Objects, 2006.
- 257 с.
7. Пентланд
А.С. Распознавание лиц для интеллектуальных сред [Текст] А.С. Пентланд, Т.
Чаудхари // Открытые Системы, №03, 2006.
. Техническое
зрение роботов [Текст] : пер с англ. / под ред. А.Пью - М.: Машиностроение,
2006. - 320 с.
.Глазунов, А.
Компьютерное распознавание человеческих лиц [Текст] А. Глазунов // Открытые
Системы, №03, 2007 - 107 с.
. Абламейко
С.В. Обработка изображений: Технология, методы, применение [Текст] / С.В.
Абламейко, Д.М. Лагуновский - Мн:, 2009. - 300 с.
.Соломатин,
Н.М. Логические элементы ЭВМ [Текст] : учеб. пособие / Н.М. Соломатин, М. Высш.
шк. 2007г. 160 с.: ил.
.Якушенков
Ю.Г. Техническое зрение роботов [Текст] / Ю.Г. Якушенков - М.: Машиностроение,
2007. - 272 с.: ил.
13.Canny
J.F. Finding edges and lines in images. [Текст] / J.F. Canny MIT, Cambridge, USA, 2006.
14.Прэтт У.
Цифровая обработка изображений [Текст] / У. Прэтт М.: Мир, 2008. - 784 с.
15.Smith
S.M. SUSAN - a new approach to Low Level Image Processing [Текст] / S.M. Smith, J.M. Brady // DRA
Technical Report TR95SMMS1b. - 2008. -57p.
.Kaas
M. Snakes: Active Contour Models. [Текст] / M. Kaas, A. Witkin, D. Terzopoulos // Int. Journal of Computer Vision. - 2007,
N1, -p.312-331.
. Форсайт
Компьютерное зрение. Современный подход [Текст] : пер. с англ. / Форсайт, Понс,
Девид, Жан - М.: Издательский дом «Вильямс». 2006. - 928 с.
. Брагин В..
Системы очувствления и адаптивные промышленные роботы [Текст] / В. Брагин, Ю.
Войлов, Ю.Жаботинский : под ред. К.Попова - М.: Машиностроение, 2006. - 256 с.
. Ямпольский
Л.С. Промышленная робототехника [Текст] / Л.С. Ямпольский, Е.Г. Вайсман - К.:
Техника, 2006. - 264 с.
. Техническое
зрение роботов [Текст] / В.И. Мошкин, А.А. Петров, В.С. Титов, Ю.Г Якушенков;
под общ. ред. Ю.Г. Якушенкова. - М..: Машиностроение, 2008. 272с.; ил.
. Павлидис Т.
Алгоритмы машинной графики и обработки изображений. [Текст] / Т. Павлидис - М.:
Радио и связь, 2006. - 399 с.
. Введение в
компьютерное зрение. [Электронный ресурс] . - Режим доступа : www/ URL:
#"535131.files/image128.gif">
Рисунок 1.А - Интерфейс окна программы
Приложение Б Тест программы 2
#include "cv.h"
#include "cxcore.h"
#include "highgui.h"
#include "math.h"
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <conio.h>
#include <sstream>namespace std;angle( CvPoint* pt1,
CvPoint* pt2, CvPoint* pt0 )
{dx1 = pt1->x - pt0->x;dy1 = pt1->y - pt0->y;dx2
= pt2->x - pt0->x;dy2 = pt2->y - pt0->y;(dx1*dx2 +
dy1*dy2)/sqrt((dx1*dx1 + dy1*dy1)*(dx2*dx2 + dy2*dy2) + 1e-10);}* findSquares4(
IplImage* img, CvMemStorage* storage )
{ double s = 0, t = 0;* contours = NULL;* result = NULL;*
squares = cvCreateSeq( 0, sizeof( CvSeq), sizeof( CvPoint), storage );( img,
storage, &contours, sizeof( CvContour), СV_RETR_LIST, CV_CHAIN_APPROX_SIMPLE, cvPoint( 0, 0) );( contours )
{ result = cvApproxPoly( contours, sizeof( CvContour),
storage, CV_POLY_APPROX_DP, cvContourPerimeter( contours)*0.02, 0 );(
result->total == 4 && fabs( cvContourArea( result, СV_WHOLE_SEQ)) > 1000 &&
fabs( cvContourArea( result, CV_WHOLE_SEQ)) <( img->height *
img->width/2 ) && cvCheckContourConvexity( result) )
{ s = 0;( int i = 0; i < 5; i++ )
{ if( i >= 2 ) { t = fabs( angle( ( CvPoint*)cvGetSeqElem(
result, i ), ( CvPoint*)cvGetSeqElem( result, i-2 ), ( CvPoint*)cvGetSeqElem(
result, i-1 )));= s > t ? s : t; } }( s < 0.5 )for( int i = 0; i < 4;
i++ )cvSeqPush( squares, (CvPoint*)cvGetSeqElem( result, i )); }=
contours->h_next; }<<">>> rectangles: "<<
squares->total/4 <<endl;squares;}drawSquares(IplImage *img, CvSeq*
squares )
{ CvFont font;( &font, CV_FONT_HERSHEY_SIMPLEX, 0.4f,
0.4f, 0,1, 8 );i,j = 0;reader;( squares, &reader, 0 );( i = 0; i <
squares->total; i += 4 )
{ j++;pt[4], *rect = pt;count = 4;
// read 4 vertices_READ_SEQ_ELEM( pt[0], reader
);_READ_SEQ_ELEM( pt[1], reader );_READ_SEQ_ELEM( pt[2], reader
);_READ_SEQ_ELEM( pt[3], reader );( img, pt[1], 2, CV_RGB(200,0,0),1, 8, 0 );(
img, pt[2], 4, CV_RGB(200,0,0),1, 8, 0 );( img, pt[1], pt[2],
CV_RGB(255,255,255),1, 8, 0 )angle =
abs(pt[1].y-pt[2].y)/sqrt((pt[1].x-pt[2].x)*(pt[1].x-pt[2].x)+(pt[1].y-pt[2].y)*(pt[1].y-pt[2].y)+0.00001);char
st[255]; sprintf(st, "%2f", angle);( img,
cvPoint(0,img->height/2), cvPoint(img->width,img->height/2),
CV_RGB(200,200,200),1, 8, 0 );( img, cvPoint(img->width/3,0),
cvPoint(img->width/3,img->height), CV_RGB(200,200,200),1, 8, 0 );( img,
cvPoint(img->width/3*2,0), cvPoint(img->width/3*2,img->height),
CV_RGB(200,200,200),1, 8, 0 );( img, st, pt[1], &font, CV_RGB(200,0,0));(
img, &rect, &count, 1, 1, CV_RGB(255,255,255), 1, CV_AA, 0 );}}main() {
int c = 0;* capture =
cvCaptureFromCAM(0);(!cvQueryFrame(capture)){cout<<"Video capture
failed, please check the camera."<<endl;}else{cout<<"Video
camera capture status: OK"<<endl;};sz =
cvGetSize(cvQueryFrame(capture));( "out", 0);( "src", 1);*
src = cvCreateImage( sz, 8, 3 );* gray = cvCreateImage( sz, 8, 1 );* pyr =
cvCreateImage( cvSize(sz.width/2, sz.height/2), 8, 3 );* tgray = cvCreateImage(
sz, 8, 1 );* storage = cvCreateMemStorage(0);* contours = NULL;* mainStorage =
cvCreateMemStorage(0);* cstorage = cvCreateMemStorage( 0);* circles = NULL;(c
!= 27) {IplImage* img = NULL;* out = NULL;= cvQueryFrame( capture);=
cvCloneImage( src); out = cvCloneImage( src);( img, pyr, 7 ); cvPyrUp( pyr,
img, 7 );( img, 2 );( img, tgray, 0 );( tgray, gray, 100, 255, CV_THRESH_BINARY
);( "src", gray);( gray, storage, &contours, sizeof(CvContour),
CV_RETR_LIST, CV_CHAIN_APPROX_SIMPLE, cvPoint(0,0) );= cvHoughCircles( gray,
cstorage, CV_HOUGH_GRADIENT, 1, gray->height/16, 8, 10, 4, 50
);<<"Total circles: "<< circles->total <<endl;(
int i = 0; i < circles-> total; i++ )
{float* p = ( float*)cvGetSeqElem( circles, i );( out,
cvPoint( cvRound( p[0]), cvRound( p[1])), 2, CV_RGB( 200, 0, 0), -1, 8, 0 );(
out, cvPoint( cvRound( p[0]), cvRound( p[1])), cvRound( p[2]), CV_RGB( 200, 0,
0), 1, 8, 0 );}(out,findSquares4(gray,mainStorage));( &img);(
"out", out);( &out);= cvWaitKey(10); }( &capture );
cvDestroyAllWindows();}
Интерфейс окна программы:

Рисунок 1.Б - Интерфейс окна программы 2
Приложение В Демонстрационный графический материал