Решение смешанной краевой задачи для гиперболического уравнения разностным методом
Введение
Дифференциальные уравнения в частных производных
имеют широкое приложение в математической физике, гидродинамике, акустике и
других областях знаний. Большинство таких уравнений в явном виде не решаются.
Поэтому широкое распространение получили методы приближенного их решения,
например метод сеток, частным случаем которого является разностный метод [2].
Это универсальный и эффективный метод. Он позволяет сводить приближенное
решение уравнений в частных производных к решению систем алгебраических уравнений
[3].
Цели курсовой работы:
). Обзор литературы по теме «Решение смешанной
краевой задачи для гиперболического уравнения разностным методом».
). Реализация разностного метода применительно к
смешанной краевой задачи для гиперболического уравнения в системе
программирования Borland C++ Version 3.1.
Курсовая работа состоит из введения, двух глав,
заключения, списка литературы и приложения. Первая глава посвящена обзору
основных понятия, касающихся разностных схем. Во второй главе рассматривается
смешанная краевая задача, для которой приведен алгоритм построения разностной
схемы, а также описание программы «smesh_giperb» и её тест на конкретном
примере. В приложении представлен код программы, позволяющий получить
приближенное решение смешанной краевой задачи с граничными условиями третьего
рода.
Глава 1. Разностные методы решения
дифференциальных уравнений
Характерной особенностью различных разностных
методов является то, что в качестве приближенного решения выбирается сеточная
функция. Выделим основные пункты построения и исследования разностных схем.
. Заменить область непрерывного изменения
аргумента на дискретную область изменения. Это дискретное множество точек
называется сеткой или решеткой, а отдельные точки этого множества - узлами
сетки. Чаще всего сетка выбирается прямоугольной и равномерной.
. Заменить в узлах этой сетки производные
искомой функции разностными отношениями, использовав формулы численного
дифференцирования.
. Проверить условие аппроксимации разностной
схемы.
. Доказать устойчивость построенной разностной
схемы. Это один из наиболее важных и сложных вопросов. Если схема обладает
аппроксимацией и устойчивостью, то о сходимости разностной схемы судят о
теореме доказанной ниже.
В результате получилась система алгебраических
уравнений для определения приближённого решения. Такая система часто называется
разностной схемой. Точно так же можно заменить и частные производные и свести
краевую задачу для дифференциального уравнения в частных производных к
алгебраической системе. Функция, определенная в узлах сетки называется сеточной
функцией.
Сетка. Аппроксимация частных производных
разностными отношениями.
Мы ввели уже понятие сетки, узлов сетки,
разностной схемы и сеточной функции.
Обозначим
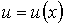 - искомая функция,
- искомая функция,
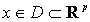 ,
,
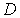 - открытая область
с границей
- открытая область
с границей 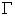 ,
,
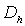 - сетка на
- сетка на 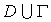 ,
где h - вещественный положительный параметр, характеризующий густоту точек на
сетке.
,
где h - вещественный положительный параметр, характеризующий густоту точек на
сетке.
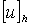 - сеточная функция,
совпадающая с точным решением дифференциальной краевой задачи
- сеточная функция,
совпадающая с точным решением дифференциальной краевой задачи 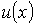 во
всех узлах сетки
во
всех узлах сетки 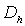 , называемая точным
решением на сетке или точным сеточным решением.
, называемая точным
решением на сетке или точным сеточным решением.
Теперь рассмотрим примеры сеток.
Пример 1.
Равномерная сетка на отрезке. Разобьем единичный
отрезок [0, 1] на N равных частей. Расстояние между соседними узлами 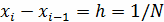
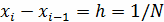 назовем шагом
сетки. Точки деления
назовем шагом
сетки. Точки деления 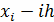
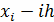 - узлы сетки.
Множество всех узлов
- узлы сетки.
Множество всех узлов
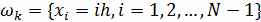
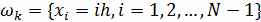 и составляет сетку
(рис. 1), в данном случае введенную на отрезке.
и составляет сетку
(рис. 1), в данном случае введенную на отрезке.
В это множество можно включить граничные точки 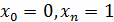
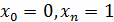 . Обозначим
. Обозначим 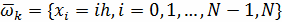
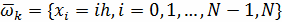
На отрезке [0, 1] вместо функции непрерывного
аргумента y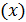
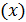 будем
рассматривать функцию дискретного аргумента
будем
рассматривать функцию дискретного аргумента 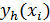
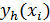 . Значения этой
функции вычисляются в узлах сетки
. Значения этой
функции вычисляются в узлах сетки 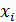
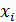 ,а сама функция
зависит от шага сетки h как от параметра.
,а сама функция
зависит от шага сетки h как от параметра.
Пример 2.
Неравномерная сетка на отрезке. Рассмотрим
отрезок 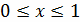
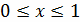 . Вводя
произвольные точки
. Вводя
произвольные точки 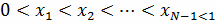
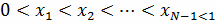 , разобьем его на N
частей. Множество узлов
, разобьем его на N
частей. Множество узлов 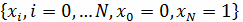
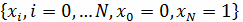 образует
неравномерную сетку
образует
неравномерную сетку 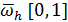
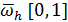 . Расстояние между
соседними узлами шаг сетки, равно
. Расстояние между
соседними узлами шаг сетки, равно 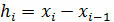
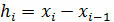 и зависит уже от
номера
и зависит уже от
номера 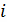
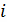 узла, т. е.
является сеточной функцией. Шаги сетки удовлетворяют условию нормировки
узла, т. е.
является сеточной функцией. Шаги сетки удовлетворяют условию нормировки
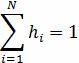
Затем рассмотрим пример замены в узлах сетки
производные искомой функции разностными отношениями.
Для начала определим разностные отношения,
которые будут использоваться в дальнейших примерах.
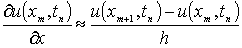 , (1.1.1)
, (1.1.1)
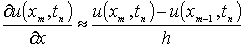 , (1.1.2)
, (1.1.2)
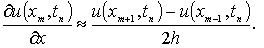 (1.1.3)
(1.1.3)
Аналогично получаются приближённые разностные
аналоги для частной производной по переменной t:
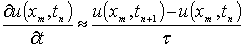 , (1.1.4)
, (1.1.4)
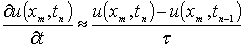 , (1.1.5)
, (1.1.5)
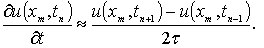 (1.1.6)
(1.1.6)
Для приближенного вычисления частных производных
второго порядка также можно использовать формулы численного дифференцирования,
например,
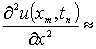
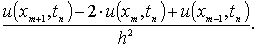 (1.1.7)
(1.1.7)
Пример 3
Рассмотрим задачу Коши для дифференциального
уравнения первого порядка. Требуется найти функцию 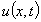 ,
определённую, непрерывную и имеющую частные производные первого порядка в
области
,
определённую, непрерывную и имеющую частные производные первого порядка в
области  удовлетворяющую
дифференциальному уравнению
удовлетворяющую
дифференциальному уравнению
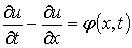 (1.1.8)
(1.1.8)
и начальному условию
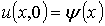 ,
, 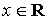 .
(1.1.9)
.
(1.1.9)
Здесь Т - заданная постоянная, а 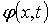 и
и
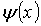 -
заданные функции. Если эти функции являются непрерывными, то задача будет иметь
единственное решение - функцию
-
заданные функции. Если эти функции являются непрерывными, то задача будет иметь
единственное решение - функцию 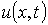 . Это решение
задачи Коши мы будем называть точным.
. Это решение
задачи Коши мы будем называть точным.
Введём в области D сетку:
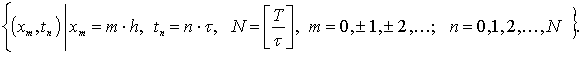
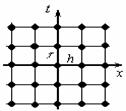
Рис. 1
Здесь h и 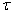 -
заданные шаги сетки, а квадратными скобками обозначена операция вычисления
целой части вещественного числа.
-
заданные шаги сетки, а квадратными скобками обозначена операция вычисления
целой части вещественного числа.
Будем искать приближённое решение этой задачи на
сетке D. Поскольку 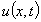 является точным
решением нашей дифференциальной краевой задачи, в каждом узле сетки
является точным
решением нашей дифференциальной краевой задачи, в каждом узле сетки 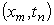 будет
выполняться дифференциальное уравнение
будет
выполняться дифференциальное уравнение
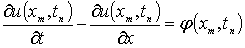
и в каждом узле, лежащем на нижней границе
области D (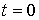 ), будут
выполняться начальные условия
), будут
выполняться начальные условия
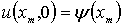 .
.
Заменим частные производные, входящие в
дифференциальное уравнение, разностными отношениям (1.1.4) и (1.1.1) и получим
в результате систему приближённых равенств, связывающих значения функции 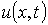 в
узлах сетки:
в
узлах сетки:
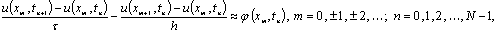 (1.1.10)
(1.1.10)
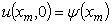 ,
,  (1.1.11)
(1.1.11)
Для вычисления приближённого решения мы получили
следующую систему линейных алгебраических уравнений:
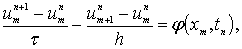 (1.1.12)
(1.1.12)
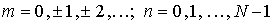 ,
,
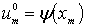 ,
, 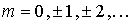 (1.1.13)
(1.1.13)
Для решения системы (10.1.12) - (10.1.13)
выразим из (1.1.12) 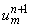 и получим
рекуррентную формулу:
и получим
рекуррентную формулу:
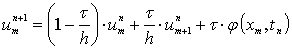 , (1.1.14)
, (1.1.14)
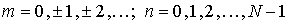 .
.
Зная 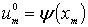 ,
по этой рекуррентной формуле при
,
по этой рекуррентной формуле при 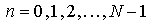 последовательно
находим
последовательно
находим 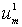 ,
,
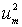 ,
…,
,
…, 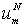 .
Таким образом, система (1.1.12) - (1.1.13), действительно, имеет единственное
решение. Но получить его практически невозможно, поскольку сетка содержит
бесчисленное множество узлов.
.
Таким образом, система (1.1.12) - (1.1.13), действительно, имеет единственное
решение. Но получить его практически невозможно, поскольку сетка содержит
бесчисленное множество узлов.
Операторная форма записи дифференциальных
краевых задач
Введём общее обозначение для любой
дифференциальной краевой задачи. Запишем её в виде операторного уравнения:
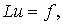 (1.2.1)
(1.2.1)
где 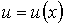 -
искомая функция,
-
искомая функция, 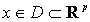 ,
, 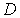 -
открытая область с границей
-
открытая область с границей 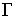 , f - заданная
функция, L - заданный дифференциальный оператор, действующий на функцию
, f - заданная
функция, L - заданный дифференциальный оператор, действующий на функцию 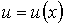 .
Будем считать, что задача (1.2.1) имеет единственное решение
.
Будем считать, что задача (1.2.1) имеет единственное решение 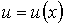 ,
которое мы в дальнейшем будем называть точным решением.
,
которое мы в дальнейшем будем называть точным решением.
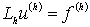 . (1.2.2)
. (1.2.2)
Здесь 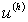 -
сеточное решение разностной краевой задачи, которое называется также
приближённым сеточным решением дифференциальной краевой задачи
-
сеточное решение разностной краевой задачи, которое называется также
приближённым сеточным решением дифференциальной краевой задачи 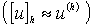 .
.
Пример 4
Построение разностной схемы для смешанной
краевой задачи для уравнения параболического типа.
Требуется найти функцию 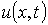 ,
определённую, непрерывную и имеющую частные производные второго порядка в
области
,
определённую, непрерывную и имеющую частные производные второго порядка в
области 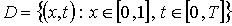 ,
удовлетворяющую дифференциальному уравнению
,
удовлетворяющую дифференциальному уравнению
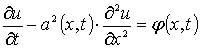 , (1.2.3)
, (1.2.3)
начальному условию
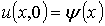 ,
, 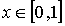 (1.2.4)
(1.2.4)
и граничным условиям
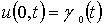 ,
, 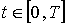 ,
(1.2.5)
,
(1.2.5)
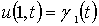 ,
, 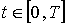 ,
(1.2.6)
,
(1.2.6)
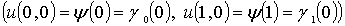 .
.
Здесь Т - заданная постоянная, а 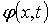 ,
,
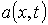 ,
,
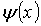 ,
,
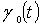 ,
,
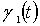 -
заданные функции. Дифференциальное уравнение (1.2.3) описывает процесс
распространения тепла в прямолинейном стержне. Поэтому его называют уравнением
теплопроводности. Будем считать, что выполнены все условия, при которых
сформулированная краевая задача имеет единственное решение - функцию
-
заданные функции. Дифференциальное уравнение (1.2.3) описывает процесс
распространения тепла в прямолинейном стержне. Поэтому его называют уравнением
теплопроводности. Будем считать, что выполнены все условия, при которых
сформулированная краевая задача имеет единственное решение - функцию 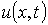 .
.
Введём в области D сетку (рис. 3):
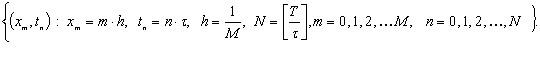
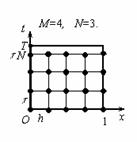
Рис. 2
Значения целой постоянной М и шага 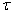 считаются
заданными. Будем искать приближённое решение этой задачи на сетке. Поскольку
считаются
заданными. Будем искать приближённое решение этой задачи на сетке. Поскольку 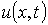 является
точным решением нашей дифференциальной краевой задачи, в каждом узле сетки
является
точным решением нашей дифференциальной краевой задачи, в каждом узле сетки 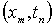 будет
выполняться дифференциальное уравнение
будет
выполняться дифференциальное уравнение
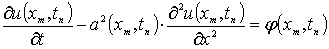 ,
,
в каждом узле, лежащем на нижней границе области
D (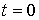 ),
будет выполняться начальное условие
),
будет выполняться начальное условие
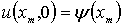 ,
,
в каждом узле, лежащем на левой границе области
D ( ),
будет выполняться граничное условие
),
будет выполняться граничное условие
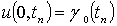 ,
,
в каждом узле, лежащем на правой границе области
D ( ),
будет выполняться начальное условие
),
будет выполняться начальное условие
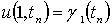 .
.
Заменим частные производные, входящие в
дифференциальное уравнение, разностными отношениями (1.1.4) и (1.1.7) и получим
в результате систему приближённых равенств, связывающих значения функции 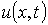 в
узлах сетки:
в
узлах сетки:
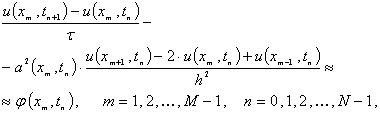 (1.2.7)
(1.2.7)
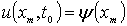 ,
, 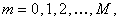 (1.2.8)
(1.2.8)
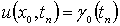 ,
, 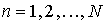 ,
(1.2.9)
,
(1.2.9)
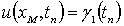 ,
, 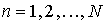 .
(1.2.10)
.
(1.2.10)
Поскольку равенства (1.2.7) являются
приближёнными, решив систему (1.2.7) - (1.2.10), мы получим, не точные значения
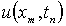 ,
а приближённые. Обозначим их через
,
а приближённые. Обозначим их через 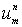 (
(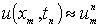 ).
В результате для определения
).
В результате для определения 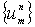 получим разностную
схему:
получим разностную
схему:
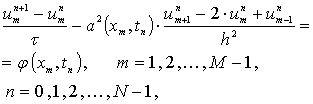 (1.2.11)
(1.2.11)
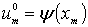 ,
, 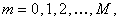 (1.2.12)
(1.2.12)
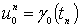 ,
, 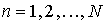 ,
(1.2.13)
,
(1.2.13)
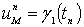 ,
, 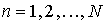 .
(1.2.14)
.
(1.2.14)
Выразим 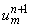 из
(1.2.11). В результате получается рекуррентная формула
из
(1.2.11). В результате получается рекуррентная формула
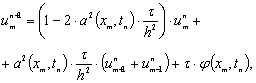 (1.2.15)
(1.2.15)
применяя которую последовательно при  ,
можно, зная
,
можно, зная 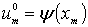 ,
, 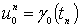 и
и
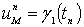 ,
в явном виде определить
,
в явном виде определить 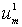 ,
, 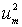 ,
…,
,
…, 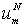 .
По этой причине построенная разностная схема получила название явной разностной
схемы для уравнения теплопроводности. И другие разностные схемы, обладающие
этим свойством, получили название явных схем.
.
По этой причине построенная разностная схема получила название явной разностной
схемы для уравнения теплопроводности. И другие разностные схемы, обладающие
этим свойством, получили название явных схем.
Если вместо формулы (1.1.4) для аппроксимации
частной производной использовать аналогичную формулу (1.1.5),то в результате
вместо системы уравнений (10.1.23) получится система:
 (1.2.16)
(1.2.16)
Разностная схема (1.2.16), (1.2.12)-(1.2.14)
получила название неявной разностной схемы для уравнения теплопроводности, так
как для её решения не удалось получить явной рекуррентной формулы, типа
(1.2.15).
Погрешность замены частных производных
разностными отношениями стремится к нулю при h и 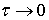 .
Поэтому можно ожидать, что и погрешность приближённого решения также будет
стремиться к нулю при h и
.
Поэтому можно ожидать, что и погрешность приближённого решения также будет
стремиться к нулю при h и 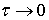 , и за счёт
уменьшения шагов сетки h и
, и за счёт
уменьшения шагов сетки h и 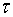 можно получать
приближённые решения с любой заданной точностью.
можно получать
приближённые решения с любой заданной точностью.
Требуется записать её в виде операторного
уравнения (1.2.2) и выяснить, что представляют собой основные объекты (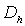 ,
,
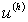 ,
,
 и
и
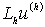 )
операторной записи. Сетка
)
операторной записи. Сетка

Густоту сетки регулируют два параметра: М (или
hрh) и 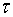 .
Один из них можно сделать основным, например, h, а второй параметр сделать
зависимым от него, введя функцию
.
Один из них можно сделать основным, например, h, а второй параметр сделать
зависимым от него, введя функцию 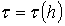 ,
такую, что
,
такую, что 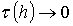 при
при  .
Тогда густота сетки будет определяться только параметром h.
.
Тогда густота сетки будет определяться только параметром h.
Приближённое решение удобно представить в виде
вектора с  компонентами:
компонентами: 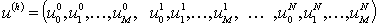 .
Точное сеточное решение представляется аналогичным вектором:
.
Точное сеточное решение представляется аналогичным вектором:
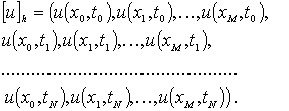
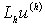 и
и 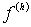 также
представим в виде векторов:
также
представим в виде векторов:
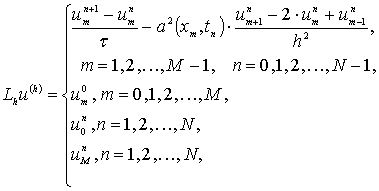
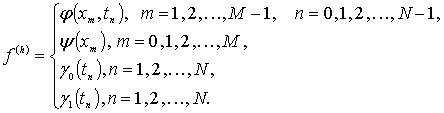
Количество компонент этих векторов равно 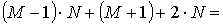
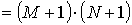 .
.
Введём целую постоянную 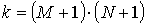 и
заметим, что величины
и
заметим, что величины 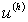 ,
, 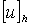 ,
,
 и
и
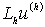 принадлежат
векторному пространству
принадлежат
векторному пространству 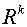 . Рассмотренный
пример показал, что практически любую дифференциальную краевую задачу можно
представить в виде (1.2.1). При этом Lu и f будут представлять собой
вектор-функции.
. Рассмотренный
пример показал, что практически любую дифференциальную краевую задачу можно
представить в виде (1.2.1). При этом Lu и f будут представлять собой
вектор-функции.
Нормы. Погрешность приближённого решения.
Сходимость. Порядок сходимости
Обозначим через 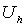 нормированное
векторное пространство, которому принадлежат точное
нормированное
векторное пространство, которому принадлежат точное 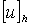 и
приближённое
и
приближённое 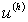 сеточные решения,
а через
сеточные решения,
а через 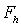 -
нормированное векторное пространство, которому принадлежат величины
-
нормированное векторное пространство, которому принадлежат величины 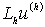 и
и
 .
Нормы элементов v, введенные в этих пространствах, будем обозначать
.
Нормы элементов v, введенные в этих пространствах, будем обозначать 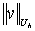 и
и
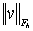 соответственно.
Нормы в векторном пространстве можно вводить разные, и от их выбора будут
зависеть свойства разностной схемы, описываемые ниже. Везде далее норма в
пространстве
соответственно.
Нормы в векторном пространстве можно вводить разные, и от их выбора будут
зависеть свойства разностной схемы, описываемые ниже. Везде далее норма в
пространстве 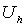 будет выбираться
по формулам
будет выбираться
по формулам 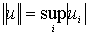 или
или 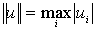 .Норму
в пространстве
.Норму
в пространстве 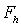 мы будем указывать
особо для каждой рассматриваемой задачи.
мы будем указывать
особо для каждой рассматриваемой задачи.
Погрешностью приближённого сеточного решения 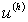 называется
величина
называется
величина 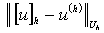 .
.
Для того чтобы можно было получить приближённое
решение с заданной точностью, необходимо, чтобы погрешность приближённого
решения стремилась к нулю при  . Это свойство
получило название сходимости. Дадим его развёрнутое определение.
. Это свойство
получило название сходимости. Дадим его развёрнутое определение.
Пусть существует положительное вещественное
число H, такое, что 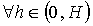 существует
единственное решение разностной краевой задачи
существует
единственное решение разностной краевой задачи 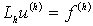 .
Если
.
Если
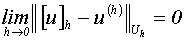 , (1.3.1)
, (1.3.1)
то говорят, что решение разностной краевой
задачи сходится к решению дифференциальной краевой задачи при  .
.
Если существуют положительные постоянные C и p,
такие, что 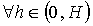 выполняется
неравенство
выполняется
неравенство
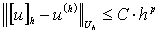 ,
,  (1.3.2)
(1.3.2)
то говорят, что приближённое решение сходится к
точному при  с p-м порядком
относительно h. Из условия (1.3.1), очевидно, следует равенство (1.3.2).
с p-м порядком
относительно h. Из условия (1.3.1), очевидно, следует равенство (1.3.2).
Разность
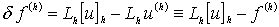 (1.3.3)
(1.3.3)
называется невязкой разностной схемы 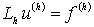 на
точном решении дифференциальной краевой задачи. Напомним, что
на
точном решении дифференциальной краевой задачи. Напомним, что 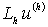 и
и
 принадлежат
к нормированному векторному пространству
принадлежат
к нормированному векторному пространству 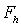 .
Величины
.
Величины 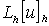 и
и
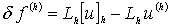 ,
очевидно, также будут принадлежать
,
очевидно, также будут принадлежать 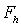 .
.
Величиной невязки 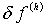 называется
её норма в этом пространстве:
называется
её норма в этом пространстве:
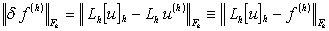 . (1.3.4)
. (1.3.4)
Пусть существует положительное вещественное
число H, такое, что 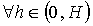 существует
единственное решение разностной краевой задачи
существует
единственное решение разностной краевой задачи 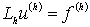 .
Если
.
Если
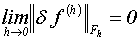 , (1.3.5)
, (1.3.5)
то говорят, что разностная схема 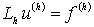 аппроксимирует
задачу
аппроксимирует
задачу 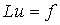 на
её точном сеточном решении
на
её точном сеточном решении 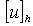 . Если, сверх того,
найдутся вещественное положительное число
. Если, сверх того,
найдутся вещественное положительное число 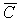 и
положительное число p, такие, что
и
положительное число p, такие, что 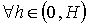 будет
выполнено неравенство
будет
выполнено неравенство
то говорят, что разностная схема 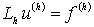 аппроксимирует
задачу
аппроксимирует
задачу 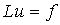 на
её точном сеточном решении с порядком p относительно h (или с порядком
на
её точном сеточном решении с порядком p относительно h (или с порядком  ).
).
Устойчивость
Пусть существует положительное вещественное
число H, такое, что 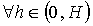 существует
единственное решение разностной краевой задачи
существует
единственное решение разностной краевой задачи 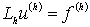 .
Эта разностная схема называется устойчивой на паре пространств
.
Эта разностная схема называется устойчивой на паре пространств 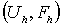 ,
если существуют положительные постоянные
,
если существуют положительные постоянные 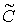 и
и
 ,
такие, что
,
такие, что 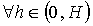 и
и 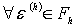 ,
удовлетворяющего условию
,
удовлетворяющего условию 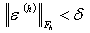 , разностная
краевая задача
, разностная
краевая задача
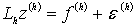 (1.4.1)
(1.4.1)
имеет единственное решение 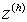 ,
причём
,
причём
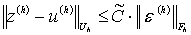 (1.4.2)
(1.4.2)
Устойчивость разностной схемы означает, что
малому возмущению правой части разностной схемы отвечает малое возмущение
решения разностной краевой задачи. Это внутреннее свойство разностных схем, не
имеющее никакого отношения к исходной дифференциальной краевой задаче. Поэтому
исследовать устойчивость несколько легче, чем исследовать сходимость. Если
оператор 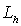 является
линейным (
является
линейным (
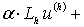
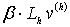 ), то определение
устойчивости можно переформулировать.
), то определение
устойчивости можно переформулировать.
Дадим определение устойчивости для линейных
разностных схем.
Разностная схема 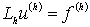 с
линейным оператором
с
линейным оператором 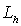 называется
устойчивой на паре пространств
называется
устойчивой на паре пространств 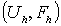 , если существует
положительная постоянная
, если существует
положительная постоянная  , такая, что
, такая, что 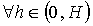 и
и
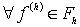 разностная
краевая задача
разностная
краевая задача
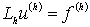 (1.4.3)
(1.4.3)
имеет единственное решение 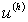 ,
причём
,
причём
 . (1.4.4)
. (1.4.4)
Понятия аппроксимации и устойчивости связаны с
понятием сходимости и позволяют облегчить её исследование. Эта связь
устанавливается следующей теоремой.
Теорема 1
Если разностная краевая задача 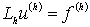 аппроксимирует
дифференциальную краевую задачу
аппроксимирует
дифференциальную краевую задачу 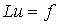 с порядком
с порядком  и
является устойчивой на паре пространств
и
является устойчивой на паре пространств 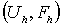 ,
то приближённое решение
,
то приближённое решение 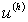 сходится к точному
сеточному решению
сходится к точному
сеточному решению 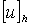 с порядком p
относительно h.
с порядком p
относительно h.
Доказательство:
Из того, что разностная краевая задача
аппроксимирует дифференциальную краевую задачу, следует, что 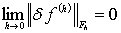 .По
определению этого предела для положительного числа
.По
определению этого предела для положительного числа  (из
определения устойчивости) найдётся положительное число H, такое, что
(из
определения устойчивости) найдётся положительное число H, такое, что 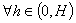 будет
выполнено неравенство
будет
выполнено неравенство 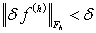 . Здесь учтено, что
h положительно, а норма неотрицательна. Зададим любое h из
. Здесь учтено, что
h положительно, а норма неотрицательна. Зададим любое h из 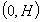 и
положим
и
положим 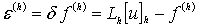 .
Тогда
.
Тогда 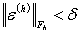 и,
согласно(1.4.2), разностная краевая задача
и,
согласно(1.4.2), разностная краевая задача
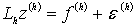
будет иметь единственное решение 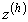 .
Заметим, что правая часть этого уравнения
.
Заметим, что правая часть этого уравнения 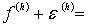
 и, следовательно,
выполняется равенство
и, следовательно,
выполняется равенство 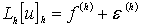 . Это означает, что
. Это означает, что
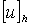 является
решением этой же разностной краевой задачи, а поскольку решение этой задачи
единственно,
является
решением этой же разностной краевой задачи, а поскольку решение этой задачи
единственно, 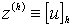 . Тогда из(1.4.18)
получим:
. Тогда из(1.4.18)
получим:
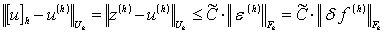 .
.
производная аппроксимация краевой
задача
Из того, что разностная краевая задача 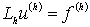 аппроксимирует
дифференциальную краевую задачу
аппроксимирует
дифференциальную краевую задачу 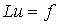 с порядком
с порядком  ,
следует, что
,
следует, что 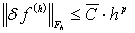 . Отсюда
. Отсюда 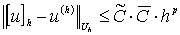 .
Что и требовалось доказать.
.
Что и требовалось доказать.
Доказанная теорема позволяет проводить
исследование сходимости приближённого решения к точному в 2 этапа. Вначале
находится порядок аппроксимации разностной схемы, а затем доказывается её
устойчивость. Как показывает пример 4, определение порядка аппроксимации
разностных схем особого труда не составляет. Более того, обычно решается более
сложная задача - это задача построения разностной схемы с заданным порядком
аппроксимации. Один из методов её решения мы и рассмотрим в следующем
параграфе.
Глава 2. Решение смешанной краевой
задачи для гиперболического уравнения разностным методом
2.1 Общая постановка задачи
Рассмотрим общую постановку смешанной краевой
задачи для гиперболического уравнения.
В области D={0<y<Y,
α<x<β} найти дважды непрерывно
дифференцируемую функцию 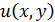
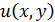 , которая в этой
области удовлетворяла бы уравнению:
, которая в этой
области удовлетворяла бы уравнению:
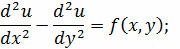 ( 2.1.1)
( 2.1.1)
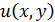
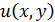 -точное решение
уравнения.
-точное решение
уравнения.
А на границе Г области D при y=0 - начальным
условиям:
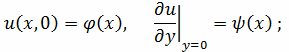 (2.1.2)
(2.1.2)
И при 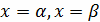
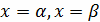 - одному из трех
граничных условий:
- одному из трех
граничных условий:
а) условия первого рода
 ; (2.1.3)
; (2.1.3)
б) условия второго рода
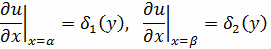 (2.1.4)
(2.1.4)
в) условия третьего рода 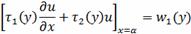
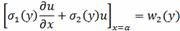 (2.1.5)
(2.1.5)
Где 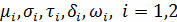
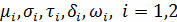 - известные
функции.
- известные
функции.
Коэффициенты 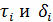
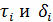 подчинены
естественным условиям
подчинены
естественным условиям

Условия (2.1.3) и (2.1.4) являются частным
случаем условий (2.1.5)
2.2 Смешанная краевая задача с
граничными условиями третьего рода
Уравнение
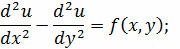 (2.2.1)
(2.2.1)
задано в области D={0<y≤Y<+∞,
α<x<β}
Начальные условия:
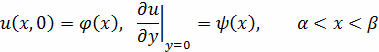 (2.2.2)
(2.2.2)
Граничные условия третьего рода:
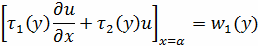
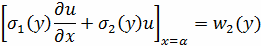 (2.2.3)
(2.2.3)
Предположим смешанная краевая задача (2.2.1)-
(2.2.3) имеет единственное решение в области 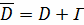
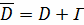 , где Г-контур
области D, и это решение вместе с производными до 4- го порядка включительно
непрерывно в области
, где Г-контур
области D, и это решение вместе с производными до 4- го порядка включительно
непрерывно в области 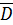
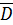
Выберем прямоугольную равномерную сетку, положив
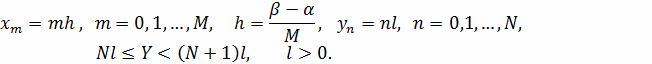
Получаемую при этом сеточную область 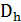
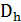 разобьем на два
множества: множество
разобьем на два
множества: множество 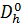
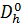 внутренних узлов,
внутренних узлов,
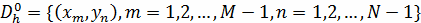
и множество 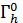
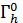 граничных узлов,
граничных узлов,
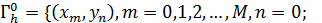
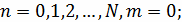
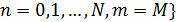
Граничные условия на прямых 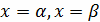
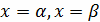 заменим по
формулам полиномиального численного дифференцирования:
заменим по
формулам полиномиального численного дифференцирования:
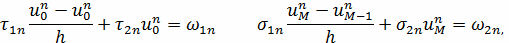 (2.4)
(2.4)
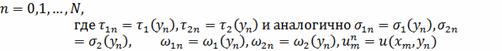
Разностные граничные условия аппроксимируют
граничные условия с погрешностью порядка 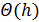
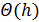
На основании формул численного дифференцирования
получаем схему, аппроксимирующую граничную задачу с погрешностью 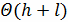
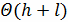
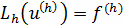
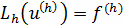 (2.5)
(2.5)
Где 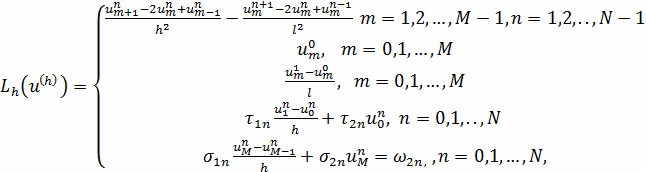
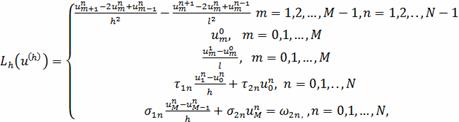
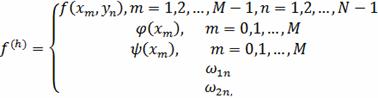
Замечание. Если 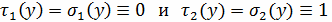
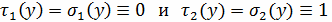 то разностная
схема аппроксимирует граничную задачу с погрешностью
то разностная
схема аппроксимирует граничную задачу с погрешностью 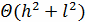
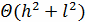
Алгоритм:
Найти приближенное решение на нулевом слое:
Найти приближенное решение на первом слое:
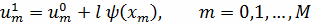
Найти приближенное решение на втором слое для
узлов с номерами 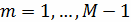
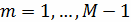
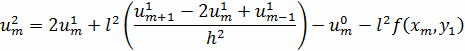
Найти приближенное решение на втором слое при 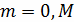
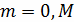
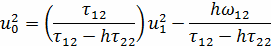
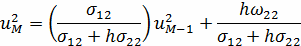
Найти приближенное решение на остальных слоях 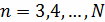
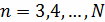

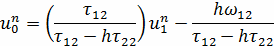
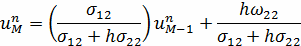
Достаточным условием для устойчивости по
начальным данным разностной схемы 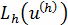
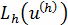 является
ограничение, налагающее на шаги h и l:
является
ограничение, налагающее на шаги h и l:
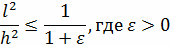
Данный алгоритм реализован в программе
smesh_giperb на языке программирования С++, листинг которой приведен в
приложении.
Описание программы:
Исходные данные:M которые задают количество
узлов по оси OX alfa, betta, Y задают прямоугольную область (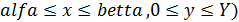
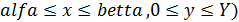
Вся программа состоит из функций. Опишем для
чего предназначена каждая из них.f(double x,double y)-задает функцию
f(x,y).fi(double x), double psi(double x)- задаются функции fi(x)и psi(x) из
начальных условий.tau1(double y), double tau2(double y), double w1(double y),
double w2(double y), double sigma1(double y), double sigma2(double y)- задаются
функции tau1(y), tau2(y),sigma1(y),sigma2(y),w1(y),w2(y) из граничных
условий.zapis_sloya(int nomer)- функция,записывающая номер
слоя.zapis_v_file(float x)- функция, записывающая значение приближенной функции
u(x,y) в узлах на слое.()- основное тело программы, в которой реализовывается
разностная схема. Изначально вычисляется значение на нулевом слое, затем на
первом, далее на всех остальных. Для вычисления например 2го слоя используются
значения на нулевом и первом, которые хранятся в массивах u0 и u1
соответственно. Значения же третьего слоя записываются в массив u2. Для
вычисления на третьем слое используются значения на первом и втором, которые
хранятся в массивах u1 и u2 соответственно. Значения же третьего слоя
записываются в массив u0. Для вычисления на четвертом слое используются
значения на втором и третьем слоях, которые хранятся в массивах u2 и u0
соответственно. Значения же третьего слоя записываются в массив u1. И так далее
до последнего слоя. Выбор буферного массива реализуется оператором switch
(octatok), где аргумент octatok- остаток от деления номера слоя на 3.
Проверим правильность работы программы на
конкретном примере.
Рассмотрим cмешанную краевую задачу (2.2.1)-
(2.2.3).
Она имеет точное решение при указанных ниже
начальных, граничных условиях и функции f(x,y) в области D={0<y≤Y=1<+∞,
0=α<x<β=1}.
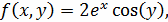
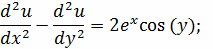
Начальные условия:

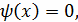
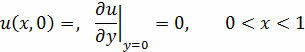
Граничные условия:
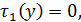
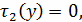
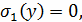
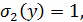
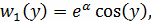
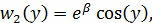
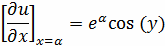
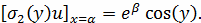 Данное уравнение
имеет точное решение
Данное уравнение
имеет точное решение 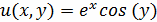
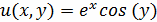 , поэтому мы можем
найти погрешность приближенных значений искомой функции в узлах разбиения.
Возьмем определенный узел (0.6,0.8)
, поэтому мы можем
найти погрешность приближенных значений искомой функции в узлах разбиения.
Возьмем определенный узел (0.6,0.8)
Выберем M=10, N=20, следовательно 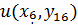
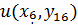 , h=0.1, l=h/2=0.05
получаем
, h=0.1, l=h/2=0.05
получаем
|
Приближенное
решение
|
Точное
решение
|
Погрешность
|
|
1,304615736000000
|
1,269482393459680
|
0,035133342540324
|
Сгущаем сетку в 2 раза M=20, N=40,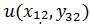
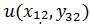 ,
,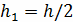
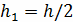 ,
, 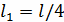
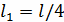 получаем
получаем
|
Приближенное
решение
|
Точное
решение
|
Погрешность
|
|
1,287504077000000
|
1,269482393459680
|
0,018021683540324
|
Сгущаем сетку в 4 раза M=40, N=80, 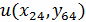
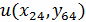 ,
,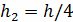
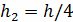 ,
, 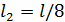
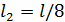 получаем
получаем
|
Приближенное
решение
|
Точное
решение
|
Погрешность
|
|
1,278385997000000
|
1,269482393459680
|
0,008903603540324
|
Сгущаем сетку в 8 раза M=80, N=160,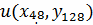
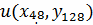 ,
, 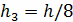
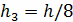 ,
, 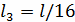
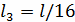 получаем
получаем
|
Приближенное
решение
|
Точное
решение
|
Погрешность
|
|
1,273945808000000
|
1,269482393459680
|
0,004463414540324
|
Сгущаем сетку в 16 раза M=160, N=320, 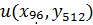
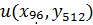 ,
, 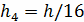
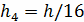 ,
, 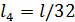
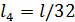 получаем
получаем
|
Приближенное
решение
|
Точное
решение
|
Погрешность
|
|
1,271712422000000
|
1,269482393459680
|
0,002230028540324
Заключение
К основным результатам курсовой работы можно
отнести:
Обзор литературы по теме «Решение смешанной
краевой задачи для гиперболического уравнения разностным методом».
Программа «smesh_giperb», разработанная в
Borland C++ Version 3.1, код которой приведен в приложении.
Список используемой литературы
1. Трубников
С.В. Численные методы. Часть 3: Решение дифференциальных уравнений. Учебное
пособие для студентов вузов. - Брянск: БГУ, 2005.
2. Крылов
В.И. и др. Вычислительные методы, т.II. М.: Наука, 1977.
. Самарский
А.А. Теория разностных схем. М.: Наука, 1983.
. Крылов
В.И, Бобков В.В, Монастырный П.И. Численные методы, т II. M.: Наука, 1977.
. Стефан
Р.Д. C++ для "чайников", 4-е издание: Пер. с англ.: - М.:
Издательский дом '"Вильяме", 2003.
. Трубников
С.В. Задачник - практикум по численным методам. Часть 4. Описание библиотеки
программ. Учебное пособие для студентов вузов. - Брянск: БГУ, 2005.
. Подбельский
В.В. Язык Си++: Учебное пособие.-5-е издание - М.: Финансы и статистика, 2003.
Приложение
/* {Программа smesh_giperb предназначена для
решения смешанной краевой задачи для уравнения гиперболического типа разностным
методом.
Рассматривается смешанная краевая задача для
дифференциального уравнения гиперболического типа:_xx (x,y)-u_yy
(x,y)=f(x,y),0<y<Y<,alfa<x<betta (x,0) = fi(x),
alfa<x<betta,_y (x,0)=psi(x)(y) u_x (alfa,y)+tau2(y)u(alfa,y)=w1(y)(y)
u_x (betta,y)+sigma2(y)u(betta,y)=w2(y)
Ищется функция u(x,y)
В прямоугольной области
(alfa<=x<=betta,0<=y<=Y), вводится сетка с шагами h и l по оси x и
y соответственно.
Число отрезков разбиения по оси x - M, а по оси
y - N. h=(alfa-betta)/MM, l= sqrt(h*h/2) - шаги сетки.
Приближённые значения решения u(x,y) в узлеах
сетки с координатами x_j=h*j и y_i=i*l (j=0,1,...,M, i=0,1,...,N) ищутся
разностным методом методом и записываются в файл rezultat.txt послойно. То есть
значения ?u(x?_m,y_n) вычисляются последовательно:
На временном слое 0. При n=0 и для всех m от 0
до M,
На временном слое 1. При n=1 и для всех m от 0
до M,
................................
На временном слое N. При n=N и для всех m от 0
до M.
Записываются приближенные значения решения
u(x_m,y_n) в файл rezultat.txt в следующем порядке:
sloi(x_0,y_0) u(x_1,y_0) … u(x_M,y_0)
sloi(x_0,y_1) u(x_1,y_1) … u(x_M,y_1)
sloi(x_0,y_N) u(x_1,y_N) … u(x_M,y_N)
Для временного хранения приближенного решения
при вычислениях по рекуррентным формулам используются также три массива
u0[m],u1[m]и u2[m].
В начале вычисляется приближенное решение на
нулевом временном слое. При вычислении оно помещается в массив u0 записывается
в файл rezultat.txt.
Затем, зная решение на нулевом слое, по рекуррентной
формуле находится решение на следующем, первом слое. При вычислении оно
помещается в массив u1 и записывается в файл rezultat.txt.
Затем, зная решение на первом слое по
рекуррентной формуле находится решение на следующем, втором слое. При
вычислении это решение помещается в массив u2 и записывается в файл
rezultat.txt
................................................................
Этот процесс продолжается до тех пор, пока не
будет вычислено и записано в файл приближенное решение на последнем слое.
Массивы u0,u1 и u2 используются в качестве
буферов, в которые временно помещается приближенное решение на очередном
временном слое до записи его в файл. */
#include <iostream.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <fstream.h>
#include <string.h>
#include <conio.h>buffer[128],
buffer_nomer[4];*copy;//указатель на переменную в которой хранится строка *
fp;* st;M,N,i,j,octatok;alfa, betta, l,Y,NN;h;
# define NDEC 10
//задается функция f(x,y)f(double x,double y)
{(2*exp(x)*cos(y));
}
// задаются функции fi(x)и psi(x) из начальных
условийfi(double x)
{(exp(x));
}psi(double x)
{x=0;x;
}
// задаются функции tau1(y),
tau2(y),sigma1(y),sigma2(y),w1(y),w2(y) из граничных условийtau1(double y)
{y=1;y;
}tau2(double y)
{y=0;y;
}w1(double y)
{(exp(alfa)*cos(y));
}
w2(double y)
{(exp(betta)*cos(y));
}sigma1(double y)
{y=0;y;
}sigma2(double y)
{ y=1;y;
}
//функция для записи в файл номера
слояzapis_sloya(int nomer)
{fp=fopen("d:\\rezultat.txt","a");(nomer,buffer_nomer,10);=new
char[strlen(buffer_nomer)+1];(st,buffer_nomer);(st,"sloi ");(fp,
"\n\r" );(fp, st );(fp, "\n\r" );(fp);st;
}
//функция для записи в файл значений на слое
?u(x?_m,y_n)zapis_v_file(float x)
{fp=fopen("d:\\rezultat.txt","a");(x,NDEC,buffer);=new
char[strlen(buffer)+1];//строка длиной 'длина строковой переменной
buffer+1',плюс 1 для нулевого символа(copy,buffer);(copy," ");(fp,
copy );(fp);copy;//освобождение памяти
}()
{<<"введите число узлов на оси
OX";cin>>M;<<"vvedite
alfa";cin>>alfa;cout<<endl;<<"vvedite
betta";cin>>betta;cout<<endl;<<"vvedite
Y";cin>>Y;=(betta-alfa)/M;cout<<h<<endl;//вычисление и
вывод шага h=h/2;cout<<l<<endl;// вычисление и вывод шага
l=fmod(Y,l);(octatok==0) NN=Y/l;NN=floor(Y/l); // вычисление
N=NN;cout<<N;*u0;*u1;*u2;=(float*) malloc(M*sizeof(float));=(float*)
malloc(M*sizeof(float));=(float*)
malloc(M*sizeof(float));=fopen("d:\\rezultat.txt","w");
{[j]=fi(j*h);_v_file(u0[j]);
}
//вычисление и запись в файл первого слоя_sloya(1);(j=0;j<=M;j++)
{[j]=psi(j*h)*l+u0[j];_v_file(u1[j]);
}
/*вычисление и запись в файл все с остальных
слоев i=2,..N
Схема трехслойная, для вычисления одного слоя
необходимы значения функции в узлах на предыдущих 2-х слоях.
Для вычисления, например 2го слоя используются
значения на нулевом и первом, которые хранятся в массивах u0 и u1
соответственно. Значения же третьего слоя записываются в массив u2.
Для вычисления на третьем слое используются
значения на первом и втором, которые хранятся в массивах u1 и u2
соответственно. Значения же третьего слоя записываются в массив u0.
Для вычисления на четвертом слое используются
значения на втором и третьем слоях, которые хранятся в массивах u2 и u0
соответственно. Значения же третьего слоя записываются в массив u1.
И так далее до последнего
слоя.*/(i=2;i<=N;i++)
{
octatok=fmod(i,3);(octatok)
{//вычисляются значения на слоях с i=3,6,9,...0:
_sloya(i);(j=1;j<M;j++)[j]=2*u2[j]+l*l*(u2[j+1]-2*u2[j]+u2[j-1])/(h*h)-u1[j]-l*l*f(j*h,i*l);[0]=tau1(i*l)*u0[1]/(tau1(i*l)-h*tau2(i*l))-h*w1(i*l)/(tau1(i*l)-h*tau2(i*l));[M]=sigma1(i*l)*u0[M-1]/(sigma1(i*l)+h*sigma2(i*l))+h*w2(i*l)/(sigma1(i*l)+h*sigma2(i*l));(j=0;j<=M;j++)_v_file(u0[j]);;
//вычисляются значения на слоях с i=4,7,11,...1:
zapis_sloya(i);(j=1;j<M;j++)[j]=2*u0[j]+l*l*(u0[j+1]-2*u0[j]+u0[j-1])/(h*h)-u2[j]-l*l*f(j*h,i*l);[0]=tau1(i*l)*u1[1]/(tau1(i*l)-h*tau2(i*l))-h*w1(i*l)/(tau1(i*l)-h*tau2(i*l));[M]=sigma1(i*l)*u1[M-1]/(sigma1(i*l)+h*sigma2(i*l))+h*w2(i*l)/(sigma1(i*l)+h*sigma2(i*l));(j=0;j<=M;j++)_v_file(u1[j]);;
//вычисляются значения на слоях с i=2,5,8,...2:
zapis_sloya(i);(j=1;j<M;j++)[j]=2*u1[j]+l*l*(u1[j+1]-2*u1[j]+u1[j-1])/(h*h)
-u0[j]-l*l*f(j*h,i*l);[0]=tau1(i*l)*u2[1]/(tau1(i*l)-h*tau2(i*l))-h*w1(i*l)/(tau1(i*l)-h*tau2(i*l));[M]=sigma1(i*l)*u2[M-1]/(sigma1(i*l)+h*sigma2(i*l))+h*w2(i*l)/(sigma1(i*l)+h*sigma2(i*l));(j=0;j<=M;j++)_v_file(u2[j]);;
}
}(u0);(u1);(u2);();0;
}
Похожие работы на - Решение смешанной краевой задачи для гиперболического уравнения разностным методом
|