Научно-методические основы управления состоянием хвостохранилищ горно-металлургического производства
Методическое пособие
Научно-методические основы управления состоянием хвостохранилищ
горно-металлургического производства
УДК 622.03:628.511:614.838.12:622:349.5
Гурин А.А., Радченко И.С., Гурин Ю.А.,
(Криворожский технический университет)
Ляшенко В.И. (ГП «УкрНИПИИ промтехнологии»)
Приведены основные
научные и практические результаты аналитических исследований процесса оседания
твердых частиц в неподвижной воде. Изложена методика определения скорости их
оседания, установлены условия, при которых частицы поднимаются вверх.
Ключевые слова: твердые частицы,
вода, оседание, сопротивление давлению.
Актуальность проблемы
Оседание частиц в воде наблюдается
при ее осветлении в отстойниках, при формировании хвостохранилищ, при бурении
нисходящих скважин на карьерах и др. Например, при проектировании отстойников
для осветления воды основным параметром является скорость оседания моно- или
полидисперсных твердых частиц. В отстойнике в результате оседания твердых
частиц образуется три зоны: осветления воды, гравитационного осаждения частиц,
сгущение частиц в суспензии. На дне отстойника скапливается слой осадка
(шлама), который периодически или же постоянно удаляется. На стадии
проектирования отстойников обычно пользуются известными расчетными и эмпирическими
формулами [1], что усложняет процедуру расчета, а полученные результаты часто
не удовлетворяют требованиям заказчика по габаритам отстойника.
хвостохранилище отстойник вода
оседание
Методика численного моделирования
При оседании твердых частиц в
неподвижной воде или ее потоке возникает сила сопротивления движению.
Рассмотрим механизм возникновения такого сопротивления.
Для этого воспользуемся
подходом Ньютона [1, 3, 4,]. Предположим, что среда состоит из большого числа
дискретных частиц, которые в первом приближении мы будем рассматривать как
материальные точки. Эти частицы или покоятся или движутся потоком воды и не
связаны между собой. Движущееся тело в среде будет испытывать столкновение с
заполняющими среду частицами и передавать им часть своего импульса. Масса
частиц, действующих на тело за 1 с, равна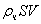 
, где 
-
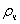масса частиц в единице объема (плотность среды), кг/м3; S -
площадь проектирования тела на плоскости, которая перпендикулярна вектору
скорости тела, м2; V - скорость тела, м/с.
При каждом столкновении
частицы с телом ему сообщается некоторая скорость1 величина которой
пропорциональна начальной скорости V, т.е.
,
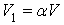где
α - безразмерный
коэффициент пропорциональности
Следовательно, изменение
импульса тела в 1 с составит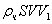 
.
Скорость изменения
импульса тела равна силе сопротивления (или просто сопротивлению) среды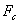 
:
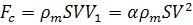
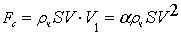(1)
Импульс, переданный
среде, зависит от того является ли столкновение тела с водяными молекулами
упругим или не упругим.
Характер столкновений в
общем случае можно учесть постоянной α. При
оценке величины α в расчет необходимо брать не только проекцию площади частицы на
плоскость перпендикулярную вектору скорости частиц (площадь поперечного
сечения). В зависимости от типа потока молекулы жидкости могут получать импульс
от тела или сообщать телу импульс с обратной стороны. В то же время края тела
могут испытывать такое же воздействие молекул, по тому в общем случае, следует
учитывать не только площадь проекции тела, а всю его поверхность.
Существует три вида
сопротивления среды, которые зависят от характера движения тела через среду.
Деформационное или вязкостное сопротивление - сила, необходимая для деформации
среды, чтобы тело могло проходить в ней. Эта деформация может происходить на
больших расстояниях от тела впереди и сзади него. Второй вид сопротивления -
сопротивление трения на поверхности тела. Третий вид сопротивления -
сопротивление давления, обусловленное сжатием среды. Два последних вида
сопротивления называют «приповерхностным трением» тела. При малых числах
Рейнольдса (Re) [5,6] преобладает деформационное сопротивление. В этом случае
сопротивление среды в первую очередь связано с проекцией тела на площадь
перпендикулярную потоку жидкости. При больших числах Рейнольдса результаты
подхода Ньютона согласуются с экспериментальными данными, даже если
предположение о постоянстве параметра α не
совсем верно.
Обычно уравнение для
сопротивления среды [6] записывается как
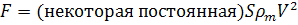
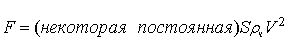. (2)
Если использовать член V2/2
(подобный члену уравнения Бернули, содержащему скорость), то
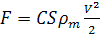
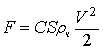, (3)
где С -
коэффициент сопротивления среды.
Для сферы диаметром d
имеем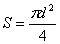 
.
Тогда
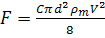
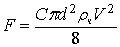. (4)
Из формулы (4) следует,
что сила сопротивления движению частиц пропорционально квадрату диаметра.
При турбулентном потоке
коэффициент сопротивления среды является постоянным и равен приблизительно 0,4.
Численный пример 1.
Вычислим силу сопротивления для частицы диаметром d=5∙10-3
м, плотностью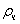 
=1000
кг/м3, которая движется в воде со скоростью V=0,1 м/с,
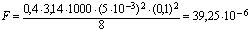Н
Первоначально считали,
что для данной формы тела, его положения и относительной скорости коэффициент С
будет иметь постоянное значение. Однако коэффициент С непостоянен, и
существует много случаев возникновения сопротивлению течению, зависящего от
числа Рейнольдса.
Коэффициент
сопротивления среды постоянен для данной формы и положения тела в потоке в тех
случаях, когда полное сопротивление среды является преимущественно
сопротивлением давления. это всегда будет при больших числах Рейнольдса.
Если имеется сходство
потоков вокруг тел сходной формы для случаев, когда сходно отношение сил у
поверхности тел, то можно сказать, что это эквивалентно существованию подобия
сил сопротивления, когда числа Рейнольдса двух тел тождественны. Но тогда
коэффициенты сопротивления среды для этих двух случаев также тождественны.
Следовательно,
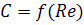
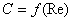, (5)
где Re - число
Рейнольдса.
В некотором интервале
чисел Рейнольдса коэффициент С можно определить аналитически. В других
случаях коэффициент С определяется эмпирически. Для номинального потока
(Re<1) справедлива формула
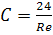
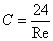. (6)
В случае промежуточного
потока (1≤Re≤1000) существует несколько эмпирических формул для
вычисления коэффициента С. Например,
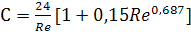
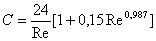, (7)
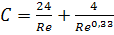
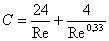. (8)
Численный пример 2.
Вычислить коэффициенты сопротивления по формулам (7) и(8) для Re=2
По уравнению (8)
.
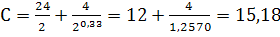
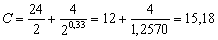По уравнению (7)
.
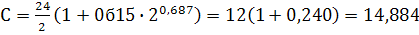
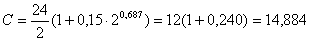Измеренная величина
коэффициента С для сфер при Re=2 равна 14,60.
Следовательно, разность
между вычисленным Св и наблюденным Сз
значениями коэффициента сопротивления составит согласно формулы (8) 4%,
согласно формулы (7) - 2%.
При малой турбулентности
(1000≤Re≤2·105) C=0,44.
При высокой
турбулентности (Re>2·105) C=0,1.
Определим скорость
оседания частиц в воде под действием силы тяжести.
На частицу, которая
движется в воде, действуют силы:
а) тяжести,
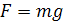
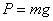, (9)
где m - масса
частицы, кг; g - ускорение силы земного притяжения, м/с2;
б) выталкивающая сила
Архимеда,
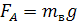
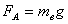, (10)
где mв
- масса вытесненной частицей воды, кг;
в) сила сопротивления F
(рис.1.).
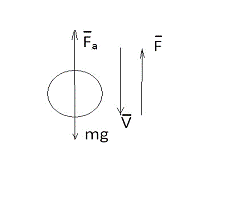
Рис. 1. К определению
скорости оседания твердых частиц в воде
При равномерном движении
частицы выполняется равенство:
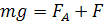
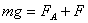(11)
Для сферических частиц
диаметра d
В то же время
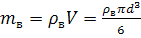
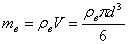, (13)
где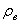 
=1000
кг/м3 - плотность воды.
В таком случае равенство
(11) переписываем в следующем виде:
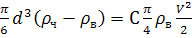
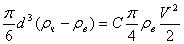. (14)
Отсюда находим скорость
оседания частиц в воде под действием силы тяжести
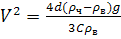
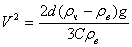. (15)
Формула (15) дает
возможность вычислить скорость оседания частиц. Однако некоторые трудности
вызываются зависимостью коэффициента сопротивления С от числа
Рейнольдса, которое в свою очередь зависит от скорости V [8]
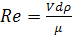
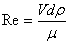, (16)
где μ
- динамическая вязкость среды, в которой оседает частица, Па·с. Кинематическая
вязкость определяется через динамическую вязкость μ
соотношением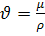 
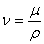, (где ρ
- плотность) Для воздуха при нормальных условиях ν=0,152
см2/с, для воды ν=0,01
см2/с.
Возводим левую и правую
части равенства (16) в квадрат и умножим на С и найдем:
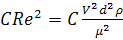
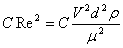. (17)
Подставляя сюда
выражение V2 из (15), получаем
,
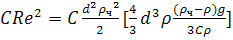
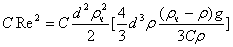или
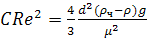
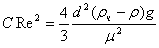. (18)
В табл. 1. приводены
экспериментально определенные в работе [9] величины С·Re2.
Таблица 1.
Экспериментальные и вычисленные по уравнению (7) значения коэффициента С
|
Re
|
экспери-мент
|
уравнение
|
CRe2
|
Re
|
экспери-мент
|
уравнение
|
CRe2
|
|
0,1
|
240
|
247,4
|
2,40
|
1,0
|
26,5
|
27,6
|
26,5
|
|
0,2
|
120
|
126,0
|
4,80
|
2
|
14,6
|
14,9
|
58,4
|
|
0,3
|
80
|
85,3
|
7,20
|
3
|
10,4
|
10,6
|
93,6
|
|
0,5
|
49,5
|
52,5
|
12,375
|
5
|
6,9
|
7,0
|
172,5
|
|
0,7
|
36,5
|
38,3
|
17,885
|
7
|
5,3
|
5,4
|
259,7
|
|
10
|
4,1
|
4,2
|
410
|
0,65
|
0,68
|
58500
|
|
20
|
2,55
|
2,61
|
1020
|
500
|
0,55
|
0,56
|
137500
|
|
30
|
2,00
|
2,04
|
1800
|
700
|
0,50
|
0,50
|
245000
|
|
50
|
1,50
|
1,54
|
3750
|
1000
|
0,46
|
0,44
|
460000
|
|
70
|
1,27
|
1,30
|
6323
|
2000
|
0,42
|
0,35
|
1680000
|
|
100
|
1,07
|
1,09
|
10700
|
3000
|
0,40
|
0,30
|
3600000
|
|
200
|
0,77
|
0,81
|
30800
|
|
|
|
|
Следовательно, для вычисления
скорости оседания частиц необходимо придерживаться следующей
последовательности:
) задать диаметр частицы d,
плотность материала частиц ρч, плотность жидкости ρ, в которой осаждается
частица и ее динамическую вязкость μ по формуле (18) вычисляем величину:
.
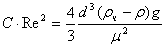
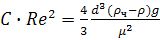2) по таблице 1 находим
величину Re. Эту же величину можно найти из уравнения (7), которое в этом
случае удобно записать в следующем виде
,
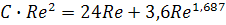
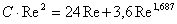из которого при известной величине С·Re2
находим значение Re.
) При известной величине Re
по формуле
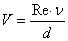
находим скорость оседания частиц.
Численный пример 3. Определить
скорость оседания частиц песка диаметром d=2,5 мм =2,2·10-1
см =2,5·10-3 м; ρч=2,65·103
кг/м3 в воздухе (μ=1,83·10-4
π=1,83·10-5 Па·с) и воде (μ=1,01·10-3 Па·с)
Для воды имеем:
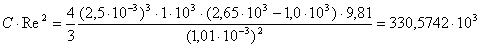
Из табл. 1 находим для
данного значения С·Re2 величину Re=854.
Кинематическая вязкость
для воды равна
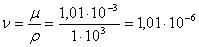
Скорость оседания такой
частицы равна:
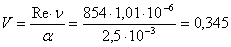, м/с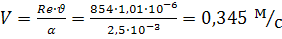
Значительный
практический интерес представляет вопрос о движении совокупности частиц
насыпного материала в воде (например, гранул ВВ в обводненной скважине).
В работе [10]
исследовано движение водяных капель в атмосфере, насыщенной водяными парами или
мельчайшими твердыми частицами, где показано, что при этом происходит рост
частиц и определена их скорость с учетом и без учета сопротивления движению.
Так как движение капель происходило в воздухе, то в работе [11] не учитывалась
сила Архимеда, действующая на частицы ввиду ее малости.
При движении частиц в
воде необходимо учитывать силу Архимеда. В таком случае активная сила,
действующая на частицы равна
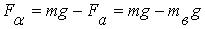
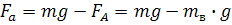, (19)
где mв
- масса, вытесненной частицей воды. Для сферических частиц, плотность материала
которых равна ρч,
из (19) имеем
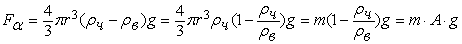
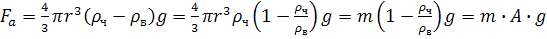, (20)
.
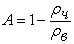
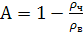Радиус падающей в воде
частицы увеличивается как за счет присоединения мельчайших твердых частиц, так
и за счет присоединения молекул растворенного в воде воздуха. Для простоты, как
в работе [11], будем считать, что масса частицы возрастает пропорционально ее
поверхности, т.е.
,
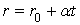
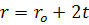где ro
- начальный радиус частицы; α -
некоторый коэффициент, который характеризует быстроту увеличения радиуса
частицы (м/с). Если сила сопротивления пропорциональна площади максимального
поперечного сечения частицы и скорости частицы:
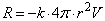
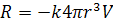, (21)
где k -
коэффициент, который учитывает свойства поверхности частицы (Н·с/м3).
Составим дифференциальное уравнения движения частицы переменной массы
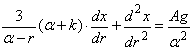
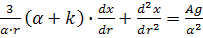. (22)
(получение и решение
подобного уравнения детально описано в работе [11]. Ось Х направлена
вертикально вниз).
Из уравнения (22)
находим скорость частицы как функцию времени падения частицы
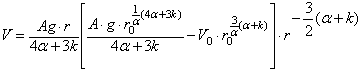
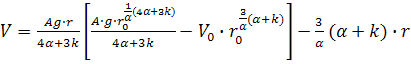, (23)
и высоту положения
частицы
. 
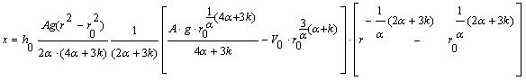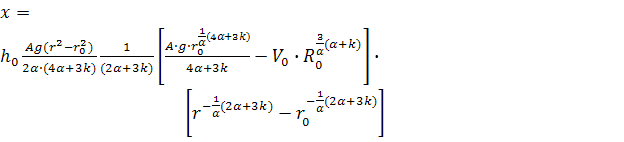(24)
Исследуем уравнение
(23)и (24) в предельном случае. При k=0 из (23) следует равенство
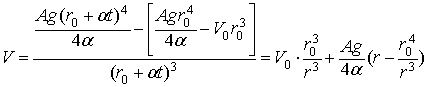
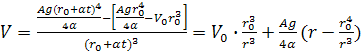(25)
Разложим соответствующие
выражения в формуле (25) в ряды
;
,
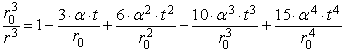
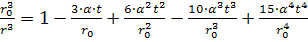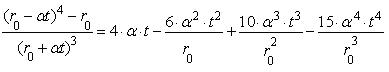
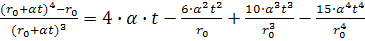Подставим эти разложения
в (25) и ограничиваясь первыми слагаемыми при α=0,
найдем
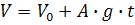. (26)
Для определения высоты
падающей частицы мы нашли, что
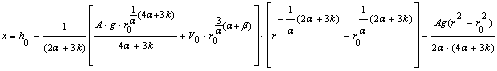
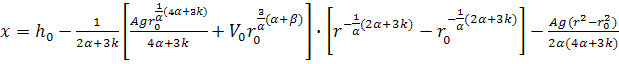(27)
При k=0
(сопротивление падению частицы не учитывается) из (27) находим
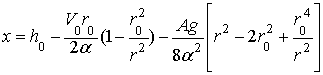
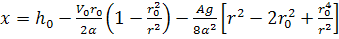. (28)
При α=0
(без учета прилипания частичек) из (28) имеем
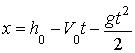
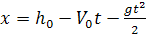, (29)
где h0
- первоначальная высота нахождения частицы, м.
На рис.2. приведены
вычисленные зависимости скорости падения сферической частицы в воде для разных
значений коэффициента α.
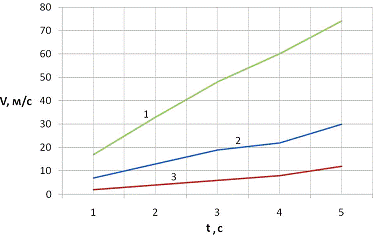
Рис. 2. Зависимость
скорости оседания частиц в воде при А=0,9; V0=0,05
м/с; r0=0,005 м: кривая 1 - α=0;
2 - α=0,02; 3 - α=0,04.
Из рисунка видим, что с
увеличением числа захваченных данной частицей (мельчайших частиц или молекул)
скорость падения уменьшится. Это приводит к тому, что такие частицы захватывают
на своем пути большое количество инородных молекул или частиц.
Частица с захваченными
ею молекулами газа может подниматься в воде вверх. В грубом приближении условие
такого поднимания можно записать в виде
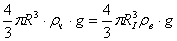
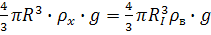, (30)
где RI
- радиус частицы с захваченными молекулами газа, м. Из (30) находим
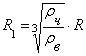
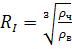. (31)
При известных величинах R
и RI находим объем газовой оболочки
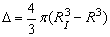
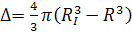. (32)
и при известном радиусе
молекул газа Rм определяем их число
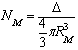
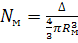. (33)
Например, для частиц
песка (ρч=2,65
г/см3) с 2R=10·10-4 cм число захваченных молекул
кислорода или азота (Rм=0.15·10-7 см) Nм=4,8·107.
Выводы
1. Полученные формулы
позволяют установить процесс оседания различных частиц в воде на разных
стадиях.
. Скорость оседания частиц
зависит от захвата ими других частиц и молекул. С увеличением числа захваченных
частиц скорость оседания уменьшится.
. При захвате частицами
молекул газа они могут подниматься вверх (например гранулы ВВ в обводненной
скважине).
Библиографический список
1. Запольский А.К. Водопостачання, водовідведення та якість
води. К.: «Вища школа» 2005. - 670 с.
2. Гурин А.А., Домничев Н.В., Ляшенко В.И. Природоохранные
технологи пылеподавления на хвостохранилищах горно-металлургического
производства// Экология и промышленность. 2010. №4. С. 24 - 30
. Ньютон И. математические начала натуральной философии.
Перевод с английского в книге: А.Н. Крылов. Собрание трудов. Т. 7. М - Л., 1936
. Ландау Л.Д., Лифшиц Е.М. Механика сплошных сред. М., 1964
. Седов Л.И. Введение в механику сплошных сред. М., 1978
. Pradt L. Tietjens O. Fundamentals of Hydro- and
Aeromechanics. New York. 1975
. Алешко П.И. Механика жидкости и газа. Харьков. 1977
. C.Ozz et al. J.Met, Vol. 15 Р. 40. 1985
. Чигаев Ф.Ф. Гидравлика (техническая механика жидкостей) -
4-е издание. - М. Энергоиздат. 1982 - 672 с.
. Perry R.H., Chilton C.H. Chemical Engineers. Hardbooc. Th
Ed., Megraw - Hill, New York. 1973. Р. 549
. Гурин А.А., Гурин Ю.А., Ратушный В.М., Радченко И.С. О
коагуляции частиц аэрозолей// Сб. научн. Трудов. Качество минерального сырья.
Кривой Рог. - 2008. - с. 441 - 450.