Исследование данных в линейной регрессионной модели
Московский государственный институт
электронной техники (Технический Университет)
Контрольная
работа по теории вероятностей
Анализ данных в линейной
регрессионной модели
Москва 2008
Постановка
задачи
Пусть требуется измерить некоторую величину а. Результаты
измерений х1(ω), х2(ω), ... хn(ω) естественно рассматривать как
значения случайных величин х1(ω), х2(ω), ... , хn(ω), полученные в данном опыте с исходом
w.Если измерительный прибор не даёт
систематической ошибки, то Мхk = а. Таким образом, по результатам наблюдений
х1, х2, ... хn нужно определить неизвестный параметр
а - это типичная задача оценки неизвестных параметров.
Общая ошибка измерения часто складывается из большого числа ошибок, каждая из
которых невелика. В такой ситуации на основании центральной предельной теоремы
становится правдоподобным следующее предположение (гипотеза): СВ хk имеют нормальное распределение. Таким
образом, мы пришли к задаче статистической проверки гипотезы о законе
распределения.
К задачам оценки параметров часто относят задачи, в которых нужно
установить зависимость между переменными. Пусть, например, из некоторых
соображений известно, что переменная у линейно зависит от
переменных х1, х2, ... хn: у = А0
+ А1х1 + ... + Аkхk. Коэффициенты А0, А1,
... ,Аk
неизвестны. При различных наборах (хi1, хi2, ... , хin), i=1,…,n,
измеренных значения уi = А0 + А1хi1 + ... + Аkхik +di , где di - ошибки измерения у
при наборе (хi1, хi2, ... , хin). По значениям (уi , хi1, хi2, … , хin) требуется оценить коэффициенты А0,
А1, ... ,Аk . Задачи такого типа называют регрессионными.
вектор линейный регрессия дисперсия
Статистическое
описание и выборочные характеристики двумерного случайного вектора
Пусть
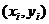 ,
,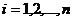 - выборка объема
- выборка объема 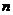 из
наблюдений случайного двумерного вектора (X, Y).
Предварительное представление о двумерной генеральной совокупности можно
получить, изображая элементы выборки точками на плоскости с выбранной
декартовой системой координат. Это представление выборки называется диаграммой
рассеивания.
из
наблюдений случайного двумерного вектора (X, Y).
Предварительное представление о двумерной генеральной совокупности можно
получить, изображая элементы выборки точками на плоскости с выбранной
декартовой системой координат. Это представление выборки называется диаграммой
рассеивания.
Распределением
двумерной выборки называется
распределение двумерного дискретного случайного вектора, принимающего значения 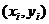 ,
,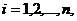 с вероятностями, равными
с вероятностями, равными 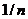 . Выборочные числовые характеристики вычисляются как
соответствующие числовые характеристики двумерного случайного вектора
дискретного типа.
. Выборочные числовые характеристики вычисляются как
соответствующие числовые характеристики двумерного случайного вектора
дискретного типа.
Выборочная
линейная регрессия 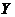 на
на 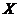 по
выборке
по
выборке 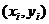 ,
,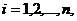 определяется уравнением
определяется уравнением
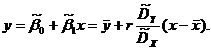

Выборочные средние находятся по формулам:
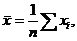
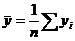 .
.
Вычислим суммы квадратов отклонений от среднего и произведений отклонений
от средних:
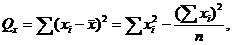
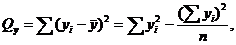
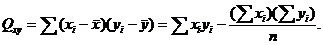
Дисперсия находится по
формулам: 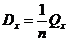 ,
,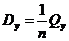 ; коэффициент корреляции считается как
; коэффициент корреляции считается как
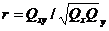 .
.
Линейная
регрессия
В
регрессионном анализе изучается связь между зависимой переменной 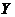 и одной или несколькими независимыми переменными.
Пусть переменная
и одной или несколькими независимыми переменными.
Пусть переменная 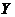 зависит от одной переменной
зависит от одной переменной 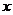 . При этом предполагается, что переменная
. При этом предполагается, что переменная 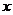 принимает фиксированные значения, а зависимая
переменная
принимает фиксированные значения, а зависимая
переменная 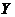 имеет случайный разброс из-за ошибок измерения,
влияния неучтенных факторов и т.д. Каждому значению переменной
имеет случайный разброс из-за ошибок измерения,
влияния неучтенных факторов и т.д. Каждому значению переменной 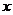 соответствует некоторое вероятностное распределение
случайной величины
соответствует некоторое вероятностное распределение
случайной величины 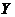 . Предположим, что случайная величина
. Предположим, что случайная величина 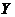 в среднем линейно зависит от значений переменной
в среднем линейно зависит от значений переменной 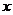 . Это означает, что условное математическое ожидание
случайной величины
. Это означает, что условное математическое ожидание
случайной величины 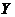 при заданном значении переменной
при заданном значении переменной 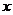 имеет вид
имеет вид
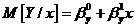
Функция
переменной, определяемая правой частью формулы, называется линейной регрессией 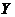 на
на 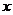 , а
параметры
, а
параметры 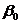 и
и 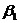 -
параметрами линейной регрессии. На практике параметры линейной регрессии
неизвестны и их оценки определяют по результатам наблюдений переменных
-
параметрами линейной регрессии. На практике параметры линейной регрессии
неизвестны и их оценки определяют по результатам наблюдений переменных 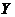 и
и 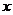 .
.
Пусть
проведено 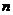 независимых наблюдений случайной величины
независимых наблюдений случайной величины 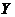 при значениях переменной
при значениях переменной 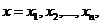 при этом измерения величины
при этом измерения величины 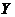 дали следующие результаты:
дали следующие результаты: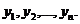
Так
как эти значения имеют "разброс" относительно регрессии, то связь
между переменными 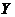 и
и 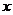 можно
записать в виде линейной регрессионной модели:
можно
записать в виде линейной регрессионной модели:
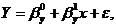
где
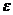 - случайная ошибка наблюдений, причем
- случайная ошибка наблюдений, причем 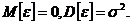 Значение дисперсии ошибок наблюдений
Значение дисперсии ошибок наблюдений 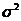 неизвестно, и оценка ее определяется по результатам
наблюдений.
неизвестно, и оценка ее определяется по результатам
наблюдений.
Задача
линейного регрессионного анализа состоит в том, чтобы по результатам наблюдений
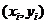 ,
,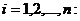
· получить
наилучшие точечные и интервальные оценки неизвестных параметров 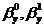 и
и 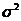 модели;
модели;
· проверить статистические
гипотезы о параметрах модели;
· проверить
достаточно ли хорошо модель согласуется с результатами наблюдений.
Задача
линейного регрессионного анализа решается в предположении, что случайные ошибки
не коррелированны, имеют 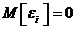 и одну и ту же дисперсию
и одну и ту же дисперсию 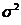 и нормально распределены, т.е.
и нормально распределены, т.е. 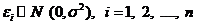 . В этом случае ошибки наблюдений также являются
независимыми СВ.
. В этом случае ошибки наблюдений также являются
независимыми СВ.
Для
нахождения оценок параметров регрессии по результатам наблюдений используется
метод наименьших квадратов. По этому методу в качестве оценок параметров
выбирают такие значения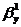 и
и 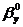 , которые
минимизируют сумму квадратов отклонений наблюдаемых значений случайных величин
, которые
минимизируют сумму квадратов отклонений наблюдаемых значений случайных величин 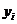 , i=1,2,…,n , от их математических ожиданий, т. е. сумму
, i=1,2,…,n , от их математических ожиданий, т. е. сумму
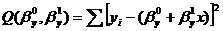 .
.
Из
необходимых условий минимума функции 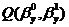 :
:
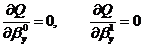
Получим, что МНК-оценки параметров линейной регрессии имеют вид:
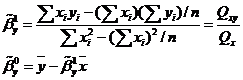
Аналогично определяются линейная регрессия X на Y
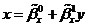 .
.
Коэффициенты
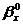 и
и 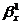 находятся
по формулам:
находятся
по формулам:
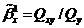 ,
,
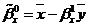 .
.
Для
контроля правильности расчетов используется соотношение: 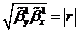 .
.
Прямые
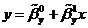 ,
, 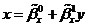 пересекаются
в точке с координатами
пересекаются
в точке с координатами 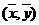 .
.
Оценки
параметров линейной регрессии, получаемые по методу наименьших квадратов, при
любом законе распределения ошибок наблюдений 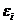 , i=1,2,….n,
имеют следующие свойства:
, i=1,2,….n,
имеют следующие свойства:
. Они
являются линейными функциями результатов наблюдений 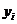 , i=1,2,…,n, и несмещенными оценками параметров, т.е.
, i=1,2,…,n, и несмещенными оценками параметров, т.е. 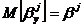 , j=0,1.
, j=0,1.
. Они
имеют минимальные дисперсии в классе не смещенных оценок, являющихся линейными
функциями результатов наблюдений. Если ошибки наблюдений 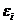 не коррелированны и имеют нормальное распределение,
т.е.
не коррелированны и имеют нормальное распределение,
т.е. 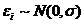 , то в дополнение к свойствам 1, 2 выполняется
свойство:
, то в дополнение к свойствам 1, 2 выполняется
свойство:
. МНК
- оценки совпадают с оценками, вычисляемыми по методу максимального подобия.
Функция
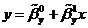 определяет выборочную регрессию Y на X .
Последняя является оценкой предполагаемой линейной регрессией по результатам
наблюдений. Разности между наблюдаемыми значениями переменной Y при
определяет выборочную регрессию Y на X .
Последняя является оценкой предполагаемой линейной регрессией по результатам
наблюдений. Разности между наблюдаемыми значениями переменной Y при
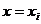 , i=1,2,…,n, и расчетными значениями
, i=1,2,…,n, и расчетными значениями 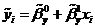 называются остатками и обозначаются
называются остатками и обозначаются 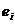 :
: 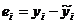 .
.
Качество
аппроксимации результатов наблюдений 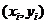 ,
,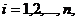 выборочной регрессии определяется величиной остаточной
дисперсии, вычисляемой по формуле:
выборочной регрессии определяется величиной остаточной
дисперсии, вычисляемой по формуле:
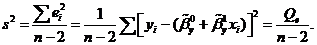
Величина
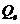 , определяется выражением
, определяется выражением
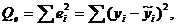
и называется остаточной суммой квадратов.
В практических вычислениях остаточную сумму квадратов получают из
тождества
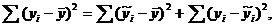
которое записывается в виде
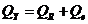 ,
,
где
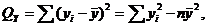
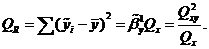
Величина
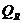 называется суммой квадратов, обусловленной
регрессией.
называется суммой квадратов, обусловленной
регрессией.
Линейная
регрессионная модель называется незначимой, если параметр 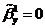 . Если эта гипотеза отклоняется, то говорят, что
регрессионная модель статистически значима
. Если эта гипотеза отклоняется, то говорят, что
регрессионная модель статистически значима
Полезной
характеристикой линейной регрессии является коэффициент детерминации 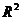 , вычисляемый по формуле
, вычисляемый по формуле
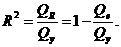
Коэффициент
детерминации 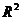 равен той доле разброса результатов наблюдений
равен той доле разброса результатов наблюдений 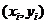 ,
,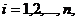 относительно горизонтальной прямой
относительно горизонтальной прямой 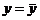 , которая объясняется выборочной регрессией.
, которая объясняется выборочной регрессией.
Величина
R является оценкой коэффициента корреляции между результатами наблюдений 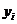 и вычисленными значениями
и вычисленными значениями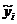 , предсказываемыми регрессией. В случае линейной
регрессии Y на X (одной независимой переменой X) между
коэффициентом R и выборочным коэффициентом корреляции
, предсказываемыми регрессией. В случае линейной
регрессии Y на X (одной независимой переменой X) между
коэффициентом R и выборочным коэффициентом корреляции 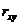 имеется следующее соотношение:
имеется следующее соотношение:
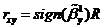 .
.
Доверительным
интервалом для параметра 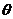 называется интервал
называется интервал 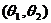 ,
содержащий истинное значение с заданной вероятностью
,
содержащий истинное значение с заданной вероятностью 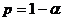 , т.е.
, т.е. 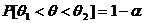 . Число
. Число 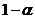 называется доверительной вероятностью, а
значение
называется доверительной вероятностью, а
значение 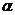 - уровнем значимости. Статистики
- уровнем значимости. Статистики 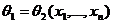 , определяемые по выборке из генеральной совокупности
с неизвестным параметром
, определяемые по выборке из генеральной совокупности
с неизвестным параметром 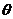 , называются нижней и верхней границами доверительного
интервала.
, называются нижней и верхней границами доверительного
интервала.
Границы
доверительных интервалов для параметров линейной регрессии имеют вид:
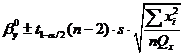 ,
,
где
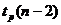 - квантиль распределения Стьюдента с n-2
степенями свободы.
- квантиль распределения Стьюдента с n-2
степенями свободы.
Границы
доверительного интервала для среднего значения 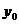 ,
соответствующего заданному значению
,
соответствующего заданному значению 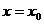 ,
определяются формулой:
,
определяются формулой:
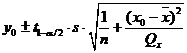 .
.
Доверительный
интервал для дисперсии ошибок при неизвестном 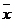 и при
доверительной вероятности
и при
доверительной вероятности 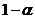 имеет вид
имеет вид 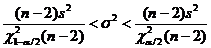 , где
, где 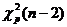 - квантиль распределения
- квантиль распределения 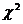 с n-2 степенями свободы.
с n-2 степенями свободы.
Проверка
гипотезы о равенстве средних двух нормальных совокупностей при неизвестных дисперсиях
1.Проверить
гипотезу о равенстве дисперсий Н0:

a) Zв=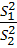
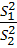 (
(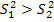
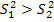 ) ,
) , 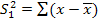
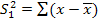 2/(n-1) - несмещённая оценка дисперсии
2/(n-1) - несмещённая оценка дисперсии
б)
если Zв<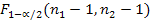
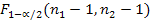 ,
гипотеза Н0 принимается на уровне значимости
,
гипотеза Н0 принимается на уровне значимости 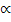
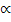
.Проверить
гипотезу о равенстве средних с неизвестными неравными дисперсиями 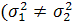
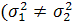 )
)
а)
Zв=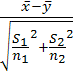
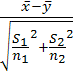
б)
если 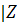
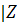 в|<
в|<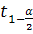
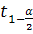 (k),
где k=
(k),
где k=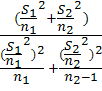
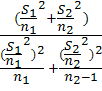 , то
гипотеза m1=m2 принимается.
, то
гипотеза m1=m2 принимается.
.Гипотеза
о равенстве средних с неизвестными равными дисперсиями (
 )
)
а)
Zв=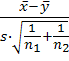
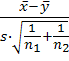 , где s=
, где s=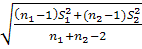
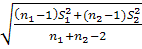
б)если
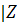
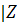 в|<
в|<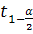
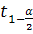 (
(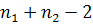
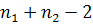 ), то Н0:
m1=m2
принимается.
), то Н0:
m1=m2
принимается.
Практическая
часть
Выборочная
регрессия Y на X по выборке 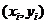 ,
,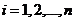 определяется уравнением
определяется уравнением 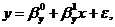
Найдем
средние значения X и Y:
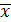
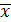 =1/ n
=1/ n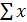
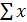 i=250,34/50=5,0068
i=250,34/50=5,0068
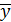
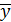 =1/n
=1/n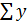
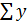 i=597,78/50=11,9556
i=597,78/50=11,9556
2) Найдем суммы квадратов отклонений от среднего и произведений
отклонений от средних значений по формулам:
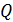
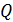 x=
x=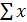
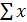 i2-(
i2-(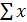
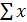 i) 2/
n=1370,51 - (250,34)2/50=117,1079y=
i) 2/
n=1370,51 - (250,34)2/50=117,1079y=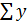
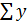 i2-(
i2-(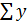
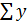 i) 2/
n=7273,65 - (597,78)2/50=126,8358
i) 2/
n=7273,65 - (597,78)2/50=126,8358
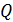
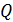 xy=
xy=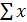
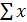 iyi-((
iyi-((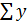
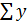 i)
i)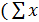
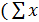 i)) / n =3102,39
- (250,34
i)) / n =3102,39
- (250,34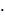
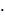 597,78)/50=109,425x=
597,78)/50=109,425x=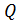
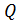 x
x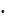
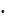 1/n=117,1079/50=2,3422
1/n=117,1079/50=2,3422
Dy=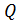
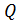 y
y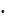
 1/n=126,8358/
1/n=126,8358/ 50=2,5367
50=2,5367
3)
Получим коэффициенты регрессии Y на X (определяется уравнением
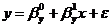 :
:
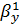
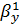 =
=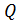
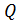 xy/
xy/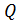
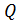 x=0,8628
x=0,8628
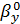
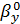 =
=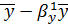
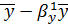 =-5,3076
=-5,3076
у
= -5,3076 + 0,8628*x
4) Получим коэффициенты регрессии X на Y
(определяется уравнением
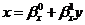 ):
):
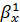
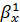 =
=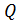
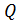 xy/
xy/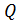
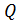 y=0,9344
y=0,9344
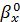
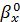 =
=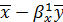
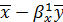 =7,2773
=7,2773
x =
7,2773+0,9344*y
5) Найдём коэффициент корреляции:
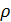
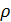 =
=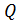
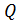 xy/
xy/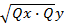
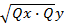 =0,8978
=0,8978
6) Найдём остатки и остаточные суммы квадратов по формулам:
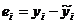
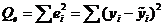 =24,5897
=24,5897
7) Найдём остаточную дисперсию (несмещённая оценка дисперсии ошибок
измерений):
S2=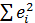
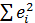 /n-2=
/n-2=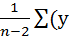
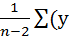 i-
i-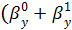
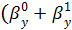 )2=
)2=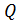
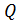 e/n-2=0,5123=0,7157
e/n-2=0,5123=0,7157
8) Сумма квадратов, обусловленной регрессией:
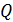
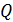 R=
R=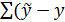
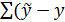 i)2=
i)2=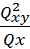
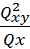 =
=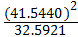 102,2461
102,2461
9) Коэффициент детерминации:
R2=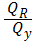
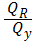 = 1 -
= 1 - 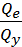
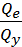 =0,8061
=0,8061
Значит,
полученное уравнение регрессии на 80% объясняет разброс относительно прямой 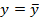
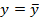 =11,9556
=11,9556
С
помощью коэффициента детерминации R получим коэффициент
корреляции:
rxy=sign(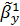
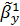 )R=0,8978
)R=0,8978
10) Доверительные интервалы для коэффициентов регрессии (уровень
значимости a=0.1):
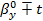
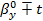 1-α/2(n-2)
1-α/2(n-2)
 s
s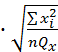
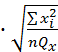 =
= 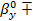
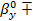 0,1066
0,1066
Доверительный
интервал для 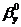 : (6,6962; 7,8583).
: (6,6962; 7,8583).
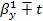
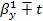 1-α/2(n-2)
1-α/2(n-2)
 s
s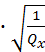
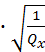 =
= 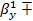
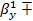 0,5810
0,5810
Доверительный
интервал для 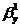 : (0,8234; 1,0410).
: (0,8234; 1,0410).
Из
этого следует, что гипотеза H0: 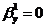 отклоняется на уровне значимости a=0.1, т.к доверительный интервал не накрывает нуль с доверительной
вероятностью 0.9. Таким образом, модель статистически значима.
отклоняется на уровне значимости a=0.1, т.к доверительный интервал не накрывает нуль с доверительной
вероятностью 0.9. Таким образом, модель статистически значима.
)
Доверительный интервал для среднего значения у0,
соответствующего заданному значению х=х0:
y0 ±t1-α/2∙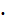 S
S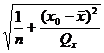
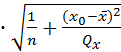 =
=
(7,2773+0,9344x0)±1.6780*0.7157*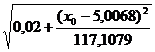
12) Доверительный интервал для дисперсии ошибок:
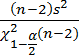
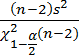 <
<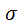
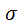 2 <
2 < 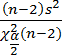
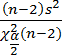
,3803
<σ2 <
0,7407
13) Проверка гипотезы о равенстве средних двух нормальных совокупностей
при неизвестных дисперсиях.
Проверяем гипотезу о равенстве дисперсий H0: σ12=σ22
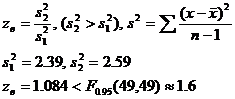
гипотеза H0 принимается на уровне значимости
0,1.
Проверяем гипотезу о равенстве средних с неизвестными равными дисперсиями
H0: σ12 = σ22.
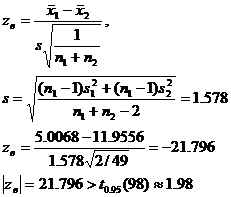
Гипотеза о равенстве средних не подтверждается расчетами.