Теория вероятностей
Задача 1
В первой урне содержится 10 шаров, из них 8
белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли
по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти
вероятность того, что взят белый шар.
Решение:
Введем обозначения событий: 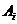 - событие,
состоящее в том, что шар, извлеченный из
- событие,
состоящее в том, что шар, извлеченный из 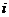 -ой урны оказался белым (
-ой урны оказался белым (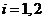 ). Тогда
). Тогда 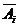 - событие,
состоящее в том, что шар, извлеченный из
- событие,
состоящее в том, что шар, извлеченный из 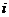 -ой урны оказался не белым. Так как
в 1-ой урне из 10 шаров 8 белые, то
-ой урны оказался не белым. Так как
в 1-ой урне из 10 шаров 8 белые, то 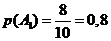 (из 10 исходов появлению события
(из 10 исходов появлению события 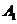 благоприятствуют
8), а
благоприятствуют
8), а 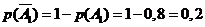 . Аналогично
рассуждая, имеем:
. Аналогично
рассуждая, имеем: 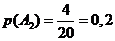 и
и 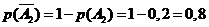 .
.
Обозначим: 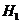 - событие,
состоящее в том, что после извлечения по одному шару из каждой урны, среди них
не оказалось ни одного белого шара,
- событие,
состоящее в том, что после извлечения по одному шару из каждой урны, среди них
не оказалось ни одного белого шара, 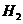 - событие, состоящее в том, что
после извлечения по одному шару из каждой урны, среди них оказался один белый
шара,
- событие, состоящее в том, что
после извлечения по одному шару из каждой урны, среди них оказался один белый
шара, 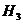 - событие,
состоящее в том, что после извлечения по одному шару из каждой урны, среди них
не оказалось два белых шара.
- событие,
состоящее в том, что после извлечения по одному шару из каждой урны, среди них
не оказалось два белых шара.
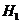 произойдет тогда и только тогда,
когда произойдут события
произойдет тогда и только тогда,
когда произойдут события 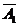 и
и 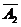 .
Следовательно,
.
Следовательно, 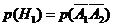 =(так как
события независимы)= =
=(так как
события независимы)= =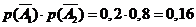 .
.
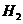 произойдет тогда и только тогда,
когда произойдут события
произойдет тогда и только тогда,
когда произойдут события 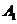 и
и 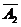 , либо
, либо 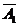 и
и 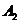 .
Следовательно,
.
Следовательно, 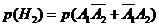 =(так как
события несовместны)=
=(так как
события несовместны)=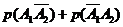 =(так как
события независимы)= =
=(так как
события независимы)= =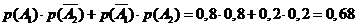 .
.
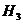 произойдет тогда и только тогда,
когда произойдут события
произойдет тогда и только тогда,
когда произойдут события 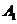 и
и 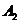 . Следовательно,
. Следовательно,
 =(так как
события независимы)= =
=(так как
события независимы)= =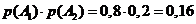 .
.
Обозначим: 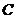 - событие,
состоящее в том, что после извлечения из двух (уже извлеченных по одному из каждой
урны) шаров, вынутый шар оказался белым. Очевидно,
- событие,
состоящее в том, что после извлечения из двух (уже извлеченных по одному из каждой
урны) шаров, вынутый шар оказался белым. Очевидно, 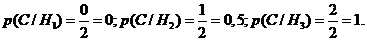
События 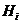 (i=1,2,3)
образуют полную группу попарно несовместных событий, и по формуле полной
вероятности имеем:
(i=1,2,3)
образуют полную группу попарно несовместных событий, и по формуле полной
вероятности имеем:
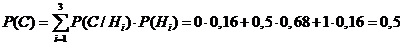 - вероятность извлечь белый шар из
двух извлеченных по одному из каждой урны шаров.
- вероятность извлечь белый шар из
двух извлеченных по одному из каждой урны шаров.
Задача 2
Случайная величина 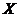 задана
функцией распределения
задана
функцией распределения
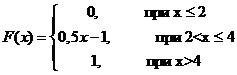
Найти математическое ожидание и
дисперсию случайной величины 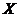 , а также вероятность того, что в
результате испытания
, а также вероятность того, что в
результате испытания 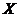 примет
значение: а) меньшее 0,2; б) меньшее 3; в) не меньшее 3; г) не меньшее 5.
примет
значение: а) меньшее 0,2; б) меньшее 3; в) не меньшее 3; г) не меньшее 5.
Решение:
Плотность распределения 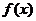 случайной
величины
случайной
величины 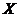 найдем из
условия
найдем из
условия 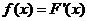 . Тогда:
. Тогда:
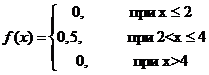
Математическое ожидание найдем по
формуле:
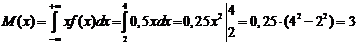 .
.
Дисперсию найдем по формуле:
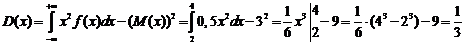 .
.
Далее
a) 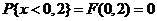 ;
;
б) 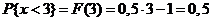 ;
;
в) 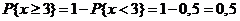 ;
;
г) 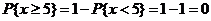 .
.
Задача 3
Построить гистограмму распределения
случайной величины 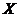 по данному
распределению выборки.
по данному
распределению выборки.
|
Границы интервалов
|
0-0,6
|
0,6-1
|
1-1,4
|
1,4-1,8
|
1,8-2,2
|
2,2-2,6
|
2,6-3
|
3-3,4
|
3,4-3,8
|
|
Частоты
|
9
|
12
|
18
|
16
|
15
|
12
|
8
|
6
|
4
|
Определить математическое ожидание и
дисперсию случайной величины 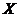 .
.
Решение:
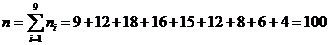 . Обозначим
. Обозначим 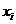 - середины
интервалов (
- середины
интервалов (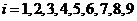 ). Имеем
). Имеем
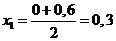 ;
;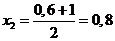 ;
;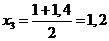 ;
;
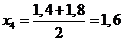 ;
; 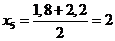 ;
;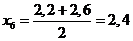 ;
;
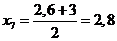 ;
; 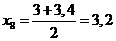 ;
; 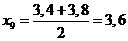 .
.
Математическое ожидание:
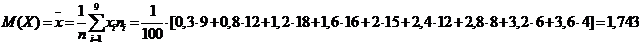
Дисперсия:
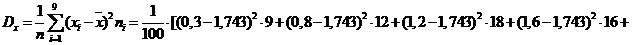
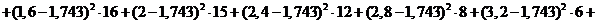
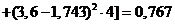 .
.
Среднее квадратическое отклонение: 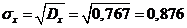 .
.
Найдем относительные частоты: 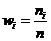 . Имеем:
. Имеем:
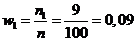 ;
; 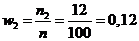 ;
; 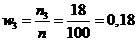 ;
;
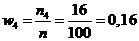 ;
; 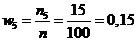 ;
; 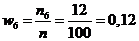 ;
;
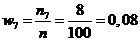 ;
;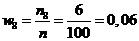 ;
; 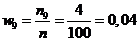 .
.
Для построения гистограммы
относительных частот составим таблицу:
|
Границы
интервалов
|
0-0,6
|
0,6-1
|
1-1,4
|
1,8-2,2
|
2,2-2,6
|
2,6-3
|
3-3,4
|
3,4-3,8
|
|
Частоты
|
9
|
12
|
18
|
16
|
15
|
12
|
8
|
6
|
4
|
|
Относительные
частоты
(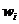 )0,090,120,180,160,150,120,080,060,04 )0,090,120,180,160,150,120,080,060,04
|
|
|
|
|
|
|
|
|
|
|
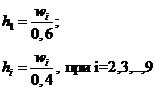 0,150,30,450,40,3750,30,20,150,1 0,150,30,450,40,3750,30,20,150,1
|
|
|
|
|
|
|
|
|
|
математическое
ожидание дисперсия квадратическое отклонение
Гистограмма относительных частот:
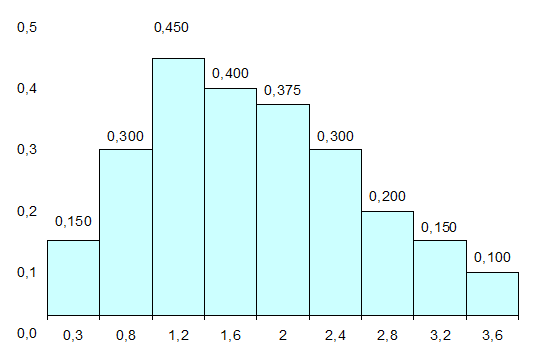
Задача 4
По условию задачи 3 по критерию
согласия хи-квадрат при уровне значимости 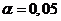 проверить гипотезу о том, что
случайная величина
проверить гипотезу о том, что
случайная величина 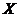 имеет
распределение Релея. Неизвестный параметр распределения Релея оценить по
начальному выборочному моменту второго порядка (Прилож. 4).
имеет
распределение Релея. Неизвестный параметр распределения Релея оценить по
начальному выборочному моменту второго порядка (Прилож. 4).
Решение:
Распределение Релея задается плотностью:

Функция распределения имеет вид:
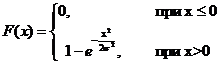
В качестве оценки параметра 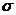 рассмотрим
начальный выборочный момент второго порядка. Известно, что математическое
ожидание распределения Релея с параметром
рассмотрим
начальный выборочный момент второго порядка. Известно, что математическое
ожидание распределения Релея с параметром 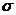 равно
равно 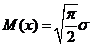 , дисперсия
равна
, дисперсия
равна 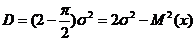 . Тогда
. Тогда
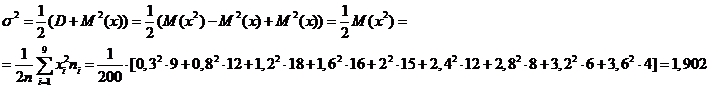 и
и 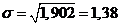 - оценка параметра распределения
Релея на основании начального выборочного момента второго порядка. Рассмотрим
значения
- оценка параметра распределения
Релея на основании начального выборочного момента второго порядка. Рассмотрим
значения 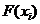 , где
, где 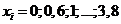 - границы
интервалов, а
- границы
интервалов, а
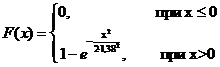 -
-
функция распределения Релея с
параметром 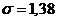 .
.
Составим таблицу:
|
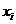 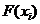  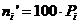 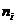 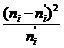
|
|
|
|
|
|
|
 0 0
|
|
|
|
|
|
|
0,6
|
0,0903
|
0,0903
|
9,03
|
9
|
0,0001
|
|
1
|
0,2312
|
0,1409
|
14,09
|
12
|
0,3092
|
|
1,4
|
0,4026
|
0,1715
|
17,15
|
18
|
0,0423
|
|
1,8
|
0,5733
|
0,1707
|
17,07
|
16
|
0,0668
|
|
2,2
|
0,7198
|
0,1465
|
14,65
|
15
|
0,0084
|
|
2,6
|
0,8309
|
0,1110
|
11,10
|
12
|
0,0723
|
0,9061
|
0,0753
|
7,53
|
8
|
0,0297
|
|
3,4
|
0,9521
|
0,0460
|
4,60
|
6
|
0,4279
|
|
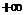 10,04794,7940,1299 10,04794,7940,1299
|
|
|
|
|
|
|
Итого
|
1,09
|
Значение 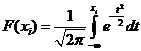 находим по
методичке А.М. Карлова - Приложение 1 (стр.46-48), с учетом того, что F(-x) =1 - F(x).
находим по
методичке А.М. Карлова - Приложение 1 (стр.46-48), с учетом того, что F(-x) =1 - F(x).
При уровне значимости α=0,05 и
к=9-1-1=7 степенях свободы по таблице критических точек распределения χ2 находим
критическое значение: χ2крит(0,05;7)=14,07
(См. Приложение 2 методички А.М.Карлова (стр. 49)).=> χ2набл=1,09 < χ2крит , и
гипотеза о распределении генеральной совокупности по закону распределения Релея
в соответствии с критерием χ2 (Пирсона) при уровне значимости α=0,05
принимается.
Число степеней свободы k находят из
равенства k=s-r-1 , где s - число
групп (частичных интервалов) выборки (в нашем случае s=9);r - число
параметров предполагаемого распределения, которые оценены по данным выборки (в
нашем случае сравниваем с распределением Релея и по выборке оценивали один
параметр - 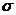 ). То есть k=9-1-1=7.
). То есть k=9-1-1=7.
Таким образом, можно считать, что
генеральная совокупность, выборка из которой приведена в №3, распределена по
закону распределения Релея с параметром 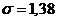 .
.
Литература
1. Вентцель Е.С. Теория
вероятностей., М, Высшая школа, 1998.
2. Гмурман В.Е. Теория
вероятностей и математическая статистика., М, Высшая школа, 1998.
. Гмурман В.Е. Руководство к
решению задач по теории вероятностей и математической статистике., М, Высшая
школа, 1997.
. Карлов А.М. Теория
вероятностей и математическая статистика: Учебное пособие., Калининград, БИЭФ,
1998.