Регуляризация обратной задачи бигармонического уравнения
Содержание:
Аннотация
. Постановка
задачи
. Сведение
дифференциальной задачи к интегральному уравнению для бигармонического
уравнения
3. Расчетные
формулы
4. Корректно
и некорректно поставленные задачи
. Метод
регуляризации Тихонова А.Н. для решения систем линейных алгебраических
уравнений
. Дискретная
регуляризация для бигармонического уравнения
. Оценка
погрешности метода дискретной регуляризации для бигармонического уравнения
Список
литературы
Приложение
Аннотация
В данной работе рассматривается применение метода
дискретной регуляризации для нахождения приближённого решения в обратной задаче
для однородного бигармонического уравнения в круге.
Такое уравнение возникает из задачи о колебаниях
тонкой пластины с закрепленными краями, на которую действует внешняя сила,
распределенная равномерно с плотностью f(x,y).
Для нахождения приближенного решения используется
метод сведения к системе интегральных уравнений Фредгольма I рода (и, следовательно, некорректно
поставленной задаче), к которой, после дискретизации посредством квадратурных
формул, применяется метод регуляризации Тихонова А.Н. [2], [3].
В приложении приведены расчётные формулы; программа и
результаты численного счета на ЭВМ.
1.
Постановка задачи
Уравнение
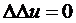 (1`) называется бигармоническим, а его
решения, имеющие производные до 4-го порядка включительно, называются
бигармоническими функциями.
(1`) называется бигармоническим, а его
решения, имеющие производные до 4-го порядка включительно, называются
бигармоническими функциями.
Основная
первая краевая задача для бигармонического уравнения ставится следующим образом
[1]:
Найти
функцию u(х,у), непрерывную вместе с первой производной в
замкнутой области S+C, имеющую производные до 4-го порядка в S,
удовлетворяющую уравнению (1) или (1`) внутри S и
граничным условиям на С:

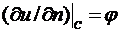 ,
,
где
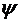 и
и 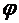 непрерывные
функции.
непрерывные
функции.
Задан
круг SR радиуса R с центром в начале координат и
границей С . В этом круге SR рассматривается
краевая задача для бигармонического уравнения:
. В этом круге SR рассматривается
краевая задача для бигармонического уравнения:
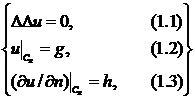 (1)
(1)
где
дифференциальный оператор
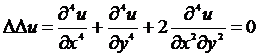
и
int SR -
внутренность круга.
Предполагая,
что значения g и h неизвестны, но известно решение на простой замкнутой
гладкой кривой L, лежащей внутри круга SR,
т.е. известно значение функции u(х,у) и значение производной функции u(х,у)
по внешней нормали на кривой L. Кривая L определена параметрически как x = x(t), y =
y(t), t 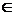 [
[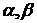 ]. Функции x = x(t), y = y(t) - непрерывно
дифференцируемы на [
]. Функции x = x(t), y = y(t) - непрерывно
дифференцируемы на [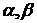 ].
].
 (1*)
(1*)
где
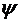 (t) и
(t) и 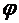 (t)
непрерывные функции.
(t)
непрерывные функции.
Требуется
найти решение в круге SR.
Таким образом, имеем обратную краевую задачу о восстановлении решения по
заданной информации внутри области.
2.
Сведение обратной задачи к системе двух интегральных уравнений
Рассмотрим бигармоническое уравнение
 внутри SR
внутри SR
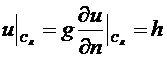
и
замкнутую гладкую кривую
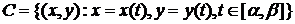
с непрерывно дифференцируемыми x(t), y(t) и известными значениями решения
u(x,y) на L:
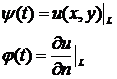
при
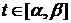 . Здесь функции g, h - предполагаются неизвестными.
. Здесь функции g, h - предполагаются неизвестными.
Так
как начало координат совпадает с центром окружности, то по [1] воспользуемся
известным представлением решения задачи (1) для круга:
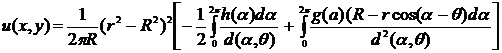 , (2.2)
, (2.2)
где
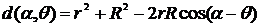 ;
;
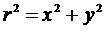 , ( r,
, ( r, 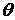 - полярные координаты)
- полярные координаты)
Введём
обозначения:
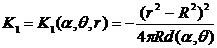

Тогда
формула (2.2) запишется в виде:
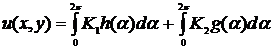
Для
определения функций h и g воспользуемся условиями (1.4), (1.5):
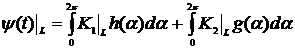 (2.3)
(2.3)
 (2.4)
(2.4)
Введём
вектора 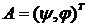 , X = (h,g)T и
матрицу:
, X = (h,g)T и
матрицу:
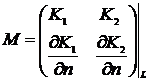
Запишем
систему уравнений (2.3), (2.4) в виде одного векторно-матричного интегрального
уравнения:
 (2.5)
(2.5)
Тем
самым получили интегральное уравнение Фредгольма I рода. Как
известно решение такого уравнения является некорректной задачей.
Найдя
вектор X из (2.5) и подставив в формулу (2.2) получим решение
задачи (2.1) по формуле (2.2), описывающей решение внутри круга SR.
3. Расчетные формулы
Введем используемые обозначения:
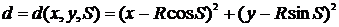

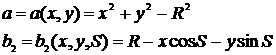
Уравнения
ядер будут выглядеть следующим образом:
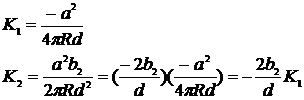
используем:
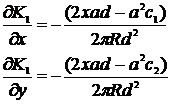

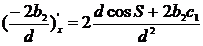

и
косинусы внешней нормали к кривой L:
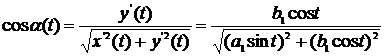
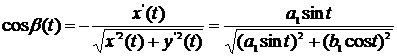
получаем:
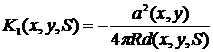
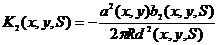

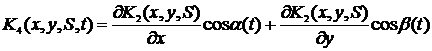
4.
Корректно и некорректно поставленные задачи
Математической
моделью многих практических задач является линейное уравнение Az = u
(4.1), где z - искомый элемент
и u - правая часть принадлежат соответствующим
нормированным пространствам Z, U; А - линейный оператор, действующий из Z в U.
Среди
задач (4.1) выделяется класс задач некорректно поставленных.
Они
характеризуются тем, что сколь угодно малые изменения исходных данных могут
приводить к произвольно большим изменениям решений.
Следуя
Тихонову А.Н., задача (4.1) называется корректно поставленной, или
просто корректной, если выполняются следующие условия:
решение
задачи (4.1) существует для любого элемента u 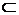 U;
U;
1) решение определено однозначно по u;
решение
задачи устойчиво, т.е. для любой точности  > 0
можно указать такое
> 0
можно указать такое 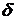 (
( ) > 0, что если
) > 0, что если 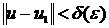 , то ||
, то ||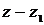 || <
|| <  , где
, где 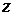 и
и 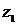 решения (3.1), соответствующие правым частям
решения (3.1), соответствующие правым частям 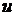 и
и 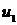 .
.
Если
оператор А обратим и ограничен, т.е. существует оператор 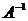 , то
, то
z = A u и R=A
u и R=A . Условие
3) означает непрерывность оператора R. Если задача (4.1) не
удовлетворяет хотя бы одному из условий 1), 2), 3), то она называется
некорректной. в случае ограниченного оператора A
. Условие
3) означает непрерывность оператора R. Если задача (4.1) не
удовлетворяет хотя бы одному из условий 1), 2), 3), то она называется
некорректной. в случае ограниченного оператора A имеем корректность по Адамару.
имеем корректность по Адамару.
Уравнение
Фредгольма I рода является некорректной задачей, так как решение
задачи не устойчиво [2].
Уточним
понятие решения для некорректно поставленных задач. Действительно, если
выполняется условие 1), но не выполняется условие 2), то точных решений много.
Если же не выполняется 1), то решений вообще нет. В таких случаях говорят о
нормальных решениях.
Определение:
элемент z называется нормальным решением уравнения Az=u,
если ||z
называется нормальным решением уравнения Az=u,
если ||z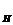 ||=
||=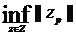 , где Z
-множество всех решений
, где Z
-множество всех решений 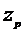 , для уравнения Az
, для уравнения Az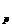 =u.
=u.
5. Метод
регуляризации Тихонова А.Н. для решения систем линейных алгебраических
уравнений
Пусть
в пространстве 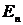 задана система линейных алгебраических уравнений Ах =
b с матрицей А = (
задана система линейных алгебраических уравнений Ах =
b с матрицей А = (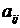 ) и
вектором b = (
) и
вектором b = (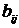 ), i,j = l,...,n.
Эта система может быть однозначно разрешимой, вырожденной и неразрешимой.
Введём в этих случаях понятие псевдорешения [2].
), i,j = l,...,n.
Эта система может быть однозначно разрешимой, вырожденной и неразрешимой.
Введём в этих случаях понятие псевдорешения [2].
Определение:
Псевдорешением системы Ах = b называют вектор х, минимизирующий
невязку || Ах-b || = 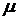 (x) на
всём пространстве
(x) на
всём пространстве 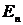 .
.
Очевидно,
если у системы Ах = b есть решение  , то оно
же будет и псевдорешением. В этом случае невязка
, то оно
же будет и псевдорешением. В этом случае невязка 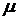 (
( ) = 0. Система может иметь не одно псевдорешение.
Возникает вопрос о выделении среды псевдорешений какого-либо одного,
обладающего определёнными свойствами. Введём понятие нормального решения.
) = 0. Система может иметь не одно псевдорешение.
Возникает вопрос о выделении среды псевдорешений какого-либо одного,
обладающего определёнными свойствами. Введём понятие нормального решения.
Определение:
Вектор  называется нормальным решением системы Ах = b,
если он имеет минимальную норму среди всех псевдорешений,
называется нормальным решением системы Ах = b,
если он имеет минимальную норму среди всех псевдорешений,
т.е.
|| хн || = inf || х || для всех x 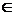 FA
FA
(где
FA - множество псевдорешений).
||
х || = 
Нормальное
решение для любой системы Ах = b существует и единственно [4]. Если система имеет
единственное решение, то оно же будет и нормальным решением.
Задача
нахождения нормального решения некорректна. Поэтому для получения его
целесообразно применять регуляризирующий метод, в основе которого лежит идея
регуляризирующего оператора [2], [3].
Есть
точная система Ах = b и есть приближённая система
Ah х
=b ,
,
где
|| A-Ah || 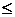 h ,
|| b- b
h ,
|| b- b ||
|| 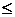
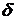 .
.
Требуется
найти вектора ха, где 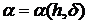 , такие,
что
, такие,
что 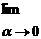 || ха-хн || = 0. Эти вектора ха
называются приближениями к нормальному решению хн уравнения Ах = b. Их
можно находить путём минимизации функции Тихонова А.Н.:
|| ха-хн || = 0. Эти вектора ха
называются приближениями к нормальному решению хн уравнения Ах = b. Их
можно находить путём минимизации функции Тихонова А.Н.:
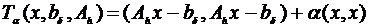
В
[2] показывается, что для любых 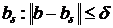 и матриц
Ah: || A-Ah ||
и матриц
Ah: || A-Ah || 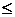 h,
чисел
h,
чисел 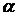 > 0 существует единственный вектор ха,
минимизирующий функцию Тихонова А.Н. Та(х, b
> 0 существует единственный вектор ха,
минимизирующий функцию Тихонова А.Н. Та(х, b , Ah) на всём пространстве
, Ah) на всём пространстве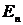 . При
этом вектор ха удовлетворяет уравнению:
. При
этом вектор ха удовлетворяет уравнению:
gradx Та(х,
b , Ah) = 0 или
, Ah) = 0 или
AhTAhxa + 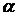 xa=AhTb
xa=AhTb (4.1)
(4.1)
Устанавливается
также в [2], что для всех 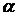 > 0 определён оператор
> 0 определён оператор
R(b , Ah,
, Ah,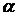 ) = xa, который будет регуляризирующим. Именно существует
зависимость
) = xa, который будет регуляризирующим. Именно существует
зависимость 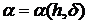 , при которой вектора xa = R(b
, при которой вектора xa = R(b , Ah,
, Ah, ) сходятся к нормальному решению системы Ах = b при
h,
) сходятся к нормальному решению системы Ах = b при
h,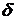 -> 0. Эти ха находятся из системы (4.1)
для заданного уровня погрешностей h,
-> 0. Эти ха находятся из системы (4.1)
для заданного уровня погрешностей h, 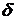 .
.
Определение:
Оператор R(b, A,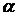 ), зависящий от параметра
), зависящий от параметра 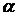 , со значениями в Rn,
называется регуляризирующим оператором для уравнения
, со значениями в Rn,
называется регуляризирующим оператором для уравнения
Ах
= b, если он обладает свойствами [2], [3]:
)существует
такая пара положительных чисел (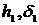 ), что
оператор
), что
оператор
R(b , Ah,
, Ah,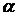 ) определён для всякого
) определён для всякого 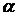 > 0 и
любых
> 0 и
любых  и матриц Ah размера (n
и матриц Ah размера (n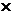 n): || b-b
n): || b-b ||
|| , || Ah-A ||
, || Ah-A ||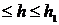 ;
;
)существует
такая функция 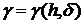 ,
,  , что для
любого
, что для
любого  > 0найдётся пара чисел
> 0найдётся пара чисел 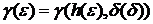 , такая, что если
, такая, что если 
при
|| Ah-A || 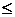 h
h 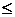 h(
h( ),|| b-b
),|| b-b ||
||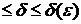 , будет
|| ха-х0||
, будет
|| ха-х0||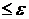 ,
,
где
ха = R(b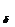 , Ah,
, Ah, ) , х0 - точное решение системы Ах = b.
) , х0 - точное решение системы Ах = b.
В этом определении не предполагается однозначность
оператора
R(b, A,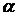 ), отметим, что функция
), отметим, что функция  зависит
от b
зависит
от b и Ah .
и Ah .
Итак,
в качестве приближённых решений уравнения Ahx =
b можно брать значения регуляризирующего оператора: ха
= R(b
можно брать значения регуляризирующего оператора: ха
= R(b , Ah,
, Ah, ), где пара-
), где пара-
метр
регуляризации  согласован с погрешностью исходных данных Ah, b
согласован с погрешностью исходных данных Ah, b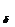 . Полученные таким образом регуляризованные решения
устойчивы к малым изменениям исходных данных.
. Полученные таким образом регуляризованные решения
устойчивы к малым изменениям исходных данных.
Выбор
параметра регуляризации по обобщенной невязке.
) Введём
функцию 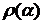 , называемую обобщённой невязкой:
, называемую обобщённой невязкой:
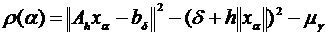
где
 - мера несовместимости системы
- мера несовместимости системы 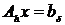 ,
, 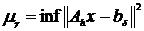 для всех
х
для всех
х 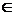
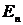 .
Очевидно, что если система Ahx = b
.
Очевидно, что если система Ahx = b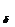 имеет решение, то
имеет решение, то  = 0.
= 0.
Обобщенный
принцип невязки для выбора параметра регуляризации 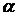 :
:
а)
пусть выполнено условие 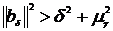 и для любого
и для любого 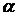 > 0
векторха определяется из системы (4.1). Тогда обобщённая невязка
> 0
векторха определяется из системы (4.1). Тогда обобщённая невязка 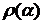 определена при всех
определена при всех 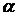 > 0 и
имеет положительный корень
> 0 и
имеет положительный корень 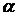 * > 0
или
* > 0
или 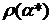 = 0. В этом случае приближённое решение уравнения Ах
= b полагается ха*;
= 0. В этом случае приближённое решение уравнения Ах
= b полагается ха*;
б)
если же 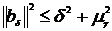 , то полагаем приближённое решение системы Ах = b
равным нулю.
, то полагаем приближённое решение системы Ах = b
равным нулю.
Показывается
в [2] и [3], что для || Ah-A || 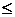 h, ||
b
h, ||
b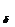 -b ||
-b || 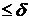 и
и 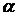 , выбранному согласно принципу обобщённой невязки,
будет
, выбранному согласно принципу обобщённой невязки,
будет 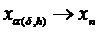 при
при 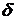 ,h
,h 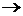 0.
0.
) Устанавливается,
что обобщённая невязка 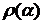 - строго возрастающая функция. Поэтому для нахождения
корня
- строго возрастающая функция. Поэтому для нахождения
корня 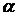 *:
*: 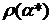 = 0
можно сделать следующее. Берётся конечный отрезок монотонной последовательности
чисел
= 0
можно сделать следующее. Берётся конечный отрезок монотонной последовательности
чисел 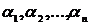 , например, отрезок геометрической прогрессии
, например, отрезок геометрической прогрессии
ak = aoqk, k= l,...,n; 0<q< 1
.
Для каждого значения ak находится вектор xak из решения уравнения (4.1) и
вычисляется
p(ak) = || Ahxak-b ||2 - (
||2 - (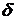 + h||xak||)2 -
+ h||xak||)2 -  .
.
За
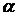 * берётся такое
* берётся такое 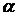 k*, для которого с
требуемой точностью
k*, для которого с
требуемой точностью  выполняется неравенство |
выполняется неравенство |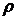 (
(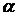 k*)| <
k*)| <  . Тогда за приближённое решение системы Ах= b
берём ха*к. Корень
. Тогда за приближённое решение системы Ах= b
берём ха*к. Корень 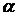 *, для
которого
*, для
которого 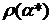 = 0, можно находить, используя метод половинного
деления.
= 0, можно находить, используя метод половинного
деления.
Если
система 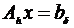 имеет решение, то
имеет решение, то  = 0 и
обобщённая невязка имеет вид:
= 0 и
обобщённая невязка имеет вид: 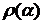 = || Ahxa-b
= || Ahxa-b ||2 - (
||2 - (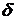 + h||x
+ h||x ||)2.
||)2.
Замечание:
В [3] устанавливается, что в принципе
невязки можно не учитывать  (т.е.
положим
(т.е.
положим  = 0), поэтому можно записать:
= 0), поэтому можно записать:
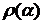 = || Ahxa-b
= || Ahxa-b ||2 - (
||2 - ( + h||x
+ h||x ||)2
||)2
Для
нашей задачи в системе уравнений Ах = b мы будем возмущать лишь правую
часть (п.5), поэтому невязка запишется следующим образом:
 (5.1)
(5.1)
6.
Дискретная регуляризация для бигармонического уравнения
Ранее было установлено равенство:
где
g и h находятся из системы интегральных уравнений (2.2),
(2.3).
К
интегралу Пуассона (2.1) и к системе интегральных уравнений (2.2), (2.3)
применим какую либо квадратурную формулу. В результате получим:
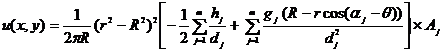 (6.1)
(6.1)
k=  и A
и A -
квадратурные коэффициенты.
-
квадратурные коэффициенты.
Так
для формулы прямоугольников:
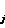 =
=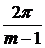 , j =
, j =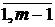 , A
, A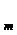 =0
=0
и
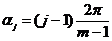 , j =
, j = .
.
Для формулы трапеций:
 , A
, A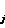 =
=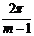 , j =
, j =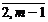
и
 , j =
, j = .
.
Полагая
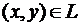 и осуществляя дискретизацию по t, получаем
и осуществляя дискретизацию по t, получаем
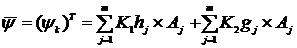
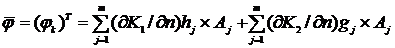
систему
линейных алгебраических уравнений.
Запишем
систему уравнений в векторном виде.
Введём
обозначения блочной матрицы А и векторов х, b:
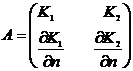 ,
, 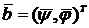 ,
, 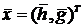 , где
, где
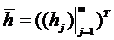 ,
, 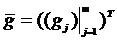
Ax = b -
система линейных алгебраических уравнений порядка (2m) относительно 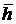 и
и 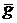 .
.
Далее
осуществляем возмущение правой части: b = b+
= b+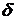 , где
, где 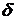 = (
= (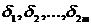 )т,
)т,  > 0 и
применим метод регуляризации Тихонова А.Н. к возмущённой системе, описанный в
пункте 4.
> 0 и
применим метод регуляризации Тихонова А.Н. к возмущённой системе, описанный в
пункте 4.
Для
останова используем обобщённую невязку 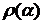 .
.
Далее
найдя регуляризованное решение ха, где 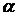 =
= 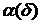 -
параметр регуляризации, который находится изложенным выше способом, подставляем
в квадратурную формулу:
-
параметр регуляризации, который находится изложенным выше способом, подставляем
в квадратурную формулу:
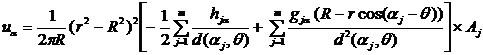
Здесь
ua = ua(x,y) для любой точки, принадлежащей внутренности круга S .
.
Тем
самым получили приближение ua к точному решению u(х,у).
. Оценка
погрешности метода дискретной регуляризации для бигармонического уравнения
Дадим оценку погрешности метода дискретной
регуляризации для бигармонического уравнения:
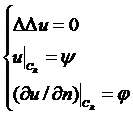
Имеем
точные интегральные уравнения:
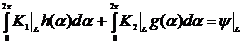
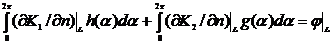
А также приближённые:
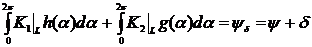
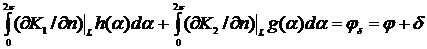
Применим
к системе приближённых уравнений метод дискретной регуляризации (ограничимся
квадратурной формулой прямоугольников):
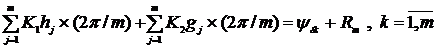
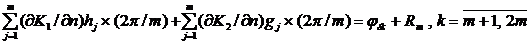
Заменяем:
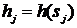 ;
; 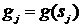
Отбрасываем
остаток, так как это маленькая величина, и получим:


Тогда
получаем:
h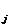
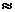 h(s
h(s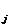 ); g
); g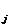
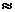 g(s
g(s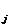 )
)
Нам
известна оценка остатка для квадратурной формулы прямоугольников |R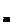 | = o(h)
| = o(h) 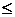 Bh
Bh
Будем
считать:
Ax = b - точной
системой,
- точной
системой,
Ax = b + R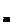 -
приближенной системой.
-
приближенной системой.
Погрешность
правой части можно оценить:
||
b - (b + R
- (b + R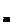 )||
)|| 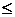 ||
||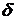 || + ||R
|| + ||R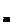 ||
||
Или
||x - x
- x ||
||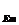
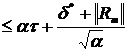
где
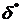 =
=  , ||R
, ||R || =
|| = 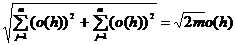
Шаг
интегрирования в формуле прямоугольников h=2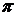 /m, то есть
/m, то есть
m=2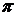 /h
/h
Тогда
формулу для оценки погрешности можно записать следующим образом:
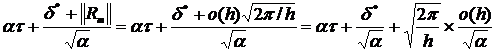
дискретный регуляризация интегральный бигармонический
Список
литературы
1. Тихонов А.Н., Самарский А.А. «Уравнения математической физики».
-Главная редакция физико-математической литературы издательства «Наука», - М.,
1966.
2. Тихонов А.Н., Арсенин В.Я. «Методы решения некорректных задач». -
Главная редакция физико-математической литературы издательства «Наука», - М.,
1974.
. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г.
«Численные методы решения некорректных задач». - М., Наука, 1990.
. Воеводин В.В., Кузнецов Ю.А. «Матрицы и вычисления». - М.:
Наука, 1984г.
. Вержбицкий В.М. «Численные методы. Математический анализ и
обыкновенные дифференциальные уравнения». - М.: Высшая школа, 2001г.
. Верлань А.Ф., Сизиков В.С. «Интегральные уравнения: методы,
алгоритмы, программы», - Киев, 1986
Приложение
Описание переменных в программе:- число точек деления.
K1, K2,
К3, К4 - функция ядер.- правая часть.- точное решение,- регуляризованное
решение.- невязка.
Текст программы:;clc;disp("INVERSE
PROBLEM for BIGARMONIC
EQUATION:");("d^4U/dx^4+2d^4U/(dxdy)^2+d^4U/dy^4=0 for(x,y)in
CR");("U(x,y)=FI(t),dU/dn=PCI(t) on L in CR CALCULATE
U(x,y)");("SYSTEM 1D-FR1:intg{s0,s1;K(t,s)z(s)ds}=FP(t),t0<=t<=t1");("K(t,s)=[K1(t,s)
K2(t,s); K3(t,s)
K4(t,s)]");("FP(t)=[FI(t);PSI(t)]");=input("ENTER N-NUMBER
of KNOTS for FR1");=input("Enter delta-error for FI(t),PCI(t) on
L");=input("Enter eps(<0.0001)for
nev<=eps");("R-radius for CR");=input('Enter R(test
R=4)');("(xp,yp)-center L as xp^2+yp^2<R^2");=input ('Enter
xp');=input ('Enter yp');=(R-sqrt (xp^2+yp^2))^2("Enter a1,b1-parameter
for L as a1^2+b1^2<RL2");=input('Enter a1-(test a1=3 for
xp,yp=0)');=input('Enter b1-(test b1=2 for xp,yp=0)');=0; s1=2*%pi; t0=0; t1=2*%pi;
N1=N-1;
//--------------------------------------------------------------
//disp("PRAM");hs=(s1-s0)/N;ht=(t1-t0)/N;for
j=1:N;A(j)=hs;end;P=input('ENTER
P={0;0.5;1}');("TRAP");P=1;hs=(s1-s0)/N1;ht=(t1-t0)/N1;A(1)=hs/2;A(N)=hs/2;for
j=2:N1;A(j)=hs;end
//---------------Кривая L в CR ---------------------------------z=xL(t), z=a1*cos(t)+xp,
endfunctionz=yL(t), z=b1*sin(t)+yp, endfunction
//Производные параметров кривой L по x,y
//Косинус(alfa) внешней нормали к кривой L
function
z=cosal(t),z=dyL(t)/sqrt((dxL(t))^2+(dyL(t))^2),
endfunction
//Косинус(beta) внешней нормали к кривой L
function
z=cosbe(t),z=-dxL(t)/sqrt((dxL(t))^2+(dyL(t))^2),
endfunction
//Функции для расчётных формул(из теории)
function z=a(x,y),
z=x^2+y^2-R^2,endfunctionz=d(x,y,s),=(x-R*cos(s))^2+(y-R*sin(s))^2,z=c1(x,s),
z=x-R*cos(s), endfunctionz=c2(y,s), z=y-R*sin(s),endfunctionz=b2(x,y,s),
z=R-x*cos(s)-y*sin(s),
endfunctionz=K1(x,y,s),=-a(x,y)^2/(4*%pi*R*d(x,y,s)),z=K2(x,y,s),=a(x,y)^2*b2(x,y,s)/(2*%pi*R*d(x,y,s)^2),
endfunction
//Производная K1(x,y,s) по х
function
z=DK1X(x,y,s),=-(2*x*d(x,y,s)*a(x,y)-c1(x,s)*a(x,y)^2)/(2*%pi*d(x,y,s)^2*R),
endfunction
//Производная K1(x,y,s) по у
function
z=DK1Y(x,y,s),=-(2*y*d(x,y,s)*a(x,y)-c2(y,s)*a(x,y)^2)/(2*%pi*d(x,y,s)^2*R),
endfunction
//Производная K1(x,y,s) по внешней нормали L
function
z=K3(x,y,s,t),=DK1X(x,y,s)*cosal(t)+DK1Y(x,y,s)*cosbe(t), endfunction
//Производная K2(x,y,s) по х
function z=DK2X(x,y,s),=2*(d(x,y,s)*cos(s)+2*b2(x,y,s)*c1(x,s))*K1(x,y,s)/d(x,y,s)^2-
2*(b2(x,y,s)*DK1X(x,y,s))/d(x,y,s),
endfunction
//Производная K2(x,y,s) по у
function
z=DK2Y(x,y,s),=2*(d(x,y,s)*sin(s)+2*b2(x,y,s)*c2(y,s))*K1(x,y,s)/d(x,y,s)^2-
2*(b2(x,y,s)*DK1Y(x,y,s))/d(x,y,s),
endfunction
//Производная K2(x,y,s) по внешней нормали L
function
z=K4(x,y,s,t),=DK2X(x,y,s)*cosal(t)+DK2Y(x,y,s)*cosbe(t),
//Точное
решение Бигармонического уравненияz=UT(x,y), z=(x^2+y^2)/2,
endfunction
//FI(t)-значение решения UT(x,y) на L
function z=FI(t), z=UT(xL(t),yL(t)),
endfunction
//Производная UT(x,y) по х
function z=UTx(x,y), z=x, endfunction
//Производная UT(x,y) по у
function z=UTy(x,y), z=y, endfunction
//PSI(t)-производная UT(x,y)по внешней нормали к L
function z=PSI(t),=UTx(xL(t),yL(t))*cosal(t)+UTy(xL(t),yL(t))*cosbe(t),
endfunction
//Построение С.Л.А.У.(дискретизация системы FR)
for
i=1:N(i)=t0+(i-P)*ht;j=1:N(j)=s0+(j-P)*hs;(i,j)=K1(xL(t(i)),yL(t(i)),s(j))*A(j);(i,j)=K2(xL(t(i)),yL(t(i)),s(j))*A(j);(i,j)=K3(xL(t(i)),yL(t(i)),s(j),t(i))*A(j);(i,j)=K4(xL(t(i)),yL(t(i)),s(j),t(i))*A(j);(i)=FI(t(i))+delta*(2*rand(t(i))-1);(i)=PSI(t(i))+delta*(2*rand(t(i))-1);;
end;=[F1;F2]; M=[M1 M2;M3 M4];
//Регуляризация Тихонова А.Н. С.Л.А.У.
K=10;
q=0.1;=(M'*M+q^7*eye(2*N,2*N))\M'*F;=norm(M*zp-F)^2;n=1:K;=q^n;=(M'*M+alfa*eye(2*N,2*N))\M'*F;=abs(norm(M*z-F)^2-delta^2-mu);nev<=eps
then break; end;("Exit alfa,nev when nev<=eps");=alfa=nev=6;
x0=-2; x1=2; y0=-2;
y1=2;i=1:Sj=1:S(i)=x0+(i-1)*(x1-x0)/(S-1);(j)=y0+(j-1)*(y1-y0)/(S-1);(i,j)=UT(xk(i),yk(j));=0;
us2=0;k=1:N=us1+A(k)*z(k)/d(xk(i),yk(j),s(k));=us2+A(k)*z(k+N)*b2(xk(i),yk(j),s(k))/d(xk(i),yk(j),s(k))^2;
end;
//Приближённое решение UR(x,y) уравнения
UR(i,j)=a(xk(i),yk(j))^2/(2*%pi*R)*((-0.5)*us1+us2);;
end; S=S=input('Enter 1<=S1<=S for rezults'); m=1;i=1:S1j=1:S1(m,1)=xk(i);
RES(m,2)=yk(j);(m,3)=Ut(i,j); RES(m,4)=UR(i,j);(m,5)=UR(i,j)-Ut(i,j);=m+1; end;
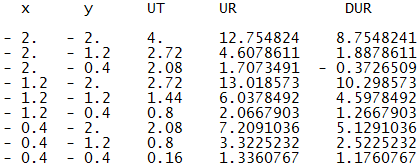
end; DUR=UR-Ut;("EXIT REZULTS");(" x y UT UR DUR
");('v',10); disp(RES); H=100;
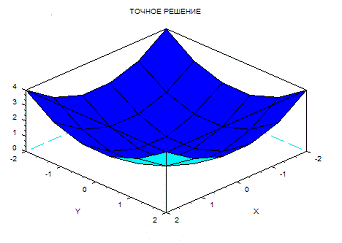
//Графики(поверхности)j=1:H(j)=t0+(j-1)*(t1-t0)/H;(j)=xL(tL(j));(j)=yL(tL(j));(j)=R*cos(tL(j));(j)=R*sin(tL(j));;(2,2,1)d(xk,yk,Ut)("ТОЧНОЕ РЕШЕНИЕ")(2,2,2)d(xk,yk,UR)("ПРИБЛИЖЁННОЕ РЕШЕНИЕ")(2,2,3)d(xk,yk,DUR)("ПОГРЕШНОСТЬ")(2,2,4)(XL,YL)(CRx,CRy) ("КРИВАЯ L в КРУГЕ CR")
Тестовый пример
В качестве замкнутой гладкой кривой L выберем
x = a*cos(t)= b*sin(t)
Рассмотрим однородную задачу:
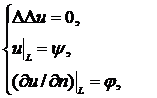
Для
иллюстрации результата выберем произвольные 9 точек.
u(х,у) =(x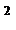 +y
+y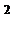 )/2.
)/2.
Возьмем
кривую с параметрами a=3, b=4; R=5; количество точек разбиения n=30: