Теоретическое исследование моделей программы, решающей заданную задачу

Теоретическое исследование моделей программы, решающей заданную задачу

Федеральное агентство связи

Сибирский государственный университет телекоммуникаций и информатики

Пояснительная записка к курсовой работе по дисциплине: “Теория вычислительных процессов”

на тему: “Теоретическое исследование моделей программы, решающей заданную задачу”

Задание к курсовой работе

Написать программу решения задачи, номер которой совпадает с номером в журнале (вариант №5).

Составить и исследовать ССП в линейной и графовой формах.

Указать интерпретацию ССП и составить протокол выполнения программы.

Построить и исследовать инварианты и ограничения цикла(ов).

Доказать частичную и полную правильность программы.

Представить схему программы в виде сети Петри и осуществить анализ ее свойств на основе дерева достижимости.

Задача к курсовой работе

Вариант 5

Задано множество прямых на плоскости (коэффициентами своих уравнений). Подсчитать количество точек пересечения этих прямых.

Стандартные схемы программ

Базис класса стандартных схем программ.

Стандартные схемы программ (ССП) характеризуются базисом и структурой схемы.

Базис класса фиксирует символы, из которых строятся схемы, указывает их роль (переменные, функциональные символы и др.), задает вид выражений и операторов схем.

Полный базис В класса стандартных схем состоит из 4-х непересекающихся, счетных множеств символов и множества операторов - слов, построенных из этих символов.

Множества символов полного базиса:

Х = {x, х1, х2..., у, у1 у2..., z, z1, z2...} - множество символов, называемых переменными;= {f(0), f(1), f(2)..., g(0), g(1), g(2)..., h(0), h(1), h(2)...}- множество функциональных символов; верхний символ задает местность символа; нульместные символы называют константами и обозначают начальными буквами латинского алфавита a, b, c...;

Р = {р(0), р(1), р(2)...; q(0), q(1), q(2)...; } - множество предикатных символов; р(0), q(0) - ; нульместные символы называют логическими константами;

{start, stop, ...,:= ит. д.}- множество специальных символов.

Термами (функциональными выражениями) называются слова, построенные из переменных, функциональных и специальных символов по следующим правилам:

односимвольные слова, состоящие из переменных или констант, являются термами;

слово τ вида f(n)(τ1, τ2...τn), где τ1, τ2...τn - термы, является термом;

те и только те слова, о которых говорится в п.п. 1,2, являются термами.

Примеры термов: х, f(0), а, f(1)(х), g(2)(x, h(3)(y, a)).

Тестами (логическими выражениями) называются логические константы и слова вида р(n)(τ1, τ2,...,τn). Примеры: p(0), p(0)(х), g(3)(x, y, z), p(2) (f(2(x, y)). Допускается в функциональных и логических выражениях опускать индексы местности, если это не приводит к двусмысленности или противоречию.

Множество операторов включает пять типов:

начальный оператор - слово вида start(х1, х2...хк), где k ≥0, а х1, х2...хк - переменные, называемые результатом этого оператора;

заключительный оператор - слово вида stop(τ1, τ2...τn), где n ≥0, а τ1, τ2...τn - термы; вхождения переменных в термы τ называются аргументами этого оператора;

оператор присваивания - слово вида х := τ, где х - переменная (результат оператора), а τ - терм; вхождения переменных в термы называются аргументами этого оператора;

условный оператор (тест) - логическое выражение; вхождения переменных в логическое выражение называются аргументами этого оператора;

оператор петли - односимвольное слово loop.

Среди операторов присваивания выделим случаи: когда τ - переменная, то оператор называется пересылкой (х:=у) и когда τ - константа, то оператор называется засылкой (х:=а).

Подклассы используют ограниченные базисы. Так, например, подкласс У1 имеет базис:

{х1, х2}, {а, f(1)}, {p(1)},{start,stop, (,),:=, ,}и множество операторов {start(х1, х2); х1:=f(x1), x2=f(x2), x1:=а, х2:=а, р(х1), р(х2), stop(х1,х2)}, т. е. схемы из этого подкласса используют две переменные, константу а, один одноместный функциональный символ, один предикатный символ и операторы указанного вида.[1]

Графовая форма стандартной схемы

Представим стандартную схему программ как размеченный граф, вершинам которого приписаны операторы из некоторого базиса В.

Стандартной схемой в базисе В называется конечный (размеченный ориентированный) граф без свободных дуг и с вершинами следующих пяти видов:

Начальная вершина (ровно одна) помечена начальным о1ператором. Из нее выходит ровно одна дуга. Нет дуг, ведущих к начальной вершине.

Заключительная вершина (может быть несколько). Помечена заключительным оператором. Из нее не выходит ни одной дуги.

Вершина-преобразователь. Помечена оператором присваивания. Из нее выходит ровно одна дуга.

Вершина-распознаватель. Помечена условным оператором (называемым условием данной вершины). Из нее выходит ровно две дуги, помеченные 1 (левая) и 0 (правая).

Вершина-петля. Помечена оператором петли. Из нее не выходит ни одной дуги.

Конечное множество переменных схемы S составляют ее память ХS.

Из определения следует, что один и тот же оператор может помечать несколько вершин схемы.

Вершины именуются (метки вершины) целым неотрицательным числом (0, 1, 2...). Начальная вершина всегда помечается меткой 0.

Схема S называется правильной, если на каждой дуге заданы все переменные.

Вершины изображены прямоугольниками, а вершина-распознаватель - овалом. Операторы записаны внутри вершины. [1]

Линейная форма стандартной схемы

Для использования линейной формы СПП множество специальных символов расширим дополнительными символами {:,goto, if, then, else}. СПП в линейной форме представляет собой последовательность инструкций, которая строится следующим образом:

если выходная дуга начальной вершины с оператором start(х1,..., хn) ведет к вершине с меткой L, то начальной вершине соответствует инструкция:

0: start(х1,..., хn) goto L;

если вершина схемы S с меткой L - преобразователь с оператором присваивания х:=τ, выходная дуга которого ведет к вершине с меткой L1, то этому преобразователю соответствует инструкция:

L: x: =τgotoL1;

если вершина с меткой L - заключительная вершина с оператором stop(τ1,...τm), то ей соответствует инструкция

L:stop(τ1,..., τm);

если вершина с меткой L - распознаватель с условием р(τ1,...τk), причем 1-дуга ведет к вершине с меткой L1, а 0-дуга - к вершине с меткой L0, то этому распознавателю соответствует инструкция

L: if р(τ1,...τk) then L1 else L0;

если вершина с меткой L - петля, то ей соответствует инструкция : loop. [1]

Интерпретация стандартных схем программ

ССП не является записью алгоритма, поэтому позволяет исследовать только структурные свойства программ, но не семантику вычислений. При построении «семантической» теории схем программ вводится понятие интерпретация ССП. Определим это понятие.

Пусть в некотором базисе В определен класс ССП. Интерпретацией базиса В в области интерпретации D называется функция I, которая сопоставляет:

каждой переменной х из базиса В - некоторый элемент d = I(x) из области интерпретации D;

каждой константе а из базиса В - некоторый элемент d = I(а) из области интерпретации D;

каждому функциональному символу f(n) - всюду определенную функцию F(n)=I(f(n));

каждой логической константе р(0) - один символ множества { 0,1 };

каждому предикатному символу р(n) - всюду определенный предикат P(n) = I(p(n)).

Определим понятие выполнения программы.

Состоянием памяти программы (S,I) называют функцию W: XS® D, которая каждой переменной x из памяти схемы S сопоставляет элемент W(x) из области интерпретации D.

Значение терма τ при интерпретации I и состоянии памяти W (обозначим τI(W)) определяется следующим образом:

) если τ=х, x - переменная, то τI(W) = W(x);

2) если τ=a, a - константа, то τI(W) = I(a);

3) если τ=f(n)(τ1, τ2..., τn), то τI(W)= I(f(n))(τ1I(W), τ2I(W),..., τnI(W)).

Аналогично определяется значение теста p при интерпретации I и состоянии памяти W или pI(W): если p=р(n)(τ1, τ2..., τn), то pI(W)= I(p(n))(τ1I(W), τ2I(W),... τnI(W)), n ≥0.

Конфигурацией программы называют пару U=(L,W), где L - метка вершины схемы S, а W - состояние ее памяти. Выполнение программы описывается конечной или бесконечной последовательностей конфигураций, которую называют протоколом выполнения программы (ПВП).

Протокол (U0, U1,..., Ui, Ui+1,...) выполнения программы (S,I) определяем следующим образом (ниже ki означает метку вершины, а Wi - состояние памяти в i-й конфигурации протокола, Ui=(ki,Wi)):=(0, W0), W0 - начальное состояние памяти схемы S при интерпретации I.

Пусть Ui=(ki, Wi) - i-я конфигурация ПВП, а О - оператор схемы S в вершине с меткой ki. Если О - заключительный оператор stop(τ1, τ2... τn), то Ui - последняя конфигурация, так что протокол конечен. В этом случае считают, что, программа (S,I) останавливается, а последовательность значений τ1I(W), τ2I(W),..., τnI(W) объявляют результатомval(S,I) выполнения программы (S,I). В противном случае, т. е. когда О - не заключительный оператор, в протоколе имеется следующая, (i+1)-я конфигурация Ui+1 = (ki+1, Wi+1), причем

а) если О - начальный оператор, а выходящая из него дуга ведет к вершине с меткой L, то ki+1 = L и Wi+1 = Wi;

б) если О - оператор присваивания х:=τ, а выходящая из него дуга ведет к вершине с меткой L, то ki+1 = L, Wi+1 = Wi, Wi+1(х) = τ1(Wi);

в) если О - условный оператор p и pI(Wi) = Δ, где Δ Î{0,1}, а выходящая из него дуга ведет к вершине с меткой L, то ki+1 = L и Wi+1 = Wi;

г) если О - оператор петли, то ki+1 = L и Wi+1 = Wi, так что протокол бесконечен.

Таким образом, программа останавливается тогда и только тогда, когда протокол ее выполнения конечен. В противном случае программа зацикливаетсяи результат ее выполнения не определен. [1]

Построение циклов исходя из инвариантов и ограничений

Существуют две стратегии построения циклов при данных предусловии Q, постусловии R, инварианте Р и ограничивающей функции t. Первая приводит к циклу с одной охраняемой командой: doB>Sod. Во второй учитываются преимущества, предоставляемые гибкостью конструкции повторения. [1]

Условия для проверки циклов.

. Покажите, что инвариант цикла Р истинен перед началом выполнения цикла.

. Покажите, что "i: 1 £i£n{P AND Bi} Si {P} - выполнение охраняемой команды завершается при истинном Р.

3. Покажите, что P AND NOT BB . R - в момент завершения цикла R результат истинен.

4. Покажите, что P AND NOT BB . (t > 0) - до завершения цикла ограничение снизу справедливо.

. Покажите, что "i: 1 £i£n{P AND Bi} t1 := t; Si {t < t1} - каждый шаг цикла приводит к уменьшению ограничивающей функции t. [1]

Стратегия построения циклов №1.

. Построить охрану В такую, что P AND NOT B ÞR;

. Построить тело цикла так, чтобы оно уменьшало ограничивающую функцию при сохранении инварианта цикла. [1]

Стратегия построения циклов №2.

. Стройте охраняемые команды так, чтобы каждая из них приближала цикл к завершению, а соответствующая охрана обеспечивала сохранение инварианта.

. Завершайте процесс создания охраняемых команд, если их создано достаточно для доказательства P AND NOT BB ÞR[1].

Метод индуктивных утверждений

Метод индуктивных утверждений независимо сформулирован К. Флойдом и П. Науром. Суть этого метода состоит в следующем:

) формулируются входное и выходное утверждения: входное утверждение описывает все необходимые входные условия для программы (или программного фрагмента), выходное утверждение описывает ожидаемый результат;

) предполагая истинным входное утверждение, строится промежуточное утверждение, которое выводится на основании семантики операторов, расположенных между входом и выходом (входным и выходным утверждениями); такое утверждение называется выведенным утверждением;

) формулируется теорема (условия верификации): из выведенного утверждения следует выходное утверждение;

) доказывается теорема; доказательство свидетельствует о правильности программы (программного фрагмента).

Пусть А - утверждение, описывающее предполагаемые свойства данных в программе, аС - утверждение, описывающее то, что по предположению требуется получить в результате выполнения программы (утверждение о правильности). Программа частично правильна, если при каждом ее выполнении с данными, удовлетворяющими предположению А, будет справедливо утверждение С при условии, что программа закончится.

Программа полностью правильна, если она частично правильна и заканчивается при всех данных удовлетворяющих предположению А. [1]

Доказательство правильности программ с помощью индуктивных утверждений

Для доказательства частичной правильности свяжем утверждение А с началом программы, а утверждение с конечной точкой программы. Выявим закономерности, относящиеся к значениям переменных, и свяжем соответствующие утверждения (условия верификации), по крайней мере, с одной из точек в каждом цикле. Для каждого пути в программе, ведущего из точки i, связанной с утверждением Аi, в точку j, связанную с утверждением Аj, (при условии, что на этом пути нет точек с какими-либо дополнительными утверждениями), докажем, что если мы попали в точку i и справедливо с утверждение Аi, а затем прошли от точки i до точки j, то при попадании в точку j будет справедливо с утверждение Аj. Для циклов точки i и j могут быть одной и той же точкой. Для доказательства полной правильности программы сначала методом индуктивных утверждений нужно доказать ее частичную правильность, а затем уже доказать, что программа когда-нибудь завершится. Алгоритм доказательства правильности программы методом индуктивных утверждений:

) Построить структуру программы.

) Выписать входное и выходное утверждения.

) Сформулировать для всех циклов индуктивные утверждения.

) Составить список выделенных путей.

) Построить условия верификации.

) Доказать условие верификации.

) Доказать, что выполнение программы закончится. [1]

Cети Петри

сеть петри модель программа

Сети Петри это инструмент для математического моделирования и исследования сложных систем. Цель представления системы в виде сети Петри и последующего анализа этой сети состоит в получении важной информации о структуре и динамическом поведении моделируемой системы. Эта информация может использоваться для оценки моделируемой системы и выработки предложений по ее усовершенствованию. Впервые сети Петри предложил немецкий математик Карл Адам Петри. [2]

Теоретико-множественное определение сетей Петри

Пусть мультимножество это множество, допускающее вхождение нескольких экземпляров одного и того же элемента.

Сеть ПетриN является четверкой N=(P,Т,I,O), где = {p1, p2,..., pn} - конечное множество позиций, n ³ 0;= {t1, t2,..., tm} - конечное множество переходов, m ³ 0;: T ® P* - входная функция, сопоставляющая переходу мультимножество его входных позиций;

О: T ® P* - выходная функция, сопоставляющая переходу мультимножество его выходных позиций.

Позиция pÎP называется входом для перехода tÎT, если pÎI(t). Позиция pÎP называется выходом для перехода tÎT, если pÎO(t). Структура сети Петри определяется ее позициями, переходами, входной и выходной функциями.

Маркировка сетей Петри

Маркировка - это размещение по позициям сети Петри фишек, изображаемых на графе сети Петри точками. Фишки используются для определения выполнения сети Петри. Количество фишек в позиции при выполнении сети Петри может изменяться от 0 до бесконечности.

Маркировка m сети Петри N=(P,T,I,О) есть функция, отображающая множество позиций P во множествоNat неотрицательных целых чисел. Маркировка m, может быть также определена как n-вектор m=<m(p1), m(p2),…, m(pn)>, где n- число позиций в сети Петри и для каждого 1 £ i £ n m(pi) Î Nat - количество фишек в позиции pi.

Маркированная сеть Петри N=(P,Т,I,О,m) определяется совокупностью структуры сети Петри (P,T,I,О) и маркировки m.

Анализ сетей Петри

Моделирование систем сетями Петри, прежде всего, обусловлено необходимостью проведения глубокого исследования их поведения. Для проведения такого исследования необходимы методы анализа свойств самих сетей Петри. Этот подход предполагает сведения исследования свойств реальной системы к анализу определенных свойств моделирующей сети Петри.

Свойства сетей Петри

Позиция pÎP сети Петри N=(P,Т,I,O) c начальной маркировкой m является k-ограниченной, если m’(p)£k для любой достижимой маркировки m’ÎR(N,m). Позиция называется ограниченной, если она является k-ограниченной для некоторого целого значения k. Сеть Петри ограниченна, если все ее позиции ограниченны.

Позиция pÎP сети Петри N=(P,Т,I,O) c начальной маркировкой m является безопасной, если она является 1-ограниченной.Сеть Петри безопасна, если безопасны все позиции сети.

Сеть Петри N=(P,Т,I,O) с начальной маркировкой m является сохраняющей, если для любой достижимой маркировки m’ÎR(N,m) справедливо следующее равенство.

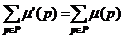
Тупик в сети Петри - один или множество переходов, которые не могут быть запущены. Определим для сети Петри N с начальной маркировкой m следующие уровни активности переходов:

Уровень 0: Переход t обладает активностью уровня 0 и называется мёртвым, если он никогда не может быть запущен.

Уровень 1: Переход t обладает активностью уровня1 и называется потенциально живым, если существует такаяm’ÎR(N,m), что t разрешён в m’.

Уровень 2: Переход t, обладает активностью уровня2 и называется живым, если для всякой m’ÎR(N,m) переход t является потенциально живым для сети Петри N с начальной маркировкой m’.

Сеть Петри называется живой, если все её переходы являются живыми.

Задача покрываемости: Для данной сети Петри N с начальной маркировкой m и маркировки m’ определить, существует ли такая достижимая маркировка m”ÎR(N,m), что m">³m’.

(Отношение m"³m’ истинно, если каждый элемент маркировки m" не меньше соответствующего элемента маркировки m’.)

Сети Петри присуще некоторое поведение, которое определяется множеством ее возможных последовательностей запусков переходов или ее множеством достижимых маркировок. Понятие эквивалентности сетей Петри определяется через равенство множеств достижимых маркировок.

Сеть Петри N=(P,Т,I,O) с начальной маркировкой m и сеть Петри N’=(P’,Т’,I’,O’) с начальной маркировкой m’ эквивалентны, если справедливо R(N,m)=R(N’,m’).

Понятие эквивалентности сетей Петри может быть определено также через равенство множеств возможных последовательностей запусков переходов.

Более слабым, по сравнению с эквивалентностью, является свойство включения, определение которого совпадает с определением эквивалентности, с точностью до замены = на Í.

Анализ свойств сетей Петри на основе дерева достижимости

Анализ безопасности и ограниченности. Сеть Петри ограниченна тогда и только тогда, когда символ w отсутствует в ее дереве достижимости.

Присутствие символа w в дереве достижимости (m[х](p)=w для некоторой вершины x и позиции p) означает, что для произвольного положительного целого k существует достижимая маркировка со значением в позиции p, большим, чем k (а также бесконечность множества достижимых маркировок). Это, в свою очередь, означает неограниченность позиции p, а следовательно, и самой сети Петри.

Отсутствие символа wв дереве достижимости означает, что множество достижимых маркировок конечно. Следовательно, простым перебором можно найти верхнюю границу, как для каждой позиции в отдельности, так и общую верхнюю границу для всех позиций. Последнее означает ограниченность сети Петри. Если граница для всех позиций равна 1, то сеть Петри безопасна.

Анализ сохранения. Так как дерево достижимости конечно, для каждой маркировки можно вычислить сумму начальной маркировки. Если эта сумма одинакова для каждой достижимой маркировки, то сеть Петри является сохраняющей. Если суммы не равны, сеть не является сохраняющей. Если маркировка некоторой позиции совпадает с w, то эта позиция должна был исключена из рассмотрения.

Анализ покрываемости. Задача покрываемости требуется для заданной маркировки m' определить, достижима ли маркировкаm"³m'. Такая задача решается путём простого перебора вершин дерева достижимости. При этом ищется такая вершина х, что m[x]³m'. Если такой вершины не существует, то маркировка m' не является покрываемой. Если она найдена, то m[x] определяет покрывающую маркировку для m' Если компонента маркировки m[x], соответствующая некоторой позиции p совпадает с w, то конкретное её значение может быть вычислено. В этом случае на пути от начальной маркировки к покрывающей маркировке имеется повторяющаяся последовательность переходов, запуск которой увеличивает значение маркировки в позиции p. Число таких повторений должно быть таким, чтобы значение маркировки в позиции p превзошло или сравнялось с m'(p).

Анализ живости. Переход t сети Петри является потенциально живым, тогда и только тогда, когда он метит некоторую дугу в дереве достижимости этой сети.

Доказательство очевидно.

Ограниченность метода дерева достижимости. Как видно из предыдущего, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, эквивалентности. Решение этих задач ограничено существованием символа w. Символ w означает потерю информации: конкретные количества фишек отбрасываются, учитывается только существование их большого числа.[2]

Программная реализация

Программная реализация решения задачи выполнена наC# в VisualStudio 2008.calc() // нахождение количества точек пересечия

{i, j;_per = 0;(i = 0; i < num - 1; i++)(j = i + 1; j < num; j++)

{(b_arr[i] != b_arr[j]) all_per++;

}

}

Результаты проведённого исследования ССП в графовой форме

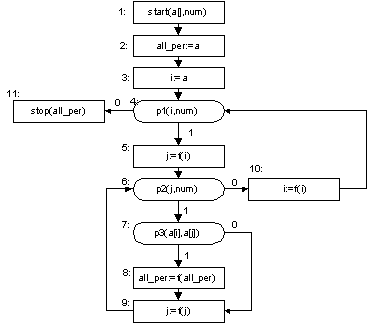
Рисунок 1

ССП в линейной форме

1: start(a[],num) goto 2

2: all_per:=a goto 3

: i:=b goto 4

: if p1(i,num) then goto 5 else goto 11

: j:=f(i)i goto 6

: if p2(j,num) then goto 7 else goto 10

: if p3(a[i],a[j]) then goto 8 else goto 9

: all_per:=f(all_per) goto 9

: j:=f(j) goto 6

: i:=f(i) goto 4

11: stop (all_per)

Интерпретация

Константы:

I(a)=0;

Функции(f)=F, F(x)=x+1;

Предикаты(p1)=P1, P1(i,x)=true, еслиi<x-1;(p2)=P2, P2(j,x)=true, еслиj<x;(p3)=P3, P3(x,y)=true, еслиx<>y;

Протокол выполнения

На вход подан массив угловых коэффициентов уравнений a= {1,2,2}

Инварианты и ограничения циклов

Внешний цикл по i

Предусловие Q:i < num - 1

Постусловие R: i=num - 1

Ограничивающая функция t: num -1- i

ИнвариантP:0≤ i≤ num-1

Внутренний цикл по j

Предусловие Q:j<num

Постусловие R:j = num

Ограничивающая функция t:num - j

Инвариант P: 1≤j≤ num

Доказательство частичной и полной правильности программы

Доказательство частичной правильности подразумевает доказательство того, что цикл перебирает все пары. А полное, подразумевает, что после получения ответа программа завершится.

Для доказательства частичной правильности необходимо показать, что цикл переберёт все пары. Это можно сделать с помощью метода индуктивных утверждений.

При первом попадании в точку Т1 i=0. Утверждение 0 ≤ i≤ num-1верно.

Предположим, что в результате выполнения программы было попадание в точку Т1 с i=n. Докажем, что будет попадание в точку Т1 с i=n+1.

В точке Т1 при i=t отношение 0 ≤ i≤ num-1истинно, так как n<numи n≥0. Следовательно, цикл выполнится ещё раз, c увеличится на 1, произойдёт попадание в точку Т1 с i=n+1.

Для доказательства полной правильности необходимо показать, что цикл когда-нибудь завершится. Так как на каждой итерации iувеличивается на 1, а величина num-1 не изменяется, то когда-нибудь значение cстанет равно n, следовательно, выражение i<num-1 перестанет выполняться, и цикл завершится.

Таким образом, доказана частичная и полная правильность основного цикла программы. На основании этого можно сделать вывод, что программа решает поставленную задачу правильно.

Схема программы в виде сети Петри

a: read(a[],num);: all_per=0;: i=0;: i< num-1;: j=i+1;: g<num;: a[i]==a[j];: all_per=all_per+1;

i: j=j+1;: i=i+1;

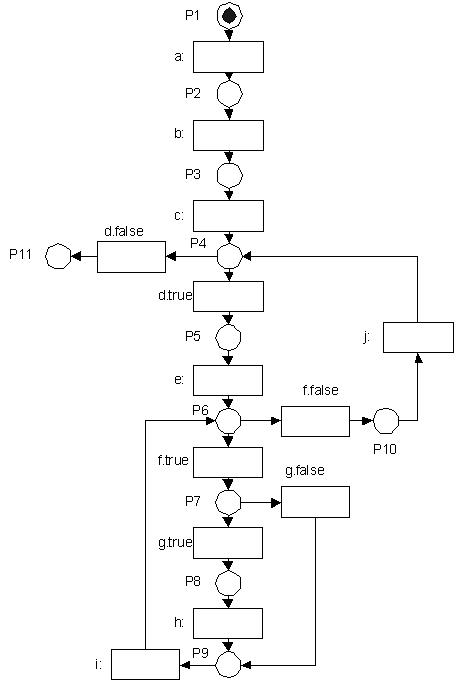
Рисунок 2

Дерево достижимости

Рисунок 3

Анализ свойств сетей Петри на основе дерева достижимости

Анализ безопасности и ограниченности.

Сеть Петри ограниченна тогда и только тогда, когда символ w отсутствует в ее дереве достижимости. Отсутствие символа wв дереве достижимости означает, что множество достижимых маркировок конечно. Следовательно, простым перебором можно найти верхнюю границу, как для каждой позиции в отдельности, так и общую верхнюю границу для всех позиций. Последнее означает ограниченность сети Петри. Полученная сеть Петри безопасна, потому что граница для всех позиций равна 1.

Анализ сохранения.

Так как дерево достижимости конечно, для каждой маркировки можно вычислить сумму начальной маркировки. Сеть Петри является сохраняющей, так как для каждой маркировки сумма начальной маркировки равна 1. Она одинакова для каждой достижимой маркировки.

Анализ покрываемости.

В данной сети Петри ни одна маркировка m' не является покрываемой, так как среди вершин дерева достижимости не существует такой вершины x, что m[x]³m'.

Анализ живости.

Переход t сети Петри является потенциально живым, тогда и только тогда, когда он метит некоторую дугу в дереве достижимости этой сети. Все переходы t сети Петри являются потенциально живыми, т.к. существует такая µ´ÎR(N, µ), что t разрешен в µ´.

Вывод

В результате выполнения курсовой работы была написана программа, решающая поставленную задачу, а именно, подсчет количества пересечений прямых, заданных двумя точками. Была представленная стандартная схема программы, решающей заданную задачу. Алгоритм вычислений был охарактеризован приведенной интерпретацией. Был составлен протокол выполнения программы в виде последовательности конфигураций. Из которого видно, каким образом изменяются переменные в ходе работы программы и какие значения получаются в результате. Доказательства частичной и полной правильности программ позволяют сделать вывод, что программа не зациклится и за конечное время будет получен результат. Была построена сеть Петри, и на основе дерева были исследованы ее свойства: построенная сеть Петри является потенциально живой, ограниченной, безопасной, и сохраняющей.

Таким образом, результат данных исследований позволяет сделать вывод о правильности программы.

Список используемой литературы

1. Рабинович Е.В. Теория вычислительных процессов, учебное пособие - Новосибирск, 2004.

. Котов В.Е. Сети Петри - М.: Наука, 1984.