Основные динамические свойства и их классификация
Федеральное
агентство по образованию
ГОУ
ВПО ''Магнитогорский государственный университет''
Кафедра
алгебры и геометрии
Курсовая
работа на тему:
Основные
динамические свойства и их классификация
Выполнил:
студент 38 гр., ФМФ
Шунин А.
Проверила:
проф., кандидат техн. наук
Кадченко А. И.
дата сдачи:
дата защиты:
оценка:
Магнитогорск
Содержание
Введение
Глава I, §2. Функционирующие и
развивающиеся системы
Основные переменные в динамике
систем
Определение функционирующей системы
Некоторые способы задания
функционирующих систем. Система процессов
Определение системы процессов;
процессы
Некоторые замечания о природе
процессов и среды
Глава II, §4. Основные динамические
свойства и их классификация
Основные и неосновные переменные
динамики систем, множества их значений, типовые кванторы
Определения динамических свойств
Классификация динамических свойств
Заключение
Список литературы
Введение
Одной из важных научных проблем естествознания
является решение задачи предсказания поведения изучаемого объекта во времени и
пространстве на основе определенных знаний о его начальном состоянии. Эта
задача сводится к нахождению некоторого закона, который позволяет по имеющейся
информации об объекте в начальный момент времени t0 в точке пространства x0
определить его будущее в любой момент времени t > t0. В зависимости от
степени сложности самого объекта этот закон может быть детерминированным или
вероятностным, может описывать эволюцию объекта только во времени, только в
пространстве, а может описывать пространственно-временную эволюцию.
Предметом нашего анализа будут не объекты
вообще, а динамические системы в математическом понимании этого термина, будут
рассмотрены основные динамические свойства систем процессов и проведена их
классификация.
К примеру, об актуальности данной темы, основным
классическим строгим методом анализа многих динамических свойств нелинейных
систем является метод функций Ляпунова. Созданный для исследования устойчивости
движения он широко применяется в настоящее время благодаря работам Н. Г.
Четаева, Е. А. Барбашина, Н. Н. Красовского, Т. Иосидзава и других ученых для
анализа многих динамических свойств, таких, как устойчивость при постоянно
действующих возмущениях, ограниченность, диссипативность, существование и
единственность периодических решений дифференциальных уравнений, существование
и корректность решений, устойчивость и другие динамические свойства
инвариантных множеств и т. д.
I. Функционирующие и
развивающиеся системы
. Основные переменные в динамике систем
Для описания систем в динамике целесообразно
прежде всего рассмотреть абстрактные аналоги времени, входов (начальные данные,
возмущения, управления), движений (процессов) и выходов (или состояний), а
также соответствующие множества (пространства), определяющие области их изменения.
При классическом описании (классическая
динамическая система, общая система В. И. Зубова и др.) время принимает
значения из вещественной оси (времени) 𝑅1
= (-∞, +∞) (непрерывное время) или ее подмножества (например, из
множества натуральных чисел N
(дискретное время)), обладающего естественным отношением порядка, евклидовой
нормой, свойством группы или полугруппы и т. д. Такое представление о времени
слишком ограничительно, так как часто возникает необходимость рассматривать
время, принимающее значения в плоскости комплексных чисел 𝐶
(Ляпунов, 1956) или даже в конечномерном пространстве 𝑅n
(например, при изучении многомерных дифференциальных уравнений (Перов, 1966) и
т. д.).
Поэтому, в ряде работ проанализированы более
общие определения времени, принимающего значения из частично упорядоченного
множества (Барбашин, 1946), топологической (Немыцкий, 1946) или произвольной (Sullivan,
1970; Сибирский, 1970) группы, локально-компактной полугруппы (Gilbert,
Knops, 1967), частичного
группоида (Windeknecht,
Mesarovic, 1967) и т. д.
Попытка охватить большую часть перечисленных подходов приводит к следующему
определению, используемому в дальнейшем.
Время t
принимает значения из множества T,
наделенного некоторой структурой 𝒯.
Любой элемент t множества T
называется моментом времени.
В множестве T
выделяется непустое подмножество T0
⊆
T начальных моментов
времени t0 ∊
T0 (с сужением 𝒯0
на него структуры 𝒯 из T).
Выделение множества T0 начальных
моментов времени объясняется тем, что изучение решений некоторых задач и
функционирования ряда систем оказывается возможным, если начальный момент
времени t0 фиксирован (T0
- singl) или принадлежит
некоторому собственному подмножеству (T0
⊂
T). Например, при t0
∊
T0 решение задачи
Коши может существовать, а при t0
∉
T0 - нет.
Здесь структуры 𝒯,
𝒯0
понимаются в смысле Н. Бурбаки (1965а) и охватывают структуры порядка,
линейные, топологические и др. Далее будем опираться также на следующее общее
понятие пространства.
Пространством называется множество с введенным
на нем некоторым семейством собственных подмножеств. В частности,
топологическое или векторное пространство есть множество с определенной на нем
топологической или линейной структурой, задающей семейство его открытых
множеств, соответственно линейных подпространств.
Вход 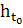 при
t0 ∊
T0 понимается как
совокупность начальных данных
при
t0 ∊
T0 понимается как
совокупность начальных данных 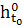 (при данном t0
∊
T0), возмущений
(при данном t0
∊
T0), возмущений 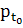 и
управлений
и
управлений 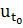 .
.
Начальные данные для обыкновенных
дифференциальных и разностных уравнений представляют элементы конечномерного
пространства 𝑅n,
для систем с последействием или с распределенными параметрами - элементы
функциональных пространств. Возмущения и управления обычно также задаются
некоторыми функциями и, значит, могут быть представлены как элементы некоторых
функциональных пространств. Таким образом, их совокупность (вход 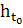 )
- элемент некоторого пространства входов
)
- элемент некоторого пространства входов 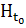 ,
являющегося прямым произведением пространств начальных данных
,
являющегося прямым произведением пространств начальных данных 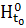 ,
возмущений
,
возмущений 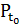 и управлений
и управлений 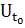 ,
в котором в зависимости от классов этих пространств может быть введена
индуцированная из них некоторая метрика, топология или другая структура,
определяющая систему окрестностей, открытых множеств или вообще некоторое
семейство
,
в котором в зависимости от классов этих пространств может быть введена
индуцированная из них некоторая метрика, топология или другая структура,
определяющая систему окрестностей, открытых множеств или вообще некоторое
семейство 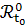 множеств
множеств 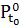 .
.
В различных задачах, связанных с описанием
некоторыми классами интегральных, интегродифференциальных и других уравнений, 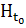 и
и
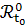 могут
существенно зависеть от t0
(для
могут
существенно зависеть от t0
(для 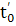 ,
,
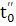 ∊
∊
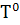 ,
,
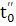 ≠
≠
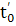 ,
вообще
,
вообще 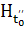 может
не совпадать с
может
не совпадать с 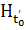 и
и 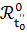 может
не совпадать с
может
не совпадать с 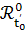 ). Например, в
некоторых системах встречается описание на различных промежутках времени
обыкновенными дифференциальными уравнениями различной размерности. При этом
размерность начальных данных в задаче Коши будет зависеть от выбора t0
того или иного из указанных промежутков времени.
). Например, в
некоторых системах встречается описание на различных промежутках времени
обыкновенными дифференциальными уравнениями различной размерности. При этом
размерность начальных данных в задаче Коши будет зависеть от выбора t0
того или иного из указанных промежутков времени.
Для любого t0
∊
T0 будем считать
заданным пространство входов как непустое множество 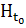 входов
входов
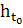 с
определенным на нем семейством
с
определенным на нем семейством 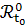 множеств
множеств 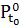 .
.
Упорядоченная пара h
≡
(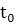 ,
,
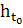 )
образует исходные данные. Вводится пространство исходных данных
)
образует исходные данные. Вводится пространство исходных данных
H
≡
{h = (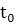 ,
,
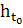 ):
):
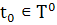 ,
,
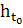 ∊
∊
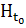 }
(1)
}
(1)
с определенным на нем семейством 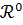 начальных
оценочных множеств
начальных
оценочных множеств
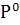 ≡ {h
∊
H:
≡ {h
∊
H: 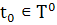 ,
,
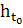 ∊
∊
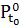 }.
(2)
}.
(2)
Некоторые или все множества 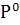 ⊂
⊂
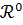 могут
быть пустыми.
могут
быть пустыми.
Вводится также множество
H
≡
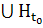 ,
,
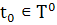 .
(3)
.
(3)
Выход также понимается обобщенно, и ему
приписывается различный смысл в зависимости от вида описания системы.
Например, для абстрактной динамической
управляемой системы (Калман и др., 1971) при так называемом внешнем описании
системы выход будет пониматься в смысле Калмана как значение в текущий момент
времени некоторой выходной функции времени и состояния системы в текущий и
(или) некоторые предшествующие моменты времени. При внутреннем описании
определяется лишь состояние системы в текущий момент времени. В нашем изложении
оно и будет пониматься в качестве выхода (в отличие от Р. Калмана). При полном
описании системы выход в нашем смысле - совокупность состояния и выхода в
смысле Калмана. Такая гибкая трактовка выхода, входа и времени позволит
унифицировать различные описания систем.
Выход в этом обобщенном смысле представляет в
каждый момент времени t
элемент x некоторого
пространства выходов  (конечномерного,
функционального или другого), являющегося, может быть, прямым произведением
пространства состояний и пространства внешних выходов в обычном смысле с индуцированными
из них метрикой, топологией или другой структурой и соответственно системой
окрестностей, открытых множеств или вообще семейством множеств
(конечномерного,
функционального или другого), являющегося, может быть, прямым произведением
пространства состояний и пространства внешних выходов в обычном смысле с индуцированными
из них метрикой, топологией или другой структурой и соответственно системой
окрестностей, открытых множеств или вообще семейством множеств 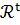 .
В ряде известных случаев пространство выходов (состояний) системы может
существенно изменяться с течением времени. Такой пример системы с непрерывным
временем уже приводился. Пример системы с дискретным временем - численный
процесс (Бабушка и др., 1969), в котором на каждом шаге вычислений возникает
новое нормированное пространство состояний. При моделировании развивающихся
организационных и экономических систем, живых организмов и т. д. также могут
появиться пространства входов и выходов, изменяющиеся с течением времени, т. е.
для
.
В ряде известных случаев пространство выходов (состояний) системы может
существенно изменяться с течением времени. Такой пример системы с непрерывным
временем уже приводился. Пример системы с дискретным временем - численный
процесс (Бабушка и др., 1969), в котором на каждом шаге вычислений возникает
новое нормированное пространство состояний. При моделировании развивающихся
организационных и экономических систем, живых организмов и т. д. также могут
появиться пространства входов и выходов, изменяющиеся с течением времени, т. е.
для 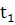 ,
,
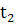 ∊
T,
∊
T, 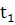 ≠
≠
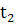 вообще
вообще
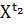 ≠
≠
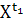 .
.
Учитывая это, для любого t
∊
T будем считать
заданным пространство выходов как непустое множество  выходов
x ∊
выходов
x ∊
 с
определенным на нем семейством
с
определенным на нем семейством 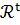 множеств
множеств 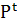 .
.
Семейства 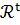 ,
,
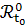 множеств
множеств
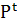 ,
,
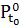 при
этом могут задаваться, например, с помощью некоторых отношений r(
при
этом могут задаваться, например, с помощью некоторых отношений r(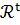 ),
r(
),
r(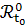 ),
аксиом 𝔄(
),
аксиом 𝔄(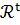 ),
𝔄(
),
𝔄(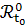 )
(пространств выходов и входов).
)
(пространств выходов и входов).
Упорядоченная пара (t,
x) называется
позицией.
Вводится пространство позиций как множество
позиций
𝚵 ≡ {(t,
x): t
∊
T, x
∊
 }
(4)
}
(4)
с определенным на нем множеством ℛ
текущих оценочных множеств
P
≡
{(t, x)
∊
𝚵:
t ∊
T, x
∊
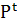 }
(5)
}
(5)
(некоторые или все множества P
могут оказаться пустыми). Вводится также множество
X
≡
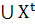 ,
t ∊
T. (6)
,
t ∊
T. (6)
Теперь  ,
,
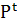 (соответственно
(соответственно
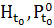 )
можно рассматривать как сечения множеств 𝚵,
P (соответственно H,
)
можно рассматривать как сечения множеств 𝚵,
P (соответственно H,
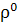 )
при t
∊
T (соответственно
при
)
при t
∊
T (соответственно
при 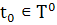 ).
С другой стороны, множества 𝚵
и H определяют
отображения
).
С другой стороны, множества 𝚵
и H определяют
отображения
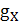 : t
→
: t
→
 ,
T →
,
T →
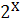 ,
(7)
,
(7)
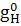 :
: 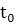 →
→
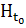 ,
,
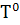 →
→
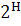 ,
(8)
,
(8)
где 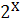 (соответственно
(соответственно
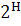 )
- множество всех подмножеств множества X
(соответственно множества H).
)
- множество всех подмножеств множества X
(соответственно множества H).
Очевидно, всегда 𝚵
⊆
T ×
X, H
⊆
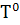 ×
H.
×
H.
(∀t
∊
T)  =
X ≡
=
X ≡
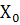 ,
(∀
,
(∀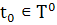 )
)
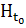 =
H ≡
=
H ≡
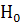 .
.
Для них 𝚵
= T × 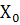 =
T × X,
H =
=
T × X,
H = 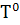 ×
×
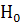 =
=
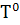 ×
H.
×
H.
Замечание. Здесь и далее используются формулы с
типовыми кванторами (Бурбаки, 1965а), т. е. формулы с кванторами общности и
существования вида
(∀𝔄z)
𝔅 ≡
(∀z)
𝔄 ⟹
𝔅
(что означает: для любого значения операторной
переменной z из типовой формулы
𝔄
следует формула 𝔅),
(∃𝔄z)
𝔅
≡ (∃z)
𝔄 ∧
𝔅
(что означает: существует такое значение
операторной переменной, что имеют место типовая формула 𝔄
и формула 𝔅). Часто типовая
формула 𝔄
имеет вид (z
∊
Z) ∧
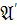 ,
для таких формул с типовыми кванторами используются записи
,
для таких формул с типовыми кванторами используются записи
(∀z
∊
Z: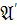 )
𝔅 ≡
(∀𝔄z)
𝔅
)
𝔅 ≡
(∀𝔄z)
𝔅
(для любого z
из множества Z, удовлетворяющего
условию 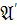 ,
выполняется формула 𝔅),
,
выполняется формула 𝔅),
(∃z
∊
Z: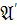 )
𝔅 ≡
(∃𝔄z)
𝔅
)
𝔅 ≡
(∃𝔄z)
𝔅
(существует элемент z
множества
Z, удовлетворяющий
условию 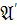 ,
такой, что выполняется формула 𝔅).
,
такой, что выполняется формула 𝔅).
Например, для классической динамической системы
в метрическом пространстве R
T
≡
𝑅1, 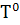 ≡
{0} (или
≡
{0} (или 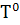 ≡
𝑅1),
≡
𝑅1),  =
X ≡
R ≡
=
X ≡
R ≡
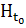 =
H, 𝚵
= 𝑅1 ×
R, H
= {0} × R,
где {0} - множество, состоящее из одной точки 0 ∊
𝑅1.
=
H, 𝚵
= 𝑅1 ×
R, H
= {0} × R,
где {0} - множество, состоящее из одной точки 0 ∊
𝑅1.
Движения, или процессы, в абстрактной динамике
по смыслу должны представлять частичные функции (однозначные) времени t
(области их определения включены в T)
такие, что для всякого t
из области определения функции ее значение принадлежит пространству выходов  (график
частичной функции является подмножеством пространства позиций 𝚵).
Такие частичные функции обозначаются
(график
частичной функции является подмножеством пространства позиций 𝚵).
Такие частичные функции обозначаются
x: t
→
x(t),
dom x
→
X
dom x ⊆
T, (∀t
∊ dom x) x(t) ∊
 .
(9)
.
(9)
В соответствии с этим вводится множество таких
частичных функций времени со значениями в пространствах выходов
Ф ⊆
{{x: t
→
x(t),
dom x
→
X}:
dom x
⊆
T, (∀t
∊
dom x)
x(t)
∊
 }.
(10)
}.
(10)
Иногда его будем называть пространством движений
(или пространством процессов).
Таким образом, выделены пять основных переменных
динамики систем со значениями:
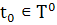 ,
, 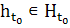 ⊆
H, x
∊
Ф, t ∊
T, x
∊
⊆
H, x
∊
Ф, t ∊
T, x
∊
 ⊆
X.
⊆
X.
При построении абстрактной динамики систем как
аксиоматической теории эти основные переменные считаются заданными apriori
исходными символами (неопределяемые предметные переменные), хотя, конечно, на
них могут и будут накладываться условия, сужающие множества их значений.
. Определение функционирующей системы
Пусть даны множество T
(значений абстрактного времени) с некоторой структурой 𝒯,
определенной на нем; его непустое подмножество T0
⊆
T (начальных
моментов времени) с сужением 𝒯0
на него структуры 𝒯). Для
любого t
∊
T задано
пространство выходов  (множество
(множество  с
определенным на нем семейством
с
определенным на нем семейством 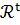 ⊂
⊂
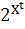 множеств
множеств
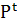 ⊂
⊂
 ),
а для любого
),
а для любого 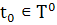 , кроме того,
задано пространство входов
, кроме того,
задано пространство входов 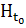 (множество
(множество 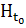 с
определенным на нем семейством
с
определенным на нем семейством 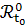 ⊂
⊂
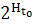 множеств
множеств
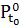 ⊂
⊂
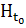 ).
).
На них в соответствии с (1) - (10) вводятся
пространство исходных данных H
(множество H, образованное по
формуле (1) с определенным на нем семейством 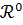 ⊂
⊂
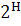 начальных
оценочных множеств
начальных
оценочных множеств 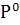 ⊂
H (по (2));
множество H (по (3)) и
отображение
⊂
H (по (2));
множество H (по (3)) и
отображение 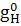 (по (8));
пространство позиций 𝚵 (множество 𝚵
(по (4)) с определенным на нем семейством
(по (8));
пространство позиций 𝚵 (множество 𝚵
(по (4)) с определенным на нем семейством 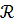 ⊂
⊂
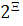 текущих
оценочных множеств P
⊂
𝚵
(по (5))); множество X
(по
(6)) и отображение
текущих
оценочных множеств P
⊂
𝚵
(по (5))); множество X
(по
(6)) и отображение 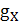 (по (7));
множество Ф (по (10)) частичных функций x
(9) времени t со значениями в
пространствах выходов
(по (7));
множество Ф (по (10)) частичных функций x
(9) времени t со значениями в
пространствах выходов  . Совокупность этих
множеств и пространств
. Совокупность этих
множеств и пространств
< T,
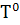 ,
,
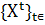 ,
,
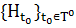 ,
H, 𝚵,
Ф >
,
H, 𝚵,
Ф >
Называется средой. При ее определении задание
структуры 𝒯 и семейств 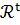 ,
,
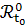 может
производиться с использованием отношений r(𝒯),
r(
может
производиться с использованием отношений r(𝒯),
r(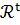 ),
r(
),
r(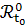 )
и аксиом 𝔄(𝒯),
𝔄(
)
и аксиом 𝔄(𝒯),
𝔄(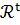 ),
𝔄(
),
𝔄(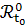 )
(отношения и аксиомы среды).
)
(отношения и аксиомы среды).
Функционирующей системой в среде называется
отношение r между
пространством исходных данных H
и множеством Ф (частичных функций x
времени t со значениями в
пространствах выходов  ), удовлетворяющее
вообще некоторым аксиомам 𝔄.
), удовлетворяющее
вообще некоторым аксиомам 𝔄.
Аксиомы 𝔄
функционирующей системы могут и отсутствовать. Отношение r
между множествами H и Ф
представляет собственное подмножество их прямого произведения Ф ×
H, т. е. r
⊂
Ф ×
H.
Принадлежность (x, h)
∊
r обозначается xrh.
Таким образом, чтобы определить функционирующую
систему Ф, надо знать кортеж множеств и пространств
< r, Ф,
H, 𝚵,
T, 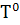 ,
,
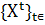 ,
,
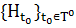 >,
>,
Удовлетворяющих аксиомам 𝔄,
условиям r
⊂
Ф ×
H (условие
отношения),
Ф ⊆
{{x: t
→
x(t)}:
dom x
⊆
T, (∀t
∊
dom x)
x(t)
∊
 }
}
(условие функционирования системы),
H = {h
= (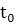 ,
,
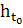 ):
):
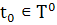 ,
,
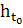 ∊
∊
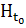 },
},
𝚵 = {(t,
x): t
∊
T, x
∊
 }
}
(условия образования множеств H
и 𝚵),
условиям образования структуры 𝒯
и семейств множеств 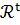 ,
, 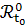 (например,
выраженным через отношения и аксиомы среды), условиям образования семейств
множеств
(например,
выраженным через отношения и аксиомы среды), условиям образования семейств
множеств 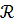 и
и
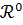 ((2),
(5) с заменой символа ≡ на =).
((2),
(5) с заменой символа ≡ на =).
Отношению r
⊂
Ф ×
H функционирующей
системы отвечают область его определения (в пространстве H
исходных данных h)
dom
r ≡
pr2r
≡
{h ∊
H: (∃x
∊
Ф) xrh}
⊆
H
и множество значений (в множестве Ф частичных
функций x)
range
r ≡
pr1r
≡
{x ∊
Ф: (∃h
∊
H) xrh}
⊆
Ф.
Любая частичная функция x
∊
range r
называется движением. Исходные данные h
∊
dom r
называются допустимыми.
Отношению r,
определенному на множествах Ф и H
функционирующей системы, отвечает частичное многозначное отображение из H
в Ф, при котором образом элемента h
∊
dom r
⊆
H (соответственно
множества 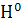 ⊂
dom r)
является непустое множество движений rh
≡
{x ∊
range r:
xrh}
⊂
Ф (соответственно r
⊂
dom r)
является непустое множество движений rh
≡
{x ∊
range r:
xrh}
⊂
Ф (соответственно r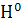 ≡ {x
∊
range r:
(∃h
∊
≡ {x
∊
range r:
(∃h
∊
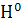 )
xrh}
⊆
Ф), называемое функционированием системы при данном h
(соответственно при
)
xrh}
⊆
Ф), называемое функционированием системы при данном h
(соответственно при 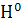 ).
).
Можно сказать, что функционирующая система Ф
характеризуется частичным мультиотображением r
из множества H в множество Ф,
удовлетворяющим аксиомам 𝔄, условиям
функционирования и образования множеств H,
𝚵,
структуры 𝒯, семейств 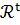 ,
,
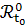 ,
,
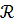 ,
,
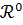 .
.
Каждый элемент x
∊
rh (при h
∊
dom r)
называется движением с исходными данными h
и обозначается x( ∙ , h)
или x( ∙ , 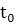 ,
,
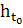 ).
Оно представляет частичную функцию времени со значениями в пространствах
выходов x( ∙ , h):
t →
x(t,
h), dom
x( ∙ , h)
→ X.
).
Оно представляет частичную функцию времени со значениями в пространствах
выходов x( ∙ , h):
t →
x(t,
h), dom
x( ∙ , h)
→ X.
Область определения движения x(
∙ , h) обозначается T(x,
h) ≡ dom
x( ∙ , h)
⊆
T; значение
частичной функции x( ∙ , h)
при t
∊
T(x,
h) обозначается x(t,
h) (подробнее x(t,
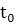 ,
,
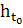 ))
и принадлежит
))
и принадлежит  . Множество x(T(x,
h), h)
= Ux(t,
h) ⊂
X точек x(t,
h) ∊
X для всех t
∊
T(x,
h) называется
траекторией движения x(
∙ , h).
. Множество x(T(x,
h), h)
= Ux(t,
h) ⊂
X точек x(t,
h) ∊
X для всех t
∊
T(x,
h) называется
траекторией движения x(
∙ , h).
Функционирование rh
системы при данном h
∊
dom r,
т. е. множество всех движений с данными h,
определяет функцию достижимости f(
∙ , h) при данном h
как частичное отображение из T
в 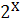 :
f( ∙ , h):
(t, h)
→ f(t,
h), dom
f( ∙ , h)
→
:
f( ∙ , h):
(t, h)
→ f(t,
h), dom
f( ∙ , h)
→ 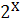 ,
задаваемое равенством
,
задаваемое равенством
f(t, h) = 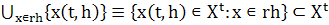 .
.
Множество моментов времени t
∊
T, для которых f(t,
h) ≠
Ø, называется областью определения функции
достижимости f( ∙ , h)
при данном h и обозначается
T(f,
h) ≡ dom
f( ∙ , h)
= 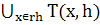 ≡
{t ∊
T: f(t,
h) ≠
Ø} ⊆ T.
≡
{t ∊
T: f(t,
h) ≠
Ø} ⊆ T.
Множество

называется множеством достижимости при исходных
данных h, а f(t,
h) - множеством
достижимости в момент времени t
при исходных данных h.
Функционирования rh
системы при различных h
∊
dom r
определяют функцию достижимости f
как частичное отображение из T
× dom
r в 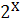
f: (t, h) → f(t, h), dom f →
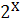 ,
,
задаваемое равенством
f(t,
h) ≡ 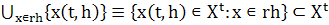 .
.
Множество пар (t,
h) ∊
T × dom
r, для которых f(t,
h) не пусто,
называется областью определения функции достижимости и обозначается
dom
f ≡
{(t, h)
∊
T × dom
r: f(t,
h) ≠
Ø} = {(t, h)
∊
T × H:
h ∊
dom r,
t ∊
T(f,
h)}.
Множество
{x
∊
X: (∃(t,
h) ∊
dom f)
x ∊
f(t,
h)} ≡ 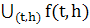
называется множеством достижимости системы, а
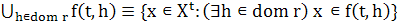
- множеством достижимости системы в момент
времени t.
Прообразом любого движения x
при частичном многозначном отображении r
является непустое множество исходных данных xr
≡
{h ∊
dom r:
xrh}
⊆
H.
В дальнейшем системы с изменяющимся с течением
времени пространством выходов  называются
развивающимися, а с постоянным пространством выходов (
называются
развивающимися, а с постоянным пространством выходов ( = X = X0)
- неразвивающимися.
= X = X0)
- неразвивающимися.
Классические пространственно-временные системы,
изучавшиеся в динамике, являются неразвивающимися. Примеры развивающихся систем
- численный процесс И. Бабушки и др. (1969) и система с непрерывным временем и
с пространством выходов (состояний) меняющейся размерности на разных
промежутках времени, приведенная в п. 1.
3. Некоторые способы задания функционирующих
систем
Все системы и другие конструкции, упомянутые во
введении, при соответствующем выборе r,
Ф, H могут быть
представлены как функционирующие системы (ФС) и, таким образом, рассмотрены как
различные их конкретизации, определяющие, по существу, некоторые способы
задания функционирующих систем.
В качестве первых примеров разберем наиболее
общие.
Пусть даны некоторая группа G,
топологическое пространство R
и функция f: G
× R
→
R, удовлетворяющая
следующим условиям.
°. (Аксиома начальных данных): (∀p
∊
R) f(Θ,
p) = p,
где Θ
- нуль
группы G.
°. (Аксиома непрерывности): (∀g
∊
G) функция f(g,
∙ ) непрерывна (по второму аргументу) в топологии пространства R.
°. (Аксиома группы): (∀p
∊
R) (∀g1,
g2 ∊
G) f(g2,
f(g1,
p)) = f(g1
+ g2, p).
Общая динамическая система задается тройкой <f,
R, G>.
Она называется непрерывной, если группа G
является топологической, а функция f
непрерывна по совокупности аргументов в топологиях пространств R
и G. Понятие общей
непрерывной динамической системы введено В. В. Немыцким (1946) в предположении,
что G - локально-компактная
топологическая группа, а затем рассмотрено в статьях В. В. Немыцкого (1948,
1950), Е. А. Барбашина (1948а, 1950а, 1951) и других, в монографиях Х.
Готшалка, Г. А. Хедлунда (Gottschalk,
Hedlund, 1955), И. У.
Бронштейна (1969) и др. Очевидно, классическая динамическая система (КДС) (Markoff,
1931) представляет частный случай общей непрерывной динамической системы В. В.
Немыцкого.
Общая динамическая система называется
дискретной, если группа G
- циклическая (существует g0
∊
G такой, что любой
элемент g
∊
G кратен g0).
Частным случаем дискретных общих динамических систем являются введенные и
изученные М. Морсом (Morse,
1966) символические динамические системы, у которых G
есть множество всех целых чисел Z,
а R = Sm
- пространство двухсторонних последовательностей из m
элементов (m
≥
2). КДС очевидным образом порождает дискретную общую динамическую систему <f,
R, {kt0}>,
где t0 ∊
R1, k
= 0, ±1, ±2, … (см. Birkhoff,
1950; Жидков, 1952; Reddy,
1968; и др.).
Е. А. Барбашин (1946), введя в группу G
непрерывной
общей динамической системы отношение частичной упорядоченности, пришел к
понятию частично упорядоченной динамической системы, имеющей глубокие аналоги с
КДС (см. также Барбашин, 1948а, б, 1950а-в, 1951а, б; 1954; Сибирский и др.,
1960; Стахи, 1965, 1967, 1968; и др.). Подробнее эти концепции изложены в
лекциях К. С. Сибирского (1970).
Функция f(
∙ , p) называется
движением, а множество f(G,
p) - траекторией
общей динамической системы при исходных (начальных) данных (θ,
p) ∊
G × R.
Общая динамическая система определяет два
способа задания функционирующей системы, соответствующих выбору T0:
1) T0 = {θ} - singl;
) T0 = G.
В остальном среда ФС находится однотипно с
помощью G и R:
T = G,
𝒯
- структура группы,  = X
=
= X
= 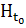 =
H ≡
R,
=
H ≡
R, 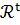 =
=
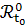 -
семейство открытых множеств топологического пространства R,
H = T0
× R, 𝚵
= G × R,
Ф ≡ ℱ X
(T) = ℱ
R (G)
≡ {x: G
→
R} - множество всех
функций, отображающих группу G
в топологическое пространство R
(такое представление Ф может быть сделано, если учесть, что любое движение f(
∙ , p) общей
динамической системы определено на всей группе G,
имеет место аксиома группы).
-
семейство открытых множеств топологического пространства R,
H = T0
× R, 𝚵
= G × R,
Ф ≡ ℱ X
(T) = ℱ
R (G)
≡ {x: G
→
R} - множество всех
функций, отображающих группу G
в топологическое пространство R
(такое представление Ф может быть сделано, если учесть, что любое движение f(
∙ , p) общей
динамической системы определено на всей группе G,
имеет место аксиома группы).
Отношение r
является функциональным, т. е.
(∀h
= (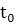 ,
,
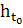 )
∊ T0 × R) {x} = rh
- singl
)
∊ T0 × R) {x} = rh
- singl
(при любом h
= (g0, p)
функционирование описывается единственным движением и определяется при любом t0
= g0 ∊
G равенствами:
1) x(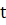 ,
,
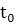 ,
,
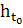 )
= x(g, θ, p) = f(g, p);
)
= x(g, θ, p) = f(g, p);
) x(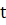 ,
,
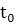 ,
,
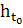 )
= x(g, g0, p) = f(g - g0, p).
)
= x(g, g0, p) = f(g - g0, p).
Область определения процесса x(
∙ , h) совпадает с G(T(x,
h) = G)
для любого h
∊
T0 × R.
Аксиома начальных данных приводит к равенству x(t0,
h) = 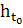 .
.
Общая система в смысле И. Е. Гильберта и Р. Т.
Кнопса (Gilbert,
Knops, 1967).
T -
локально-компактная полугруппа, T0
⊂
T,  =
X - топологическое
пространство,
=
X - топологическое
пространство, 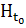 ⊆
X (в
⊆
X (в 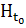 используется
другая топология), H
⊆
𝚵
= T × X;
задано множество B(X,
T) ⊂
ℱ
X (T);
мультиотображение r из H
в Ф = ℱ
X (T)
определяется условием
используется
другая топология), H
⊆
𝚵
= T × X;
задано множество B(X,
T) ⊂
ℱ
X (T);
мультиотображение r из H
в Ф = ℱ
X (T)
определяется условием
(∀h
∊
H) rh
= {x ∊
B(X,
T): x(t0)
= 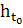 }.
}.
Предпроцесс О. Гаека (1967б, в).
Пусть P
- произвольное множество, T
⊆
R1 - упорядоченное
естественным образом подмножество вещественной оси. Бинарное отношение p
на T × P
называется предпроцессом в P
над T тогда и только
тогда, когда выполняются следующие аксиомы.
°. (Аксиома упорядоченности времени): (∀t,
t0 ∊
T) (∀y,
y0 ∊
P) (t,
y)p(t0,
y0) ⟹
t ≥
t0.
°. (Аксиома начальных данных): (∀t0
∊
T) (∀y,
y0 ∊
P) (t0,
y)p(t0,
y0) ⟹
y = y0.
Для предпроцесса можно ввести его индивидуальные
отношения 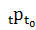 на P:
на P:
(∀t,
t0 ∊
T) y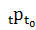 y0
⟺ (t,
y)p(t0,
y0).
y0
⟺ (t,
y)p(t0,
y0).
Важными типами предпроцессов являются суженный
предпроцесс, характеризуемый соотношением
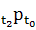 ⊃
⊃
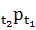 ∘
∘
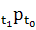 для
всех t2 ≥ t1
≥ t0 в T,
для
всех t2 ≥ t1
≥ t0 в T,
и транзитивный предпроцесс, для которого
выполняется свойство
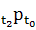 ⊃
⊃
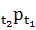 ∘
∘
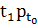 для
всех t2 ≥ t1
≥ t0 в T.
для
всех t2 ≥ t1
≥ t0 в T.
Положим T0
= T (подмножество R1
c наследованными из R1
свойствами); 𝒯 - структура
естественного порядка из R1,
(∀t0
∊
T0) 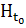 =
H = P,
H = T0
× P, (∀t
∊
T)
=
H = P,
H = T0
× P, (∀t
∊
T)  =
X =
=
X = 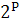 ,
𝚵
= T ×
,
𝚵
= T × 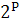 ;
;
Ф - множество функций x
из T в X
с dom x
⊆
T; r
- функциональное отношение между H
и Ф такое, что
dom r = dom p, (∀h
∊ dom r) rh ≡
{x( ∙ , h)} = {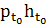 },
},
где 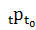 -
индивидуальное отношение предпроцесса, движение x(
∙ , h) с исходными
данными h
∊
H имеет область
определения T(x,
h) ⊆
{t ∊
T: t0
≤ t}.
Таким образом, значение функции x(
∙ , h) с исходными
данными h = (t0,
-
индивидуальное отношение предпроцесса, движение x(
∙ , h) с исходными
данными h
∊
H имеет область
определения T(x,
h) ⊆
{t ∊
T: t0
≤ t}.
Таким образом, значение функции x(
∙ , h) с исходными
данными h = (t0,
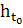 )
∊
dom r
при t
∊
T(x,
h) здесь
отождествляется со значениями отношения
)
∊
dom r
при t
∊
T(x,
h) здесь
отождествляется со значениями отношения 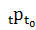 на
элементе
на
элементе 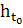 и
является множеством x(t,
h) =
и
является множеством x(t,
h) = 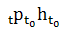 в
P, т. е. элементом
множества 2P = X.
Множество достижимости f(t,
h) одноэлементно в X.
Из приведенного построения следует выполнение условий функционирования и
образования множеств H
и 𝚵.
Следовательно, предпроцесс О. Гаека задает функционирующую систему с
единственностью движений в пространстве выходов, являющемся множеством
подмножеств P.
в
P, т. е. элементом
множества 2P = X.
Множество достижимости f(t,
h) одноэлементно в X.
Из приведенного построения следует выполнение условий функционирования и
образования множеств H
и 𝚵.
Следовательно, предпроцесс О. Гаека задает функционирующую систему с
единственностью движений в пространстве выходов, являющемся множеством
подмножеств P.
Переходная система Т. Г. Уиндекнехта и М. Д.
Месаровича (Windeknecht,
Mesarovic, 1967), как легко
показать, также задает некоторую ФС. Но в нее не вводится аксиома начальных
данных (в отличие от предыдущих случаев, в которых выполнена классическая
аксиома начальных данных).
При исследовании динамики систем целесообразно
использовать ослабленную аксиому начальных данных, что иллюстрируется следующим
примером.
Система решений функционально-дифференциального
уравнения с последействием (Красовский, 1959; Hale,
1971).
Пусть дано уравнение с последействием
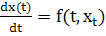 ,
(11)
,
(11)
где f:
[0, τ) × 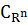 ([-η,
0]) →
([-η,
0]) → 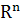 .
.
Здесь в качестве решений рассматриваются
непрерывные функции x( ∙ ),
определенные на промежутке [-η, τ) или
[-η
+ t0, t0
+ τx) (0 ≤ t0
< t0 + τx
≤
τ), имеющие значения в 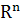 ,
дифференцируемые справа на [0, τ) (соответственно
на [t0, t0
+ τx)). Для них и для t
∊
[0, τ) (соответственно t
∊
[t0, t0
+ τx)) вводятся функции
,
дифференцируемые справа на [0, τ) (соответственно
на [t0, t0
+ τx)). Для них и для t
∊
[0, τ) (соответственно t
∊
[t0, t0
+ τx)) вводятся функции
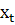 ∊
∊
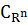 ([-η,
0]) такие, что (∀θ ∊
[-η, 0])
([-η,
0]) такие, что (∀θ ∊
[-η, 0]) 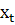 (θ)
= x(t
+ θ); они фигурируют в правой части уравнения.
Производная в левой части уравнения понимается как правая.
(θ)
= x(t
+ θ); они фигурируют в правой части уравнения.
Производная в левой части уравнения понимается как правая.
Пусть t0
∊
[0, τ) - заданное число, 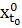 -
заданная функция из
-
заданная функция из 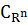 ([-η,
0]). Функция x(
([-η,
0]). Функция x(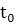 ,
,
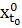 )(
∙ ) называется решением уравнения (11) с начальными данными (
)(
∙ ) называется решением уравнения (11) с начальными данными (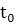 ,
,
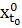 ),
если существует число τx
такое, что t0 + τx
≤
τ, x(
),
если существует число τx
такое, что t0 + τx
≤
τ, x(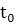 ,
,
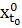 )(
∙ ) определена на [t0
- η, t0 + τx),
дифференцируема справа по t
∊
[t0, t0
+ τx), удовлетворяет
уравнению (11) и
)(
∙ ) определена на [t0
- η, t0 + τx),
дифференцируема справа по t
∊
[t0, t0
+ τx), удовлетворяет
уравнению (11) и 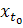 (
(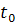 ,
,
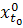 )
=
)
= 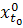 .
.
Покажем, что множество всех решений уравнения
(11) с начальными условиями (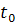 ,
, 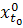 )
∊
[0, τ) ×
)
∊
[0, τ) × 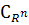 ([-η,
0]) является функционирующей системой.
([-η,
0]) является функционирующей системой.
Положим T
= [-η, τ)
⊃
T0, 𝒯
- структура естественного порядка из R1,
T0 = [0, τ),
(∀t0
∊
T0) 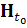 =
H =
=
H = 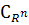 ([-η,
0]), (∀t
∊
T)
([-η,
0]), (∀t
∊
T) 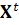 =
X =
=
X = 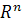 ,
H = T0
× H, 𝚵
= T × X;
,
H = T0
× H, 𝚵
= T × X;
Ф - множество нерперывных дифференцируемых
справа функций x из [t0
- η, t0 + τx)
⊆
T в X;
r - отношение между H
и Ф, которое каждым начальным данным h
≡
(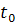 ,
,
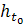 )
= (
)
= (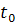 ,
,
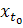 )
∊
dom r
⊆
H ставит в
соответствие множество rh
всех решений уравнения (11) с этими начальными данными; функция x(
∙ , h) ∊
rh отождествляется с
решением x(
)
∊
dom r
⊆
H ставит в
соответствие множество rh
всех решений уравнения (11) с этими начальными данными; функция x(
∙ , h) ∊
rh отождествляется с
решением x(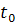 ,
,
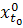 )(
∙ ) уравнения (11) и принимается T(x,
h) = [t0
- η, t0 + τx).
Выполнение условия функционирования и других при этом очевидно, что и
требовалось. Начальное условие
)(
∙ ) уравнения (11) и принимается T(x,
h) = [t0
- η, t0 + τx).
Выполнение условия функционирования и других при этом очевидно, что и
требовалось. Начальное условие 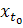 (
(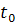 ,
,
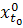 )
=
)
= 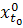 здесь
не влечет выполнения аксиомы начальных данных в обычной (классической) форме
здесь
не влечет выполнения аксиомы начальных данных в обычной (классической) форме
x(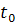 ,
,
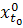 )(
)(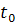 )
=
)
= 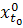 .
.
Оно обеспечивает лишь выполнение условия
(∀(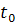 ,
,
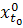 )
∊ dom r) x(
)
∊ dom r) x(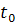 ,
,
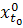 )(
)(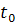 )
= {
)
= {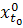 (0)}
- singl,
(0)}
- singl,
которое можно истолковать как ослабленную
аксиому начальных данных.
II. Система
процессов
Как отмечено в главе I,
большая часть известных математических концепций систем укладывается в понятие
ФС, которое, однако, из-за чрезмерной общности не учитывает некоторые важные
особенности динамики систем. Например, время T
с произвольной структурой 𝒯
на нем не позволяет при эволюции системы отличить ее прошлое от будущего (что
наглядно видно в примерах 3.1, 3.2 гл. I),
т. е. в ФС не оговаривается основная особенность времени T
- его направленность. Это можно сделать, предположив 𝒯
структурой порядка, как в примерах 3.1 (случай частично упорядоченной
динамической системы), 3.3 и 3.5 гл. I.
Наиболее общий из них первый случай, когда 𝒯
является структурой частичного порядка, заданной отношением частичной
упорядоченности “≤”. В этом случае T
- частично упорядоченное множество, т. е. множество T
с заданным на нем бинарным отношением r(𝒯)
≡ (≤), удовлетворяющим известным аксиомам частичного порядка (𝔄(𝒯)):
(𝒯1).
(Аксиома рефлексивности): t
≤
t.
(𝒯2).
(Аксиома транзитивности): (t1
≤ t2) ⋀
(t2 ≤ t3)
⟹
t1 ≤ t3.
(𝒯3).
(Аксиома антисимметричности): (t1
≤ t2) ⋀
(t2 ≤ t1)
⟹
t1 = t2.
Например, если множество T
значений времени t является v-мерным
векторным пространством 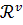 , то естественна
покомпонентная частичная упорядоченность векторов, определяемая следующим
образом:
, то естественна
покомпонентная частичная упорядоченность векторов, определяемая следующим
образом:
для
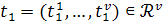 ,
, 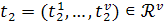 ,
,
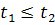 ⟺
⟺
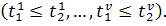
Представляется также желательным более полное
описание множеств достижимости и выходов (состояний) системы, соответствующих
начальному моменту времени. В частности, как отмечено в п. 3 гл. I,
в динамике систем целесообразно использовать ослабленную аксиому начальных
данных (в качестве аксиомы 𝔄
функционирующей системы).
При таких аксиомах 𝔄(𝒯)
и 𝔄 движение ФС при
данных h можно трактовать
как процесс с этими исходными данными (достаточно общей природы).
Полученная конкретизация среды и аксиомы
функционирующей системы при этом естественно приводит к понятию системы
процессов. В теории системы процессов, как более богатой, чем теория ФС,
удается глубже исследовать различные динамические задачи.
1. Определение системы процессов; процессы
Функционирующая система r
в среде называется системой процессов (СП), если выполняются следующие аксиомы:
𝔄(𝒯).
(Аксиома времени): T - частично
упорядоченное множество (с отношением частичной упорядоченности ≤).
𝔄. (Аксиома
исходных данных): (∀h
∊
dom r)
(∀x
∊
rh) t0
∊
T(x,
h) ⋀
f(t0,
h) = {x(t0,
h)} - singl.
Смысл аксиомы 𝔄
состоит в следующем. Для любых исходных данных h
= (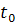 ,
,
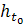 )
из области определения отношения r
и для любых движений x(
∙ , h) функционирующей
системы r с исходными
данными h выполняются два
условия:
)
из области определения отношения r
и для любых движений x(
∙ , h) функционирующей
системы r с исходными
данными h выполняются два
условия:
) начальный момент времени принадлежит области
определения T(x,
h) движения x(
∙ , h);
) множество достижимости из h
в начальный момент времени t0
является одноэлементным множеством {x(t0,
h)}, состоящим из
одного элемента - выхода (в указанном движении) в начальный момент времени t0
(значения всех функций x
∊
rh в начальный момент
времени совпадают).
Более сильным условием была бы
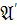 . (Классическая
аксиома начальных данных):
. (Классическая
аксиома начальных данных):
(dom
r = H
⊆
𝚵)
⋀
(∀h
∊
H) (∀x
∊
rh) t0
∊
T(x,
h) ⋀
x(t0,
h) = 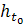 .
.
Для выполнения 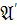 ,
очевидно, требуется выполнение всех условий аксиомы 𝔄
и, кроме того, следующее. Область определения отношения r
совпадает с H, (∀t0
∊
T0)
,
очевидно, требуется выполнение всех условий аксиомы 𝔄
и, кроме того, следующее. Область определения отношения r
совпадает с H, (∀t0
∊
T0) 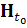 ⊆
⊆
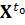 ,
т. е. для начальных моментов времени пространства входов (начальных состояний)
совпадают или являются подмножествами пространств выходов (состояний), все
движения x( ∙ , h)
c любыми исходными
данными h
∊
H в начальные
моменты времени t0
определены, и выходы (состояния) совпадают с входами (начальными состояниями).
,
т. е. для начальных моментов времени пространства входов (начальных состояний)
совпадают или являются подмножествами пространств выходов (состояний), все
движения x( ∙ , h)
c любыми исходными
данными h
∊
H в начальные
моменты времени t0
определены, и выходы (состояния) совпадают с входами (начальными состояниями).
В примерах 3.1, 3.2 классическая аксиома
начальных данных 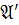 выполняется, но в
примерах 3.3, 3.5 (для решений функционально-дифференциального уравнения с
запаздыванием) она не выполнена (тогда как ослабленная аксиома начальных данных
𝔄 выполняется). Ниже
будут приведены и другие примеры, подтверждающие целесообразность введения
аксиомы исходных данных в форме 𝔄.
выполняется, но в
примерах 3.3, 3.5 (для решений функционально-дифференциального уравнения с
запаздыванием) она не выполнена (тогда как ослабленная аксиома начальных данных
𝔄 выполняется). Ниже
будут приведены и другие примеры, подтверждающие целесообразность введения
аксиомы исходных данных в форме 𝔄.
Введем теперь важное для дальнейшего изложения
понятие процесса.
В системе процессов каждая частичная функция x
∊
range r
⊆
Ф называется процессом, а при фиксированном h
∊
dom r
всякая частичная функция x
∊
rh называется
процессом с данным h и
обозначается  .
.
Таким образом, если функционирующая система
является системой процессов, то ее движения называются процессами, а при
фиксированном h
∊
dom r
всякое движение x( ∙ , h)
∊
rh называется
процессом с исходными данными h
и обозначается  . Иными словами,
процесс с исходными данными h
есть движение x( ∙ , h)
такой функционирующей системы, для которой выполняются аксиомы времени и
исходных данных.
. Иными словами,
процесс с исходными данными h
есть движение x( ∙ , h)
такой функционирующей системы, для которой выполняются аксиомы времени и
исходных данных.
Для процессов с исходными данными h
вводятся сокращения в обозначениях: T(x,
h) ≡ T( )
- область определения процесса
)
- область определения процесса  ;
;  (t)
≡ x(t,
h) = x(t,
t0,
(t)
≡ x(t,
h) = x(t,
t0, 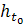 )
- выход в процессе
)
- выход в процессе  в момент времени t
∊
T(x,
h).
в момент времени t
∊
T(x,
h).
2. Некоторые замечания о природе процессов и
среды
Поскольку множества и отношения, участвующие в
описании СП, имеют произвольный характер, введенная математическая модель
достаточно общая и может использоваться при описании процессов самой
разнообразной природы.
Представление о времени как о произвольном
частично упорядоченном множестве является довольно широким и охватывает большую
часть реальных ситуаций. Чаще всего в качестве T
принимается множество на вещественной прямой с естественным отношением порядка
на нем. В системах с непрерывным временем T
- обычно вся вещественная ось R1
или ее упорядоченные невырожденные интервалы (один или несколько). Но,
например, в работе Е. А. Барбашина (1946) T
- частично упорядоченная топологическая группа, в статье В. В. Немыцкого (1946)
T -
локально-компактная топологическая группа, в которой можно ввести частичный
порядок, а Г. Д. Саливаном (Sullivan,
1970) рассмотрена пространственно-временная полисистема Д. Башо с понятием
времени более общим, чем в классической механике и теории относительности
(моменты времени упорядочены и зависят от состояний системы). В дискретных
системах (автоматы, численные процессы и т. п.) время T
- либо множество целых чисел Z,
либо какие-то его естественным образом упорядоченные подмножества, например,
множество натуральных чисел N.
В принципе не исключены случаи, когда множество T
имеет смешанный дискретно-непрерывный характер, что выполняется, например, в
гибридных системах, когда одни подсистемы функционируют в непрерывном времени,
а другие - в дискретном (T
= 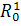 ×
N).
×
N).
Природа входов (элементов 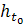 множества
множества
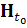 )
может быть весьма разнообразна. Это начальные состояния системы, как в задаче
Коши для уравнений различных классов; разнообразные входные воздействия (в
обычном смысле), вызванные взаимодействием рассматриваемой системы с другими
системами (открытые системы); комплексные сигналы, несущие информацию о
начальных состояниях и возмущениях и т. п.
)
может быть весьма разнообразна. Это начальные состояния системы, как в задаче
Коши для уравнений различных классов; разнообразные входные воздействия (в
обычном смысле), вызванные взаимодействием рассматриваемой системы с другими
системами (открытые системы); комплексные сигналы, несущие информацию о
начальных состояниях и возмущениях и т. п.
Пусть система процессов такова, что
(∀t0
∊
T0) 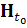 =
=
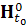 ×
×
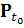 ,
,
где 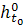 ∊
∊
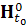 -
начальное состояние системы в начальный момент времени t0,
а
-
начальное состояние системы в начальный момент времени t0,
а 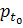 ∊
∊
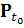 -
функция (возможно, многозначная), действующая из dom
-
функция (возможно, многозначная), действующая из dom
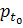 ⊆
𝚵
или dom
⊆
𝚵
или dom
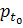 ⊆
T в некоторое
множество и представляющая входной сигнал или возмущающее воздействие; при этом
исходные данные h = (t0,
⊆
T в некоторое
множество и представляющая входной сигнал или возмущающее воздействие; при этом
исходные данные h = (t0,
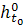 ,
,
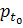 ).
Тогда СП r называется
открытой, или возмущаемой, системой.
).
Тогда СП r называется
открытой, или возмущаемой, системой.
Выходами (элементами x
=  (t)
множества
(t)
множества 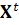 ) могут являться
текущие состояния системы, ее выходные сигналы и воздействия, различные
интересующие нас смешанные и интегральные характеристики системы, как-то
показатели надежности, качества, энергоемкости и т. п.
) могут являться
текущие состояния системы, ее выходные сигналы и воздействия, различные
интересующие нас смешанные и интегральные характеристики системы, как-то
показатели надежности, качества, энергоемкости и т. п.
Наконец, желание подчеркнуть, что с одними и
теми же исходными данными h
≡
(t0, 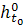 )
система может вести себя по-разному, что, в частности, наблюдается в уравнениях
с неединственностью решений задачи Коши, а также в системах с различными видами
неопределенностей, когда в зависимости от воздействия тех или иных неучтенных
факторов реализуется тот или иной процесс в системе, привело к введению
произвольного (а не функционального) отношения r
между множествами исходных данных H
и функций Ф, описывающего функционирование системы.
)
система может вести себя по-разному, что, в частности, наблюдается в уравнениях
с неединственностью решений задачи Коши, а также в системах с различными видами
неопределенностей, когда в зависимости от воздействия тех или иных неучтенных
факторов реализуется тот или иной процесс в системе, привело к введению
произвольного (а не функционального) отношения r
между множествами исходных данных H
и функций Ф, описывающего функционирование системы.
Впервые понятие системы процессов было введено в
работе Л. Ю. Анапольского и В. М. Матросова (1972). Там в определении СП кроме
аксиом 𝔄(𝒯)
и 𝔄 требовалось еще
выполнение следующего
𝔄(r).
(Аксиома реализуемости):
(∀h
≡
(t0, 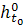 )
∊
dom r)
(∀
)
∊
dom r)
(∀ ∊
rh) (∀t1
∊
T(x,
h)) t0
≤ t1 ⟹
[t0, t1]
⊆
T(x,
h).
∊
rh) (∀t1
∊
T(x,
h)) t0
≤ t1 ⟹
[t0, t1]
⊆
T(x,
h).
Аксиома реализуемости означает, что если процесс
 определен
в момент времени t1 (t0
≤ t1, t1
≠ t0), то он определен
на всем отрезке [t0, t1]
≡ {t
∊
T: t0
≤ t
≤
t1} частично
упорядоченного множества T.
Для рассматриваемых ниже примеров аксиома реализуемости приемлема, однако ее
справедливость в дальнейшем при развитии теории, в частности при построении
метода сравнения, не играет существенной роли. Поэтому, начиная с работы В. М.
Матросова (1974), мы не стесняем себя этим дополнительным требованием и в
дальнейшем будем пользоваться определением СП из п. 1.
определен
в момент времени t1 (t0
≤ t1, t1
≠ t0), то он определен
на всем отрезке [t0, t1]
≡ {t
∊
T: t0
≤ t
≤
t1} частично
упорядоченного множества T.
Для рассматриваемых ниже примеров аксиома реализуемости приемлема, однако ее
справедливость в дальнейшем при развитии теории, в частности при построении
метода сравнения, не играет существенной роли. Поэтому, начиная с работы В. М.
Матросова (1974), мы не стесняем себя этим дополнительным требованием и в
дальнейшем будем пользоваться определением СП из п. 1.
III. Основные
динамические свойства и их классификация
динамика система процесс квантор
В этой главе вводится унифицированное
представление основных динамических свойств в виде некоторых формул
математической логики. Производится их логический анализ и классификация.
Согласно идеям качественной теории Ляпунова и
Пуанкаре, строгое качественное изучение системы должно начинаться с введения
определений свойств, интересующих исследователя. Так, при построении теории
устойчивости движения А. М. Ляпуновым были даны фундаментальные определения устойчивости
движения (неустойчивости), условной и асимптотической устойчивости.
При развитии теории устойчивости исследовались
различные другие определения свойств устойчивости движения: равномерная по t0
устойчивость, экспоненциальная устойчивость (Персидский, 1937, 1946),
равномерная по (t0, x0)
(Малкин, 1954) и равномерная по x0
(Красовский, 1956а) (равностепенная) асимптотическая устойчивость, (A,
λ, t0, T)-устойчивость
(Четаев, 1962), устойчивость на конечном интервале времени (Каменков, 1971),
устойчивость при постоянно действующих возмущениях малых в каждый момент
(Дубошин, 1940), ограниченных в среднем (Гермаидзе, Красовский, 1957),
ограниченных интегрально (Красовский, 1959), устойчивость при параметрических
возмущениях (Кузьмин, 1957), абсолютная устойчивость (Лурье, Постников, 1944),
асимптотическая устойчивость в целом (Барбашин, Красовский, 1952), устойчивость
относительно части переменных (Румянцев, 1957) и относительно двух метрик
(Мовчан, 1960) и т. д.
Позднее введены и изучены определения устойчивости
множества относительно одной (Зубов, 1957; Yoshizawa,
1966) и двух (Матросов, 1969) метрик, устойчивости системы, а также аналогичные
всем предыдущим, но более общие определения устойчивости в каждом смысле
относительно двух функционалов, совокупностей функционалов (Матросов, 1971,
1973, 1975) и двух семейств множеств (Матросов, Анапольский, 1972, 1975). В
литературе накопилось несколько десятков только определений устойчивости (в
детальной классификации), обзор которых сделан Н. Д. Моисеевым (1949), В. Ханом
(Hahn, 1967), В. М.
Матросовым (1971, 1973, 1974, 1975). Выбор того или иного определения при
решении прикладной задачи диктуется ее смыслом, требованиями и каждый раз
должен быть индивидуальным.
Аналогичное положение с ограниченностью движений
(решений) после введения определений ограниченности в детальной классификации
Т. Йосидзава (Yoshizawa,
1966), притяжением - в детальной классификации Н. П. Батья и Дж. Д. Сегё (Bhatia,
Szegö, 1967) и
некоторыми другими динамическими свойствами решений дифференциальных уравнений
(Lakshmikantham, Leela,
1969) и движений динамических систем (Bhatia,
Szegö, 1967).
Д. Башо (Bushaw,
1969) предложил записи определений свойств типа устойчивости в смысле Ляпунова
и Пуассона для потоков, заданных на метрическом пространстве с помощью
некоторых формул математической логики и, таким образом, унифицировал
представление этих динамических свойств, а также провел их частичное
упорядочение. П. Хабетс и К. Пейффер (Habets,
Peiffer, 1973, 1975),
используя идеи Д. Башо, наметили классификацию свойств устойчивости,
ограниченности и притяжения относительно множеств для решений обыкновенных
дифференциальных уравнений с единственностью в 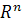 .
.
В развитие этих исследований динамические
свойства (ДС) системы процессов описываются в данном параграфе, по существу, на
языке теории первого порядка (Мендельсон, 1971), более сильной, чем
аксиоматическая теория множеств (дается в неформальном изложении), но с
различными областями значений отдельных предметных переменных. В этом описании
выделены основные и неосновные переменные динамики систем, константы, формулы и
типовые кванторы, в которых в качестве типовых условий используются формулы
принадлежности значений операторных переменных областям их значений, каждая из
которых указывается отдельно и фиксируется.
Вводится унифицированное представление
определений ДС с помощью формул (теории I
порядка) “квазипренексного” вида, содержащих основные переменные динамики
систем в качестве операторных переменных типовых кванторов с указанием областей
их значений, стоящих перед заключительной формулой. В дальнейшем типовые
кванторы обозначаются строчными, а заключительные формулы - прописными
готическими буквами и, таким образом, определение динамического свойства записывается
в виде слова, составленного из готических букв. Такая сжатая запись определений
ДС значительно облегчает их логический анализ и классификацию, а в дальнейшем -
получение принципа сравнения.
ДС частично упорядочены с помощью импликации,
введены типы, классы, семейства ДС и проведена основанная на них классификация
ДС.
. Основные и неосновные переменные динамики
систем, множества их значений, типовые кванторы
Как указывалось в гл. I,
в качестве основных переменных в динамике систем используются исходные данные t0,
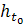 ,
движения или процессы x
(движения, процессы
,
движения или процессы x
(движения, процессы  с исходными
данными h), время t
и выходы (или состояния) - x.
Значения этих переменных могут вообще в динамике выбираться из множеств и
пространств, образующих среду:
с исходными
данными h), время t
и выходы (или состояния) - x.
Значения этих переменных могут вообще в динамике выбираться из множеств и
пространств, образующих среду:
t0 ∊
T0, 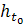 ∊
∊
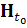 ,
(h ∊
H), x
∊
Ф, t ∊
T, x
∊
,
(h ∊
H), x
∊
Ф, t ∊
T, x
∊
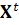 ((t,
x) ∊
𝚵).
((t,
x) ∊
𝚵).
Применительно к СП с выбранной ВФС множества
значений исходных данных h
сужаются до dom
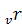 ,
процессы
,
процессы  с
любыми такими исходными данными h
принадлежат rh, значения
времени t для всякого такого
прцоесса принадлежат T(
с
любыми такими исходными данными h
принадлежат rh, значения
времени t для всякого такого
прцоесса принадлежат T( )
⊆
)
⊆
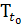 ,
а текущий выход (состояние) процесса x
=
,
а текущий выход (состояние) процесса x
=  (t).
(t).
С другой стороны, пространства входов 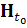 ,
исходных данных H, выходов
,
исходных данных H, выходов 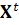 и
позиций 𝚵
оснащены семействами
и
позиций 𝚵
оснащены семействами 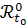 ,
, 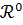 ,
,
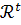 ,
,
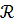 оценочных
множеств
оценочных
множеств 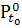 ⊂
⊂
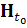 ,
,
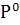 ⊂
H,
⊂
H, 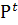 ⊂
⊂
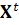 ,
P ⊂
𝚵,
которые могут рассматриваться как неосновные переменные динамики систем,
характеризующие среду.
,
P ⊂
𝚵,
которые могут рассматриваться как неосновные переменные динамики систем,
характеризующие среду.
При изучении динамических свойств относительно
этих семейств множеств в дальнейшем предполагаются выполненными следующие
условия, относящиеся к аксиомам среды:
(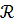 ): (∀P
∊
): (∀P
∊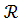 )
(∀t
∊
T) Ø ≠
)
(∀t
∊
T) Ø ≠
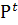 ⊆
⊆
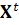 ,
,
(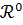 ): (∀
): (∀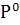 ∊
∊
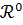 )
(∀t0
∊
T0) Ø ≠
)
(∀t0
∊
T0) Ø ≠
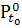 ⊆
⊆
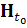 ,
,
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Обычно введенные системы оценочных множеств 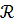 ,
,
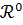 играют
роль систем окрестностей и могут задаваться весьма разнообразно. Например, как
открытые окрестности некоторого множества (Bhatia,
Szegö, 1967) или
с помощью неравенств для модулей фазовых координат (Ляпунов, 1956), нормы
вектора состояния (Четаев, 1962), метрики (Зубов, 1957), квазиметрики (Мовчан,
1960), неотрицательного функционала (Сиразетдинов, 1971), модулей нескольких
скалярных функций (Ляпунов, 1956), конечной совокупности неотрицательных
функционалов (Матросов, 1973, 1975) и т. д.
играют
роль систем окрестностей и могут задаваться весьма разнообразно. Например, как
открытые окрестности некоторого множества (Bhatia,
Szegö, 1967) или
с помощью неравенств для модулей фазовых координат (Ляпунов, 1956), нормы
вектора состояния (Четаев, 1962), метрики (Зубов, 1957), квазиметрики (Мовчан,
1960), неотрицательного функционала (Сиразетдинов, 1971), модулей нескольких
скалярных функций (Ляпунов, 1956), конечной совокупности неотрицательных
функционалов (Матросов, 1973, 1975) и т. д.
В частности, если заданы совокупности ρ
= (ρ1, …, 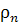 ),
), 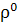 =
(
=
(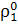 ,
…,
,
…, 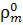 )
неотрицательных функционалов
)
неотрицательных функционалов
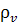 : (t,
x) → ρ(t,
x), 𝚵
→
: (t,
x) → ρ(t,
x), 𝚵
→ 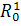 ,
v = 1, …, n,
,
v = 1, …, n,
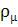 : h →
: h → 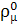 (h),
dom
(h),
dom 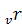 →
→ 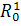 , μ = 1, …, m,
, μ = 1, …, m,
то семейства оценочных множеств образуются в
виде
P(ε)
= {(t, x)
∊
𝚵:
ρ(t,
x) < ε
∊
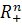 }
(при любом ε
∊
}
(при любом ε
∊
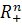 ),
),
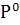 (δ)
= {h ∊
dom
(δ)
= {h ∊
dom 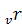 :
:
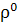 (h)
< δ
∊
(h)
< δ
∊
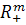 }
(при любом δ
∊
}
(при любом δ
∊
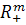 ),
),
где 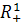 =
(0, +∞), и равенства между векторами понимаются как покомпонентные. В
этом случае, если
=
(0, +∞), и равенства между векторами понимаются как покомпонентные. В
этом случае, если
M = {(t,
x) ∊
𝚵:
ρ(t,
x) = 0}, M0
= {h ∊
dom 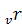 :
:
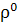 (h)
= 0}
(h)
= 0}
и
(∀t
∊
T) Ø ≠
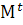 ⊂
⊂
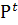 ,
(∀t0
∊
T0) Ø ≠
,
(∀t0
∊
T0) Ø ≠
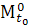 ⊂
⊂
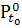 ,
,
то ρ(t,
x(t))
∊
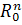 называется
отклонением в момент t
процесса x от множества
называется
отклонением в момент t
процесса x от множества 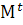 ⊂
⊂
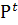 ,
,
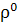 (h)
∊
(h)
∊
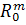 -
начальным отклонением входа
-
начальным отклонением входа 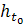 от
от 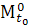 ⊂
⊂
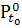 (аналогично
А. А. Мовчану (1960), В. М. Матросову (1973), где m
= n = 1). Но вообще
условия
(аналогично
А. А. Мовчану (1960), В. М. Матросову (1973), где m
= n = 1). Но вообще
условия 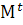 ≠
Ø,
≠
Ø, 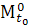 ≠
Ø не обязательны.
≠
Ø не обязательны.
Начальные оценочные множества 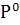 ,
,
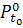 ,
являясь значениями неосновных переменных, накладывают также ограничения на
множества значений основных переменных h,
,
являясь значениями неосновных переменных, накладывают также ограничения на
множества значений основных переменных h,
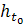 ,
которые при этом сужаются до
,
которые при этом сужаются до
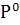 (r, v) ≡
(r, v) ≡ 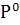 ∩ dom
∩ dom 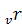 ;
; 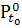 (r,
v) ≡ (
(r,
v) ≡ (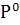 ∩
dom
∩
dom 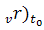 .
.
Различные практические обстоятельства делают
целесообразным дальнейшее сужение областей изменения входов 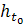 и
исходных данных h до
некоторых подмножеств
и
исходных данных h до
некоторых подмножеств 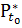 ⊆
⊆
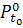 (r,
v) (здесь вводится
еще семейство
(r,
v) (здесь вводится
еще семейство 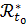 начальных
оценочных множеств
начальных
оценочных множеств 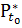 ,
, 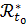 ≡
{
≡
{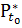 },
а также в дальнейшем семейство
},
а также в дальнейшем семейство 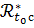 ≡ {
≡ {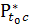 }),
при этом предполагается
}),
при этом предполагается
(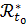 ): (∀t0
∊
dom
): (∀t0
∊
dom 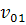 )
(∀
)
(∀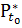 ∊
∊
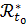 )
)
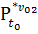 ≡
≡
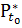 ∩
∩
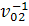 (
(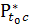 )
≠
Ø.
)
≠
Ø.
В качестве неосновных переменных динамики систем
могут входить также моменты времени t1
∊
T1, t2
∊
T2, …. Множества
T1 ⊆
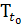 ≡
{t ∊
T: t0
≤ t},
≡
{t ∊
T: t0
≤ t},
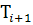 ⊆
⊆
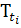 ≡
{t ∊
T:
≡
{t ∊
T: 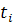 ≤
t}
(i = 1, …)
≤
t}
(i = 1, …)
должны задаваться дополнительно. Например, T1
= 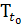 или
T1 =
или
T1 = 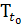 (x,
h) ≡
(x,
h) ≡ 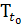 ∩
T(x,
h), ….
∩
T(x,
h), ….
Суженная область изменения основной переменной t
принимается T( )
≡ T(x,
h) ∩ T(t0)
∩ T(t1)
∩ …, где множества T(
)
≡ T(x,
h) ∩ T(t0)
∩ T(t1)
∩ …, где множества T(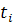 )
⊆
)
⊆
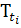 определяются
отдельно.
определяются
отдельно.
Типовые кванторы общности и существования по
основным и неосновным переменным динамики систем, как операторным переменным, в
которые в качестве типовой формулы входят формулы принадлежности значений этих
переменных указанным суженным множествам их значений, обозначаются в дальнейшем
соответствующими строчными готическими буквами (может быть, с индексами). В
частности, для кванторов общности используются строчные готические буквы без
индексов ∨ сверху, а для кванторов
существования - буквы с индексом ∨
сверху.
Основные и неосновные переменные динамики
систем, множества их значений и обозначения соответствующих им типовых
кванторов приводятся в табл. 1.
Строчные готические буквы 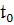 ,
,
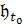 ,
𝔥,
𝔯,
,
𝔥,
𝔯,
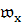 (соответственно
(соответственно
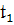 ,
…,
,
…, 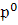 ,
𝔭),
отвечающие основным (неосновным) переменным, называются основными (неосновными)
буквами.
,
𝔭),
отвечающие основным (неосновным) переменным, называются основными (неосновными)
буквами.
Пусть 𝔚
- некоторое слово, составленное из строчных готических букв (с индексами).
Далее 𝔞
∊
𝔚
(соответственно 𝔞, 𝔟
∊
𝔚)
означает вхождение буквы 𝔞
(соответственно 𝔞, 𝔟)
в слово 𝔚.
2. Определения динамических свойств
Динамическое свойство описывается формулой
абстрактной динамики систем, представимой в препексном виде 𝔚
𝕽,
где 𝕽
- формула, не содержащая кванторов, 𝔚
- некоторое слово, составленное из строчных готических букв (с индексами),
служащих сокращающими символами для кванторов общности (буквы без ингдексов ∨
сверху) и существования (буквы с индексом ∨)
с указанием принятых в табл. 1 областей изменения связанных ими переменных,
удовлетворяющей следующим условиям:
а) основные переменные t0,
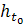 ,
x, t
связанно входят в его формулу; x
=
,
x, t
связанно входят в его формулу; x
= 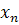 (t)
входит последней в 𝔚;
(t)
входит последней в 𝔚;
б) из каждой строки табл. 1 в слово 𝔚
может входить только одна буква из третьей или четвертой колонки;
Пример. Рассмотрим определение свойства 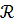 ,
,
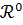 -устойчивости
(на T) системы процессов
r, полагая
-устойчивости
(на T) системы процессов
r, полагая 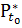 =
=
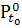 (r,
v), T(
(r,
v), T( )
=
)
= 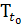 (
( ,
h), 𝕽
≡ (x
∊
,
h), 𝕽
≡ (x
∊
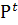 ).
Его формула
).
Его формула
𝔚𝕽 ≡ (∀t0
∊
T0) (∀P
∊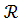 )
(∃
)
(∃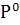 ∊
∊
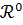 )
(∀
)
(∀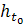 ∊
∊
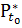 )
(∀
)
(∀ ∊
rh)
∊
rh)
(∀t
∊
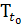 (
( ,
h)) (∀x
∊
,
h)) (∀x
∊
 (t))
(x ∊
(t))
(x ∊
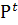 )
≡
)
≡ 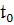 𝔭
𝔭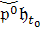 𝔯𝔱
𝔯𝔱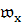 𝕽.
𝕽.
Эта формула охватывает классическое определение
А. М. Ляпунова (1956), определения устойчивости при постоянно действующих
возмущениях (Дубошин, 1940; 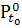 (δ)
= {(
(δ)
= {(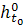 ,
,
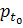 ):
||
):
||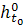 ||
< δ1, ||
||
< δ1, ||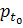 ||
< δ2}),
||
< δ2}), 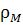 ,
,
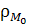 -устойчивости)
(Матросов, 1973;
-устойчивости)
(Матросов, 1973; 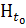 =
= 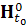 ,
,
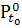 =
=
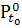 (δ)
(m = 1),
(δ)
(m = 1), 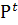 =
=
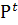 (ε)
(n = 1)) и др.
(ε)
(n = 1)) и др.
Таблица 1
|
Переменная
|
Область изменения
|
Квантор общности
|
Квантор существования
|
Название
|
|
|
|
|
|
|
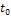
|
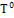
|
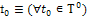
|
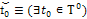
|
Начальное время
|
|
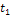
|
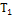
|
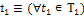
|
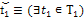
|
Последующий момент
|
|
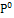
|
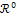
|
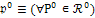
|

|
Начальное оценоч-ное множество
|
|
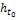
|
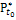
|
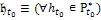
|
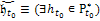
|
Вход
|
|
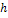
|
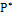
|
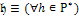
|
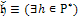
|
Исходные данные
|
|
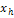
|
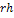
|
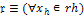
|
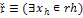
|
Процесс, соответст-вующий данному 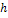
|
|
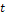
|
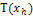
|
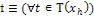
|
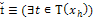
|
Текущий момент времени
|
|
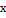
|
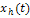
|
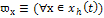
|
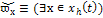
|
Выход (состояние)
|
|
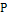
|
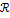
|
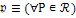
|
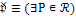
|
Текущее оценочное множество
|
|
(Другие неосновные переменные)
|
|
3. Классификация динамических свойств
Классификация проводится в трех аспектах,
связанных с видом формулы 𝕽
и вхождением основных и неосновных букв в слово 𝔚.
Формула 𝕽
определяет тип ДС. Множество динамических свойств с фиксированной формулой 𝕽
называется ДС типа 𝕽.
По-видимому, можно образовать бесконечное множество типов ДС, но не все из них
будут непересекающимися. Наиболее важными представляются типы ДС, в формулы 𝕽
которых не входят процессы  , но входят
множества P
∊
, но входят
множества P
∊
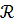 ,
переменные t и x.
Основным является тип 𝕽 ≡ (x
∊
,
переменные t и x.
Основным является тип 𝕽 ≡ (x
∊
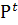 ),
причем в нем наиболее изучен тип 𝕽(ε)
≡ (ρ(t,
x) < ε).
),
причем в нем наиболее изучен тип 𝕽(ε)
≡ (ρ(t,
x) < ε).
Если в формуле 𝔚𝕽
все
переменные из первой колонки табл. 1 связаны, то мы имеем дело с динамическим
свойством системы процессов r
в среде с семействами множеств 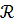 ,
, 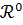 ,
…, которое для основного типа 𝕽,
как правило, обозначается
,
…, которое для основного типа 𝕽,
как правило, обозначается 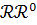 …𝔇𝔅
системы процессов r (за
исключением некоторых случаев, когда часть букв 𝔭,
…𝔇𝔅
системы процессов r (за
исключением некоторых случаев, когда часть букв 𝔭,
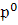 ,
… входит в слово 𝔚 с индексом ∨,
в их обозначении соответствующее семейство множеств заменяется его элементом с
этим индексом).
,
… входит в слово 𝔚 с индексом ∨,
в их обозначении соответствующее семейство множеств заменяется его элементом с
этим индексом).
Если некоторые переменные 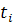 ,
P, P0,
… остаются свободными, то получается динамическое свойство системы процессов и
этих переменных относительно остальных семейств множеств. Для основного типа 𝕽
в его обозначении участвуют свободные переменные. Они заменяют семейства
множеств, которым принадлежат их значения.
,
P, P0,
… остаются свободными, то получается динамическое свойство системы процессов и
этих переменных относительно остальных семейств множеств. Для основного типа 𝕽
в его обозначении участвуют свободные переменные. Они заменяют семейства
множеств, которым принадлежат их значения.
Вводится иерархия семейств ДС.
С точки зрения структуры слова 𝔚
множество ДС делится на 16 семейств, отличающихся вхождением в слова 𝔚
основных букв. Целесообразно ввести следующие названия ДС: t0
- безусловное, если t0 ∊
𝔚; t0
- условное, если 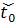 ∊
𝔚;
∊
𝔚;
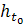 -
безусловное, если
-
безусловное, если 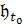 ∊
𝔚;
∊
𝔚;
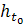 -
условное, если
-
условное, если 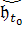 ∊
𝔚;
сильное, если 𝔯 ∊
𝔚;
слабое, если 𝔯 ∊
𝔚;
универсальное, если 𝔱 ∊
𝔚;
экзистенциональное, если
∊
𝔚;
сильное, если 𝔯 ∊
𝔚;
слабое, если 𝔯 ∊
𝔚;
универсальное, если 𝔱 ∊
𝔚;
экзистенциональное, если 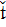 ∊
𝔚.
∊
𝔚.
Для данного типа 𝕽
и одинакового вхождения всех неосновных букв в 𝔚
импликацией ДС этих 16 семейств могут быть частично упорядочены, причем
вводится иерархическая структура из 5 уровней (рис. 1). Здесь импликация
семейств ДС понимается как совокупность импликаций тех их свойств, которые
имеют один и тот же тип и одинаковое вхождение всех неосновных букв в слово 𝔚
(с учетом их порядка и индексов ∨).
И, значит, принадлежат одному классу ДС (см. ниже). Вид вхождения x
в 𝔚
не является существенным при классификации семейств (и не рассматривается), так
как
x
∊
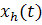 ,
а
,
а 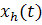 =
singl, поэтому
=
singl, поэтому 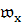 =
=
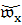 .
.

На первом (верхнем) уровне - одно семейство
безусловных сильных универсальных ДС, называемое основным семейством ДС; на
пятом (нижнем) - одно семейство (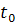 ,
,
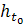 )
- условных слабых экзистенциональных ДС; на 2, 3, 4-м уровнях - промежуточные
(по силе) семейства ДС.
)
- условных слабых экзистенциональных ДС; на 2, 3, 4-м уровнях - промежуточные
(по силе) семейства ДС.
Дальнейшая классификация ДС связана с понятием
ранга r ДС, равного числу
неосновных букв в его слове 𝔚
(r = 0, 1, 2, …).
Слово 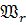 ,
составленное из r неосновных
букв (с их индексами), взятых в том порядке, в котором они входят в слово 𝔚
данного ДС ранга r, называется
представлением слова 𝔚 и задает
класс ДС.
,
составленное из r неосновных
букв (с их индексами), взятых в том порядке, в котором они входят в слово 𝔚
данного ДС ранга r, называется
представлением слова 𝔚 и задает
класс ДС.
Представлениями 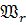 слов
𝔚
определяется разбиение множества ДС на непересекающиеся классы. Классы ДС
данного типа, семейства и ранга упорядочены с помощью импликации (частично).
слов
𝔚
определяется разбиение множества ДС на непересекающиеся классы. Классы ДС
данного типа, семейства и ранга упорядочены с помощью импликации (частично).
В классе динамических свойств данного типа и
семейства ДС частично упорядочены с помощью импликации и формально отличаются
лишь вхождением основных букв в слово 𝔚
относительно неосновных, т. е. “степенью равномерности (равностепенности)
относительно 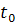 ,
, 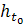 ,
x, t”.
В частности, если в слово 𝔚
входит одна экзистенциональная буква
,
x, t”.
В частности, если в слово 𝔚
входит одна экзистенциональная буква 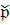 (или
(или
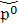 ),
предшествующая
),
предшествующая 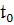 , то это ДС влечет
динамическое свойство того же класса, отличающееся лишь тем, что в его слове
, то это ДС влечет
динамическое свойство того же класса, отличающееся лишь тем, что в его слове 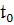 предшествует
предшествует
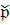 (или
(или
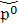 ).
).
𝔚𝕽 ≡ (∀P
∊
𝕽) (∃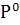 ∊
∊
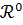 )
(∀t0
∊
T0) (∀
)
(∀t0
∊
T0) (∀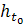 ∊
∊
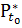 )
(∀
)
(∀ ∊
rh)
∊
rh)
(∀t
∊
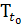 (
( ,
h)) (∀x
∊
,
h)) (∀x
∊
 (t))
(x ∊
(t))
(x ∊
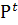 )
≡ 𝔭
)
≡ 𝔭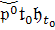 𝔯𝔱
𝔯𝔱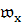 𝕽.
𝕽.
Вместе с ДС 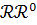 -устойчивости
(пример п. 2) оно образует класс
-устойчивости
(пример п. 2) оно образует класс 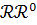 -устойчивости
𝔭
-устойчивости
𝔭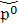 (
(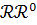 𝔇𝔅)
системы процессов r второго
ранга, основного семейства, основного типа.
𝔇𝔅)
системы процессов r второго
ранга, основного семейства, основного типа.
Динамические свойства 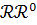 -устойчивости
и равномерной
-устойчивости
и равномерной 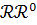 -устойчивости упорядочены
с помощью импликации
-устойчивости упорядочены
с помощью импликации
𝔭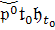 𝔯𝔱
𝔯𝔱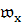 𝕽
⟹
𝕽
⟹
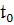 𝔭
𝔭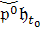 𝔯𝔱
𝔯𝔱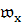 𝕽,
𝕽,
т. е. равномерная по t0
∊
T0 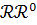 -устойчивость
на T СП r
является более сильным свойством, чем
-устойчивость
на T СП r
является более сильным свойством, чем 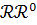 -устойчивость
на T СП r.
ДС равномерной по t0
-устойчивость
на T СП r.
ДС равномерной по t0 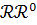 -устойчивости
на T охватывает
свойство равномерной устойчивости по К. П. Персидскому, равномерной
устойчивости при постоянно действующих возмущениях по С. Г. Горщину и др.
-устойчивости
на T охватывает
свойство равномерной устойчивости по К. П. Персидскому, равномерной
устойчивости при постоянно действующих возмущениях по С. Г. Горщину и др.
ДС основного типа 𝕽
≡ (x
∊
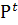 )
и основного семейства (безусловных сильных универсальных динамических свойств)
называются основными динамическими свойствами (ОДС).
)
и основного семейства (безусловных сильных универсальных динамических свойств)
называются основными динамическими свойствами (ОДС).
В классических и современных математических
работах и в литературе по динамике исследовались главным образом основные
динамические свойства.
Примеры определений неосновных ДС.
. Пусть 𝕽
≡ (x
∊
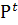 ),
ДС
),
ДС 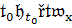 𝕽
содержится в семействе (
𝕽
содержится в семействе (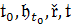 ) безусловных
слабых универсальных свойств, имеет основной тип, нулевой ранг и называется
слабой P, P0-оценкой
СП r. Оно обобщает
понятия A, λ-оценки
Н. Г. Четаева (1962), (A,
λ, t0, T)-устойчивости
по Н. Г. Четаеву и т. п.
) безусловных
слабых универсальных свойств, имеет основной тип, нулевой ранг и называется
слабой P, P0-оценкой
СП r. Оно обобщает
понятия A, λ-оценки
Н. Г. Четаева (1962), (A,
λ, t0, T)-устойчивости
по Н. Г. Четаеву и т. п.
2. Пусть T
= T0 = R1,
(∀t
∊
T) X
= 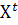 .
Рассмотрим ДС типа 𝕽 ≡ (
.
Рассмотрим ДС типа 𝕽 ≡ (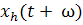 =
= 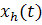 )
(не основного), предполагая
)
(не основного), предполагая
(∀t0
∊ T0) 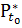 =
(P0 ∩ dom r
=
(P0 ∩ dom r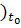 ,
,
T( )
=
)
= 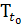 ∩ T(x, h) ∩ {t ∊
T: t +
∩ T(x, h) ∩ {t ∊
T: t + 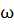 ∊
T(x, h)}
∊
T(x, h)}
и считая области изменения всех переменных
формулы 𝔚𝕽
непустыми. Пусть 𝔚 ≡ 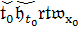 .
Свойство 𝔚𝕽 относится к
семейству
.
Свойство 𝔚𝕽 относится к
семейству 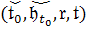 (
(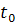 ,
,
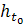 )
- условных сильных универсальных свойств нулевого ранга и называется P0-сильной
ω-периодичностью
на T СП r.
ДС 𝔚𝕽
≡
)
- условных сильных универсальных свойств нулевого ранга и называется P0-сильной
ω-периодичностью
на T СП r.
ДС 𝔚𝕽
≡ 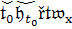 𝕽
(того же типа, что и предыдущее динамическое свойство), содержится в семействе
𝕽
(того же типа, что и предыдущее динамическое свойство), содержится в семействе 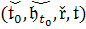 условных
слабых универсальных ДС, имеет нулевой ранг и называется P0-слабой
ω-периодичностью
на T СП r.
Как легко заметить,
условных
слабых универсальных ДС, имеет нулевой ранг и называется P0-слабой
ω-периодичностью
на T СП r.
Как легко заметить,
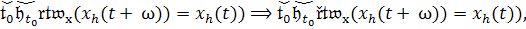
т. е. P0-сильная
ω-периодичность
на T СП имплицирует P0-слабую
ω-периодичность.
Заключение
В данной курсовой работе дано строгое
математическое определение динамической (функционирующей) системы и приведены
некоторые способы задания динамических систем (глава 1); во второй главе дается
определение системы процессов; в третьей приводится определение основных
динамических свойств, ДС частично упорядочены с помощью импликации, введены
типы, классы, семейства ДС и проведена основанная на них классификация ДС,
приведены примеры.
Список литературы
1.
Матросов В.М., Анапольский Л.Ю., Васильев С.Н. Метод сравнения в математической
теории систем. - Новосибирск: Наука, 1980.