Динамика шпиндельного узла

Динамика шпиндельного узла

ДИНАМИКА ШПИНДЕЛЬНОГО УЗЛА

ДЕМПФИРУЮЩИЕ СВОЙСТВА ШПИНДЕЛЬНОГО УЗЛА

Шпиндельный узел станка представляет собой чаще всего корпусную деталь с установленным на подшипниковые опоры шпинделем. Шпиндельный узел может быть неподвижно закреплен на базовой детали станка (токарные, фрезерные, сверлильные станки) или перемещаться, выполняя еще и движение подачи (расточные, шлифовальные станки). Сам шпиндель в шпиндельном узле также может быть неподвижным или выдвигаться с пинолью. Любой ШУ обладает радиальной, осевой и угловой податливостями, которые изменяют свои значения в процессе работы, регулировки и за время эксплуатации станка. Податливости ШУ в большей степени определяются податливостями шпиндельных опор и самого шпинделя и в меньшей степени податливостями корпусной детали.

Кроме того, все элементы конструкции ШУ - отдельные детали, подвижные и неподвижные соединения (стыки) обладают различной демпфирующей способностью. Демпфирующая способность деталей зависит как от материала изготовления, так и от формы детали (колокол - пример детали с низкими демпфирующими свойствами). Основное демпфирование колебаний происходит в стыках между деталями.

Демпфирующие свойства шпиндельного узла можно количественно оценить с помощью логарифмического декремента затухания колебаний l

l = ln(An/An+1) > [l],

где    Ап, Ап+1 - амплитуды соседних по периоду свободных затухающих колебаний шпиндельного узла;

[l] - допустимое минимальное значение логарифмического декремента колебаний шпиндельного узла данного типа станка.

Для некоторых типов станков значение допустимого логарифмического декремента следующие:

[l] = 0,13 - для радиально-сверлильных станков;

[l] = 0,23 - для токарных станков;

[l] = 0,27 - для фрезерных станков;

[l] = 0,30 - для шлифовальных станков.

Приближенно величину логарифмического декремента затухания колебаний l можно рассчитать по формуле

,

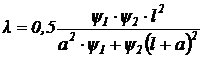где y1, y2 - относительное рассеяние энергии (демпфирующее свойство) передней и задней опоры;

a, l - консоль и пролет шпинделя.

При установке в шпиндельную опору нескольких подшипников качения относительное рассеяние опоры yS равно сумме демпфирующих свойств y0 установленных в ней подшипников

yS = Sy0i

Для расчетов можно принимать следующие значения демпфирующих свойств подшипников качения:

y0 = 0,21 - радиально-упорный однорядный шарикоподшипник;

y0 = 0,23 - радиальный однорядный шарикоподшипник;

y0 = 0,26 - упорный однорядный шарикоподшипник;

y0 = 0,35 - радиально-упорный конический однорядный роликоподшипник;

y0 = 0,36 - радиальный однорядный роликоподшипник;

y0 = 0,40 - радиальный двухрядный роликоподшипник.

ОПРЕДЕЛЕНИЕ СОБСТВЕННОЙ ЧАСТОТЫ КОЛЕБАНИЙ ШПИНДЕЛЯ

Динамический расчет ШУ сводится к определению амплитуд радиальных, осевых и крутильных установившихся колебаний шпинделя от гармонических силовых возмущающих воздействий со стороны процесса резания и привода главного движения при различных частотах вращения. При этом особое внимание уделяется частотам вращения близким к частоте собственных колебаний шпинделя. Как правило, частоты вращения шпинделя ниже его собственный частот колебаний, поэтому достаточно определить низшую (первую, основную) собственную частоту, чтобы судить о ее влиянии на ШУ.

Теоретическое определение частоты собственных колебаний шпинделя, установленного на опоры с несколькими сосредоточенными массами является весьма сложной задачей. Поэтому часто определяют приближенно значение частоты собственных изгибных колебаний первого тона по формуле (Г.С. Маслов, стр. 173)

,

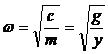где    ω=2pf - круговая частота, с-1;

f - частота колебаний, Гц;

y - прогиб от собственного веса наиболее длинного пролета, м;

с - жесткость наиболее длинного пролета, Н/м;

т - масса наиболее длинного пролета, кг;

g - ускорение свободного падения, м/с2.

Приближенно можно определить круговую частоту w, с-1 и частоту f, Гц собственных колебаний шпинделя, не имеющего больших сосредоточенных масс и по другой формуле (Кузнецов Ю.Н. Станки с ЧПУ, стр.176)

,               ,

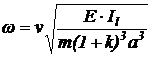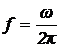где    k = a/l;

a - длина консоли;

l - длина пролета;

n = f(k) - коэффициент, который для k =2,5…3,5 лежит в пределах n =2,3…2,4;

m - масса шпинделя;

Il - момент инерции сечения на длине пролета.

При точном проектировании необходимо учитывать все сосредоточенные и распределенные массы шпинделя и жесткость каждой опоры.

В простейших случаях, когда шпиндельный узел можно свести к двухопорной балке массой m1 с одним пролетом l и одной консолью a , имеющей в пролете и на консоли по одной сосредоточенной массе m01, m02, определение собственных частот колебаний может быть выполнено на основе использовании коэффициентов влияния. Суть метода заключается в том, что дифференциальное уравнение свободных колебаний каждой из п масс системы описывается уравнением

,

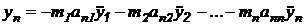где     аni - прогиб (перемещение) в точке, где сосредоточена п-я масса, приложенная в i-той точке (в месте сосредоточения массы);

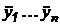 - вторые производные этих перемещений по времени;

m1…mn - сосредоточенные массы.

Коэффициенты влияния - прогибы от единичной силы определяются в каждой точке обычными методами сопротивления материалов.

,

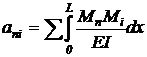где     Мп, Мi - изгибающие моменты, вызванные соответствующими единичными силами;

L - общая длина расчетной балки;

EI - характеристика изгибной жесткости сечения.

Функцию перемещения (прогиба) принимают в виде

yi = Aisin(wit+j),

где    Аi, wi - i-я неизвестная амплитуда и i-я неизвестная частота.

Подставляя это выражение в дифференциальное уравнение перемещений, получают систему алгебраических уравнений относительно неизвестных амплитуд Аi и частот wi.

Например, для двухмассовой системы:

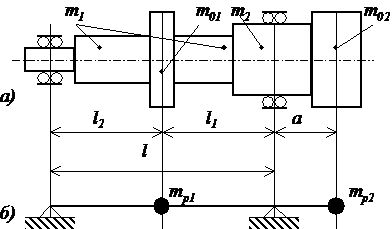
Рис. 1. Конструктивная а) и расчетная б) схемы шпинделя с двумя сосредоточенными массами

,

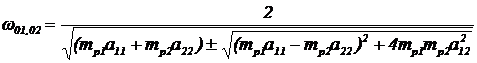где    а11, а12, а22 - коэффициенты влияния;

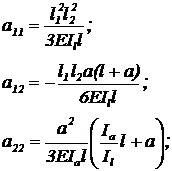
mp1, mp2 - расчетные приведенные массы:

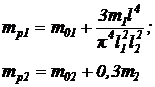
m01, m02, m1, m2 - сосредоточенные массы в центре пролета и на консоли; масса пролета и консоли шпинделя;

l, - длина пролета;

l1, l2 - длина от передней опоры до сосредоточенной массы, длина от сосредоточенной массы до задней опоры;

КРИТИЧЕСКАЯ ЧАСТОТА ВРАЩЕНИЯ ДВУХОПОРНОГО ШПИНДЕЛЯ

Если вращать двухопорный шпиндель жесткостью j с одной сосредоточенной массой т в виде диска (например, зубчатого колеса) между опорами, то можно отметить, что всегда, при любой доступной точности, существует некоторый эксцентриситет е на величину которого смещен центр тяжести диска относительно оси вращения. При вращении центробежная сила FЦ уравновешивается силой упругости FУ. Ось шпинделя прогнется при этом на величину у.

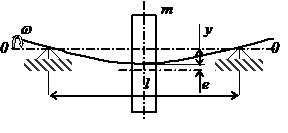
Рис. 2. Расчетная схема для определения критической частоты вращения

FЦ = FУ ,                              m2(y + e) = jy,

m2y + m2e = сy,              сy - m2y = m2e.

Разделим правую и левую часть уравнения на с

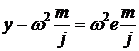
Выражение с/m является квадратом круговой частоты собственных колебаний шпинделя w02, тогда

y - 2y/w02 = 2e/w02,

y(1 - 2/w02) = e2/w02,

.

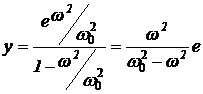Из уравнения следует, что прогиб шпинделя растет с увеличением угловой скорости. При равенстве частоты вращения и собственной круговой частоты  =w0 (критическая частота вращения) наступает резонанс, когда теоретический прогиб y стремится к бесконечности и должна случиться поломка. Однако в действительности, так как в системе имеются потери энергии, которые не учитываются расчетом, жесткости вала оказывается достаточно, чтобы поломка не произошла.

Следует отметить, что критическая частота вращения не зависит от эксцентриситета и не может быть изменена никакой балансировкой.

При увеличении частоты вращения выше критической  > w0 изменяется знак прогиба на противоположный, что говорит о том, что центр тяжести диска находится между осью вращения 0-0 и изогнутой осью шпинделя. С дальнейшим увеличением частоты вращения происходит самоцентрирование диска - прогиб уменьшается.

Для определения влияния жесткости опор на критическую частоту вращения предположим, что на шпинделе с эксцентриситетом равным нулю (e = 0) симметрично относительно опор (l1=l2=l/2, реакция опор R1=R2=R) расположен диск массой m (см. рис. 3). Шпиндель, имеющий изгибную жесткость равную с, установлен на подшипниках с одинаковой жесткостью (с1=с2=с0).

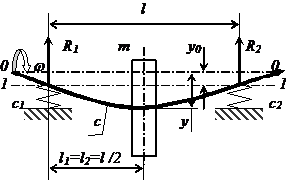
Рис. 3. Расчетная схема для определения критической частоты вращения с учетом жесткости опор

Под действием центробежной силы FЦ шпиндель прогнется на величину y, а опоры просядут на величину y0 от первоначального положения 0-0. Ось шпинделя при вращении займет положение 1-1.

Осадка (податливость) подшипников зависит от реакции опор, которые, в свою очередь, зависят от центробежной силы

шпиндель колебание вращение

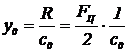
Центробежная сила возникает из-за первоначального прогиба под весом диска и пропорциональна величине прогиба

FЦ = mw2кр y.

Сила упругости FУпр пропорциональна величине прогиба и изгибной жесткости шпинделя и равна центробежной силе

FУпр = с(y - y0) = 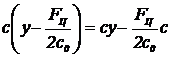 = FЦ = mw2кр y,

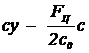= mw2кр y,

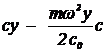= mw2кр y.

Откуда определяется критическая частота вращения двухопорного шпинделя жесткостью j с одной сосредоточенной массой m посредине пролета при равенстве жесткостей передней и задней опор j0

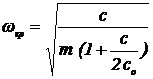
Следовательно, критическая частота вращения снижается с уменьшением жесткости опор. Этим часто пользуются на практике. Для возможности повышения частоты вращения шпинделя целесообразно устанавливать подшипники качения в промежуточные упругие опоры, жесткость которых во много раз (в 5…8) меньше жесткости шпиндельных подшипников.

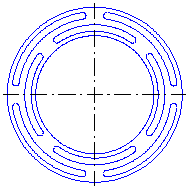
Рис. 4. Промежуточная упругая подшипниковая опора

Литература

1.  Орликов М.Л. Динамика станков. - 2-е изд. перераб. и доп. - К.: Выща школа. Головное изд-во, 1989. - 272 с.; 8 табл.; 138 ил. - Билиогр.: 70 назв.

2.      Металлорежущие станки и автоматы: Учебник для машиностроительных втузов / Под ред. А.С. Проникова. - М.: Машиностроение, 1981. - 479 с., ил. (стр. 144-184).

.        Кудинов В.А. Динамика станков. - М.: Машиностроение, 1967. - 360 с.

.        Металлорежущие станки: Учебник для машиностроительных втузов / Под ред. В.Э.Пуша. - М.: Машиностроение, 1985. - 256 с., ил. (стр. 357-411).

.        Попов В.И., Локтев В.И. Динамика станков. - К.: Технiка, 1975. - 135 с.

.        Детали и механизмы металлорежущих станков, т. 1. / Под ред. Д.Н. Решетова. - М.: Машиностроение, 1972. - 664 с.

.        Детали и механизмы металлорежущих станков, т. 2. / Под ред. Д.Н. Решетова. - М.: Машиностроение, 1972. - 520 с.

.        Кедров С.С. Колебания металлорежущих станков. М., «Машиностроение», 1978, 199 с. с ил.

.        Ривин Е.И. Динамика привода станков. - М.: Машиностроение, 1966, 203 с.

.        Маслов Г.С. Расчеты колебаний валов. Справочное пособие. - М.: Машиностроение, 1968.

.        Проников А.С. Программный метод испытания металлорежущих станков. - М.: Машиностроение, 1985. - 288 с., ил.

.        ЭНИМС, Типовые методики и программы испытаний металлорежущих станков. Методические рекомендации. - М.: НИИмаш, 1984.