Використання можливостей системи Wolfram Mathematica при вивчені математичного аналізу
Вступ
На сьогоднішній день в широких колах користувачів
обчислювальних машин став досить популярним і широко використовуваним термін
«комп'ютерна математика». Дане поняття включає сукупність як теоретичних і
методичних засобів, так і сучасних програмних і апаратних засобів [10].
Попит на універсальні і спеціалізовані програмні пакети для
вирішення різних прикладних завдань викликав появу на ринку програмних
продуктів систем комп'ютерної математики (СКМ), які швидко стали популярними.
В останні роки в процес математичної освіти дедалі
наполегливіше і успішніше впроваджуються такі системи, як DERIVE, MatLab,
Maple, MuPAD, Mathematica та ін. Вони
звільняють користувача від проведення громіздких, рутинних викладок, однотипних
обчислень і дозволяє зосередитися безпосередньо на аналізі модельованого явища.
Діалог з пакетом СКМ відбувається на досить природній мові, використовуються
традиційні позначення і способи написання формул. Безсумнівним достоїнством
сучасних СКМ є прекрасні графічні можливості, що дозволяє зробити наочними
багато математичних понять і методів.
У викладацькому середовищі математиків існує обґрунтоване
побоювання, що використання систем комп'ютерної математики "зіпсує"
математичну підготовку студентів, подібно до того, як "калькулятор розучив
їх рахувати". Вихід бачиться у роз'ясненні призначення та використання
СКМ. Очевидно, що успішне використання СКМ можливо лише за умови знання основ
математики. Більше того, щоб використати всі можливості таких пакетів як
MatLab, Maple, Mathematica потрібна дужа висока математична культура [7, c. 3].
А також, при залученні СКМ для обчислень потрібно пам'ятати,
що використовувати обчислювальну систему не завжди просто. Для одних і тих же
завдань система може пропонувати кілька варіантів виконання, і студент, який
застосовує систему, повинен вміти вибрати найбільш ефективний варіант. Далі,
будь-яка система комп'ютерної математики не застрахована від локальних помилок,
і користувач повинен пам'ятати про способи контролю проведених обчислень. Тобто
потрібно, в певному сенсі, вміти відслідковувати процес виконання перетворень.
Також потрібно мати уявлення про способи подання даних в СКМ.
В даній курсовій роботі об'єктом дослідження є процес
вивчення математичного аналізу.
Предметом дослідження - використання СКМ Wolfram Mathematica
при вивченні математичного аналізу.
Мета даної роботи - продемонструвати можливості системи Wolfram Mathematica при вивчені
математичного аналізу.
Актуальність роботи полягає в тому, що за допомогою системи WM, студент може самостійно перевіряти
себе, тобто, контролювати рівень формування навичок і умінь, представляти
результати у найбільш наочній формі, будувати без труднощів складні тривимірні
поверхні і т.д. При цьому звільняти час для обдумування алгоритмів, більш
глибокого вивчення математичної сутності розв'язуваних задач і їх рішень
різними методами.
Для досягнення поставленої мети визначені наступні задачі:
. розглянути програму навчальної дисципліни
«Математичний аналіз» та самостійну роботу студентів по цій дисципліні;
. розглянути та проаналізувати сучасні СКМ;
. розглянути загальні відомості про систему Wolfram
Mathematica;
. розглянути особливості та інтерфейс системи WM;
. продемонструвати обчислення границь функцій у WM;
. продемонструвати обчислення похідних і інтегралів у
WM;
. продемонструвати побудову графіків на плоскості та у
просторі в WM;
. продемонструвати розкладання функцій в ряди Тейлора
і Маклорена.
.
Розділ
1. Теоретичні аспекти математичного аналізу та системи Wolram Mathematica
1.1 Деякі відомості математичного аналізу
Математичний аналіз займає центральне місце в ряду
математичних і технічних дисциплін, які вивчаються. Він є базою, стартовим
матеріалом для їх розуміння та засвоювання.
В процесі навчання математичного аналізу студенти отримують
знання та навички як найпростішого, так і складного аналізу. Вони вчаться
використовувати методи диференціального та інтегрального числення функцій
однієї або декількох змінних. Широко ознайомлюються з дослідженнями функцій та
способами їх представлення, вивчають різноманітні прийоми та оператори для
логічного та грамотного запису виразів. Більш повний зміст курсу представлений
у програмі навчальної дисципліни "Математичний аналіз", яка приведена
у додатку 1.
Методи математичного аналізу, засновані на доказах теорем,
лем, наслідках та ін., привчають студентів до строгості математичного мислення,
абстрактності в підходах до розв’язання задач, до бачення та прогнозування
аналогових ситуацій. Оволодіння методами математичного аналізу дозволяє
використовувати їх в дослідницьких та практичних цілях, домагаючись реальності
результатів та необхідної точності розрахунків [6, c. 3].
Міцне засвоєння сучасних математичних методів дає змогу
випускнику університету розв’язувати в своїй діяльності актуальні практичні
задачі та розуміти написані на сучасному науковому рівні результати інших
дослідників і тим самим удосконалювати свою проф. майстерність [6, c. 4].
Однак, курс математичного аналізу дуже широкий і складний,
він охоплює великий об’єм матеріалу. Проте, виділених годин на практичні
заняття не достатньо для якісного засвоєння необхідного матеріалу та для
формування навичок і умінь по цій дисципліні. Тому, приблизно 1/3 відводиться
на самостійну роботу студентів.
Самостійна навчальна робота не лише формує у студентів навички
і вміння самостійного здобування знань, що важливо для здійснення неперервної
освіти протягом усієї подальшої трудової діяльності, а й має важливе виховне
значення, оскільки формує самостійність як рису характеру, що відіграє істотну
роль у структурі особистості сучасного спеціаліст вищої кваліфікації.
Вагомим підґрунтям для самостійної роботи має стати лекція,
на якій викладач не просто закликає до самостійної роботи, а й порушує
проблеми, пропонує конкретні завдання, рекомендує певну літературу чи системи
комп’ютерної математики, визначає час для виконання роботи, повідомляє види й
терміни її контролю, наголошує на можливості отримати консультацію [8,c. 126].
Використання СКМ у самостійній роботі студентів при вивчені
математичного аналізу дає змогу поєднати високі обчислювальні можливості з
перевагами графічного подання інформації. Це сприяє розвиткові геометричної
інтуїції, графічних навичок, евристичної діяльності студентів і дає змогу
враховувати їхні індивідуальні здібності. Також системи комп’ютерної математики
можна паралельно використовувати як потужні електронні довідники з великою
кількістю прикладів [8, c. 140].
1.2 Короткий огляд та аналіз сучасних
систем комп’ютерної математики
Нові інформаційні технології докорінно змінили порядок вирішення
математичних завдань. Тепер рішення завдань і виконання математичних
перетворень доцільно проводити за допомогою спеціальних програм. Саме огляду і
короткому аналізу таких програмних продуктів і присвячений даний підрозділ [4, c. 15].
За функціональністю сучасні математичні системи діляться в
цілому на дві категорії: пакети, призначені в основному для чисельних
розрахунків (MatLab, S-PLUS) і системи комп’ютерної алгебри (Derive,
Mathematica, Maple, Macsyma, частково, MathCad) - вони також називаються системами
символьних чи аналітичних обчислень (Symbolic Manipulation Program). Це
найбільш універсальні математичні програми, здатні вирішувати най різноманітні
задачі, причому як чисельно, так і точно - аналітично [11].
Опис та особливості системи Mathematica будуть розглянуті в
підрозділі 1.3.
) DERIVE
Система Derive, повна назва якої Derive a Mathematical
Assistant (математичний помічник Derive), фірми Soft Warehouse, Inc., являється
маловимогливим до ресурсів пакетом символьної математики, орієнтованим в першу
чергу на студентів та шкільних викладачів. Однак він з успіхом використовується
також для серйозних наукових досліджень [3, c. 11]. є зручним інструментом при
диференціюванні, інтегруванні, розкладанні функцій в ряди, знаходженні границь.
Система має повний набір вбудованих елементарних функцій, а також безліч
статистичних і спеціальних математичних функцій. Система дозволяє працювати з
матрицями, проводити перетворення Фур’є і Лапласа. Здатність системи працювати
з комплексними числами робить її привабливою для радіотехнічних і
електротехнічних розрахунків. Загалом, можливості системи повністю покривають
потреби класичних курсів елементарної та вищої математики [1, c. 23].
2) MAPLE
Даний продукт компанії Waterloo Maple Software, Inc.
(#"525686.files/image001.gif">.
Приклади обчислення невизначених інтегралів представлені на
рис. 2.3.1.
Тут вхідна комірка у першому прикладі представлена у форматі
введення (Input-Form), а в інших прикладах - в стандартному форматі
(StandardForm), при використанні палітри. При записі інтегралів останній формат
кращий зважаючи на наочності, оскільки при цьому знаки інтеграла мають
природний математичний вигляд.
Наступна серія прикладів (рис. 2.3.2) ілюструє обчислення
визначених інтегралів звичайного виду та інтегралів з межами-функціями.
Система Mathematica має найширші можливості обчислення
інтегралів. Ядро системи увібрало в себе формули інтегрування з усіх відомих
довідників.здатна обчислювати навіть кратні інтеграли з фіксованими і змінними,
верхнім або нижнім, межами.
На рис. 2.3.3 представлено обчислення декількох подвійних визначених
інтегралів. Хоча обчислення подвійного інтеграла передбачено в синтаксисі
функції Integrate, це не завжди дає результат. Як правило, обчислення кратних
інтегралів краще виробляти, використовуючи послідовне обчислення однократних
інтегралів, вкладених один в одного.
При обчисленні складних інтегралів, наприклад які не мають
представлення через елементарні функції, система Mathematica 2 зверталася до
своїх пакетів розширень в спробі знайти рішення, яке може бути представлене
через спеціальні математичні функції. Mathematica наступних версій вже не
акцентує увагу користувача на свої проблеми і, як правило, видає результат
інтегрування. Однак деколи він може мати досить незвичайний вигляд (рис.
2.3.4).
Ці приклади наочно показують, що обчислення первісних в
системі може дати результати, далекі від тривіального обчислення невизначених
інтегралів, приведених у звичайних довідниках з математики. До речі, і при
обчисленні тривіальних інтегралів результат може бути іншим, ніж у довідниках,
із-за різних перетворень, застосованих для отримання кінцевих формул. Часом
можуть знадобитися певні зусилля для отримання результату в заданій формі. Як
підінтегральний вираз, так і результати обчислень можуть містити як
елементарні, так і спеціальні математичні функції.
Необхідно зазначити, що результати символьного інтегрування в
системах Mathematica різних версій нерідко різняться. Більше того, вони можуть
різнитися і в межах однієї версії Mathematica, так як ядро системи постійно
вдосконалюється. Звичайно більш пізні версії дають більш точні результати
обчислень особливих інтегралів, хоча часом вони і виглядають більш складними і
навіть незвичайними. Це говорить про необхідність вдумливо ставитися до
одержуваних результатів.
Для обчислення чисельних значень визначених інтегралів
використовується функція NIntegrate [f, {x, xmin, xmax}], яка повертає чисельне
наближення інтеграла від функції f по змінній х в межах від xmin до xmax.
Вона має ряд опцій, які можна отримати, виконавши команду
Options [Nlntegrate]. Наведемо приклади чисельного інтегрування (рис. 2.3.5).
Ці приклади показують, що функція NIntegrate з успіхом може
застосовуватися для обчислення як однократних, так і багатократних визначених
інтегралів, в тому числі зі змінними межами.
4. Побудова графіків на площині
У відношенні графіки система Mathematica є лідером серед
систем комп'ютерної алгебри. Велика кількість опцій дозволяє оформляти графічні
образи практично в будь-якому бажаному вигляді.
Графіки в системі Mathematica є об'єктами і тому вони можуть
бути значеннями змінних.
Почнемо розгляд графічних можливостей системи з побудови
найпростіших графіків функцій однієї змінної виду у = f (x) або просто f (x).
Графік таких функцій будується на площині, тобто в двовимірному просторі. При
цьому використовується прямокутна (декартова) система координат. За
замовчуванням будуються і лінії координатної системи.
Для побудови двовимірних графіків функцій виду f(x)
використовується вбудована в ядро функція Plot: [f, {x, xmin,
xmax}] - повертає об'єкт, що представляє собою графік функції f аргументу х в
інтервалі від xmin до xmax; [{f1, f2 ,...}, {x, xmin, xmax}] - повертає об'єкт
у вигляді графіків ряду функцій fi.
Функція Plot використовується для побудови однієї або кількох
ліній, що дають графічне представлення для зазначених функцій f, f1, f2 і т. д.
Приклади застосування функції Plot показані на рис. 2.4.1.Зауважимо, що графіки
побудовані без використання будь-яких опцій (точніше, з набором опцій за
замовчуванням).
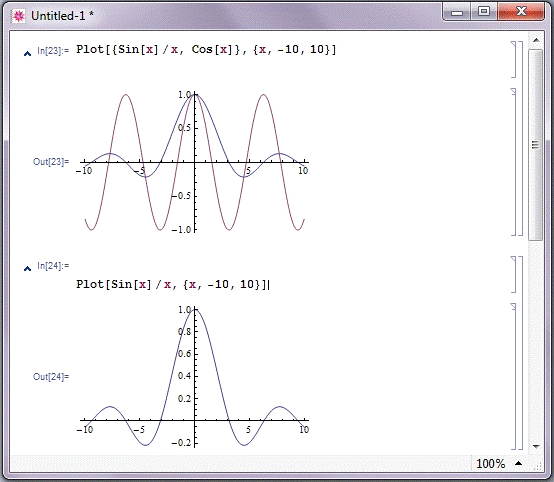
Рис. 2.4.1. Приклади Побудови графіків на площині
В міру ускладнення задач користувачеві рано чи пізно
перестануть влаштовувати графіки, одержувані при автоматичному виборі їх стилю
та інших параметрів. Для точного налаштування графіків Mathematica використовує
спеціальні опції графічних функцій. Для виведення їх списку треба
використовувати команду Options [Plot].
Ще одним важливим засобом настроювання графіків є графічні
директиви. Синтаксис їх подібний синтаксису функцій. Однак директиви не
повертають об'єктів, а лише впливають на їх характеристики. Застосування
графічних директив спільно з опціями дозволяє створювати графіки самого різного
виду. Так як список опцій і директив дуже великий, то не будемо на ньому
зупинятися.
Також часто виникає необхідність побудови графіка по точках.
Це забезпечує вбудована в ядро графічна функція ListPlot:
• ListPlot [{yl, у2 ,...}] - виводить графік списку величин.
Координати х приймають значення 1, 2, ...;
• ListPlot [{{x1, y1}, {х2, у2 },...}]- виводить графік списку
величин з зазначеними х і y координатами.
У найпростішому випадку (рис. 2.4.2) ця функція сама задає
значення координати х = 0, 1, 2, 3, ...і будує на графіку точки з координатами
(х, у), вибираючи у послідовно зі списку координат. Функція ListPlot, особливо
в її другій формі (із заданими координатами х і у), зручна для виведення на
графік експериментальних точок.
Система Mathematica також дозволяє будувати графіки функцій в
полярній системі координат. Побудова графіків в полярній системі координат можливо
двома способами. Перший спосіб ґрунтується на використанні звичайної декартової
системи координат. Координати кожної точки при цьому задаються в параметричному
вигляді: x = f x(t) і у = f у(t), де незалежна змінна t змінюється
від мінімального значення tmin до максимального tmах. Особливо зручне
застосування таких функцій для побудови замкнутих ліній, таких як кола, еліпси,
циклоїди і т. д.
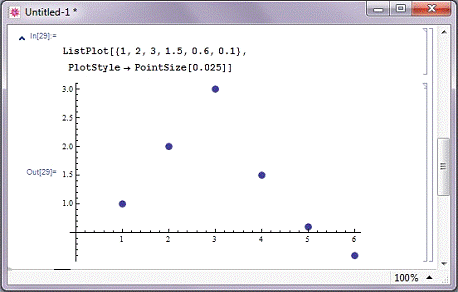
Рис. 2.4.2. Приклад Побудови графіка по точках
Для побудови параметрично заданих функцій використовуються
наступні графічні засоби:
• ParametricPlot [{fx, fy}, {t, tmin, tmax}] - будує
параметричний графік з координатами fх і fу (відповідними х і у), одержуваними
як функції від t;
• ParametricPlot [{{fx, fy}, {gx, gy },...}, {t, tmin, tmax}]
- будує графіки декількох параметричних кривих.
Функції fx, fу можуть бути як безпосередньо вписані в список
параметрів, так і визначені як функції користувача.
Рисунок 2.4.3 показує побудову параметрично заданої фігури
Ліссажу. Вона задається функціями синуса і косинуса з постійним параметром R і
аргументами, кратними t.
Тепер розглянемо другий спосіб побудови графіків в полярній
системі координат (рис. 2.4.4). Для цього використовується функція PolarPlot:
[f, {t, tmin, tmax}] - будує графік в полярній системі координат. [{f1, f2, f3,
...}, {t, tmin, tmax}] - будує графіки функцій в полярній системі координат.
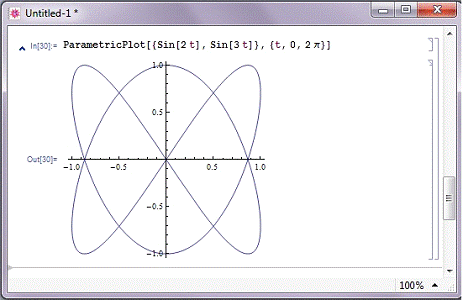
Рис. 2.4.3. Побудова фігури Ліссажу

5. Побудова
графіків поверхонь
Функція двох змінних z = f (x, у) утворює в просторі деяку
тривимірну поверхню або фігуру. Для їх побудови доводиться використовувати
координатну систему з трьома осями координат: x, у і z. Оскільки екран дисплея
плоский, то насправді об'ємність фігур лише імітується.
Для побудови графіків тривимірних поверхонь в системі
Mathematica використовується основна графічна функція Plot3D:
• Plot3D [f, {x, xmin, xmax}, {у, ymin, ymax}] - будує
тривимірний графік функції f (х, у);
• Plot3D [{f, s}, {x, xmin, xmax}, {y, ymin, ymax}] - будує
тривимірний графік, в якому висоту поверхні визначає параметр f, а затінення -
параметр s.
На рис. 2.5.1 показаний приклад побудови поверхні, що
описується функцією двох змінних cos (xу) при х і у, що міняються від -3 до
3.Поверхня будується у вигляді каркасу з прямокутними комірками з використанням
функціонального забарвлення. Всі опції задані за замовчуванням.
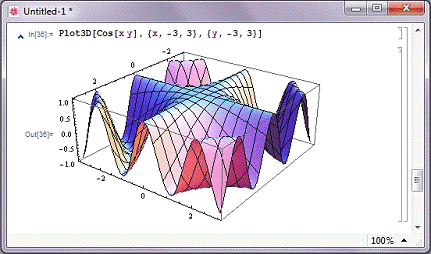
Рис. 2.5.1. Приклад побудови поверхні
Поверхні, також як і графіки на площині, можна будувати по
точкам та в параметричній формі використовуючи при цьому відповідні функції ListPointPlot3D і ParametricPlot3D.
Для модифікації тривимірних графіків можуть використовуватися
численні опції та директиви. Їх застосування дозволяє будувати велику кількість
графіків різних типів навіть при завданні однієї і тієї ж поверхні.
6. Розкладання функцій в ряди Тейлора і Маклорена
Одна із широко розповсюджених математичних задач -
розкладання заданої аналітичної функції в степеневий ряд Тейлора щодо деякої
вузлової точки з абсцисою х0.
Для розкладу в ряд використовуються наступні функції системи
Mathematica: [f, {х, х0, n}] - виконує розкладання в степеневий ряд функції f в
околі точки х = х0 за ступенями (х-х0) ^ n; [f, {х, х0, nх }, {у, у0, nу}] -
послідовно шукає розкладання в ряд спочатку по змінній у, потім по х; [s, n] -
повертає коефіцієнт при змінної n-го ступеня ряду s;
Суть розкладання функції в степеневий ряд добре видно з
розкладу функції f (х) = 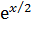 , представленої на рис. 2.6.1 (вихідні комірки мають
стандартний формат).
, представленої на рис. 2.6.1 (вихідні комірки мають
стандартний формат).
У першому прикладі розкладання йде відносно початкової точки
х0 = 0, що відповідає спрощеному ряду Тейлора, який називається рядом
Маклорена. У другому випадку розкладання йде відносно початкової точки х0,
відмінною від нуля. Зазвичай таке розкладання складніше і дає велику залишкову
похибку. Відповідно до прийнятої математичної символікою ця похибка
позначається як О[x]i з показником ступеня, що вказує на порядок похибки.

Рис. 2.6.1. Приклад розкладу в степеневий ряд
Слід зазначити, що розкладання в ряд використовує особливий
формат виводу, частиною якого і є член залишкової похибки. На рис. 2.6.2
показано розкладання в ряди Тейлора і Маклорена для декількох функцій.
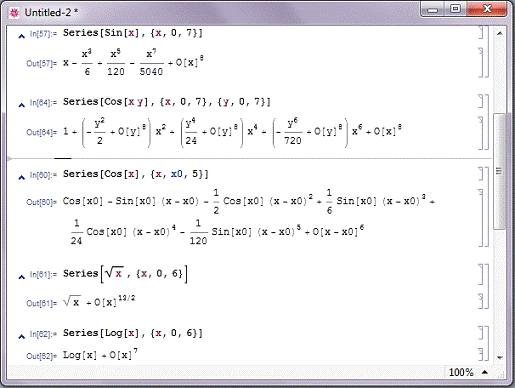
Рис. 2.6.2. Приклади розкладу в раді Тейлора і Маклорена
Неважко помітити, що не всі функції розкладаються в ряд
Маклорена, і відповідно в ряд Тейлора, системою Mathematica. Наприклад, не
мають розкладання логарифм і квадратний корінь - вони повертаються в
початковому вигляді.
Із-за особливого формату результати розкладання в ряд не
можна явно використовувати для розрахунків (наприклад, для побудови графіка
функції за даними її розкладу в ряд). Для усунення залишкового члена та
отримання прийнятних для розрахунків виразів можна використовувати функції
Collect і Normal. Нижче показані приклади застосування цих функцій.

Рис. 2.6.3. Приклади Видалення залишкового члена ряду
Похибка розкладання в ряд зростає із зростанням відхилення
від вузлової точки. При великих відхиленнях навіть якісний опис функції може
різко порушуватися - наприклад, монотонно зростаюча функція при обчисленні по
розкладання в ряд може спадати або навіть прагнути до нескінченності. Для
оцінки того, наскільки і в якій області вихідної точки розкладання в ряд
адекватно розкладається функції, корисно побудувати на одному рисунку графік
вихідної функції і графік вираження, відповідного отриманого ряду (без
залишкової похибки). Іншими словами, потрібна графічна візуалізація розкладання
в ряд.
Приклад графічної візуалізації розкладання в ряд
представлений на рис. 2.6.4. На ньому добре помітно розбіжність за межами
області, що примикає до оперної точці функції. Як зазначалося, похибка
зменшується, якщо х0 = 0 (ряд Маклорена). На жаль, при великому числі членів
ряду його поведінка стає важко передбачуваним, і похибка наближення
катастрофічно наростає.
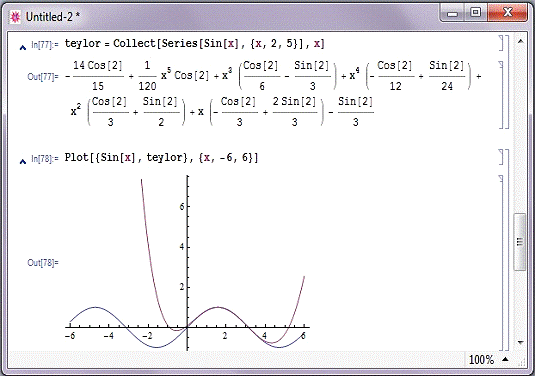
Рис. 2.6.4. Представлення синусоїдальної функції рядом
Тейлора з графічною ілюстрацією його точності
Висновки
У результаті виконання курсової роботи було:
. розглянуто програму навчальної дисципліни
«Математичний аналіз» та самостійну роботу студентів по цій дисципліні;
. розглянуто та проаналізовано сучасні СКМ;
. розглянуто теоретичні аспекти системи Wolfram
Mathematica;
. продемонстровано обчислення границь функцій у WM;
. продемонстровано обчислення похідних і інтегралів у
WM;
. продемонстровано побудову графіків на плоскості та у
просторі в WM;
. продемонстровано розкладання функцій в ряди Тейлора
і Маклорена.
Розглядаючи програму навчальної дисципліни «Математичний
аналіз» ми побачили, що дана дисципліна дуже широка і складна, вона охоплює
великий об’єм матеріалу. Тому, приблизно 1/3 всіх годин відводиться на
самостійну роботу студентів. Використання СКМ у самостійній роботі студентів
при вивчені мат. аналізу дає змогу поєднати високі обчислювальні можливості з
перевагами графічного подання інформації.
При розгляді сучасних СКМ прийшли до висновку, що на
сьогоднішній день існує дуже велике різноманіття цих систем на будь-який смак.
Починаючи від малих систем для шкільної освіти Derive і MuPAD, продовжуючи універсальними системами «для всіх» класу Mathcad і закінчуючи гігантами
комп’ютерної алгебри - системами Mathematica та Maple. Особливе місце займає елітна
матрична система MATLAB з пакетами її розширення. Всі ці системи широко
використовуються на Заході, а останнім часом і у нас, у практиці шкільного,
вузівського і університетської освіти.
Після розгляду теоретичних відомостей про систему Mathematica
можна зробити висновок, що багаті чисельні і символьні можливості цієї системи,
потужні графічні можливості (включаючи анімацію), вбудована мова програмування,
велика довідкова система і зручні засоби побудови гіпертекстових зв'язків між
документами роблять цю систему привабливою як для дослідницької та практичної
діяльності, так і для навчання студентів.
Так як система Wolfram Mathematica дозволяє вирішувати
широкий спектр завдань, то було продемонстровано лише основну частину
можливостей цієї системи при вивчені математичного аналізу.
Підбиваючи підсумки всієї роботи, можна сказати, що сучасні
СКМ слід розглядати не тільки як електронні довідники нового покоління, але і
як системи для самонавчання та дистанційного навчання математики. Однак для
цього вони повинні бути забезпечені грамотно складеними (насамперед у
методичному відношенні) електронними уроками або книгами. У той же час, при
відсутності таких уроків застосування математичних систем може мати негативні
наслідки для освіти - небезпечна підміна навчання основам математики навчанням
основам роботи з математичними системами.
Однак, працювати з сучасними СКМ просто, приємно і повчально.
Завдяки цьому освоєння системи Mathematica сприймається учнями та студентами з
великим інтересом, що служить спонукальним мотивом до їх впровадження в систему
освіти, причому не тільки вищої, а й середньої.
Список
використаних джерел
1. Дьяконов В. П. Комп'ютерні математичні системи
в освіті. Інформаційні технології. - М.: «Пітер», 1997. -40 с.
2. Дьяконов В. П. Комп'ютерна математика. Теорія
і практика. - М.: «Пітер», 2001. -1296 с.
. Дьяконов В. П. Системи комп'ютерної алгебри
Derive. - М.: «Пітер», 2002. -374 с.
. Жалдак М.І. Комп'ютер на уроках математики. -
Посібник для вчителів - Київ: Техніка, 1997. -303 с.
. Половко О.М. Mathematica для студента - СПб.:
«БХВ-Петербург», 2007. - 368 с.
. Рубцов М.О. Математичний аналіз. - Програма
навчальної дисципліни для студентів спеціальності «Інформатика». - МДПУ, 2008.
- 13с.
. Семенов С.П., Славський В.В., Татаринцев
П.Б.. Системи комп'ютерної математики. Навчальний посібник для студентів
математичного факультету АМУ. - Барнаул: Алт. ун-ту, 2004 . - 128 с.
. Слєпкань З.І. Наукові зсади педагогічного
процесу у вищій школі. - Навчальний посібник. - К.: Вища шк., 2005. -239 с.
. Електронний підручник з Wolfram Mathematica
http://lib.qrz.ru/book/export/html/10482
. Морзеэв Ю.М. Сучасні системи комп’ютерної
математики. - Стаття -
http://www.compress.ru/article.aspx?id=12530&iid=474#begin, 2001.
11. Житніков В. Г.
Комп'ютери, математика і свобода. - Стаття
-<http://www.computerra.ru/gid/266002/>, 2006.
. Виговський
Л.С. Введення в Wolfram Mathematica. - Стаття -http://www.exponenta.ru/educat/news/vygovskiy/vygovskiy.asp
13. www.wolfram.com <http://www.wolfram.com>