Прямоугольный диэлектрический волновод

Содержание

Ведение

1.       Теория диэлектрического прямоугольного волновода

2. Решение основных уравнений

3. Полученные результаты

. Вывод

Список литературы

Приложение А

Приложение Б

Введение

Целью данной работы является то, что нам надо было решить уравнения Максвелла, дисперсионные уравнения, размеры волновода, а также такие составляющие как сопротивление в волноводе, коэффициент дисперсии, длину волны критическую, фазовую и групповые скорости. Значения мощностей предельных и допустимых, коэффициенты распространения волны. Также надо построить поля для волн H_x, H_z, E_y.

1. Теория диэлектрического прямоугольного волновода

Плоская диэлектрическая пластина с параметрами m₀e_а толщиной 2d в направлении координаты x,бесконечно протяженная вдоль координаты y и оси z (рис.1.1) помещена в воздухе. При z<0 пластина обрывается и входит в рупор, также бесконечно протяженный вдоль оси y и создающий электромагнитное поле, излучаемое вдоль оси z. В результате воздействия этого поля в пластине и вокруг неё создается волна, параметры которой необходимо определить.

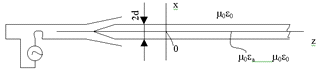
Рис. 1.1

В рупоре, где осуществляется возбуждение пластины, вектор Пойтинга возбуждающего поля может иметь различное направление относительно нормали к пластине, совпадающей с осью x. Если угол, составленный вектором Пойтинга и осью x, меньше угла полного внутреннего отражения, то в соответствии с анализом подобных процессов волна, попавшая изнутри диэлектрика на границу раздела диэлектрик - воздух, преломится на границе и выйдет в воздух. Если угол, составленный вектором Пойтинга и осью x, равен или больше угла полного внутреннего отражения, то такая волна отразится от границы раздела с воздухом и, попав под тем же углом на другую границу раздела, вновь отразится от нее. Этот процесс будет продолжаться по мере продвижения волны вдоль оси z. В результате в диэлектрической пластине возникает волна обычного волнового типа, распространяющаяся в пластине с фазовой скоростью, превышающей скорость света в диэлектрике c. То есть в пластине будет распространяться быстрая волна. В соответствии с явлением полного внутреннего отражения в воздухе у поверхностей пластины образуется медленная волна, распространяющаяся вдоль оси z, с фазовой скоростью, меньшей скорости света в воздухе c₀.. обе волны (внутренняя и внешняя) образуют единое электромагнитное поле с одной и той же фазовой скоростью u_ф, удовлетворяющей неравенству

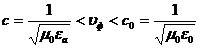 (1.1)

та к как с<c₀, соблюдение этого равенства возможно.

Таким образом, волна, обладающая фазовой скоростью u_ф внутри и вне диэлектрика, по отношению к скорости света в диэлектрике может быть быстрой, а по отношению к скорости света в воздухе - медленной.

Бесконечно протяженная пластина представляет собой идеализацию реальных волновых систем , однако это существенно упрощает анализ и позволяет наглядно проследить процессы, происходящие в волноводах медленных волн.

2. Решение основных уравнений

Чтобы вычислить основные параметры надо решить уравнения Максвелла

    (2.1)

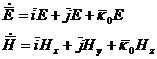       (2.2)

равенство векторов выполняется, если выполняется равенство проекций:

                    (2.3)

подставляя экспоненциальные составляющие в дифференциальные уравнения, и, решая их, получим

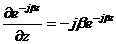
подставляя полученное выражение в уравнение максвелла, получим

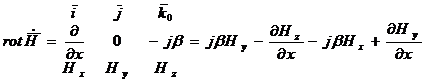 (2.4)

 (2.5)

приравнивая уравнения (1.1) и (1.4), (1.5) получим

 (2.6)

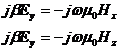 (2.7)

Произведя некоторые преобразования, т.е. сделать замену c²=k²-b², где k=w²em, получим систему уравнений

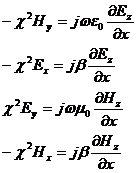
  (2.8)

так как волна типа H, то E_z=0, E_x=0, H_z=0, H_y=0

и тогда система уравнений (2.8) получится такая

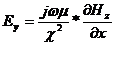 (2.9)

 (2.10)

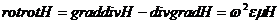
пусть w² em=k², тогда

для H_z получим

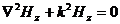
так как 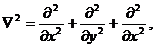 тогда

,

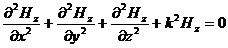но 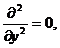 , тогда

поскольку здесь участвует две среды, то уравнения для H_z можно записать для диэлектрика

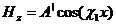 (2.11)

а для воздуха ,

Но коэффициент  не удовлетворяет условия теоремы единственности и тогда для воздуха уравнение примет вид

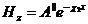 (2.12)

подставим полученные значения для H_z в уравнения в (2.9) и (1.10) получаем

 (2.13)

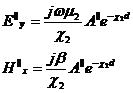 (2.14)

для определения поперечных волновых чисел c₁, c₂ необходимо применить граничные условия на границе диэлектрик воздух. Составляющие H_x, E_y, определяющие вектор Пойтинга, ориентированный вдоль оси z , изменяется по закону sin(cd), т.е. представляет собой нечетные функции по координате x.

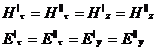
Получаем

 (2.15)

 (2.16)

где m₁₌ m₂₌m₀

чтобы получить дисперсионные уравнения необходимо почленно разделить (2.16) на (2.17), находим

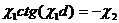 (2.17)

умножим обе части уравнения (2.17) на d получаем трансцендентное уравнение, связывающее поперечные волновые числа c₁, c₂

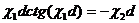 (2.18)

 (2.19)

помножим (2.19) на d²

введем обозначение

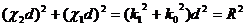
тогда получаем

 (2.21)

Соотношение (2.21) представляет собой уравнение окружности в координатах c₁d, cd радиуса R. Решая совместно трансцендентное уравнение (2.18) и уравнение (2.21) находим значения поперечных волновых чисел c₁, c₂. Решаем уравнения с помощью ЭВМ. Точки пересечения окружностей с кривыми (2.18) дают значения c₁, c₂, откуда для заданной полутолщины пластины d определяют поперечные волновые числа (смотри приложение Б).

Волна типа H₁₀ может существовать только при R>0, а существование волн H_m0 будет

 (2.22)

подставляя значения R из выражения (2.20), получаем

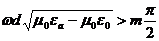
при заданных параметрах пластины это выражение позволяет получить значения критической частоты

 (2.23)

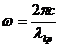
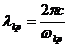
из уравнения (2.23) возможно найти толщину пластины, путем простейших выводов формул и решения промежуточных уравнений получили

 (2.24)

зная критическую длину можно найти коэффициент дисперсии

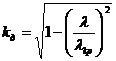 (2.25)

где l в одном случае l_min, а в другом l_max

вычислив коэффициент дисперсии можно найти ряд параметров, найдем длину волны в волноводе

 (2.26)

 (2.27)

теперь найдем в волноводе волновое сопротивление

 (2.28)

фазовую и групповую скорость можно найти также при помощи коэффициента дисперсии

 (2.29)

 (2.30)

зная значения c₁ и c₂ можно вычислить значения коэффициента распространения волны H₁₀

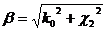 (2.31)

вычислим предельную мощность волновода, зная толщину диэлектрика и коэффициент дисперсии

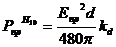 (2.32)

где Е_пр=30 кВ/см

у каждого волновода есть своя предельная мощность

 (2.33) где gизменяется от 4 до 5

. Полученные результаты

Результаты получены для двух длин волн l₁ и l₂ распишем полученные значения

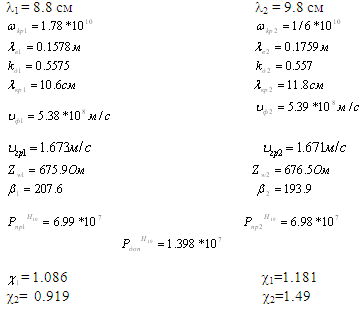
Вывод

Проделав данную работу, я ознакомился с таким понятием как диэлектрический волновод, познал, как распространяется волна в волноводе. Также приобрел навык расчета уравнений Максвелла, уравнений Гельмгольца, дисперсионных уравнений. прямоугольного волновода и рассчитал все положенные параметры расчета.

диэлектрический волновод максвелл дисперсионный

Список литературы

1. Вольман В.И. Техническая электродинамика. - М.: Связь, 1971 486 с.

.Федоров Н.Н. Основы электродинамики. - М.: Высшая школа, 1980, 399 с.

.Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. - М.: Наука, 1989, 540 с.

.Никольский В.В. Теория электромагнитного поля. - М.: Высшая школа, 1964, 379 с.

Приложение А

Структура электрического поля в прямоугольном волноводе с длиной волны H₁₀.

Приложение Б

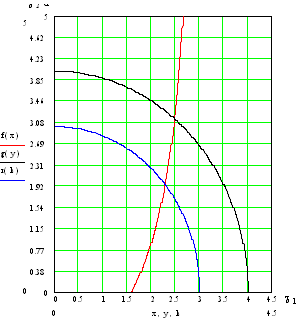
Решение трансцендентных уравнений