Матричное планирование экспериментов, выбор и расчет циклонов

1. Матричное планирование экспериментов

При проведении опытных исследований различают пассивный и активный эксперимент.

Методология пассивного экспериментирования предполагает проведение большой серии опытных исследований с поочередным варьированием значений входных переменных 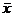 и анализом результатов измерений выходной переменной y (лабораторный эксперимент или эксперимент на пилотной установке). К пассивному эксперименту принято относить также и сбор опытных данных в режиме эксплуатации промышленной установки - т.н. промышленный эксперимент. Обработка результатов пассивного эксперимента проводится методами регрессионного и корреляционного анализа, и выбор вида эмпирической модели (уравнения регрессии), т.е. решение задачи структурной идентификации является достаточно сложной задачей.

Это связано с тем, что вид уравнения регрессии необходимо определять по характеру изменения переменных на графике эмпирической линии регрессии, полученной по выборке экспериментальных данных.

Для решения этой задачи для одной входной переменной x предложены эффективные методы, в которых предусматривается преобразование системы координат как для входной (x), так и для выходной переменной (y). При большем числе входных переменных (x₁,… x_m) надёжных методов определения вида уравнения регрессии (вида эмпирической модели) в настоящее время не существует.

Активный эксперимент проводится по заранее составленному плану, в соответствии с которым ставится задача не только определения оптимальных условий проведения эксперимента, но и оптимизации процесса (оптимальное планирование эксперимента).

При этом уравнения регрессии (эмпирические модели) описывают данные активного эксперимента, в основном, в двух ограниченных областях и имеют следующий вид:

в дали от экстремального значения выходной переменной y:

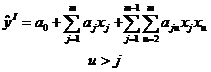
в близи экстремального значения выходной переменной y («в почти стационарной области»):

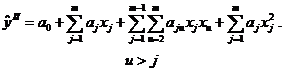
Приведённые уравнения являются линейными относительно коэффициентов регрессии 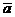 и имеют достаточно простой вид.

Они включают слагаемые с двойным взаимодействием входных переменных:

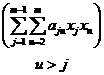
и не учитывают взаимодействия более высоких порядков (тройные, четверные и т.д.), вероятность которых существенно меньше.

Последнее уравнение включает слагаемые с квадратами входных переменных

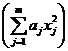
и его коэффициенты получаются при обработке результатов активных экспериментов II-го порядка (верхний индекс II при 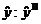) - например, ОЦКП - ортогонального центрального композиционного плана эксперимента.

Предпоследнее уравнение не включает слагаемые с квадратами входных переменных и его коэффициенты получаются при обработке результатов активных экспериментов I-го порядка - верхний индекс I при 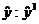 - например, ПФЭ - полный факторный эксперимент.

При определении оптимальных условий проведения процесса с использованием эмпирических моделей (например, методом Бокса-Вильсона) выходная переменная 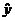 является критерием оптимальности или целевой функцией.

В теории активного экспериментирования выходную (зависимую) переменную принято называть функцией отклика, а входные (независимые) переменные - факторами. Соответственно - координатное пространство с координатами (x₁, x₂, …x_m) - факторным пространством, а геометрическое изображение функции отклика в факторном пространстве - поверхностью отклика.

Активный эксперимент планируется таким образом, чтобы упростить обработку его результатов методами регрессионного и корреляционного анализа. Ортогональные планы экспериментов, используемые при активном экспериментировании, обеспечивают диагональный вид корреляционной матрицы 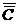 при регрессионном анализе и, соответственно, статистическую независимость коэффициентов регрессии.

К другим достоинствам активного экспериментирования относятся: возможность предсказания количества опытов, которые следуют провести; определение точек факторного пространства, где следует проводить опыты; отсутствие проблем, связанных с выбором вида уравнения регрессии; возможность определения оптимальных параметров процесса экспериментально-статистическим методом; сокращение объёма опытных исследований.

ПФЭ и обработка его результатов. Полный факторный эксперимент (ПФЭ) относится к экспериментам I-го порядка, т. к. описывающее его уравнение 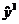 не включает факторы в квадрате. Для двух факторов (x₁ и x₂) и без учёта взаимодействия факторов соответствующая эмпирическая модель может быть записана: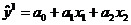

В соответствии с теорией ПФЭ при проведении опытных исследований каждый из факторов варьируется только на двух уровнях - минимальном (кодированное значение -1) и максимальном (кодированное значение +1).

При этом реализуются возможные комбинации минимальных и максимальных значений факторов, в результате чего общее число опытов (n) в ПФЭ равно 2^m и полный факторный эксперимент обычно называется ПФЭ типа 2^m. Для определения числа опытов применяется формула: n = 2^m

В последнее уравнение включаются кодированные значения факторов z_j вместо x_j, значения которых получаются по следующей схеме кодирования:

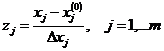
где

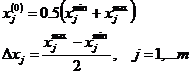
В результате план проведения эксперимента с учётом вышесказанного и кодирования факторов имеет вид: (число факторов равно 2 - m = 2, число опытов n = 2^m = 2² = 4)

При этом уравнение регрессии, описывающее эти опытные данные, записывается с использованием кодированных факторов z_j (j = 0,1,2) и соответственно кодированных коэффициентов регрессии :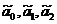

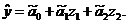
В кодированном факторном пространстве в соответствии с указанным планом проведения эксперимента проведённые опыты представляются точками вершин квадрата:

Для параметрической идентификации кодированного уравнения регрессии используется метод регрессионного анализа, включающий три этапа: определение кодированных коэффициентов уравнения регрессии 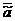 методом наименьших квадратов; оценка значимости кодированных коэффициентов регрессии с использованием t - критерия Стьюдента; проверка адекватности кодированного уравнения регрессии с использованием F - критерия Фишера.

Реализация двух последних этапов возможна при выполнении свойства однородности дисперсий (одно из требований регрессионного анализа) и проведении параллельных опытов, например, в точке с координатами z₁ = 0 и z₂ = 0 (центр плана, на рисунке - тёмная точка).

При проведении k параллельных опытов в центре плана 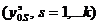 среднее значение  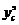определяется как среднее арифметическое результатов измерений во всех параллельных опытах:

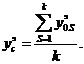
В этом случае используется применяемая при линейном регрессионном анализе матричная формула метода наименьших квадратов (МНК), которая с учётом кодирования факторов имеет вид:

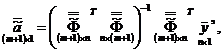
где кодированная матрица, зависящая от независимых переменных для двух факторов включает только +1 и -1 и имеет вид:

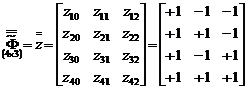
Матрица 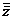 при активном экспериментировании называется матрицей планирования и обладает тремя оптимальными свойствами:

·        симметричности: сумма элементов всех столбцов матрицы, кроме первого (точнее, нулевого) равна нулю

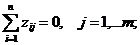
·        ортогональности: скалярное произведение двух любых столбцов матрицы равно нулю

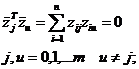
·        нормировки: скалярное произведение двух одинаковых столбцов матрицы равно n (n = 2^m в ПФЭ)

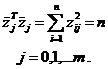
Благодаря перечисленным оптимальным свойствам матрицы планирования 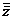 информационная матрица в ПФЭ при m=2 равна

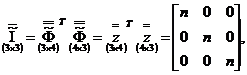
т.е. она является диагональной с одинаковыми элементами на главной диагонали, равными n=2²=4. Соответственно, корреляционная матрица 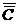 также будет диагональной и с одинаковыми элементами главной диагонали:

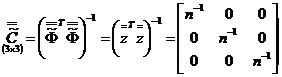
Результатом подстановки последних соотношений в матричную формулу для определения кодированных коэффициентов регрессии будет простая формула:

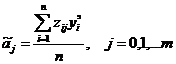
При учёте взаимодействия двух факторов z₁ и z₂ кодированное уравнение регрессии принимает вид: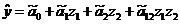

и в матрицу планирования 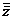 включается ещё один дополнительный последний столбец, каждый элемент которого равен произведению элементов столбцов, соответствующих взаимодействующим факторам:

В теории ПФЭ доказывается, что при увеличении числа факторов (m >2) матрица планирования  строится с использованием рассмотренной методики, в том числе и с учётом взаимодействия факторов (не только двойного, но и тройного, четверного и т.д.).

В этом случае число столбцов матрицы p зависит от числа учёта взаимодействий факторов n = 2^m и матрица планирования сохраняет перечисленные оптимальные свойства.

Поэтому для определения кодированных коэффициентов регрессии используются приведённые выше формулы.

Для расчёта натуральных значений коэффициентов в кодированное уравнение регрессии вместо кодированных факторов z_j (j = 1, … m) следует подставить выражения для последних через натуральные значения факторов x _j (j = 1, … m) в соответствии с приведённой выше схемой кодирования.

Определение значимости кодированных коэффициентов регрессии (ПФЭ). Незначимость кодированных коэффициентов регрессии определяется с использованием квантиля t - распределения Стьюдента 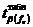 при помощи неравенства:

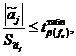 где

β - доверительная вероятность (в инженерных расчётах равная 0,95); fe - число степеней свободы дисперсии воспроизводимости (при одной серии параллельных опытов равная k -1).

Выборочное значение квадратного корня дисперсии кодированного коэффициента регрессии определяется по формуле:

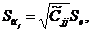 где

S_e - квадратный корень из дисперсии воспроизводимости, определяемой по k параллельным опытам в центре плана эксперимента:

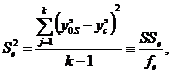 где

SS_e - сумма квадратов дисперсии воспроизводимости; f_e - число степеней свободы дисперсии воспроизводимости.

Как было показано выше, диагональные элементы корреляционной матрицы в ПФЭ при кодировании факторов одинаковы и равны 1/n, вследствие чего:

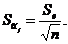
В результате условие незначимости кодированных коэффициентов регрессии принимает вид:

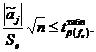
Так как корреляционная матрица 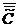 в этом случае является диагональной, то кодированные коэффициенты регрессии статистически независимы и при одновременной незначимости нескольких кодированных коэффициентов регрессии они (в отличие от процедуры обработки пассивного эксперимента) могут быть сразу, все вместе, исключены из кодированного уравнения регрессии.

Проверка адекватности уравнения регрессии (ПФЭ. Проводится так же, как и при проведении пассивного эксперимента, с использованием табличного значения критерия Фишера, выбранного при доверительной вероятности β (чаще всего равной 0,95) и числе степеней свободы остаточной дисперсии f_R и дисперсии воспроизводимости f_e.

Условие адекватности проверяется с использованием неравенства:

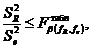
где остаточная дисперсия, характеризующая точность уравнения, определяется по формуле:

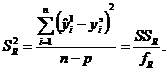
При этом f_R = n - p, где n - число экспериментов при различных значениях факторов; p - число значимых коэффициентов регрессии. К недостаткам ПФЭ относится резкое увеличение числа опытов при возрастании количества факторов больше, чем 5 (при m = 5 n = 2⁵ = 32).

Для проведения регрессионного анализа при пренебрежении целым рядом несущественных взаимодействий факторов достаточно проводить меньшее число опытов. В этом случае можно реализовать часть ПФЭ, т.н. дробный факторный эксперимент (ДФЭ), который здесь не рассматривается.

ОЦКП и обработка его результатов. Ортогональный центральный композиционный эксперимент (ОЦКП) относится к экспериментам II - го порядка, так как описывающее его уравнение 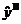 включает факторы в квадрате и поэтому может описывать поверхности функций отклика в окрестности их экстремальных значений.

Для двух факторов (x₁ и x₂) с учётом только двойного взаимодействия факторов соответствующая эмпирическая модель может быть записана:

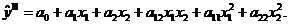
В соответствии с методикой ортогонального центрального композиционного плана эксперимента (ОЦКП) здесь, также как и для ПФЭ, осуществляется кодирование факторов по приведённой выше схеме, и для обеспечения ортогонального свойства матрицы планирования эксперимента в уравнение регрессии 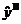 включается некоторая постоянная S.

В результате уравнение регрессии при m = 2 принимает вид:

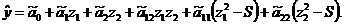
Для определения большего числа кодированных коэффициентов, чем при обработке ПФЭ, и описания поверхности функции отклика вблизи её экстремума («почти стационарной области»), количество опытов в этом случае увеличивается. При этом опыты, проводимые при ПФЭ n = 2^m, дополняются опытами в «звёздных» точках факторного пространства n_α = 2m и опытами в центре плана с координатами z₁ = 0 и z₂ = 0 (n_c).

«Звёздные» точки в факторном пространстве располагаются на осях координат на расстоянии + α и - α от центра плана эксперимента; причём величина α называется «звёздным» плечом и её значения, так же как величина S, определяются из условия ортогональности матрицы планирования 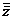 для ОЦКП. Общее число опытов N в ортогональном центральном композиционном эксперименте определяется по формуле:

N = n + n_α + n_c,

или с учётом приведённых выше равенств: N = 2^m + 2m + n_c.

Для случая двух факторов (m = 2): N = 8 + n_c.

Расположение опытных точек в факторном пространстве для случая двух факторов в приведённой ранее кодированной системе координат может быть представлено:

План проведения экспериментов в этом случае может быть представлен:

Матрица планирования 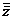 представляет собой часть плана проведения эксперимента без горизонтальных и вертикальных заголовков таблицы и вектора наблюдения 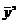(правого столбца). Определение величины «звёздного плеча» α и S из условия ортогональности матрицы планирования 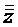.Матрица планирования  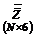была бы ортогональной, если бы выполнялись следующие равенства:

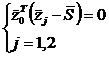                          и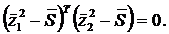                

Раскрывая первое равенство, можно получить:

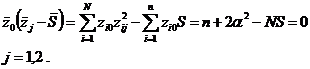
Откуда:

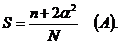
Раскрывая второе равенство, получаем:

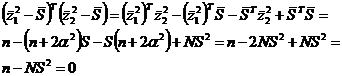
Откуда:

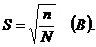
Последнее выражение используется для определения S.

Приравнивая правые части двух выражений для S, можно найти формулу для определения α:

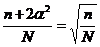
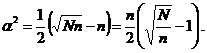
В результате звёздное плечо α можно определить по формуле:

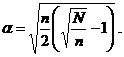
Определение кодированных коэффициентов регрессии (ОЦКП). В соответствии с методом наименьших квадратов эти коэффициенты определяются по матричной формуле:

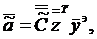 где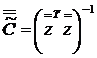                             

Из-за свойства ортогональности матрицы планирования 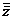 необходимо определить только диагональные элементы информационной матрицы:

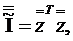
а затем диагональные элементы корреляционной матрицы:

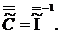
Определение диагональных элементов информационной и корреляционной матриц. Обобщая уравнение регрессии на случай m факторов и учитывая только все двойные взаимодействия факторов, число которых определяется по формуле:

общее число коэффициентов уравнения регрессии для m факторов равно:

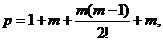
диагональные элементы информационной матрицы 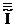 определяются: i₀₀ = N - число таких элементов равно 1;

i_jj = n + 2α² (j = 1, …m);

i_ju = n (u > j) - число таких элементов равно: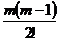

Для определения при квадратах факторов i_jj можно записать:

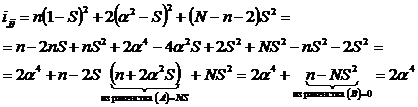
Количество таких диагональных элементов - m. Диагональная матрица 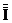 имеет размер: 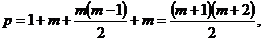что соответствует числу определяемых параметров p.

В результате диагональная корреляционная матрица 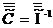 размером р х р для m факторов и с учётом их двойных взаимодействий имеет вид:

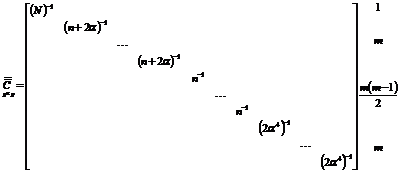
Элементы корреляционной матрицы определяются по матричной формуле МНК:

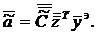
Кодированные коэффициенты регрессии определяются:

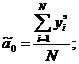
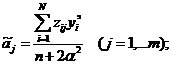
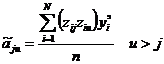 (число коэффициентов )

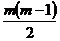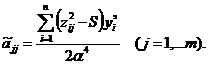
Для пересчёта этих коэффициентов регрессии в натуральные значения необходимо вместо кодированных факторов z подставить их натуральные величины x_j в соответствии с приведённой схемой кодирования.

Определение значимости кодированных коэффициентов регрессии (ОЦКП). В отличие от ПФЭ значимость коэффициентов регрессии определяется по разным формулам для различных коэффициентов, так как диагональные элементы корреляционной матрицы 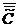 отличаются друг от друга.

С учётом общей формулы для определения незначимости коэффициентов регрессии

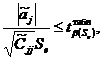
Незначимость каждого вида коэффициентов регрессии определяется:

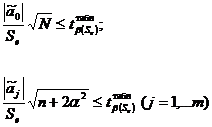
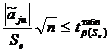 (число коэффициентов )

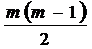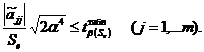
Проверка адекватности уравнения регрессии (ОЦКП) осуществляется с использованием критерия Фишера - так же, как и в случае с ПФЭ.

Определение экстремума функции отклика. Уравнение регрессии с m факторами вида:

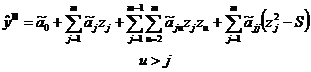
может применяться для определения экстремума функции отклика с использованием необходимого условия экстремума функции многих переменных:

Полученная система линейных уравнений (СЛАУ) позволяет расчётным путём определить 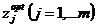 и после подстановки их величин в исходное уравнение 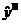 получить максимальное или минимальное значение функции отклика.

2. Выбор и расчет циклонов

эксперимент матричный планирование циклон

Среди аппаратов, применяемых, как правило, только для улавливания сравнительно крупных частиц (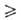5 мкм), максимальной эффективностью обладают циклоны. Взвешенные частицы отделяются в них от газа под действием центробежных сил, возникающих в результате спирально-поступательного движения газового потока вдоль ограничивающей поверхностисти аппарата. При гидравлическом сопротивлении 0,5-1,5 кПа эффективность сепарации в циклонах частиц пыли размерами около 5 и около 20 мкм составляет соотвляют 40-70 и 97-99%.

Подобрать циклон, обеспечивающий степень эффективности очистки газа от пыли не менее h = 0.87 Циклоны предназначены для сухой очистки газов от пыли со средним размером частиц 10…20 мкм.

Все практические задачи по очистке газов от пыли с успехом решаются циклонами НИИОГАЗа: цилиндрическим серии ЦН и коническим серии СК. Избыточное давление газов, поступающих в циклон, не должно превышать 2500 Па. Температура газов во избежание конденсации паров жидкости выбирается на 30…500С выше температуры точки росы, а по условиям прочности конструкции - не выше 4000С.

Производительность циклона зависит от его диаметра, увеличиваясь с ростом последнего. Цилиндрические циклоны серии ЦН предназначены для улавливания сухой пыли аспирационных систем. Их рекомендуется использовать для предварительной очистки газов при начальной запыленности до 400 г./м³ и устанавливать перед фильтрами и электрофильтрами. Конические циклоны серии СК, предназначенные для очистки газов от сажи, обладают повышенной эффективностью по сравнению с циклонами типа ЦН за счет большего гидравлического сопротивления. Входная концентрация сажи не должна превышать 50 г./м³.

Произведем расчет циклона на примере: Исходные данные: количество очищаемого газа - Q = 1,4 м³/с; плотность газа при рабочих условиях - r = 0,89 кг/м³; вязкость газа - m = 22,2×10-6 Н×с/м²; плотность частиц пыли - rП = 1750 кг/м³; плотность пыли - d_П = 25 мкм; дисперсность пыли - lgsп = 0,6; входная концентрация пыли - С_вх = 80 г./м³.

Расчет: Задаёмся типом циклона и определяем оптимальную скорость газа wопт, в сечении циклона диаметром Д: Выберем циклон ЦН-15, оптимальная скорость газа, в котором w_опт = 3,5 м/с. Определяем диаметр циклона, м

Ближайшим стандартным сечением является сечение в 700 мм. По выбранному диаметру находим действительную скорость газа в циклоне, м/с, где n - число циклонов. Вычисляем коэффициент гидравлического сопротивления одиночного циклона: где К₁ - поправочный коэффициент на диаметр циклона; К₂ - поправочный коэффициент на запыленность газа; 500 - коэффициент гидравлического сопротивления одиночного циклона диаметром 500 мм. Определяем гидравлическое сопротивление циклона. По таблице определяем значение параметров пыли и lgsh: Для выбранного типа циклона - =4,5 мкм lgsh=0,352. Ввиду того, что значения, приведенные в таблице, определены по условиям работы типового циклона (Дт = 0,6 м; rпт = 1930 кг/м³; mт = 22,2×10-6; wт = 3,5 м/с), необходимо учесть влияние отклонений условий работы от типовых на величину d50: мкм.

Рассчитываем параметр x: по таблице находим значение параметра Ф(x): Ф(x)=0,8413 Определяем степень эффективности очистки газа в циклоне: Расчетное значение h = 0,92 больше необходимого условия h = 0,87, таким образом, циклон выбран верно.

Литература

1.      Мельников, В.Г., Основы стандартизации строительных работ, допуски, посадки и технические измерения: учебник [Текст] / В.Г. Мельников, Л.С. Казанов. - М.: «Высш. шк», 1988. - 253 с.

2.      Миронов, А.В. Методология, методика социологических исследований [Текст] / А.В. Миронов, В.В. Панферова, Н.С. Субочев // Социально - политический журнал. - 1999. - №9 - 10. - С. 22-28.

.        Фокин, С.В. Столярно-плотничные работы [Текст] / С.В. Фокин, О.Н. Шпоротько. - М.: Альфа-М: ИНФРА, 2006. - 334 с.

.        Экономика и социология труда: учебник [Текст] / Под ред. проф. А.Я. Кибанова. - М.: ИНФРА-М, 2003. - 584 с.

.        Экономика промышленных и строительных материалов: метод. указания и задания к выполнению контрольных работ для студентов специальности 080502 «Экономика и управление на предприятиях промышленности строительных материалов» [Текст] / Сост. И.А. Адамчук. - Губкин: БГТУ им. В.Г. Шухова, 2006. - 12 с.