Конечно-разностные схемы моделирования распространения волн
Оглавление
Оглавление
. Введение
. Явная схема
.1 Постановка задачи
.2 Теоретическая часть
.3 Начальные условия
.4 Граничные условия
.5 Условие Куранта - Фридрихса - Леви
.6 Условие устойчивости
.7 Алгоритм решения
.8 Блок-схема
.9 Реализация
.9.1 Таблица идентификаторов для программы
.9.2 Реализация на языке С/С++ программы
.9.3 Исходный код программы для вывода в среде MATLAB
.10 Тестовые примеры для программы, реализующей явную
схему
. Неявная схема
.1 Постановка задачи
.2 Теоретическая часть
.3 Начальные условия
.4 Граничные условия
.5 Алгоритм решения
.6 Блок-схема
.7 Реализация
.7.1 Таблица идентификаторов для программы
.7.2 Реализация на языке С/С++ программы
.7.3 Исходный код программы для вывода в среде MATLAB
.8 Тестовые примеры для программы, реализующей явную
схему
. Заключение
1. Введение
Разностная схема - это конечная система алгебраических уравнений,
поставленная в соответствие какой-либо дифференциальной задаче, содержащей
дифференциальное уравнение и дополнительные условия (например краевые условия
и/или начальное распределение). Таким образом, разностные схемы применяются для
сведения дифференциальной задачи, имеющей континуальный характер, к конечной
системе уравнений, численное решение которых принципиально возможно на
вычислительных машинах. Алгебраические уравнения, поставленные в соответствие
дифференциальному уравнению, получаются применением разностного метода, что
отличает теорию разностных схем от других численных методов решения
дифференциальных задач[1].
Уравнения мелкой воды - система гиперболических дифференциальных
уравнений в частных производных, которая описывает потоки под поверхностью
жидкости[2].
2.
Явная схема
2.1 Постановка задачи
Пусть система дифференциальных уравнений, моделирующая поведение волн,
имеет вид
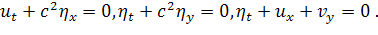 (1)
(1)
Для этой системы выберем разностную схему №11 [3]
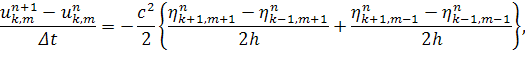
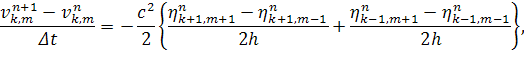
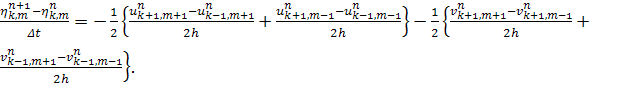 (2)
(2)
Шаги по горизонтальным осям (Δx и Δy) возьмём равными, выразив их как h = Δx = Δy.
С помощью полученной схемы реализовать программу, позволяющую
моделировать поведение волн.
2.2 Теоретическая часть
Для моделирования поведения волн, как уже было описано выше, мы
использовали систему дифференциальных уравнений (1) и построенную к ней
конечно-разностную схему в которой: c - фазовая скорость, u и v -векторы скорости, а η
- высота волны.
Легко заметить, что данная схема является явной, а использование
осреднения по пространственным переменным придёт схеме параболический характер.
Для её решения будем использовать алгоритм бегущего счёта. Что по первому
слою (который задаётся из начальных условий), мы можем вычислить второй, по
второму - третий и т.д. пока не добьёмся желаемого результата. Для этого нам
потребуется однозначно выразить искомые значения через уже известные:
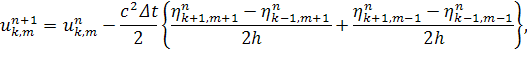
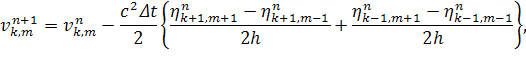
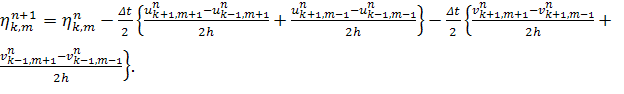 (3)
(3)
Теперь, когда уравнения для поиска новых значений построены, требуется
задать начальные и граничные условия.
2.3 Начальные
условия
В качестве начального состояния поверхности рассмотрим гладкую
поверхность с «колокольчиком» в центре.
Для того, что бы её задать будем использовать следующую формулу.
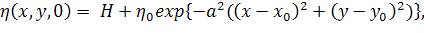 (2)
(2)
где 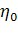 - высота «колокольчика»,
- высота «колокольчика», 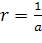 - радиус, H - глубина бассейна, a
- радиус, H - глубина бассейна, a 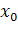 и
и 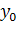 - координаты центра. Для конкретного
примера зададим высоту равную 1, радиус равный 5, глубину равной 1, а
расположен он будет в центре расчётной области. В итоге, поверхность в
начальный момент времени будет иметь такой вид (Рисунок 1):
- координаты центра. Для конкретного
примера зададим высоту равную 1, радиус равный 5, глубину равной 1, а
расположен он будет в центре расчётной области. В итоге, поверхность в
начальный момент времени будет иметь такой вид (Рисунок 1):
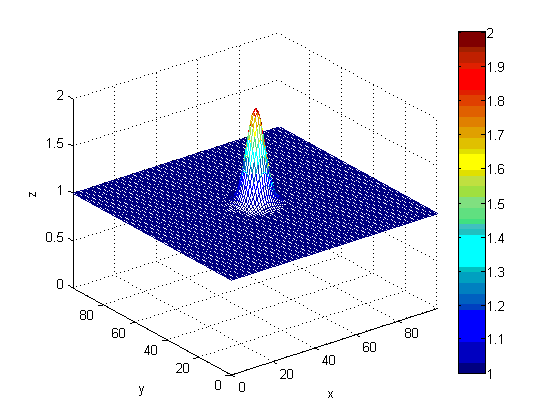
Рисунок
1 - поверхность в начальный момент.
2.4 Граничные
условия
Для того, что бы удачно осуществить алгоритм, так же потребуются и
граничные условия. Для данной задачи рассмотрим условия со свободной границей
(волна будет проходить сквозь границу, а не отражаться от неё).
Для описания «свободных» границ в задачах о распространении волн цунами
было выбрано условие Зоммерфельда, согласно которому предполагается перенос в
направлении внешней нормы с постоянной скоростью, определяемой глубиной
бассейна у границы и без изменения формы волны:
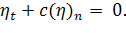 (3)
(3)
В тех случаях, когда это необходимо, нормальная компонента скорости у
свободной границы рассчитывается из соотношения
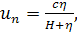 (4)
(4)
а касательная компонента скорости
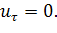 (5)
(5)
Переходя к рассмотрению численных алгоритмов, реализующих условия
свободного прохода, предположим, что в приграничных точках поведение волны
описывается уравнением (3). Тогда значение 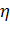 на границе в момент времени (n+1)Δt определяется из соотношения
на границе в момент времени (n+1)Δt определяется из соотношения
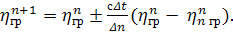 (6)
(6)
где 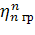 - значение высоты волны в точке, ближайшей к границе по
направлению
- значение высоты волны в точке, ближайшей к границе по
направлению 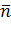 . Соотношение (6) является интерполяционной формулой,
устойчивость которой обеспечивается выполнением критерия Куранта
. Соотношение (6) является интерполяционной формулой,
устойчивость которой обеспечивается выполнением критерия Куранта 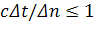 .
.
Для простоты расчётов будем считать, что 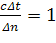 , тогда уравнение (6) принимает вид
, тогда уравнение (6) принимает вид
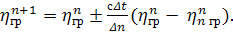 (7)
(7)
На рисунке 2 графически изображён этот принцип: красными показаны искомые
граничные узлы, зелёными - граничные узлы на предыдущем слое, синие - ближайшие
узлы предыдущего слоя к искомым граничным узлам.
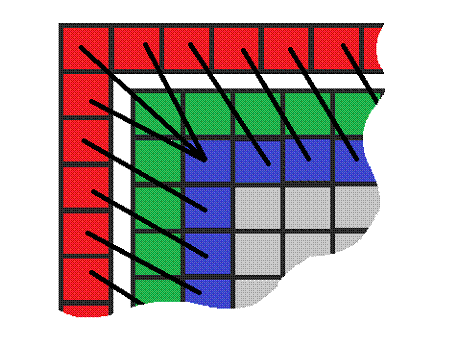
Рисунок
2 - наглядное изображение выбранного принципа отыскания граничных условий
2.5 Условие
Куранта - Фридрихса - Леви
Критерий Куранта-Фридрихса-Леви - необходимое условие устойчивости явного
численного решения некоторых дифференциальных уравнений в частных производных.
Как следствие, во многих компьютерных симуляциях временной шаг должен быть
меньше определённого значения, иначе результаты будут неправильными[1].
Критерий КФЛ применяется к гиперболическим уравнениям. В двумерном случае
он будет иметь вид:
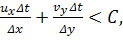 (8)
(8)
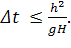 (10)
(10)
где 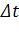 - шаг по времени, h - шаг по пространственным осям, g - ускорение силы тяжести, H - глубина.
- шаг по времени, h - шаг по пространственным осям, g - ускорение силы тяжести, H - глубина.
Исследует нашу схему на устойчивость.
Уравнение 1.
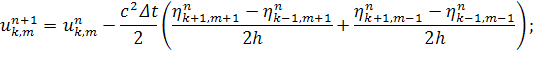
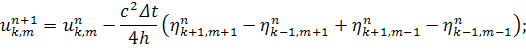
Заменим 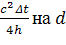 .
.
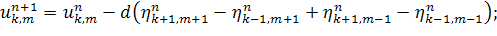
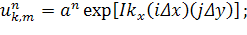
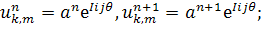
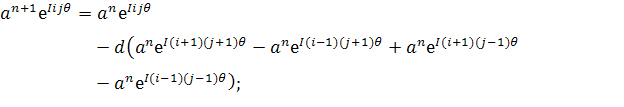
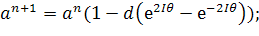
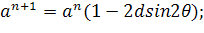
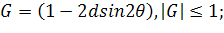
Для этого должно выполняться условие 
Выразим отсюда Δt:
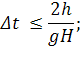
Уравнение 2.
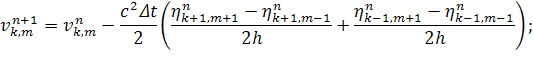
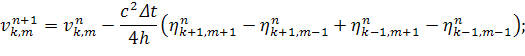
Заменим 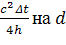 .
.
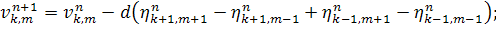
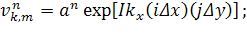
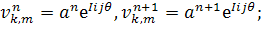
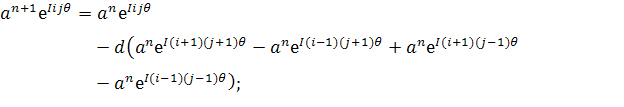
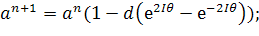
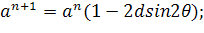
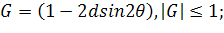
Для этого должно выполняться условие 
Выразим отсюда Δt:
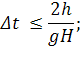
Уравнение 3.
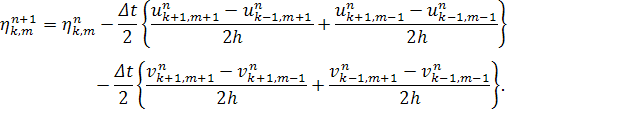
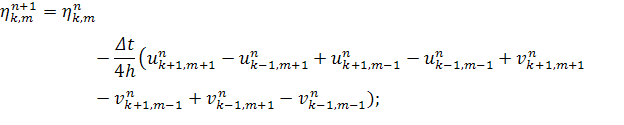
Заменим 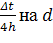 .
.
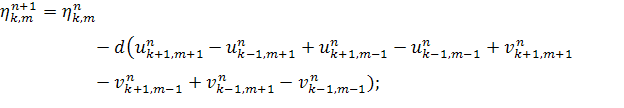
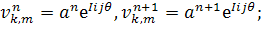
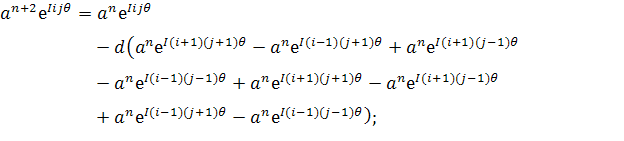
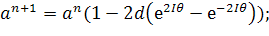
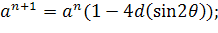
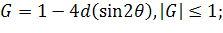
Для этого должно выполняться условие 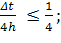
Выразим отсюда Δt:
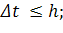
Условие 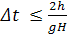 является самым сильным из полученных. Если усилить его до
является самым сильным из полученных. Если усилить его до 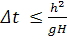 (при h < 1), то получим искомое неравенство.
(при h < 1), то получим искомое неравенство.
2.7 Алгоритм
решения
1) Задать параметры расчётной сетки.
) Задать начальные значения.
) Рассчитать следующий слой.
) Задать граничные условия на новом слою.
) Вернуться к пункту 3, если слой не последний.
) Вывести полученные данные о высотах и характеристиках в файлы.
) Отобразить поведение волн.
2.8 Блок-схема
На рисунке 3 изображена блок-схема алгоритма.
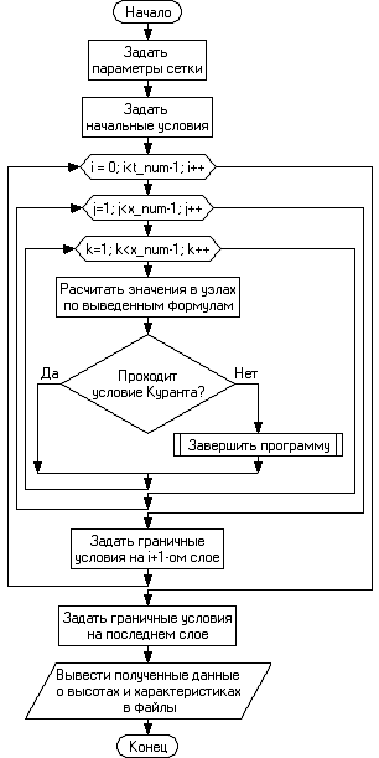
Рисунок
3 - блок-схема алгоритма
2.9 Реализация
2.9.1 Таблица
идентификаторов для программы
В таблице 1 представлены идентификаторы переменных, функций и процедур
для языков C/C++, используемых в реализации программ.
|
Таблица 1 - Идентификаторы
|
|
|
Данные
|
Идентификатор на языке C/C++
|
|
Переменные и методы Scheme:
|
|
|
Массив значений u
|
double *** u
|
|
Массив значений v
|
double *** v
|
|
Массив значений высот
|
double *** eta
|
|
Кол-во моментов времени
|
t_num
|
|
Кол-во точек на осях
|
x_num
|
dt
|
|
Шаг по оси (метры)
|
dx
|
|
Глубина бассейна
|
H
|
|
Вывод массива значений
|
outArray(char *,
double ***)
|
|
Очистка массивов
|
clear()
|
|
Вывод информации о схеме
|
ouput()
|
|
Переменные и методы SchemeN:
|
|
|
Фазовая скорость
|
c
|
|
Задать начальные условия
|
setInitialConditions()
|
|
Задать граничные условия на
n шагу
|
setBoundaryConditions(int
n)
|
|
Начать расчёты
|
calculate()
|
|
Переменные:
|
|
|
Счётчики
|
i, j, k
|
|
Начальная координата x
|
x0
|
|
Начальная координата y
|
y0
|
|
Начальная высота
|
eta0
|
|
a
|
a
|
|
Тестовая схема
|
test
|
|
|
|
2.9.2 Реализация
на языке С/С++ программы
Представлена реализация алгоритма на языке C/C++.
Реализация явной схемы на языке C/C++
#include <stdlib.h>
#include <stdio.h>
#include <math.h>Scheme{:*** u; // Массив значений u*** v; //
Массив значений v*** eta; // Массив значений etaH; //
Глубина бассейнаt_num; // Кол-во моментов времениx_num; //
Кол-во точек на оси Xdt; // Шаг по времени (секунды)dx; //
Шаг по оси (метры)outArray(char * name, double *** out_array){* fout =
fopen(name, "w");(int i = 0; i < t_num; i++){(int j = 0; j <
x_num; j++){(int k = 0; k < x_num; k++){(fout, "%f\t",
out_array[i][j][k]);
}(fout, "\n");
}(fout, "\n\n");
}(fout);
}:void setInitialConditions() = 0;void setBoundaryConditions(int n) =
0;void calculate() = 0;(int N, int M, double Dx, double H_temp){= Dx;= H_temp;=
(dx*dx)/(10*H*10);_num = N;_num = M;= new double**[t_num];= new
double**[t_num];= new double**[t_num];(int i = 0; i < t_num; i++){[i] = new
double*[x_num];[i] = new double*[x_num];[i] = new double*[x_num];(int j = 0; j
< x_num; j++){[i][j] = new double[x_num];[i][j] = new double[x_num];[i][j] =
new double[x_num];
}
}
}
~Scheme(){(int i = 0; i < t_num; i++){(int j = 0; j < x_num;
j++){[] u[i][j];[] v[i][j];[] eta[i][j];
}[] u[i];[] v[i];[] eta[i];
}[] u;[] v;[] eta;
}clear(){(int i = 0; i < t_num; i++){(int j = 0; j < x_num;
j++){(int k = 0; k < x_num; k++){[i][j][k] = 0.0;[i][j][k] = 0.0;[i][j][k] =
0.0;
}
}
}
}ouput(){* foutConfig = fopen("config.txt",
"w");(foutConfig, "%d\n%lf\n", x_num, dx);(foutConfig,
"%d\n%lf\n", t_num, dt);(foutConfig);("eta.txt", eta);
}
};SchemeN: public Scheme {c;:void setInitialConditions(){x0 =
double(x_num)*dx/2.0;y0 = double(x_num)*dx/2.0;eta0 = 1.0;a = 0.2;(int i = 0; i
< x_num; i++){(int j = 0; j < x_num; j++){[0][i][j] = 0.0;[0][i][j] =
0.0;[0][i][j] = H + eta0*exp( - a*a*((dx*i-x0)*(dx*i-x0) +
(dx*j-y0)*(dx*j-y0)));
}
}
}void setBoundaryConditions(int n){(n < 1 || n > t_num - 1);(int i
= 1; i < x_num-1; i++){[n][0][i] = eta[n-1][1][i];[n][x_num-1][i] =
eta[n-1][x_num-2][i];[n][i][0] = eta[n-1][i][1];[n][i][x_num-1] =
eta[n-1][i][x_num-2];[n][0][i] = u[n-1][1][i];[n][x_num-1][i] =
u[n-1][x_num-2][i];[n][i][0] = u[n-1][i][1];[n][i][x_num-1] =
u[n-1][i][x_num-2];[n][0][i] = v[n-1][1][i];[n][x_num-1][i] =
v[n-1][x_num-2][i];[n][i][0] = v[n-1][i][1];[n][i][x_num-1] =
v[n-1][i][x_num-2];
}[n][0][0] = eta[n-1][1][1];[n][x_num-1][0]
= eta[n-1][x_num-2][1];[n][0][x_num-1] =
eta[n-1][1][x_num-2];[n][x_num-1][x_num-1] =
eta[n-1][x_num-2][x_num-2];[n][0][0] =
u[n-1][1][1];[n][x_num-1][0] = u[n-1][x_num-2][1];[n][0][x_num-1] =
u[n-1][1][x_num-2];[n][x_num-1][x_num-1] = u[n-1][x_num-2][x_num-2];[n][0][0]
= v[n-1][1][1];[n][x_num-1][0] = v[n-1][x_num-2][1];[n][0][x_num-1]
= v[n-1][1][x_num-2];[n][x_num-1][x_num-1] = v[n-1][x_num-2][x_num-2];
}void calculate(){(int i = 0; i < t_num-1; i++){(int j = 1; j <
x_num-1; j++){(int k = 1; k < x_num-1; k++){[i+1][j][k] = u[i][j][k] -
((c*c*dt)/2.0)*((eta[i][j+1][k+1] - eta[i][j-1][k+1])/(2.0*dx) +
(eta[i][j+1][k-1] - eta[i][j-1][k-1])/(2.0*dx));[i+1][j][k] = v[i][j][k]
-
((c*c*dt)/2.0)*((eta[i][j+1][k+1] - eta[i][j+1][k-1])/(2.0*dx) +
(eta[i][j-1][k+1] - eta[i][j-1][k-1])/(2.0*dx));[i+1][j][k] =
eta[i][j][k] +*(-0.5*((u[i][j+1][k+1] - u[i][j-1][k+1])/(2.0*dx) +
(u[i][j+1][k-1] -[i][j-1][k-1])/(2.0*dx)) - 0.5*((v[i][j+1][k+1] -
v[i][j+1][k-1])/(2.0*dx)
+ (v[i][j-1][k+1] - v[i][j-1][k-1])/(2.0*dx)));(dt*(u[i+1][j][k] +
v[i+1][j][k])/dx >= c){("Courant-Friedrichs-Lewy condition
failed/n");();
}
}
}(i+1);
}(t_num-1);
}(int N, int M, double Dx, double H_temp): Scheme(N, M, Dx, H_temp),
c(sqrt(10*H_temp)) {}
}
2.9.3 Исходный
код программы для вывода в среде MATLAB
Представлен исходный код программы для вывода в среде MATLAB.
Исходный код программы для вывода в среде MATLAB
clear;config.txt;= config(2);= config(4);=
0:dx:(config(1)-1)*dx;= x;= config(3);= moviein(num);= 1;eta.txt;= 0;=
dx*(config(1)-1);r = 1:num= eta(n:n+config(1)-1,:);(x,y,z);([0 xmax 0 xmax -0
2]);('x');('y');('z');(:,r) = getframe;= n+config(1);= 0;= 10;(M, repeat, fps);
2.10 Тестовые
примеры для программы, реализующей явную схему
Программа реализованная на C/C++ в качестве выходных данных имеет 2
файла: config.txt - содержащий информацию о расчётной сетке и eta.txt - содержащую карту высот. Примеры выходных данных
можно посмотреть в прикреплённых файлах.
На рисунках 4 - 9 изображены результаты работы программы строящей графики
в среде MATLAB в разные моменты времени:
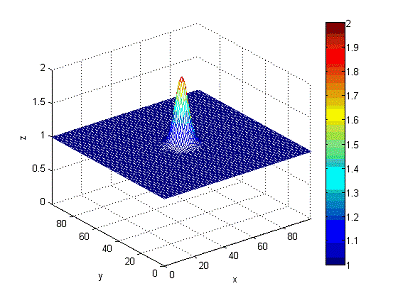
Рисунок
4 - состояние волны в начальный момент времени
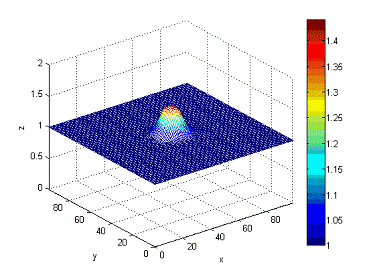
Рисунок
5 - состояние волны в момент времени t = 1с
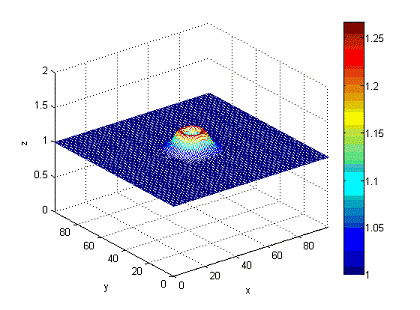
Рисунок
6 - состояние волны в момент времени t=1,5c
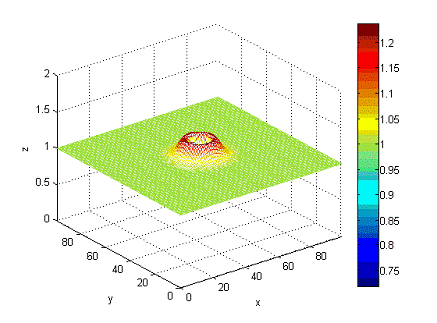
Рисунок
7 - состояние волны в момент времени t=2c
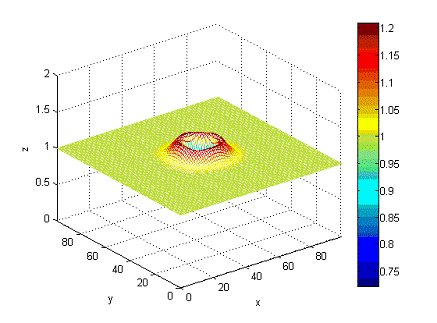
Рисунок
8 - состояние волны в момент времени t=3c
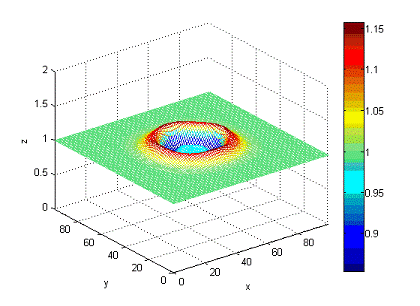
Рисунок
9 - состояние волны в момент времени t=6c
3. Неявная
схема
3.1 Постановка задачи
Пусть система дифференциальных уравнений, моделирующая поведение волн,
имеет вид
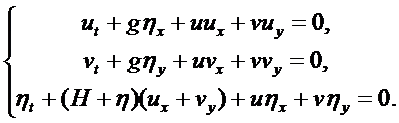 (11)
(11)
Для этой системы выберем неявную конечно-разностную схему с пересчётом
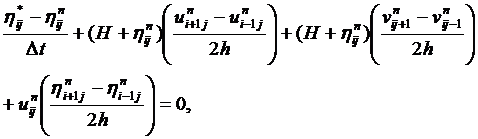 (12)
(12)
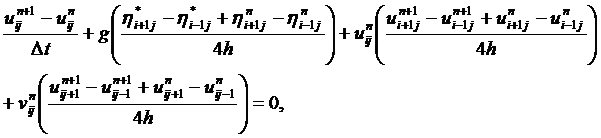 (13)
(13)
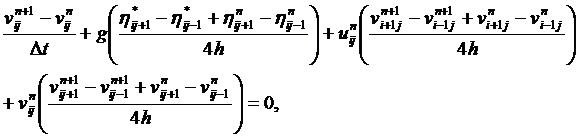 (14)
(14)
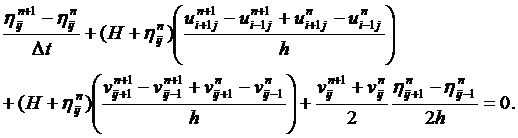 (15)
(15)
Шаги по горизонтальным осям (Δx и Δy) возьмём равными, выразив их как h = Δx = Δy, а глубину бассейна будем считать
постоянной, т.е. H = const.
С помощью полученной схемы реализовать программу, позволяющую
моделировать поведение волн.
3.2 Теоретическая
часть
Для моделирования поведения волн, как уже было описано выше, мы
использовали систему дифференциальных уравнений (11) и построенную к ней
конечно-разностную схему в которой: u и v -векторы скорости, а η
- высота волны, η*
- вспомогательное
значение высота волны, H -
глубина бассейна.
Данная схема является неявной с пересчётом. Главной особенностью неявных
схем является то, что они являются безусловно устойчивыми.
Мы выделили η*, которая не зависит от элементов на следующем слое.
Пользуясь этим приёмом, мы может находить скорости независимо от значения
скоростей на следующем шаге. Это позволяет нам использовать метод прогонки для
отыскания значений скоростей на новом слое. Для этого нам потребуется выразить
скорости из уравнений (13) и (14), а заодно и однозначно выразить η
и η*:
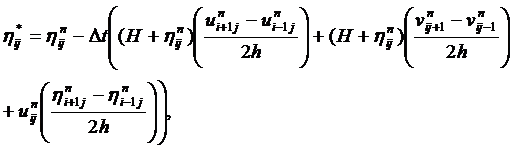 (16)
(16)
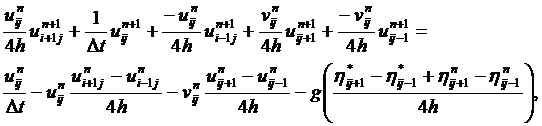 (17)
(17)
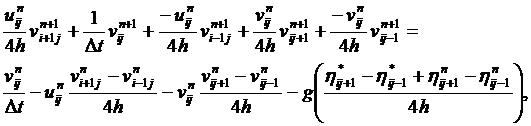 (18)
(18)
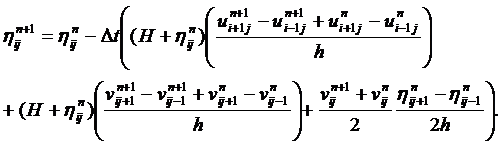 (19)
(19)
Для того, что бы отыскать значения на n+1 слое, опираясь на предыдущий слой, нужно будет решать
систему линейных уравнений. Обычно, для этого используются итерационные методы,
вместо более долгих точных методов. То такие методы имеют один большой
недостаток - они решают систему приближенно. Но особый вид неявной схемы
позволяет нам использовать решать всего лишь трёхдиагональную матрицу. Для
этого используется метод «прогонки».
Теперь, когда уравнения для поиска новых значений построены, требуется
задать начальные и граничные условия.
3.3
Начальные условия
В данной задаче начальное состояние волны зададим при помощи функции
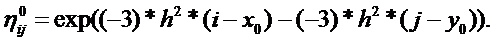 (20)
(20)
Скорости
начальный момент равны 0. h = 0.1, 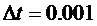 , а
высота бассейна равна 1.
, а
высота бассейна равна 1.
На
рисунке 10 изображено начальное состояние волны.
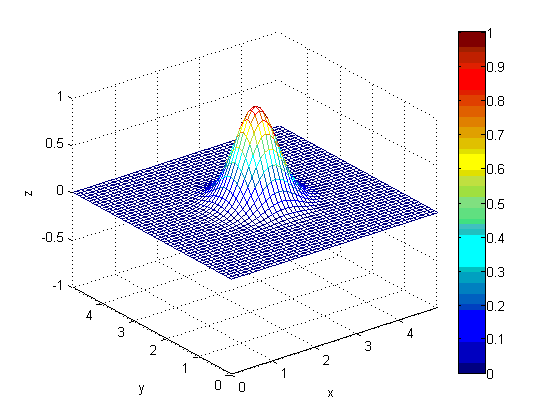
Рисунок
10 - состояние в начальный момент времени
3.4
Граничные условия
Для данной схемы рассмотрим в качестве граничных условий «свободные»
границы. Для этого будем использовать условие протекания:
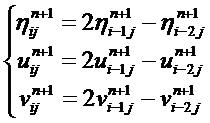 (21)
(21)
3.5 Алгоритм
решения
1) Задать параметры расчётной сетки.
) Задать начальные значения.
) Рассчитать временные высоты.
) Рассчитать используя метод прогонки распределение скоростей на
новом слою
) .Рассчитать высоты на новом слою.
) Задать граничные условия на новом слою.
) Вернуться к пункту 3, если слой не последний.
) Вывести полученные данные о высотах и характеристиках в файлы.
) Отобразить полученные результаты.
3.6 Блок-схема
На рисунке 11 изображена блок-схема алгоритма.

Рисунок
11 - блок-схема алгоритма
3.7 Реализация
3.7.1 Таблица
идентификаторов для программы
В таблице 4 представлены идентификаторы переменных, функций и процедур
для языков C/C++, используемых в реализации программ.
|
Таблица 4 - Идентификаторы
|
|
|
Данные
|
Идентификатор на языке C/C++
|
|
Переменные и методы Scheme:
|
|
|
Массив значений u
|
double *** u
|
|
Массив значений v
|
double *** v
|
|
Массив значений высот
|
double *** eta
|
|
Временный массив значений
высот
|
double **
etaTemp
|
|
Кол-во моментов времени
|
|
Кол-во точек на осях
|
x_num
|
|
Шаг по времени (секунды)
|
dt
|
|
Шаг по оси (метры)
|
dx
|
|
Глубина бассейна
|
H
|
|
Вывод массива значений
|
outArray(char *,
double ***)
|
|
Очистка массивов
|
clear()
|
|
Вывод информации о схеме
|
ouput()
|
|
Переменные и методы SchemeN:
|
|
|
Фазовая скорость
|
c
|
|
Задать начальные условия
|
setInitialConditions()
|
|
Задать граничные условия на
n шагу
|
setBoundaryConditions(int
n)
|
|
Начать расчёты
|
calculate()
|
|
Подготовить временные
высоты
|
prepareEtaTemp()
|
|
Метод прогонки
|
solveMatrix()
|
|
Рассчитать значений высот
|
calculateEta()
|
|
Рассчитать Ux
|
calculateUx()
|
|
Рассчитать Uy
|
calculateUy()
|
|
Рассчитать Vx
|
calculateVx()
|
|
Рассчитать Vy
|
calculateVy()
|
|
Переменные:
|
|
|
Счётчики
|
i, j, k
|
|
Начальная координата x
|
x0
|
|
Начальная координата y
|
y0
|
|
Начальная высота
|
eta0
|
|
Вспомогательные массивы
|
a, b, c, f, d, e
|
|
Тестовая схема
|
test
|
|
|
|
3.7.2 Реализация
на языке С/С++ программы
Gредставлена
реализация алгоритма на языке C/C++.
Реализация явной схемы на языке C/C++
#include <stdlib.h>
#include <stdio.h>
#include <math.h>double g = 9.8;Scheme{:*** u; //
Массив значений u*** v; // Массив значений v*** eta; //
Массив значений eta** etaTemp; // Массив вспомогательных значений
etaH; // Глубина бассейнаt_num; // Кол-во моментов
времениx_num; // Кол-во точек на оси Xdt; // Шаг по
времени (секунды)dx; // Шаг по оси (метры)outArray(char * name,
double *** out_array){* fout = fopen(name, "w");(int i = 0; i <
t_num; i++){(int j = 0; j < x_num; j++){(int k = 0; k < x_num; k++){(fout,
"%f\t", out_array[i][j][k]);
}(fout, "\n");
}(fout, "\n\n");
}(fout);
}:void setInitialConditions() = 0;void setBoundaryConditions(int n) =
0;void calculate() = 0;(int N, int M, double Dx, double H_temp){= Dx;= H_temp;=
dx/100;_num = N;_num = M;= new double**[t_num];= new double**[t_num];= new
double**[t_num];(int i = 0; i < t_num; i++){[i] = new double*[x_num];[i] =
new double*[x_num];[i] = new double*[x_num];(int j = 0; j < x_num;
j++){[i][j] = new double[x_num];[i][j] = new double[x_num];[i][j] = new
double[x_num];
}
}= new double*[x_num];(int i = 0; i < x_num; i++){[i] = new
double[x_num];
}
}() {}
~Scheme(){(int i = 0; i < t_num; i++){(int j = 0; j < x_num;
j++){[] u[i][j];[] v[i][j];[] eta[i][j];
}[] u[i];[] v[i];[] eta[i];
}[] u;[] v;[] eta;(int i = 0; i < x_num; i++){[] etaTemp[i];
}[] etaTemp;
}clear(){(int i = 0; i < t_num; i++){(int j = 0; j < x_num;
j++){(int k = 0; k < x_num; k++){[i][j][k] = 0.0;[i][j][k] = 0.0;[i][j][k] =
0.0;
}
}
}
}
}ouput(){* foutConfig = fopen("config.txt",
"w");(foutConfig, "%d\n%lf\n", x_num, dx);(foutConfig,
"%d\n%lf\n", t_num, dt);(foutConfig);
("eta.txt", eta);
}
};SchemeN: public Scheme {* a;* b;* c;* f;* u_temp;* v_temp;* d;* e;:void
setInitialConditions(){x0 = x_num/2;y0 = x_num/2;eta0 = 1.0;a = 0.2;(int i = 0;
i < x_num; i++){(int j = 0; j < x_num; j++){[0][i][j] = 0.0;[0][i][j] =
0.0;
//eta[0][i][j] = H + eta0*exp( - a*a*((dx*i-x0)*(dx*i-x0) +
(dx*j-y0)*(dx*j-y0)));[0][i][j]= exp(-dx*(i-x0)*3*dx*(i-x0)-dx*(j-y0)*dx*3*(j-y0));[1][i][j]
= eta[0][i][j];
}
}
}void setBoundaryConditions(int n){(int i = 1; i < x_num-1;
i++){[n][0][i] = 2*eta[n][1][i] - eta[n][2][i];[n][x_num-1][i] =
2*eta[n][x_num-2][i] - eta[n][x_num-3][i];[n][i][0] = 2*eta[n][i][1] -
eta[n][i][2];[n][i][x_num-1] = 2*eta[n][i][x_num-2] -
eta[n][i][x_num-3];[n][0][i] = 2*u[n][1][i] - u[n][2][i];[n][x_num-1][i] =
2*u[n][x_num-2][i] - u[n][x_num-3][i];[n][i][0] = 2*u[n][i][1] -
u[n][i][2];[n][i][x_num-1] = 2*u[n][i][x_num-2] - u[n][i][x_num-3];[n][0][i]
= 2*v[n][1][i] - v[n][2][i];[n][x_num-1][i] = 2*v[n][x_num-2][i] -
v[n][x_num-3][i];[n][i][0] = 2*v[n][i][1] - v[n][i][2];[n][i][x_num-1] =
2*v[n][i][x_num-2] - v[n][i][x_num-3];
}[n][0][0] = 2*eta[n][1][0] - eta[n][2][0];[n][x_num-1][0]
= 2*eta[n][x_num-1][1] - eta[n][x_num-1][2];[n][0][x_num-1] =
2*eta[n][1][x_num-1] - eta[n][2][x_num-1];[n][x_num-1][x_num-1] =
2*eta[n][x_num-1][x_num-2] - eta[n][x_num-1][x_num-3];[n][0][0]
= 2*u[n][1][0] - u[n][2][0];[n][x_num-1][0] = 2*u[n][x_num-1][1] -
u[n][x_num-1][2];[n][0][x_num-1] = 2*u[n][1][x_num-1] -
u[n][2][x_num-1];[n][x_num-1][x_num-1] = 2*u[n][x_num-1][x_num-2] -
u[n][x_num-1][x_num-3];[n][0][0] = 2*v[n][1][0] -
v[n][2][0];[n][x_num-1][0] = 2*v[n][x_num-1][1] -
v[n][x_num-1][2];[n][0][x_num-1] = 2*v[n][1][x_num-1] -
v[n][2][x_num-1];[n][x_num-1][x_num-1] = 2*v[n][x_num-1][x_num-2] -
v[n][x_num-1][x_num-3];
}solveMatrix(double * a,
double * b, double *c, double * f, double * x){[1] = -b[0]/c[0];[1] = f[0]/c[0];(int
i = 1; i < x_num-1; ++i) {[i+1] = -b[i] / (a[i]*d[i]+c[i]);[i+1] = (f[i] -
a[i]*e[i]) / (c[i]+a[i]*d[i]);
}[x_num-1] = (f[x_num-1] -
a[x_num-1]*e[x_num-1]) / (c[x_num-1]+a[x_num-1]*d[x_num-1]);(int i = x_num-2; i
> 0; --i) {[i] = d[i+1]*x[i+1]+e[i+1];
}
}prepareEtaTemp(int n){(int i
= 1; i < x_num-1; i++){(int j = 1; j < x_num-1; j++){[i][j] =
eta[n][i][j] - dt*((H + eta[n][i][j])*(u[n][i+1][j] - u[n][i-1][j])/(2.0*dx)
+ (H +
eta[n][i][j])*(v[n][i][j+1] - u[n][i][j-1])/(2.0*dx)
+ u[n][i][j]*(eta[n][i+1][j]
- eta[n][i-1][j])/(2.0*dx));
}
}
}calculateEta(int n){(int i =
1; i < x_num-1; i++){(int j = 1; j < x_num-1; j++){[n+1][i][j] =
eta[n][i][j] - dt*((H + eta[n][i][j])*(u[n+1][i+1][j] - u[n+1][i-1][j] +
u[n][i+1][j] - u[n][i-1][j])/dx
+ (H +
eta[n][i][j])*(v[n+1][i][j+1] - v[n+1][i][j-1] + v[n][i][j+1] -
v[n][i][j-1])/dx
+ ((v[n+1][i][j] +
v[n][i][j])/2.0)*((eta[n][i][j] - eta[n][i][j-1])/(2*dx)));
}
}
}calculateVx(int n){(int j =
1; j < x_num-1; j++){[0] = a[x_num-1] = 0;[0] = b[x_num-1] = 0;[0] =
c[x_num-1] = 1;(int i = 0; i < x_num; i++) {_temp[i] = v[n][i][j];
}[0] = v_temp[0];[x_num-1] =
v_temp[x_num-1];(int i = 1; i < x_num-1; i++) {[i] =
-u[n][i][j]/(4.0*dx);[i] = 1.0/dt;[i] = u[n][i][j]/(4.0*dx);[i] =
-v[n][i][j]/(4.0*dx)*v[n+1][i][j+1] + v[n][i][j]/(4.0*dx)*v[n+1][i][j-1]
+
v[n][i][j]/dt-u[n][i][j]*(v[n][i+1][j] - v[n][i-1][j])/(4.0*dx)
v[n][i][j]*(v[n][i][j+1] -
v[n][i][j-1])/(4.0*dx)
g*(etaTemp[i][j+1] -
etaTemp[i][j-1] + eta[n][i][j+1] - eta[n][i][j-1])/(4.0*dx);
}(a, b, c, f, v_temp);(int i
= 0; i < x_num; i++) {[n+1][i][j] = v_temp[i];
}
}
}calculateVy(int n){(int i =
1; i < x_num-1; i++){[0] = a[x_num-1] = 0;[0] = b[x_num-1] = 0;[0] =
c[x_num-1] = 1;(int j = 0; j < x_num; j++) {_temp[j] = v[n][i][j];
}[0] = v_temp[0];[x_num-1] =
v_temp[x_num-1];(int j = 1; j < x_num-1; j++) {[j] =
-v[n][i][j]/(4.0*dx);[j] = 1.0/dt;[j] = v[n][i][j]/(4.0*dx);[j] =
(-v[n][i][j]/(4.0*dx))*v[n+1][i+1][j] + (u[n][i][j]/(4.0*dx))*v[n+1][i-1][j]
+ v[n][i][j]/dt -
u[n][i][j]*(v[n][i+1][j]-v[n][i-1][j])/(4.0*dx)
v[n][i][j]*(v[n][i][j+1] -
v[n][i][j-1])/(4.0*dx)
g*(etaTemp[i][j+1] -
etaTemp[i][j-1] + eta[n][i][j+1] - eta[n][i][j-1])/(4.0*dx);
}(a, b, c, f, v_temp);(int j
= 0; j < x_num; j++) {[n+1][i][j] = v_temp[j];
}
}
}calculateUx(int n){(int j =
1; j < x_num-1; j++){[0] = a[x_num-1] = 0;[0] = b[x_num-1] = 0;[0] =
c[x_num-1] = 1;(int i = 0; i < x_num; i++) {_temp[i] = u[n][i][j];
}[0] = u_temp[0];[x_num-1] =
u_temp[x_num-1];(int i = 1; i < x_num-1; i++) {[i] =
-u[n][i][j]/(4.0*dx);[i] = 1.0/dt;[i] = u[n][i][j]/(4.0*dx);[i] =
(-v[n][i][j]/(4.0*dx))*u[n+1][i][j+1] + (v[n][i][j]/(4.0*dx))*u[n+1][i][j-1]
+ u[n][i][j]/dt -
u[n][i][j]*(u[n][i+1][j] - u[n][i-1][j])/(4.0*dx)
v[n][i][j]*(u[n][i][j+1] -
u[n][i][j-1])/(4.0*dx)
g*(etaTemp[i+1][j] -
etaTemp[i-1][j] + eta[n][i+1][j] - eta[n][i-1][j])/(4.0*dx);
}(a, b, c, f, u_temp);(int i
= 0; i < x_num; i++) {[n+1][i][j] = u_temp[i];
}
}
}calculateUy(int n){(int i =
1; i < x_num-1; i++){[0] = a[x_num-1] = 0;[0] = b[x_num-1] = 0;[0] =
c[x_num-1] = 1;(int j = 0; j < x_num; j++) {_temp[j] = u[n][i][j];
}[0] = u_temp[0];[x_num-1] =
u_temp[x_num-1];(int j = 1; j < x_num-1; j++) {[j] =
-v[n][i][j]/(4.0*dx);[j] = 1.0/dt;[j] = v[n][i][j]/(4.0*dx);[j] =
(-u[n][i][j]/(4.0*dx))*u[n+1][i+1][j] + (u[n][i][j]/(4.0*dx))*u[n+1][i-1][j]
+ u[n][i][j]/dt -
u[n][i][j]*(u[n][i+1][j] - u[n][i-1][j])/(4.0*dx)
v[n][i][j]*(u[n][i][j+1] -
u[n][i][j-1])/(4.0*dx)
g*(etaTemp[i+1][j] -
etaTemp[i-1][j] + eta[n][i+1][j] - eta[n][i-1][j])/(4.0*dx);
}(a, b, c, f, u_temp);(int j
= 0; j < x_num; j++) {[n+1][i][j] = u_temp[j];
}
}
}void calculate(){(int i = 0;
i < t_num-1; i++){(i);(i);(i);(i);(i);(i);(i);
}
}(int N, int M, double Dx,
double H_temp){= Dx;= H_temp;= dx/100;_num = N;_num = M;= new double**[t_num];=
new double**[t_num];= new double**[t_num];(int i = 0; i < t_num; i++){[i] =
new double*[x_num];[i] = new double*[x_num];[i] = new double*[x_num];(int j =
0; j < x_num; j++){[i][j] = new double[x_num];[i][j] = new
double[x_num];[i][j] = new double[x_num];
}
}
= new double*[x_num];(int i =
0; i < x_num; i++){[i] = new double[x_num];
}= new double[x_num];= new
double[x_num];= new double[x_num];= new double[x_num];= new double[x_num];= new
double[x_num];_temp = new double[x_num];_temp = new double[x_num];
}
};main(){test(200, 50, 0.1,
1.0);.clear();.setInitialConditions();.calculate();.ouput();("pause");1;
}
3.7.3 Исходный
код программы для вывода в среде MATLAB
Представлен исходный код программы для вывода в среде MATLAB.
код программа дифференциальный уравнение
Исходный код программы для вывода в среде MATLAB
clear;config.txt;= config(2);= config(4);=
0:dx:(config(1)-1)*dx;= x;= config(3);= moviein(num);= 1;eta.txt;= 0;=
dx*(config(1)-1);r = 1:num= eta(n:n+config(1)-1,:);(x,y,z);([0 xmax 0 xmax -0
2]);('x');('y');('z');(:,r) = getframe;= n+config(1);= 0;= 10;(M, repeat, fps);
На рисунках 12 - 13 изображены результаты работы программы строящей
графики в среде MATLAB в разные
моменты времени.
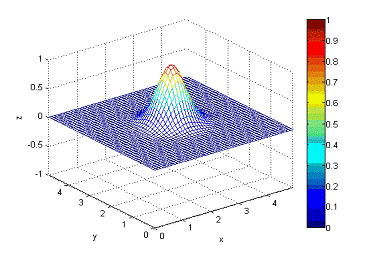
Рисунок
12 - состояние волны в начальный момент времени
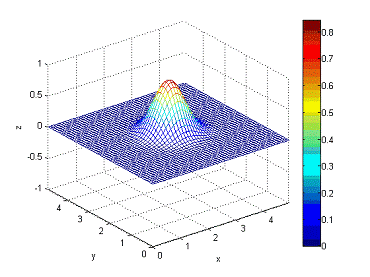
Рисунок
13 - состояние волны в момент времени t = 0.2с
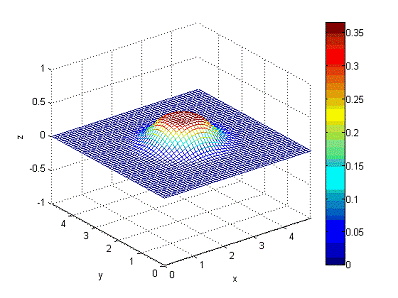
Рисунок
14 - состояние волны в момент времени t=0.5с
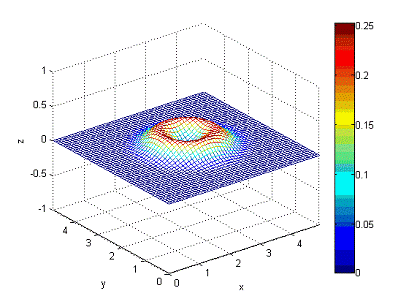
Рисунок
15 - состояние волны в момент времени t=0.75c
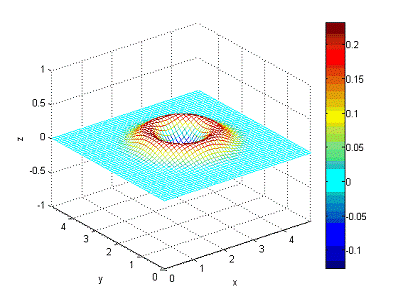
Рисунок
16 - состояние волны в момент времени t=1c.
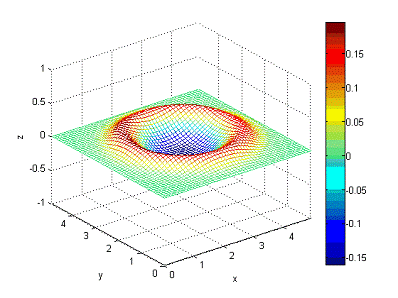
Рисунок
17 - состояние волны в момент времени t=2c.
4. Заключение
Данная работа позволила нам изучить и научиться работать с разностными
схемами. В современной науке моделирование является важнейшим инструментом в
изучении новых явлений. Разностные схемы же позволяют легко решать
дифференциальные задачи в естествознании.
Например, моделирование волн цунами, позволяет прогнозировать
распространение волн в мировом океане, а следовательно, избежать разрушений и
жертв среди мирного населения.
Основной сложностью является подбор корректных начальных и краевых
условий.
Никогда не стоит забывать о верно подобранных параметрах схемы, удовлетворяющих
критерию устойчивости.
Единственная сложность, которую сейчас всё ещё трудно обойти - высокие
требование к вычислительной машине. Требования к большому количеству
оперативной памяти и нагрузки на процессор, но позволяют оперативно получать
данные.