Информатика и прикладные программы в ЭВМ в управлении экономикой фирмы
Информатика
и прикладные программы в ЭВМ в управлении экономикой фирмы
Введение
Для решения многих нелинейных
уравнений чаще всего используют Методы: простой итерации, половинного деления,
Ньютона. Нелинейные решения нужны современному инженеру, ученому, экономисту в
его профессиональной деятельности. Например, экономист с помощью таких
уравнений может находить прибыль предприятия и просчитывать его на К лет.
Таким образом, развитие этих методов
получает широкое развитие в мире.
Теоретические
сведения
Методы решения
Методы решения
нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют
записать корни в виде некоторого конечного соотношения (формулы). Из школьного
курса алгебры нам известны такие методы для решения тригонометрических,
логарифмических, показательных, а также простейших алгебраических уравнений.
Однако
встречающиеся на практике уравнения не удаётся решить такими простыми методами.
Для их решения используются итерационные методы, т.е. методы последовательных
приближений. Алгоритм нахождения корня уравнения с помощью итерационного метода
состоит из двух этапов: а) отыскания приближённого значения корня или
содержащего его отрезка; б) уточнения приближённого значения до некоторой
заданной степени точности.
Итерационный
процесс состоит в последовательном уточнении начального приближения Хо. Каждый
такой шаг называется итерацией. В результате итераций находится
последовательность приближённых значений корня Х1, Х2,…, Xn - Если эти значения с ростом n приближаются к истинному значению
корня, то говорят, что итерационный процесс сходится.
А теперь рассмотрим
3 итерационных метода решения трансцендентных, алгебраических уравнений. Метод
деления отрезка пополам, Ньютона, простой итерации.
Метод деления отрезка пополам (метод
дихотомии)
Пусть действительный
корень уравнения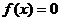 
отделен
и функция 
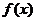непрерывна
на интервале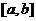 
отделения
корня. Построим процесс сужения интервала 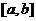так, чтобы искомый
корень всегда находился внутри суженного интервала. Очевидно, что в этом случае
погрешность приближённого значения корня не превышает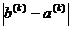 
,
где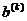 
,
−
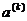граничные точки интервала на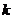 
-ой итерации. Найдём
середину отрезка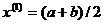 
и
вычислим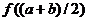 
.
Составим произведения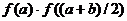 
и
.
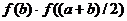Из двух половин отрезков выберем тот, в котором произведение является
отрицательной величиной, и обозначим новые границы отрезка через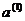 
,
.
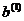Затем новый отрезок разделим пополам, вновь составим аналогичные произведения и
выберем тот из отрезков, в котором произведение − величина отрицательная.
Погрешность метода
половинного деления, который также называется методом дихотомии, определяется
достаточно очевидным соотношением (которое, впрочем, может быть строго
доказано)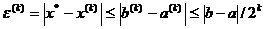 
,
которое указывает на скорость сходимости метода: с увеличением 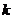погрешность
стремиться к нулю не медленнее геометрической прогрессии со знаменателем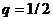 
.
Метод дихотомии прост и надёжен, всегда сходиться, хотя и медленно, устойчив к
ошибкам округления.
Метод простой итерации
С начало приводим
нелинейное уравнение 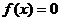к
виду, удобному для итерации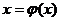 
. Для этого умножим
исходное уравнение на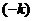 
и
прибавим к обеим частям уравнения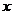 
:
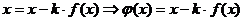. (1)
В качестве начального
приближения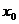 
можно
выбрать любое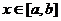 
.
Итерационный процесс
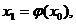
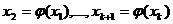
заканчивается при
выполнении условия
.
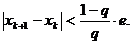
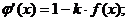
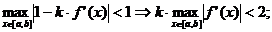
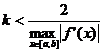Недостатком метода
является малая скорость сходимости приближённого решения к точному. К
достоинствам метода относятся более широкая область сходимости и простота по
сравнению с методами Ньютона, хорд и секущих. На рис. 1 приводиться блок-схема
алгоритма метода. Она проста, алгоритм полностью совпадает с приведённым выше в
тексте. Обозначения переменных ясных из текста.
Найти корни уравнения
методом простой итерации можно с помощью электронных таблиц. В столбце 
вычисляются
последовательные приближения к корню.
Метод Ньютона
Рассмотрим в точке 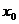касательную
к кривой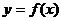 
,
задаваемую уравнением
.
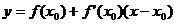Положив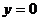 
,
находим точку 
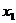пересечения
касательной с осью абсцисс:
.
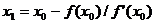Функция 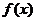на
отрезке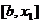 
(рис.
2) заменяется прямой и 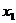является
приближённым значением корня 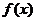. Построив касательную в
точке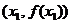 
получим
точку пересечения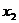 
этой
касательной с осью ,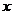
таким же способом получаем любую точку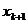 
:
.
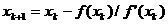Последовательность
значений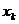 
сходиться
к точному решению (корню) значительно быстрее, чем в методе половинного
деления. Итерации можно прекратить, если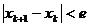 
.
Теорема.
Если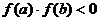 
,
причём 
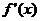и
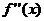отличны
от нуля и сохраняют определённые знаки на 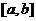, то исходя из
начального приближения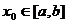 
,
удовлетворяющего неравенству: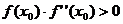 
, можно вычислить
методом Ньютона единственный корень уравнения 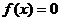с любой точностью.
Существование решения
следует из непрерывности 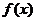на
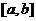и
условия .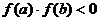
Единственность решения следует из монотонности 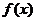на 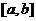(так
как 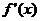сохраняет
знак).
После ввода начальной
точки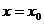 
,
точности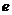 
и
предельного числа итераций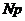 
следует обнуления
счётчика итераций. Затем следует итерационный цикл: вычисление приближённого
значения корня по формуле Ньютона и сравнение погрешности решения с заданной
точностью. Если погрешность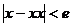 
или число итераций 
,
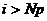то на экран (принтер) выводиться приближённое значение корня и числа итераций.
На этом вычисление заканчиваются. Если погрешность вычисления корня больше
заданной, то итерация продолжается: вычисляются новое приближённое значения
корня, его погрешность сравнивается с заданной так далее.
Для уточнения корня
методом Ньютона можно использовать электронные таблицы. В столбец записываем
формулу Ньютона,
в 
,
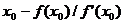в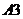 
,
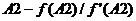затем копируем выражение
из 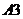в
клетки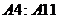 
.
В этих клетках появляются значения выражений.
Во второй строке в
результате подстановки в формулу Ньютона нулевого приближения 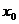появляется
первое приближение корня .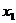
В третьей строке в результате подстановки в формулу Ньютона приближения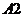 
появиться
второе приближение корня и так далее.
Установлено, что прибыль
учебного заведения вычисляется по формуле Z. При этом прибыль связана
нелинейной зависимостью с количеством студентов, принимаемых по контракту. Дать
прогноз на К лет о количестве принимаемых студентов по контракту для
обеспечения изменения прибыли на Pr%.
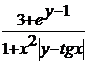
K=20,
Pr= 30%
Решение задачи сделать
следующим образом:
1. Переменную из формулы Z подобрать с помощью двух вариантов:
1. Программно, используя
методы простой итерации, половинного деления, Ньютона
2. Результаты работы
представить в PowerPoint.
· В качестве
переменной использовать любую переменную из заданных в выражении (выбирать
необходимо нелинейную зависимость, а значения остальных переменных выбрать
произвольно). Количество точек построения равно K, а интервал изменения
переменной подобрать так, чтобы величина изменения функции при изменении переменной
составляла Pr%.
· Из найденного
решения по п. 1.1 и 1.2 построить график функции по формуле Z (Таблица 1.1).
Для построения графика использовать электронную таблицу Excel из офисного
программного обеспечения со сформированными данными из Раscal на диске.
Результаты работы сохранить в виде файлов *.pas, *.dat, *.xls. Вид формулы Z,
величины Рr, K взять из вариантов по заданию преподавателя
· Переменные
необходимо задать на стадии выполнения программы вводом с клавиатуры или
дискового устройства.
· В программе
предусмотреть выходы из возможных некорректных программных прерываний типа
(1/0, ln(-2) и т.п.
· Исходный текст
программы и результаты расчетов и построений продублировать на бумажном
носителе, оформив их в Word, а график функции в Excel.
Фиксируем левую границу интервала: x0=4.71; y=1 - const. Для нахождения правой границы необходимо решить уравнение: z(x)=1.3z(x0) или f=z(x) - 1.3z(x0)=0. Уравнение решаем в
цикле К раз. Решение на каждом шаге является левой границей интервала x0 для следующего шага.
program
d;lambda=-0.01;=0.0000001;=30;=20;=1;t: text;:real;:integer;z
(x:real):real;(1+abs (y-sin(x)/cos(x))*x*x=0) then
begin('Error');;(n);;:=(3+exp (y-1))/(1+x*x*abs (y-sin(x)/cos(x)));;f (x:real):
real;:=z(x) - (1+Pr/100)*z(x0);;df (x:real): real;:=(f (x+0.00001) -
f(x))/0.00001;;
{Metod polovinnogo
deleniyaя}delenie;a1, b1, x, c: real;: integer;(t, 'C:\20\delenie.txt');(t);(t,
' x ', ' z(x) ');i:=1 to k do begin(t, x0:2:4,' ', z(x0):3:4);:=x0;:=a1*0.9;abs
(b1-a1)>=e do begin:=(a1+b1)/2;f(a1)*f(c)<0 then b1:=ca1:=c;;:=c;;(t);;
{Metod Nyutona}newton;x,
x1, b:real;:integer;(t, 'C:\20\newton.txt');(t);(t, ' x ', ' z(x) ');i:=1 to k
do begin(t, x0:2:4,' ', z(x0):3:4);:=0.9*x0;
x1:=x;:=x1-f(x1)/df(x1);abs
(x-x1)<=e;
:=x;;(t);;
{Metod prostoy
iteracii}iterac;x, x1, b: real;:integer;(t, 'C:\20\iterac.txt');(t);(t, ' x ',
' z(x) ');i:=1 to k do begin(t, x0:2:4,' ',
z(x0):3:4);:=0.9*x0;:=x;:=x1-f(x1)*lambda;abs (x-x1)<=e;:=x;;(t);;
нелинейный уравнение итерация
трансцендентный
begin:=4.71;
delenie;:=4.71; newton;:=4.71; iterac;.
Вывод
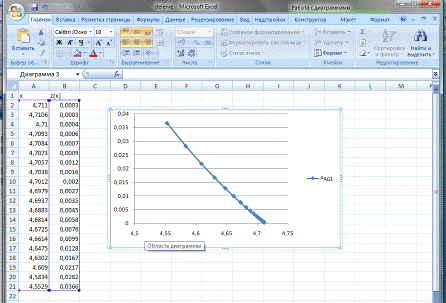
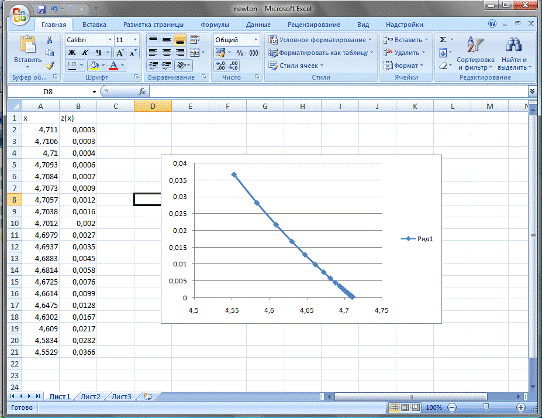
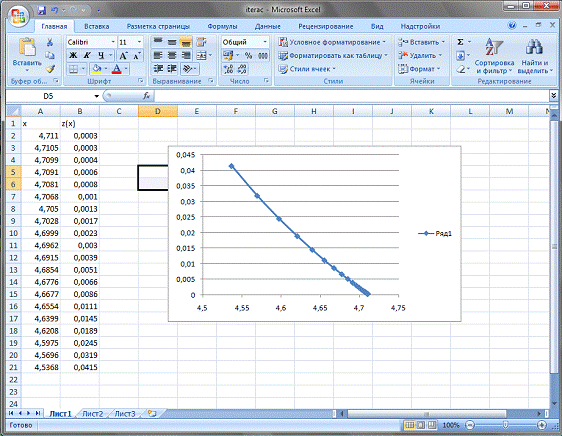
Таблица решений по каждому из
методов записана в соответствующие текстовые файлы (delenie.txt, newton.txt, iterac.txt). Все методы сходятся к
одним и тем же значениям. Видно, что z(x) на следующем шаге на 30% больше значения на текущем шаге.
Решение на Microsoft Excel.
Задаем x0=4,71. Запишем формулу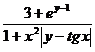 
и вычислим z(x0). Затем найдем z(x) увеличивая каждое последующее z
на 30%. Теперь будем подбирать x
с помощью «подбор параметра».
Когда все x и z найдены построим
график.
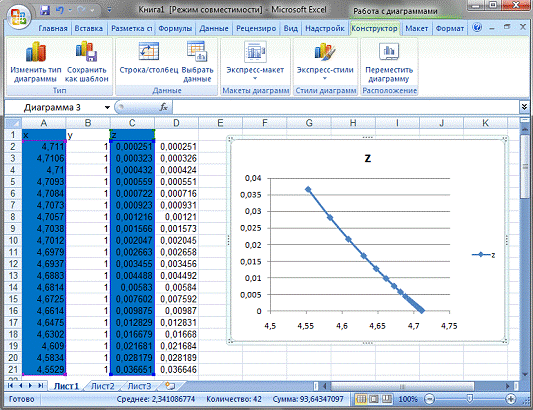
Видно, что задача,
решенная четырьмя методами, дает одно и тоже решение. Следовательно, можно
предполагать, что она выполнена правильно.