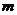 - характерная масса -
- характерная масса - 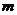 = 1кг.
= 1кг.
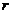 - характерный радиус -
- характерный радиус - 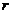 = 0.1м.
= 0.1м.
с - коэффициент жесткости - с = 4000
Н/м.
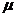 - коэффициент сопротивления
- коэффициент сопротивления 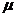 = 100 Н
= 100 Н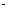 сек/м.
сек/м.
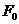 - амплитуда возмущающей силы
- амплитуда возмущающей силы 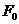 = 50 Н.
= 50 Н.
р - частота возмущающей силы р =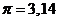 рад/c.
рад/c.
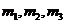 - массы тел механической системы.
- массы тел механической системы.
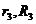 - радиусы ступеней блока 3.
- радиусы ступеней блока 3.
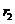 - радиус подшипника 2.
- радиус подшипника 2.
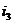 - радиус инерции блока 3.
- радиус инерции блока 3.
Часть 1. ПРИМЕНЕНИЕ ОСНОВНЫХ ТЕОРЕМ ДИНАМИКИ
МЕХАНИЧЕСКОЙ
СИСТЕМЫ
.1 Постановка второй основной задачи динамики
системы
Расчетная схема представлена на рис. 2.
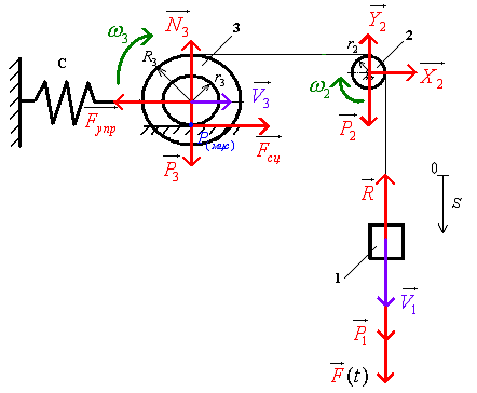
рис.2
На рис.2 обозначено:
 - силы тяжести,
- силы тяжести,
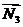 - нормальная реакция опорной
плоскости,
- нормальная реакция опорной
плоскости,
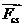 - сила сцепления,
- сила сцепления,
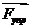 - упругая реакция пружины,
- упругая реакция пружины,
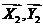 - реакции подшипника 2,
- реакции подшипника 2,
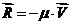 - сила вязкого сопротивления,
- сила вязкого сопротивления,
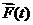 - возмущающая сила.
- возмущающая сила.
Рассматриваемая механическая система
имеет одну степень свободы (нити нерастяжимые, качение блока 2 происходит без
скольжения). Будем определять её положение с помощью координаты S . Начало
отсчета координаты совместим с положением статического равновесия центра масс
груза 1.
Для построения дифференциального
уравнения движения системы используем теорему об изменении кинетической энергии
механической системы в форме:
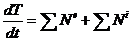 , (1.1)
, (1.1)
где Т - кинетическая энергия
системы,
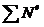 - сумма мощностей внешних сил,
- сумма мощностей внешних сил,
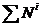 - сумма мощностей внутренних сил.
- сумма мощностей внутренних сил.
Теорема (1.1) формулируется так:
"Производная по времени от кинетической энергии механической системы равна
алгебраической сумме мощностей внутренних и внешних сил, действующих на точки механической
системы".
Вычислим кинетическую энергию
системы как сумму кинетических энергий тел 1-3:
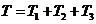 . (1.2)
. (1.2)
Груз 1 совершает поступательное
движение. Его кинетическая энергия равна:
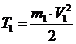 . (1.3)
. (1.3)
Подшипник 2 совершает вращательное
движение вокруг неподвижной оси. Его кинетическая энергия равна:
где 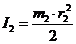 - момент инерции подшипника
относительно центральной оси,
- момент инерции подшипника
относительно центральной оси,
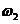 - угловая скорость подшипника.
- угловая скорость подшипника.
Блок 3 совершает плоскопараллельное
движение, поэтому его кинетическая энергия определяется по теореме Кенига:
 , (1.5)
, (1.5)
где 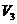 - скорость центра масс блока 3,
- скорость центра масс блока 3,
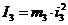 - момент инерции блока 3
относительно центральной оси ,
- момент инерции блока 3
относительно центральной оси ,
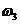 - угловая скорость блока 3.
- угловая скорость блока 3.
Тогда кинетическая энергия всего
механизма будет равна:
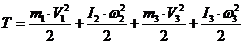 . (1.6)
. (1.6)
Выразим  через
скорость груза 1. Положив
через
скорость груза 1. Положив 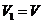 , получим:
, получим:
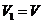 ;
; 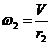 ;
; 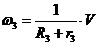 ;
;  . (1.7)
. (1.7)
Подставляя (1.3), (1.4), (1.5) в
(1.6) с учетом (1.7), получаем:
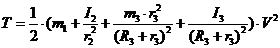 (1.8)
(1.8)
или
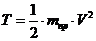 , (1.9)
, (1.9)
где
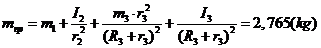 . (1.10)
. (1.10)
Величину 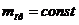 будем
называть приведенной массой.
будем
называть приведенной массой.
Найдём производную от кинетической
энергии по времени:
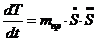 . (1.11)
. (1.11)
Теперь вычислим правую часть уравнения
(1.1) - сумму мощностей внешних и внутренних сил.
Мощность силы равна скалярному
произведению вектора силы на скорость точки её приложения:
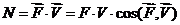 . (1.12)
. (1.12)
Рассматриваемая нами механическая
система является неизменяемой, т.е. тела, входящие в систему, недеформируемы и
скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей
всех внутренних сил будет равняться нулю:
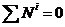 . (1.13)
. (1.13)
Будут равняться нулю и мощности некоторых
внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из
расчетной схемы:
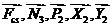 .
.
Найдем мощности остальных внешних
сил:
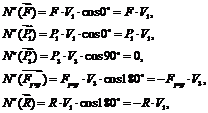 (1.14)
(1.14)
Тогда сумма мощностей внешних сил
будет равна:
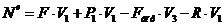 . (1.15)
. (1.15)
С учетом кинематических соотношений
(1.7) сумму мощностей внешних сил преобразуем к виду:
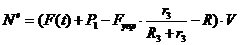 (1.16)
(1.16)
или
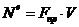 , (1.17)
, (1.17)
где
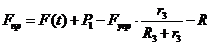 . (1.18)
. (1.18)
Величину 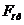 будем называть
приведенной силой.
будем называть
приведенной силой.
Преобразуем выражение (1.18).
Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение
пружины f равно сумме
статического 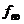 и
динамического
и
динамического  удлинений:
удлинений:
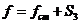 ,
,
причем из выражения (1.7) для 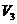 следует,
что
следует,
что 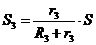 .
.
Тогда упругая сила будет равна:
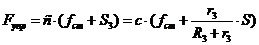 . (1.19)
. (1.19)
Сила вязкого сопротивления 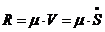 .
Приведенную силу с учетом последних формул для
.
Приведенную силу с учетом последних формул для 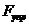 и
и 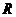 запишем в виде:
запишем в виде:
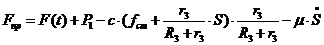 ,
,
раскрывая скобки получим:
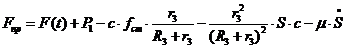 , (1.20)
, (1.20)
В состоянии покоя приведенная сила
равна нулю. Полагая (1.20) 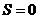 ,
, 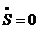 и
и 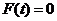 , получаем условие равновесия
системы:
, получаем условие равновесия
системы:
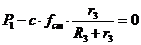 , (1.21)
, (1.21)
Из уравнения (1.21) определяется
статическое удлинение пружины:
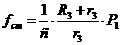 . (1.22)
. (1.22)
Учитывая (1.22) и (1.20), получаем
окончательное выражение для приведенной силы:
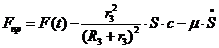 . (1.23)
. (1.23)
Подставим выражения для производной
от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом
(1.23) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения
системы:
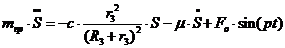 . (1.24)
. (1.24)
Запишем последнее уравнение в виде:
 , (1.25)
, (1.25)
где введены коэффициенты, имеющие
определенный физический смысл:
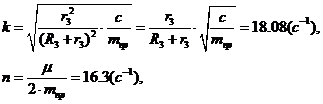
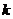 - циклическая частота свободных
колебаний,
- циклическая частота свободных
колебаний,
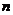 - показатель степени затухания
колебаний.
- показатель степени затухания
колебаний.
Запишем начальные условия движения:
 . (1.26)
. (1.26)
Выражения (1.25) и (1.26) совместно
представляют математическую модель для решения второй задачи динамики.
.2 Определение закона движения
системы
Проинтегрируем дифференциальное уравнение
(1.25). Пусть возмущающая сила изменяется по гармоническому закону:
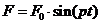 , (2.1)
, (2.1)
где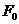 - амплитуда возмущающей силы,
- амплитуда возмущающей силы,
p -
циклическая частота возмущения.
Общее решение S
неоднородного дифференциального уравнения (1.25) складывается из общего решения
однородного 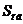 и частного
решения
и частного
решения 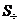 неоднородного:
неоднородного:
 . Однородное
дифференциальное уравнение, соответствующее данному неоднородному (1.25) ,
имеет вид:
. Однородное
дифференциальное уравнение, соответствующее данному неоднородному (1.25) ,
имеет вид:
Решение этого уравнения ищем в виде
функции:
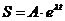 , (2.3)
, (2.3)
где 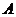 и
и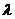 - постоянные величины.
- постоянные величины.
Подставляя (2.3) в (2.2), получаем:
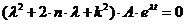 .
.
Так как мы ищем нетривиальное
решение, то 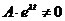 .
Следовательно, должно выполняться условие:
.
Следовательно, должно выполняться условие:
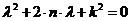 . (2.4)
. (2.4)
Уравнение (2.4) называется
характеристическим уравнением дифференциального уравнения (2.2). Это уравнение
имеет два корня:
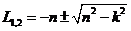 . (2.5)
. (2.5)
В нашем случае 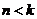 -
подкоренное выражение (2.5) отрицательно, следовательно корни
комплексно-сопряженные. Общее решение уравнения (2.2) имеет вид:
-
подкоренное выражение (2.5) отрицательно, следовательно корни
комплексно-сопряженные. Общее решение уравнения (2.2) имеет вид:
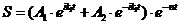 , (2.6)
, (2.6)
где 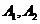 - постоянные интегрирования,
- постоянные интегрирования,
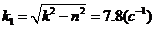 . (2.7)
. (2.7)
Решение (2.6), используя известные
формулы Эйлера
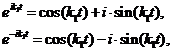
нетрудно представить в виде:
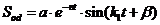 , (2.8)
, (2.8)
где 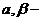 постоянные интегрирования.
постоянные интегрирования.
Определим частное решение
неоднородного дифференциального уравнения
 . (2.9)
. (2.9)
Частное решение ищем в виде правой
части
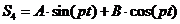 . (2.10)
. (2.10)
Подставляя (2.10) в (2.9), после
несложных преобразований получаем
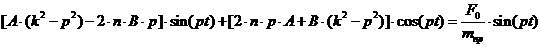
Сравнивая коэффициенты при соответствующих
тригонометрических функциях справа и слева, получаем систему алгебраических
уравнений для определения постоянных А и В:
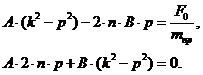
Решая эту систему, получаем
следующие выражения для коэффициентов А и В:
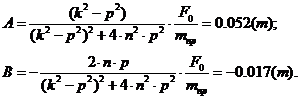 (2.11)
(2.11)
Таким образом, решение (2.10)
определено. Складывая (2.8) и (2.10), получаем общее решение неоднородного
уравнения (2.9):
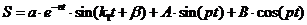 . (2.12)
. (2.12)
Константы 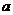 и
и 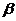 определяются
из начальных условий (1.26). Для этого найдем производную по времени от (2.12):
определяются
из начальных условий (1.26). Для этого найдем производную по времени от (2.12):
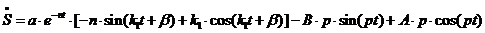 . (2.13)
. (2.13)
Подчинив (2.12) и (2.13) начальным
условиям, получим систему уравнений относительно искомых констант:
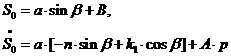 (при t=0).
(при t=0).
Решая эту систему, получаем:
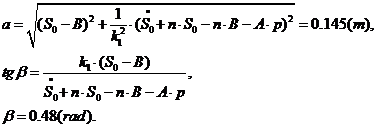 (2.14)
(2.14)
Подставляя (2.14) в (2.12), получаем
закон движения механизма:
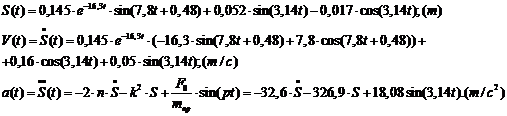 (2.15)
(2.15)
.3 Определение реакций внешних и
внутренних связей
Для решения этой задачи расчленяем механизм на
отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис.3).
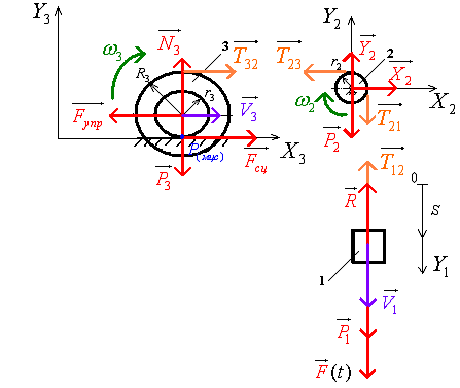
рис.3
Определение реакций связей проведем с помощью
теоремы об изменении количества движения:
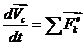 , (3.1)
, (3.1)
и теоремы об изменении кинетического
момента относительно центра масс:
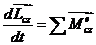 , (3.2)
, (3.2)
В соответствии с расчетными схемами
(рис.3) записываем уравнения (3.1) и (3.2) в проекциях на оси координат:
тело 1: 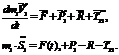 (3.3)
(3.3)
тело 2: 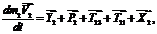
на ось 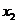 :
: 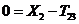 , (3.4)
, (3.4)
на ось 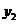 :
: 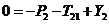 , (3.5)
, (3.5)
 (3.6)
(3.6)
тело 3: 
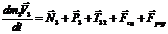
на ось 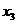 :
: 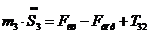 , (3.7)
, (3.7)
на ось 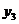 :
: 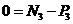 , (3.8)
, (3.8)
 (3.9)
(3.9)
С учетом кинематических соотношений (1.7)
систему уравнений (3.3) - (3.9) преобразуем к виду:
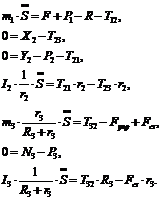 (3.10)
(3.10)
Уравнения (3.10) составляют систему
алгебраических уравнений относительно функций:
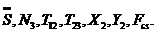
Решая эту систему, получаем и
дифференциальное уравнение системы, и выражения для определения реакций:
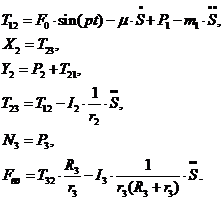 (3.11)
(3.11)
Часть 2. ВЫЧИСЛЕНИЕ КОНСТАНТ,
РЕАКЦИЙ СВЯЗЕЙ И ЗНАЧЕНИЙ ФУНКЦИЙ
2.1 Вычисление
констант
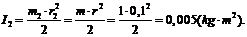
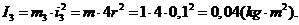
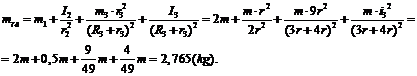
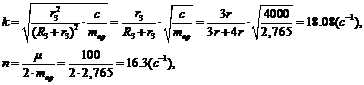
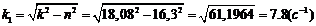
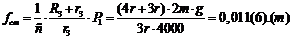
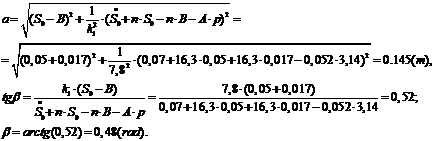
.2 Вычисление значений функций в момент времени t
Для момента времени 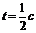 вычислим
значения функций
вычислим
значения функций  и
и 
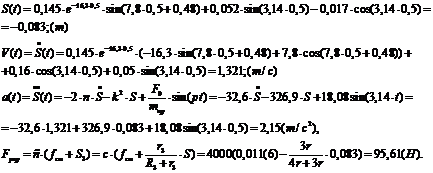
.3 Вычисление реакций связей

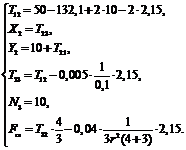
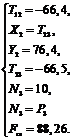
Такая механическая система
неработоспособна, для её оптимизации необходимо изменить параметры, такие как
масса, жесткость пружины и частота возмущающей силы.
Часть 3. ПРИМЕНЕНИЕ ПРИНЦИПА
ДАЛАМБЕРА-ЛАГРАНЖА И УРАВНЕНИЙ ЛАГРАНЖА ВТОРОГО РОДА
.1 Составление дифференциального
уравнения движения механизма с помощью принципа Даламбера-Лагранжа
Общее уравнение динамики системы есть
математическое выражение принципа Даламбера-Лагранжа:
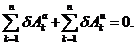 (3.1)
(3.1)
Здесь 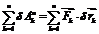 - сумма элементарных работ всех
активных сил на возможном перемещении системы;
- сумма элементарных работ всех
активных сил на возможном перемещении системы; 
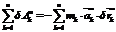 - сумма элементарных работ всех сил
инерции на возможном перемещении системы.
- сумма элементарных работ всех сил
инерции на возможном перемещении системы.
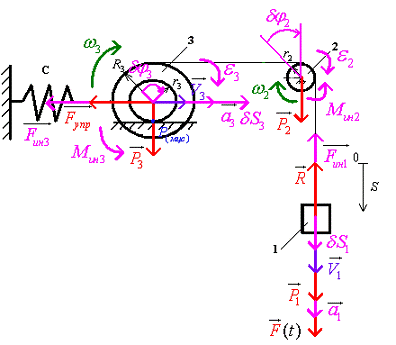
рис.4
Изобразим на рисунке активные силы и
силы инерции (рис.4). Идеальные связи 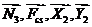 не учитываем и не отображаем на
расчетной схеме, поскольку по определению работа их реакций на любом возможном
перемещении системы равна нулю.
не учитываем и не отображаем на
расчетной схеме, поскольку по определению работа их реакций на любом возможном
перемещении системы равна нулю.
Пружина является неидеальной связью.
Введем реакцию этой связи в число активных сил.
Сообщим системе возможное
перемещение. Возможная работа активных сил определяется как сумма следующих
элементарных работ:
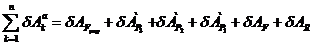 (3.2)
(3.2)
Вычислим последовательно
элементарные работы активных сил:

Суммируя эти работы получаем:
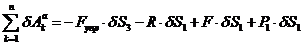 (3.3)
(3.3)
С учетом кинематических соотношений
(1.7) получим:
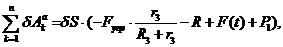
где 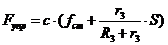 ,
,
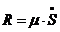
Окончательно получаем:
 (3.4)
(3.4)
Аналогичное выражение для
приведенной силы 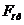 получено
ранее [см.(1.23)].
получено
ранее [см.(1.23)].
Найдем возможную работу сил инерции:
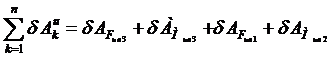 (3.5)
(3.5)
Вычислим последовательно
элементарные работы сил инерции:
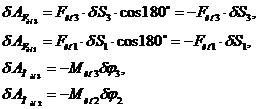 , где
, где 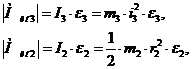 (3.6)
(3.6)
Суммируя эти работы получаем:
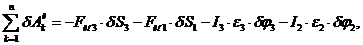 (3.7)
(3.7)
где 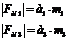
Используя кинематические соотношения (1.7),
можно записать:
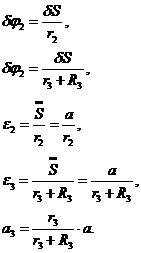 (3.8)
(3.8)
Тогда возможную работу сил инерции
можно преобразовать к виду:

 (3.9)
(3.9)
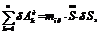 (3.10)
(3.10)
где 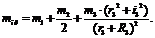 (3.11)
(3.11)
Аналогичное выражение для
приведенной массы системы было получено ранее [(1.10)]. Подставляя выражения
(3.4) и (3.10) в общее уравнение динамики (3.1) получаем:
 (3.12)
(3.12)
Поделив (3.12) на 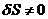 , получим
дифференциальное уравнение вынужденных колебаний системы:
, получим
дифференциальное уравнение вынужденных колебаний системы:
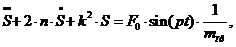 (3.13)
(3.13)
где 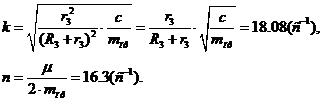 (3.14)
(3.14)
Дифференциальное уравнение (3.13) полностью
совпадает с полученным ранее уравнением (1.25).
.2 Составление
дифференциального уравнения движения механизма с помощью уравнений Лагранжа
второго рода
Составим теперь уравнения Лагранжа второго рода.
Для механической системы с одной степенью свободы дифференциальное уравнение
движения в обобщенных координатах имеет вид:
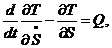 (3.15)
(3.15)
где Т - кинетическая энергия
системы;
Q -
обобщенная сила;
S -
обобщенная координата;
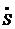 - обобщенная скорость.
- обобщенная скорость.
Выражение для кинетической энергии
системы было найдено ранее:
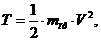
где 
Учитывая, что 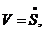 получаем:
получаем:
 (3.16)
(3.16)
Производные от кинетической энергии
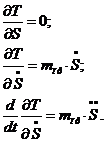 (3.17)
(3.17)
Для определения обобщенной силы Q сообщим
системе возможное перемещение 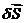 (рис.4) и вычислим сумму
элементарных работ всех активных сил на возможных перемещениях точек их
приложения [cм. (3.4)]:
(рис.4) и вычислим сумму
элементарных работ всех активных сил на возможных перемещениях точек их
приложения [cм. (3.4)]:
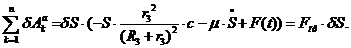 (3.18)
(3.18)
С другой стороны для системы с одной
степенью свободы
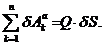 (3.19)
(3.19)
Сравнивая формулы (3.18) и (3.19)
получим:
 (3.20)
(3.20)
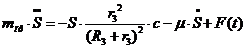
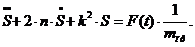 (3.21)
(3.21)
Полученное уравнение (3.21)
совпадает с уравнениями (1.25) и (3.13).