Механика деформирования и разрушения
История разрушений и катастроф
Прочность -
это способность тел быть целыми под действием нагрузки, не поддаваясь
разрушению. В истории накопилось много примеров последствий разрушений:
27г. Н.э. - разрушение Амфитеатра для
гладиаторских боев недалеко от Рима. Причина аварии в отступлении от законов
строительства и недостаточном обследовании надежности грунта
Франция, 13в.- рухнула башня одного из самых
больших соборов в городе Бова. Причина- незнание законов прочности несущих
конструкций.
США, 1940г. - катастрофа Такомского моста.
Причина- мост был рассчитан только на статическую ветровую нагрузку до 50 м/с,
а разрушился при ветре 19 м/с из-за динамических колебаний.
1942г. - разрушение судов типа
"либерти". Причина- возникновение трещин в корабельной стали в местах
вырезов в остром углу люка на палубе. Эта трещина росла под действием нагрузки,
достигла критической длины и мнгновенно перерезала корпус судна.
Россия, 2009г.- катастрофа на Саяно-Шушинской
ГЭС. Причина- отрыв турбины от основания из-за постепенного разрушения
крепежных шпилек.
Чтобы не допустить разрушения, надо хорошо знать
и уметь применять механику деформирования и разрушения твердых тел под
действием механических нагрузок.
История науки о прочности и сопротивление
разрушению.
Существует 3 этапа.
этап (16-18вв)- Сопромат. Здесь простейшее
одноосное напряженное состояние. Леонардо да Винчи впервые количественно
определил несущую способность проволок, подвешивая на них корзины и постепенно
наполняя их песком. Следующий шаг сделал Галилей, испытав на разрыв деревянные
брусья. Он нашел, что разрушающая нагрузка растет пропорционально площади
поперечного сечения бруса и не зависит от его длины. Он ввел представление о
прочности σ в как
о некоторой константе материала. Дальше Роберт Гук нашел, что напряжение
пропорционально деформации, что позволило сформулировать закон Гука:
σ= E·ε,
где E- модуль упругости; σ=
F/S; ε= Δl/l-
относительное удлинение
σ< σ в- разрушения
нет
этап (19век)- теория упругости. Развита
знаминитыми французами- Каши, Пуассоном, Новье. Они рассмотрели трехмерное
напряженное состояние. Сложными математическими приемами они научились
рассчитывать напряженно-деформированное состояние в любой точке различных
объемных тел под действием нагрузок. Казалось, что классическая теория упругости
позволяет рассчитать все, и разрушений больше не будет.
этап (20век)- механика разрушения. Если в теории
упругости сам процесс разрушения не рассматривался, то в механике разрушения он
стал рассматриваться. В 20 веке продолжались катастрофические разрушения на
суше, в воде и в воздухе. Взрывались паровые котлы, разрушались корабли, хотя
рассчитаны они были по всем правилам науки о прочности. Прочность корабельной
стали составляет 400 Мпа. Эксперименты в шторм обнаружили напряжение не выше 90
Мпа, т.е. корабли не должны были разрушаться, но они разрушались. Почему?
Накапливаемый
печальный опыт показал, что опасными местами на корабле являются люки,
отверстия, вырезы. Именно вокруг них появлялись трещины, которые от
неравномерной загрузки трюма или от удара волны могли со скоростью пули
перерезать судно. Инженеры долго не могли понять, почему отверстия так опасны.
Ведь при малом диаметре отверстия напряжения возрастают незначительно.
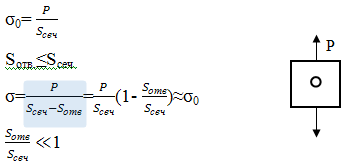
Решение нашел в 1898 году немец Кирш, решив
задачу об одноосном растяжении прямоугольной пластины с малым круговым
отверстием
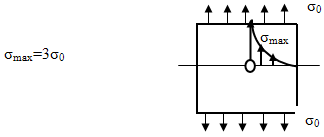
Он обнаружил резкий пик напряжений на краю
отверстия. Еще более удивительные результаты получил Колосов в 1909 году для
эллипсического отверстия.
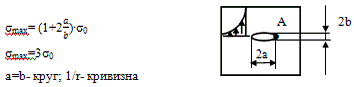
Из рисунка видно, что наиболее опасные пиковые
напряжения определяются кривизной отверстия и достигают максимума в точке А.
=3b,
σmax=7σ0
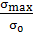 - коэффициент
концентрации напряжений, он показывает, что
самые опасные ситуации возникают у острых вырезов у острых материалов.
- коэффициент
концентрации напряжений, он показывает, что
самые опасные ситуации возникают у острых вырезов у острых материалов.
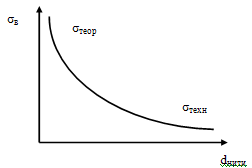
Известно, что теоретическая прочность,
рассчитанная для идеального кристаллического тела, является очень большой,
реальная же техническая прочность σтех=
(0,001-0,1)σтеор
значительно меньше. Причина- наличие трещин и дислокаций. Это подтвердили опыты
академика Иофа с кристаллами каменной соли. Если кристалл погрузить ненадолго в
горячую воду, а затем измерить прочность, то она возрастет в десятки раз.
Объясняется это растворением поверхностного слоя с дефектами, царапинами и
трещинами. Также увеличивается прочность стекла в тонких нитях.
При увеличении размера тела кристаллическая
решетка становится менее совершенной и в нем возникают дефекты больших
размеров. Англичанин Гриффитс показал, что возможности роста трещины зависит от
ее длины l:
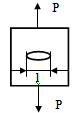
Он разработал энергетическую теорию прочности:
для роста трещины необходимо затрачивать работу на образование новых
поверхностей. С другой стороны при росте трещины освобождается упругая
деформация в области трещины. Для малых трещин освобожденной энергии
недостаточно для образования новых поверхностей, т.е. для разрыва материала.
Для больших трещин этой энергии хватает на разрыв и трещина рванется вперед с
громадной скоростью если материал хрупкий. Он рассчитал критическое значение
длины трещины (lкр), при l<lкр-
трещина не растет, а при l>lкр- трещина растет и разрывает тело.
Правильность этой теории Гриффитс подтвердил
экспериментально на стеклянных колбах и цилиндрических трубках. На них
наносилась трещина определенной длины, и с помощью сжатого воздуха создавалось
внутреннее давление. В ходе экспериментальных измерений внутреннее давление и
длина трещины в момент ее страгивания, которое всегда заканчивалось разрушением
сосуда на мелкие осколки. Стекло очень хрупкий материал и энергетическая теория
к нему хорошо применима (1920г). Но к пластичным металлам эта теория оказалась
не
очень
применима и только через 30 лет Ирвин и Орован предложили теорию квазехрупкого
разрушения, которая оказалась применима для Ме. Они в теории Гриффитса
константу равную поверхностной энергии материала,
которую надо затратить на продвижение трещины, заменили на удельную работу
пластической деформации в малой окрестности вблизи вершины трещины. Работа
пластической деформации при квазехрупком разрушении в сотни и тысячи раз
превосходит поверхностную деформацию при образовании поверхности. Вместо
рассмотрения энергетического баланса тела они изучили поле напряжений у конца
трещины. Из решения этой задачи следовало, что единственным параметром,
определяющим напряженное состояние концевой зоны и возможность распространения
трещины является коэфициентом интенсивности напряжений- КИН. Понятие о КИН
стало фундаментальным в механике разрушения и критическое значение КИН стало
использоваться в инженерной практике расчетов на прочность, сделав их более
точными и заменив в таких расчетах величину σв-
предел прочности, которая использовалась в сопромате. Теория Гриффится и
силовая теория Ирвина-Орована для квазехрупкого разрушения составляет линейную
механику разрушения. В отличие от сопромата и теории упругости, она
рассматривала сам процесс разрушения, развитие трещины и рассматриваемое тело
как неидеальное, с наличием дефектов- это главные черты третьего этапа науки о
прочности.
В первых двух этапах тело считают идеальным и
расчеты велись до момента разрушения, процесс разрушения не рассматривается.
Растяжение и сжатие.
Это простейшие одноосные воздействия нагрузки
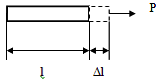
Упругое деформирование подчиняется закону Гука
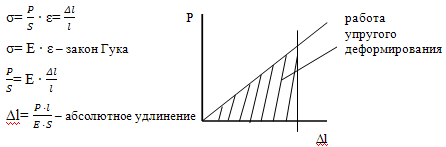
Элементарная работа:
dA= P · d(Δl)= 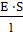 ·Δl
· d(Δl)
·Δl
· d(Δl)
после интегрирования получаем:
=  P
· Δl=
P
· Δl=  ·
·
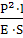
Это работа или потенциальная энергия упругого
деформирования стержня.
Напряженное состояние стержня.
Определим напряжение в некоторой наклонной
площадке с углом α в плоскости
нормального сечения
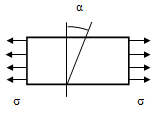
Отбросим левую часть стержня и рассмотрим
равновесие правой части
P- полные напряжения
на наклонной площадке.
P · Sα=
σ · S,
где Sα-
площадь наклонного сечения
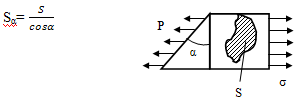
Разложим полное напряжение на нормальное и
касательное
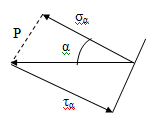
σα=
P · cosα
τα=
P · sinα
P= σ
· cosα
σα=
σ · cos2α
τα=
 ·
σ · sin2α
·
σ · sin2α
α= 0; σα=
σ; τα=
0
α= 900; σα=
0; τα=
0
τmax=
 при
α=
при
α=
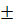 450
450
Для касательных напряжений выполняется закон
парности, согласно которому касательные напряжения на перпендикулярных
площадках равны.
Деформированное состояние в стержне.
Практика показывает, что продольное удлинение в
стержне сопровождается его поперечным сужением.
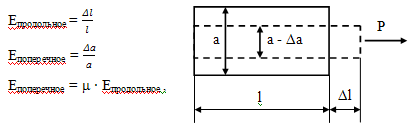
где μ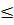 0,5-
коэффициент Пуассона. μ= 0,5 для
несжимаемого материала, который не изменяет своего объема при деформировании.
Чем пластичнее материал, тем μ ближе
к 0,5 (пластелин). Для Ме μ= 0,25-0,5 и
приводится в справочниках.
0,5-
коэффициент Пуассона. μ= 0,5 для
несжимаемого материала, который не изменяет своего объема при деформировании.
Чем пластичнее материал, тем μ ближе
к 0,5 (пластелин). Для Ме μ= 0,25-0,5 и
приводится в справочниках.
При растяжении возникают не только линейные, но
и угловые деформации.
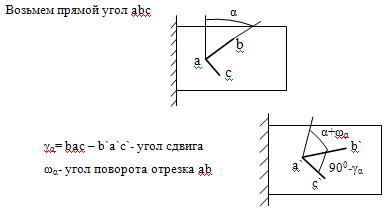
Из геометрических соображений ωα=
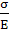 (1+μ)
sinα · cosα, увеличивая
α
на
900,
найдем угол поворота отрезка ac:
(1+μ)
sinα · cosα, увеличивая
α
на
900,
найдем угол поворота отрезка ac:
ωα+90=
- 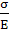 (1+μ)
sinα · cosα
(1+μ)
sinα · cosα
Угол сдвига равен разности углов поворота этих
отрезков
γα= ωα-
ωα+90= 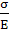 (1+μ)
sin2α, так как τα=
(1+μ)
sin2α, так как τα=
 σ
sin2α, то
σ
sin2α, то
γα=
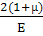 ·
τα- закон Гука для сдвига
·
τα- закон Гука для сдвига
γ=  , где G=
, где G= 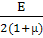 -
модуль упругости (сдвига) 2-ого рода
-
модуль упругости (сдвига) 2-ого рода
Закон Гука записывается в двух идентичных
формах:
σ= E · ε-
для нормальных напряжений и линейных деформаций
τ= G
· γ- для касательных напряжений
и сдвиговых деформаций
Величины E, G, μ
приведены в справочниках.
Скаляры, векторы, тензоры.
Все величины в природе- тензоры, но тензоры
разного ранга. Ранг тензора определяется числом его компонент. Число компонент
тензора N= 3r,
где r- ранг тензора.=0;N=1-
скаляр (масса, температура, время)- эта величина полностью определяется
значением одного числа
r=1;N=3-
вектор (скорость, сила, перемещение)- эта величина определяется тремя числами и
имеет направление в пространстве.
r=2;N=9-
тензор второго ранга (напряжение на площадке, деформация по направлению)- эта
величина определяется девятью числами и является вектором на площадке любой
ориентации. Если ориентация площадки изменяется, то изменяется и вектор.
Аналогично и деформации, которые зависят от направления.
r=3;N=27-
тензор третьего ранга (электро-магнитные поля в анизотропных средах).
Напряженное состояние в точке.
При растяжении и сжатии стержня мы видели, что
напряжение на площадке, проходящее через заданную точку, зависят от ориентации
площадки.
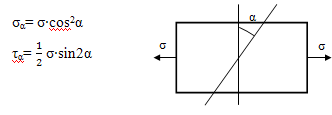
С поворотом площадки (изменение угла α),
изменяются
напряжения. Совокупность напряжений, возникающих на множестве площадок,
проходящих через рассматриваемую точку, называется напряженным состоянием в
точке.
Для его характеристики рассмотрим очень
маленький элементарный кубик около этой точки. Напряжения на его гранях будут
характеризовать напряженное состояние в точке при стягивании кубика в точку.
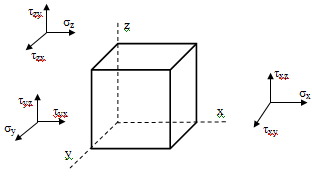
Полное напряжение на каждой грани кубика можно
разложить на 3 составляющие или компоненты: σ и
2τ.
Для
индексикации этих компонент используют правило:
. Нормальные напряжения σ
индексируются
осью, вдоль которой они направлены
. В касательных напряжениях ставятся два
индекса: первый обозначает ось перпендикулярные площадке, второй- ось, вдоль
которой направлено напряжение.
. Нормальные напряжения σ>0-
для
растяжения, σ<0- для сжатия.
. Касательные напряжения положительны, если
перпендикуляр к площадке совпадает с направлением оси, а направление τ
совпадает
с соответствующей осью и наоборот.
. Для касательных напряжений соблюдается закон
парности. На двух взаимно перпендикулярных площадках τ
перпендикулярные
к общему ребру равны и направлены либо обе к ребру, либо от ребра
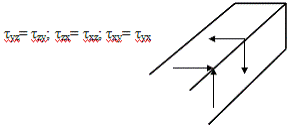
. При написании формул для компонент тензора
используется правило наращивания индексов с заменой:
x→y→z→x
Совокупность напряжений на гранях кубика можно
записать в виде таблицы или матрицы:
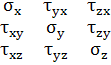
Эти 9 напряжений и образуют тензор напряжений.
По закону парности τxy=
τyx;
τyz=
τzy.
Вследствие закона парности получается 6 независимых компонент напряжений (а не
9!). Горизонтальные строчки в тензоре показывают напряжение вдоль одной оси для
всех площадок. Вертикальные колонки показывают все компоненты на одной
площадке.
Итак, тензор напряжений можно записать в виде
матрицы:
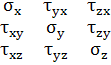
Компоненты тензора в общем виде записываются pij,
где i и j
принимают по очереди значения x, y, z. При i=j pij=
σi,
при i≠j
pij= τij.
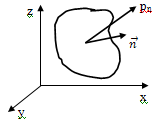
Знание тензора напряжения, т.е. напряжения на гранях элементарного кубика,
позволит находить напряжения на любой площадке с единичным вектором 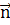 .
Полное напряжение на этой площадке
.
Полное напряжение на этой площадке 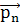 =
‖p‖
·
=
‖p‖
· 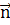 .
.
Компоненты единичного вектора:
nx= cos(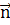 ;
;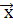 )
)
ny= cos(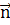 ;
;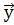 )z=
cos(
)z=
cos(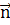 ;
;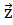 )
)
В общем виде 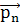 =
‖p‖
·
=
‖p‖
· 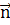 нам
даст pnk=
pik · ni,
k= x, y, z.
нам
даст pnk=
pik · ni,
k= x, y, z.
pnx=
σxnx
+ τyxny
+ τzxnz
pny=
τxynx
+ σyny
+ τzynz
pnz=
τxznx
+ τyzny
+ σznz
Тензор напряжения показывает напряжения на
гранях элементарного кубика. Он нужен, чтобы найти напряжения на любой
площадке. Поэтому напряженное состояние в точке является тензором второго ранга
с шестью независимыми компонентами.
Компоненты тензора напряжения зависят от
ориентации осей (ориентации кубика). При изменении осей (повороте кубика) эти
компоненты изменяются, но при любой ориентации они дают один и тот же результат
при нахождении напряжения на какой-то площадке.
Элементарный кубик можно повернуть так, т.е.
найти такое его положение, что на всех его гранях касательные напряжения будут
равны нулю. На этих гранях будут действительно только нормальные напряжения σ.
Такие
площадки называются главными, а σ на
них будут главными напряжениями. В порядке возрастания они обозначаются σ3,σ2,σ1.
Таким образом, в каждой точке напряженного тела существует такая система осей
x,y,z, в которой касательные напряжения:
τxy=
τyz=
τzx=
0
Такие оси называются главными. В таких осях в
системах напряжения на кубике существенно упрощаются.
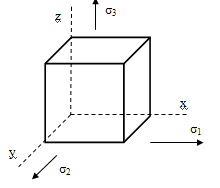
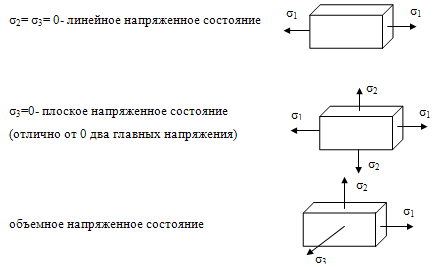
Вместо 9 напряжений остается максимум 3. С
помощью главных осей и напряжений удобно показывать три вида напряженного
состояния:
Тензор- направленная величина из 9 компонент,
характеризующая напряженное состояние в точке, где компоненты- напряжения на
гранях кубика. Позволяет находить напряжение на любой площадке, проходящей
через эту точку:
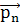 = ‖p‖
·
= ‖p‖
· 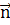
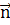 = ║
= ║  ║
║
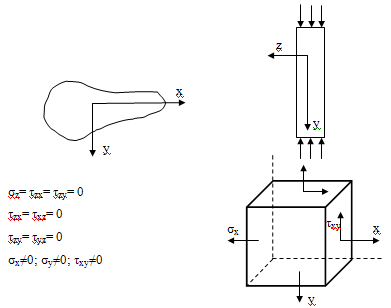
Плоское напряженное состояние (ПНС)
Здесь одно главное напряжение равно нулю, а два-
отличны от нуля. ПНС реализуется в тонких пластинах, которые нагружаются
напряжениями, приложенными на границе плоской пластины и равномерно
распределены по ее толщине. Напряжение на обеих поверхностях пластины равны
нулю.
Найдем напряжения на наклонной площадке при ПНС.
Разрежем кубик наклонным сечением и отбросим правую часть:
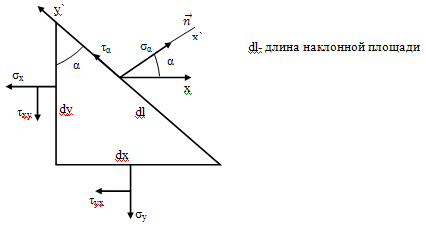
Выберем новые оси x` и y`. Чтобы найти σα
и
τα
рассмотрим
условия равновесия Δ, проектируя
все силы на оси x` и y`.
Проекция на ось x` при единичной толщине пластины:
σα·dl
- σx·dy·cosα
- σy·dx·sinα
- τyx·dx·cosα
- τxy·dy·sinα=
0
Проекция на ось y`:
τα·dl
+ σx·dy·sinα
- σy·dx·cosα
+ τxy·dx·sinα
- τyx·dy·cosα=
0
Учтем, что dy= dl·cosα;
dx= dl·sinα,
следовательно для оси x:
σα·dl
- σx·cos2α·dl
- σy·sin2α·dl
- τyx· sin2α·dl
- τxy·
sin2α·dl
- τxy· sin2α
sin2α
cos2α
- sin2α=
cos2α
cos2α=
 (1
+ cos2α)
(1
+ cos2α)
sin2α=
 (1
- cos2α)
(1
- cos2α)
σα= σx·cos2α
+ σy·sin2α
+ τxy·sin2α
(1)
τα=
-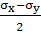 · sin2α + τxy·cos2α
(2)
· sin2α + τxy·cos2α
(2)
Выражение (1) перепишем по-другому:
σα=
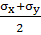 +
+
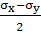 ·
cos2α
- τxy·sin2α
(3)
·
cos2α
- τxy·sin2α
(3)
На перпендикулярной наклонной площадке α+900:
σα+90=
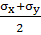 -
-
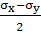 ·
cos2α
- τxy·sin2α
·
cos2α
- τxy·sin2α
По закону парности τα+90=
τα:
Сумма нормальных напряжений на взаимно
перпендикулярных площадках не зависит от угла α, т.е.
постоянно в данной точке или является инвариантом, независящем от выбора осей
координат.
Главные напряжения в ПНС. Если поворачивать
площадку, т.е. изменять угол α, то
при каком-то значении α0-
σα достигнет максимума, а σα+90˚-
минимума. Найдем этот максимум:
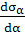 = -
= - 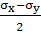 ·
2sin2α
+ τxy·2cos2α,
используя (2) получим:
·
2sin2α
+ τxy·2cos2α,
используя (2) получим:
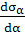 = 2τα
= 2τα
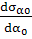 = 0 при τα=
0
= 0 при τα=
0
При нулевом касательном напряжении на площадке
получим главную площадку и нормальное напряжение на ней будет главным:
g2α0=
 (4)
(4)
(4) определяет два взаимно перпендикулярных
направления, по которым действуют главные напряжения σmax
и σmin.
Подставив (3) α= α0:
σα0=
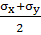 +
(
+
(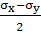 + τxy·tg2α0) · cos2α,
с учетом (4):
+ τxy·tg2α0) · cos2α,
с учетом (4):
cos2α0=
± 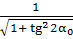 =
±
=
± 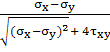
σ1,2=
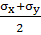 ±
±

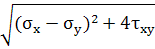 (5)
(5)
+ для σmax=
σ1
- для σmin=
σ2
В главных осях тензор запишется:
‖p‖=

tgα1,2=
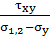
Совместим оси x и y с направлениями σ1
и
σ2,
т.е. выберем главные оси:
σx=
σ1;
σy=
σ2;
τxy=
0
Угол α отсчитывается
от направления σ1,
тогда выражения (2) и (3) упростятся:
σα=
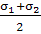 +
+
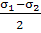 ·
cos2α (6)
·
cos2α (6)
τα=
- 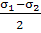 ·
sin2α (7)
·
sin2α (7)
α= - 450,
sin2α= -1
τmax=
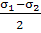 (8)
(8)
τmax
равно
полуразности главных напряжений, действующих под углом 45˚ к главным осям.
Подставляя (5) в (8) получим выражение τmax
через
исходные компоненты:
τmax=

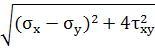
На площадке под углом 45˚ к главным осям:
σ±45º =
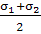 =
=
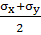
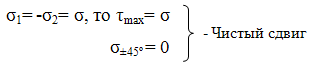
Круг напряжений Мора.
Обозначим (6) и (7):
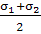 = a
= a 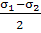 =
R
=
R
σα=
a + R·cos2α
(9)
τα=
- R·sin2α
(10)
В координатах σ и
τ
эти
равенства являются уравнениями окружности R в параметрической формуле (α-параметр)
и дают круг напряжений Мора, который позволяет графически находить напряжения
на любой наклонной площадке с углом α
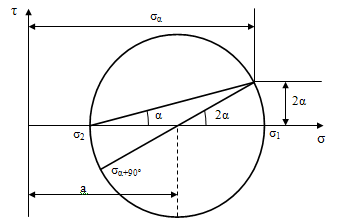
Круг Мора можно построить и не по главным
напряжениям, т.е. σx,
σy,
τxy.
Объемное напряженное состояние (ОНС)
Оно определяется полным тензором напряжений с
шестью независимыми компонентами, представляющими собой нормальные и
касательные напряжения на гранях элементарного кубика, расположенного в системе
координат x,y,z. Этот тензор позволяет находить напряжения на любой наклонной
площадке с единичным вектором 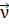 (νx,
νy,
νz)
(νx,
νy,
νz)
νx=
cos(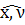 )
)
νy=
cos(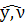 )
)
νz=
cos(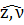 )
)
Вывод формул ведется как и для ПНС. Элементарный
кубик пересекается наклонной плоскостью, правая часть отбрасывается и рассматривается
равновесие левой. Из условий равновесия получаем кубическое уравнение для
определения главных напряжений
σ1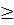 σ2
σ2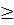 σ3
σ3
т.е. наша наклонная площадка выбрана главной:
σ3
+ I1σ2
+ I2σ
- I3=
0 (11)
Коэффициенты (11) являются инвариантами, которые
не зависят от выбора осей координат, поскольку при любых исходных площадках они
должны давать одни и те же значения главных напряжений (σ1,
σ2, σ3).
Величины I1, I2,
I3
называют первым, вторым и третьим инвариантом (т.е. при повороте площадки
значение не меняется) тензора напряжений:
1=
σx
+ σy + σz
I2=
σxσy
+ σyσz
+ σzσx
- 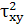 -
-
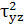 -
-
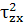
I3= σxσyσz
- σx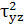 - σy
- σy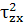 - σz
- σz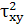 - 2τxyτyzτzx
- 2τxyτyzτzx
Круг Мора для ОНС.
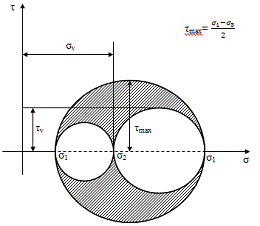
Заштрихованная часть определяет напряженное
состояние на наклонных площадках. Здесь более сложные построения, чем для
плоского напряженного состояния.
Обобщенный закон Гука.
В линейном состоянии закон Гука имеет самый простой
вид σ=
E·ε.
Но и в более общем объемном напряженном
состоянии между компонентами тензоров напряжений и деформации существует
определенная зависимость. При малых упругих деформациях эта зависимость
является линейной и называется обобщенный закон Гука. Он особенно прост в
случае изотропного тела, свойства которого не зависят от направления.
γxy=
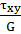 -
модуль сдвига, модуль упругости 2 рода
-
модуль сдвига, модуль упругости 2 рода
γyz=
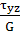
γzx=
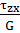
Т.е. здесь сдвиговая деформация определяется
одним соответствующим или тангенциальным напряжением. В случае линейной
деформации они зависят от всех трех нормальных напряжений.
εx=
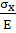 -
μ
-
μ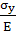 - μ
- μ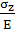
εy=
 ·[σy
- μ·(σx -
σz)]
·[σy
- μ·(σx -
σz)]
εz=
 ·[σz
- μ·(σz -
σy)]
·[σz
- μ·(σz -
σy)]
Сложив линейные деформации, получим
относительное изменение объема:
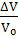 = εx
+ εy
+ εz=
= εx
+ εy
+ εz=
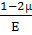 ·
(σx
+ σy
+ σz)
·
(σx
+ σy
+ σz)
Потенциальная энергия деформирования.
В элементарном объеме определяются суммой работ
сил, действующих на поверхности этого объема. Например, сила σxdyσz
совершает работу на перемещение εxdx
по оси x, вызванном всеми действующими силами:
 σxεydz
· εxdx
σxεydz
· εxdx
Касательная сила τyzdydx
на перемещение γyzdz
дает работу:
 τyxdydx
· γyzdx
τyxdydx
· γyzdx
Все остальные компоненты дают аналогичные
выражения. В итоге для энергии деформирования элементарного объема получим:
Разделив на единицу объема dxdydz,
и выразив деформации через напряжение, получим выражение для энергии
деформирования единичного объема:
0=
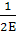 [
[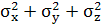 - 2μ·(σxσy
+ σyσz
+ σzσx)
+
- 2μ·(σxσy
+ σyσz
+ σzσx)
+ 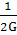 ·
(
·
(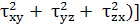
Или в главных напряжениях:
0=
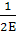 [
[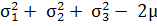 ·(σ1σ2
+ σ2σ3
+ σ3σ1)]
·(σ1σ2
+ σ2σ3
+ σ3σ1)]
Эта энергия деформирования состоит из двух
частей: из энергии изменения объема и из энергии изменения формы.
0=
Uи.об.
+ Uи.ф.и.об.=
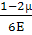 ·
(σ1
+ σ2
+
·
(σ1
+ σ2
+ 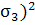
Uи.ф.=
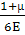 ·
(
·
(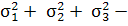 σ1σ2
- σ2σ3
- σ3σ1)
σ1σ2
- σ2σ3
- σ3σ1)
В другой форме:
Uо.ф.=
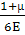 ·
[(
·
[(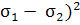 +
+ 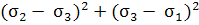 ]
]
Для неглавных осей получим:
о.ф.=
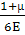 ·
[(
·
[(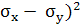 +
+ 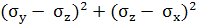 +
+
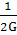 ·
(
·
(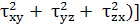
Теории предельных напряженных состояний.
В зависимости от условий нагружения, материал
может находиться в механических состояниях:
упругом (при небольших внешних силах)
пластическом (при больших силах)
разрушения (при очень больших силах и
образовании трещин)
Предельное напряженное состояние- это такое
состояние, при котором происходит переход из одного сотояния в другое:
для хрупких- упругое переходит в разрушение
для пластичных- упругое переходит в пластичное с
большой остаточной деформацией
Предельное напряженное состояние характеризует
свойства материала. При расчете конструкции на прочность обычно максимальные
напряжения сопоставляют с предельными для данного материала. Если σmax<σпредел,
то разрушения нет- конструкция работает нормально.
Но как определяется предельное напряженное
состояние?
. Это очень просто для одноосного напряженного
состояния. Испытания на растяжение позволяют найти предел текучести σт
и
предел прочности σв-
эти величины и будут предельными напряжениями:
- σт
для пластичных материалов;
- σв
для хрупких материалов
. Также просто и в случае чистого сдвига,
испытывая на кручение тонкостенную трубку, находят предельное значение τт,
τв. Если касательные
напряжения в конструкции (трубке) меньше этих предельных значений, то
конструкция не разрушается- она работоспособна.
. Значительно сложнее в случае объемного
напряженного состояния, когда отличаются от нуля σ1,
σ2, σ3.
Здесь для каждого набора этих главных напряжений надо было бы проводить
испытания материала и находить предельное состояние, но таких наборов σ1,
σ2, σ3
может быть очень много, что потребует очень многих испытаний и с практической
точки зрения неприемлимо.
Выход- в замене этого напряженного состояния на
равноопасное, простое растяжение с главным напряжением σэкв.
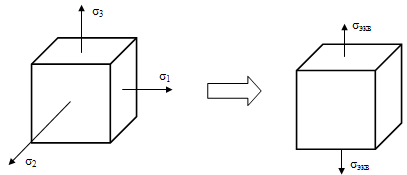
σэкв-
эквивалентное напряжение- это такое напряжение, которое следует создавать в
растянутом образце, чтобы его напряженное состояние стало равноопасным с
заданным объемом, тогда набор величин σ1,
σ2, σ3
заменяется на одну величину σэкв,
сравнивая которую с предыдущими характеристиками растяжения σт
и σв
мы делаем вывод о том, наступит разрушение или нет
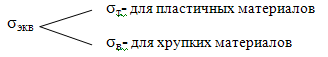
Теории прочности.
Они определяют правила перехода от объемного
напряженного состояния σ1,
σ2, σ3
к простому растяжению σэкв,
т.е. правила замены σ1,
σ2, σ3
на σэкв.
теория - наибольшего нормального растяжения. σэкв=
σ1, не учет σ2,
σ3 является
недостатком.
теория - наибольшей линейной деформации.
εэкв=
ε1=
 ·(σ1
- μ·(σ2+σ3)=
·(σ1
- μ·(σ2+σ3)=
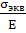
σэкв=
σ1 - μ·(σ2+σ3)
Физический смысл этой теории- разрушение
наступает, когда расстояние между молекулами становится слишком большим,
подходит для хрупких материалов.
теория - наибольшего касательного напряжения.
Подходит для пластичных материалов. Означает, что пластические деформации
возникают, когда τmax
достигает некоторого предельного значения:
τmax=
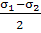 =
=
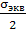
σэкв=
σ1-σ3
Недостаток - не учет σ2,
кроме того дает погрешность для материалов, имеющих различные характеристики σт
и σв
при растяжении и сжатии, но для Ме это самая хорошая теория.
теория - энергетическая. Предельное напряжение
материала наступает тогда, когда энергия его формы изменения достигает
предельного значения:
о.ф.
= 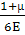 ·
[(
·
[(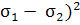 +
+ 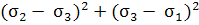 ]
]
Uо.ф.
= 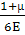 ·2
·2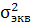
σэкв=
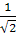
σэкв=
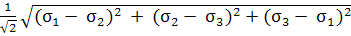
5 теория - Мора. Теория применяется для
материалов, обладающих различными значениями пределов текучести и прочности (σт
и σв)
при растяжении и сжатии.
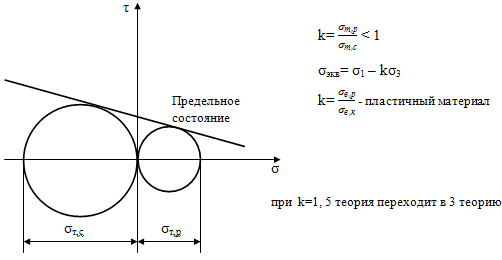
Различные теории прочности применяются для
различных материалов, находящихся в различных напряженных состояниях. Наиболее
подходящая теория дает наилучшее совпадение с экспериментом. Универсальной
теории нет для всех условий нагружения материала, поэтому надо думать, когда
какую теорию лучше применить. А лучше применить несколько теорий и по ним
сделать наиболее обоснованный вывод.
Механика разрушения. Виды разрушений.
Разрушение- сложный процесс, протекающий во
времени в результате воздействия внешних и внутренних разрушений и
завершающийся разделением тела на части или наступлением беспрепятственного
пластичного течения.
хрупкое. Процесс разрушения неразрывно связан с
развитием реальных дефектов твердых тел: трещин и дислокаций. Из-за них реальная
прочность на 1-3 порядка меньше теоретической, рассчитанной для идеального
твердого тела. В хрупких материалах за разрушение ответственны внутренние и
поверхностные трещины, являющиеся концентрациями напряжений. Причиной
разрушения является то, что одна или несколько трещин пробегает через весь
материал с очень большой скоростью. При растяжении образца из хрупкого
материала, шейка перед разрушением не образуется. Все это придает
катастрофический характер разрушению, т.к. оно происходит без видимых изменений
тела внезапно и очень быстро. Поверхность разрушения представляет собой гладкий
скол по кристаллографическим плоскостям с низкими индексами.
вязкое (пластичное). В таких материалах, которые
пластически деформируются перед разрушением, наблюдаются большие необратимые
искажения формы (шейка при растяжении образца). Если в хрупком материале
разрушения происходят путем полного разделения двух соседних слоев атомов при
растяжении, то в пластичных материалах наблюдается интенсивное пластичное
течение. При этом соседние атомные пласты не разделяясь, сдвигаются
относительно друг друга подобно колоде карт, что объясняется дислокациями. При
растяжении образца из пластичного материала несущая способность в ходе течения
сначала возрастает, а затем после образования шейки, падает и тело разрушается.
Шейка возникает в наиболее слабом сечении образца, и вся дальнейшая деформация
сосредотачивается в шейке, здесь возникают микропоры и микротрещины, которые
постепенно объединяются с образованием трещины. Эта трещина медленно растет, и
процесс заканчивается сдвигом под углом 45˚ к оси с
образованием характерной чашки и конусного излома. Поверхность излома имеет
шероховатый вид из-за слияния микротрещин и интенсивного пластичного течения.
Так как процесс разрушения развивается медленно, наблюдается необратимое
искажение формы, то разрушение не носит катастрофического характера.
усталостное разрушение. Однако надо иметь в
виду, что пластичные материалы могут катастрофически внезапно хрупко
разрушаться без заметной пластичной деформации, причем при напряжениях
значительно меньших пределу прочности. Объясняется это постепенным очень
медленным ростом трещин при повторной колебательной нагрузки и катастрофически
быстром ростом трещин после достижения критической длины. Это усталостное
разрушение при циклических нагрузках. Оно, в частности, объяснило серию
катастроф в военное время с американскими судами типа "либерти",
построенных из пластичной малоуглеродистой стали. Такое разрушение является и
причиной других катастроф: с самолетами, мостами, резервуарами и т.д.
при ползучести. Ползучесть- медленная
непрерывная пластичная деформация твердого тела под действием постоянной
нагрузки. Разрушение происходит через длительное время по механизму пластичного
разрушения. Типичная кривая ползучести:
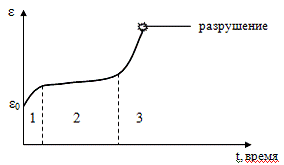
Состоит из трех участков: неустановившейся
ползучестью с уменьшением скорости пластичной деформации (1), установившейся с
постоянной скоростью (2), ускоренной ползучести (3), когда в образце возникают
микропоры и микротрещины, что заканчивается разрушением.
Коррозионное разрушение- под совместным
действием длительной нагрузки и коррозионной среды, которая ускоряет процесс
распространения трещины, чем значительно снижает прочность материала. Особенно
сильно проявляется в случае высокопрочных низкопластичных материалах.
Динамическое разрушение- под действием
динамических нагрузок. Главным образом гармонических (например, изменяющихся во
времени по синусоиде) и ударных. Здесь существенную роль в процессах
распространения трещин начинают играть возникающие при динамических нагрузках
упругие волны, возникающие в объеме или на поверхности тела.
Тепловой удар- разрушение под действием
внутренних температурных напряжений. Например, стакан лопается при наливании
горячей воды или дерево лопается в сильный мороз. Здесь внутренние более горячие
слои материала расширяются и давят на холодные внешние слои, вызывая в них
растягивающие напряжения. При наличии трещин (царапин на поверхности) эти
напряжения приводят к хрупкому разрушению. Часто температурные разрушения
вызываются различием коэффициента термического расширения (КТР)
Обобщая можно сказать, что разрушение есть
процесс зорождения и роста трещин под действием нагрузки.
Теоретическая прочность.
Это максимально возможная расчетная прочность
идеального кристаллического тела. Сила межатомного взаимодействия зависят от
межатомного расстояния x.
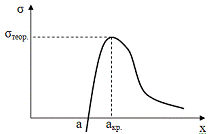
При равновесном межатомном расстоянии x=a=1Å=10-10м
эти силы равны 0. При меньших расстояниях x<a
атомы отталкиваются и σ<0; при
больших- притягиваются и σ>0. На
критическом расстоянии акрит. Сила притяжения максимально возможна и
они определяют теоретическую прочность на разрыв σтеор.
Если прикладные напряжения σ>σтеор.,
то атомные слои беспрепятственно удаляются друг от друга, т.е. разрываются на
части- разрушается. Кривую σ(х)
можно условно принять за синусоиду, тогда:
σ= σтеор·sin( ·
· 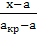 ),
a ≤ x ≤ aкр
),
a ≤ x ≤ aкр
На начальной стадии находится почти линейный
участок, который и обеспечивает справедливость закона Гука σ=Е·ε,
где
ε-
относительная
деформация:
ε= 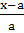 при
малых x, sinx≈x
при
малых x, sinx≈x
sin ·
· 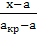 ≈
≈  ·
· 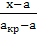
Однако очень тонкие нити (стальные, стеклянные)
имеют прочность, приближенные к 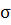 теор.,
также и нитевидные кристаллы, выращенные в особых условиях, которые практически
не имеют дефектов.
теор.,
также и нитевидные кристаллы, выращенные в особых условиях, которые практически
не имеют дефектов.
Концентрация напряжений.
Всякого рода отверстия, вырезы, трещины в
упругом теле приводят к существенному повышению напряжений в непосредственной
близости от таких мест.
Возникновение локального, часто весьма опасного
пика напряжений называется концентрацией напряжений.
Рассматриваемые растяжения пластичны
эллиптическим вырезом, где 2а- ось, 2в- малая ось эллипса
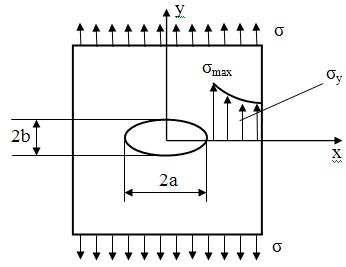
Колосов и Инглис решили задачу о распределении
напряжений и показали, что на поверхности вершины эллипса оно максимально:
σmax=
σ·(1+2 )
)
Теория Гриффитса для хрупкого разрушения.
Молодой английский ученый Гриффитс (27лет) в
1920году опубликовал статью "Явление разрушения и течения твердого
тела", совершившую революцию в механике твердого тела. Он попытался
достичь теоретической прочности на стекле, которое при 20˚С является
упругим вплоть до разрушения. Он брал свежевытянутые тончайшие нити и определял
их прочность на разрыв. Обнаружил, что с уменьшением диаметра нити их прочность
повышается и становится сравнима с теоретической.
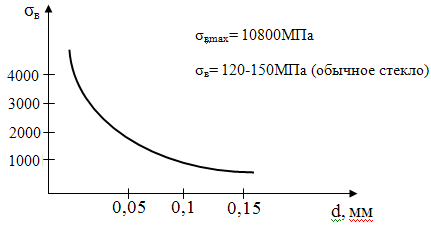
Сильное отличие σреал
от σтеор
Гриффитс объяснил наличием трещин, может быть и невидимых, но значительно
превышающих по размеру межатомное расстояние. Эти трещины образуются
самопроизвольно при изготовлении стеклянного волокна, чем больше диаметр
волокна, тем больше может быть размер трещин, поэтому с ростом диаметра-
прочность падает.
Но главная заслуга Гриффитса состоит в том, что
он связал причины развития (роста трещины в теле) с процессами накопления и
освобождения энергии упругой деформации тела (энергетический подход Гриффитса).
Он рассматривал концентрацию напряжений на дефекты микроскопических размеров.
Но одной концентрации напряжений у вершины трещины мало для того, чтобы трещина
росла и разорвала тело. Для роста трещины необходимо затрачивать работу на
образование новых поверхностей материала. Эта работа совершается в процессе
распространения трещины за счет упругой разгрузки объема материала, прилегающего
к трещине.
Гриффитс нашел условия, при которых
освобожденной упругой энергии хватает на образование новых поверхностей
материала трещины и трещина самопроизвольно распространяется, приводя к
разрушению тела. Это энергетическая теория Гриффитса.
Возьмем прямоугольную пластину единичной толщины
с размерами а и в и растянем ее напряжением σ и
жестко закрепим края.
В закрепленной пластине запасается упругая
энергия:
W0= 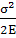 ·
ab
·
ab
W0= 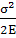 -
в единицу площади
-
в единицу площади
Появление сквозной трещины 2l приведет к
уменьшению деформации в зоне у трещины. С площадью с·l2, где с-
множитель, который Гриффитс нашел из решения Инглиса с=2π.
Таким
образом,
освобождается упругая энергия ΔW=
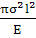 .
.
Эта энергия поступает в вершину трещины, где
возникла концентрация напряжений и там затрачивается на разрушение, т.е. на
образование новой поверхности.
Работа образования трещины длиной 2l равна:
Г=
4γl
γ- удельная работа
образования единицы площади новой поверхности (поверхностная энергия
материала).
При увеличении длины трещины на малую величину Δl-
высвободится энергия упругой деформации:
ΔW= 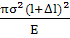 -
-
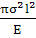 ≈
≈ 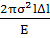
На увеличение длины трещины должна быть
затрачена энергия
ΔГ= 4γ·(l+Δl)
- 4γl= 4γΔl
В критическом состоянии при ΔW=
ΔГ:
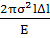 = 4γΔl
= 4γΔl
σкр=
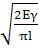
Если ΔW>ΔГ,
то освобожденной энергии хватает на разрушение материала и трещина
самопроизвольно распространяется. Если ΔW<ΔГ,
то освобожденной энергии недостаточно и трещина остается неподвижной.
Если σ<σкр,
то трещина не распространяется; если σ>σкр-
трещина распространяется и тело разрушается. Формула Гриффитса позволила найти
напряжение разрушаемого тела, т.е. прочность тела при наличии трещины. При σ=σкр,
трещина длиной 2l становится опасной. Критическое условие Гриффитса можно
представить также в виде критической длины трещины:
кр=
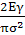
растяжение
деформированный тензор квазехрупкий
При l<lкр- освобожденной энергии
недостаточно для разрыва материала. Для больших трещин l>lкр-
энергии хватает на разрыв и трещина с огромной скоростью начинает расти,
разрывая тело на части.
Выше рассматривались только внутренние трещины,
но эта теория справедлива и для поверхностных трещин с глубиной l. Причем
появление трещины более вероятно именно на поверхности тела.
Теория Ирвина и Орована для квазехрупкого
разрушения.
Теория Гриффитса справедлива для идеально
хрупкого разрушения, когда материал деформируется упруго вплоть до разрушения,
поэтому металлы остались вне сферы ее применения. Константа Ɣ
представляет собой поверхностную энергию материала, которую очень трудно
определить. По этим двум причинам теория Гриффитса не нашла широкого
практического применения.
Англичанин Ирвин и венгр Орован экспериментально
исследовали разрушение металлов и показали, что когда трещина развивается, то в
малой окрестности вблизи вершины трещины происходит необратимая пластическая
деформация. Так как размеры объема пластической деформации малы по сравнению с
длиной, то освобождение упругой энергии по-прежнему можно вычислять из упругого
решения, но затраты на разрушение следует отнести к работе пластической
деформации. Это концепция квазехрупкого разрушения. Она позволила использовать
теорию Гриффитса, но константу Ɣ,
равную поверхностной энергии материала заменить на удельную работу пластической
деформации, которая в сотни и тысячи раз может превосходить Ɣ.
Такой шаг позволил перейти от идеально хрупкого материала в схеме Гриффитса к
реальным металлическим материалам и применить теорию Гриффитса для решения
инженерных проблем.
Ирвин не стал рассматривать общий энергетический
баланс всего тела, а изучил поле напряжений в вершине трещины и сформулировал
силовой критерий разрушений. Силовой критерий Ирвина и энергетическая теория
Гриффитса оказались эквивалентны.
Ирвин показал, что единственным параметром,
определяющим напряженной состояние в концевой зоне трещины является КИН
(коэффициент интенсивности напряжений)
Структура полей напряжений и смещений вблизи
вершины трещины оказалась практически одинаковой для трещин разного вида в
теории упругости. Существует 3 вида трещин:
. Трещина отрыва
. Трещина поперечного сдвига
. Трещина продольного сдвига
Для трещин 1 вида:
σx=
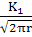 ·
cos
·
cos · (1 - sin
· (1 - sin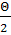 · sin
· sin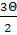 )
+…
)
+…
σy=
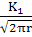 ·
cos
·
cos · (1 + sin
· (1 + sin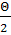 · sin
· sin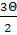 )
+…
)
+…
τxy=
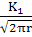 ·
sin
·
sin · cos
· cos · cos
· cos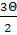 +…
+…
τxz=
τyz=
0, σz=
ν·(σx
+ σy)=
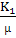 ·
·
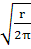 ·
cos
·
cos · (1 - 2ν +
· (1 - 2ν + 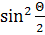 ) + …=
) + …= 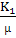 ·
·
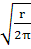 ·
sin
·
sin · (1 - 2ν +
· (1 - 2ν + 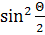 ) + …
) + …
здесь r-
расстояние от вершины трещины
Θ- угловая координата
ν- коэффициент
Пуассона
μ- модуль
сдвигасмещение по координате x
v- смещение по
координате y
K1-
КИН
Многоточиями обозначаются слагаемые, пренебрежимо
малые, по сравнению с выписанными. Аналогична структура формул для трещин 2 и
3-его видов, но в них вместо К1 будут К2 и К3.
Итак, вблизи вершины трещины любого вида, поля
напряжений и смещений имеют одну и ту же структуру и отличаются множителем К, который
зависит от внешних нагрузок и геометрических размеров тела. Распределение
напряжений и смещений по радиальным и угловым координатам всегда одинаково.
Отметим, что приведенные формулы дают, что σ→∞
при r→0, но эти формулы нельзя использовать для очень малых r,
где наблюдаются не упругие, а пластические деформации. Радиус пластической зоны
и начало упругой зоны:
y=
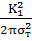 ,
где σт-
предел текучести
,
где σт-
предел текучести
Трещина получает возможность распространения,
если КИН достигает критической величины Кс. Для случая плоской
деформации величину К1с называют вязкостью разрушения или более
точно трещиностойкостью. При этом рассматриваются трещины 1-ого вида, т.к.
именно такой вид трещинонагружения в наибольшей степени определяет ее рост.
Величину К1с определяют в эксперименте непосредственно на
стандартных образцах с трещиной. При К<К1с- трещина не растет при
К>К1с- происходит разрушение.
КИН и вязкость разрушения.
Как показал Ирвин, КИН является единственным
параметром, определяющим напряженное состояние у вершины трещины. Критическое
значение КИН, которое характеризует сопротивление материала разрушению (чем
больше К1с, тем труднее материал разрушается), явилось
фундаментальным для механики разрушения. В связи с этим, КИН стал объектом
обширного аналитического и экспериментального исследования и к настоящему
времени составлены таблицы аналитических выражений КИН для тел различных
конфигураций и схем нагружения. Это позволяет проводить инженерные расчеты на
прочность различных тел с трещинами.
|
№
|
Форма
образца и схема нагружения
|
Условия
нагружения
|
Формула
для КИН
|
|
1
|
|
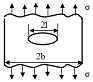
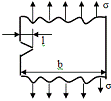
Полоса
с центральной поперечной трещиной. Осевое растяжение.
|
K= σ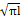 · Y(λ) λ=
· Y(λ) λ=
 (λ<0,7)
Y(λ)= 1+0,128λ-0,288 (λ<0,7)
Y(λ)= 1+0,128λ-0,288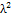 +1,525 +1,525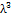
|
|
Полоса
с краевой поперечной трещиной. Осевое растяжение.
|
K= σ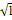 · Y(λ) λ=
· Y(λ) λ=
 (λ<0,7)
Y(λ)=
1,99-0,41λ+18,70 (λ<0,7)
Y(λ)=
1,99-0,41λ+18,70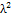 -38,48 -38,48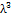 +53,85 +53,85
|
|
3
|
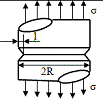
|
Цилиндр
с внешней кольцевой трещиной. Осевое растяжение.
|
K= σ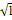 · Y(λ) λ=
· Y(λ) λ=  λ=
0,03; 0,05; 0,1; 0,2; 0,4. Y= 1,88; 1,82; 1,66; 1,41; 1,01. λ=
0,03; 0,05; 0,1; 0,2; 0,4. Y= 1,88; 1,82; 1,66; 1,41; 1,01.
|
|
4
|
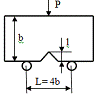
|
Балка
с краевой поперечной трещиной, изгиб, сосредоточенный силой, h- толщина
балки.
|
K=
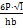 ·
Y(λ) λ= ·
Y(λ) λ=
 (λ<0,6)
Y(λ)= 1,93-3,07λ+14,53λ2-25,1λ3+25,8λ4 (λ<0,6)
Y(λ)= 1,93-3,07λ+14,53λ2-25,1λ3+25,8λ4
|
|
5
|
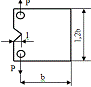
|
Компактный
образец, растяжение сосредоточенное силами, h- толщина
|
K= 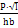 ·
Y(λ) λ= ·
Y(λ) λ=  Y(λ)=
29,6-185λ+655λ2-1017λ3+639λ4 Y(λ)=
29,6-185λ+655λ2-1017λ3+639λ4
|
КИН обычно представляют в виде:
= σ·(πl)·Y
или K= σ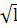 · Y
· Y
- безразмерный множитель, называемый "K-тарировка".
Этот множитель зависит от отношения длины трещины l к размеру тела b,
т.е. от λ=l(b)
и обычно представляется в виде:
(λ)=
C0
+ C1λ
+ C2λ2
+ C3λ3
+ …
Если известна "K-тарировка",
то задача расчета упрощается. Отметим, что в схемах 1 и 2 при b→∞,
получим переход от полосы к неограниченной плоскости, когда λ=
 =0,
формулы для K резко упрощаются:
=0,
формулы для K резко упрощаются:
1. K=
σ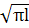
. K=
2σ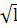
Знание k1с
позволяет найти критическое значение напряжения или критическую длину трещины,
приводящую к разрушению.
При какой длине трещины 2l эксплуатировать такую
панель нельзя?
1c=
σ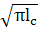 · Y(λ)
· Y(λ)
lc=
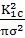 =
=
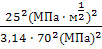 =
40мм
=
40мм
Усталостные трещины.
Усталость- накопление дефектов в материале под
действием циклической нагрузки и разрушение при σ<σв.
Рост усталостных трещин при циклической нагрузке
описывается формулой Париса:
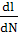 = A·(Kmax
- Kmin
= A·(Kmax
- Kmin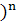
- длина трещины
N- число циклов
нагрузки
Kmax-
Kmin - перепад
КИН в одном цикле нагружения
A, n-
эмпирический коэффициент. Показатель степени n для разных материалов
располагается в интервале 2-7. Чаще всего n=4.
Эта формула позволяет через число циклов N
рассчитать усталостную долговечность:
τy=
N · τцикла
по времени роста трещины от начальной длины l0
до критической lc.
КИН при наличии коррозионной среды.
Коррозионные среды сильно снижают усталостную
долговечность конструкционных материалов, в первую очередь, за счет ускорения
процесса распространения трещин. Поэтому при расчетах на так называемое
коррозионное растрескивание под напряжением использует необычное значение КИН k1c,
а значение меньшее k1scc,
ниже которого докритический рост трещины отсутствует. Значения k1c
и k1scc
могут быть близкими у материалов, не чувствительных к действию коррозионной
среды.
Вязкость разрушения КМ.
До сих пор мы рассматривали гомогенные
однородные материалы, однокомпонентные: сталь, алюминий, стекло и т.д.
КМ являются гетерогенными, неоднородными
материалами, состоящими из нескольких компонентов, обычно матрицы и
упрочнителя. Чаще всего в качестве упрочнителя используют волокна. Помимо
возможности использования весьма высокой прочности волокон, большим
достоинством КМ является то, что они обладают высоким сопротивлением
распространения трещин или высокой вязкостью разрушения.
В этом отношении КМ имеют преимущества перед
большинством высокопрочных гомогенных материалов, обеспечивая высокую прочность
при их небольшой массе.
У обычных гомогенных материалов вязкость
разрушения резко снижается с увеличением их прочности.
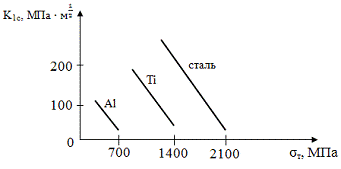
Без армирования практически невозможно получать
вязкие высокопрочные материалы. В случае КМ работают такие механизмы повышения
вязкости разрушения, какие принципиально невозможны в гомогенных материалах.
Во-первых, это наличие внутренних поверхностей раздела матрицы и волокон с
относительно небольшой прочностью сцепления, которые являются ловушками трещин,
делая КМ вязким. Это механизм торможения трещин по Куку- Гордану, которые
объяснили его.
Анализ напряженного состояния у вершины трещины,
что в области перед трещиной имеется наряду с компонентой напряжения
нормального разрыва σy
также компонента напряжения σx,
действующая в плоскости распространения трещины.
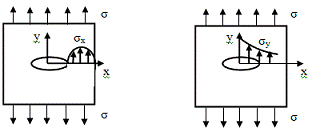
Если максимальная σy
достигается
в вершине трещины, то пик растягивающего напряжения σx
наблюдается
на некотором расстоянии от вершины трещины. Этот пик примерно в 5 раз меньше
максимального нормального напряжения σy.
Поэтому, если прочность сцепления материала на границе матрица- волокно в 5 и
более раз меньше прочности волокон, то растягивающее напряжение σx
вызывает
отслоение волокна от матрицы, затупление вершины трещины и прекращение ее
распространения.

В результате, вместо одной большой сквозной
трещины, которая бы разрушила бы материал полностью, в КМ образуются мелкие,
так называемые ответвленные трещины, поэтому КМ сохраняет определенную несущую
способность. Изобрела этот механизм сама природа. В биологических материалах,
например в кости или древесине может быть множество внутренних поверхностей
раздела. Эти поверхности не ослабляют материал в целом, а делают его вязким,
т.е. упрочняют. Такой механизм торможения трещин обеспечивает и рекордную
трещиностойкость искусственных композитов. Даже если такой композит как
стеклопластик, состоящий из хрупких стеклянных волокон, погруженных в хрупкую
эпоксидную матрицу, он обладает большой вязкостью за счет множественных
торможений магистральной трещины на поверхностях раздела волокон и связующего.
Поэтому один из способов увеличения
сопротивления распространения трещин- снижение прочности связей между волокнами
и матрицей. Однако на это можно идти в разумных пределах, не нанося большого
ущерба прочности КМ.
Если прочность сцепления матрицы и волокна будет
большой, отслоения на границе раздела происходить не будет, трещина будет
проходить через эту границу, рвать волокно и идти дальше по матрице.
Второй механизм повышения вязкости разрушения,
тоже присущий только КМ- вытягивание волокон из матрицы в процессе раскрытия
трещины. Если длина волокон не превышает критической, то такие волокна при
распространении трещины не разрушаются, а сдвигаются относительно матрицы. За
счет сил трения между волокном и матрицей совершается работа вытягивания, увеличиваются
затраты энергии на продвижение трещины и вследствие этого повышается вязкость
разрушения. Этот механизм срабатывает также и в случае длинных волокон l>lс,
если их концы находятся на расстоянии менее lc/2
от поверхности разрушения. Такие концы волокон не разрываются при раскрытии
трещины, а вытягиваются из матрицы.
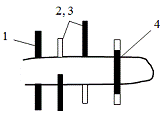
- непрерывное длинное волокно (разрыв волокна),
2,
3- длинные волокна, концы которых меньше lc/2
(вытягивание волокон), 4-
короткое волокно l ≤ lc
(вытягивание
волокна)
Если длина волокон значительно превышает
критическое lc,
то большинство волокон рвутся, а не вытягиваются и вклад работы вытягивания
волокон в общую вязкость разрушения невелик. При коротких волокнах l< lc
основной вклад в работу разрушения КМ вносит работа вытягивания. Поэтому работа
разрушения КМ, армированных короткими волокнами больше, чем у КМ с непрерывными
волокнами. Но у последней больше предел прочности, поэтому приходится идти на
компромисс, выбирая между повышением прочности и вязкостью разрушения. Часто
целесообразно создавать материал с заведомо меньшей прочностью, но зато с
повышенным сопротивлением распространения трещины. В первую очередь это
относится к ККМ (КМ с керамической матрицей). За счет армирования керамики короткими
волокнами удается в десятки раз увеличить ее ударную вязкость, термостойкость,
усталостную прочность. Но для этого должны быть обеспечены оптимальные значения
длины армированных волокон, их диаметра и прочности связи на границе раздела.
Вязкость разрушения можно увеличить, повышая объемную долю и прочность волокон,
их диаметр и уменьшая прочность связи. Однако заметно уменьшать прочность связи
нельзя, т.к. заметно снижается прочность КМ перпендикулярно оси волокон.
Целесообразно армировать матрицу толстыми волокнами с диаметром 0,05-0,5 мм.
В большинстве случаев энергетические затраты на
вытягивание волокон существенно больше работы разрушения связей на границе
раздела. Это позволяет создавать КМ с высокой вязкостью разрушения даже в
случае хрупкой матрицы и волокна. Если механизм вытягивания волокон действует,
то затраты энергии на вытягивание значительно превосходят работу разрушения
каждого компонента в отдельности. Если в таком КМ волокна разрушаются, а не
вытягиваются, то вязкость КМ остается низкой.
В композициях хрупкая матрица- пластическое
волокно наряду с вытягиванием волокон существенны процессы разрушения самих
волокон при распространении трещины. Поскольку вязкость разрушения таких
волокон высока, они до определенного предела тормозят распространение трещины,
"замораживая" ее.
В композициях пластическая матрица
-
хрупкое волокно. Существенную роль в обеспечении вязкости играет пластичность
самой матрицы, она уменьшает напряжения на фронте трещины, поглощая энергию во
время пластичного течения, и предотвращает распространение хрупкого разрушения
от одного волокна к другому. Сопротивление распространения трещин тем выше, чем
меньше объемная доля волокон и чем больше их диаметр, а также чем больше
пластичность и прочность матрицы.