Математика
Федеральное
государственное образовательное учреждение высшего профессионального
образования
Тюменская
государственная сельскохозяйственная академия
Салехардский
филиал
Математика
Салехард 2008
Тема 1. Элементы линейной алгебры
.1 Определитель и его свойства
Определение.
Определителем квадратной матрицы А=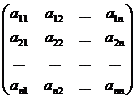
называется
число, которое может быть вычислено по элементам матрицы по формуле: ΔA = 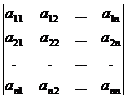 .
.
Замечание.
Определитель можно вычислить только для квадратных матриц.
Определение.
Матрица, называется квадратной, если число ее строк равно числу столбцов.
Свойства
определителей.
Свойство1.
Определитель матрицы А равен определителю матрицы AT,
транспонированной для матрицы А.
ΔA = Δ AT;
Свойство 2.
Δ ( A ± B) = ΔA ± ΔB.
Свойство
3.
Δ ( A* B) = ΔA * ΔB
Свойство
4. Если в квадратной матрице поменять местами какие-либо две строки (или
столбца), то определитель матрицы изменит знак, не изменившись по абсолютной
величине.
Свойство
5. При умножении столбца (или строки) матрицы на число ее определитель
умножается на это число.
Свойство
6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель
равен нулю.
Свойство
7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель
равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно
именно по нулевой строке или столбцу.)
Свойство
8. Определитель матрицы не изменится, если к элементам одной из его
строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные
на какое-либо число, не равное нулю.
Свойство
9. Если для элементов какой- либо строки или столбца матрицы верно соотношение:
d = d1 ± d2 , e = e1 ± e2 , f = f1 ± f2 , то верно:
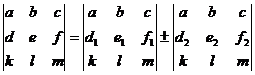
Пример.
Вычислить определитель матрицы А = 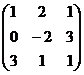
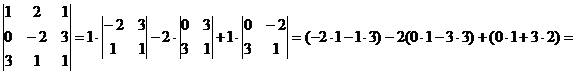
=
-5 + 18 + 6 = 19.
Пример:.
Даны матрицы А = 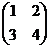 , В =
, В = 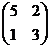 . Найти det (AB).
. Найти det (AB).
1-й способ:
A = 4 - 6 = -2; B = 15 - 2 = 13; (AB) = det A ×det B = -26.
2-
й способ:
AB = 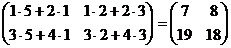 ,
,
det (AB) =
7×18 - 8×19 = 126 - -
152 = -26.
1.2
Элементарные преобразования матрицы
Определение.
Элементарными преобразованиями матрицы назовем следующие преобразования: 1)
умножение строки на число, отличное от нуля; 2) прибавление к элементам одной
строки элементов другой строки; 3) перестановка строк; 4) вычеркивание
(удаление) одной из одинаковых строк (столбцов); 5) транспонирование; Те же
операции, применяемые для столбцов, также называются элементарными
преобразованиями.
С помощью элементарных преобразований можно к какой-либо строке или
столбцу прибавить линейную комбинацию остальных строк (столбцов).
Миноры.
Выше
было использовано понятие дополнительного минора матрицы. Дадим определение
минора матрицы.
Определение.
Если в матрице А выделить несколько произвольных строк и столько же
произвольных столбцов, то определитель, составленный из элементов,
расположенных на пересечении этих строк и столбцов называется минором матрицы
А. Если выделено s строк и столбцов, то полученный минор называется
минором порядка s.
Заметим,
что вышесказанное применимо не только к квадратным матрицам, но и к
прямоугольным.
Если
вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то
определитель полученной матрицы будет являться дополнительным минором.
Алгебраические дополнения.
Определение.
Алгебраическим дополнением минора матрицы называется его дополнительный минор,
умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов
минора матрицы.
В частном случае, алгебраическим дополнением элемента матрицы называется
его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и
строки, на которых стоит элемент, есть число четное и с противоположным знаком,
если нечетное.
Теорема Лапласа. Если выбрано s строк матрицы с номерами i1, …
,is, то определитель этой матрицы равен
сумме произведений всех миноров, расположенных в выбранных строках на их
алгебраические дополнения.
1.3 Эквивалентные матрицы
Как
было сказано выше, минором матрицы порядка s называется определитель матрицы,
образованной из элементов исходной матрицы, находящихся на пересечении каких -
либо выбранных s строк и s столбцов.
Определение.
В матрице порядка m´n минор порядка r называется базисным, если он не
равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют
вовсе, т.е. r совпадает с меньшим из чисел m или n.
Столбцы
и строки матрицы, на которых стоит базисный минор, также называются базисными.
В
матрице может быть несколько различных базисных миноров, имеющих одинаковый
порядок.
Определение.
Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А.
Очень
важным свойством элементарных преобразований матриц является то, что они не
изменяют ранг матрицы.
Определение. Матрицы, полученные в результате элементарного
преобразования, называются эквивалентными.
Надо отметить, что равные матрицы и эвивалентные матрицы - понятия
совершенно различные.
Теорема. Наибольшее число линейно независимых столбцов в матрице равно
числу линейно независимых строк.
Т.к. элементарные преобразования не изменяют ранг матрицы, то можно
существенно упростить процесс нахождения ранга матрицы.
Пример. Определить ранг матрицы.
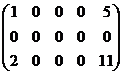 ~ ~
~ ~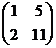 ,
, 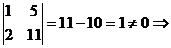 RgA
RgA
.
Пример: Определить ранг матрицы.
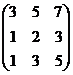 ~
~ 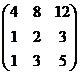 ~
~ 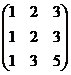 ~
~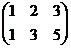 ,
, 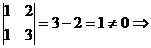 Rg = 2.
Rg = 2.
Если
с помощью элементарных преобразований не удается найти матрицу, эквивалентную
исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с
вычисления миноров наивысшего возможного порядка. В вышеприведенном примере -
это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы
равен порядку этого минора.
Теорема
о базисном миноре.
Теорема. В произвольной матрице А каждый столбец (строка) является
линейной комбинацией столбцов (строк), в которых расположен базисный минор.
Таким образом, ранг произвольной матрицы А равен максимальному числу
линейно независимых строк (столбцов) в матрице.
Если А- квадратная матрица и det A = 0, то по
крайней мере один из столбцов - линейная комбинация остальных столбцов. То же
самое справедливо и для строк. Данное утверждение следует из свойства линейной
зависимости при определителе равном нулю.
1.4 Решение произвольных систем линейных уравнений
Как
было сказано выше, матричный метод и метод Крамера применимы только к тем
системам линейных уравнений, в которых число неизвестных равняется числу
уравнений. Далее рассмотрим произвольные системы линейных уравнений.
Определение. Система m
уравнений с n неизвестными в общем виде
записывается следующим образом:
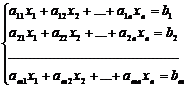 ,
,
где
aij - коэффициенты, а bi - постоянные.
Решениями системы являются n чисел, которые при подстановке в систему превращают
каждое ее уравнение в тождество.
Определение.
Если система имеет хотя бы одно решение, то она называется совместной. Если
система не имеет ни одного решения, то она называется несовместной.
Определение.
Система называется определенной, если она имеет только одно решение и неопределенной,
если более одного.
Определение.
Для системы линейных уравнений матрица
А
= 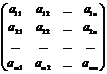 называется матрицей системы, а матрица
называется матрицей системы, а матрица
А*=
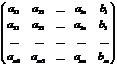 называется расширенной матрицей системы
называется расширенной матрицей системы
Определение.
Если b1, b2, …,bm = 0, то система называется однородной. однородная
система всегда совместна, т.к. всегда имеет нулевое решение.
1.5
Элементарные преобразования систем
К
элементарным преобразованиям относятся:
1)Прибавление к обеим частям одного уравнения соответствующих частей
другого, умноженных на одно и то же число, не равное нулю.
)Перестановка уравнений местами.
)Удаление из системы уравнений, являющихся тождествами для всех х.
Теорема Кронекера - Капели (условие совместности системы).
(Леопольд Кронекер (1823-1891) немецкий математик)
Теорема:
Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг
матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1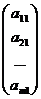 + x2
+ x2 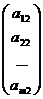 + … + xn
+ … + xn 
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная
комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу,
т.е. переход А®А* не изменяют
ранга.
2)
Если RgA = RgA*, то это означает, что они имеют один и тот же
базисный минор. Столбец свободных членов - линейная комбинация столбцов
базисного минора, те верна запись, приведенная выше.
Пример.
Определить совместность системы линейных уравнений:
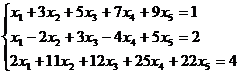 =
= 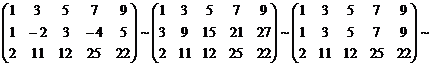
~
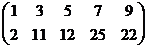 .
. 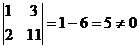 RgA =
2.
RgA =
2.
A* = 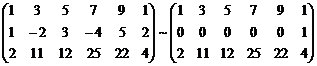 RgA* = 3
RgA* = 3
Система
несовместна.
Пример.
Определить совместность системы линейных уравнений.
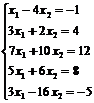 А =
А = 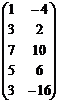 ;
; 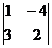 = 2 + 12
= 14 ¹ 0; RgA = 2;
= 2 + 12
= 14 ¹ 0; RgA = 2;
A* = 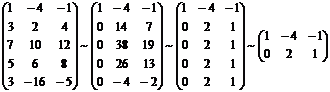
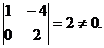 RgA*
= 2.
RgA*
= 2.
Система
совместна. Решения: x1 = 1; x2 =1/2.
Тема
2. Элементы векторной алгебры
.1
Базис. Линейная зависимость векторов
Определение.
)
Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в
определенном порядке.
)
Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в
определенном порядке.
)Базисом
на прямой называется любой ненулевой вектор.
Определение.
Если  - базис в пространстве и
- базис в пространстве и 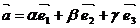 , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора 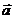 в этом базисе.
в этом базисе.
В
связи с этим можно записать следующие свойства:
3
равные векторы
имеют одинаковые координаты,
4
при умножении
вектора на число его компоненты тоже умножаются на это число,
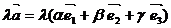 =
= 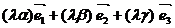
3
при сложении
векторов складываются их соответствующие компоненты.
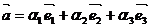 ;
; 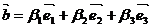 ;
;
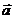 +
+ 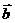 =
= 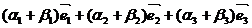 .
.
Линейная
зависимость векторов
Определение.
Векторы 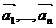 называются линейно зависимыми, если существует такая
линейная комбинация
называются линейно зависимыми, если существует такая
линейная комбинация 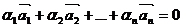 , при не равных нулю одновременно ai , т.е.
, при не равных нулю одновременно ai , т.е. 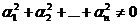 .
.
Если
же только при ai = 0
выполняется 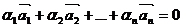 , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.
Свойство
1. Если среди векторов 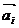 есть нулевой вектор, то эти векторы линейно зависимы.
есть нулевой вектор, то эти векторы линейно зависимы.
Свойство
2. Если к системе линейно зависимых векторов добавить один или несколько
векторов, то полученная система тоже будет линейно зависима.
Свойство
3. Система векторов линейно зависима тогда и только тогда, когда один из
векторов раскладывается в линейную комбинацию остальных векторов.
Свойство
4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно
зависимые векторы коллинеарны.
Свойство
5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно
зависимые векторы компланарны.
Свойство
6. Любые 4 вектора линейно зависимы.
2.2
Система координат
Для
определения положения произвольной точки могут использоваться различные системы
координат. Положение произвольной точки в какой- либо системе координат должно
однозначно определяться. Понятие системы координат представляет собой
совокупность точки начала отсчета (начала координат) и некоторого базиса. Как
на плоскости, так и в пространстве возможно задание самых разнообразных систем
координат. Выбор системы координат зависит от характера поставленной
геометрической, физической или технической задачи. Рассмотрим некоторые
наиболее часто применяемые на практике системы координат.
Декартова
система координат
Зафиксируем
в пространстве точку О и рассмотрим произвольную точку М.
Вектор
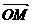 назовем радиус- вектором точки М. Если в пространстве
задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел -
компоненты ее радиус- вектора.
назовем радиус- вектором точки М. Если в пространстве
задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел -
компоненты ее радиус- вектора.
Определение.
Декартовой системой координат в пространстве называется совокупность точки и
базиса. Точка называется началом координат. Прямые, проходящие через начало координат
называются осями координат.
-я
ось - ось абсцисс
-я
ось - ось ординат
-я
ось - ось апликат
Чтобы
найти компоненты вектора нужно из координат его конца вычесть координаты
начала.
Если
заданы точки А(x1, y1, z1), B(x2, y2, z2), то 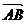 = (x2 - x1, y2 - y1, z2 - z1).
= (x2 - x1, y2 - y1, z2 - z1).
Определение.
Базис называется ортонормированным, если его векторы попарно ортогональны и
равны единице.
Определение.
Декартова система координат, базис которой ортонормирован называется декартовой
прямоугольной системой координат.
Пример.
Даны векторы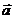 (1; 2; 3),
(1; 2; 3), 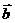 (-1; 0;
3),
(-1; 0;
3), 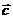 (2; 1; -1) и
(2; 1; -1) и 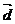 (3; 2; 2)
в некотором базисе. Показать, что векторы
(3; 2; 2)
в некотором базисе. Показать, что векторы 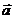 ,
, 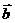 и
и 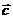 образуют
базис и найти координаты вектора
образуют
базис и найти координаты вектора 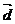 в этом
базисе.
в этом
базисе.
Векторы
образуют базис, если они линейно независимы, другими словами, если уравнения,
входящие в систему:
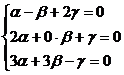
линейно
независимы.
Тогда
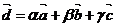 .
.
Это
условие выполняется, если определитель матрицы системы отличен от нуля.
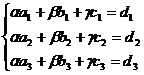
Для
решения этой системы воспользуемся методом Крамера.
D1 = 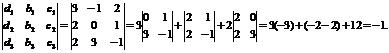
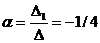 ;
;
D2 = 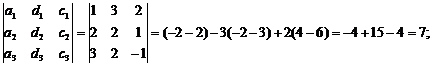
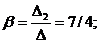
D3 = 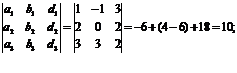
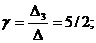
Итого,
координаты вектора 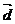 в базисе
в базисе 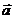 ,
, 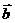 ,
, 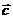 :
: 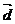 { -1/4, 7/4, 5/2}.
{ -1/4, 7/4, 5/2}.
2.3
Уравнение поверхности в пространстве
Определение.
Любое уравнение, связывающее координаты x, y, z
любой точки поверхности является уравнением этой поверхности.
2.3.1
Общее уравнение плоскости
Определение.
Плоскостью называется поверхность, все точки которой удовлетворяют общему
уравнению:
Ax + By + Cz + D =
0,
где
А, В, С - координаты вектора
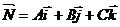
вектор
нормали к плоскости. Возможны следующие частные случаи:
А
= 0 - плоскость параллельна оси Ох
В
= 0 - плоскость параллельна оси Оу
С
= 0 - плоскость параллельна оси Оz
D = 0 -
плоскость проходит через начало координат
А
= В = 0 - плоскость параллельна плоскости хОу
А
= С = 0 - плоскость параллельна плоскости хОz
В
= С = 0 - плоскость параллельна плоскости yOz
А
= D = 0 - плоскость проходит через ось Ох
В
= D = 0 - плоскость проходит через ось Оу
С
= D = 0 - плоскость проходит через ось Oz
А
= В = D = 0 - плоскость совпадает с плоскостью хОу
А
= С = D = 0 - плоскость совпадает с плоскостью xOz
В
= С = D = 0 - плоскость совпадает с плоскостью yOz
2.3.2
Уравнение плоскости, проходящей через три точки
Для
того, чтобы через три какие- либо точки пространства можно было провести
единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой. Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в
общей декартовой системе координат. Для того, чтобы произвольная точка М(x, y, z)
лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы 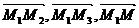 были компланарны.
были компланарны.
(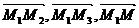 ) = 0
) = 0
Таким
образом,
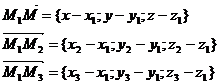
Уравнение
плоскости, проходящей через три точки:
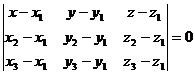
2.3.3
Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости
Пусть
заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и вектор 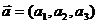 .
.
Составим
уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку
М(х, у, z) параллельно вектору 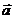 .
.
Векторы
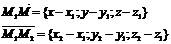 и вектор
и вектор 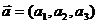 должны
быть компланарны, т.е.
должны
быть компланарны, т.е.
(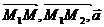 ) = 0
) = 0
Уравнение
плоскости:
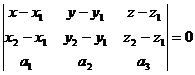
2.3.4
Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости
Пусть
заданы два вектора 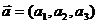 и
и 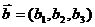 ,
коллинеарные плоскости. Тогда для произвольной точки М(х, у, z),
принадлежащей плоскости, векторы
,
коллинеарные плоскости. Тогда для произвольной точки М(х, у, z),
принадлежащей плоскости, векторы 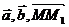 должны
быть компланарны.
Уравнение плоскости:
должны
быть компланарны.
Уравнение плоскости:
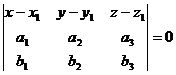
2.3.4
Уравнение плоскости по точке и вектору нормали
Теорема.
Если в пространстве задана точка М0(х0, у0, z0), то
уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали 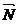 (A, B, C) имеет вид:
(A, B, C) имеет вид:
A(x - x0) +
B(y - y0) + C(z - z0) = 0.
Доказательство.
Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор 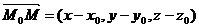 . Т.к. вектор
. Т.к. вектор 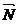 - вектор
нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и
вектору
- вектор
нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и
вектору 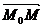 . Тогда скалярное произведение
. Тогда скалярное произведение
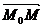 ×
×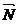 = 0
= 0
Таким
образом, получаем уравнение плоскости
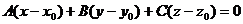
Теорема доказана.
2.3.5 Уравнение плоскости в отрезках
Если
в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D) 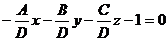 , заменив
, заменив 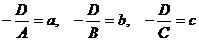 , получим
уравнение плоскости в отрезках:
, получим
уравнение плоскости в отрезках:
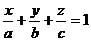
Числа
a, b, c являются точками пересечения плоскости соответственно
с осями х, у, z.
2.3.6
Уравнение плоскости в векторной форме
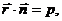
где
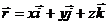 - радиус-
вектор текущей точки М(х, у, z),
- радиус-
вектор текущей точки М(х, у, z),
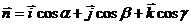 -
единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость
из начала координат.
-
единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость
из начала координат.
a, b и g - углы, образованные этим вектором с осями х, у, z.
p - длина этого
перпендикуляра. В координатах это уравнение имеет вид:
х cosa + y cosb + z cosg - p = 0.
2.3.7
Расстояние от точки до плоскости
Расстояние
от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0
равно:
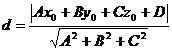
Пример.
Найти уравнение плоскости, зная, что точка Р(4; -3; 12) - основание
перпендикуляра, опущенного из начала координат на эту плоскость.
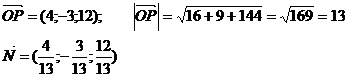
Таким
образом, A = 4/13; B = -3/13; C =
12/13, воспользуемся формулой:
A(x - x0) + B(y - y0) + C(z - z0) = 0.
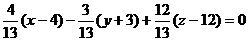
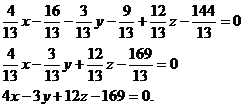
Пример.
Найти уравнение плоскости, проходящей через две точки P(2; 0; -1) и
Q(1; -1; 3)
перпендикулярно плоскости 3х + 2у - z + 5 = 0.
Вектор
нормали к плоскости 3х + 2у - z + 5 = 0 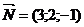 параллелен
искомой плоскости.
параллелен
искомой плоскости.
Получаем:
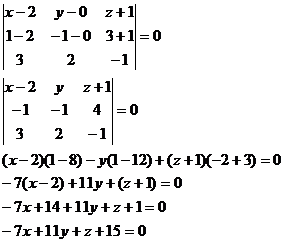
Пример.
Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1)
перпендикулярно плоскости х + у + 2z - 3 = 0.
Искомое
уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости 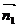 (A, B, C). Вектор
(A, B, C). Вектор 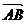 (1, 3,
-5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой
имеет вектор нормали
(1, 3,
-5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой
имеет вектор нормали 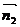 (1, 1, 2). Т.к. точки А и В принадлежат обеим
плоскостям, а плоскости взаимно перпендикулярны, то
(1, 1, 2). Т.к. точки А и В принадлежат обеим
плоскостям, а плоскости взаимно перпендикулярны, то
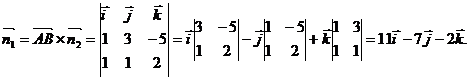
Таким
образом, вектор нормали 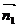 (11, -7, -2). Т.к. точка А принадлежит искомой
плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е.
11×2 + 7×1 - 2×4 + D = 0; D = -21.
(11, -7, -2). Т.к. точка А принадлежит искомой
плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е.
11×2 + 7×1 - 2×4 + D = 0; D = -21.
Итого, получаем уравнение плоскости:
x - 7y - 2z - 21 = 0.
Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) -
основание перпендикуляра, опущенного из начала координат на эту плоскость.
Находим
координаты вектора нормали 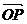 = (4, -3,
12). Искомое уравнение плоскости имеет вид:
= (4, -3,
12). Искомое уравнение плоскости имеет вид:
x - 3y +
12z + D = 0.
Для
нахождения коэффициента D подставим в уравнение координаты точки Р:
+
9 + 144 + D = 0
D = -169
Итого,
получаем искомое уравнение:
x - 3y +
12z - 169 = 0
Пример.
Даны координаты вершин пирамиды А1(1; 0; 3), A2(2; -1; 3), A3(2;
1; 1), A4(1; 2; 5).
1) Найти длину ребра А1А2.
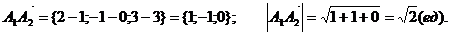
1) Найти угол между ребрами А1А2 и А1А4.
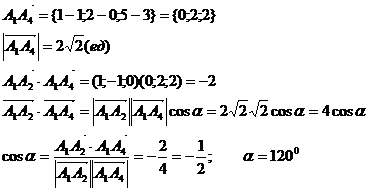
Найти
угол между ребром А1А4 и гранью А1А2А3.
Сначала
найдем вектор нормали к грани А1А2А3 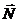 как
векторное произведение векторов
как
векторное произведение векторов 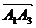 и
и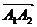 .
.
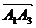 = (2-1;
1-0; 1-3) = (1; 1; -2);
= (2-1;
1-0; 1-3) = (1; 1; -2);
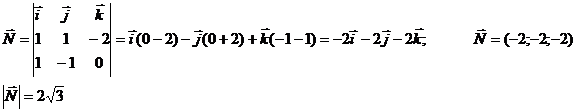
Найдем
угол между вектором нормали и вектором 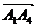 .
.
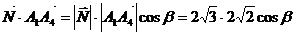
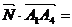 -4 - 4 =
-8.
-4 - 4 =
-8.
Искомый
угол g между вектором и плоскостью будет равен g = 900 - b.
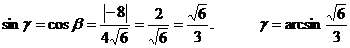
1) Найти площадь грани А1А2А3.
Найти объем пирамиды.
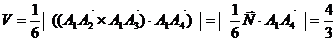 (ед3).
(ед3).
1) Найти уравнение плоскости А1А2А3.
Воспользуемся формулой уравнения плоскости, проходящей через три точки.
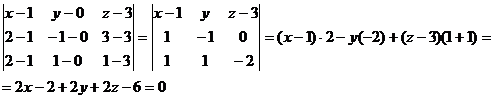
2x + 2y + 2z - 8
= 0
x + y + z - 4
= 0;
Тема
3. Элементы аналитической геометрии
.1
Уравнение линии на плоскости
Как известно, любая точка на плоскости определяется двумя координатами в
какой- либо системе координат. Системы координат могут быть различными в
зависимости от выбора базиса и начала координат.
Определение. Уравнением линии называется соотношение y = f(x) между
координатами точек, составляющих эту линию.
Отметим, что уравнение линии может быть выражено параметрическим
способом, то есть каждая координата каждой точки выражается через некоторый
независимый параметр t.
Характерный пример - траектория движущейся точки. В этом случае роль
параметра играет время.
3.2 Уравнение прямой на плоскости
Определение. Любая прямая на плоскости может быть задана уравнением
первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ¹ 0. Это уравнение первого порядка
называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные
случаи:
3
C = 0, А ¹ 0, В ¹ 0 - прямая проходит через начало
координат
4
А = 0, В ¹ 0, С ¹ 0 { By + C =
0}- прямая параллельна оси Ох
5
В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0}
- прямая параллельна оси Оу
6
В = С = 0, А ¹ 0 - прямая совпадает с осью Оу
7
А = С = 0, В ¹ 0 - прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости
от каких - либо заданных начальных условий.
3.3 Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2),
тогда уравнение прямой, проходящей через эти точки:
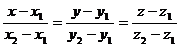
Если
какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий
числитель. На плоскости записанное выше уравнение прямой упрощается:
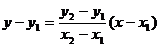
если
х1 ¹ х2 и х = х1, еслих1 = х2.
Дробь
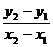 = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.
Пример.
Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Применяя
записанную выше формулу, получаем:
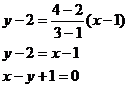
3.4
Уравнение прямой по точке и угловому коэффициенту
Если
общее уравнение прямой Ах + Ву + С = 0 привести к виду: 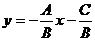
и
обозначить 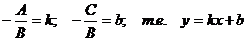 , то полученное уравнение называется уравнением прямой
с угловым коэффициентом k.
, то полученное уравнение называется уравнением прямой
с угловым коэффициентом k.
3.5
Уравнение прямой в отрезках
Если
в общем уравнении прямой Ах + Ву + С = 0 С ¹ 0, то,
разделив на -С, получим: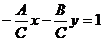 или
или 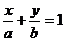 ,
,
где
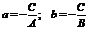
Геометрический
смысл коэффициентов в том, что коэффициент а является координатой точки
пересечения прямой с осью Ох, а b - координатой точки пересечения прямой с осью Оу.
Пример.
Задано общее уравнение прямой х - у + 1 = 0. Найти уравнение этой прямой в
отрезках. С = 1, 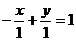 , а = -1, b = 1.
, а = -1, b = 1.
3.6
Угол между прямыми на плоскости
Определение.
Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет
определяться как
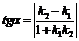 .
.
Две
прямые параллельны, если k1 = k2.
Две
прямые перпендикулярны, если k1 = -1/k2.
Теорема.
Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны
коэффициенты А1 = lА, В1 = lВ. Если еще и С1 = lС, то прямые совпадают.
Координаты точки пересечения двух прямых находятся как решение системы
уравнений этих прямых.
3.7 Уравнение прямой, проходящей через данную точку
перпендикулярно данной прямой
Определение. Прямая, проходящая через точку М1(х1, у1) и перпендикулярная
к прямой у = kx + b представляется уравнением:
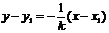
3.8
Расстояние от точки до прямой
Теорема.
Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0
определяется как
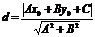 .
.
Доказательство.
Пусть точка М1(х1, у1) - основание перпендикуляра, опущенного из точки М на
заданную прямую. Тогда расстояние между точками М и М1:
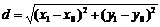 (1)
(1)
Координаты
x1 и у1 могут быть найдены как решение системы
уравнений:
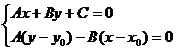
Второе
уравнение системы - это уравнение прямой, проходящей через заданную точку М0
перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к
виду:
алгебра векторный математический анализ
A(x - x0) +
B(y - y0) + Ax0 + By0 + C = 0,
то,
решая, получим:
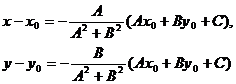
Подставляя
эти выражения в уравнение (1), находим:
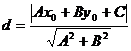 .
.
Теорема
доказана.
Пример.
Определить угол между прямыми:
y = -3x +
7; y = 2x + 1.
k1 = -3; k2 =
2 tgj = 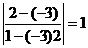 ; j = p/4.
; j = p/4.
Пример.
Показать, что прямые
х
- 5у + 7 = 0 и 10х + 6у - 3 = 0 перпендикулярны.
Находим:
k1 = 3/5, k2 = -5/3, k1k2 =
-1, следовательно, прямые перпендикулярны.
Пример.
Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти
уравнение высоты, проведенной из вершины С.
Находим
уравнение стороны АВ:
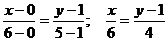 ; 4x = 6y -
6;
; 4x = 6y -
6;
x - 3y + 3
= 0; 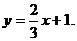
Искомое
уравнение высоты имеет вид:
Ax + By + C = 0 или y = kx + b. = 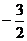 .
.
Тогда
y = 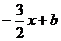 Т.к.
высота проходит через точку С, то ее координаты удовлетворяют данному
уравнению:
Т.к.
высота проходит через точку С, то ее координаты удовлетворяют данному
уравнению: 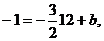 откуда b = 17. Итого:
откуда b = 17. Итого: 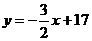 . Ответ:
3x + 2y - 34 = 0.
. Ответ:
3x + 2y - 34 = 0.
Тема
4. Введение в математический анализ
4.1
Односторонние пределы
Определение.
Если f(x) ® A1
при х ® а только при x < a, то
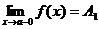 - называется пределом функции f(x) в
точке х = а слева, а если f(x) ® A2
при х ® а только при x > a, то
- называется пределом функции f(x) в
точке х = а слева, а если f(x) ® A2
при х ® а только при x > a, то
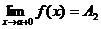 называется пределом функции f(x) в
точке х = а справа.
называется пределом функции f(x) в
точке х = а справа.
Приведенное
выше определение относится к случаю, когда функция f(x) не
определена в самой точке х = а, но определена в некоторой сколь угодно малой
окрестности этой точки. Пределы А1 и А2 называются также односторонними
пределами функции f(x) в точке х = а. Также говорят, что А - конечный
предел функции f(x).
4.2
Основные теоремы о пределах
Теорема
1.
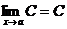 ,
,
где
С = const. Следующие теоремы справедливы при предположении, что
функции f(x) и g(x) имеют конечные пределы при х®а.
Теорема
2.
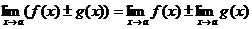
Доказательство
этой теоремы будет приведено ниже.
Теорема
3.
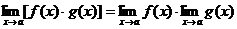
Следствие.
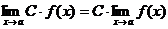
Теорема
4.
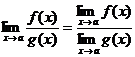 при
при 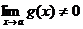
Аналогично
определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.
Теорема
6. Если g(x) £ f(x) £ u(x) вблизи точки
х = а и
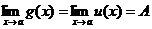 ,
,
то
и 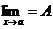 . Определение. Функция f(x)
называется ограниченной вблизи точки х = а, если существует такое число М>0,
что ïf(x)ï<M вблизи точки х = а.
. Определение. Функция f(x)
называется ограниченной вблизи точки х = а, если существует такое число М>0,
что ïf(x)ï<M вблизи точки х = а.
Теорема
7. Если функция f(x) имеет конечный предел при х®а, то она ограничена вблизи точки х = а. Доказательство. Пусть 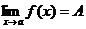 , т.е.
, т.е. 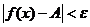 , тогда
, тогда
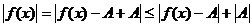 или
или
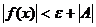 , т.е.
, т.е.
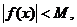 где М = e + ïАï
где М = e + ïАï
Теорема
доказана.
4.3
Бесконечно малые функции
Определение.
Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если 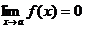 .
Бесконечно малой функция может быть только если указать к какому числу
стремится аргумент х. При различных значениях а функция может быть бесконечно
малой или нет. Пример. Функция f(x) = xn является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к.
.
Бесконечно малой функция может быть только если указать к какому числу
стремится аргумент х. При различных значениях а функция может быть бесконечно
малой или нет. Пример. Функция f(x) = xn является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. 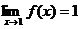 .
Теорема. Для того, чтобы функция f(x) при х®а имела предел,
равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие
.
Теорема. Для того, чтобы функция f(x) при х®а имела предел,
равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие
f(x) = A + a(x),
где
a(х) - бесконечно малая при х ® а (a(х)®0 при х ® а).
Свойства бесконечно малых функций:
1) Сумма фиксированного числа бесконечно
малых функций при х®а
тоже бесконечно малая функция при х®а.
2) Произведение фиксированного числа
бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.
3) Произведение бесконечно малой функции
на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией
при х®а.
4) Частное от деления бесконечно малой
функции на функцию, предел которой не равен нулю есть величина бесконечно
малая.
Используя понятие бесконечно малых функций, приведем доказательство
некоторых теорем о пределах, приведенных выше.
Доказательство теоремы 2. Представим
f(x) = A + a(x), g(x) = B + b(x), где
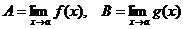 ,
,
тогда
(x) ± g(x) =
(A + B) + a(x) + b(x) + B = const,
a(х) + b(х) - бесконечно малая, значит
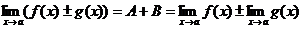
Теорема
доказана.
Доказательство
теоремы 3. Представим
f(x) = A + a(x), g(x) = B + b(x),
где
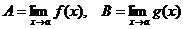 ,
,
тогда
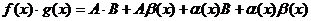 ×B = const, a(х) и b(х) - бесконечно малые, значит
×B = const, a(х) и b(х) - бесконечно малые, значит
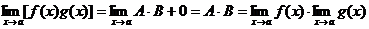
Теорема
доказана.
4.4
Бесконечно большие функции и их связь с бесконечно малыми
Определение.
Предел функции f(x) при х®а, где а- число,
равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство ïf(x)ï>M
выполняется при всех х, удовлетворяющих условию 0 < ïx - aï < D Записывается 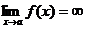 .
.
Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:
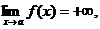
а
если заменить на f(x)<M, то:
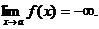
Графически
приведенные выше случаи можно проиллюстрировать следующим образом:
Определение.
Функция называется бесконечно большой при х®а, где а - чосли или
одна из величин ¥, +¥ или -¥, если 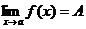 , где А - число или одна из величин ¥, +¥ или -¥. Связь бесконечно больших и
бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)®0 при х®а (если х®¥ ) и не
обращается в ноль, то
, где А - число или одна из величин ¥, +¥ или -¥. Связь бесконечно больших и
бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)®0 при х®а (если х®¥ ) и не
обращается в ноль, то
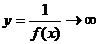
Сравнение
бесконечно малых функций. Пусть a(х), b(х) и g(х) - бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно
сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x.
Определение.
Если
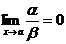 , то функция a называется
бесконечно малой более высокого порядка, чем функция b. Определение.
, то функция a называется
бесконечно малой более высокого порядка, чем функция b. Определение.
Если
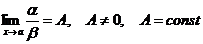 , то a и b называются бесконечно малыми одного порядка. Определение.
, то a и b называются бесконечно малыми одного порядка. Определение.
Если
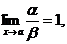 то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b. Пример. Сравним бесконечно малые при х®0 функции f(x) = x10 и f(x) = x.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b. Пример. Сравним бесконечно малые при х®0 функции f(x) = x10 и f(x) = x.
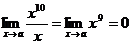
т.е.
функция f(x) = x10 - бесконечно малая более высокого порядка, чем f(x) = x.
Определение. Бесконечно малая функция a называется
бесконечно малой порядка k относительно бесконечно малой функции b, если предел 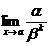 конечен
и отличен от нуля. Однако следует отметить, что не все бесконечно малые функции
можно сравнивать между собой. Например, если отношение
конечен
и отличен от нуля. Однако следует отметить, что не все бесконечно малые функции
можно сравнивать между собой. Например, если отношение 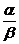 не имеет предела, то функции несравнимы. Пример. Если
не имеет предела, то функции несравнимы. Пример. Если
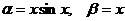 , то при х®0
, то при х®0 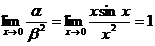 , т.е. функция a - бесконечно малая
порядка 2 относительно функции b. Пример. Если
, т.е. функция a - бесконечно малая
порядка 2 относительно функции b. Пример. Если 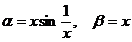 , то при х®0
, то при х®0 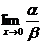 не существует, т.е. функция a и b несравнимы.
не существует, т.е. функция a и b несравнимы.
4.5
Свойства эквивалентных бесконечно малых
1)
a ~ a, 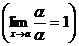
)
Если a ~ b и b ~ g, то a ~ g, 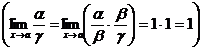
)
Если a ~ b, то b ~ a, 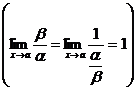
)
Если a ~ a1 и b ~ b1 и 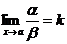 , то и
, то и 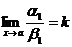 или
или 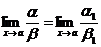 .
.
Следствие:
а) если a ~ a1 и 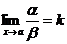 , то и
, то и 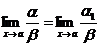 б) если b ~ b1 и
б) если b ~ b1 и 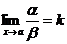 , то
, то 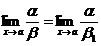
Свойство
4 особенно важно на практике, т.к. оно фактически означает, что предел
отношения бесконечно малых не меняется при замене их на эквивалентные
бесконечно малые. Этот факт дает возможность при нахождении пределов заменять
бесконечно малые на эквивалентные им функции, что может сильно упростить
вычисление пределов.
Пример.
Найти предел 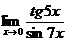
Так
как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив
функции эквивалентными бесконечно малыми, получим:
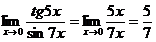
Пример.
Найти предел 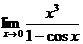 .
.
Так
как
-
cosx = 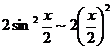
при
х®0, то 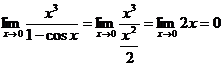 .
.
Пример.
Найти предел 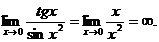 Если a и b - бесконечно малые при х®а, причем b - бесконечно малая более высокого порядка, чем a, то g = a + b - бесконечно малая, эквивалентная a. Это можно доказать
следующим равенством
Если a и b - бесконечно малые при х®а, причем b - бесконечно малая более высокого порядка, чем a, то g = a + b - бесконечно малая, эквивалентная a. Это можно доказать
следующим равенством 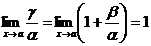 . Тогда говорят, что a - главная
часть бесконечно малой функции g. Пример. Функция х2 +х -
бесконечно малая при х®0, х - главная часть этой функции. Чтобы показать это,
запишем a = х2, b = х, тогда
. Тогда говорят, что a - главная
часть бесконечно малой функции g. Пример. Функция х2 +х -
бесконечно малая при х®0, х - главная часть этой функции. Чтобы показать это,
запишем a = х2, b = х, тогда
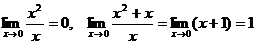 .
.
4.6
Непрерывность функции в точке
Определение.
Функция f(x), определенная в окрестности некоторой точки х0,
называется непрерывной в точке х0, если предел функции и ее значение в этой
точке равны, т.е.
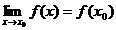
Тот
же факт можно записать иначе: 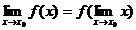 Определение.
Если функция f(x) определена в некоторой окрестности точки х0, но не
является непрерывной в самой точке х0, то она называется разрывной функцией, а
точка х0 - точкой разрыва.
Определение.
Если функция f(x) определена в некоторой окрестности точки х0, но не
является непрерывной в самой точке х0, то она называется разрывной функцией, а
точка х0 - точкой разрыва.
Свойства
непрерывных функций.
)
Сумма, разность и произведение непрерывных в точке х0 функций - есть функция,
непрерывная в точке х0.
)
Частное двух непрерывных функций 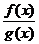 - есть
непрерывная функция при условии, что g(x) не равна нулю
в точке х0. 3) Суперпозиция непрерывных функций - есть непрерывная функция.
- есть
непрерывная функция при условии, что g(x) не равна нулю
в точке х0. 3) Суперпозиция непрерывных функций - есть непрерывная функция.
Это
свойство может быть записано следующим образом:
Если
u = f(x), v = g(x) - непрерывные функции в точке х = х0, то функция v = g(f(x)) -
тоже непрерывнаяфункция в этой точке. Справедливость приведенных выше свойств
можно легко доказать, используя теоремы о пределах.
4.7
Точки разрыва и их классификация
Рассмотрим
некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением
может быть самой этой точки. Из определения точки разрыва функции следует, что
х = х0 является точкой разрыва, если функция не определена в этой точке, или не
является в ней непрерывной.
Следует
отметить также, что непрерывность функции может быть односторонней. Поясним это
следующим образом. Если односторонний предел (см. выше) 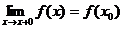 , то функция называется непрерывной справа.
, то функция называется непрерывной справа.
Определение.
Точка х0 называется точкой разрыва функции f(x),
если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке
функция f(x) имеет конечные, но не равные друг другу левый и
правый пределы.
Для
выполнения условий этого определения не требуется, чтобы функция была
определена в точке х = х0, достаточно того, что она определена слева и справа
от нее.
Из
определения можно сделать вывод, что в точке разрыва 1 - го рода функция может
иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 - го
рода еще иногда называют устранимой точкой разрыва, но подробнее об этом
поговорим ниже.
Определение.
Точка х0 называется точкой разрыва 2 - го рода, если в этой точке функция f(x) не
имеет хотя бы одного из односторонних пределов или хотя бы один из них
бесконечен.
Пример.
Функция Дирихле (Дирихле Петер Густав(1805-1859) - немецкий математик, член-
корреспондент Петербургской АН 1837г)
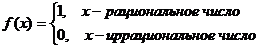
не
является непрерывной в любой точке х0.
Пример.
Функция f(x) = 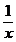 имеет в
точке х0 = 0 точку разрыва 2 - го рода, т.к.
имеет в
точке х0 = 0 точку разрыва 2 - го рода, т.к.
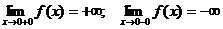 .
.

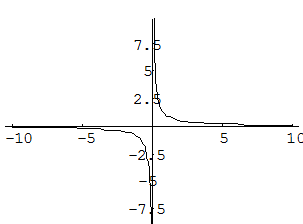
Пример.
f(x) = 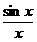
Функция
не определена в точке х = 0, но имеет в ней конечный предел 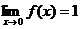 , т.е. в точке х = 0 функция имеет точку разрыва 1 -
го рода. Это - устранимая точка разрыва, т.к. если доопределить функцию:
, т.е. в точке х = 0 функция имеет точку разрыва 1 -
го рода. Это - устранимая точка разрыва, т.к. если доопределить функцию:
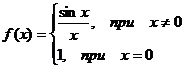
График
этой функции:
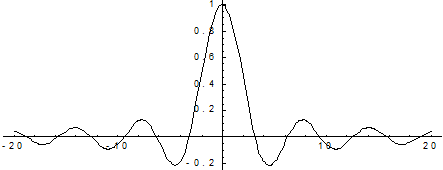
Пример.
f(x) = 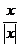 =
=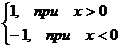
Эта
функция также обозначается sign(x) - знак х. В точке х = 0 функция не определена. Т.к.
левый и правый пределы функции различны, то точка разрыва - 1 - го рода. Если
доопределить функцию в точке х = 0, положив f(0) = 1, то
функция будет непрерывна справа, если положить f(0) = -1, то
функция будет непрерывной слева, если положить f(x)
равное какому- либо числу, отличному от 1 или -1, то функция не будет
непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в
точке х = 0 разрыв 1 - го рода. В этом примере точка разрыва 1 - го рода не
является устранимой. Таким образом, для того, чтобы точка разрыва 1 - го рода
была устранимой, необходимо, чтобы односторонние пределы справа и слева были
конечны и равны, а функция была бы в этой точке не определена.
Тема
5. Комплексные числа
5.1
Тригонометрическая форма записи комплексного числа
Определение.
Комплексным числом z называется выражение 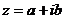 , где a и b -
действительные числа, i - мнимая единица, которая определяется соотношением:
, где a и b -
действительные числа, i - мнимая единица, которая определяется соотношением:

При
этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).
Если
a =Re z =0, то число z
будет чисто мнимым, если b = Im z = 0, то число z
будет действительным.
Определение.
Числа 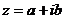 и
и 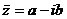 называются
комплексно - сопряженными.
называются
комплексно - сопряженными.
Определение.
Два комплексных числа 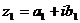 и
и 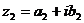 называются
равными, если соответственно равны их действительные и мнимые части:
называются
равными, если соответственно равны их действительные и мнимые части:

Определение.
Комплексное число равно нулю, если соответственно равны нулю действительная и
мнимая части.
Понятие
комплексного числа имеет геометрическое истолкование. Множество комплексных
чисел является расширением множества действительных чисел за счет включения
множества мнимых чисел. Комплексные числа включают в себя все множества чисел,
которые изучались ранее. Так натуральные, целые, рациональные, иррациональные,
действительные числа являются, вообще говоря, частными случаями комплексных
чисел.
Если
любое действительное число может быть геометрически представлено в виде точки
на числовой прямой, то комплексное число представляется точкой на плоскости,
координатами которой будут соответственно действительная и мнимая части
комплексного числа. При этом горизонтальная ось будет являться действительной
числовой осью, а вертикальная - мнимой осью.
Таким
образом, на оси ОХ располагаются действительные числа, а на оси ОY -
чисто мнимые.
С
помощью подобного геометрического представления можно представлять числа в так
называемой тригонометрической форме.
Из
геометрических соображений видно, что 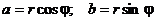 . Тогда
комплексное число можно представить в виде:
. Тогда
комплексное число можно представить в виде:
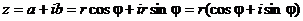
Такая
форма записи называется тригонометрической формой записи комплексного числа.
При
этом величина r называется модулем комплексного числа, а угол наклона
j - аргументом комплексного числа.
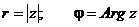 .
.
Из
геометрических соображений видно:
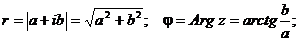
Очевидно,
что комплексно - сопряженные числа имеют одинаковые модули и противоположные
аргументы.
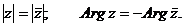
5.2
Действия с комплексными числами
Основные
действия с комплексными числами вытекают из действий с многочленами.
)
Сложение и вычитание.
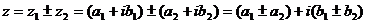
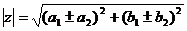
)
Умножение.
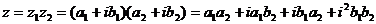
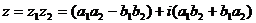
В
тригонометрической форме:
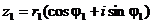 ,
,
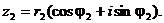
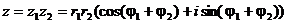
С
случае комплексно - сопряженных чисел:
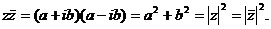
3) Деление.
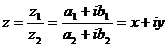
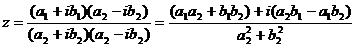
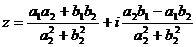
В
тригонометрической форме:
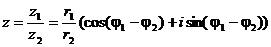
4)
Возведение в степень.
Из
операции умножения комплексных чисел следует, что
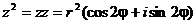
В общем случае получим:
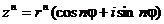 ,
,
где
n - целое положительное число.
Это
выражение называется формулой Муавра.
(Абрахам
де Муавр (1667 - 1754) - английский математик)
Формулу
Муавра можно использовать для нахождения тригонометрических функций двойного,
тройного и т.д. углов.
Пример.
Найти формулы sin2j и cos2j.
Рассмотрим
некоторое комплексное число
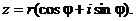
Тогда
с одной стороны
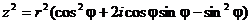 .
.
По
формуле Муавра:
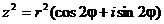
Приравнивая,
получим
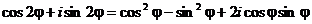
Т.к.
два комплексных числа равны, если равны их действительные и мнимые части, то
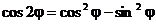
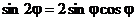
Получили
известные формулы двойного угла.
)
Извлечение корня из комплексного числа.
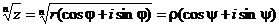
Возводя
в степень, получим:
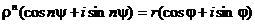
Отсюда:
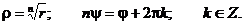
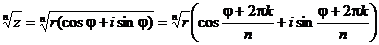
Таким
образом, корень n - ой степени из комплексного числа имеет n
различных значений.
5.3
Показательная форма комплексного числа
Рассмотрим
показательную функцию 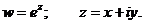
Можно
показать, что функция w может быть записана в виде:
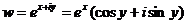
Данное
равенство называется уравнением Эйлера. Вывод этого уравнения будет рассмотрен
позднее. (См. ).
Для
комплексных чисел будут справедливы следующие свойства:
)
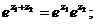
)
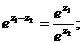
)
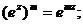 где m - целое число.
где m - целое число.
Если
в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то
получаем:
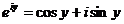
Для
комплексно - сопряженного числа получаем:
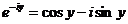
Из
этих двух уравнений получаем:
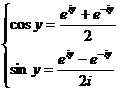
Этими
формулами пользуются для нахождения значений степеней тригонометрических
функций через функции кратных углов.
Если
представить комплексное число в тригонометрической форме:
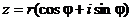
и
воспользуемся формулой Эйлера:
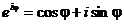
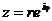
Полученное
равенство и есть показательная форма комплексного числа.