Прогноз заработной платы
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ
СООБЩЕНИЯ
Воронежский
филиал
(МИИТ)
КОНТРОЛЬНАЯ
РАБОТА
по
«Эконометрике»
Воронеж
-
Задание № 1
Вариант № 1
По данным таблицы 1.1 требуется:
1. Для характеристики зависимости 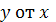
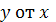 рассчитать параметры следующих
функций:
рассчитать параметры следующих
функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы.
. Оценить каждую модель через среднюю ошибку
аппроксимации и F-критерий
Фишера.
Таблица 1.1
|
Номер
региона
|
Расходы
на покупку продовольственных товаров в общих расходах, %, Y
|
Среднедневная
заработная плата одного работающего, руб., X
|
|
1
|
2
|
3
|
|
1
|
49,1
|
61,1
|
|
2
|
48,6
|
60,8
|
|
3
|
50,1
|
60,18
|
|
4
|
52,2
|
59,2
|
|
5
|
53,6
|
58,1
|
|
6
|
58,1
|
55,2
|
|
7
|
69,1
|
49,1
|
Решение:
а) В
соответствии с методом наименьших квадратов уравнение линейной регрессии имеет
вид:

 ,
,
где
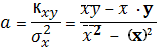
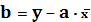
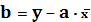 - параметры уравнения парной
линейной регрессии.
- параметры уравнения парной
линейной регрессии.
При этом
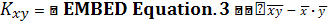
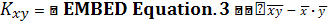 -
-
эмпирический корреляционный момент
случайных величин 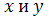
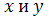


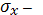
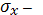 среднее квадратическое отклонение
случайной величины
среднее квадратическое отклонение
случайной величины 
 ,
,
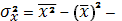
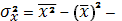 дисперсия случайной величины
дисперсия случайной величины 
 ,
,
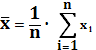
выборочное среднее значение
случайной величины 
 ,
,
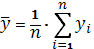
выборочное среднее значение
случайной величины 
 ,
,
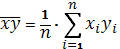
- выборочное среднее значение
случайной величины 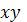
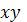 ,
,
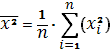
- выборочное среднее значение
случайной величины 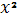
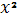 ,
,
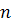
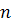 - объем выборки.
- объем выборки.
В нашем случае 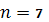
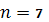 . Вычислим все необходимые суммы.
Результаты расчетов представим в виде таблицы:
. Вычислим все необходимые суммы.
Результаты расчетов представим в виде таблицы:
Таблица 1.2
|
Номер
региона
|
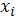
|
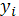
|
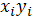
|
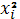
|
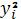
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
61,1
|
49,1
|
3000,01
|
3733,21
|
2410,81
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
2
|
60,8
|
48,6
|
2954,88
|
3696,64
|
2361,96
|
|
3
|
60,18
|
50,1
|
3015,018
|
3621,6324
|
2510,01
|
|
4
|
59,2
|
52,2
|
3090,24
|
3504,64
|
2724,84
|
|
5
|
58,1
|
53,6
|
3114,16
|
3375,61
|
2872,96
|
|
6
|
55,2
|
58,1
|
3207,12
|
3047,04
|
3375,61
|
|
7
|
49,1
|
69,1
|
3392,81
|
2410,81
|
4774,81
|
|
Итого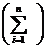 403,68380,821774,23823389,582421031 403,68380,821774,23823389,582421031
|
|
|
|
|
|
|
Среднее
 57,668654,43110,60543341,36893004,4286 57,668654,43110,60543341,36893004,4286
|
|
|
|
|
|
Получаем:
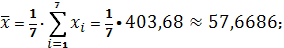
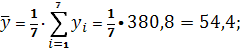
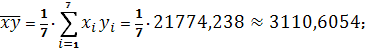
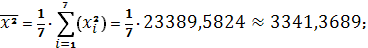
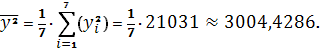
Тогда 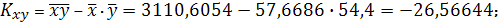
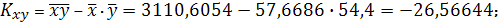
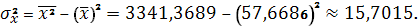
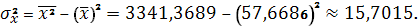
Параметры линейного регрессионного
уравнения:
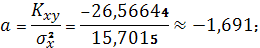
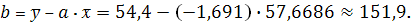
Следовательно, уравнение линейной
регрессии 
 имеет вид:
имеет вид: 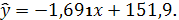
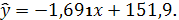
Значит с увеличением 
 на 1
на 1 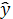
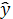 уменьшается в среднем на 1,691.
уменьшается в среднем на 1,691.
Таким образом, с увеличением
среднедневной заработной платы работающего на 1 руб. доля расходов на покупку
продовольственных товаров (в общих расходах) снижается в среднем на 1,691 %.
Найдем линейный коэффициент парной
корреляции 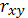
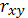 , являющийся мерой тесноты связи
между переменными
, являющийся мерой тесноты связи
между переменными 
 и
и 
 . Для этого воспользуемся формулой:
. Для этого воспользуемся формулой:
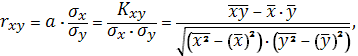
где
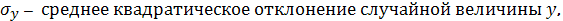
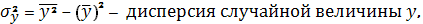

Итак, 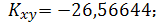
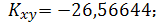
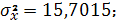
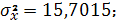
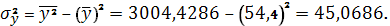
Значит линейный коэффициент парной
корреляции:
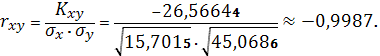
Коэффициент корреляции характеризует
зависимость 
 от
от 
 и меняется от -1 до 1.
и меняется от -1 до 1.
По коэффициенту корреляции можно
сделать вывод, что линейная связь между 
 и
и 
 обратная (так как
обратная (так как 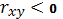
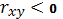 ) и весьма сильная, так как
) и весьма сильная, так как 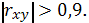
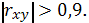
Коэффициент детерминации 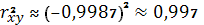
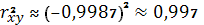 позволяет сделать вывод о том, что
линейное уравнение
позволяет сделать вывод о том, что
линейное уравнение 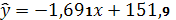
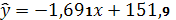 вполне адекватно описывает
зависимость между
вполне адекватно описывает
зависимость между 
 и
и 
 (вариация
(вариация 
 на 99,7 % объясняется влиянием
показателя
на 99,7 % объясняется влиянием
показателя 
 ).
).
Точность модели характеризуется
величиной отклонения расчетных значений от фактических. Средняя относительная
ошибка аппроксимации - среднее отклонение расчетных значений от фактических,
определяется по формуле:
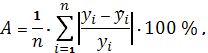
где
n - объем
выборки,
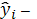
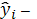 значение регрессионной функции.
значение регрессионной функции.
Составим расчетную таблицу:
Таблица 1.3
|
Номер
региона
|
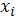
|
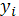
|
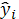
|
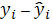
|
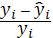
|
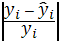
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
61,1
|
49,1
|
48,5799
|
0,5201
|
0,010592668
|
0,010592668
|
|
2
|
60,8
|
48,6
|
49,0872
|
-0,4872
|
-0,01002469
|
0,01002469
|
|
3
|
60,18
|
50,1
|
50,13562
|
-0,03562
|
-0,00071098
|
0,00071098
|
|
4
|
59,2
|
52,2
|
51,7928
|
0,4072
|
0,007800766
|
0,007800766
|
|
5
|
58,1
|
53,6
|
53,6529
|
-0,0529
|
-0,00098694
|
0,00098694
|
|
6
|
55,2
|
58,1
|
58,5568
|
-0,4568
|
-0,00786231
|
0,00786231
|
|
7
|
49,1
|
69,1
|
68,8719
|
0,2281
|
0,003301013
|
0,003301013
|
|
Итого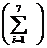 403,68380,8380,677120,122880,0021095310,041279363 403,68380,8380,677120,122880,0021095310,041279363
|
|
|
|
|
|
|
В нашем случае
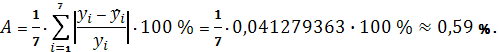
Таким образом, в среднем расчетные значения
линейной модели
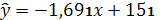
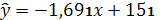 отклоняются от фактических на 0,59
%.
отклоняются от фактических на 0,59
%.
Проверим значимость 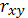
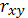 с доверительной вероятностью
с доверительной вероятностью 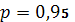
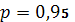 (то есть на уровне значимости
(то есть на уровне значимости 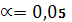
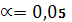 ) с помощью
) с помощью 
 критерия Фишера.
критерия Фишера.
Наблюдаемое (фактическое) значение 
 критерия Фишера определяется как
критерия Фишера определяется как
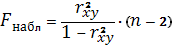
Критическое значение 
 критерия Фишера определяется как
критерия Фишера определяется как
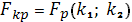
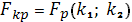 по таблице критических точек
по таблице критических точек 
 распределения Фишера - Снедекора,
где
распределения Фишера - Снедекора,
где
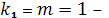
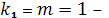 число степеней свободы большей
дисперсии,
число степеней свободы большей
дисперсии,
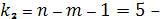
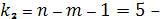 число степеней свободы меньшей
дисперсии
число степеней свободы меньшей
дисперсии
(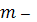
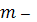 число факторных переменных,
определяющих модель).
число факторных переменных,
определяющих модель).
При 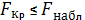
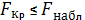 гипотеза об отсутствии линейной
связи (то есть о том, что
гипотеза об отсутствии линейной
связи (то есть о том, что 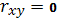
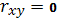 ) отклоняется, и соответственно
коэффициент парной корреляции
) отклоняется, и соответственно
коэффициент парной корреляции 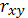
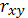 является значимым.
является значимым.
При 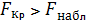
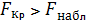 гипотеза об отсутствии связи
линейной верна, и соответственно коэффициент парной корреляции
гипотеза об отсутствии связи
линейной верна, и соответственно коэффициент парной корреляции 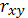
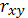 является незначимым.
является незначимым.
В нашем случае
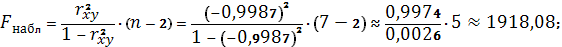
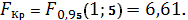
Оказалось, что 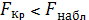
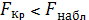 , следовательно, гипотеза об
отсутствии линейной связи неверна, и соответственно коэффициент парной
корреляции
, следовательно, гипотеза об
отсутствии линейной связи неверна, и соответственно коэффициент парной
корреляции
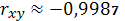
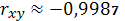 является значимым.
является значимым.
Таким образом, найденное линейное
уравнение 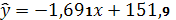
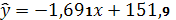 в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах).
в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах).
б) Найдем
уравнение степенной регрессии:
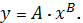
Прологарифмируем обе части уравнения
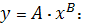
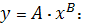


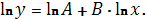
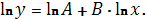
После замены переменных 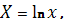
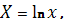
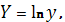
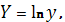
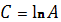
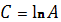 получим линейную модель
получим линейную модель 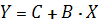
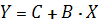 , то есть
, то есть 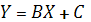
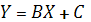 .
.
В соответствии с методом наименьших
квадратов параметры уравнения линейной регрессии 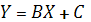
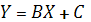 определим по формулам:
определим по формулам:
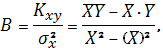
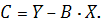
Вычислим все необходимые суммы.
Результаты расчетов представим в виде таблицы:
Таблица 1.4
|
Номер
региона
|
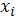
|
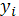
|
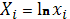
|
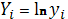
|
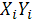
|
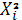
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
61,1
|
49,1
|
4,112511866
|
3,893859035
|
16,01354149
|
16,91275385
|
|
2
|
60,8
|
48,6
|
4,107589789
|
3,883623531
|
15,95233236
|
16,87229387
|
|
3
|
60,18
|
50,1
|
4,097340071
|
3,914021008
|
16,03707512
|
16,78819566
|
|
4
|
59,2
|
52,2
|
4,080921542
|
3,955082495
|
16,14038135
|
16,65392063
|
|
5
|
58,1
|
53,6
|
4,062165664
|
3,981549068
|
16,17371191
|
16,50118988
|
|
6
|
55,2
|
58,1
|
4,010962953
|
4,062165664
|
16,29319599
|
16,08782381
|
|
7
|
49,1
|
69,1
|
3,893859035
|
4,235554731
|
16,49265306
|
15,16213818
|
|
Итого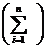 403,68380,828,3653509227,92585553113,1028913114,9783159 403,68380,828,3653509227,92585553113,1028913114,9783159
|
|
|
|
|
|
|
|
Среднее 57,668654,44,05223,989416,15755616,4255 57,668654,44,05223,989416,15755616,4255
|
|
|
|
|
|
|
Получаем:
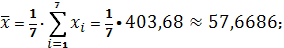
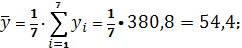
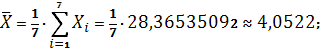
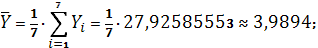
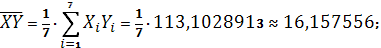
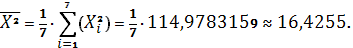
Тогда
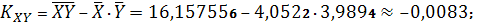
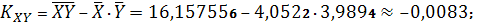
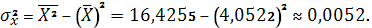
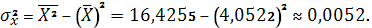
Параметры линейного регрессионного
уравнения 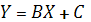
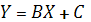 :
:
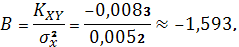
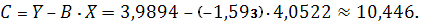
Соответственно параметры степенного
регрессионного уравнения 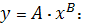
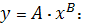
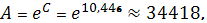
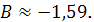
Следовательно, уравнение степенной
регрессии имеет вид: 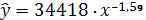
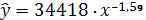
Найдем коэффициент нелинейной парной
корреляции (индекс корреляции) 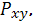
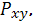 являющийся мерой тесноты связи
между переменными
являющийся мерой тесноты связи
между переменными 
 и
и 
 . Для этого воспользуемся формулой:
. Для этого воспользуемся формулой:

где
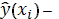
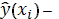 значение регрессионной функции в
точке
значение регрессионной функции в
точке 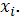
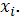
Таблица 1.5
|
Номер
региона
|
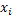
|
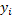
|
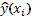
|
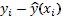
|
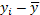
|
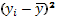
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
61,1
|
49,1
|
49,1611442
|
-0,0611442
|
0,003738614
|
-5,3
|
28,09
|
|
2
|
60,8
|
48,6
|
49,54812545
|
-0,94812545
|
0,898941861
|
-5,8
|
33,64
|
|
3
|
60,18
|
50,1
|
50,36377814
|
-0,26377814
|
0,069578905
|
-4,3
|
18,49
|
|
4
|
59,2
|
52,2
|
51,69840583
|
0,501594167
|
0,251596708
|
-2,2
|
4,84
|
|
5
|
58,1
|
53,6
|
53,26636385
|
0,333636146
|
0,111313078
|
-0,8
|
0,64
|
|
6
|
55,2
|
58,1
|
57,79319168
|
0,30680832
|
0,094131345
|
3,7
|
13,69
|
|
7
|
49,1
|
69,1
|
69,64546034
|
-0,54546034
|
0,29752698
|
14,7
|
216,09
|
|
Итого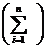 403,68380,8381,4764695-0,676469491,72682749
1,42109315,48 403,68380,8381,4764695-0,676469491,72682749
1,42109315,48
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Среднее 57,668654,454,4966385-0,09663850,2466896412,0301245,06857143 57,668654,454,4966385-0,09663850,2466896412,0301245,06857143
|
|
|
|
|
|
|
|
Следовательно, индекс корреляции для
степенной модели 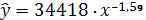
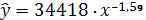 :
:
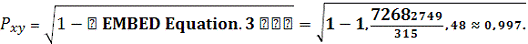
По индексу корреляции можно сделать
вывод, что степенная связь между 
 и
и 
 весьма сильная, так как
весьма сильная, так как 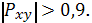
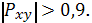
Коэффициент детерминации 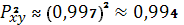
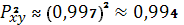 позволяет сделать вывод о том, что
степенное уравнение
позволяет сделать вывод о том, что
степенное уравнение 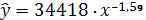
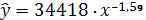 вполне адекватно описывает
зависимость между
вполне адекватно описывает
зависимость между 
 и
и 
 (вариация
(вариация 
 на 99,4 % объясняется влиянием
показателя
на 99,4 % объясняется влиянием
показателя 
 ).
).
Для нахождения средней относительной
ошибки аппроксимации составим расчетную таблицу:
Таблица 1.6
|
Номер
региона
|
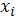
|
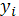
|
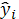
|
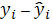
|
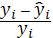
|
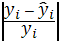
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
61,1
|
49,1
|
49,1611442
|
-0,0611442
|
-0,0012453
|
0,001245299
|
|
2
|
60,8
|
48,6
|
49,54812545
|
-0,94812545
|
-0,01950875
|
0,01950875
|
|
3
|
60,18
|
50,1
|
50,36377814
|
-0,26377814
|
-0,00526503
|
0,00526503
|
|
4
|
59,2
|
52,2
|
51,69840583
|
0,501594167
|
0,009609084
|
0,009609084
|
|
5
|
58,1
|
53,6
|
53,26636385
|
0,333636146
|
0,006224555
|
0,006224555
|
|
6
|
55,2
|
58,1
|
57,79319168
|
0,30680832
|
0,005280694
|
0,005280694
|
|
7
|
49,1
|
69,1
|
69,64546034
|
-0,54546034
|
-0,00789378
|
0,00789378
|
|
Итого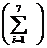 403,68380,8381,4764695-0,67646949-0,0127985360,055027201 403,68380,8381,4764695-0,67646949-0,0127985360,055027201
|
|
|
|
|
|
|
В нашем случае
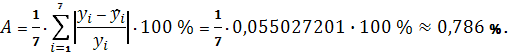
Таким образом, в среднем расчетные значения
степенной модели
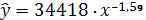
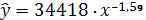 отклоняются от фактических на 0,786
%.
отклоняются от фактических на 0,786
%.
Проверим значимость 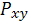
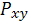 с доверительной вероятностью
с доверительной вероятностью 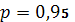
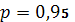 (то есть на уровне значимости
(то есть на уровне значимости 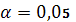
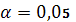 ) с помощью
) с помощью 
 критерия Фишера.
критерия Фишера.
Наблюдаемое (фактическое) значение 
 критерия Фишера определяется как:
критерия Фишера определяется как:
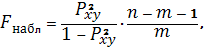
где 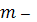
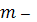 число параметров при переменных
число параметров при переменных 
 ,
,
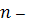
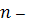 число наблюдений.
число наблюдений.
Критическое значение 
 критерия Фишера определяется как
критерия Фишера определяется как
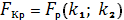
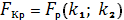 по таблице критических точек
по таблице критических точек 
 распределения Фишера - Снедекора,
где
распределения Фишера - Снедекора,
где
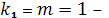
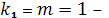 число степеней свободы большей
дисперсии,
число степеней свободы большей
дисперсии,
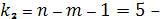
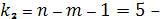 число степеней свободы меньшей
дисперсии,
число степеней свободы меньшей
дисперсии,
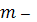
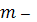 число параметров при переменных
число параметров при переменных 
 .
.
При 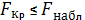
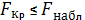 гипотеза об отсутствии нелинейной
связи (то есть о том, что
гипотеза об отсутствии нелинейной
связи (то есть о том, что 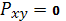
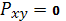 ) отклоняется, и соответственно
индекс корреляции
) отклоняется, и соответственно
индекс корреляции 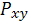
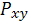 является значимым.
является значимым.
При 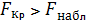
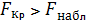 гипотеза об отсутствии нелинейной
связи верна, и соответственно индекс корреляции
гипотеза об отсутствии нелинейной
связи верна, и соответственно индекс корреляции 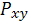
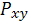 является незначимым.
является незначимым.
В нашем случае
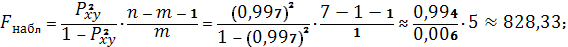
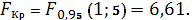
Оказалось, что 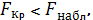
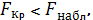 следовательно, гипотеза об
отсутствии нелинейной связи неверна, и соответственно индекс корреляции
следовательно, гипотеза об
отсутствии нелинейной связи неверна, и соответственно индекс корреляции 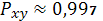
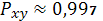 является значимым.
является значимым.
Таким образом, найденное степенное
уравнение 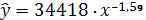
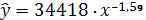 в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах.) При этом
характеристики степенной модели указывают, что она несколько хуже линейной
функции описывает эту зависимость.
в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах.) При этом
характеристики степенной модели указывают, что она несколько хуже линейной
функции описывает эту зависимость.
в) Найдем
уравнение показательной (экспоненциальной) регрессии:
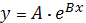
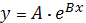
Прологарифмируем обе части уравнения
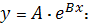
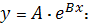
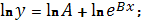
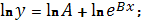
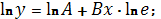
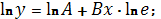
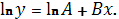
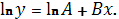
После замены 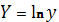
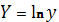 ,
, 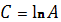
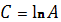 получим линейную модель
получим линейную модель 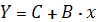
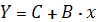 , то есть
, то есть 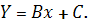
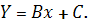
В соответствии с методом наименьших
квадратов параметры уравнения линейной регрессии 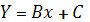
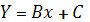 определим по формулам:
определим по формулам:
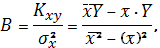
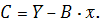
Вычислим все необходимые суммы.
Результаты расчетов представим в виде таблицы:
Таблица 1.7
|
Номер
региона
|
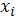
|
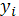
|
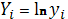
|
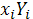
|
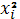
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
61,1
|
49,1
|
3,893859035
|
237,914787
|
3733,21
|
|
2
|
60,8
|
48,6
|
3,883623531
|
236,1243107
|
3696,64
|
|
3
|
60,18
|
50,1
|
3,914021008
|
235,5457843
|
3621,6324
|
|
4
|
59,2
|
52,2
|
3,955082495
|
234,1408837
|
3504,64
|
|
5
|
58,1
|
53,6
|
3,981549068
|
231,3280009
|
3375,61
|
|
6
|
55,2
|
58,1
|
4,062165664
|
224,2315446
|
3047,04
|
|
7
|
49,1
|
69,1
|
4,235554731
|
207,9657373
|
2410,81
|
|
Итого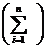 403,68380,827,925855531607,25104823389,5824 403,68380,827,925855531607,25104823389,5824
|
|
|
|
|
|
|
Среднее 57,668654,43,9894229,60733341,3689 57,668654,43,9894229,60733341,3689
|
|
|
|
|
|
Получаем:
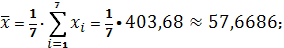
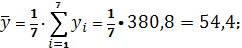
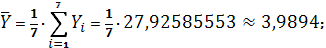
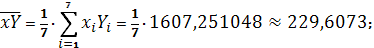
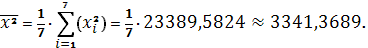
Тогда
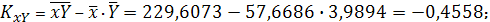
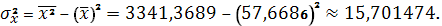
Параметры линейного регрессионного
уравнения 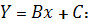
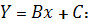
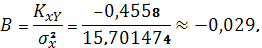
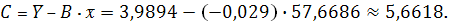
Соответственно параметры
показательного регрессионного уравнения 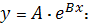
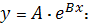
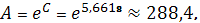
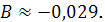
Следовательно, уравнение
показательной регрессии имеет вид:
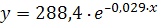
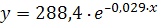 , то есть
, то есть 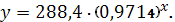
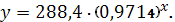
Найдем коэффициент нелинейной парной
корреляции (индекс корреляции) 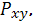
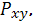 являющийся мерой тесноты связи
между переменными
являющийся мерой тесноты связи
между переменными 
 и
и 
 . Для этого воспользуемся формулой:
. Для этого воспользуемся формулой:

где 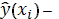
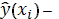 значение регрессионной функции в
точке
значение регрессионной функции в
точке 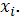
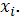
Таблица 1.8
|
Номер
региона
|
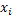
|
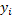
|
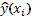
|
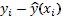
|
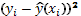
|
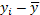
|
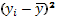
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
61,1
|
49,1
|
48,9800375
|
0,119962497
|
0,014391001
|
-5,3
|
28,09
|
|
2
|
60,8
|
48,6
|
49,40827409
|
-0,80827409
|
0,653307009
|
-5,8
|
33,64
|
|
3
|
60,18
|
50,1
|
50,30519793
|
-0,20519793
|
0,042106191
|
-4,3
|
18,49
|
|
4
|
59,2
|
52,2
|
51,75624082
|
0,44375918
|
0,196922209
|
-2,2
|
4,84
|
|
5
|
58,1
|
53,6
|
53,43487723
|
0,16512277
|
0,027265529
|
-0,8
|
0,64
|
|
6
|
55,2
|
58,1
|
58,12598539
|
-0,02598539
|
0,000675241
|
3,7
|
13,69
|
|
7
|
49,1
|
69,1
|
69,38121864
|
-0,28121864
|
0,079083921
|
14,7
|
216,09
|
|
Итого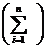 403,68380,8381,3918316-0,59183161,0137511011,42109315,48 403,68380,8381,3918316-0,59183161,0137511011,42109315,48
|
|
|
|
|
|
|
|
|
Среднее 57,668654,454,48454737-0,084547370,1448215862,0301245,06857143 57,668654,454,48454737-0,084547370,1448215862,0301245,06857143
|
|
|
|
|
|
|
|
Следовательно, индекс корреляции для
показательной модели
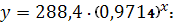
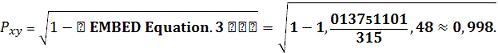
По индексу корреляции можно сделать
вывод, что показательная связь между 
 и
и 
 весьма сильная, так как
весьма сильная, так как 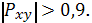
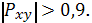
Коэффициент детерминации 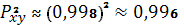
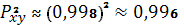 позволяет сделать вывод о том, что
показательное уравнение
позволяет сделать вывод о том, что
показательное уравнение 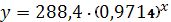
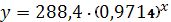 вполне адекватно описывает
зависимость между
вполне адекватно описывает
зависимость между 
 и
и 
 (вариация
(вариация 
 на 99,6 % объясняется влиянием
показателя
на 99,6 % объясняется влиянием
показателя 
 ).
).
Для нахождения средней относительной
ошибки аппроксимации составим расчетную таблицу:
Таблица 1.9
|
Номер
региона
|
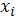
|
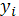
|
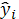
|
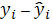
|
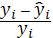
|
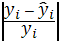
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
61,1
|
49,1
|
48,9800375
|
0,119962497
|
0,002443228
|
0,002443228
|
|
2
|
60,8
|
48,6
|
49,40827409
|
-0,80827409
|
-0,01663115
|
0,01663115
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
3
|
60,18
|
50,1
|
50,30519793
|
-0,20519793
|
-0,00409577
|
0,00409577
|
|
4
|
59,2
|
52,2
|
51,75624082
|
0,44375918
|
0,008501134
|
0,008501134
|
|
5
|
58,1
|
53,6
|
53,43487723
|
0,16512277
|
0,003080649
|
0,003080649
|
|
6
|
55,2
|
58,1
|
58,12598539
|
-0,02598539
|
-0,00044725
|
0,00044725
|
|
7
|
49,1
|
69,1
|
69,38121864
|
-0,28121864
|
-0,00406973
|
0,00406973
|
|
Итого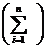 403,68380,8381,3918316-0,5918316-0,0112188980,039268919 403,68380,8381,3918316-0,5918316-0,0112188980,039268919
|
|
|
|
|
|
|
В нашем случае
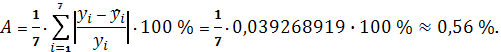
Таким образом, в среднем расчетные
значения показательной модели 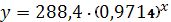
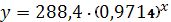 отклоняются от фактических на 0,56
%.
отклоняются от фактических на 0,56
%.
Проверим значимость 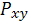
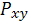 с доверительной вероятностью
с доверительной вероятностью 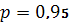
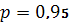 (то есть на уровне значимости
(то есть на уровне значимости 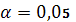
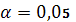 ) с помощью
) с помощью 
 критерия Фишера.
критерия Фишера.
В нашем случае
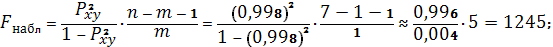
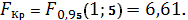
Оказалось, что 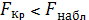
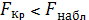 , следовательно, гипотеза об
отсутствии нелинейной связи неверна, и соответственно индекс корреляции
, следовательно, гипотеза об
отсутствии нелинейной связи неверна, и соответственно индекс корреляции 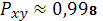
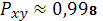 является значимым.
является значимым.
Таким образом, найденное
показательное уравнение 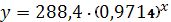
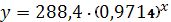 в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах). При этом
характеристики показательной модели указывают, что она с примерно той же точностью,
что и линейная функция описывает эту зависимость.
в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах). При этом
характеристики показательной модели указывают, что она с примерно той же точностью,
что и линейная функция описывает эту зависимость.
г) Найдем
уравнение гиперболической регрессии:
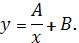
После замены 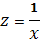
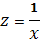 получим линейную модель
получим линейную модель 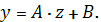
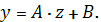
В соответствии с методом наименьших
квадратов параметры уравнения линейной регрессии 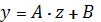
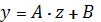 определим по формулам:
определим по формулам:
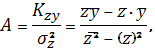
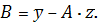
Вычислим все необходимые суммы.
Результаты расчетов представим в виде таблицы:
Таблица 1.10
|
Номер
региона
|
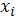
|
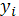
|
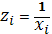
|
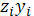
|

|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
61,1
|
49,1
|
0,016366612
|
0,803600655
|
0,000267866
|
|
2
|
60,8
|
48,6
|
0,016447368
|
0,799342105
|
0,000270516
|
|
3
|
60,18
|
50,1
|
0,016616816
|
0,832502493
|
0,000276119
|
|
4
|
59,2
|
52,2
|
0,016891892
|
0,881756757
|
0,000285336
|
|
5
|
58,1
|
53,6
|
0,017211704
|
0,922547332
|
0,000296243
|
|
6
|
55,2
|
58,1
|
0,018115942
|
1,052536232
|
0,000328187
|
|
7
|
49,1
|
69,1
|
0,020366599
|
1,407331976
|
0,000414798
|
|
Итого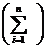 403,68380,80,1220169336,6996175490,002139065 403,68380,80,1220169336,6996175490,002139065
|
|
|
|
|
|
|
Среднее 57,668654,40,01740,9570880,0003056 57,668654,40,01740,9570880,0003056
|
|
|
|
|
|
Получаем:
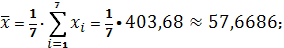
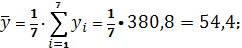
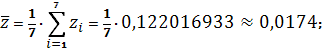
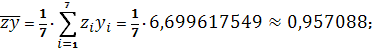
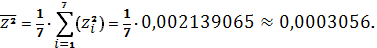
Тогда
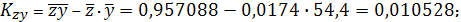
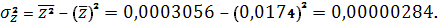
Параметры линейного регрессионного
уравнения 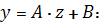
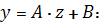
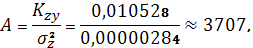
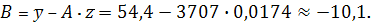
Соответственно параметры
гиперболического регрессионного уравнения 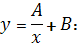
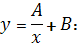
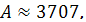
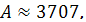
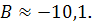
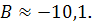
Следовательно, параметры
гиперболической регрессии имеет вид:
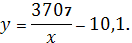
Найдем коэффициент нелинейной парной
корреляции (индекс корреляции) 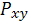
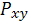 , являющийся мерой тесноты связи
между переменными
, являющийся мерой тесноты связи
между переменными 
 и
и 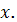
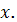 Для этого воспользуемся формулой:
Для этого воспользуемся формулой:

где 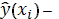
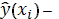 значение регрессионной функции в
точке
значение регрессионной функции в
точке 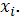
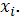
Таблица 1.11
|
Номер
региона
|
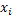
|
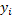
|
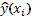
|
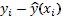
|
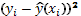
|
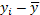
|
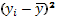
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
61,1
|
49,1
|
50,5710311
|
-1,4710311
|
2,163932487
|
-5,3
|
28,09
|
|
2
|
60,8
|
48,6
|
50,87039474
|
-2,27039474
|
5,154692261
|
-5,8
|
33,64
|
|
3
|
60,18
|
50,1
|
51,49853772
|
-1,39853772
|
1,955907755
|
-4,3
|
18,49
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
4
|
59,2
|
52,2
|
52,51824324
|
-0,31824324
|
0,101278762
|
-2,2
|
4,84
|
|
5
|
58,1
|
53,6
|
53,70378657
|
-0,10378657
|
0,010771653
|
-0,8
|
0,64
|
|
6
|
55,2
|
58,1
|
57,0557971
|
1,044202899
|
1,090359693
|
3,7
|
13,69
|
|
7
|
49,1
|
69,1
|
65,39898167
|
3,70101833
|
13,69753668
|
14,7
|
216,09
|
|
Итого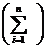 403,68380,8381,6167721-0,8167721424,174479291,42109315,48 403,68380,8381,6167721-0,8167721424,174479291,42109315,48
|
|
|
|
|
|
|
|
|
Среднее 57,668654,454,51668173-0,116681733,4534970412,0301245,06857143 57,668654,454,51668173-0,116681733,4534970412,0301245,06857143
|
|
|
|
|
|
|
|
Следовательно, индекс корреляции для
гиперболической модели
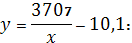
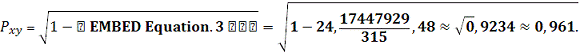
По индексу корреляции можно сделать
вывод, что гиперболическая связь между 
 и
и 
 весьма сильная, так как
весьма сильная, так как 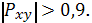
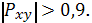
Коэффициент детерминации 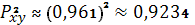
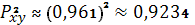 позволяет сделать вывод о том, что
гиперболическое уравнение
позволяет сделать вывод о том, что
гиперболическое уравнение 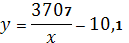
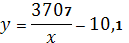 вполне адекватно описывает
зависимость между
вполне адекватно описывает
зависимость между 
 и
и 
 (вариация
(вариация 
 на 92,34 % объясняется влиянием
показателя
на 92,34 % объясняется влиянием
показателя 
 ).
).
Для нахождения средней относительной
ошибки аппроксимации составим расчетную таблицу:
Таблица 1.12
|
Номер
региона
|
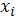
|
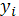
|
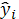
|
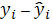
|
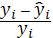
|
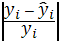
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
61,1
|
49,1
|
50,5710311
|
-1,4710311
|
-0,0299599
|
0,0299599
|
|
2
|
60,8
|
48,6
|
50,87039474
|
-2,27039474
|
-0,04671594
|
0,04671594
|
|
3
|
60,18
|
50,1
|
51,49853772
|
-1,39853772
|
-0,02791492
|
0,02791492
|
|
4
|
59,2
|
52,2
|
52,51824324
|
-0,31824324
|
-0,00609661
|
0,00609661
|
|
5
|
58,1
|
53,6
|
53,70378657
|
-0,10378657
|
-0,00193632
|
0,00193632
|
|
6
|
55,2
|
58,1
|
57,0557971
|
1,044202899
|
0,017972511
|
0,017972511
|
|
7
|
49,1
|
69,1
|
65,39898167
|
3,70101833
|
0,053560323
|
0,053560323
|
|
Итого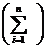 403,68380,8381,6167721-0,81677214-0,0410908620,184156531 403,68380,8381,6167721-0,81677214-0,0410908620,184156531
|
|
|
|
|
|
|
В нашем случае
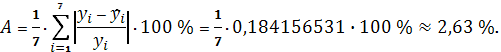
Таким образом, в среднем расчетные
значения гиперболической модели 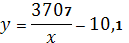
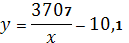 отклоняются от фактических на 2,63
%.
отклоняются от фактических на 2,63
%.
Проверим значимость 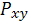
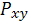 с доверительной вероятностью
с доверительной вероятностью 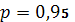
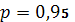 (то есть на уровне значимости
(то есть на уровне значимости 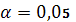
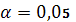 ) с помощью
) с помощью 
 критерия Фишера.
критерия Фишера.
В нашем случае
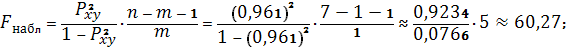
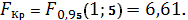
Оказалось, что 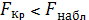
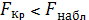 , следовательно, гипотеза об
отсутствии нелинейной связи неверна, и соответственно индекс корреляции
, следовательно, гипотеза об
отсутствии нелинейной связи неверна, и соответственно индекс корреляции 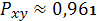
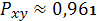 является значимым.
является значимым.
Таким образом, найденное
гиперболическое уравнение 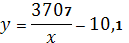
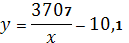 в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах). При этом
характеристики гиперболической модели указывают, что она несколько хуже
линейной функции описывает эту зависимость.
в целом довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах). При этом
характеристики гиперболической модели указывают, что она несколько хуже
линейной функции описывает эту зависимость.
Ответ: а) линейная модель 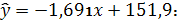
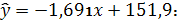
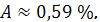
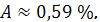
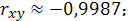
б) степенная модель 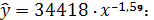
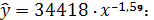
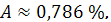
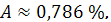
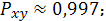
в) показательная модель 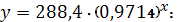
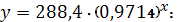
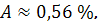
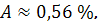
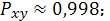
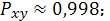
г) гиперболическая модель 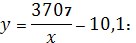
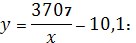
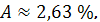
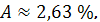


все модели довольно точно описывает
зависимость между среднедневной заработной платой работающего и долей расходов
на покупку продовольственных товаров (в общих расходах); при этом самыми
точными являются линейная модель 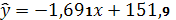
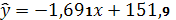 и показательная модель
и показательная модель 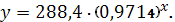
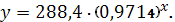
модель
аппроксимация прогноз точность
Задание № 2
Вариант № 1
По данным таблицы 2.1 требуется:
1. Построить линейное уравнение
парной регрессии 
 от
от 
 .
.
. Рассчитать линейный коэффициент
парной корреляции и среднюю ошибку аппроксимации.
. Оценить статистическую значимость
параметров регрессии и корреляции.
. Выполнить прогноз заработной платы

 при прогнозном значении
среднедушевого прожиточного минимума
при прогнозном значении
среднедушевого прожиточного минимума 
 , составляющем 107 % от среднего
уровня.
, составляющем 107 % от среднего
уровня.
. Оценить точность прогноза,
рассчитать ошибку прогноза и его доверительный интервал.
Таблица 2.1
|
Номер
региона
|
Среднедушевой
прожиточный минимум в день одного трудоспособного, руб., 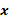 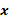 Среднедневная
заработная плата, руб., Среднедневная
заработная плата, руб., 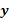 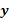
|
|
|
1
|
2
|
3
|
|
1
|
71
|
131
|
|
2
|
76
|
142
|
|
3
|
81
|
136
|
|
4
|
67
|
134
|
|
5
|
79
|
141
|
|
6
|
149
|
|
7
|
88
|
151
|
|
8
|
78
|
147
|
|
9
|
89
|
150
|
|
10
|
91
|
153
|
Решение:
) В соответствии с методом наименьших квадратов
уравнение линейной регрессии имеет вид:
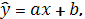
где
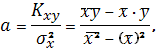
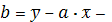
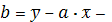 параметры уравнения парной линейной
регрессии.
параметры уравнения парной линейной
регрессии.
При этом
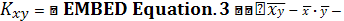
- эмпирический корреляционный момент
случайных величин 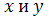
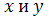


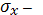
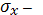 среднее квадратическое отклонение
случайной величины
среднее квадратическое отклонение
случайной величины 
 ,
,
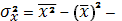
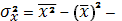 дисперсия случайной величины
дисперсия случайной величины 
 ,
,
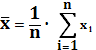
выборочное среднее значение
случайной величины 
 ,
,
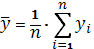
- выборочное среднее значение
случайной величины 
 ,
,
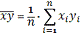
- выборочное среднее значение
случайной величины 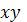
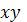 ,
,
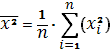
выборочное среднее значение
случайной величины 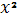
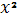 ,
,
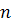
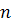 - объем выборки.
- объем выборки.
В нашем случае 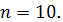
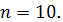 Вычислим все необходимые суммы.
Результаты расчетов представим в виде таблицы:
Вычислим все необходимые суммы.
Результаты расчетов представим в виде таблицы:
Таблица 2.2
|
Номер
региона
|
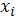
|
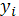
|
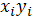
|
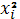
|
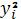
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
71
|
131
|
9301
|
5041
|
17161
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
2
|
76
|
142
|
10792
|
5776
|
20164
|
|
3
|
81
|
136
|
11016
|
6561
|
18496
|
|
4
|
67
|
134
|
8978
|
4489
|
17956
|
|
5
|
79
|
141
|
11139
|
6241
|
19881
|
|
6
|
82
|
149
|
12218
|
6724
|
22201
|
|
7
|
88
|
151
|
13288
|
7744
|
22801
|
|
8
|
78
|
147
|
11466
|
6084
|
21609
|
|
9
|
89
|
150
|
13350
|
7921
|
22500
|
|
10
|
91
|
153
|
13923
|
8281
|
23409
|
|
Итого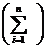 802143411547164862206178 802143411547164862206178
|
|
|
|
|
|
|
Среднее
 80,2143,411547,16486,220617,8 80,2143,411547,16486,220617,8
|
|
|
|
|
|
Получаем:
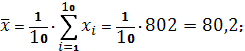
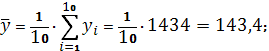
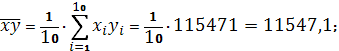
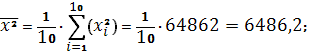
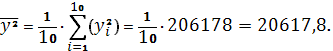
Тогда
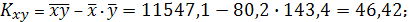
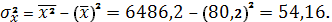
Параметры линейного регрессионного уравнения:
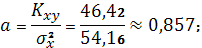
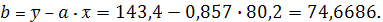
Следовательно, уравнение линейной
регрессии 
 имеет вид:
имеет вид: 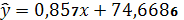
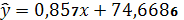 . Значит с увеличением
. Значит с увеличением 
 на 1
на 1 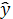
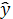 увеличивается в среднем на 0,857.
увеличивается в среднем на 0,857.
Таким образом, с увеличением
среднедушевого прожиточного минимума в день на 1 руб. среднедневная заработная
плата увеличивается в среднем на 0,857 руб.
2) Найдем линейный коэффициент
парной корреляции 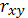
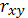 , являющийся мерой тесноты связи
между переменными
, являющийся мерой тесноты связи
между переменными 
 и
и 
 . Для этого воспользуемся формулой:
. Для этого воспользуемся формулой:
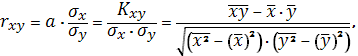
где 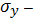
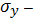 среднее квадратическое отклонение
случайной величины
среднее квадратическое отклонение
случайной величины 
 ,
,

 дисперсия случайной величины
дисперсия случайной величины 
 ,
,
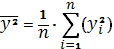
выборочное среднее значение
случайной величины 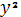
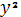 .
.
Итак,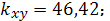
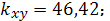
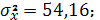
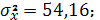
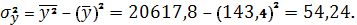
Значит линейный коэффициент парной
корреляции:
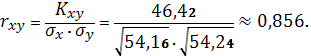
Коэффициент корреляции характеризует
зависимость 
 и
и 
 и меняется от -1 до 1.
и меняется от -1 до 1.
По коэффициенту корреляции можно
сделать вывод, что линейная связь между 
 и
и 
 прямая (так как
прямая (так как 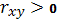
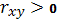 ) и очень сильная, так как
) и очень сильная, так как 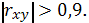
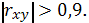
Коэффициент детерминации 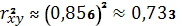
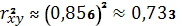 позволяет сделать вывод о том, что
линейной уравнение
позволяет сделать вывод о том, что
линейной уравнение 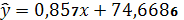
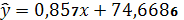 вполне адекватно описывает
зависимость между
вполне адекватно описывает
зависимость между 
 и
и 
 (вариация
(вариация 
 на 73,3 % объясняется влиянием
показателя
на 73,3 % объясняется влиянием
показателя 
 ).
).
Точность модели характеризуется
величиной отклонения расчетных значений от фактических. Средняя относительная
ошибка аппроксимации - среднее отклонение расчетных значений от фактических,
определяется по формуле:
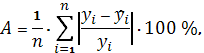
где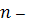
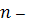 объем выборки,
объем выборки,
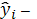
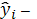 значение регрессионной функции
значение регрессионной функции 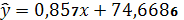
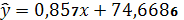 в точке
в точке 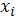
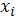 .
.
Составим расчетную таблицу:
Таблица 2.3
|
Номер
региона
|
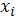
|
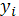
|
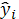
|
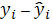
|
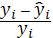
|
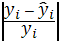
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
71
|
131
|
135,5156
|
-4,5156
|
-0,03447023
|
0,03447023
|
|
2
|
76
|
142
|
139,8006
|
2,1994
|
0,015488732
|
0,015488732
|
|
3
|
81
|
136
|
144,0856
|
-8,0856
|
-0,05945294
|
0,05945294
|
|
4
|
67
|
134
|
132,0876
|
1,9124
|
0,014271642
|
0,014271642
|
|
5
|
79
|
141
|
142,3716
|
-1,3716
|
-0,00972766
|
0,00972766
|
|
6
|
82
|
149
|
144,9426
|
4,0574
|
0,027230872
|
0,027230872
|
|
7
|
88
|
151
|
150,0846
|
0,9154
|
0,006062252
|
0,006062252
|
|
8
|
78
|
147
|
141,5146
|
5,4854
|
0,037315646
|
0,037315646
|
|
9
|
89
|
150
|
150,9416
|
-0,9416
|
-0,00627733
|
0,00627733
|
|
10
|
91
|
153
|
152,6556
|
0,3444
|
0,00225098
|
0,00225098
|
|
Итого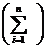 802143414340-0,0073080380,212548288 802143414340-0,0073080380,212548288
|
|
|
|
|
|
|
В нашем случае
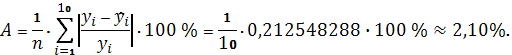
Таким образом, в среднем расчетные значения
линейной модели
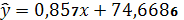
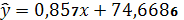 отклоняются от фактических на 2,1
%.
отклоняются от фактических на 2,1
%.
) Оценим статистическую значимость
параметров регрессии и корреляции
Проверим значимость 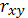
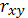 с доверительной вероятностью
с доверительной вероятностью 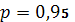
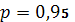 (то есть на уровне значимости
(то есть на уровне значимости 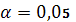
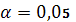 ) с помощью
) с помощью 
 критерия Фишера.
критерия Фишера.
Наблюдаемое (фактическое) значение 
 критерия Фишера определяется как:
критерия Фишера определяется как:
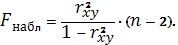
Критическое значение 
 критерия Фишера определяется как
критерия Фишера определяется как
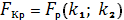
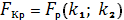 по таблице критических точек
по таблице критических точек 
 распределения Фишера - Снедекора,
где
распределения Фишера - Снедекора,
где
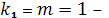
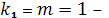 число степеней свободы большей
дисперсии,
число степеней свободы большей
дисперсии,
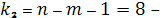
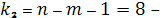 число степеней свободы меньшей
дисперсии,
число степеней свободы меньшей
дисперсии,
(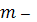
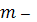 число факторных переменных,
определяющих модель).
число факторных переменных,
определяющих модель).
При 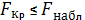
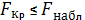 гипотеза об отсутствии линейной
связи (то есть о том, что
гипотеза об отсутствии линейной
связи (то есть о том, что 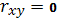
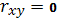 ) отклоняется, и соответственно
коэффициент парной корреляции
) отклоняется, и соответственно
коэффициент парной корреляции 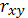
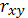 является значимым.
является значимым.
При 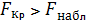
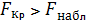 гипотеза об отсутствии связи
линейной верна, и соответственно коэффициент парной корреляции
гипотеза об отсутствии связи
линейной верна, и соответственно коэффициент парной корреляции 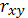
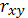 является незначимым.
является незначимым.
В нашем случае
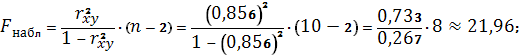
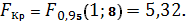
Оказалось, что 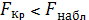
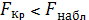 , следовательно, гипотеза об
отсутствии линейной связи неверна, и соответственно коэффициент парной
корреляции
, следовательно, гипотеза об
отсутствии линейной связи неверна, и соответственно коэффициент парной
корреляции
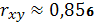
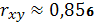 является значимым.
является значимым.
Таким образом, найденное линейное
уравнение 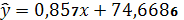
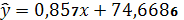 в целом довольно точно описывает
зависимость между среднедневной заработной платой и среднедушевым прожиточным
минимумом в день.
в целом довольно точно описывает
зависимость между среднедневной заработной платой и среднедушевым прожиточным
минимумом в день.
Значимость параметра 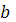
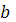 линейного уравнения парной
регрессии
линейного уравнения парной
регрессии 
 проверим с помощью критерия
Стьюдента.
проверим с помощью критерия
Стьюдента.
Наблюдаемое (фактическое) значение 
 критерия Стьюдента определяется
как:
критерия Стьюдента определяется
как:

где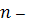
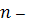 число фактических наблюдений (в
нашем случае
число фактических наблюдений (в
нашем случае 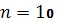
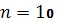 );
);
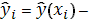
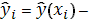 значение регрессионной функции
значение регрессионной функции 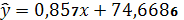
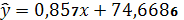 в точке
в точке 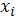
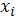 .
.
Критическое значение 
 критерия Стьюдента определяется как
критерия Стьюдента определяется как

 по таблице критических точек
распределения Стьюдента.
по таблице критических точек
распределения Стьюдента.
При 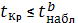
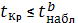 гипотеза о равенстве нулю параметра
гипотеза о равенстве нулю параметра
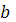
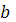 линейного уравнения парной
регрессии
линейного уравнения парной
регрессии 
 отклоняется, и соответственно
параметр
отклоняется, и соответственно
параметр 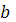
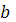 является значимым.
является значимым.
При 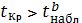
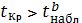 параметр
параметр 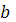
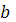 линейного уравнения парной
регрессии
линейного уравнения парной
регрессии 
 является незначимым, его можно
считать равным нулю.
является незначимым, его можно
считать равным нулю.
Вычислим
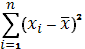
и
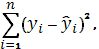
для чего составим расчетную таблицу:
Таблица 2.4
|
Номер
региона
|
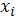
|
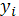
|
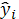
|
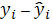
|
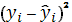
|
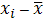
|
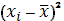
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
71
|
131
|
135,5156
|
-4,5156
|
20,39064336
|
-9,2
|
84,64
|
|
2
|
76
|
142
|
139,8006
|
2,1994
|
4,83736036
|
-4,2
|
17,64
|
|
3
|
81
|
136
|
144,0856
|
-8,0856
|
65,37692736
|
0,8
|
0,64
|
|
4
|
67
|
134
|
132,0876
|
1,9124
|
3,65727376
|
-13,2
|
174,24
|
|
5
|
79
|
141
|
142,3716
|
-1,3716
|
1,88128656
|
-1,2
|
1,44
|
|
6
|
82
|
149
|
144,9426
|
4,0574
|
16,46249476
|
1,8
|
3,24
|
|
7
|
88
|
151
|
150,0846
|
0,9154
|
0,83795716
|
7,8
|
60,84
|
|
8
|
78
|
147
|
141,5146
|
5,4854
|
30,08961316
|
-2,2
|
4,84
|
|
9
|
150
|
150,9416
|
-0,9416
|
0,88661056
|
8,8
|
77,44
|
|
10
|
91
|
153
|
152,6556
|
0,3444
|
0,11861136
|
10,8
|
116,64
|
|
Итого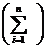 802143414340144,53880541,6 802143414340144,53880541,6
|
|
|
|
|
|
|
|
|
Среднее 80,2143,4 80,2143,4
|
|
|
|
|
|
|
|
Таким образом,
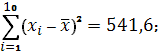
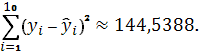
В нашем случае
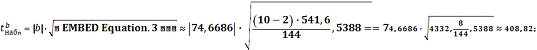
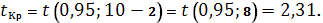
Оказалось, что 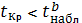
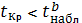 , следовательно, гипотеза о
равенстве нулю параметра
, следовательно, гипотеза о
равенстве нулю параметра 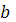
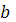 линейного уравнения парной
регрессии
линейного уравнения парной
регрессии 
 отклоняется, и соответственно
параметр
отклоняется, и соответственно
параметр 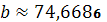
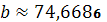 является значимым.
является значимым.
Значимость параметра 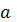
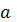 линейного уравнения парной
регрессии
линейного уравнения парной
регрессии 
 также проверим с помощью критерия
Стьюдента.
также проверим с помощью критерия
Стьюдента.
Наблюдаемое (фактическое) значение 
 критерия Стьюдента определяется
как:
критерия Стьюдента определяется
как:

где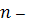
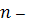 число фактических наблюдений (в нашем
случае
число фактических наблюдений (в нашем
случае 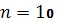
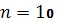 );
);
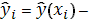
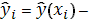 значение регрессионной функции
значение регрессионной функции 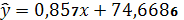
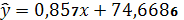 в точке
в точке 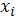
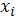 .
.
Критическое значение 
 критерия Стьюдента определяется как
критерия Стьюдента определяется как

 по таблице критических точек
распределения Стьюдента.
по таблице критических точек
распределения Стьюдента.
При 
 гипотеза о равенстве нулю параметра
гипотеза о равенстве нулю параметра
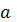
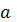 линейного уравнения парной
регрессии
линейного уравнения парной
регрессии 
 отклоняется, и соответственно
параметр
отклоняется, и соответственно
параметр 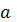
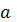 является значимым.
является значимым.
При 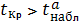
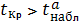 параметр
параметр 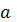
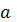 линейного уравнения парной
регрессии
линейного уравнения парной
регрессии 
 является незначимым, его можно
считать равным нулю.
является незначимым, его можно
считать равным нулю.
Ранее было найдено
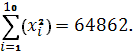
В нашем случае
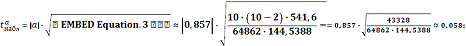
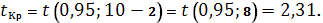
Оказалось, что 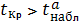
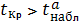 , следовательно, параметр
, следовательно, параметр 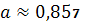
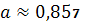 линейного уравнения парной регрессии
линейного уравнения парной регрессии

 является незначимым.
является незначимым.
4) Выполним прогноз заработной платы

 при прогнозном значении
среднедушевого прожиточного минимума
при прогнозном значении
среднедушевого прожиточного минимума 
 , составляющем 107 % от среднего
уровня, то есть при
, составляющем 107 % от среднего
уровня, то есть при
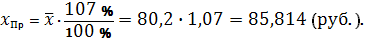
Прогнозное значение заработной платы
определим по регрессионному уравнению 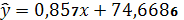
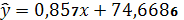 , подставив в него прогнозное
значение среднедушевого прожиточного минимума:
, подставив в него прогнозное
значение среднедушевого прожиточного минимума:
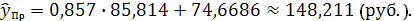
) Оценим точность прогноза,
рассчитав ошибку прогноза и его доверительный интервал.
Определим доверительный интервал
прогноза для уровня значимости 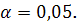
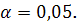
Средняя квадратическая ошибка
прогноза находится по формуле:
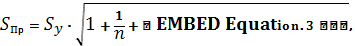
где
 планируемая (прогнозируемая)
величина среднедушевого прожиточного минимума (в нашем случае
планируемая (прогнозируемая)
величина среднедушевого прожиточного минимума (в нашем случае 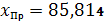
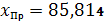 );
);
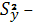
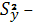 дисперсия отклонений фактических
наблюдений от расчетных;
дисперсия отклонений фактических
наблюдений от расчетных;

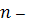
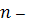 число фактических наблюдений (в
нашем случае
число фактических наблюдений (в
нашем случае 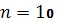
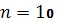 );
);
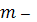
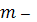 число нормальных уравнений,
связывающих независимые наблюдения случайной величины (в нашем случае
число нормальных уравнений,
связывающих независимые наблюдения случайной величины (в нашем случае 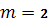
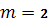 );
);
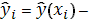
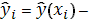 значение регрессионной функции в
точке
значение регрессионной функции в
точке 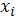
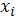 , то есть значение заработной платы,
рассчитанное по регрессионному уравнению
, то есть значение заработной платы,
рассчитанное по регрессионному уравнению
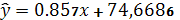
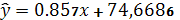 .
.
В нашем случае
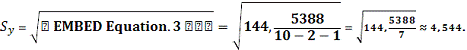
Значит средняя квадратическая ошибка
прогноза
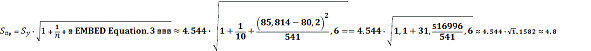
Предельная ошибка прогноза
определяется по формуле:
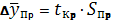
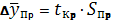 ,
,
где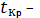
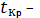 критическое значение
критическое значение 
 критерия Стьюдента, определяется
как
критерия Стьюдента, определяется
как 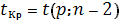
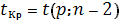 по таблице критических точек
распределения Стьюдента;
по таблице критических точек
распределения Стьюдента;
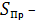
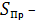 средняя квадратическая ошибка
прогноза.
средняя квадратическая ошибка
прогноза.
Следовательно, в нашем случае
предельная ошибка прогноза
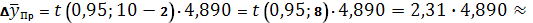
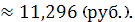
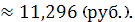
Значит, доверительный интервал
прогноза:
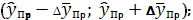
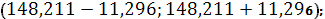

Таким образом, с вероятностью 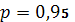
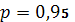 можно утверждать, что если
среднедушевой прожиточный минимум составит
можно утверждать, что если
среднедушевой прожиточный минимум составит 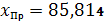
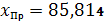 руб. (107 % от среднего уровня), то
среднедневная заработная плата будет заключена в пределах от 136,915 (руб.) до
159,507 (руб.).
руб. (107 % от среднего уровня), то
среднедневная заработная плата будет заключена в пределах от 136,915 (руб.) до
159,507 (руб.).
Ответ:1) 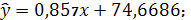
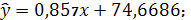
) 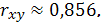
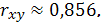
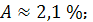
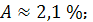
) 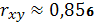
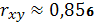 является значимым; параметр
является значимым; параметр 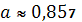
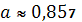 является незначимым, а параметр
является незначимым, а параметр 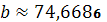
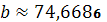 является значимым;
является значимым;
) 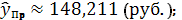
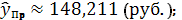
) с вероятностью 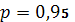
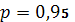
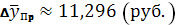
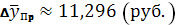 ,
,
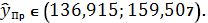
Список использованной литературы
.
Елисеева И.И., Курышева С.В., Горденко Н.М. и др. Эконометрика/Под ред. И.И.
Елисеевой. - М.: Изд-во «Финансы и статистика», 2001.
.
Доугерти К. Введение в эконометрику. - М.: Изд-во Финансы и статистика, 1999.
.
Магнус Я.Р., Катышев П. К., Пересецкий А.А. Эконометрика: Начальный курс. - М.:
Изд-во «Дело», 1998.