Разработка факультативного курса 'Алгебраические числа' для учащихся общеобразовательной школы
Московский
городской педагогический университет
Математический
факультет
Кафедра
алгебры, геометрии и методики их преподавания
Дипломная
работа
Разработка факультативного курса «Алгебраические числа» для
учащихся общеобразовательной школы
Студента:
Пчелинцева Алексея
Сергеевича
Научный руководитель:
к.п.н., доцент Чуйкова
Н.В.
Москва
- 2010
Оглавление
Актуальность исследования
Глава 1. Сущностная характеристика дополнительного математического
образования с точки зрения системного подхода
§ 1. История развития дополнительного математического образования
и внеклассной работы в России
§ 2. Педагогические условия организации дополнительного
математического образования в 8-10 классах общеобразовательной школы
§ 3. Психологические особенности учащихся 8-10 классов, влияющие
на содержание и формы организации факультативных занятий
Глава 2. Условия внедрения факультатива «Алгебраические числа» в
практику общеобразовательной школы
§1. Содержание факультативного курса
Раздел 1. История развития числовых понятий
Раздел 2. Симметрические многочлены
Раздел 3. Алгебраические числа
§2. Примерная программа факультатива «Алгебраические числа»
§3. Методические рекомендации по организации изучения
факультативного курса «Алгебраические числа»
Заключение
Библиография
Актуальность исследования
Математическое развитие является
важным фактором, обеспечивающим готовность человека к непрерывному образованию
и самообразованию в самых различных областях человеческой деятельности.
Общеобразовательная школа не в состоянии
в полной мере удовлетворить такие потребности. Однако дополнительное
математическое образование учащихся в форме внеклассных занятий, понимаемое как
«образовательный процесс, имеющий свои педагогические технологии, формы и
средства их реализации», по программам государственных стандартов
общеобразовательной школы является необходимым условием диверсификации
образования, дает возможность учитывать всех школьников, сильных, слабых и тех,
чьи интересы лежат в другой области.
Важной причиной дополнительного
изучения математических наук в школе является связь абстрактных математических
понятий с объективной действительностью.
Существенные изменения в концепции
школьного математического образования, произошедшие за последние десятилетия,
заставляют вернуться к обсуждению вопроса о более углубленном изучении чисел и
многочленов в средней школе. В настоящее время рассматриваемая тема
предлагается в системе углубленного изучения математики. Так изучение этой темы
затронуто в учебнике Н.Я. Виленкина для 8 классов с углубленным изучением
математики. Она связана с расширением существующего содержания, по сравнению с
общеобразовательным курсом, и учитель имеет право ее не изучать. Актуальность
изучения темы «Алгебраические числа» в 8-10 классах общеобразовательной школы
обосновывается преемственностью этой темы в вузах, вооружением учащихся
простыми и эффективными методами решения более широкого, по сравнению с
общеобразовательной школой класса задач. Эта тема является продолжением
числовой линии, изучению которой посвящается достаточно большое количество
часов в школы.
Изучение этой темы в содержании
общеобразовательной школы представляется целесообразным ввиду очевидных тесных
связей с материалом, изучаемым в вузах: комплексные числа, многочлены, матрицы,
… Обсуждение симметрических многочленов и комплексных чисел уже в 8 классе,
овладение учащимися основными применениями этой теории, дают им возможность
решать более широкий круг задач, и, что особенно важно - осваивать новые
математические идеи, т.е. качественно повышать уровень своей математической
подготовки [17, 18].
Изучением данной темы занимались
Н.Я. Виленкин, Э.Б. Винберг, Г.В. Дорофеев, В.В. Прасолов, С.Л. Табачников и
другие.
Возможно, что изучение темы
«Алгебраические числа» окажется для учащихся 8-10 классов достаточно трудным,
даже в классах с углубленным изучением математики. Однако при соответствующей
методике изучения этой темы, ориентированной, прежде всего, на знакомство с
рядом новых идей и понятий, такой курс может вызвать у учащихся живой интерес к
математике, показать им ее красоту. Математическая техника и отработка
конкретных навыков должны отойти на задний план.
Прикладные аспекты изучения
различных разделов факультативного курса практически лишены мотивационной
значимости, поскольку довести их до реальных приложений невозможно, и вряд ли
целесообразно. Учащиеся, способные освоить соответствующий материал, не
нуждаются в мотивации изучения предлагаемых разделов.
Итак, можно сделать вывод, что
изучение дополнительных разделов и тем в курсе математики на этапе 8 - 10
классов является важным фактором, обеспечивающим готовность человека к
непрерывному образованию и самообразованию в самых различных областях
человеческой жизни.
Цель исследования. Разработать
факультативный курс «Алгебраические числа» для школьников 8-10 классов и
проанализировать условия его внедрения в процесс дополнительного
математического образования.
Задачи исследования.
Изучить историю развития
дополнительного математического образования и внеклассной работы в России.
Выявить педагогические условия
организации дополнительного математического образования в 8-10 классах
общеобразовательной школы.
Сформулировать психологические
особенности учащихся 8-10 классов, влияющие на содержание и формы организации
факультативных курсов.
Выявить научно-методические аспекты
определения содержания факультативного курса «Алгебраические числа».
Предложить примерную программу
факультативного курса «Алгебраические числа».
Разработать методические
рекомендации по организации изучения дополнительного курса «Алгебраические
числа».
Методы исследования.
Метод изучения
психолого-педагогической литературы по теме;
Метод теоретического поиска;
Метод обобщения и систематизации
передового педагогического опыта, относящегося к проблемам дополнительного образования.
Структура дипломной работы.
Работа состоит из введения, двух
глав, заключения и библиографии. Она изложена на 60 страницах; библиография
включает 41 наименование.
В главе 1 раскрывается сущность
организации дополнительного образования в средней школе и рассматриваются
следующие вопросы:
история развития дополнительного
математического образования и внеклассной работы в России,
педагогические условия организации
дополнительного математического образования в 8-10 классах общеобразовательной
школы,
психологические особенности учащихся
8-10 классов, влияющие на содержание и формы организации дополнительных
математических курсов.
В главе 2 представлено содержание
факультативного курса «Алгебраические числа» и его методическое обеспечение.
Она состоит из трех параграфов. В первом параграфе предлагается детально
проработанный факультативный курс, включающий в себя исторический раздел,
раздел посвященный основной теореме о симметрических многочленах с рядом
важнейших следствий (симметрические многочлены по наборам переменных, формулы
Виета) и раздел, посвященный собственно алгебраическим числам, - комплексные
числа, алгебраическая замкнутость поля алгебраических чисел, теоремы Кантора о
счетности множества алгебраических чисел и несчетности множества точек на
отрезке [0; 1]. Во втором параграфе обсуждаются основные требования к учащимся,
предлагается примерная программа курса и система задач по данному курсу. В
третьем параграфе обсуждаются методические рекомендации по данному курсу.
В заключении отражены основные
выводы проведенного исследования.
Глава 1. Сущностная характеристика
дополнительного математического образования с точки зрения системного подхода
§ 1. История развития
дополнительного математического образования и внеклассной работы в России
Дополнительное образование
школьников и внеклассная работа взаимосвязаны и входят в состав непрерывного
математического образования, поэтому об их истории и развитии необходимо
говорить в контексте общего школьного математического образования.
А.К. Бруднов относил дополнительное
образование «к сфере наибольшего благоприятствования для становления личности
каждого ребенка», отмечал, что «в его процессе неисчерпаемы возможности
создания ситуации успеха для каждого ребенка, что благотворно сказывается на
воспитании и укреплении его личностного достоинства», что это «мощное средство
развития личности». Он считал, что этот вид образования изначально ориентирован
на свободный выбор различных видов и форм деятельности, формирования
собственных представлений о мире, развития познавательной мотивации и
способностей. [39, 40]
В.Б. Новичков, зам. директора
Московского института развития образовательных систем, считает, что
дополнительное образование может дополнять образовательную сферу по-разному:
оно может расширять предметные области; оно может увеличивать «вооруженность»
личности; оно способно многократно усиливать мотивацию образовательной
деятельности. [39, 40]
Таким образом, одной из значимых
характеристик российской системы образования, как отмечалось выше, является то,
что в ее структуре рассматривается дополнительное образование. При этом, само
дополнительное образование интерпретируется как бы с разных позиций. Одни
исследователи (В.В. Безлепкин, А.М. Новиков и др.) дополнительным образованием
называют послевузовское образование в системе повышения квалификации или
получение второй специальности. С другой стороны, ряд исследователей (А.К.
Бруднов, В.А. Березина, Л.И. Виноградова, В.В. Белова и др.) дополнительным
образованием называет дополнительное образование только детей и молодежи с 6 до
18 лет, сюда непосредственно относят и школьные кружковые внеурочные занятия.
Такая ситуация, с одной стороны, свидетельствуя о неоднозначности определения
понятия дополнительного образования, выявляет то, что объединяет позиции; точки
зрения разных исследователей.
А именно, сущностной характеристикой
дополнительного образования является его связь с базовым образованием, что
позволяет рассматривать это образование в контексте общей макросистемы
образования как одну из его составляющих, подструктур наряду с подструктурой
базового.
Дополнительное образование это
изначально ориентированное на свободный выбор каждым ребенком той или иной
области знаний и предлагающее услуги всем детям без всякого принуждения на
привлекательной для детей и юношества основе добровольности. Это формирует
особую образовательную среду и атмосферу заинтересованности, взаимозаботы,
творчества. [35]
Продолжая анализ понятия
«дополнительное образование» отметим, в программе «Столичное образование - 3»
Московского департамента образования, отдельный раздел посвящен дополнительному
образованию детей. В программе дополнительное образование определяется как
«неотъемлемая часть системного обучения, призванного раскрыть способности
ребенка, реализовать его тяготение к познанию, творчеству».
Проблемы истории школьного
математического образования исследовались в трудах И. К. Андронова, Ю.М.
Колягина, В.И. Лысенко, Г.Г. Масловой и др.
Т.С. Полякова дает систематическое
изложение истории отечественного математического образования и делит её на 9
этапов:
этап зарождения,
этап становления,
этап создания российской модели
классической системы школьного математического образования,
этап движения за реформацию,
этап поиска новых моделей
математического образования,
этап реставрации отечественных
традиций, создания советской модели классической системы школьного
математического образования,
этап её реформирования,
этап контреформации,
современный этап.
На каждом этапе можно выделить
структуры, относящиеся по своему характеру и целям к дополнительному
математическому образованию. [32]
Но сделаем акцент на 6 этапе. В 1931
г. восстанавливается предметное преподавание основных наук, вводятся стабильные
программы, в том числе и по математике, появляются стабильные учебники.
В 40 - 50х. гг. отечественная модель
классического школьного образования достигла наиболее оптимального
функционирования. Именно в этот период и начала функционировать система
внеклассной работы отечественной школы. Под внеклассной работой по
математическим наукам понимаются необязательные систематические занятия
учащихся с преподавателем во внеурочное время.
Следует различать два вида
внеклассной работы по математике:
работа с учащимися, отстающими от
других в изучении программного материала (дополнительные внеклассные занятия);
работа с учащимися, проявляющими к
изучению математики повышенный, по сравнению с другими, интерес и способности
(собственно внеклассная работа в традиционном понимании смысла этого термина).
Такие занятия отвечают следующим
основным целям:
пробуждение и развитие устойчивого
интереса учащихся к математике и ее приложениям.
расширение и углубление знаний
учащихся по программному материалу.
оптимальное развитие математических
способностей у учащихся и привитие учащимся определенных навыков научно-исследовательского
характера.
воспитание культуры математического
мышления.
развитие у учащихся умения
самостоятельно и творчески работать с учебной и научно-популярной литературой.
расширение и углубление
представлений учащихся о культурно-исторической ценности математики, о роли
отечественной математической школы в мировой науке.
установление более тесных деловых
контактов между учителем математики и учащимися и на этой основе более глубокое
изучение познавательных интересов и запросов школьников.
Предполагается, что эти цели
частично реализуются на уроках. Однако в процессе классных занятий,
ограниченных рамками учебного времени и программы, сделать это с достаточной
полнотой не удается. Поэтому окончательная реализация целей переносится на
внеклассные занятия. [20]
К 60-м годам 20 века школьное
математическое образование все более отдалялось от развития современной
математики, не было связано с бурно развивающейся информатикой и вычислительной
техникой, не учитывало новейших достижений педагогики и психологии. Назрела
необходимость радикального его пересмотра. Все это требовало новых, более
эффективных форм внеклассной работы и дополнительного математического
образования. Учащимся были нужны новые знания, а вузам - хорошо подготовленные
абитуриенты. Поэтому возникли весьма разнообразные формы внеклассной работы с
учащимися по математике: публичные лекции для учащихся, юношеские
математические школы, специальные школы (программистов-вычислителей),
общематематические школы и классы, вечерние и заочные математические школы,
школы - интернаты, летние и зимние математические школы. [26]
Начался первый этап введения
факультативных и дополнительных занятий в школу.
Факультативные занятия - одна из
форм дифференцированного обучения. Попытки дать толкования понятию
"дифференциация обучения" предпринимаются учеными давно. Чтобы
отчетливее представить движение научной мысли относительно содержания
рассматриваемого понятия, обратимся к различным определениям этого понятия.
Как считает З.И. Калмыкова,
дифференциация обучения - это создание специализированных классов и школ,
рассчитанных на учете психологических особенностей школьников.
И.Э. Унт утверждал, что это учет
индивидуальных особенностей учащихся в той или иной форме, когда учащиеся
группируются на основании каких-либо особенностей для раздельного обучения.
Г.В. Дорофеев, С.Б Суворова., В.В.
Фирсов, П.В. Кузнецов поддерживали мнение о том, что - это такая система
обучения, при которой каждый ученик, овладевая некоторым минимумом
общеобразовательной подготовки, являющейся общезначимой и обеспечивающей
возможность адаптации в постоянно меняющихся жизненных условиях, получает право
и гарантированную возможность уделять преимущественное внимание тем
направлениям, которые в наибольшей степени отвечают его склонностям.
Когда речь идет о дифференцированном
обучении, то говорится о комплексе организационно-управленческих,
социально-экономических и правовых аспектов обучения, которые создают статус
учебного заведения.
Если речь идет о дифференцированном
подходе, то имеется в виду технология индивидуального подхода к учащимся с
целью определения уровня их способностей и возможностей, их профильной
ориентации, максимального развития каждой личности на всех этапах обучения.
Если дифференциацию рассмотреть как систему, то, на наш взгляд,
дифференцированный подход немыслим без дифференцированного обучения, т.е. от
организации учебно-воспитательного процесса во всех его звеньях непосредственно
зависит результативность технологии индивидуального подхода к учащимся. [11,
12]
Индивидуальный подход к учащимся
предполагает частичное, временное изменение ближайших задач и отдельных сторон
содержания учебно-воспитательной работы, постоянное варьирование её методов и
организационных форм с учетом общего и особенного в личности каждого ученика
для обеспечения всестороннего ее развития.
Первые факультативные курсы
назывались "Дополнительные главы и вопросы математики" в
"Специальные курсы". В журнале "Математика в школе" в 1980
году были опубликованы программы этих факультативных курсов. В это время
факультативные курсы были ориентированы на новую программу по математике и
являлись местом апробации новых тем. После широкой экспериментальной проверки
на факультативных занятиях некоторые темы были включены в основной курс
математики. Например, "Метод координат", "Множества в операции
над ними", "Бесконечные множества", "Геометрические
преобразования”, "Производная".
В практику работы школы
факультативные занятия вошли в 1967-1968 учебном году. Уже в конце 1968 года в
Москве состоялось Всесоюзное совещание по опыту углубленного изучения отдельных
школьных предметов по выбору учащихся. Совещание обсудило итоги первого года
внедрения факультативных занятий в школу, рассмотрело широкий круг вопросов,
связанных с содержанием и организацией факультативов и поставило ряд серьезных
проблем, связанных, прежде всего, с методикой их проведения, оценкой знаний
учащихся, комплектованием групп, местом факультативных занятия в
учебно-воспитательном процессе, связи с другими занятиями по математике. [27]
По мере внедрения в жизнь новых
программ обязательного курса математики программа факультативного курса
"Дополнительные главы и вопросы математики" претерпевала ряд
изменений. Так в 1973-1974 учебном году, в связи о переходом на новые программы
была принята усовершенствованная программа факультативных курсов, которая, как
было отмечено выше, не включила ряд тем, переведенных в основной курс.
К 1980 году был завершен переход
средней школы на новую
программу по математике.
Факультативный курс "Дополнительные главы и вопросы математики" с
успехом выполнил свои функции и был заменен на новый курс. Начался второй этап
внедрения факультативных занятий в школе. Новый курс включил в себя три
следующих раздела:
избранные вопросы математики;
математика в приложениях;
алгоритмы и программирование.
Последний раздел заменил специальные
курсы по математике. Программа данных факультативных курсов была опубликована в
журнале "Математика в школе". Для раздела "Математика в
приложениях" журнал поместил примерное теоретическое планирование с
указанием рекомендуемых форм проведения занятий и списком литературы. Для
проведения занятии по первому разделу "Избранные вопросы математики"
издательство "Просвещение" выпустило соответствующую литературу в
помощь учителю, ведущему факультативные занятия по этому курсу, были изданы
методические пособия.
Современный этап развития школьного
математического образования характеризуется кардинальными изменениями,
связанными, прежде всего, с отказом от концепции единообразия отечественной
школы, что привело к распаду образовательной моносистемы советского периода.
[27]
Современная образовательная ситуация
отличается многовариантностью систем, существующих в образовательном
пространстве России.
§ 2. Педагогические условия
организации дополнительного математического образования в 8-10 классах
общеобразовательной школы
При разработке занятий для
дополнительного изучения предмета необходимо учитывать некоторые педагогические
условия организации таких видов дополнительного образования в форме внеклассных
занятий.
Сформулируем цели и задачи
построения таких внеурочных занятий:
Углубление и расширение знаний по
математике.
Развитие интереса учащихся к
предмету.
Развитие их математических
способностей.
Воспитание у школьников интереса и
вкуса к самостоятельным
занятиям математикой.
Воспитание и развитие инициативы и
творчества.
Интеллектуальное развитие.
Подготовка к практической творческой
деятельности по любой
специальности.
Повышение общего уровня развития
учащихся.
Подготовка школьников к дальнейшему
образованию и самообразованию.
Расширение и углубление знаний
учащихся по программному
материалу.
Оптимальное развитие математических
способностей у учащихся и привитие учащимся определенных навыков
научно-исследовательского характера.
Воспитание высокой культуры
математического мышления.
Развитие у учащихся умения
самостоятельно и творчески работать с учебной и научно-популярной литературой.
Расширение и углубление
представлений учащихся о практическом значении математики в технике, экономике,
математическом моделировании.
Расширение и углубление
представлений учащихся о культурно - исторической ценности математики, о роли
ведущих ученых математиков в развитии мировой науки.
Одна из задач, которые возлагаются
на дополнительное образование - улучшать подготовку учащихся к обучению в
вузах. Но если эта задача становиться главной, то занятия сводятся к прямым
тренировкам и повторению. А это дискредитирует саму идею дополнительного
образования. Поэтому сознательное, глубокое усвоение идей, методов школьного
курса и новых тем является лучшей подготовкой. [11, 34]
Для того чтобы показать
целесообразность общего психолого-педагогического подхода к нашей теме,
сформулируем вывод: критерий совершенствования содержания и методики
организации занятий, носящих дополнительный характер, должен быть комплексным.
Он заключается в учете и всесторонней оценке всего педагогического,
психологического и математического единства, которым должны быть связаны
учебная работа по математике и дополнительные занятия. Определяющую роль в этом
единстве играет учебная работа.
Говоря о единстве, мы подразумевали
здесь взаимосвязь и преемственность в содержании, формах и методах организации
учебной работы, внеклассных занятий и дополнительного образования по
математике.
Определенная зависимость
дополнительных занятий от учебной и внеклассной работы по математике очевидна.
Однако это обстоятельство не затрудняет, а облегчает выполнение следующей
основной задачи дополнительных занятий: учитывая интересы и склонности
учащихся, расширить и углубить усвоение ими программного материала, ознакомить
с некоторыми общими идеями современной математики, раскрыть приложения
математики на практике.
Решение актуальных задач определения
содержания дополнительного образования по математике, разработки методики его
организации требует изучения ряда более общих вопросов. Решение этих задач
должно базироваться на анализе соответствующей педагогической и
методико-математической литературы, анализе результатов специальных
исследований по затронутым проблемам, на передовом педагогическом опыте.
Внеклассная работа, несмотря на
некоторую свою произвольность и специфическую воспитательную направленность,
всегда строится на основе программного материала. Но это не исключает
возможность рассматривать и дополнительные вопросы, лишь бы они были доступны и
весьма интересны для изучения их учащимися. [20, 30]
Из сказанного следует, что единым
фундаментом в научном содержании всех занятий по математике (классных,
внеклассных, дополнительного образования) является программный учебный
материал. Таким образом, учитель должен помнить, что внеклассная работа и
дополнительное образование должны строиться с учетом завершения задач обучения
математике; уроки математики должны подготавливать учащихся к внеклассной
работе и дополнительным занятиям. Учитывая, что дополнительное образование по
математике вводится только с 7 класса, учителю следует совершенствовать
методику проведения уроков. [29, 40]
Научные линии, по которым содержание
математики усваивается школьниками, в сложившемся сейчас школьном курсе
определились следующие: алгоритмическая, формально-логическая линии,
функциональная и графическая линии, линия геометрических преобразований и др.
Некоторые из них подчинены друг другу (линия уравнений и неравенств входит
составной частью в функциональную линию) или тесно связаны (как, например,
функциональная и графические линии). Эти линии служат учебно-познавательным
целям (усвоение установленных программой математических фактов, математического
языка, методов математического исследования, развитие научного мышления.
В настоящее время еще нет полной
ясности в вопросе об учебно-познавательных целях, реализацию которых должен
взять на себя курс математики средней школы в целом. Их выявление помогло бы
дать важные рекомендации, касающиеся содержания классных, внеклассных занятий и
дополнительного образования по математике.
Для определения содержания
внеклассных и дополнительного образования по математике, для разработки их
эффективной методики сформулируем некоторые общие требования взаимосвязанного
построения уроков и других видов занятий.
Преемственность в содержании,
методах и формах организации уроков, внеклассных занятий и дополнительного
образования по математике должна определяться целями обучения математике,
всестороннего развития и воспитания учащихся. [38, 28]
Взаимосвязанное построение уроков,
внеклассных занятий и дополнительного образования по математике не должно
противоречить дидактическим принципам в обучении математики.
Не должно быть противоречий с научно
обоснованными психолого-педагогическими требованиями, например, такими, как:
изучение новых понятии на основе известных понятий; включение этих понятий в
круг имеющихся у учащихся знаний; опора при изучении математических абстракций
на конкретные модели; использование практических возможностей приложения
математики не только на завершающем этапе изучения данного вопроса, но и в
качестве мотива, обосновывающего необходимость изучений этого раздела, вопроса.
[38, 32]
Не должно быть несогласованности и с
директивными нормами организации работы общеобразовательной школы. Например,
нельзя часы, отведенные на дополнительное образование, использовать для
внеклассной работы по математике (хотя бы потому, что это не предусмотрено
финансированием школы и противоречит идее занятий по выбору и интересам
учащихся).
Главным критерием эффективности
взаимосвязанного построения уроков, внеклассных занятий и дополнительного
образования по математике должна быть в конечном счете результативность
неразрывно связанных между собой процессов обучения, развития и воспитания
школьников. [31]
Поскольку результативность
учебно-воспитательного процесса зависит главным образом от «массовости»
занятий, то преемственность и взаимосвязь уроков, внеклассных занятий и
дополнительного образования должны рассматриваться в такой последовательности:
уроки математики - внеклассные занятия - дополнительное образования. Самая
массовая форма обучения - уроки - главное звено этой цепи. Дополнительно
образование не может охватить всех учащихся, а отдельные внеклассные занятия -
могут. [39, 2]
Примечательной особенностью
дополнительного образования является то, что программа курса для каждого класса
составлена из рада основных тем, содержание которых непосредственно примыкает к
общему курсу математики. Однако содержание учебной работы учащихся на курсах
дополнительного образования определяется не только математическим содержанием
изучаемых тем и разделов, но и различными методическими факторами: характером
объяснения учителя, соотношением теории и учебных упражнений, содержанием познавательных
вопросов и задач, сочетанием самостоятельной работы и коллективного обсуждения
полученных каждым учащимся результатов.
Кроме того, в условиях работы по
новым программам и учебникам математики определилась неизученная область
внеклассной работы, касающаяся ее взаимосвязи с дополнительным образованием.
В дополнительном образовании
школьников, в частности в математическом, на наш взгляд, необходимо
использовать основные психологически ориентированные модели школьного обучения,
понимая под этим следующее: содержание и формы школьного образования,
дополнительного в частности, должны соответствовать психологии ребенка, его
правам и интересам. [27]
Основными методическими моделями,
построенными с учетом психологических механизмов умственного развития учащихся,
являются:
«Свободная мысль», в которой в
максимальной мере учитывается инициатива ребенка. Сторонники данной модели: Р.
Штейнер, Ф.Г. Кумбе, Ч. Сильберман, В.С. Библер, С. Ю. Курганов считали, что
при наличии определенной помощи со стороны учителя ребенок, тем не менее, сам
определяет интенсивность и продолжительность своих учебных занятий, свободно
планирует собственное время, самостоятельно выбирает средства обучения.
Ключевой психологический элемент - «свобода индивидуального выбора».
«Личностная модель». Представители
данной линии Л.В. Занков, И.И. Аргинская, И.В. Нечаева утверждали, что основной
психологической целью данной модели является общее развитие учащегося, в том
числе развитие его познавательных, эмоционально-волевых, нравственных и эстетических
возможностей. Ключевой психологический элемент - «целостный личностный рост».
«Развивающая модель». В центре
внимания оказывается перестройка учебной деятельности ребенка как на уровне
содержания, так и на уровне формы ее организации с тем, чтобы обеспечить
появление некоторых новых психологических качеств: теоретического мышления,
рефлексии, самостоятельности в решении разнообразных учебных задач и т.д.
Ключевой психологический элемент - «способы деятельности». Ученые, разделяющие
данную теорию: Д.Б. Эльконин, В.В. Давыдов, В.В. Репкин, А.З. Зак.
«Активизирующая модель», направлена
на повышение уровня познавательной активности учащихся за счет включения в
учебный процесс проблемных ситуаций, опоры на познавательные потребности и
интеллектуальные чувства. Ключевой психологический элемент - «познавательный
интерес». Это мнение разделяли А.М. Матюшкин, М.М. Махмутов, М.Н. Скаткин, Г.И.
Щукина.
«Формирующая модель».
Предполагается, что влиять на умственное развитие ребенка - это значит
осуществлять целенаправленное управление процессом усвоения знаний и умений.
П.Я. Гальперин, Н.Ф. Талызина, И.П. Калошина, В.П. Беспалько, СИ. Шапиро
считали, что при условии прохождения учеником всех необходимых этапов с учетом
специально организованной учителем ориентировочной основы действий можно
гарантировать сформированность знаний и умений с наперед заданными качествами.
Разновидностью этой модели являются программированное и алгоритмическое
обучение. Ключевой психологический элемент - «умственное действие».
Все перечисленные модели несомненно
способствуют повышению эффективности школьного обучения, поскольку на первом
плане оказывается ребенок как субъект деятельности и основные педагогические
усилия направляются на его познавательное и личностное развитие. [25, 26]
Поэтому неудивительно, что на уровне конкретных методических приемов эти модели
в той или иной степени взаимопересекаются.
«Обогащенная модель». Ее ключевой
элемент - «индивидуальный ментальный опыт». М.А. Холодная, сторонник данной
модели, считает, что цель данной модели - помочь ребенку выстроить собственный
(личный или ментальный) мир. В качестве показателей интеллектуальной зрелости
можно рассматривать характеристики индивидуального умозрения, например такие:
широта умственного кругозора;
гибкость к многовариантность оценок
происходящего;
готовность к принятию необычной
информации;
умение осмысливать происходящее
одновременно в терминах
прошлого (причин) и в терминах
будущего (последствий);
ориентация на выявление
существенных, объективно значимых аспектов происходящего;
склонность мыслить в категориях
вероятного в рамках ментальной модели «как если бы».
Имея необходимые интеллектуальные
ресурсы, ребенок впоследствии самостоятельно сможет решить, над чем и как он
будет думать.
Роль учителя здесь заключается в
«выстраивании» с помощью определенного материала учебного арсенала субъективных
средств продуктивного интеллектуального отношения к действительности.
В период становления дополнительного
образования встал вопрос о методах, используемых на этих занятиях, не всегда
находил правильное решение. Нередко использовались те же методы обучения, что и
на основных уроках математики или методы кружковой работы. В первом случае
дополнительное образование превращались во внеклассные занятия по математике, в
другом - носили поверхностный, легковесный характер. [27, 28]
В исследованиях, посвященных
проблемам постановки и организации дополнительного образования, говорится о
важном значении поисковой исследовательской деятельности, которая является
результатом проблемного обучения; о постановке самостоятельных работ и
организации самообучения учащихся на базе дополнительного образования.
Высказываются некоторые рекомендации
относительно выбора форм и методов обучения при дополнительном образовании, а
именно:
организация самостоятельной работы
учащихся на всех этапах обучения.
построение процесса изучения
математики как совместной исследовательской деятельности учащихся.
индивидуализация и увеличение объема
самостоятельной работы каждого учащегося.
Были выделены следующие критерии
отбора методов организации дополнительного образования:
Критерии преемственности методов.
Критерий соответствия целям и
задачам обучения.
Критерии соответствия содержанию
занятий.
Критерии соответствия возрастным и
индивидуальным особенностям развития старшеклассников.
Рассмотрим теперь каждый из этих
критериев в отдельности и
определим его место и роль в решении
образовательных, воспитательных и развивавших задач обучения. [37, 40]
Критерий преемственности методов,
применяемых на основных занятиях и дополнительном образовании по математике
означает, что методы, используемые при дополнительном образовании находятся не
в отрыве, а являются естественным продолжением методов, используемых на
основных уроках. Этот критерии предполагает, что на основных уроках,
предшествующих дополнительному образованию, заложена некоторая база и созданы
условия - расширения применяемых методов в сторону постепенного приближения к
методам обучения, носящим самостоятельный, творческий характер.
Критерий соответствия целям и
задачам обучения предполагает, что при выборе методов обучения необходимо
учесть цели обучения, задачи образования, воспитания и развития, которые будут
реализовываться на данном этапе урока и на протяжении изучения всего материала
дополнительного курса. Методы обучения играют первостепенную роль в выработке
не только знаний, но и умений, навыков учащихся. Среди таких умений и навыков,
выработка которых необходима при дополнительном образовании, выделим следующие:
умение по решению задач, доказательству
теорем и т.д.;
умение слушать объяснение нового
материала, выделять главное, существенное, вести конспект занятий;
умение работать с книгой: учебниками
по математике, учебно-методической и научно-популярной литературой;
умение подготовить и сделать доклад
или сообщение по прочитанному материалу;
умение написать статью для
стенгазеты, реферат на определенную тему, с самостоятельным изучением подбором
литературы;
умение проводить самостоятельное
исследование поставленной проблемы, включающее в себя: изучение необходимой
литературы, поиски и нахождение решения проблемы, доказательство полученных
результатов, доклад по итогам проведенных исследований.
Критерий соответствия содержанию
занятий предполагает, что использование тех или иных методов обучения при дополнительном
образовании непосредственно зависит от содержания материала.
Таким образом, условиями организации
дополнительного курса образования является определение некоторой модели:
«Свободная мысль», «Личностная модель», «Развивающая модель», «Активизирующая
модель», «Формирующая модель», «Обогащенная модель», где заложены свои критерии
и система методов: критерии преемственности методов, критерий соответствия
целям и задачам обучения, критерии соответствия содержанию занятий, критерии
соответствия возрастным и индивидуальным особенностям развития
старшеклассников. А также при построении курса дополнительного математического
образования необходимо учитывать комплексный подход к разработке такого курса.
§ 3. Психологические особенности
учащихся 8-10 классов, влияющие на содержание и формы организации
факультативных занятий
Подростковый возраст называют
переходным. Психологическое состояния подросткового возраста связано с двумя
«переломными» моментами этого возраста: психофизиологическим - половым созреванием,
и всё, что с ним связано, и социальным - конец детства. Вступление в мир
взрослых.
Но, будучи по типу логики мышления
равным взрослому, по жизненному опыту и содержанию сознания подросток остается
еще ребенком. Главным противоречием подросткового возраста можно считать
противоречие между рассудочной формой возникновения в сознание подростка
рефлексии, ставшей для него ведущей формой сознательного отношения к миру, и
неличным миром взрослых, не укладывающейся в рамки рассудочности, и в то же
время провозглашающим рассудочность (сознательность) своего бытия. [12]
Нам при планировании факультативных
занятий необходимо рассмотреть вопрос развития мышления в переходном возрасте.
Основная разница между маленьким школьником и подростком, легко обнаруживаемая
даже самым поверхностным наблюдением над их поведением - общеизвестная
склонность подростка и юноши к рассуждениям. Это эпоха - эпоха рассуждающего
мышления. Подростковый возраст - возраст проблем, рассуждений и споров.
Находящаяся в разгаре своего созревания функция мышление начинает проявлять
себя с большой энергией, и огромное место занимает мышление в жизни подростка и
юноши. Они забрасывают в школе учителей вопросами, а дома усиленно думают над
решением порой труднейших проблем. Дружить для них в значительной степени, -
значит иметь партнёров для рассуждений, а содержание их учебных предметов в
большей мере состоит из рассуждений и доказательств. И в школе, и вне школы они
имеют репутацию спорщиков, причём в этих спорах уже большое место занимает доказательство
своих собственных положений. Порой мышление проявляется с такой избыточной
энергией, что производит впечатление как бы игры: спорят ради спора,
рассуждают, чтобы рассуждать, и думают над проблемами с виду эксцентричными.
Абстрактное мышление ещё далеко от
полной зрелости. В подростковом возрасте лишь начинается интенсивное развитие
абстрактных понятий, но это развитие продолжается с ещё большей интенсивностью
в юношеском возрасте.
Как ни интенсивно развивается
мышление подростка, как ни сильно оно выходит за пределы личных восприятий,
ограниченных местом и временем, как ни активно оно проявляется по отношению к
памяти, всё же оно недостаточно широко и глубоко, ещё недостаточно всёсторонне.
На его мышлении лежит ещё тень не преодоленной метафизичности, и ему ещё не
хватает в должной мере диалектичности. Ему недостаёт ещё философского
диалектического мышления.
Мышление - одна из тех функций,
которые в онтогенезе (ранняя стадия развития), как и в филогенезе (более
позднее развитие), развиваются позднее ряда многих других функций. Влияние
школы на мышление, начинающееся с первого дня поступления ребёнка в школу,
особенно ярко выступает в подростковом возрасте. Ключом ко всем проблемам
развития мышления в переходном возрасте является тот установленный рядом
исследований факт, что подросток впервые овладевает процессом образования
понятий, что он переходит к новой и высшей форме интеллектуальной деятельности
- к мышлению в понятиях.
Это центральное явление всего
переходного возраста, и недооценка оттеснить на задний план изменения
интеллектуального характера по сравнению с эмоциональными и другими сторонами
кризиса, присущие большинству современных теорий переходного возраста,
объясняются в первую очередь тем, что образование понятий представляет собой в
вышей степени сложный процесс, отнюдь не аналогичный простому вызреванию
элементарных интеллектуальных функций, а потому не поддающийся внешнему
констатированию, грубому определению на глаз. Этот процесс знаменует собой
действительно революционные изменения как в области содержания, так и в области
форм мышления. Именно высшие формы мышления, в частности логическое мышление,
раскрываются в своём значении перед подростком.
Без мышления в понятиях нет
понимания отношений, лежащих за явлениями. Целый мир глубоких связей, лежащих
за внешней видимостью явлений, мир сложных взаимозависимостей и отношений
внутри каждой сферы действительности и между её отдельными сферами раскрывается
только перед тем, кто подходит к нему с ключом понятия.
Мир внутренних переживаний, закрытый
от ребёнка раннего возраста, сейчас раскрывается перед подростком и составляет
чрезвычайно важную сферу в содержании его мышления.
В соответствии с требованиями,
предъявляемыми современной школой, обучение в ней должно ориентироваться на
развитие продуктивного, творческого мышления, обеспечивающего возможность
самостоятельно приобретать новые знания, применять их в многообразных условиях
окружающей действительности.
Исследование процесса усвоения и
применения знаний показали, что обычно учащиеся усваивают содержательную
сторону знаний и непосредственно с ней связанные конкретные приемы решения
довольно узкого круга задач. Лишь у школьников с высокой обучаемостью на основе
решения единичных задач формируются обобщенные приемы, методы решения целого класса
задач. Формирование такого рода обобщенных приемов умственной деятельности
чрезвычайно важно, так как оно означает существенный сдвиг в интеллектуальном
развитии, расширяет возможности переноса знаний в относительно новые условия. В
соответствие с этим одним из принципов развития творческого, продуктивного
мышления является специальное формирование обобщенных приемов умственной
деятельности.
Обобщенные приемы умственной
деятельности делятся на две большие группы - приемы алгоритмического типа и
эвристические.
Остановимся сначала на
характеристике приемов алгоритмического типа.
Это приемы рационального,
правильного мышления, полностью соответствующего законам формальной логики.
Точное следование предписаниям, даваемым такими приемами, обеспечивает безошибочное
решение широкого класса задач, на который эти приемы непосредственно
рассчитаны. Вооружение учащихся правильными, рациональными приемами мышления,
обучение тому, как определять понятия, классифицировать их, строить
умозаключения, решать в соответствии с данным алгоритмом задачи, оказывает
положительное влияние и на самостоятельное, продуктивное мышление, обеспечивает
возможность решения задач-проблем.
Формирование приемов мыслительной
деятельности алгоритмического типа, ориентирующих на формально-логический
анализ задач, является необходимым, но не достаточным условием развития
мышления. Необходимо оно, во-первых, потому, что содействует совершенствованию
репродуктивного мышления, являющегося важным компонентом творческой
деятельности (особенно на начальном и конечном этапах решения проблем).
Во-вторых, эти приемы служат тем фондом знаний, из которых ученик может черпать
«строительный материал» для создания, конструирования методов решения новых для
него задач. Недостаточным формирование алгоритмических приемов является потому,
что не соответствует специфике продуктивного мышления, не стимулирует
интенсивное развитие именно этой стороны мыслительной деятельности.
Вот почему формирование таких
приемов должно сочетаться со специальным вооружением учащихся приемами
эвристического типа.
Приемы другого типа назвали
эвристическими потому, что они непосредственно стимулируют поиск решения новых
проблем, открытие новых проблем, открытие новых для субъекта знаний и тем самым
соответствуют самой природе, специфике творческого мышления. В отличие от
приемов алгоритмического типа, эвристические приемы ориентируют не на
формально-логический, а на содержательный анализ проблем. Они направляют мысль
учеников на проникновение в суть описываемого в условии предметного содержания,
на то, чтобы за каждым словом они видели его реальное содержание и по нему
судили о роли в решении того или иного данного. Многие эвристические приемы
стимулируют включение в процесс решения проблем наглядно-образного мышления,
что позволяет использовать его преимущество перед словесно логическим мышлением
- возможность целостного восприятия, видения всей описываемой в условии
ситуации. Тем самым облегчается течение характерных для продуктивного мышления
интуитивных процессов.
Следовательно, одним из принципов
развития мышления должно быть специальное формирование как алгоритмических, так
и эвристических приемов умственной деятельности. [12]
Итак, подведем итог по вопросу
психологических особенностей данного возраста. Вся история психического
развития в переходном возрасте состоит из этого перехода функций вверх и
образования самостоятельных высших синтезов. Различные функции не развиваются
рядом друг с другом, как пучок веток, поставленных в один сосуд; они
развиваются как связанные между собой общим стволом различные ветки единого
дерева. В процессе развития все эти функции образуют сложную иерархическую
систему, где центральной, или ведущей, функцией является развитие мышления,
функция образования понятий. Все остальные функции вступают в сложную
взаимосвязь с этим новым образованием и перестраиваются на основе мышления.
Глава 2. Условия внедрения
факультива «алгебраические числа» в практику общеобразовательной школы
§ 1. Содержание факультативного
курса «Алгебраические числа»
факультативный курс математический
алгебраический
Необходимо сделать одно замечание
общего характера. В основу данного курса положены общие методические установки,
разработанные Г.В. Дорофеевым [17]. Основные методические идеи Г.В.Дорофеева
были реализованы в учебном пособии [18], на которое мы серьезно опираемся и
считаем «образцом для подражания». Предлагаемый курс можно рассматривать как
расширение темы «Многочлены от одной переменной». К сожалению, за рамками курса
остались задачи на построение с помощью циркуля и линейки, хотя в упражнениях
есть несколько задач на эту тему и при желании вполне возможно более подробное
изложение соответствующего материала.
РАЗДЕЛ 1. ИСТОРИЯ РАЗВИТИЯ ЧИСЛОВЫХ
ПОНЯТИЙ
Мы приведем примерное содержание
данного раздела. По желанию учителя материал может быть дополнен и
скорректирован. В дальнейшем по ходу изложения основного содержания также будут
приведены исторические комментарии, отсутствующие в данном разделе. Заметим,
что используемый материал взят из книг по истории математики, содержащихся в
библиографии.
Центральным
математическим понятием является число. Отметим сразу, что многочлены, поля,
множества, функции тесно связаны с понятием числа. Впрочем, последнее замечание
относится практически к любому математическому понятию. Для нас точкой отсчета
является 1600 г. Наступление 16 в. в Западной Европе ознаменовалось важными
достижениями в алгебре и арифметике. Были введены в обращение десятичные дроби
и правила арифметических действий с ними. Настоящим триумфом стало изобретение
в 1614 логарифмов Дж. Непером. С начала 16 в. более широко стали употребляться
иррациональные числа. Б.Паскаль (1623-1662) и И. Барроу (1630-1677), учитель
Ньютона в Кембриджском университете, утверждали, что такое число, как 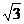 ,
можно трактовать лишь как геометрическую величину. Однако в те же годы Р.
Декарт (1596-1650) и Дж.Валлис (1616-1703) считали, что иррациональные числа
допустимы и сами по себе, без ссылок на геометрию. В это время продолжались
споры по поводу законности введения отрицательных чисел. Еще менее приемлемыми
считались возникавшие при решении квадратных уравнений комплексные числа, такие
как
,
можно трактовать лишь как геометрическую величину. Однако в те же годы Р.
Декарт (1596-1650) и Дж.Валлис (1616-1703) считали, что иррациональные числа
допустимы и сами по себе, без ссылок на геометрию. В это время продолжались
споры по поводу законности введения отрицательных чисел. Еще менее приемлемыми
считались возникавшие при решении квадратных уравнений комплексные числа, такие
как 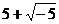 ,
названные Декартом «мнимыми». Эти числа были под подозрением даже в 18 в., хотя
великий российский математик (швейцарец по происхождению) Л.Эйлер (1707-1783) с
успехом пользовался ими.
,
названные Декартом «мнимыми». Эти числа были под подозрением даже в 18 в., хотя
великий российский математик (швейцарец по происхождению) Л.Эйлер (1707-1783) с
успехом пользовался ими.
Достижения в алгебре.
Решение задач,
сводящихся к частным видам уравнений 2-ой и 3-ей степени, можно найти еще в
древнем Вавилоне (2000 лет до н.э.). Первое изложение теории решения квадратных
уравнений дано в книге Диофанта «Арифметика» (3 в. н.э.). В 16 в. итальянские
математики Н. Тарталья (1499-1577), С. Дель Ферро (1465-1526), Л. Феррари (1522-1565)
и Дж. Кардано (1501-1576) нашли общие решения уравнений третьей и четвертой
степеней. Чтобы сделать алгебраические рассуждения и их запись более точными,
были введены символы: +, -, ×, ¤, 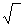 ,
=, < и другие. Самым существенным новшеством стало систематическое
использование французским математиком Ф. Виетом (1540-1603) букв для
обозначения неизвестных и постоянных величин. Это нововведение позволило ему
найти единый метод решения уравнений второй, третьей и четвертой степеней.
,
=, < и другие. Самым существенным новшеством стало систематическое
использование французским математиком Ф. Виетом (1540-1603) букв для
обозначения неизвестных и постоянных величин. Это нововведение позволило ему
найти единый метод решения уравнений второй, третьей и четвертой степеней.
Великий английский физик
и математик И.Ньютон (1643-1727) открыл соотношение между корнями и
дискриминантом [b2 - 4ac] квадратного уравнения, а именно, что уравнение ax2 +
bx + c = 0 имеет равные действительные, разные действительные или комплексно
сопряженные корни в зависимости оттого, будет ли дискриминант b2 - 4ac равен
нулю, больше или меньше нуля. В 1799 великий немецкий математик К.Гаусс
(1777-1855) доказал так называемую основную теорему алгебры: каждый многочлен
n-й степени с комплексными коэффициентами имеет ровно n комплексных корней.
В течение почти 300 лет
после открытия способов решения уравнений степени 3 и 4 делались безуспешные
попытки решить в радикалах уравнения степени 5 и выше с буквенными коэффициентами.
Такие попытки предпринимал великий немецкий математик Г. Лейбниц, но «бог
распорядился иначе». Только в 1826 г. норвежский математик Н. Абель (1802-1829)
доказал, что невозможно получить общее решение уравнения степени выше 4 с
помощью конечного числа указанных операций. Это, правда, не исключало, что
корни каждого конкретного уравнения с числовыми (а не буквенными)
коэффициентами могут быть выражены в радикалах. Тем более, что существует много
уравнений специального вида степени выше 4, допускающих такое решение.
Накануне своей гибели на
дуэли французский математик Э. Галуа (1811-1832) дал решающий ответ на вопрос о
том, какие уравнения разрешимы в радикалах. В теории Галуа использовались
перестановки корней и было введено понятие группы, которое нашло широкое
применение во многих областях математики. Примером уравнения неразрешимого в
радикалах является уравнение x5 - 25x - 5 = 0. Нельзя не отметить
теоретико-групповые и теоретико-полевые идеи и результаты великого французского
математика Ж. Лагранжа (1736-1813), приблизившие решение проблемы разрешимости
уравнений в радикалах. Кстати, весьма близок к решению проблемы был и Абель,
которого сразила смерть в 1829 году, когда он интенсивно занимался этой
проблемой и сообщил Лежандру свои результаты, уж очень близкие к результатам
Галуа. Дальнейшее развитие возникших идей привело к созданию теорий групп,
колец и полей - важнейших направлений современной алгебры.
Заметим, что
разрешимость уравнений в радикалах тесно связана с вопросом о геометрических
построениях с помощью циркуля и линейки, в частности, задача о построении
правильного n-угольника. Эта задача в полном объеме была решена Гауссом, при
этом потребовалось изучить корни n-ой степени из единицы в поле комплексных
чисел.
Аналитическая геометрия.
Аналитическая или
координатная геометрия была создана независимо видными французкими математиками
П. Ферма (1601-1665) и Р. Декартом для того, чтобы расширить возможности
евклидовой геометрии в задачах на построение. Однако Ферма рассматривал свои работы
лишь как переформулировку сочинения Аполлония. Подлинное открытие - осознание
всей мощи алгебраических методов - принадлежит Декарту. Декарт решил эту
проблему: он формулировал геометрические задачи алгебраически, решал
алгебраическое уравнение и лишь затем строил искомое решение - отрезок, имевший
соответствующую длину. Собственно аналитическая геометрия возникла, когда
Декарт начал рассматривать неопределенные задачи на построение, решениями
которых является не одна, а множество возможных длин.
Аналитическая геометрия
использует алгебраические уравнения для представления и исследования кривых и
поверхностей. Декарт считал приемлемой кривую, которую можно записать с помощью
единственного алгебраического уравнения относительно х и у.
Аналитическая геометрия
полностью поменяла ролями геометрию и алгебру. Как заметил Лагранж, «пока
алгебра и геометрия двигались каждая своим путем, их прогресс был медленным, а
приложения ограниченными. Но когда эти науки объединили свои усилия, они
позаимствовали друг у друга новые жизненные силы и с тех пор быстрыми шагами
направились к совершенству». Следует отметить, что идея введения координат и
проблемы, связанные с решением диофантовых уравнений, привели к открытию
алгебраической геометрии - одного из важных разделов современной математики.
Основания математики.
Примерно до 1870
математики пребывали в убеждении, что действуют по предначертаниям древних
греков, применяя дедуктивные рассуждения к математическим аксиомам, тем самым,
обеспечивая своими заключениями не меньшую надежность, чем та, которой обладали
аксиомы. Одним из недостатков евклидовых Начал было использование допущений, не
сформулированных в явном виде. По-видимому, Евклид не подвергал сомнению те
свойства, которыми обладали его геометрические фигуры, но эти свойства не были
включены в его аксиомы. Кроме того, доказывая подобие двух треугольников,
Евклид воспользовался наложением одного треугольника на другой, неявно
предполагая, что при движении свойства фигур не изменяются. Но кроме таких
логических пробелов, в Началах оказалось и несколько ошибочных доказательств.
Задача усиления строгости формулировок евклидовой геометрии была сравнительно
простой и сводилась к перечислению определяемых терминов, уточнению
определений, введению недостающих аксиом и восполнению пробелов в
доказательствах. Эту задачу выполнил в 1899 г. великий немецкий математик
Д.Гильберт (1862-1943). Почти в то же время были заложены и основы других
геометрий. Гильберт сформулировал концепцию формальной аксиоматики. Одна из
особенностей предложенного им подхода - трактовка неопределяемых терминов: под
ними можно подразумевать любые объекты, удовлетворяющие аксиомам. Следствием
этой особенности явилась возрастающая абстрактность современной математики.
Евклидова и неевклидова геометрии описывают физическое пространство. Но в
топологии, являющейся обобщением геометрии, неопределяемый термин «точка» может
быть свободен от геометрических ассоциаций. Для тополога точкой может быть
функция или последовательность чисел, равно как и что-нибудь другое.
Абстрактное пространство представляет собой множество таких «точек».
Аксиоматический метод
Гильберта вошел почти во все разделы математики 20 в. Однако вскоре стало ясно,
что этому методу присущи определенные ограничения. В 1880-х Кантор попытался систематически
классифицировать бесконечные множества (например, множество всех рациональных
чисел, множество действительных чисел и т.д.) путем их сравнительной
количественной оценки - мощности множества (трансфинитные числа). При этом был
обнаружен ряд парадоксов в теории множеств. Таким образом, к началу 20 в.
математикам пришлось иметь дело с проблемой их разрешения, а также с другими
проблемами оснований математики, такими, как неявное использование аксиомы
выбора; ряд сомнений вызывал и закон исключенного третьего (или доказательство
от противного). Однако ничто не могло сравниться с разрушительным воздействием
теоремы неполноты, доказанной великим К.Гёделем (1906-1978). Эта теорема
утверждает, что любая непротиворечивая формальная система, использующая
аксиоматику натурального ряда, обязательно содержит неразрешимое предложение,
т.е. утверждение, которое невозможно ни доказать, ни опровергнуть в рамках
формальной системы. Тем самым, было доказано, что абсолютного доказательства в
математике не существует. Относительно того, что такое доказательство, мнения
расходятся. Однако большинство математиков склонно полагать, что проблемы
оснований математики являются философскими. Действительно, ни одна теорема не
изменилась вследствие открытых формальных логических структур; это показывает,
что в основе математики лежит не формальная логика, а здравая интуиция.
Если математику,
известную до 1600 г., можно охарактеризовать как элементарную, то по сравнению
с тем, что было создано позднее, элементарная математика бесконечно мала.
Расширились старые области и появились новые, как чистые, так и прикладные
отрасли математических знаний. Выходят около 500 математических журналов.
Огромное количество публикуемых результатов не позволяет даже специалисту
ознакомиться со всем, что происходит в той области, в которой он работает, не
говоря уже о том, что многие результаты доступны пониманию только специалистами
узкого профиля. Ни один математик сегодня не может надеяться знать больше того,
что происходит в очень маленьком уголке науки. Однако это вовсе не означает,
что следует заниматься только узким разделом математики. Математика едина по
своей сути, ее идеи проникают из одной области в другую. Многие результаты и
направления математических исследований вызваны непосредственными потребностями
других наук.
РАЗДЕЛ 2. СИММЕТРИЧЕСКИЕ
МНОГОЧЛЕНЫ
Тема 2.1. Первичные
понятие и простейшие свойства.
Из основного курса вам
известны понятия одночлена и многочлена от нескольких переменных. Вы знакомы
также с понятием степени и знаете ее свойства: при умножении многочленов
степени складываются, при сложении многочленов степень не может увеличиться,
она может уменьшиться.
. Старшие члены
многочленов. Далее, одночлены одной степени можно сравнивать, сравнивая их
наборы показателей, например, набор (2, 3, 5) больше, чем набор (2, 3, 4),
поэтому мы считаем, что одночлен 7x2y3z5 больше одночлена 12x2y3z4. Сравнивая
одночлены, мы сравниваем только показатели сначала по первой переменной (в
данном случае по x), потом по второй переменной (это y), затем по следующей
переменной (это z). Коэффициенты при одночленах, в данном случае - это числа 7
и 12, мы никак не сравниваем.
Определение. Среди
одночленов, входящих в многочлен, имеется самый большой в указанном выше
смысле, он называется старшим членом многочлена.
Легко сообразить, что
при умножении старших членов получается старший член произведения многочленов.
Поскольку при сложении многочленов не могут появиться новые одночлены, то
старший член суммы не больше старшего члена одного из слагаемых.
. Понятие
симметрического многочлена.
Определение. Многочлен ƒ
(от нескольких переменных) называется симметрическим, если он не меняется при
любом переименовании переменных.
Рассмотрим всевозможные
переименования переменных.
Для двух переменных x и
y возможно только одно переименование: → y, y → x, которое
обозначим через (12).
Три переменные (x, y,
z): x → y, y → z, z → x (его обозначим через (123));
аналогично вводятся
переименования
(12) x → y, y →
x, z → z; (13) x → z, z → x, y →
y;
(23) x → x, y →
z, z → y; (132) x → z, z → y, y →
x и т.д.
Приведем пример
симметрического многочлена: ƒ = x2 + y2. Это
многочлен от двух переменных, поэтому рассмотрим единственное возможное
переименование переменных (12): (x2 + y2)(12) = y2 + x2 = ƒ.
Следовательно, ƒ симметричен. Но следует заметить, что он несимметричен для
переименования (23), так как (x2 + y2)(23) = y2 + z2, следовательно, данный
многочлен не является симметрическим от трех переменных.
Для дальнейшего изучения
данной темы нам потребуются два утверждения, которые мы с вами примем без
доказательства.
Критерий симметричности
многочлена. Многочлен ƒ от n переменных симметричен тогда и только тогда, когда он не
меняется при следующих двух переименованиях переменных (12) и (12…n).
Таким образом, проверять
надо только два переименования переменных, а не n! («эн» факториал)
переименований, указанных в определении симметрического многочлена. Напомним,
что факториал n! определяется как произведение чисел от 1 до n!
В частности, для
проверки симметричности многочлена ƒ
от 3 переменных нам надо проверить меняется ли он при переименованиях (12) и
(123).
Теорема. Сумма, разность
и произведение симметрических многочленов являются симметрическими
многочленами.
. Элементарные
симметрические многочлены.
Важными примерами
симметрических многочленов служат элементарные симметрические многочлены.
Приведем их для некоторых наборов переменных.
Для двух переменных (x,
y) существует два элементарных симметрических многочлена:
j1 = x + y (сумма
переменных);
j2 = xy (произведение
переменных);
. Для трех переменных
существует три элементарных симметрических многочлена:
j1 = x + y + z (сумма
переменных)
j2 = xy + xz + yz (сумма
произведений двух различных переменных)
j3 = xyz (произведение
трех переменных)
Для четырех переменных
существует четыре элементарных симметричных многочлена:
j1 = x + y + z + t (сумма
переменных)
j2 = xy + xz + xt + yz +
yt + zt (сумма произведений по два)
j3 = xyz + xzt + yzt +
xyt (сумма произведений по три)
j4 = xyzt (произведение
всех переменных)
Приведем два утверждения
о строении старших членов симметрических многочленов.
Лемма 1. Показатели
степеней старшего члена симметрического многочлена расположены в невозрастающем
порядке.
Докажем это утверждение
для 3 переменных: x, y, z; общий случай рассматривается точно также. Пусть u -
старший член; u = axiyjzk, где a - число, i, j, k - показатели степеней.
Необходимо проверить, что i ≥ j ≥ k. Допустим от противного, что
i<j. Тогда, так как f - симметричный многочлен, то f = f(12), значит, среди
одночленов, входящих в его состав, содержится одночлен: (axiyjzk)(12) =
axjyizk. Поскольку по предположению i<j, то одночлен axjyizk будет больше
старшего члена, и это противоречит определению. Следовательно, i ≥ j.
Аналогично проверяется неравенство j ≥ k. ÿ
Лемма 2. Каждый одночлен
от элементарных симметрических многочленов однозначно определяется своим
старшим членом.
Доказательство
рассмотрим на примере. Пусть дан j-одночлен S = aj1ij2jj3k,
т.е. одночлен от элементарных симметрических, зависящих от трех переменных x,
y, z (a - произвольное число, отличное от нуля). Для того чтобы найти его
старший член необходимо перемножить старшие члены элементарных симметрических
многочленов. Ясно, что старший член j1 равен x, старший член j2
равен xy, старший член j3 - это xyz. Следовательно, старший член многочлена aj1ij2
jj3k
имеет вид(xy) j(xyz)k = axi+j+k y j+k zk.
Заметим, что если
известен старший член u для j-одночлена S = aj1ij2jj3k, то можно найти числа a, i, j, k. Например, если u = 2x5y4z3,
то a = 2,+ j + k = 5, j + k = 4, k = 3,
значит, i = j = k = 1.
Тема 2.2. Основные
теоремы о симметрических многочленах.
. Представление
симметрического многочлена через элементарные.
Основная теорема. Всякий
симметричный многочлен единственным образом можно представить в виде многочлена
от элементарных симметрических.
Доказательство приведем
на конкретном примере, рассматривая симметрический многочлен f = x3 + y3 + z3.
Представление f в виде многочлена от элементарных симметрических оформим в виде
алгоритма:
Шаг 0. Вводим начальный
многочлен f0 = f, и находим его старший член - это x3. Используя лемму 2,
восстанавливаем по старшему члену соответствующий одночлен от элементарных
симметрических, в данном случае получаем s0 = φ13. Отметим
еще раз, что многочлены f0 и s0 имеют одинаковые старшие члены.
Шаг 1. Полагаем f1 = f0
- s0: = f - s0 = x3 + y3 + z3 - (x + y + z)3 = - 3(x2y + y2x + …) - 6xyz.
В последней скобке стоят
одночлены указанного вида от трех переменных; коэффициенты определяются по
формуле «куба суммы».
Далее, находим старший
член f1 - это одночлен -3x2y; и восстанавливаем по нему одночлен s1 от
элементарных симметрических: s1 = -3φ1φ2. Отметим,
что старшие члены многочленов f1 и s1 совпадают.
Шаг 2. Положим f2 =
f - s1 = - 3(x2y + y2x + …) - 6xyz + 3φ1φ2 =
= - 3(x2y + y2x + …) -
6xyz + 3(x + y + z)(xy + yz + zx) =
= (-6 + 9)xyz = 3xyz =
3φ3.
В общем случае указанный
алгоритм выдает две конечные последовательности многочленов: f0, f1, f2, … (в
нашем случае f0, f1, f2), s0, s1, s2, … (в нашем случае s0, s1). В нашем случае
f2 = 3φ3, процесс закончился на шаге 2, когда мы получили одночлен от
элементарных симметрических. Положим s3 = 3φ3, и
запишем систему равенств f0 = f,f1 = f0 - s0, f2 = f1 - s1, s2 = f2. Складывая
почленно полученные равенства, получаем s2 = f - s0 - s1, откуда находим f = s0
+ s1 + s1. Значит, f - сумма j-одночленов и в нашем случае f =j13 - 2j1j2 +
3φ3. ÿ
. Метод неопределенных
коэффициентов. Из доказательства основной теоремы вытекает
Следствие. Всякий
симметрический многочлен f представим в виде многочлена g от элементарных
симметрических, причем коэффициенты g являются целыми числами, если целыми
числами были коэффициенты многочлена f.
Отметим без
доказательства, что многочлен g, о котором идем речь в последнем утверждении
находится по многочлену f однозначно. На этом замечании основан еще один способ
представления симметрического многочлена через элементарные симметрические,
называемый методом неопределенных коэффициентов. Этот метод является более
эффективным при решении задач.
Проиллюстрируем его на
примере многочлена f = x3 + y3 + z3. Так как наш многочлен содержит 3
переменные, то давайте распишем вектор-показателей (в данном случае тройку
чисел), который отвечает показателям старшего члена при переменных x, y, z. Он
имеет вид (3,0,0) (при x - степень 3, при y - 0, при z - 0).
Согласно алгоритму,
указанному в основной теореме, на каждом шаге происходит уменьшение вектора
показателей степеней у старшего члена. Выпишем тройки чисел показателей для
всевозможных старших членов, заметив, что их компоненты располагаются в
невозрастающем порядке согласно лемме 1:
(3,0,0) - соответствует
старшему члену x3
(2,1,0) - соответствует
старшему члену x2y
(1,1,1) - соответствует
старшему члену xyz
Для каждой из троек
приведем соответствующие φ-одночлены (т.е. одночлены от элементарных симметрических
многочленов):
(3,0,0) → φ13
(2,1,0) → φ1φ2
(1,1,1) → φ3
Значит, многочлен f
можно представить в виде f = aφ13 + bφ1φ2 + cφ3, где
a,b,c - некоторые числа. Их нам надо найти.
Для того, чтобы их
отыскать надо поступить так: присвоить какие-нибудь значения переменным x, y, z
и посчитать в этой точке значения многочленов f, φ1, φ2,
φ3.
Тем самым, каждый раз
возникает линейное уравнение на числа a, b, c. Взяв необходимое число различных
точек, и решив соответствующую систему линейных уравнений, найдем a, b, c. Для
простоты вычислений точки надо выбирать так, чтобы в них было по возможности
больше нулей, и при подстановке в наше равенство получилось бы уравнение
относительно одной неизвестной. Обычно берут точки
(1,0,0), (1,1,0),
(1,1,1).
Рассмотрим точку t =
(1,0,0) и вычислим f(t) = 1, φ1(t) = 1,
φ2(t) = 0, φ3(t) = 0. Подставляя
найденные значения в равенство f = aφ13 + bφ1φ2 +
cφ3, получаем 1 = a·1, a=1, следовательно, f = φ13
+ bφ1φ2 + cφ3. Точка t = (1,1,0) приводит к
значениям(t) = 2, φ1(t) = 2, φ2(t) = 1,
φ3(t) = 0,
следовательно, после
подстановки в равенство f = φ13 + bφ1φ2 + cφ3, получаем
= 23 + 2b, b откуда = -
3, значит,
f = φ13 -
3φ1φ2 + cφ3.
Теперь считаем значения
в точке t = (1,1,1):(t) = 3, φ1(t) = 3,
φ2(t) = 3, φ3 t) = 1,
значит, 3 = 33 - 3×3×3
+ c, c = 3. Итак, f = φ13 - 3φ1φ2 + 3φ3.
Тема 2.3. Некоторые
применения основной теоремы.
. Симметрические дроби.
Определение. Дробь вида
f/g, где f, g - многочлены от нескольких переменных называется симметрической,
если она не меняется при любых переименованиях переменных.
Нетрудно понять, что
симметричность дроби не зависит от формы ее записи. Умножая числитель и
знаменатель на подходящий многочлен, можно добиться, что знаменатель станет
симметрическим многочленом, но тогда и числитель, очевидно, будет
симметрическим многочленом. Отсюда на основании основной теоремы получаем
следующий результат.
Теорема. Всякая
симметрическая дробь представима в виде отношения двух многочленов, каждый из
которых является многочленом от элементарных симметрических многочленов.
. Симметричные
многочлены по наборам переменных.
Определение. Пусть
у нас есть два набора переменных:= (x1, x2,…, xn) и y = (y1, y2,…, ys).
Многочлен f = f(x1,…,
xn, y1,…,ys) называется симметрическим по этим наборам, если он не меняется при
любых переименованиям, как переменных x, так и y (то есть он симметричен по
каждому набору отдельно).
Введем обозначения: φ1,…,φn
- элементарные симметрические от переменных x, ψ1,…,ψs
- элементарные симметрические от переменных y.
Теорема 2. Всякий
многочлен f(x1,…, xn, y1,…,ys) симметричный по двум наборам переменных
представим в виде многочлена от элементарных симметрических φ1,…,φn,
ψ1,…,ψs.
Доказательство. Запишем
f(x, y) в виде многочлена g(y); коэффициенты g - это многочлены hi(x) от набора
x. Ясно, hi(x) - симметрические многочлены от x, а g - симметрический многочлен
от y. Многочлен g по основной теореме представлен в виде многочлена от
элементарных симметрических ψ1,…,ψs, причем
его коэффициенты являются суммой многочленов hi(x), и значит, являются
многочленами от элементарных симметрических φ1,…, φn. Тем
самым, получено представление исходного многочлена через φ
и ψ. ÿ
. Формулы Виета. Вы
знаете формулы Виета для квадратного многочлена. Оказывается аналогичные формулы
справедливы для произвольного многочлена.
Возьмем для
определенности кубический многочлен f = a0x3 + a1x2 + a2x + a3. Допустим, нам
известны корни многочлена f; пусть это будут числа γ1,
γ2, γ3. Тогда по теореме Безу верно равенство: f(x) = a0(x - γ1)(x
- γ2)(x - γ3). Сравнивая коэффициента при одинаковых степенях x, получаем
a1 = - a0φ1(γ),
φ1(γ) = - a1/a0,= a0φ2(γ), φ2(γ) = a2/a0,= -
a0φ3(γ), φ3(γ) = - a3/a0.
Формулы для вычисления
значений элементарных симметрических многочленов от корней данного многочлена
называются формулами Виета. Для кубического многочлена они имеют вид φ1(γ)
= - a1/a0, φ2(γ) = a2/a0, φ3(γ)
= - a3/a0. Если коэффициенты многочлена a0x3 + a1x2 + a2x + a3
положительны, то в этих формулах знаки чередуются.
РАЗДЕЛ 3. АЛГЕБРАИЧЕСКИЕ
ЧИСЛА
Тема 3.1. Числовые поля.
С первого класса вы
изучаете различные числа, начиная с натуральных чисел и заканчивая
действительными числами. Напомним основные классы чисел.
. Основные числовые
системы.
а) Натуральные числа -
это числа, употребляемые для счета. Множество натуральных чисел обозначается
через Ν, значит, Ν = {1, 2, 3, …}.
б) Целые число - это
натуральные числа, нули и числа, противоположные натуральным. Множество целых
чисел обозначается через Z, т.е. Z = {0, 1, -1, 2, -2, …}.
в) Рациональные числа -
это отношения целых чисел, т.е. числа вида m/n, где mÎZ,
nÎN.
Каждое рациональное число может быть представлено в виде конечной десятичной
дроби или бесконечной периодической. Верно и обратное, каждая такая дробь
является рациональным числом. Такое представление неоднозначно, например, 1,(9)
= 2,(0) = 2. Множество рациональных чисел обозначается через Q.
г) Действительные числа
- можно определить как бесконечные десятичные дроби. Множество действительных
чисел обозначается через R. Каждое действительное число можно изобразить точкой
на прямой (такая прямая называется числовой осью).
д) Иррациональные числа
- это действительные числа, которые не являются рациональными. Для этого
множества будем использовать букву I. Известно, что каждое иррациональное число
однозначно представимо в виде бесконечной десятичной дроби.
Примеры: 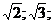 0,010010001…
(число нулей между соседними единицами неограниченно увеличивается).
0,010010001…
(число нулей между соседними единицами неограниченно увеличивается).
е) Комплексные числа -
обозначается множество комплексных чисел через C. Для вас это новое числовое
множество, поэтому необходимы соответствующие определения.
. Действия над
комплексными числами. Комплексные числа можно определять как точки на
координатной плоскости или пары действительных чисел. Сложение и умножение пар
определяется правилами:
(a, b) + (c, d) = (a +
c, b + d), (a, b)×(c, d) = (ac - bd, ad + bc).
Сложение пар определено
покоординатно, а умножение существенно более сложным образом (его смысл будет
ясен чуть позже). Отметим, что вычитание и деление можно вводить обычным
образом, как решения соответствующих уравнений:+ x = t, zx = t (z ¹
0)
где z и t данные
комплексные числа, x - неизвестное. Можно доказать, что указанные уравнения
имеют единственные решения. Кроме того, отметим, что арифметические действия
обладают известными для действительных чисел свойствами, в частности, можно по
обычным правилам преобразовывать дробные выражения.
Существенным отличием от
действительных чисел является невозможность ввести на C порядок так, чтобы были
выполнены основные свойства неравенств, в частности, почленное умножение
неравенств.
. Алгебраическая форма.
Пусть i = (0;1) и называется мнимой единицей. Любое комплексное число
представимо в виде z = a + bi, где a, b Î R, i - мнимая единица
(i2 = - 1). Это алгебраическая форма комплексного числа z. Записывая пары в
алгебраической форме, раскрывая по обычным правилам скобки, приводя подобные
члены и используя равенство i2 = - 1, получим указанные выше определения
действий сложения и умножения. В самом деле, (a, b)×(c,
d) = (a + bi)(c + di) = ac + adi + bci + bdi2 = ac + adi + bci - bd = (ac - bd)
+ (ad + bc)i = (ac - bd, ad + bc).
. Тригонометрическая
форма. Каждое комплексное число a + bi изобра-жается точкой (a, b) на
плоскости. Вместо этой пары можно рассматривать другую пару действительных
чисел, задающих ту же точку.

Проведем радиус-вектор в точку (a,
b), пусть φ - угол
между направлением оси 0x и данным радиус вектором, r - длина радиус-вектора.
Тогда число a + bi можем
описать парой чисел (r, φ). При этом φ называется аргументом комплексного числа, а r
- его модулем. Из прямоугольного треугольника имеем r2
= a2 + b2 (теорема Пифагора), значит, 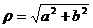 . Кроме того, используя
понятия синуса и косинуса, получаем a = r cosφ, b = r
sinφ. Тогда число z = a + bi представимо в виде: z = r
(cosφ + sinφ). Указанное представление называется тригонометрической формой числа
z. Отметим, что модуль числа находится однозначно, а аргумент с точностью до слагаемых
вида 2pn,
n - любое целое число.
. Кроме того, используя
понятия синуса и косинуса, получаем a = r cosφ, b = r
sinφ. Тогда число z = a + bi представимо в виде: z = r
(cosφ + sinφ). Указанное представление называется тригонометрической формой числа
z. Отметим, что модуль числа находится однозначно, а аргумент с точностью до слагаемых
вида 2pn,
n - любое целое число.
. Теорема Гаусса.
В множестве C
комплексных чисел мы можем вычислить корень из отрицательного числа, и вообще
корень любой натуральной степени. Всякое уравнение xn = z имеет ровно n корней.
Более того, справедлива
Теорема Гаусса. Всякий
многочлен n-ой степени с комплексными коэффициентами имеет ровно n комплексных
корней.
В частности, можно
разложить на множители сумму квадратов действительных чисел, правда,
сомножители при этом оказываются комплексными:+ b2 = (a + bi)(a - bi).
Определение. Числа a +
bi и a - bi называются комплексно сопряженными.
При этом пишут 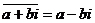 .
Перечислим свойства комплексного сопряжения:
.
Перечислим свойства комплексного сопряжения:
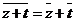 ;
; 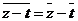 ;
;
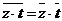 ;
;
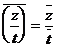 .
.
. Расположение числовых
систем. Изобразим рассмотренные выше числовые системы на диаграмме:
Эта схема характеризует
расширение понятия числа - центрального понятия во всей математике.
Подведем некоторый итог.
Итак, многочлен с рациональными коэффициентами степени n имеет ровно n корней.
Среди корней многочленов могут быть иррациональные и действительные числа.
Может случиться, что все корни будут комплексными числами.
Тема 3.2. Алгебраические
числа.
. Понятие поля.
Естественный и важный подход к выделению и изучению тех или иных множеств чисел
связан с замкнутостью множеств чисел относительно тех или иных действий.
Определение. Множество
чисел М называется замкнутым относительно некоторого действия, если для всяких
двух чисел М, для которых определен результат данного действия, число,
являющееся этим результатом, принадлежащим М.
Примеры. Множество
натуральных чисел N замкнуто относительно сложения, т.е. результат сложения
двух натуральных чисел является всегда числом натуральным. В отношении
умножения множество N так же замкнуто. Множество целых чисел Z замкнуто
относительно сложения, вычитания и умножения.
Определение. Множество
чисел k, содержащие не менее двух чисел, называется полем, если оно замкнуто
относительно действий сложения, вычитания, умножения и деления (конечно, при
условии, что знаменатель отличен от нуля).
Последнее означает, что
для любых двух чисел из множества k результаты действий a + b, a - b, a ×
b, a: b также принадлежат множеству k.
. Примеры полей. Среди
важнейших числовых полей наиболее важными являются:
поле рациональных чисел;
поле вещественных чисел;
поле комплексных чисел.
Что касается множества
всех целых чисел, то оно не является кольцом, т.е. замкнуто относительно
сложения, вычитания и умножения. Примерами нечисловых колец являются многочлены
от одной или нескольких переменных, симметрические многочлены. Примером
нечислового поля служит множество симметрических дробно - рациональных функций,
т.е. отношения симметрических многочленов.
Существует бесконечно
много числовых полей. Например, множество всех чисел вида 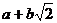 ,
где a, b - рациональны, - является полем. Заменяя
,
где a, b - рациональны, - является полем. Заменяя 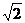 на
другую квадратичную рациональность - корень квадратного трехчлена с
рациональными коэффициентами, получим новые поля.
на
другую квадратичную рациональность - корень квадратного трехчлена с
рациональными коэффициентами, получим новые поля.
С точки зрения важного
для алгебры понятия алгебраического уравнения, естественным представляется
рассмотрение чисел, являющихся корнями алгебраических уравнений, коэффициенты
которых принадлежат заданному полю.
. Понятие
алгебраического числа.
Определение. Комплексное
число называется алгебраическим, если оно является корнем некоторого многочлена
с рациональными (или целыми) коэффициентами.
Определение.
Неалгебраическое число называется также трансцендентным.
Примерами
трансцендентных чисел являются числа p (отношение длины
окружности к ее диаметру) и e (основание натуральных логарифмов).
Трансцендентных чисел больше, чем алгебраических, однако доказательство
трансцендентности конкретного числа - трудная математическая задача.
. Простейшие свойства
алгебраических чисел.
Каждое рациональное
число a является алгебраическим, так как оно является корнем многочлена x - a с
рациональными коэффициентами.
Если a - положительное
рациональное число, то  являются
алгебраическим, как корни многочленов x2 - a, x3 - a. Можно доказать, что
корень n-ой степени из алгебраического числа является алгебраическим числом.
являются
алгебраическим, как корни многочленов x2 - a, x3 - a. Можно доказать, что
корень n-ой степени из алгебраического числа является алгебраическим числом.
Сумма алгебраического
числа γ и рационального числа a является алгебраическим числом.
Число, противоположное к
алгебраическому, является алгебраическим. Действительно, если γ
- корень многочлена c0xn + c1xn - 1 + … + cn, то - γ
- корень многочлена c0xn - c1xn - 1 + … + (- 1)ncn (знаки многочлена
чередуются).
Число, обратное к
алгебраическому, является алгебраическим. Действительно, если γ
- ненулевой корень многочлена c0xn + c1xn - 1 + … + cn, то γ
- 1 - корень многочлена c0 + c1x + … + cnxn.
. Степень
алгебраического числа.
Определение. Число n
называется степенью алгебраического числа γ, если
γ - корень некоторого многочлена n-ой степени с рациональными
коэффициентами и не существует ненулевого многочлена с рациональными
коэффициентами степени, меньшей чем n, корнем которого является γ.
Рациональные числа
являются алгебраическими числами первой степени. Любая квадратичная иррациональность
представляет собой алгебраическое число второй степени, так как, являясь корнем
квадратичного уравнения с целыми коэффициентами, она не является корнем какого
- либо линейного уравнения с целыми коэффициентами. Алгебраические числа
степени 3 часто называют кубическими иррациональностями, а степени 4 -
биквадратичными иррациональностями.
Пример. 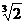 -
алгебраическое число степени 3.
-
алгебраическое число степени 3.
Действительно, это число
есть корень уравнения третьей степени с целыми коэффициентами x3 - 2 = 0 и 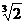 не
является корнем никакого многочлена первой или второй степени с целыми
коэффициентами. Последнее утверждение нуждается в более строгом обосновании.
Для этой цели нам потребуется определение минимального многочлена
алгебраического числа.
не
является корнем никакого многочлена первой или второй степени с целыми
коэффициентами. Последнее утверждение нуждается в более строгом обосновании.
Для этой цели нам потребуется определение минимального многочлена
алгебраического числа.
. Минимальный многочлен
алгебраического числа.
Определение. Пусть γ
- алгебраическое число. Многочлен μ(x) с
рациональными коэффициентами называется минимальным многочленом числа γ,
если выполнены два условия:
- μ(x) неприводим,
т.е. его нельзя представить в виде произведения многочленов положительной
степени;
- μ(γ) = 0, т.е.
γ - его корень.
Обычно, минимальным
многочленом числа γ называется многочлен наименьшей степени с рациональными
коэффициентами и старшим коэффициентом 1, корнем которого является γ.
Условие на старший коэффициент позволяет однозначно определить
минимальный многочлен для каждого алгебраического числа.
Важнейшее свойство
минимального многочлена числа γ - он является
делителем любого многочлена, корнем которого служит число γ.
Отсюда вытекает, что неприводимый многочлен, корнем которого
является число γ, совпадает с минимальным. Учитывая, что многочлен x3 - 2
неприводим, получаем, что он минимальный для числа 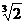 .
.
Отметим также, что
степень алгебраического числа совпадает со степенью его минимального
многочлена.
. Поле алгебраических
чисел.
Теорема. Множество A
всех комплексных алгебраических чисел является полем, т.е. сумма, разность,
произведение и частное двух алгебраических чисел a и b
(для частного b ¹ 0) являются алгебраическими числами.
Приведем доказательство
этого факта по двум причинам. Во-первых, оно совершенно не очевидно. Даже в
простом случае суммы нескольких квадратных корней достаточно трудно найти
минимальный многочлен для их суммы. Пусть, например,
g = a
+ b,
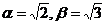 .
Тогда
.
Тогда 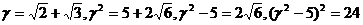 ,
т.е. g
является корнем многочлена (x2 - 5)2 - 24 = x4 - 10 x2 + 1. Это означает, что
число g
является алгебраическим.
,
т.е. g
является корнем многочлена (x2 - 5)2 - 24 = x4 - 10 x2 + 1. Это означает, что
число g
является алгебраическим.
Во-вторых, оно
совершенно отличается от традиционных тривиальных доказательств алгебраических
утверждений.
Доказательство разобьем
на три пункта.
. Если g
- алгебраическое число, то числа - g, g
- 1 также алгебраические.
Это утверждение было
доказано ранее при обсуждении простейших примеров алгебраических чисел.
. Сумма алгебраических
чисел является алгебраическим числом.
Пусть a
и b
- алгебраические числа; f и g - их минимальные многочлены;
a1 = a,
a2,...,
an
- все корни многочлена f (числа сопряженные к a),
b1 = b,
b2,...,
bs
- все числа сопряженные к b.
Рассмотрим многочлен 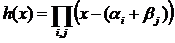 .
Коэффициенты этого многочлена не меняются при произвольной перестановке чисел a1,...,
a
n, аналогично, они не меняются при произвольной перестановке чисел b1,...,
bs,
следовательно, они являются симметрическими многочленами над Q относительно
указанных наборов переменных, но тогда по теореме Виета указанные числа
рациональны. Итак, коэффициенты многочлена h(x) рациональны. Наконец, a
+ b
- корень h(x).
.
Коэффициенты этого многочлена не меняются при произвольной перестановке чисел a1,...,
a
n, аналогично, они не меняются при произвольной перестановке чисел b1,...,
bs,
следовательно, они являются симметрическими многочленами над Q относительно
указанных наборов переменных, но тогда по теореме Виета указанные числа
рациональны. Итак, коэффициенты многочлена h(x) рациональны. Наконец, a
+ b
- корень h(x).
. Произведение
алгебраических чисел является алгебраическим числом.
Достаточно повторить
прежние рассуждения для многочлена 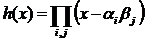 . Тем самым, теорема
доказана. ÿ
. Тем самым, теорема
доказана. ÿ
Определение. Поле L
называется алгебраически замкнутым, если всякий многочлен над L разлагается на
линейные множители.
По теореме Гаусса поле C
является алгебраически замкнутым.
Теорема. Поле A является
алгебраически замкнутым.
Иначе этот результат
можно сформулировать так: всякий корень многочлена с алгебраическими
коэффициентами сам является алгебраическим числом.
Доказательство. Пусть c
- корень многочлена f(x) = x5 + ax4 +bx3
+ gx2+
lx
+ m
с алгебраическими коэффициентами a, b,
g,
l,
m.
Числа, сопряженные к коэффициентам исходного многочлена a,
b,
g,
l,
m.,
обозначим теми же буквами с соответствующими индексами, причем a1=a,
b1=b,
g1=g,
l1=l,
m1=m.
Введем многочлены ,j,k,l,m(x) = x5 + aix4 + bjx3
+ gkx2
+ llx
+ mm
и рассмотрим их
произведение F(x). Заметим, что коэффициенты многочлена F(x) являются
симметрическими многочленами относительно каждого из наборов переменных
a1, a2,...;
b1,
b2,...;
g1,
g2,...;
l1,
l2,...;
m1,
m2,....
Следовательно, по
теореме Виета коэффициенты многочлена F(x) рациональные числа, а исходное число
c - корень F(x), т.е. является алгебраическим. ÿ
Тема 3.3. Теорема Кантора.
Этот раздел посвящен
ответу на вопрос: каких чисел больше алгебраических или трансцендентных?
Сначала надо объяснить - что означает больше, если множества бесконечные?
Конечные множества сравнивать легко, считая большим то множество, в котором больше
элементов. Конечно, математики умеют пересчитывать элементы в любом бесконечном
множестве, используя для этого так называемые кардинальные числа. Мы не будем
даже пытаться излагать эту теорию, а ограничимся совсем простыми наблюдениями.
. Счетные и несчетные
множества.
Определение. Числовое
множество называется счетным, если элементы этого множества можно пересчитать.
Следует подробнее
остановится на идее «пересчета». Пересчитать элементы бесконечного множества -
это значит установить взаимно-однозначное соответствие между данным множеством
и множеством натуральных чисел, или записать элементы данного множества в
последовательность, или присвоить каждому элементу множества какой-нибудь
номер.
Определение. Если
множество бесконечно и не является счетным, то оно называется несчетным.
Далее мы приведем
примеры счетных и несчетных множеств, отметив пока, что рациональных чисел
счетно, а действительных несчетно.
. Примеры
взаимно-однозначных соответствий.
Возьмем два отрезка
равной длины. Соединим концы данных отрезков и увидим, что каждой точке одного
отрезка соответствует точка другого:
Как установить взаимно
однозначное соответствие между окружностью и квадратом. Для этого достаточно
вписать окружность в квадрат и проводить прямые через центр окружности до
пересечения с квадратом. Тогда каждой точке окружности будет соответствовать
точка квадрата.
Легко установить
счетность множества Z целых чисел. Для этого расположим все целые числа таким
образом: 0,1, - 1, 2, - 2,… Видно, что мы представили их в виде числовой
последовательности вида a1, a2, a3, a4,… Можно было сделать иначе, указав номер
N(x) целого числа x: 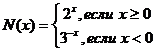 .
Правда при этом не каждое натуральное число будет номером какого-нибудь целого
числа, например, уравнение N(x) = 5 не имеет решений, значит, 5 не является
номером никакого целого числа.
.
Правда при этом не каждое натуральное число будет номером какого-нибудь целого
числа, например, уравнение N(x) = 5 не имеет решений, значит, 5 не является
номером никакого целого числа.
По существу очевиден
следующий результат.
Теорема. Бесконечное
подмножество счетного множества счетно.
Из нее вытекает, что
если каждому элементу множества удалось присвоить номер (при этом допустимо,
что у некоторых элементов может оказать даже бесконечно много номеров), то это
множество счетно.
С помощью этого
замечания можно доказать, что рациональных чисел счетное число. Каждое
рациональное число является отношением целых. Обозначим номер целого числа x
через N(x), тогда можно присвоить номер рациональному числу x/y по формуле
N(x/y) = 2N(x)3N(y). При этом каждому рациональному числу присваивается
бесконечно много номеров ввиду неоднозначности представления рационального
числа в виде дроби, однако разным рациональным числам присваиваются разные
номера. При этом конечно есть натуральные числа (например, степени 5), которые
не являются номером никакого рационального числа.
. Свойства счетных множеств.
Начнем со следующего простого факта.
Теорема. Пусть у нас
есть счетные множества А, В, С. Тогда объединение этих множеств также счетно.
Доказательство. Так как
все эти множества счетны, то они представимы в виде последовательностей: A: a1,
a2, a3, …; B: b1, b2, b3, …; C: c1, c2, c3, … Объединение этих множеств
содержит элементы каждого множества. Будем выписывать элементы объединения
множеств, двигаясь по столбцам слева направо, а в каждом столбце сверху вниз:
a1, b1, c1; a2, b2, c2; a3, b3, с3,…, т.е. объединение указанных множеств
счетно. ÿ
Следующая теорема уже не
столь очевидна.
Теорема 1. Счетное
объединение счетных множеств счетно.
Доказательство. Запишем
в виде таблицы элементы данных множеств, считая, что в первой строке
занумерованы элементы первого множества и т.д. Рассмотрим систему расширяющихся
квадратов Kn (n = 1, 2, …). Квадрат Kn находится на пересечении первых n строк
и первых n столбцов таблицы. Теперь все элементы легко записать в виде
последовательности. Сначала записываем элемент из первого квадрата, потом в
любом порядке элементы второго квадрата (можно записанные ранее элементы не
писать еще раз, а можно и писать), потом элементы третьего квадрата и т.д. ÿ
Следующий результат
совсем не очевиден, его доказательство принадлежит великому математику 20 века
Гёделю и основано на идее нумерации.
Теорема 2. Множество
конечных последовательностей рациональных чисел счетно.
Доказательство. Пусть N
какой-нибудь пересчет рациональных чисел. Найдем по формуле номер конечной
последовательности рациональных чисел
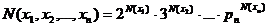 ,
,
где pn - простое число с
номером n, т.е. p1 = 2, p2 = 3, p3 = 5, … Поскольку каждое натуральное число
однозначно разлагается на простые множители, то по номеру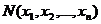 однозначно
восстанавливаются номера N(x1), N(x2), …, N(xn), а по каждому из них и
рациональные числа x1, x2, …, xn. ÿ
однозначно
восстанавливаются номера N(x1), N(x2), …, N(xn), а по каждому из них и
рациональные числа x1, x2, …, xn. ÿ
Для нас центральным в
этом пункте является следующая
Теорема 3. Множество
алгебраических чисел счетно.
Доказательство. Каждый
многочлен полностью задается своими коэффициентами, значит, многочлен с
рациональными коэффициентами полностью определяется конечной
последовательностью рациональных чисел. Следовательно, по теореме 2 таких многочленов
счетное число. Каждый из многочленов имеет конечное число корней, значит,
алгебраических чисел заданной степени счетное число. Множество алгебраических
чисел представляют собой объединение указанных множеств, значит, по теореме 1
это множество счетно. ÿ
. Число точек на отрезке
[0;1].
Теорема Кантора. Точек
на отрезке [0;1] несчетное множество.
Доказательство. Применим
так называемый процесс Кантора. Предположим от противного, что точек на отрезке
[0;1] счетное число, значит, их можно выписать в последовательность a1, a2, a3,
… Запишем каждое из чисел в виде бесконечной десятичной дроби:= 0, a11 a12 a13
…,= 0, a21 a22 a23 …,= 0, a31 a32 a33 …, и т.д.
Построим число, лежащее
на отрезке [0;1] и отличное от перечисленных. Для этого положим b = 0, b1b2 …
bn …, считая, что все цифры, входящие в запись числа b отличны от 0 и 9, а
также цифра b1 отлична от цифры a11, цифра b2 отлична от цифры a22, …, цифра bn
отлична от цифры ann, и т.д. Если b оказалось бы равным некоторому числу an, то
были бы равны цифры bn и ann, что противоречит определению числа b. ÿ
Теперь мы можем дать
ответ на сформулированный в начале пункта вопрос: каких чисел больше
алгебраических или неалгебраических? Больше чисел неалгебраических, чем
алгебраических, поскольку первое множество несчетно, а второе счетно.
У приведенной теоремы
Кантора есть один «серьезный недостаток», она не позволяет указать хотя бы одно
неалгебраическое число.
Впервые о существовании
трансцендентных чисел заявил Лиувилль в 1844 году, заметив, что иррациональные алгебраические
числа не допускают «очень сильных» приближений рациональными числами. Эрмит в
1873 году доказал трансцендентность числа e, а трансцендентность числа p
доказал Линдеман в 1882 году. Следует отметить особо, что с помощью этого факта
была решена проблема, стоявшая почти 20 веков - задача о квадратуре круга:
можно ли с помощью циркуля и линейки построить квадрат равновеликий кругу
радиуса 1?
На языке алгебраических
чисел задачу о квадратуре круга можно переформулировать так: можно ли число p
записать в виде алгебраического выражения, содержащего рациональные числа,
знаки арифметических действий и знак квадратного корня (знаки действий и корня
могут использоваться любое конечное число раз).
Так вот, Линдеман
доказал, что так получить число p нельзя, разрешив даже
использовать радикалы любой степени, а не только второй.
Одновременно и
независимо друг от друга в 1934 году советский математик Гельфонд и немецкий
математик Шнейдер доказали, что число 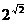 не является
алгебраическим, решив седьмую проблему Гильберта.
не является
алгебраическим, решив седьмую проблему Гильберта.
Алгебраические числа
имеют широкое применение в теории чисел, алгебре, геометрии и других разделах
математики. Изучение свойств таких чисел составляет содержание одного из
важнейших разделов современной теории чисел, называемого алгебраической теорией
чисел. Доказательство трансцендентности конкретных чисел представляет собой
решение трудных математических проблем.
§ 2. Примерная программа
факультатива «Алгебраические числа»
Введение. Тема
«Алгебраические числа» может быть рассмотрена в системе углубленного изучения
математики, однако, в соответствии с существующей на данный момент
образовательной программой не является обязательной: она связана с расширением
существующего содержания по сравнению с общеобразовательным курсом.
В 1997 году Н.Я.Виленкин
выпустил учебник «Алгебра» для учащихся школ с углубленным изучением
математики. В данном пособии он выделил отдельную главу, посвященную теории
многочленов и предлагает на рассмотрение многие вопросы, носящие скорее
необязательный характер. Среди них находится и тема «Алгебраические числа». В
этом учебнике проводится изучение симметрических многочленов на примере
многочленов от двух переменных. К сожалению, в учебнике нет алгебраических чисел,
играющих важную роль в математике, ввиду их обширных применений. В контексте
алгебраических чисел устанавливаются разнообразные связи между различными
разделами и направлениями математики. Например, многочлены, поля, комплексные
числа, построения с помощью циркуля и линейки, диофантовы уравнения - вот
далеко неполный перечень соответствующих направлений.
Как мы уже говорили,
основной целью изучения многочленов в школе является не столько изучение самой
теории многочленов, сколько совершенствование изучения математики с помощью
элементарных понятий и методов теории многочленов.
Поэтому главной задачей
изучения темы является не формирование прочных и устойчивых навыков
использования соответствующего математического аппарата при решении задач, а
демонстрация новых понятий и идей.
Раздел I. История
возникновения и развития числовых понятий
Ученик должен иметь
представление:
об истории развития
математики и возникновении основных понятий - число, уравнение, многочлен от
нескольких переменных, поле, алгебраическое число, счетное множество;
об основных задачах,
приводящих к теории алгебраических чисел;
об именах великих
математиков, внесших огромный вклад в науку.
Раздел 2. Симметрические
многочлены.
Ученик должен иметь
представление:
о понятии
симметрического многочлена;
о виде элементарных
симметрических многочленов;
о способах представления
симметрического многочлена в виде многочлена от элементарных симметрических;
Ученик должен знать:
формулировку основной
теоремы о симметрических многочленах;
формулы Виета.
Ученик должен уметь (для
степени 2 и 3):
приводить примеры
симметрических многочленов;
записывать набор
показателей старшего члена многочлена;
сравнивать старшие
члены;
восстанавливать по
старшему члену соответствующий одночлен от элементарных симметрических;
выражать симметрический
многочлен через элементарные симметрические;
применять формулы Виета.
Тема 2.1. Понятие
симметрического многочлена.
Введение понятия
симметрического многочлена. Элементарные симметрические многочлены. Утверждения
о строении старших членов симметрических многочленов.
Тема 2.2. Основные
теоремы о симметрических многочленах.
Основная теорема о
симметрических многочленах. Представление симметрического многочлена в виде
многочлена от элементарных симметрических. Метод неопределенных коэффициентов.
Тема 2.3. Некоторые
применения основной теоремы.
Симметрическая дробь, ее
свойства. Симметрические многочлены по наборам переменных. Формулы Виета.
Раздел 3. Алгебраические
числа.
Ученик должен иметь
представление:
о понятии замкнутости числового
множества;
об основные числовые
множества;
о понятии числового
поля;
о понятии алгебраически
замкнутого поля.
Ученик должен знать:
определение числового
поля;
определение
алгебраического числа;
определение минимального
многочлена;
понятия счетного и
несчетного множества;
формулировку теоремы о
множестве алгебраических чисел;
формулировку теоремы о
счетности алгебраических чисел;
диагональный процесс
Кантора.
Ученик должен уметь:
выполнять действия над
комплексными числами;
изображать комплексные
числа на плоскости;
находить модуль и
аргумент комплексного числа;
приводить примеры
алгебраических чисел;
приводить примеры
счетных и несчетных множеств;
доказывать счетность
множества целых чисел;
устанавливать
взаимно-однозначные соответствия между отрезками разной длины,
окружностями разного
радиуса; окружностью и квадратом.
Тема 3.1. Числовые поля.
Множество натуральных
чисел. Множество целых чисел. Множество рациональных чисел. Множество
иррациональных чисел. Множество действительных чисел. Множество комплексных
чисел. Числовые и нечисловые поля.
Тема 3.2. Алгебраические
числа.
Понятие алгебраического
числа. Степень алгебраического числа и свойства алгебраических чисел.
Минимальный многочлен. Поле алгебраических чисел и его алгебраическая
замкнутость.
Тема 3.2. Теорема
Кантора.
Счетность и несчетность
числовых множеств, примеры. Счетность множества алгебраических чисел.
Диагональный процесс Кантора. Несчетность множества трансцендентных чисел.
Приведем теперь
тематический план обсуждаемого факультатива.
Тематический план
|
Название
|
Количество часов
|
|
Максимум
|
Всего
|
Лекции
|
Семинары
|
Самост. работа.
|
|
Раздел I. История возникновения и развития числовых понятий
|
2
|
2
|
2
|
-
|
-
|
|
Раздел 2. Симметрические многочлены
|
15
|
15
|
5
|
5
|
4
|
|
Тема 2.1. Первичные понятие и простейшие свойства
|
4
|
4
|
1
|
2
|
1
|
|
Тема 2.2. Основные теоремы о симметрических многочленах
|
5
|
5
|
2
|
2
|
2
|
|
Тема 2.3. Некоторые применения основной теоремы
|
4
|
4
|
2
|
1
|
1
|
|
Раздел 3. Алгебраические числа
|
7
|
7
|
6
|
8
|
8
|
|
Тема 3.1. Числовые поля
|
3
|
3
|
2
|
4
|
4
|
|
Тема 3.2. Алгебраические числа
|
2
|
2
|
2
|
2
|
2
|
|
Тема 3.3. Теорема Кантора
|
2
|
2
|
2
|
2
|
2
|
|
Всего:
|
24
|
24
|
13
|
13
|
13
|
Список упражнений и задач для
контроля
Симметрические многочлены
. Напишите несколько переименований
для 5 переменных: x, y, z, p, q.
. Допустим, что мы выполнили
последовательно переименования (12) и (13). Тогда получилось новое
переименование, которое назовем произведением и запишем в виде (12)(13). Найти
произведения: (12)(13), (12)(123), (12)(123)(12).
. Приведите пример симметрического
многочлена от 3, 4, 5 переменных.
. Проверьте симметричность
многочленов относительно указанных переменных:
а) x3 + y3 + z3 - 3xyz, в)
xy + zt + x3,
б) x3 + y3 + z3 + t2, г)
x2 + y2 - xy.
. Перечислите элементарные
симметрические многочлены от x, y, z, t.
. Восстановите многочлен, если известно
его представление через элементарные симметрические многочлены:
а) f = φ13 - 3φ1φ2, в) f = φ14 - φ22 -
φ1φ3,
б) f = φ13 - 4φ1φ2 + φ3, г) f = φ12φ2 - 3φ4.
7. Выразить многочлен через
элементарные симметрические многочлены:
а) x3 + y3 + z3 - 3xyz, в)
(x + y)(y + z)(z + x),
б) x2y + xy2 + x2z + zx2 + y2z +
yz2, г) (x + y - z)(y + z - x)(z + x - y).
. Расположите в убывающем порядке
векторы показателей данной степени для старших членов, меньших данного набора:
(2,2,0,0,0), (3,0,0,0), (3,1,0,0,0),
(3,3,0,0), (2,2,2,0), (4,1,0,0).
. Сколько существует элементарных
симметрических многочленов от 3 и 4 переменных? Перечислите их.
. Как записать симметрическую дробь
f/g в виде дроби с несимметричным знаменателем?
. Почему симметрическую дробь можно
представить в виде отношения двух симметрических многочленов?
. Найти значение симметрического
многочлена S от корней многочлена f:
а) S = x12x22 + …, f = x2 - x - 1; б)
S = x12x2x3 + …, f = 2x2 - 3x + 1.
. Пусть x1, x2, x3 - корни уравнения
а) x3 - 3x + 1 = 0, в) x3 - 2x2 + 3x
- 1 = 0,
б) x3 + 3x - 1 = 0, г) x3 + 3x2 - 2x
- 1 = 0.
Составить уравнения, имеющие
указанные корни:
) а) x1 + x2, x2 + x3, x3 + x1, б)
x1 + x2 - x3, x2 + x3 - x1, x3 + x1 - x2,
) а) 1/x1, 1/x2, 1/x3, б) 1/x1 +
1/x2, 1/x2 + 1/x3, 1/x3 + 1/x1,
) а) x12, x22, x32, б) x1x2, x2x3,
x3x1.
Комплексные числа
. Вычислить:
а) (1 + 2i)(2 + 3i); б) (5 - 2i)(2 -
3i), в) (2 + 3i)(3 - 4i);
г) (1 + 2i)2, д) (1 + i)4,
е) (1 + i)100.
. Представить комплексное число в
алгебраической форме:
а) 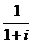 ;
б)
;
б) 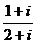 ;
в)
;
в) 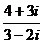 ;
г)
;
г)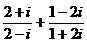 .
.
. Упростить выражение,
считая действительными числа a и b:
а) (2 + i)5 +(2 - i)5,
б) (1 + 2i)5 +(1 - 2i)5;
в)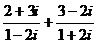 ,
г)
,
г)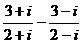 ;
;
. Какие действительные
числа a и b удовлетворяют уравнению:
а) (1 + i)a + (2 + 3i)b
= 1 + 2i; б) (1 - 2i)a + (4 - 3i)b = 6 - 7i ?
. Найти комплексные
числа, удовлетворяющие обоим уравнениям:
(3 - i)x + (4 + 2i)y =
-1 + 3i, (4 + 2i)x - (2 + 3i)y = 7.
. Найти комплексные
корни квадратного уравнения:
а) z2 + (2 - i)z - 3(1 +
i) = 0; г) z2 - 5z + 7 + i = 0;
б) z2 + (1 + i)z - 3(2 -
i) = 0; д) z2 - (2 + i) z + (-1 + 7i) = 0;
в) z2 - 3z + 3 + i = 0; е)
z2 - (3 - 2i) z + (5 - 5i) = 0.
Определение. Комплексное
число a - bi называется комплексно сопряженным к числу a + bi; обозначение 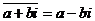 .
.
. Доказать свойства
комплексного сопряжения:
а) 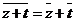 ;
б)
;
б) 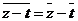 ;
в)
;
в) 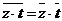 ;
г)
;
г) 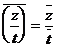 .
.
. Проверить, что
следующие числа являются комплексно сопряженными:
а) (2 + 5i)4(4 - 3i)8 и
(2 - 5i)4(4 + 3i)8; б) 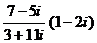 и
и 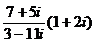 .
.
. Используя комплексные
числа, доказать тождество Эйлера:
(a2 + b2)(c2 + d2) = (ac
- bd)2 + (ad + bc)2.
. Пусть многочлен f с
действительными коэффициентами имеет комплексный корень z. Доказать, что
комплексно-сопряженное число 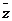 также является корнем
f.
также является корнем
f.
. Доказать, что
а) модуль произведения
комплексных чисел равен произведению модулей сомножителей; что можно утверждать
о модуле частного и модуле разности двух комплексных чисел?
б) модуль суммы
комплексных чисел не превосходит суммы модулей слагаемых;
. Решить уравнение:
а) 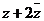 =
a + bi; б)
=
a + bi; б) 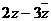 =
a + bi.
=
a + bi.
. Решить графически и
аналитически уравнение:
а) z + ½z½=
1 - i; б) z + ½z + 1½= i.
. Построить точки,
изображающие комплексные числа:
а) 1 + i, б)
1, в) -1, г) i,
д) -i, е) -1
+ 2i, ж) 2 - 3i, з) sina + icosa.
. Найти
тригонометрическую форму комплексного числа:
а) 1, б) -1, в)
i, г) - i, д) 1 + i, е) -1 + i.
. Доказать
справедливость равенств:
а) 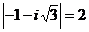 ,
arg
,
arg 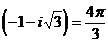 ;
;
б) 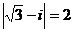 , arg
, arg
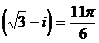 .
.
. Вычислить:
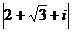 , arg
, arg 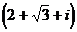 ;
;
. Нарисовать множество
точек, удовлетворяющих условиям:
а) ½z½=
1; б) ½z½£ 1; в) ½z½>
2; г) 1 £½z½£ 2;
д) arg z = 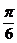 ;
е) arg z =
;
е) arg z = 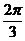 ; ж) arg z = p; з)
arg z = 0.
; ж) arg z = p; з)
arg z = 0.
. Доказать, что
расстояние между точками z и t равно ½z - t½.
. Изобразить множество
точек z таких, что
а) ½z
- i½=
1; б) ½z - i½£ 1; в) ½z
- i½<
1; г) ½z - i½³ 1.
. Какое множество точек
z задается условиями:
а) ½z
- 1½=
½z
- i½; в)
½z
+ 1½=½z
- i½=½z
+ i½;
б) ½z
+ i½=½z
+ 1 - i½; г)
½z
- 1½=½z
- 2i½=½z
+ 1 + i½.
. Найти расстояние от
точки z0 до множества M:
а) z0 = 2, M = {z½arg
z = 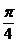 }; в)
z0 = -1 + i, M = {z½arg z = p};
}; в)
z0 = -1 + i, M = {z½arg z = p};
б) z0 = -2i, M = {z½arg
z = 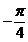 }; г)
z0 = 4 + 3i, M = {z½arg z = 0}.
}; г)
z0 = 4 + 3i, M = {z½arg z = 0}.
. Найти расстояние от
точки 2 + 3i до множества M:
а) M = {z½arg
z = 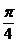 };
в) M = {z½arg z =
};
в) M = {z½arg z = 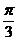 };
};
б) M = {z½arg
z = 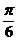 }; г)
M = {z½arg
z =
}; г)
M = {z½arg
z = 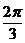 }.
}.
. Считая ½z½£
1, найти указанное значение:
а) min ½1
+ i - z½;
в) min ½3 + 2i - z½;
б) max ½1
+ i - z½; г)
max ½3
+ 2i - z½.
. Найти расстояние между
множествами точек:
а) M1 = {z½½z
- i½£
1},
M2 = {z½½z - 2 - 3i½£
1};
б) M1 = {z½½z
- 2i½£
1},
M2 = {z½arg z = 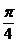 }.
}.
. Найти точку на
окружности, имеющую наименьший положительный аргумент:
а) ½z
- 3i½=
2; в) ½z - 2 - 3i½=
1;
б) ½z
- 1 - 2i½=
1; г) ½z + 1 - i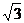 ½=
½=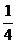 .
.
. Доказать, что для
любых комплексных чисел справедливо равенство
½x + y½2
+ ½x
- y½2
= 2(½x½2
+ ½y½2).
Объяснить его
геометрический смысл.
. Доказать, что если ½z½<
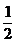 ,
то
,
то
а) ½(1
+ i)z3 + iz ½<
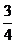 ; б)
½(2
+ 3i)z5 + (1- i)z ½<
; б)
½(2
+ 3i)z5 + (1- i)z ½<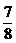 .
.
Прежде чем приступать к
решению следующих задач необходимо рассказать о произведении и частном
комплексных чисел, записанных в тригонометрической форме
. Выполнить действия над
комплексными числами:
а) (1 - i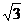 )(cosj
- i sinj);
б)
)(cosj
- i sinj);
б) 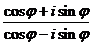 ;
;
. Найти модуль и
наименьший положительный аргумент комплексного числа:
а) (i +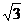 )(1
- i
)(1
- i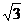 )(1
+ i); б) (1 - i)(
)(1
+ i); б) (1 - i)(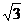 - i)
- i)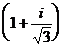 .
.
. Вывести формулу
Муавра: (cosj
+ i sinj)n
= cosnj
+ i sinnj.
Алгебраические числа
. Доказать, что
множество всех чисел указанного вида является полем
а) 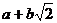 ,
б) a + bi, где a, b - рациональны, i - мнимая единица.
,
б) a + bi, где a, b - рациональны, i - мнимая единица.
. Среди чисел найти
рациональные.
а) 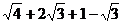 ,
б)
,
б) 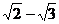 ,
в)
,
в) 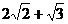 ,
г)
,
г)  .
.
. Доказать
иррациональность чисел: 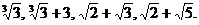
. Известно, что p
- неалгебраическое число. Какие из чисел являются алгебраическими: а) p3
+ p
+ 1, б) p
+ 1/p,
в) p
+ 1/p
+ 1.
. Можно ли построить с
помощью циркуля и линейки треугольник равновеликий кругу радиуса 1?
. Является ли число 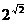 алгебраическим?
Можно ли его построить с помощью циркуля и линейки?
алгебраическим?
Можно ли его построить с помощью циркуля и линейки?
Теорема Кантора
. Как установить взаимно-однозначное
соответствие между
а) замкнутыми отрезками
разной длины;
б) окружностями разного
радиуса;
в) кругом и областью
ограниченной квадратом;
д) отрезком и лучом;
е) отрезком и прямой;
ж) прямой и окружностью?
. Как вы думаете где
больше точек на прямой, на плоскости или в пространстве?
. Докажите, что конечных
последовательностей из 0 и 1 счетное множество?
. Каким может быть
подмножество счетного множества?
. Докажите, что
бесконечных последовательностей из 0 и 1 столько же сколько точек на отрезке.
. Почему конечных
последовательностей натуральных чисел счетное число?
. Сколько можно
расположить на плоскости непересекающихся букв «Г» одного размера; а букв «О»?
§ 3. Методические
рекомендации по организации изучения факультативного курса «Алгебраические
числа»
Для разработки
рекомендаций по организации работы сформулируем некоторые общие требования
взаимосвязанного построения дополнительного образования и уроков по математике:
преемственность в содержании,
методах и формах организации занятий по математике должна определяться целями
обучения математики, всестороннего развития и воспитания учащихся.
взаимосвязанное
построение уроков и факультативных занятий по математики не должно
противоречить дидактическим принципам в обучении математики.
не должно быть
противоречий психолого-педагогическими требованиями;
не должно быть
несогласованности и с директивными нормами организации работы
общеобразовательной школы.
главным критерием
эффективности взаимосвязанного построения уроков, внеклассных занятий и
дополнительного образования по математике должна быть в конечном счете
результативность неразрывно связанных друг с другом процессов обучения,
развития и воспитания школьников.
взаимосвязь уроков и
дополнительного образования должна рассматриваться в такой последовательности:
уроки математики - внеклассные занятия - дополнительное образование. [37]
Перейдем к рассмотрению
вопроса методического обеспечения факультативного курса «Алгебраические числа».
Оперативные навыки, приобретаемые учащимися в процессе изучения темы, и
использование этих навыков на протяжении всего дальнейшего обучения имеют
безусловный приоритет по сравнению с логическими аспектами изложения теории, с
уровнем строгости и общности определений, теорем и доказательств. [17, 36]
Такой подход к изучению
темы связан с рядом обстоятельств. Прежде всего, теоретический уровень обучения
математике не должен значительно отличаться от уровня общеобразовательных
классов.
Нельзя не учитывать
также и объективные возрастные особенности учащихся, их ограниченные
возможности в усвоении абстрактных теоретических построений, и быть может,
самое главное - еще не сложившуюся внутреннюю потребность в более высоком, чем
раннее, уровне строгости - в строгой форме определений, в необходимости
доказательств теоретических утверждений в обще виде, в теоретическом
обосновании алгоритмов решения задач, ориентированных на практические
применения.
Наконец, существенное
значение имеют и общедидактические и методические соображения о значимости
логики в курсе математики, о роли формальных доказательств в процессе обучения
математики, о точности языка преподавания математики. Мы не будем детально
вдаваться в эту исключительно деликатную тему и ограничимся лишь двумя
замечаниями. [37]
Во-первых, даже для
профессионального математика некоторые доказательства «на примере», абсолютно
неприемлемые с чисто логической точки зрения, могут быть настолько
убедительными, что их логически необходимое формальное доказательство
отличается от примера лишь общими обозначениями.
Такими являются,
например, доказательства признаков делимости на 3 и на 9 в младших классах,
правило перевода бесконечной периодической дроби в обыкновенную, основанное на
домножение на степень числа 10.
В этих теоремах частные
примеры настолько адекватно моделируют общее формальное доказательство, что в
справедливости общих утверждений после таких доказательств, рассчитанных на
младших школьников, не будет сомневаться и профессионал - математик. В тоже
время доказательства в общем виде в данных случаях отличаются от примеров лишь
громоздкостью обозначений и с дидактической точки зрения не дают ничего нового,
кроме чисто формальной логической строгости.
Между тем, одна из
основных особенностей рассматриваемой темы, определяемая и ее содержанием и
целью изучения, состоит именно в том, что большая часть основных результатов
допускает дидактически допустимое обоснование с помощью примеров, адекватно
отражающих сущность формального доказательства. Это позволяет практически
всегда избегать громоздких обозначений и выкладок, существенно облегчая
погружение учащихся в рассматриваемый раздел. [17, 25]
Кроме того,
теоретические обоснования некоторых алгоритмов, ориентированных на практическое
применение, могут быть проведены сравнительно несложно, что предоставляет
учителю богатые возможности для дифференцированного подхода к учащимся.
Во-вторых, недостатки
овладения школьниками тем или иным конкретным математическим материалом, как
правило, в меньшей степени связаны с логическим уровнем его изложения.
Еще раз подчеркнем, что
выбор логического уровня изложения теории полностью отдается на усмотрение
учителя.
С начальными понятиями
теории многочленов от нескольких переменных: нормальный вид многочлена,
сложение, вычитание, умножение многочленов, степень многочлена, - учащимся уже
знакомы из курса алгебры.
Наша задача - доступно и
легко изложить материал по теме «Алгебраические числа». Сразу следует отметить,
что для изучения учащимся представлена не полная теория, а лишь основные блоки,
которые позволяют практически оперировать и то, только те которые учащиеся 8 и
9 классов могут освоить. Поэтому доказательства, задачи, определения,
утверждения доказываются для частных случаев или на примерах.
Раздел I. История
возникновения и развития числовых понятий
Для изложения материала
данного раздела мы предлагаем метод рассказа. Он предполагает устное
повествовательное изложение содержания учебного материала.
Раздел 2. Симметрические
многочлены.
Тема 2.1. Первичные
понятие и простейшие свойства. В данной теме необходимо уделить внимание
усвоению детьми определения симметрического многочлена и возможности
формирования навыков переименования переменных. Для введения понятия
переименования переменных мы предлагаем наглядно - иллюстративный метод: рассмотреть
различные переименования для конкретного числа переменных. Аналогичным способом
мы предлагаем рассматривать элементарные симметрические многочлены. Это
позволит не только сформировать навыки по записи элементарных симметрических
многочленов для конкретного числа переменных, но и понять закономерность
процесса построения таких многочленов. В данной теме приводятся четыре
утверждения, которые в последующем потребуются для доказательства более сложных
теорем и свойств. Мы посчитали целесообразным доказать только два из них
(утверждение 3, 4), так как доказательство этих фактов можно провести на
конкретном примере и оно не является слишком абстрактным для понимания детей в
8-10 классах.
Тема 2.2. Основные
теоремы о симметрических многочленах. В данной теме трудности могут возникнуть
с пониманием алгоритма выражения симметрического многочлена через элементарные
симметрические. Поэтому на данном занятии стоит сразу отработать данный
алгоритм на решении задач аналогичных примеру рассмотренному в доказательстве
теоремы.
Тема 2.3. Некоторые
применения основной теоремы. Здесь рассматриваются симметрические дроби,
симметрические многочлены по наборам переменных и формулы Виета. В рассмотрении
данной темы необходимо акцентировать внимание на вывод формул Виета. Его необходимо
провести на конкретном примере. После их вывода необходимо закрепить знания
формул при решении задач. При рассмотрении понятия симметрической дроби можно
предложить детям, интересную на наш взгляд, задачу о представлении
симметрической дроби в виде отношения двух симметрических многочленов, которая
позволит лучше понять основное свойство дроби и само понятие симметрической
дроби. Теорема о строение симметрических многочленов необходима для
доказательства теоремы о структуре множества алгебраических чисел.
Раздел 3. Алгебраические
числа.
Тема 3.1. Числовые поля.
Материал данного раздела рассматривается подробно в 8 классе, поэтому начальные
этапы рассмотрения носят скорее обобщающий характер. А вот новое в данном
вопросе - комплексные числа. При описании этого числового множества, мы
предлагаем рассмотреть пары чисел на декартовой плоскости и действия над такими
парами. Затем вводится мнимая единица i и приводится представление комплексного
числа в алгебраической форме (знакомство с формулой Эйлера и теоремой Муавра на
данном этапе почти невозможно по ряду очевидных причин, прежде всего, ввиду
отсутствия достаточных знаний по тригонометрии). Здесь же предполагается
знакомство с полярной системой координат и тригонометрической формой
комплексного числа. Основное внимание следует уделить арифметическим действиям
над комплексными числами, решению линейных и квадратных уравнений с
действительными и комплексными коэффициентами. Мы умышленно предлагаем
расширенный список задач на комплексные числа. В нем содержатся разнообразные
задачи, связанные с геометрическим представлением комплексных чисел. При
решении этих задач используются свойства прямоугольных треугольников и
окружностей, т.е. наблюдаются определенные межпредметные связи. Следует
обратить внимание на задачи, использующие понятие расстояния между точками на
плоскости и его интерпретацию на языке комплексных чисел.
Нет сомнения в том, что
задачи на комплексные числа способны вызвать живой интерес учащихся. С помощью
задач можно организовать индивидуальную самостоятельную работу, а потом
разобрать их решения на дополнительном занятии.
После рассмотрения
числовых множеств для более наглядного понимания и для закрепления удобно
привести графическую диаграмму, иллюстрирующую расположение основных числовых
множеств. Учащиеся должны понять вложение числовых множеств одно в другое.
Например, натуральные числа являются подмножеством целых чисел. Этот факт
следует даже из определения целых чисел - это натуральные числа,
противоположные к ним и нуль. Поэтому круг, изображающий множество натуральных
чисел, находится внутри круга целых чисел. Аналогичные рассуждения можно
провести и с другими множествами. Необходимо обратить внимание на расположение
рациональных и иррациональных чисел. Они не являются подмножествами друг друга.
Дети должны понять, что все действительные числа делятся на непересекающиеся
множества рациональных и иррациональных чисел.
Тема 3.2. Алгебраические
числа. Основная цель заключительных тем - демонстрация новых идей. Овладение
техникой отходит на задний план, поскольку сама техника весьма нетривиальна.
Новые красивые идеи, несомненно, способны вызвать интерес у школьников,
интересующихся математикой, открыть перед ними ее красоту.
В данной теме могут
возникнуть трудности с пониманием различных понятий: поле, алгебраически
замкнутое поле, запись многочленов с большим числом переменных. Кроме того, при
доказательстве теорем о поле алгебраических чисел используются формулы Виета и
теорема о симметрических многочленах по наборам переменных - это достаточно
тонкие рассуждения и вполне естественны трудности при понимании соответствующих
рассуждений. Вполне допустимо, если эти теоремы будут приведены на минимальном
уровне строгости, вполне допустимо ограничиться пониманием соответствующих
формулировок и их применением при решении задач.
Тема 3.3. Теорема
Кантора. При введении понятия счетности множества надо расшифровать слово
«пересчитать» в определении. Полезным является установление сначала разного
сорта взаимно-однозначных соответствий между простейшими геометрическими
фигурами, и только после этого следует переходить к доказательству счетности
различных числовых множеств. После доказательства теоремы Кантора следует
указать на его неконструктивность, т.е. невозможность указать хотя бы одно
неалгебраическое число.
Заключение
Изучение истории
дополнительного образования показало, что дополнительное образование и
внеклассная работа взаимосвязаны и входят в состав непрерывного математического
образования. В своем развитии дополнительное математическое образование и
внеклассная работа прошли несколько этапов, но наиболее важный период для
появления факультативных и внеклассных занятий - 60-е года 20 века. Это
позволило реализовать дифференцированный подход к обучению и осуществить
индивидуализацию отечественного образования. Условиями организации
дополнительного образования является определение некоторой модели: «Свободная
мысль», «Личностная модель», «Развивающая модель», «Активизирующая модель»,
«Формирующая модель», «Обогащенная модель», где заложены свои критерии и
система методов: критерии преемственности методов, критерий соответствия целям
и задачам обучения, критерии соответствия содержанию занятий, критерии
соответствия возрастным и индивидуальным особенностям развития
старшеклассников. А также при построении курса дополнительного математического
образования необходимо учитывать комплексный подход к разработке такого курса,
а также психологические особенности детей, на возрастную группу которых
рассчитан этот курс. Этим вопросам посвящена целиком первая глава.
С учетом первой главы
предложена разработка факультативного курса «Алгебраические числа», в
частности, определено содержание курса, предложена примерная программа, а также
методические рекомендации по организации работы. Предлагаемый курс является
естественным продолжением факультативного курса «Многочлены от одной
переменной», разработанного Г.В. Дорофеевым. Кроме того, предлагаемый
факультативный курс можно рассматривать как естественное продолжение одной из
важнейших линий школьного курса - числовой линии. При отборе содержания
учитывалась история возникновения и развития основных понятий, а также их связи
с другими важнейшими понятиями основного курса и значимость не только для
математики, но и для общего образования. При отборе содержания и подаче
материала мы отдавали предпочтение идеям, а не отработке технических навыков.
На наш взгляд, предложенный содержательный материал показывает единство
различных разделов математики - арифметики, алгебры, геометрии, анализа, и
способен вызвать живой интерес учащихся.
Материалы дипломной
работы могут быть использованы при внедрения данного курса в школьную практику.
Библиография
1. Азаров Ю.П. Радость учить и учиться. - М.: Политиздат, 1989.
- 335 с.
2. Алексеев А.Е. В помощь начинающему учителю по математике.
- Якутск, 1984. - 38 с.
. Альхова З.Н. Внеклассная работа по математике. -
Саратов: Лицей, 2001.
. Батурина Г.И., Кузина Т. Ф. Введение в педагогическую
профессию: Учеб. пособие для студентов сред. пед. учеб. заведений. - М.:
Издательский центр «Академия», 1998. - 176 с.
. Бурбаки Н. Очерки по истории математики. - М.: Наука,
1963. - 292 с.
. Бурбаки Н. Алгебра. Многочлены и поля. - М.: Наука,
1965. - 300 с.
. Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика
Древнего Египта, Вавилона и Греции. - М., 1959.
. Василевский А.Б. Задания по внеклассной работе по
математике: 9 - 11 кл. - Минск, 1988. - 127 с.
. Введение в педагогическую профессию: Курс лекций. //
Научные редакторы: Н.К. Сергеев и Е.И. Сахарчук. - Волгоград: Перемена, 1998.
. Винберг Э.Б. Симметрия многочленов. - М.: Изд-во Моск.
центра непрерывного мат. образования, 2001.- 24 с.
. Внеклассная работа по математике. / Под ред. Ф.С.
Королева и др. - Первиль, - 1999.
. Внеклассная работа по математике в средней школе:
Учебное пособие для студентов физ. - мат. фак. и начин. учителей по математике.
/ Под ред. В.И. Сухорукова. - Балашов: БГПИ, 1994. - 204 с.
. Возрастная и педагогическая психология. - 2-е изд.,
испр. и доп. /Под ред. А.В. Петровского. - М., 1979.
. Вопросы преподавания математики в школе. Классные и
факультативные занятия. /Под ред. Сандлера А.И. - Куйбышев, 1971. - 154с.
. Гнеденко Б.В. Математика и математическое образование в
современном мире. - М.: Просвещение, 1985. - 196 с.
. Гольховой В.М. Индивидуализация учебной деятельности
учащегося как основа дифференцированного обучения по математике. - М.: Моск.
пед. ин-тут, 1997.- 16 с.
. Дорофеев Г.В. Математика для каждого. - М.: Аякс, 1999.
- 292 с.
. Дорофеев Г.В., Пчелинцев С.В. Многочлены от одной
переменной. Книга для учащихся - М.: Просвещение, 2001. - 142 с.
. Жаров В.А. Избранные вопросы для факультативных и
внеклассных занятий по математики. - Ярославль, 1971. - 163 с.
. Зимняя И.А. Педагогическая психология: учебное пособие.
- Ростов н/Д.: Феникс, 1997.
. Кадыров. И.М. Взаимосвязь внеклассных и факультативных
занятий по математике. Книга для учителя. - М.: Просвещение,1983. - 63 с.
. Клейн Ф. Лекции о развитии математики в XIX столетии. -
М., 1989.
. Козырева А.Ю. Лекции по педагогике и психологии
творчества. - Пенза: Научно-методический центр Пензенского городского отдела
образования, 1994.- 344 с.
. Колмогоров А.Н. Математика в её историческом развитии. -
М.: Наука, 1991. - 256.
. Крутецкий В.А. Психология обучения и воспитания
школьников. - М.,1976.
. Лихачёв Б.Т. Педагогика. Курс лекций. Учебное пособие
для студентов пед. учебн. заведений и слушателей ИПК и ФПК. - М.: Прометей,
1992. - 526 с.
. Материалы для факультативных занятий по математики в
средней школе. /Под. ред. А.И. Сандлера. - Куйбышев, 1971.
. Мерлина Н.И. Дополнительное математическое образование
школьников и современная школа.- М.: Гелиос, 2001.
. Мижериков В.А., Ермоленко М.Н. Введение в педагогическую
профессию: Учебное пособие для студентов педагогических учебных заведений. -
М.: Педагогическое общество России, 1999.
. Немов Р.С. Психология: Учеб. для студ. пед. вузов: В 3
кн. - 3-е изд. - М.: Гуманит. изд. центр ВЛАДОС, 1999.
. Ожегов С.И. Словарь русского языка. - М., 1964.
. Особенности углубленного изучения математики в 8- 9
классах. Сост. Е.П. Нелин, - Киев, 1989. - 175с.
. Педагогика. Учеб. пособие для студентов пед. училищ.
/С.П. Баранов, Л.Р. Болотина, Т.В. Воликова, В.А. Сластенин. - М.: Просвещение,
1981. - 367 с.
. Педагогика. Учеб. пособие для студентов пед. ин-тов по
спец. 2121 «Педагогика и методика нач. обучен.» /С.П. Баранов, Л.Р. Болотина,
В.А. Сластенин и др.; Под ред. С.П. Баранова, В.А. Сластенина. -2-е изд., доп.
- М.: Просвещение, 1986. - 336 с.
. Педагогика: педагогические теории, системы, технологии:
Учеб. пособие для студ. пед. учеб. заведений. /С.А. Смирнов, И.Б. Котова, Е.Н.
Шиянов, Т.И. Бабаева и др.; Под ред. С.А. Смирнова. - М.: Издательский центр
«Академия», 1998. - 512 с.
. Прасолов В.В. Многочлены. - М.: МЦНМО, 2001. - 335 с.
. Рыбников К.А. История математики. - М.: Изд-во МГУ,
1994. - 310.
. Семенов В.И. Некоторые методологические и методические
аспекты углубленного изучения математики. Учебное пособие. - Кемерово, 1988. -
135 с.
. Факультативные занятия по математике. Сборник статей.
/под ред. П.С. Орехова. - Ижевск,1969.
. Факультативные курсы по математике в средней школе.
Сборник трудов. /под.ред. М.К. Андронова. -М.,1994.
. Юшкевич А.П. История математики в средние века. - М.,
1961