Задачи календарного планирования производства: модель без дефицита, модель с дефицитом

Задачи календарного планирования производства: модель без дефицита, модель с дефицитом

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Магнитогорский государственный технический университет им. Г.И. Носова»

Кафедра математических методов в экономике

КУРСОВАЯ РАБОТА

по дисциплине Математические методы и модели исследования операций

не тему: Задачи календарного планирования производства: модель без дефицита, модель с дефицитом

Исполнитель:

Барышникова В.В. студент__2__ курса, группа ФММ-08

Руководитель:

Трофимова В.Ш. доцент, к.эк.н

Магнитогорск 2010

Содержание

Введение

. Календарного планирование производства

1.1 Методы решения задачи календарного планирования

.2 Постановка задачи календарного планирования

2. Транспортная задача линейного программирования

.1 Постановка транспортной задачи

.2 Методы составления первоначальных опорных планов

2.3 Метод потенциалов

. Задача календарного планирования производства

3.1 Модель без дефицита

.2 Модель с дефицитом

Заключение

Список используемых источников

ВВЕДЕНИЕ

Управление проектами стало широко применяться, начиная с 60-х годов.

Центральной задачей в управлении проектами является задача формирования плана реализации проекта или задача календарного планирования производства. Причем собственно календарными считаются задачи, относящиеся к составлению календарных графиков по дням, сменам, часам работы. Задачи управления на уровне декады, месяца, квартала называют задачами декадного, месячного, квартального планирования.

Опыт многих преуспевающих компаний промышленных стран показывает, что в условиях рынка с его жестокой конкуренцией планирование хозяйственно-производственной деятельности является важнейшим условием их выживаемости, экономического роста и процветания. Именно оно позволяет оптимально увязать имеющиеся возможности предприятия по выпуску продукции со сложившимися на рынке спросом и предложением.

Формирование класса задач планирования связано с одной из первых попыток решения экономических проблем методами математического программирования в начале 50-х годов. С тех пор актуальность решения данных задач сильно возросла. Увеличился диапазон подходов к их решению, но одновременно сохраняются трудности их реализации. Для решения задач календарного планирования привлекаются разнообразные методы прикладной математики (методы линейного, нелинейного, динамического программирования), используются ЭВМ.

Целью данной работы является рассмотрение решения задачи календарного планирования одним из методов линейного программирования, а именно с помощью транспортной модели.

Данная работа имеет традиционную структуру: содержит введение, 3 раздела, заключение. В первом разделе говорится о методах решения задачи календарного планирования, во втором - рассматривается транспортная задача, а в третьем метод решения транспортной задачи применяется для решения задачи календарного планирования производства.

модель задача календарь планирование производство

1. Календарного планирование производства

1.1 Методы решения задачи календарного планирования

С математической точки зрения задача календарного планирования представляет собой сложную комбинаторную задачу, имеющую множество решений, среди которых необходимо найти решение, оптимальное в смысле некоторого критерия. Данная задача может быть решена точно или приближенно, в соответствии с этим и методы ее решения делятся на точные и приближенные.

Точные методы. К точным методам решения задач относятся методы линейного программирования.

Пример некоторой задачи линейного программирования. Пусть цех выпускает N наименований изделий и Xj - количество изделий j-го наименования (j=1,N). Количество станков в цехе M. Обработка одного изделия может происходить последовательно на нескольких станках, причем tij - время обработки j-го изделия на i-ом станке (i=1,M). Тогда общая трудоемкость изделий

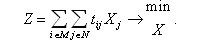 <#"521139.files/image002.gif"> <#"521139.files/image003.jpg">(1.1)

Поскольку переменные x_ij (i=1,m; j=1,n) удовлетворяют системам линейных уравнений и условию неотрицательности, обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Определение 1.1 Всякое неотрицательное решение систем линейных уравнений, определяемое матрицей X=(x_ij) (i=1,m; j=1,n), называется планом транспортной задачи.

Определение 1.2. План X^*=(x_ij^*)(i=1,m; j=1,n), при котором целевая функция принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

Обычно исходные данные транспортной задачи записываются в виде таблицы , как показано в таблице 1.

Таблица 1

Очевидно, общее наличие груза у поставщиков равно 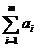, а общая потребность в грузе в пунктах назначения равна 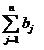. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.

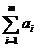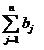= (1.2)

то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.

Теорема 1.1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство.

В случае превышения запаса над потребностью, т. е. при 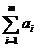>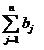, вводят фиктивный (n+1)-й пункт назначения с потребностью b_n+1=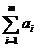- 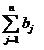и соответствующие тарифы считают равными нулю: c_in+1=0 (i=1,m). Полученная задача является транспортной задачей, для которой выполняется равенство закрытости.

Аналогично, при 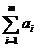<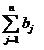, вводят фиктивный (m+1)-й пункт отправления с запасом груза a_m+1=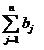- 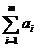и соответствующие тарифы считают равными нулю: c_m+1j=0 (j=1,n). Этим задача сводится к транспортной задаче с закрытой моделью, из оптимального плана которой получается оптимальный план исходной задачи. Поэтому в дальнейшем мы будем рассматривать только закрытую модель транспортной задачи.

Число переменных xij в транспортной задаче с m пунктами отправления и n пунктами назначения равно nm, а число уравнений в системе ограничений равно n+m. Так как предполагается, что выполняется условие закрытости, то число линейно-независимых уравнений равно n+m-1. Следовательно, опорный план транспортной задачи может иметь не более n+m-1 отличных от нуля неизвестных.

Если в опорном плане число отличных от нуля компонент равно в точности n+m-1, то план является невырожденным, а если меньше - то вырожденным. Для определения опорного плана существует несколько методов. Ниже рассматриваются два из них - метод северо-западного угла, метод минимального элемента.

Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом.

Определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана.

2.2 Методы составления первоначальных опорных планов

Метод северо-западного угла используют для нахождения произвольного опорного плана транспортной задачи.

Схема метода: 1) Полагают верхний левый элемент матрицы X

x11 = min(a1_,b1).

Возможны три случая:

а) если a1 < b1, то х11 = a1 и всю первую строку, начиная со второго элемента, заполняют нулями.

б)если a1 > b1_ь то х11 = b1 а все оставшиеся элементы первого столбца заполняют нулями.

в)если a1 = b1 то х11 = a1= b1 и все оставшиеся элементы первых столбца и строки заполняют нулями.

На этом один шаг метода заканчивается.

) Пусть проделано к шагов, (к) - й шаг состоит в следующем.

Определяют верхний левый элемент незаполненной части матрицы X. Пусть это элемент xλ_µ (λ + µ = к + λ).

Тогда полагают x_Xil = min(аλ,bµ), где

aλ(k)=aλ-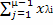 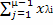и bµ(k)=bµ-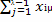 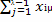(1.3)

Если aλ < bµ, то заполняют нулями λ-ю строку начиная с (µ +1) -го элемента. В противном случае заполняют нулями оставшуюся часть µ - го столбца. Метод минимального элемента позволяет построить начальный опорный план транспортной задачи и является вариантом метода северо-западного угла, учитывающим специфику матрицы С = (Cij)_m,_n. В отличие от метода северо-западного угла данный метод позволяет сразу получить достаточно экономичный план и сокращает общее количество итераций по его оптимизации.

Схема метода: элементы матрицы С нумеруют, начиная от минимального в порядке возрастания, а затем в этом же порядке заполняют матрицу Х°.

Пусть элементом с минимальным порядковым номером оказался элемент xij°.

Тогда полагают xij°= min(ai, bj)

Возможны три случая:

а) если min(ai, bj) = а;, то оставшуюся часть i-й строки заполняют нулями;

б) если min(ai, bj) = bj, то оставшуюся часть j-ro столбца заполняют нулями.

в) если ai = bj, то оставшуюся часть строки и столбца заполняют нулями.

Далее этот процесс повторяют с незаполненной частью матрицы. Пусть элементом с k-м порядковым номером оказался xλ_µ.

Тогда xλ_µ =min(aλ, bµ),где

aλ(k)=aλ-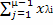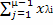(g) g=1…k-1

bµ(k)=bµ-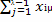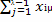(u) u=1…k-1 (1.4)

Возможны три случая:

а) aλ(k)< bµ(k)', тогда xλµ(k) = aλ(k) и оставшуюся часть строки λ заполняют нулями;

б) aλ(k)> bµ(k), тогда xλµ(k) = bµ(k) и остаток столбца µ заполняют нулями;

в) aλ(k) = bµ(k), тогда оставшуюся часть строки λ и столбца µ заполняют нулями.[4]

2.3 Метод потенциалов

Общий принцип определения оптимального плана транспортной задачи методом потенциалов: сначала находят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана.

Для определения опорного плана транспортной задачи будем пользоваться одним из методов, рассмотренных выше. Эти методы гарантируют получение m+n-1 занятых клеток в исходной таблице условий, причем в некоторых из них могут стоять нули. Полученный таким образом план следует проверить на оптимальность.

Теорема 1.2. Если для некоторого опорного плана X^*=(x_ij^*) (i=1,m; j=1,n) транспортной задачи существуют такие числа U₁, U₂, . . . , U_m, V₁, V₂, . . . , V_n, что

V_j- U_i=c_ij при x_ij>0

V_j- U_i<=c_ij при x_ij=0

для всех (i=1,m) и (j=1,n), то X*=(xij*) - оптимальный план транспортной задачи.

Определение 1. 3. Числа U_i и V_j (i=1,m; j=1,n) называются потенциалами соответственно пунктов назначения и пунктов отправления.

Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем.

1. Пусть одним из рассмотренных выше методов найдет опорный план транспортной задачи. Для каждого из пунктов отправления и назначения определяются потенциалы Ui и Vj (i=1,m; j=1,n). Эти числа находят из системы уравнений

Uj- Vi=cij

где cij - тарифы, стоящие в заполненных клетках таблицы условий транспортной задачи.

. Так как число заполненных клеток равно m+n-1, то система с m+n неизвестными содержит m+n-1 уравнений.

Поскольку число неизвестных превышает на единицу число уравнений, одно из неизвестных можно положить равным произвольному числу, например α1=0, и найти последовательно из уравнений значения остальных неизвестных.

. После того как все потенциалы найдены, для каждой из свободных клеток определяют числа Δij=Vj- Ui-cij.

4. Если среди чисел Δij (i=1,m; j=1,n) нет положительных, то найденный опорный план является оптимальным.

Если же для некоторой свободной клетки Δij>0, то исходный опорный план не является оптимальным и необходимо перейти к новому опорному плану.

Для этого рассматривают все свободные клетки, для которых Δij>0, и среди данных чисел выбирают максимальное. Клетку, которой соответствует это число, следует заполнить.

Заполняя выбранную клетку, необходимо изменить объемы поставок, записанных в ряде других занятых клеток и связанных с заполняемой клеткой, так называемым циклом.

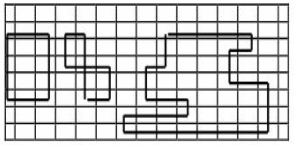
Определение 1.4. Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое в столбце.

Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.

Примеры некоторых циклов показаны на рис. 1

При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл. После того как для выбранной свободной клетки он построен, следует перейти к новому опорному плану. Для этого необходимо переместить грузы в пределах клеток, связанных циклом с данной свободной клеткой.

Это перемещение производят по следующим правилам:

) каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем свободной клетке - знак плюс, а всем остальным клеткам - поочередно знаки минус и плюс (будем называть эти клетки минусовыми и плюсовыми);

) в данную свободную клетку переносят меньшее из чисел x_ij, стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становиться занятой, а минусовая клетка, в которой стояло минимальное из чисел x_ij, считается свободной.

В результате указанных выше перемещений грузов в пределах клеток, связанных циклом с данной свободной клеткой, определяют новый опорный план транспортной задачи. Описанный выше переход от одного опорного плана транспортной задачи к другому ее опорному плану называется сдвигом по циклу пересчета.

Следует отметить, что при сдвиге по циклу пересчета число занятых клеток остается неизменным, а именно остается равным m+n-1. При этом если в минусовых клетках имеется два (или более) одинаковых числа x_ij, то освобождается лишь одну из таких клеток, а остальные остаются занятыми (с нулевыми поставками).

Полученный новый опорный план транспортной задачи проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа a_ij=V_j-U_i-c_ij для всех свободных клеток. Если среди этих чисел не окажется положительных, то это свидетельствует о получении оптимального плана. Если же положительные числа имеются, то следует перейти к новому опорному плану. В результате итерационного процесса после конечного числа шагов получают оптимальный план задачи.

3. Задача календарного планирования производства

Введем следующие обозначения для этапа i; i = 1,2,. . .,N.

сi - производственные затраты на единицу продукции при обычном режиме работы, di - производственные затраты на единицу продукции при работе в сверхурочное время (di > сi),

hi - затраты на хранение единицы продукции, переходящей из этапа i в этап i + 1, pi - потери от дефицита на единицу продукции, требуемой на этапе /, но поставляемой на этапе i + 1,

ari~ производственная мощность (в единицах продукции) при обычном режиме работы,

ati - производственная мощность (в единицах продукции) при работе в сверхурочное время,

bi - спрос (в единицах продукции).

Эквивалентность между элементами производственной и транспортной систем устанавливается следующим образом.

3.1 Модель без дефицита

В соответствии с терминологией транспортной модели поставщики представлены обычным и сверхурочным производством для различных этапов. Потребители задаются спросом соответствующих этапов. Затраты на «транспортировку» единицы продукции от любого поставщика к любому потребителю представляются суммой соответствующих производственных затрат и затрат на хранение единицы продукции.

Матрица полных затрат для эквивалентной транспортной задачи приведена в таблице 2.

Таблица 2.1 спрос на этапе j избыток

Дополнительный столбец используется для балансировки транспортной задачи, т.е.

S =∑ai - ∑bj. Затраты на единицу продукции в дополнительном столбце равны нулю.

Так как дефицит не допускается, то продукцию, выпускаемую на рассматриваемом этапе, нельзя использовать для удовлетворения спроса предыдущих этапов.

В таблице это ограничение представлено заштрихованными ячейками, что, в сущности, эквивалентно очень большим затратам на единицу продукции.

Так как задолженность в модели не допускается, то для каждого этапа к в нее необходимо включить ограничение, состоящее в том, что накопленный спрос не должен превышать соответствующий общий объем произведенной продукции, т.е.

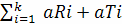
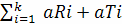 ≥ , k = 1,2,…,N (2.1)

Так как спрос на этапе i должен быть удовлетворен прежде, чем спрос на этапах i + 1, i + 2,..., N, и поскольку на функцию производственных затрат наложены специальные требования, нет необходимости применять общий алгоритм решения транспортной задачи. Сначала путем последовательного назначения максимально возможных поставок по наиболее дешевым элементам первого столбца удовлетворяется спрос на этапе 1. Затем корректируются значения ai, которые после этого определяют оставшиеся мощности для различных этапов. Далее рассматривается этап 2, и его спрос удовлетворяется наиболее дешевыми поставками в пределах новых ограничений на производственные мощности. Процесс продолжается до тех пор, пока не будет удовлетворен спрос этапа N.

3.2 Модель с дефицитом

Рассмотрим обобщение описанной выше модели при. условии, что допускается дефицит. Предполагается, что задолженный спрос должен быть удовлетворен к концу N-этапного горизонта планирования.  В каждый месяц спрос можно удовлетворить за счет

1) избытка произведенных в прошлом месяце изделий, сохраняющихся для реализации в будущем; производства изделий в течение текущего месяца; избытка производства изделий в более поздние месяцы в счет невыполненных заказов. стоимость производства в 1-й период, i = j,

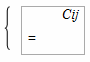
стоимость производства в i-и период + стоимость задержки от i до j, i < j, стоимость производства в i-й период + штраф за нарушение срока, i > j.

Из определения сij следует, что затраты в период i при реализации продукции в тот же период i (i = j) оцениваются только стоимостью производства. Если в период i производится продукция, которая будет потребляться позже (i < j), то имеют место дополнительные издержки, связанные с хранением. Аналогично производство в 1-й период в счет невыполненных заказов {i >j} влечет за собой дополнительные расходы в виде штрафа. Таблицу 2 можно легко модифицировать, чтобы учесть влияние задолженности, введя соответствующие удельные издержки в заблокированные маршруты. Так, например, если рi - удельные потери от дефицита (т.е. на единицу продукции) в случае, когда продукция требуется на этапе i, а поставляется на этапе i + 1, то удельные расходы, соответствующие ячейкам (Rn,i) и (ТN,1), составляют: {сN + р1 + р2 + ...+ pn-i} и {dn + p1 +p2+ … + pn-i} соответственно. Это представлено в таблице 2.2.

Таблица 2.2.

2

3

N

R1

С1

С1 + h_x

C1 + h1 + h₂

Cx + hi + ...+ hN-1

0

a_R1

Т1

d1

d1 + h1

d1 + h1+ h₂

dx + h\+ ...+ hN-1

0

a_T1

R2

С1 + р1

C₂

C₂ + h₂

C₂ + h₂+ ...+ h_N-1

0

a_R2

Т₂

d1+p1

d₂

d₂ + h₂

d₂ + h₂+ ...+ hN-1

0

an

RN

С1 + р1+ р2 + ...+ pn-i

С2 + р1+ р2 + ...+ pn-2

Cn

0

TN

d1 + p1+p2+ … + pn-i

d2 + p1+p2+ … + pn-2

d_N

0

atn

Заметим, что в общем случае описанный выше алгоритм может не привести к оптимальному решению. Поэтому задача решается как транспортная задача. Т.е. находится опорный план (например, с помощью метода минимального элемента), затем он проверяется на оптимальность. Если он оптимален, то задача календарного планирования (без дефицита) решена, если нет, то переходят к новому опорному плану, и он вновь проверяется на оптимальность. Т.е. в соответствии с алгоритмом, описанным в 1.2.3.

Заключение

Успех предпринимательской деятельности во многом зависит как от качества стратегического, так и оперативного планирования, которое тесно связано с оперативно-управленческими решениями, направленное на рациональное распределение производственных ресурсов. В этой связи разработка оптимального календарного плана производства становиться актуальной, поскольку при планировании производства возникает потребность нахождения решений для реализации поставленных целей с минимальными издержками и потерями. Одним из способов решения задачи календарного планирования производства является применение транспортной модели. Рассмотренные нами модели календарного планирования без дефицита и с дефицитом достаточно просты, но достаточно эффективны.

Список использованных источников

1. http://asy.osetiaonline.ru/docs/2-3-podsistema-operativnogo-ypravlenia-proizvodstvom.html

. Мастяева И.Н., Горбовцов Г.Я., Семенихина О.Н. Исследование операций в экономике: Учебное пособие. - М.:МЭСИ, 2003. - с. 63-68

. http://www.mmio.ru/tran_ob.html

. Мастяева И.Н., Горбовцов Г.Я., Семенихина О.Н. Исследование операций в экономике: Учебное пособие. - М.:МЭСИ, 2003. - с. 52-53