Исследование переходных процессов токов и напряжений всех ветвей электрической цепи
Содержание
1.
Классический метод расчёта
2.
Операторный метод расчёта
3.
Воздействие гармонической ЭДС
4.
Метод переменных состояния
.
Определение комплексной частотной характеристики
.
Определение временных характеристик цепи
Заключение
Литература
Аннотация
Задача анализа переходных процессов заключается в общем
случае в определении мгновенных значений токов и напряжений всех или части
ветвей электрической цепи в произвольный момент времени после коммутации.
В данном курсовом проекте необходимо выполнить следующие
расчёты: определить зависимости тока через индуктивность от времени при
воздействии постоянной ЭДС классическим и операторным методами, найти
зависимость тока через индуктивность от времени при воздействии гармонической
ЭДС, получить график зависимости тока через индуктивность от времени численным
методом, определить комплексную частотную характеристику и временные
характеристики цепи.
1.
Классический
метод расчёта
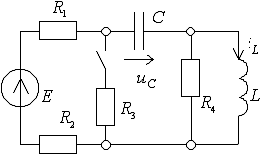
Рисунок 1.
1. Анализ цепи до коммутации. Определяется значение тока через
индуктивность 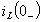 и напряжение на емкости
и напряжение на емкости 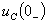 до коммутации
до коммутации 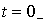 (ключ замкнут). В режиме постоянного тока
сопротивление индуктивности равно нулю, а емкости -
бесконечности. Тогда
(ключ замкнут). В режиме постоянного тока
сопротивление индуктивности равно нулю, а емкости -
бесконечности. Тогда
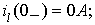
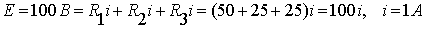
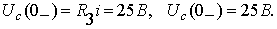
Здесь для нахождения 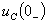 мы составили уравнение закона напряжений Кирхгоффа.
мы составили уравнение закона напряжений Кирхгоффа.
.Определение независимых начальных условий. Независимыми начальными
условиями являются ток в индуктивности и напряжение на емкости в момент времени
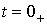 , которые определяются по первому и
второму законам коммутации:
, которые определяются по первому и
второму законам коммутации:
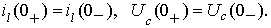
После подстановки получаем:
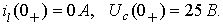
. Анализ установившегося процесса в цепи после коммутации. После
коммутации в цепи вновь установится режим постоянного тока. При этом ключ уже
разомкнут. В этом случае ток в цепи не течет и
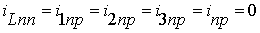 ;
;
. Определение свободной составляющей реакции цепи. Составляется
характеристическое уравнение цепи после коммутации. Для этого записывается
выражение входного сопротивления цепи относительно источника, причем в цепи
емкость заменяется на эквивалентное сопротивление 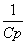 , а индуктивность заменяется на
эквивалентное сопротивление
, а индуктивность заменяется на
эквивалентное сопротивление 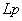 . Затем это выражение приравнивается к нулю. Уравнение
. Затем это выражение приравнивается к нулю. Уравнение 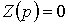 является характеристическим. В нашем
случае характеристическое уравнение может быть определено как
является характеристическим. В нашем
случае характеристическое уравнение может быть определено как
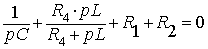
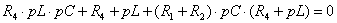
Таким образом, характеристическое уравнение имеет вид:
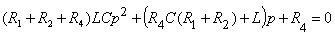
Подставляя исходные данные и решая характеристическое
уравнение, получаем корни:
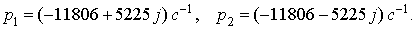
Следовательно, свободная составляющая тока при двух
комплексно-сопряженных корнях имеет вид
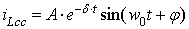 ,
,
где 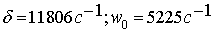
. Нахождение общего вида реакции цепи. Общий вид реакции цепи
находится путем суммирования свободной и принужденной составляющих реакции
цепи:
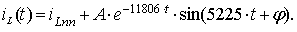
. Определение постоянных интегрирования. Для определения
постоянных интегрирования 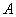 и
и 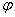 записываются уравнения для свободной составляющей тока и ее
первой производной при
записываются уравнения для свободной составляющей тока и ее
первой производной при 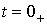 :
:

С учетом того, что 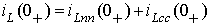 найдем
найдем
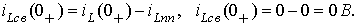
Для определения 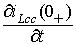 записываются уравнения Кирхгоффа для цепи в момент после
коммутации
записываются уравнения Кирхгоффа для цепи в момент после
коммутации 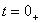 , причем в цепи емкость заменяется
источником напряжения
, причем в цепи емкость заменяется
источником напряжения 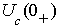 , а индуктивность - источником тока
, а индуктивность - источником тока 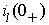 . Напряжение на индуктивности равно
. Напряжение на индуктивности равно 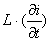 :
:
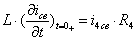 (1)
(1)
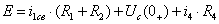 (2)
(2)
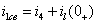 (3)
(3)
Решая эту систему, получаем
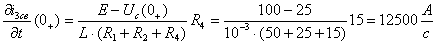
Подставив найденные величины в систему уравнений для определения
постоянных интегрирования, получим:
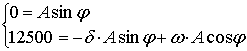
Эта система имеет решение
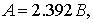
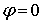
. Окончательная запись реакции цепи.
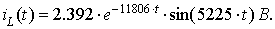
График зависимости тока 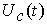 представлен на рисунке 2:
представлен на рисунке 2:

Рисунок 2. График зависимости тока 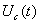
2. Операторный метод расчета
. Анализ цепи до коммутации и определение независимых
начальных условий. Независимые начальные условия определяются аналогичным
образом, как и в классическом методе:
2. Составление операторной схемы замещения цепи
после коммутации. Поскольку цепь имеет ненулевые начальные условия, то с учетом
внутренних источников ЭДС операторная схема замещения цепи после коммутации
будет иметь вид представленный на рисунке 3.
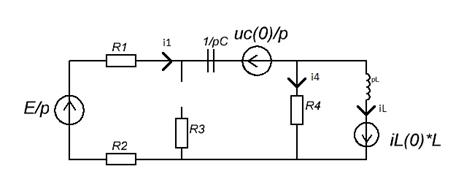
Рисунок 3 - Операторная схема замещения
Составление уравнений электрического равновесия цепи в
операторной форме. Для цепи рис.3 можно составить систему уравнений Кирхгофа:
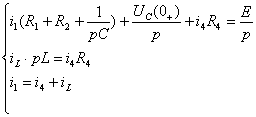
4. Решение уравнений Кирхгофа относительно изображений искомых
токов и напряжений. Полученная система уравнений решается простой подстановкой,
и решение имеет вид:
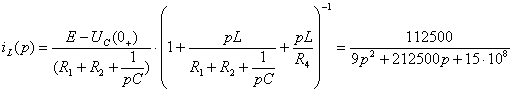
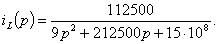
Операторное изображение напряжения 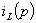 может быть представлено в виде
может быть представлено в виде 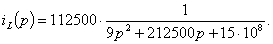
. Определение оригинала изображения искомого тока. Для этого
найдем полюсы функции изображения
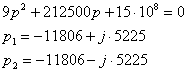
Полюсы комплексно-сопряженные, поэтому общий вид функции во
временной области
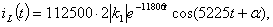
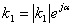 - вычет в том полюсе, у которого мнимая часть имеет положительный
знак. Вычеты определяются по общей формуле
- вычет в том полюсе, у которого мнимая часть имеет положительный
знак. Вычеты определяются по общей формуле
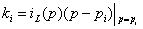 .
.
В нашем случае 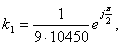 поэтому
поэтому
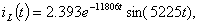
Полученное выражение совпадает с результатом, полученным при
решении классическим методом.
График зависимости тока 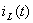
 представлен на рисунке 4:
представлен на рисунке 4:

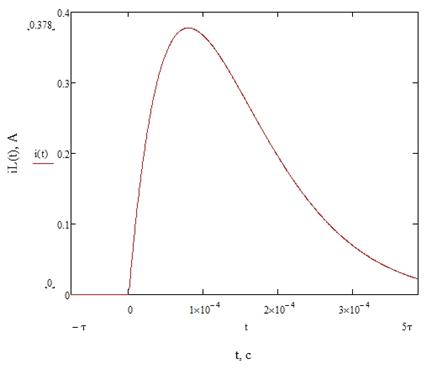
Рисунок 4. График зависимости тока 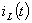
3. Воздействие гармонической ЭДС
1. Анализ цепи до коммутации. Определяется значение тока через
индуктивность 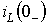 и напряжение на емкости
и напряжение на емкости 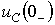 до коммутации
до коммутации 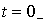 (ключ замкнут). Так как в цепи действует
источник гармонического напряжения, то для анализа следует воспользоваться
методом комплексных амплитуд.
(ключ замкнут). Так как в цепи действует
источник гармонического напряжения, то для анализа следует воспользоваться
методом комплексных амплитуд.
Для исходной схемы составляется комплексная схема замещения цепи
(рисунок 5) и определяются ее параметры следующим образом:
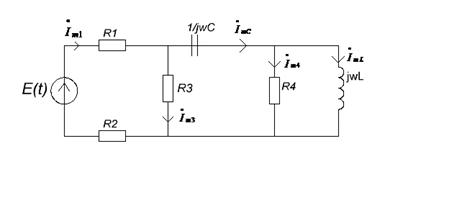
Рисунок 5. Комплексная схема замещения
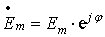 ,
, 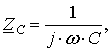
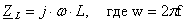
Подставляя численные значения, получаем:
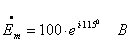
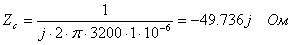
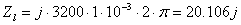 Ом
Ом
Для активных сопротивлений комплексная и действующая формы
совпадают.
Определяем ток 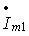 :
:
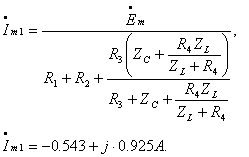
Далее запишем закон напряжений Кирхгофа для первого контура:
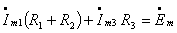 , откуда с учетом
, откуда с учетом 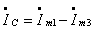 получаем
получаем
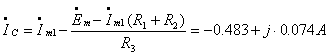
Зная значение тока 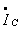 , определяется комплексное амплитудное значение напряжения на
емкости:
, определяется комплексное амплитудное значение напряжения на
емкости:
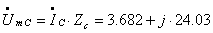
Значение напряжения на емкости к моменту коммутации 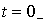 будет соответственно равно
будет соответственно равно
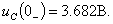
Далее записываем уравнения Кирхгофа для второго контура
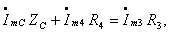
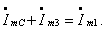
Отсюда 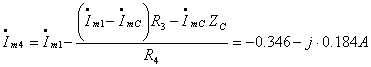
Комплексное амплитудное значение тока через индуктивность до
коммутации определяется как:
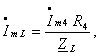
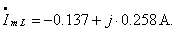
Значение тока к моменту коммутации:
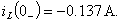
Таким образом, определены значения тока в индуктивности и
напряжения на емкости непосредственно перед коммутацией. Они составляют:
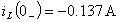 и
и 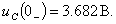
. Определение независимых начальных условий. Независимыми
начальными условиями являются ток в индуктивности и напряжение на емкости в
момент времени 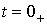 , которые определяются согласно первому и
второму законам коммутации:
, которые определяются согласно первому и
второму законам коммутации:
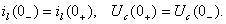
Следовательно, 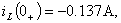
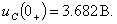
. Составление операторной схемы замещения цепи после коммутации.
Поскольку цепь имеет ненулевые начальные условия, то с учетом внутренних
источников ЭДС операторная схема замещения цепи после коммутации будет иметь
вид представленный на рисунке 6.

Рисунок 6 - Операторная схема замещения
3. Составление уравнений электрического
равновесия цепи в операторной форме. Для цепи рис.6 можно составить систему
уравнений Кирхгофа:
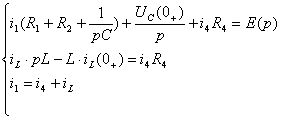
В данном случае E(p) - изображение по Лапласу гармонического
воздействия:
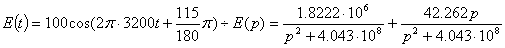
. Решение уравнений Кирхгофа относительно изображений искомых
токов и напряжений. Полученная система уравнений имеет решение
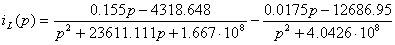
. Определение оригинала изображения искомого тока проводим по
методу, изложенному в п.2. Искомый ток
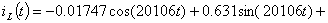
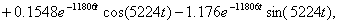
Можно сделать вывод, что вид свободной части реакции цепи
совпадает с найденным ранее. Это связано с тем, что свободная составляющая не
зависит от внешних воздействий и определяется только параметрами цепи.
График зависимости тока 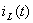 представлен на рисунке 7:
представлен на рисунке 7:
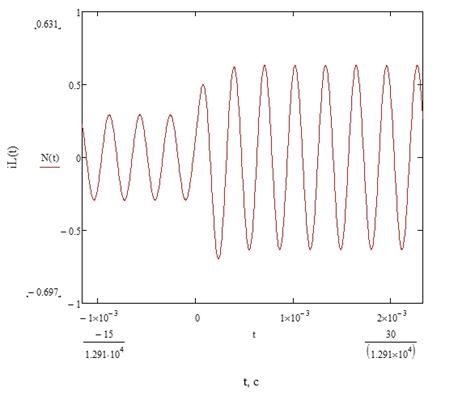
Рисунок 7. График зависимости тока 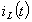
4. Метод переменных состояния
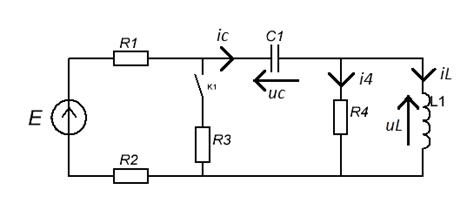
Рисунок 8.
1) Составление системы дифференциальных уравнений цепи. Для
составления системы дифференциальных уравнений записывается система уравнений
цепи по Кирхгофу:
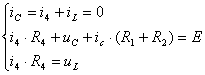
Учтем, что 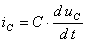 и
и 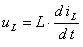 :
:

2) Эта система просто разрешается
относительно производных:
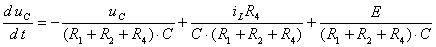
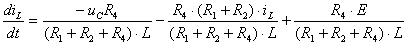
) Запишем полученную систему уравнений для переменных
состояния в матричной форме:
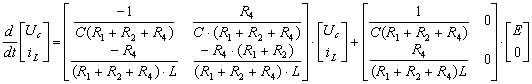
Т.е 
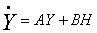 ,
,
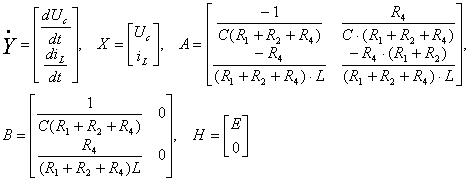
Таким образом,
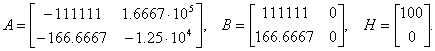
На данном этапе можно проконтролировать правильность действий. Для
этого найдем собственные числа матрицы А:
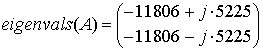
Видно, что найденные собственные числа совпадают с корнями
характеристического уравнения цепи.
) Численный метод решения
Решим численно матричное уравнение 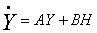 .
.
Начальные условия 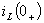 и
и 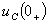 найдены в пункте 1. Итак,
найдены в пункте 1. Итак,
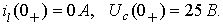
Зададим начальные значения в виде вектора
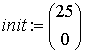
Формализованная матричная запись уравнений состояния:
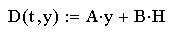
Задаём конечное значение интервала интегрирования:
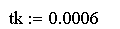
Задаём число точек интегрирования:
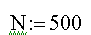
Обращаемся к программе интегрирования:
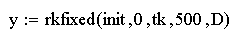
Матрица y имеет три
столбца, пронумерованные от нуля до двух. Первый из них содержит значения
времени, второй - 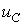 , третий -
, третий - 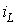 .
.
7. Строим график переменных состояния, который представлен
на рисунке 9, 10.
индуктивность ток коммутация
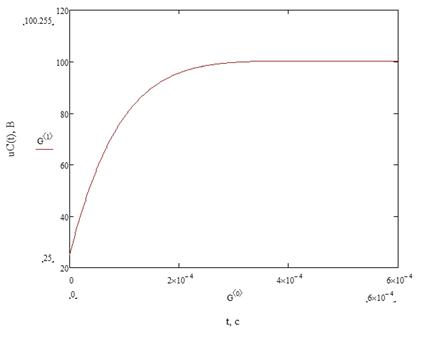
Рисунок 9
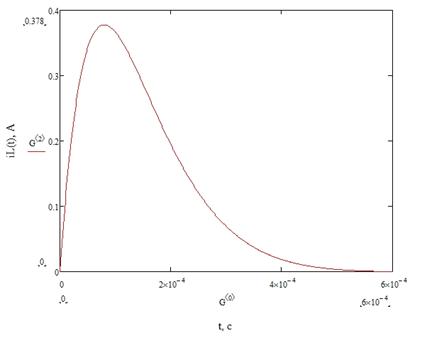
Рисунок 10
) Аналитическое решение
Для аналитического решения уравнений состояния нам понадобятся
найденные выше собственные числа матрицы коэффициентов A. Это комплексно-сопряженные числа, и по ним мы можем определить
общий вид свободной составляющей переменных состояния:
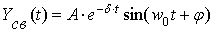 ,
,
где 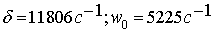 .
.
Общий вид решения
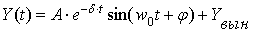
Принужденная составляющая может быть найдена непосредственным
решением уравнения 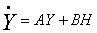 , если принять во внимание, что при постоянных
воздействиях вынужденная составляющая реакции тоже постоянна, и поэтому
производные в левой части системы уравнений состояния будут равны нулю:
, если принять во внимание, что при постоянных
воздействиях вынужденная составляющая реакции тоже постоянна, и поэтому
производные в левой части системы уравнений состояния будут равны нулю:
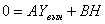 .
.
Отсюда 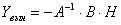 . Решая это уравнение, получаем
. Решая это уравнение, получаем
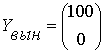 , что соответствует результатам, найденным в пункте 1.
, что соответствует результатам, найденным в пункте 1.
Независимые начальные условия были найдены также в пункте 1:
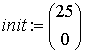 .
.
Теперь необходимо найти начальные значения производных переменных
состояния. Их можно определить непосредственно по уравнениям состояния при t=0+:
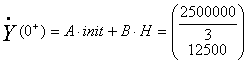
С другой стороны, 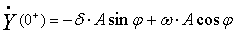 . Решая систему уравнений относительно постоянных интегрирования A и φ
. Решая систему уравнений относительно постоянных интегрирования A и φ
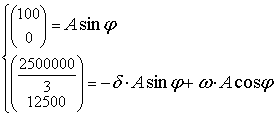 , получаем
, получаем 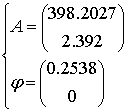 .
.
Итак, искомые переменные состояния:
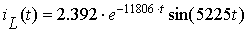
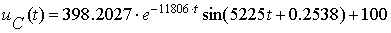
Графики этих величин можно увидеть на рисунках 9 и 10
. Определение комплексной частотной характеристики
Для нахождения операторной функции передачи цепи составим
операторную схему замещения цепи при нулевых начальных условиях (рисунок 11).
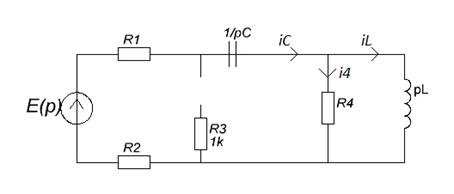
Рисунок 11. Операторная схема замещения цепи
По определению:
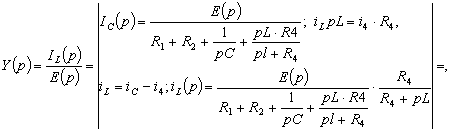
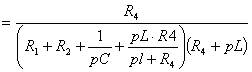
Подставив в полученное выражение значения R,L,C
окончательно получаем:
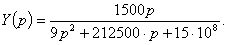
Отсюда находят комплексную передаточную проводимость:
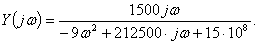
Представив полученную комплексную передаточную проводимость в
показательной форме находят:
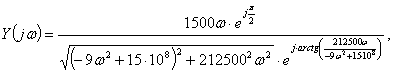
отсюда: АЧХ цепи -
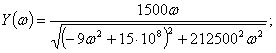
ФЧХ цепи -
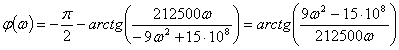 .
.
Графики АЧХ и ФЧХ приведены на рисунке 12 и рисунке 13.
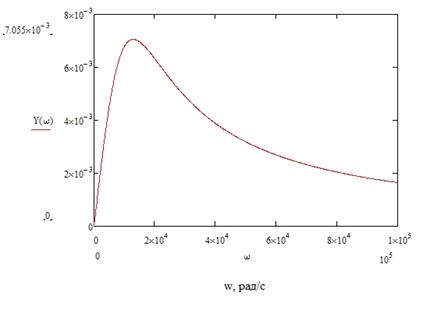
Рисунок 12 - График зависимости АЧХ комплексного входного
сопротивления
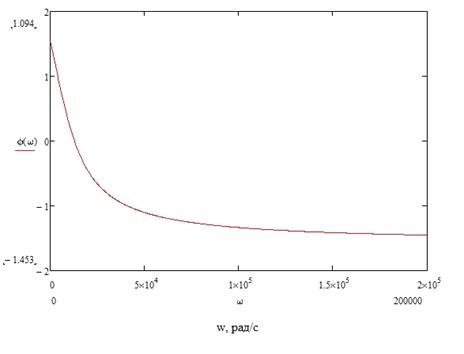
Рисунок 13 - График зависимости ФЧХ комплексного входного
сопротивления
В предыдущем примере была найдена передаточная проводимость
цепи:
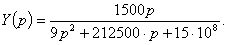
используя которую находят переходную характеристику цепи:
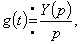 где
где 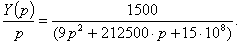 .
.
Оригинал функции 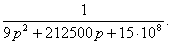 уже был найден нами в пункте 2.
уже был найден нами в пункте 2.
Поэтому сразу запишем вид g(t):
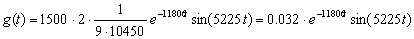
График переходной характеристики приведен на рисунке 14
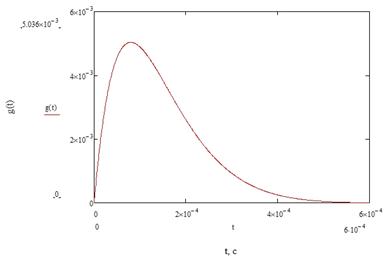
Рисунок 14. График переходной характеристики цепи
Импульсная характеристика цепи может быть определена, как
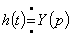 .
.
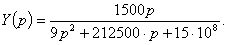
Полюса знаменателя функции Y(p) находились нами
неоднократно:
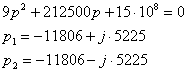
Общий вид решения, отвечающий комплексно-сопряженным корням
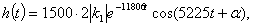
Определим k1 - вычет в точке p1:
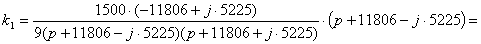
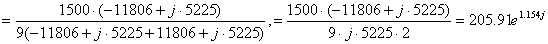
Отсюда
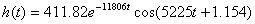
График импульсной характеристики приведен на рис. 15.
Рисунок 15 - Импульсная характеристика цепи
Заключение
В соответствии с заданием были выполнены следующие расчёты:
определение зависимости тока через индуктивность от времени при воздействии
постоянной ЭДС классическим и операторным методами, была найдена зависимость
тока через индуктивность от времени при воздействии гармонической ЭДС, получены
зависимости тока через индуктивность от времени путем решения уравнений
состояния системы как численным методом с использованием алгоритма Рунге-Кутта,
так и аналитически; были определены комплексная частотная характеристика и
временные характеристики цепи.
При воздействии постоянной ЭДС (классический метод):
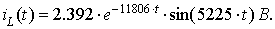
При воздействии постоянной ЭДС (операторный метод):
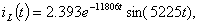
При воздействии гармонической ЭДС:
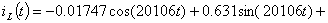
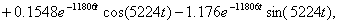
АЧХ цепи: 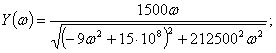
ФЧХ цепи: 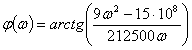 .
.
Переходная характеристика:
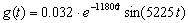
Импульсная характеристика цепи:
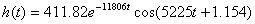
Литература
1.
Попов В.П. Основы теории цепей: Учеб. для вузов.- 3-е изд., испр.
М.:
Высш. шк., 2000. - 575 с.
.
Меренков М.Б. Основы теории цепей. Методические указания к курсовому
проектированию: Учебное пособие/ Под ред. В.И. Неволина - Челябинск: Изд-во
ЮУрГУ, 2004.- 71 с.
.
Калугин Ю.Е., Меренков М.Б. Основы теории цепей: Учебное пособие.
Челябинск:
Изд-во ЮУрГУ, 2001. - 166с.
4.
Стандарт предприятия. Курсовые и дипломные проекты. Общие требования к
оформлению.