Исследование статистической зависимости количества эритроцитов в крови от возраста человека
Содержание
Введение
Цель и задачи
Теоретическая часть
Исходные данные и их
обработка
Диаграмма рассеивания
Корреляционная таблица
Гистограммы для признаков X и
Y1
Полигоны для признаков X и Y1
Эмпирические функции для
признаков X и Y
Регрессия
Метод наименьших квадратов
Метод наименьших квадратов
для определения p, q, r
Проверка гипотез статистиками
Метод доверительных
интервалов
Заключение
Список литературы
Введение
Целью данной курсовой работы является исследование зависимости количества
эритроцитов в крови человека от его возраста в рамках науки теории вероятностей
и математической статистики.
Несомненно, здоровье является самым важным и необходимым благом для
человека, поскольку, когда человек плохо себя чувствует, все материальные и
нематериальные ценности (деньги, вещи, произведения искусства) начинают
тускнеть в его глазах и уже совсем не являются столь яркими и необходимыми в
его жизни.
В своей работе автор решил рассмотреть, в частности, изменение количества
эритроцитов с взрослением человека, так как совсем небольшие отклонения в обе
стороны могут привести к серьезным заболеваниям.
Используя такие источники, как «Популярная медицинская энциклопедия»,
«Строение и деятельность человеческого тела» и другие, автор изучил важность
учета количества красных клеток крови для нормального функционирования
человеческого организма.
Итак, немного статистических данных.
Количество эритроцитов в крови у здоровых мужчин составляет 4500000
-5500000 штук в 1мм3. У женщин 4000000 - 5000000 в 1мм3.
Общее количество в среднем 25 триллионов эритроцитов.
Средняя длительность жизни эритроцитов составляет 125 дней.
Красные клетки крови выполняют много важнейших функций в организме
человека, поэтому их изучение очень важно. Основными функциями эритроцитов
являются:
· участие в газообмене;
· поглощение кислорода гемоглобином в легких;
· транспортировка кислорода и отдача его тканям и органам;
· восприятие в тканях углекислого газа и транспортировка его в
легкие;
· регуляция кислотно-щелочного равновесия организма и другие.
Недостаток эритроцитов в крови приводит к такому заболеванию, как
белокровие, которое очень трудно излечить.
Так как большинство заболеваний, обнаруженных в самом начале их развития,
излечиваются более легко, то важно знать некоторые признаки заболевания, критерии,
по которым мы можем сказать, что человек действительно болен. Собственно
применительно к эритроцитам, важным является строгий учет их количества в крови
относительно возраста человека.
Цель и
задачи
Дана
выборка 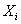 ,
, 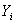 , i=1,…N, N=100,
где
, i=1,…N, N=100,
где 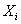 ,
, 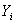 - значения
двух признаков исследуемых объектов.
- значения
двух признаков исследуемых объектов.
Задача
состоит в изучении характера зависимости между признаками X и Y.
Требуется:
. Построить
диаграмму рассеивания. Найти все выборочные числовые параметры: 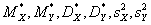 , моду и медиану выборки для признаков X и Y.
Построить гистограммы для признаков X и Y. Построить
корреляционную таблицу.
, моду и медиану выборки для признаков X и Y.
Построить гистограммы для признаков X и Y. Построить
корреляционную таблицу.
. Проверить
гипотезу 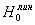 , что зависимость между признаками X и Y близка к
линейной. Методом наименьших квадратов определить числа
, что зависимость между признаками X и Y близка к
линейной. Методом наименьших квадратов определить числа 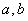 и
и 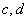 , такие,
чтобы уравнения линейных регрессий
, такие,
чтобы уравнения линейных регрессий 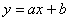 и
и 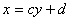 наименее отклонялись от экспериментальных данных.
Найти выборочный коэффициент корреляции
наименее отклонялись от экспериментальных данных.
Найти выборочный коэффициент корреляции 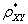 .
Изобразить обе линии регрессии на диаграмме рассеивания. Для проверки гипотезы
.
Изобразить обе линии регрессии на диаграмме рассеивания. Для проверки гипотезы 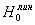 используйте статистики
используйте статистики
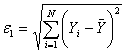 и
и 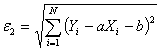 .
.
3. Проверить
гипотезу 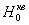 , что зависимость между признаками X и Y близка к
квадратичной. Методом наименьших квадратов определить числа
, что зависимость между признаками X и Y близка к
квадратичной. Методом наименьших квадратов определить числа 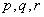 такие, чтобы линия квадратичной регрессии
такие, чтобы линия квадратичной регрессии 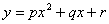 наименее отклонялась от экспериментальных данных.
Построить график линейной и параболической регрессий на диаграмме рассеивания.
Для проверки гипотезы
наименее отклонялась от экспериментальных данных.
Построить график линейной и параболической регрессий на диаграмме рассеивания.
Для проверки гипотезы 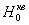 используйте статистики
используйте статистики
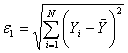 и
и 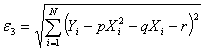
4. Сравнить между собой результаты пунктов 2 и 3 и ответить на вопрос
задания о наличии и виде зависимости между признаками X и Y.
Теоретическая
часть
Приведем основные определения и понятия из курса теории вероятностей и
математической статистики, которые будут задействованы и использованы в данной
работе.
Статистика - это наука, которая занимается получением, обработкой, а
также анализом данных и публикацией информации, характеризующей количественные
закономерности жизни общества в неразрывной связи с их качественным
содержанием. В более узком смысле статистика - это совокупность данных о
каком-либо процессе или явлении, а в естественных науках понятие статистика
означает анализ массовых явлений и основана на применении методов теории
вероятностей, которые будут достаточно широко использоваться в данной курсовой
работе.
Статистика разрабатывает специальную методологию исследования и
обработки материалов: массовые статистические наблюдения, метод группировок,
средних величин, индексов, балансовый метод, метод графических изображений. Ее
главной задачей является получение и публикация достоверных, научно
обоснованных данных о развитии и функционировании производства, об изменениях в
составе населения и уровне жизни, о наличии материальных резервов в госбюджете
и их использовании и т.д.
Итак, методами теории вероятностей и математической статистики являются
результаты наблюдений. Изучение результатов наблюдений случайных массовых
явлений позволяет установить закономерность. Задача математической статистики
состоит в том, чтобы указать методы сбора и обработки статистических данных для
получения выводов.
Теория вероятностей - раздел математики, в котором по данным вероятностям одних
случайных событий находят вероятности других событий, связанных каким - либо
образом с первым. Теория вероятностей изучает также случайные величины и
случайные процессы. Одно из основных задач теории вероятностей состоит в выяснении
закономерностей, возникающих при взаимодействии случайных факторов.
У нас имеется выборка случайных значений, объем которой равен n = 100.
Выборочной совокупностью или просто выборкой называют совокупность
случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых
производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов этой
совокупности.
Виды выборочной совокупности:
ü повторная;
ü бесповторная;
ü репрезентативная.
Повторной называют выборку, при которой отобранный объект (перед отбором
следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную
совокупность не возвращается.
Выборка должна правильно представлять пропорции генеральной совокупности.
Это требование коротко формулируют так: выборка должна быть репрезентативной
(представительной).
Наблюдаемые
значения 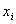 называются вариантами, а последовательность
вариант в возрастающем прядке - вариационным рядом. Частотой
называются вариантами, а последовательность
вариант в возрастающем прядке - вариационным рядом. Частотой 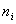 называется число, которое показывает, сколько раз
встречается данный вариант. Относительной частотой
называется число, которое показывает, сколько раз
встречается данный вариант. Относительной частотой 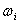 называется отношение частоты
называется отношение частоты 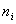 к объему выборки n.
к объему выборки n.
Случайной
величиной 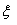 называется величина, которая может принимать
различные (случайные) значения. Она характеризуется несколькими величинами.
называется величина, которая может принимать
различные (случайные) значения. Она характеризуется несколькими величинами.
Гистограммой частот называется ступенчатая фигура,
состоящая из прямоугольников, основаниями которых служат частичные интервалы
длинной h, а высоты равны частоте 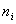 .
.
Исходные
данные и их обработка
Нам дана выборка (объемом n =
100) зависимости числа Y от
числа X (см. табл. 1).
Таблица 1
Исходные данные
|
X
|
Y
|
X
|
Y
|
X
|
Y
|
X
|
Y
|
|
15,00
|
46,80
|
5,18
|
18,30
|
8,98
|
30,50
|
4,22
|
16,10
|
|
0,21
|
4,09
|
1,87
|
9,71
|
10,60
|
34,10
|
1,06
|
4,72
|
|
17,90
|
55,10
|
6,62
|
22,80
|
16,80
|
54,40
|
9,92
|
32,80
|
|
7,68
|
28,60
|
8,06
|
27,10
|
2,70
|
9,97
|
17,10
|
54,30
|
|
18,00
|
55,60
|
8,16
|
28,10
|
7,58
|
26,50
|
9,34
|
33,10
|
|
14,90
|
46,60
|
6,76
|
23,10
|
12,30
|
37,60
|
19,20
|
58,00
|
|
13,40
|
41,70
|
13,80
|
44,50
|
4,06
|
15,40
|
3,54
|
14,40
|
|
0,36
|
4,66
|
3,14
|
11,80
|
0,24
|
3,60
|
4,64
|
18,50
|
|
0,99
|
6,96
|
6,26
|
20,90
|
4,86
|
17,40
|
9,60
|
32,20
|
|
9,78
|
33,50
|
10,80
|
36,20
|
9,48
|
30,00
|
7,48
|
25,10
|
|
5,00
|
17,80
|
6,28
|
21,70
|
15,70
|
49,50
|
6,54
|
22,80
|
|
6,68
|
22,50
|
7,54
|
25,40
|
13,50
|
43,00
|
1,10
|
6,26
|
|
17,70
|
55,40
|
3,98
|
14,60
|
16,60
|
53,70
|
19,40
|
61,50
|
|
1,99
|
10,20
|
14,30
|
44,70
|
12,10
|
39,20
|
4,52
|
15,50
|
|
19,70
|
62,90
|
10,00
|
32,70
|
15,00
|
48,90
|
8,78
|
30,50
|
|
7,16
|
23,20
|
13,50
|
42,30
|
12,20
|
40,30
|
3,54
|
13,00
|
|
10,80
|
35,70
|
6,62
|
21,10
|
8,06
|
26,00
|
16,70
|
52,50
|
|
0,65
|
3,93
|
18,40
|
59,10
|
17,60
|
54,80
|
9,70
|
31,90
|
|
9,72
|
33,80
|
1,76
|
7,68
|
19,70
|
61,70
|
1,97
|
9,22
|
|
12,60
|
42,70
|
12,40
|
40,40
|
9,98
|
33,00
|
17,10
|
53,90
|
|
4,78
|
17,90
|
11,20
|
36,30
|
16,40
|
53,10
|
6,14
|
21,50
|
|
1,36
|
5,67
|
14,60
|
48,70
|
17,80
|
57,80
|
3,24
|
15,40
|
|
4,94
|
19,40
|
1,44
|
7,04
|
5,42
|
20,00
|
8,04
|
27,90
|
|
12,30
|
41,10
|
11,00
|
35,60
|
6,98
|
24,30
|
6,70
|
23,40
|
|
4,64
|
18,70
|
17,80
|
56,10
|
5,98
|
22,60
|
9,56
|
31,00
|
|
15,00
|
46,80
|
5,18
|
18,30
|
8,98
|
30,50
|
4,22
|
16,10
|
|
0,21
|
4,09
|
1,87
|
9,71
|
10,60
|
34,10
|
1,06
|
4,72
|
|
17,90
|
55,10
|
6,62
|
22,80
|
16,80
|
54,40
|
9,92
|
32,80
|
|
7,68
|
28,60
|
8,06
|
27,10
|
2,70
|
9,97
|
17,10
|
54,30
|
Диаграмма
рассеивания
Построим диаграмму рассеивания (см. рисунок 1):
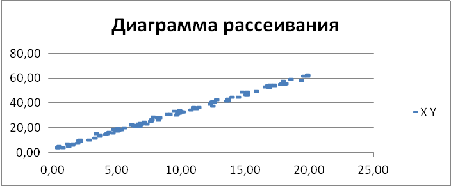
Рис. 1 Диаграмма рассеивания
Найдем некоторые характеристика для X и Y:
Ø выборочное
среднее: 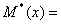 9,1947;
9,1947;
Ø выборочную
дисперсию: 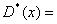 30,1964;
30,1964;
Ø исправленную
дисперсию: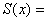 30,5014;
30,5014;
Ø среднеквадратичное
отклонение: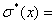 5,4951;
5,4951;
Ø оценку
среднеквадратичного отклонения: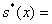 5,5228;
5,5228;
Ø выборочное
среднее: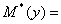 30,6331;
30,6331;
Ø выборочную
дисперсию: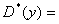 268,7818;
268,7818;
Ø исправленную
дисперсию: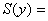 271,4968;
271,4968;
Ø среднеквадратичное
отклонение: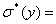 16,3946;
16,3946;
Ø оценку
среднеквадратичного отклонения: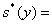 16,4772;
16,4772;
Ø выборочный
коэффициент корреляции: 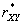 = 0,998.
= 0,998.
Найдем также моду и медиану для X и Y.
Модой случайной дискретной величины называется значение случайной величины,
которое имеет максимальную вероятность:
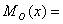 15,
15, 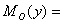 22,8.
22,8.
Медианой называется такое значение варьирующего признака,
которое приходится на середину упорядоченного ряда:
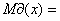 8,47,
8,47, 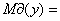 29,3.
29,3.
Корреляционная
таблица
Разобьем значения X и Y на 6 интервалов (см. табл. 2, табл. 3) и построим
корреляционную таблицу (см. табл. 4).
Таблица 2
Интервалы разбиения Х
|
Интервалы разбиения Х
|
0,212-3,46
|
3,46-6,708
|
6,708-9,96
|
9,96-13,204
|
13,204-16,452
|
16,452-19,7
|
|
Представитель интервала
|
1,84
|
5,08
|
8,33
|
11,58
|
14,83
|
18,08
|
Таблица 3
Интервалы разбиения Y
|
Интервалы разбиения Y
|
3,6-13,483
|
3,6-13,483
|
3,6-13,483
|
3,6-13,483
|
3,6-13,483
|
3,6-13,483
|
|
Представитель интервала
|
8,54
|
8,54
|
8,54
|
8,54
|
8,54
|
Таблица 4
Корреляционная таблица
|
X/Y
|
1,84
|
5,08
|
8,33
|
11,58
|
14,83
|
18,08
|
Ny
|
|
8,54
|
16
|
0
|
0
|
0
|
0
|
0
|
16
|
|
18,43
|
0
|
23
|
1
|
0
|
0
|
0
|
24
|
|
28,31
|
0
|
0
|
20
|
0
|
0
|
0
|
20
|
|
38,19
|
0
|
0
|
0
|
13
|
3
|
0
|
16
|
|
48,08
|
0
|
0
|
0
|
0
|
8
|
0
|
8
|
|
57,96
|
0
|
0
|
0
|
0
|
0
|
16
|
16
|
|
Nx
|
16
|
23
|
21
|
13
|
11
|
16
|
100
|
По корреляционной таблице найдем оценки для X.
Ø Выборочное среднее
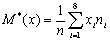 ;
;
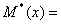 9,1947;
9,1947;
Ø выборочную дисперсию
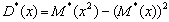 ;
;
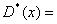 30,1964;
30,1964;
Ø исправленную дисперсию
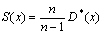 ;
;
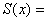 30,5014;
30,5014;
Ø среднеквадратичное отклонение
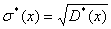 ;
;
 5,4951;
5,4951;
Ø оценку среднеквадратичного отклонения
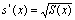 ;
;
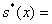 5,5228.
5,5228.
Найдем
так же оценки для Y.
Ø Выборочное среднее
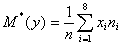 ;
;
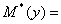 30,6331;
30,6331;
Ø выборочную дисперсию
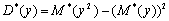 ;
;
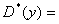 268,7818;
268,7818;
Ø исправленную дисперсию
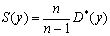 ;
;
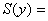 271,4968;
271,4968;
Ø среднеквадратичное отклонение
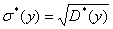 ;
;
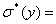 16,3946;
16,3946;
Ø оценку среднеквадратичного отклонения
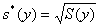 ;
;
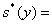 16,4772.
16,4772.
Выборочный
коэффициент корреляции:
Ø выборочный корреляционный момент
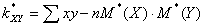 ;
;
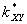 = 89,9142
= 89,9142
Ø выборочный коэффициент корреляции
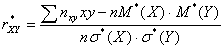 ;
;
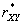 = 0,998.
= 0,998.
Оценки
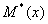 ,
, 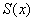 ,
, 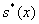 ,
, 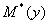 ,
, 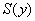 ,
, 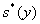 -
несмещенные оценки математического ожидания, дисперсии и среднеквадратичного
отклонения.
-
несмещенные оценки математического ожидания, дисперсии и среднеквадратичного
отклонения.
Видим,
что вычисленные величины по сгруппированным рядам - корреляционной таблице мало
отличаются от величин, вычисленных по всей выборке. В случае ручной обработки
данных использования корреляционной таблицы достаточно оправдано, ощутимо
снижая сложность вычислений.
Теперь можно построить гистограмму для признаков X и Y.
эритроцит
возраст статистический вероятность
Гистограммы
для признаков X и Y
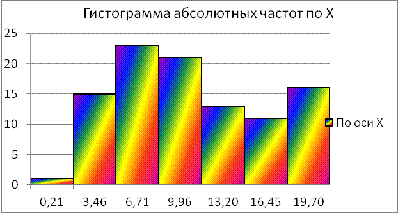
Рис. 2 Гистограмма для признаков X
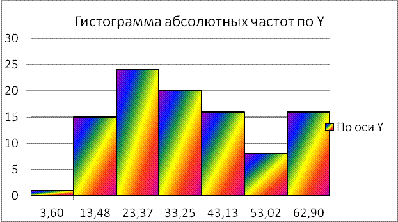
Рис. 3 Гистограмма для признаков Y
Полигоны
для признаков X и Y
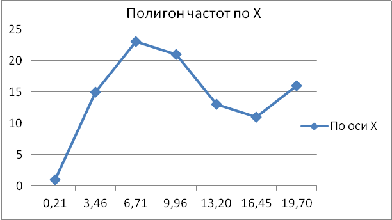
Рис. 4 Полигон для признаков X
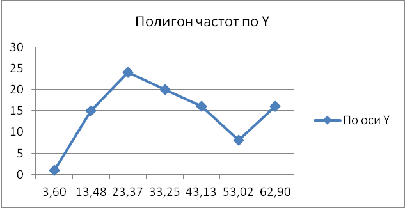
Рис. 5 Полигон для признаков Y
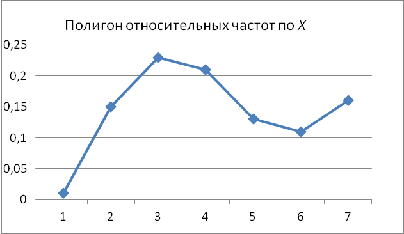
Рис. 6 Полигон отсноительных частот по X
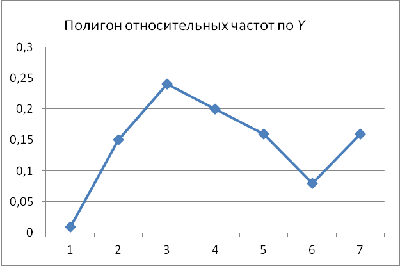
Рис. 7 Полигон отсноительных частот по Y
Эмпирические
функции для признаков X и Y
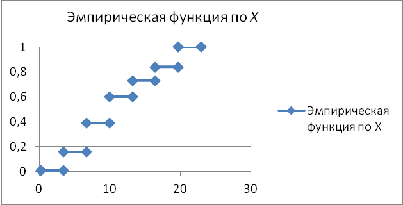
Рис. 8 Эмпирическая функция по X
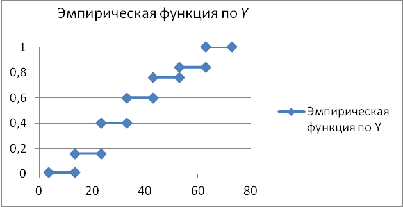
Рис. 9 Эмпирическая функция по Y
Регрессия
Регрессия - зависимость среднего значения величины Y от другой величины X. Понятие
регрессии в некотором смысле обобщает понятие функциональной зависимости
y=f(x). Только в случае регрессии одному и тому же значению x в различных
случаях соответствуют различные значения у.
Регрессионный анализ заключается в определении аналитического выражения
связи, в котором изменение одной величины (называемой зависимой или
результативным признаком) обусловлено влиянием одной или нескольких независимых
величин (факторов).
По форме зависимости различают:
1
линейную
регрессию, которая выражается уравнением прямой (линейной функцией)
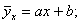
1
нелинейную
(параболическую)
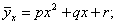
1
другие виды.
В теории вероятностей при исследовании вероятности величины Y по величине
X предполагают, что при любом фиксированном значении X величина Y является
случайной величиной с определенным (зависящим от значения X) условным
распределением вероятностей, по которому вычисляют условное математическое
ожидание:
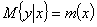
и
дисперсию
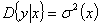 .
.
Целью
регрессионного анализа является оценка функциональной зависимости условного
среднего значения результативного признака y от факторных (x1, x2,…, xn). Основная предпосылка: только y подчиняется нормальному
закону распределения, а факторные признаки (x1, x2,…, xn) могут иметь произвольный закон распределения.
Метод
наименьших квадратов
Метод наименьших квадратов (МНК) - метод, применяемый в теории ошибок
для отыскания одного или нескольких неизвестных по результатам измерений,
содержащим случайные ошибки. МНК используется также для приближенного
представления заданной функции другими (более простыми) функциями и часто
оказывается полезным для обработки наблюдений.
В простейшем случае, когда нет систематических ошибок, а есть случайные
оценки неизвестных величин, полученные с помощью МНК, то они являются линейными
функциями от наблюдаемых значений - статистические оценки.
Если статистические оценки наблюдений независимы и подчиняются
нормальному распределению, то МНК дает оценки неизвестных с наименьшей средней
квадратичной ошибкой. В этом смысле МНК является самым лучшим среди других
способов, позволяющих находить линейные несмещенные оценки.
Если мы рассматриваем слабо формализованные системы, которые трудно
поддаются однозначным и точным описаниям, связь между величинами X и Y
изначально корреляционная. Это связано, в частности, с тем, что Y зависит не
только от X, но и от других параметров, причем такая связь часто носит
случайный характер.
В этом случае, имея экспериментальные точки, задача состоит в том, чтобы
приближённо свести корреляционную связь к функциональной с помощью подбора
такой функции, которая максимально возможным способом близка экспериментальным
точкам. Такая функция называется функцией регрессии.
Обычно вид самой функции угадывается, но она зависит от некоторых
параметров. Задача статистического и корреляционного анализа состоит в
нахождении этих параметров. Для этого и используется метод наименьших
квадратов.
Рассмотрим
случайную двумерную величину (X, Y), где 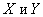 -
зависимые случайные величины. Представим одну из величин как функцию другой.
Ограничимся приближенным представлением величины
-
зависимые случайные величины. Представим одну из величин как функцию другой.
Ограничимся приближенным представлением величины 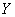 в виде
линейной функции величины X:
в виде
линейной функции величины X:
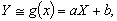
где
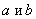 - параметры, подлежащие определению. Это можно
сделать различными способами: наиболее употребительный из них - МНК. Функцию g(x) называют
среднеквадратической регрессией Y на X.
- параметры, подлежащие определению. Это можно
сделать различными способами: наиболее употребительный из них - МНК. Функцию g(x) называют
среднеквадратической регрессией Y на X.
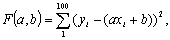
где F - суммарное квадратичное отклонение.
Подберем a и b так, чтобы сумма квадратов
отклонений была минимальной. Для того, чтобы найти коэффициенты a и b, при которых F
достигает минимального значения, приравняем частные производные к нулю:
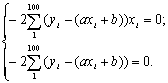
Находим a и b. Выполнив элементарные преобразования, получим систему двух
линейных уравнений относительно a и b:
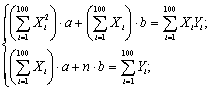
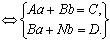 ,
,
Где
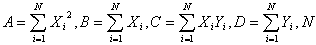 - объём
выборки.
- объём
выборки.
В
нашем случае
A = 3277; B =495; C =7188; D = 1117;N
= 100.
Найдём
a и b из этой линейной. Получим стационарную точку 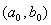 для
для 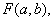 где
где 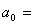 2,98;
2,98; 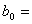 3,26.
3,26.
Следовательно,
уравнение примет вид:
Y = 2,98x+3,26
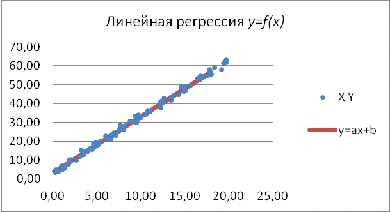
Рис. 10 Линейная регрессия y=f(x)
Построим график линейной регрессии. Для удобства наблюдения график регрессии
будет на фоне диаграммы рассеивания.
Теперь построим регрессию
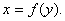
Аналогично
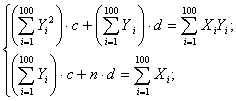
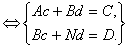 ,
,
Где
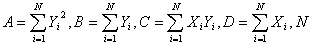 - объём
выборки.
- объём
выборки.
Теперь же A = 120716,9; B =3063,31; C =37157,64; D = 919,47; N = 100.
Найдём
c и d из этой линейной. Получим стационарную точку 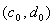 для
для 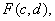 где
где 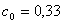 ;
; 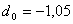 .
.
Следовательно,
уравнение примет вид:
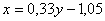
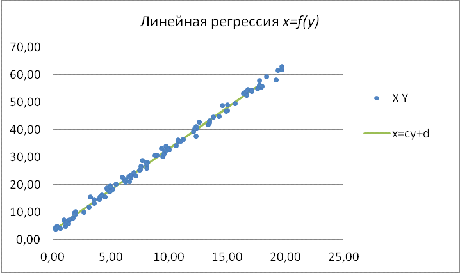
Рис. 11 Линейная регрессия x=f(y)
Теперь для наглядности изобразим обе линии линейной регрессии на
диаграмме рассеивания.
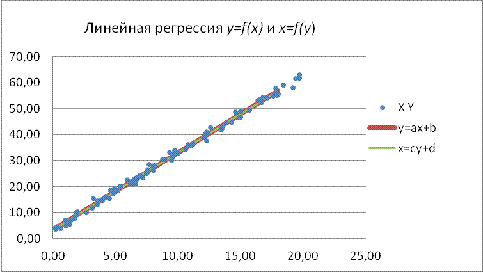
Рис. 12 Линейные регрессии y=f(x) и x=f(y)
Видно,
что они практически совпадают и пересекаются в районе математических ожиданий
признаков 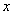 и
и 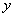 . Зелёная
линия показывает регрессию
. Зелёная
линия показывает регрессию 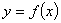 , а
красная -
, а
красная - 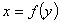 .
.
Метод
наименьших квадратов для определения p, q, r
Найдем по данным наблюдений выборочное уравнение кривой линии
среднеквадратичной (параболической в нашем случае) регрессии.
Ограничимся представлением величины Y в виде параболической функции
величины X:
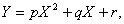
где
p, q, и r - параметры, подлежащие определению. Это можно
сделать с помощью метода наименьших квадратов.
Подберем
параметры p, q и r так, чтобы сумма квадратов отклонений была
минимальной. Так как каждое отклонение зависит от отыскиваемых параметров, то и
сумма квадратов отклонений есть функция F этих параметров:
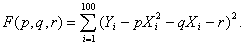
Для
отыскания минимума приравняем к нулю соответствующие частные производные:
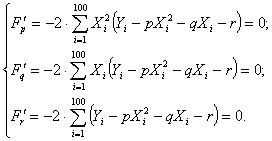
Находим
p, q и r. Выполнив элементарные преобразования, получим
систему трех линейных уравнений относительно p, q и r:
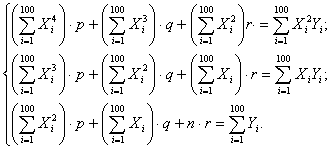
Решая
эту систему методом обратной матрицы, получим: 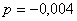 ;
; 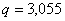 ;
; 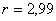 .
Следовательно, уравнение параболической регрессии примет вид:
.
Следовательно, уравнение параболической регрессии примет вид:
y= -
0,004x2+3,055x
+2,99.
Построим график параболической регрессии. Для удобства наблюдения график
регрессии будет на фоне диаграммы рассеивания (см. рисунок 13).
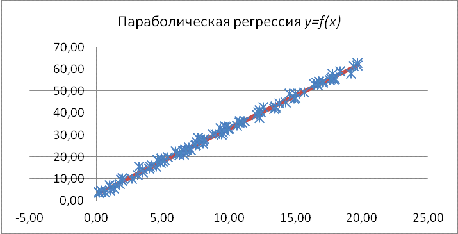
Рис. 13 Параболическая регрессия y=f(x)
Теперь
изобразим линии линейной регрессии 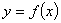 и
параболической регрессии на одной диаграмме, для наглядного сравнения (см.
рисунок 14).
и
параболической регрессии на одной диаграмме, для наглядного сравнения (см.
рисунок 14).
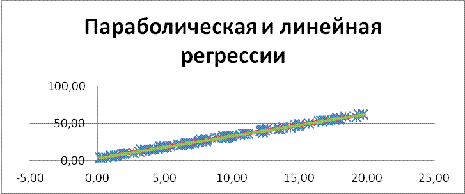
Рис. 14 Параболическая и линейная регрессии
Линейная регрессия изображена красным цветом, а параболическая - синим.
По диаграмме видно, что отличие в данном случае больше, чем при сравнении двух
линий линейных регрессий. Требуется дальнейшее исследование, какая же регрессия
лучше выражает зависимость между x и y, т. е. какой тип зависимости между x и y.
Проверка
гипотез статистиками
Для
начала рассмотрим статистику 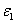 , которая
показывает отклонение значений
, которая
показывает отклонение значений 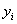 от
от 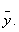
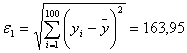
Теперь
обратимся к проверке гипотез 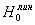 и
и 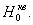 Заметим сразу, что значения, вычисленным с
использованием соответствующих статистик
Заметим сразу, что значения, вычисленным с
использованием соответствующих статистик 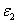 и
и 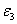 должна быть меньше значения
должна быть меньше значения 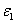 . Статистика
. Статистика 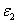 используется
для проверки гипотезы о линейной зависимости, и показывает, насколько величины
используется
для проверки гипотезы о линейной зависимости, и показывает, насколько величины 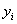 отклоняются от линии регрессии
отклоняются от линии регрессии 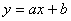 . Вычисляем
. Вычисляем
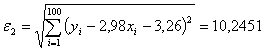 .
.
Аналогично
для гипотезы 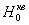 используем статистику
используем статистику 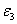 ,
которая, соответственно, показывает отклонение
,
которая, соответственно, показывает отклонение 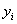 от
квадратной регрессии
от
квадратной регрессии
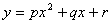
Видим
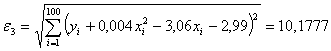 .
.
Следовательно
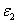 и
и 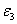 меньше
меньше 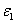 , что и требовалось доказать.
, что и требовалось доказать.
Метод
доверительных интервалов
Рассмотренные
ранее 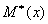 ,
, 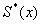 ,
, 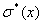 ,
, 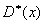 ,
, 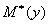 ,
, 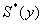 ,
, 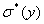 ,
, 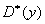 являются
точечными оценками, но наряду с ними при изучении выборки используются
интервальные оценки, так как полезно не только построить оценку, но и
охарактеризовать величину возможной при её использовании ошибки.
являются
точечными оценками, но наряду с ними при изучении выборки используются
интервальные оценки, так как полезно не только построить оценку, но и
охарактеризовать величину возможной при её использовании ошибки.
Интервальной
называют оценку, которая определяется двумя числами - концами интервала.
Интервальные оценки позволяют установить точность и надежность оценок.
Величина
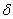 характеризует точность оценки, если выполняется
неравенство
характеризует точность оценки, если выполняется
неравенство
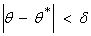 ,
,
где
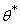 - оценка некоторого параметра
- оценка некоторого параметра 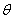 генеральной совокупности. Надежностью (доверительной
вероятностью) оценки
генеральной совокупности. Надежностью (доверительной
вероятностью) оценки 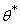 по
по 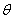 называют
вероятность
называют
вероятность 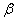 , c которой осуществляется неравенство
, c которой осуществляется неравенство
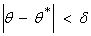
Наиболее
часто задают надежность, равную 0,95; 0,9; 0,999.
Доверительным
называют интервал 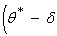 ,
, 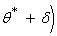 , который
покрывает известный параметр с заданной надежностью
, который
покрывает известный параметр с заданной надежностью 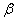 .
.
Рассмотрим доверительный интервал для математического ожидания
генеральной совокупности. Известен объем выборки n = 100;
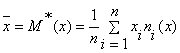 = 9,1947,
= 9,1947,
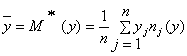 =
30,6331,
=
30,6331,
исправленное
выборочное среднеквадратичное отклонение
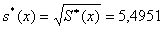 ,
, 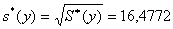 .
.
Найдем
доверительный интервал для оценки неизвестного математического ожидания по X и
Y с надежностями 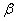 = 0,95; 0,99; 0,999.
= 0,95; 0,99; 0,999.
Если
наблюдаемая случайная величина имеет нормальное распределение, но ее
среднеквадратичное отклонение нам неизвестно, то мы можем построить
доверительный интервал по распределению Стьюдента с 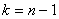 степенями свободы, то есть должно быть справедливо
неравенство:
степенями свободы, то есть должно быть справедливо
неравенство:
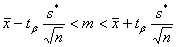 ;
;
где
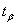 определим по заданным
определим по заданным 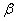 и
и 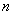 . Это соотношение выражает доверительный интервал для
. Это соотношение выражает доверительный интервал для 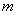 , определяемый с помощью распределения Стьюдента.
, определяемый с помощью распределения Стьюдента.
Найдем
доверительные интервалы для математического ожидания X.
При
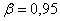 ;
; 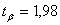 : 8,1
<
: 8,1
< 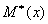 < 10,3.
< 10,3.
При
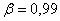 ;
; 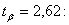 7,8 <
7,8 <
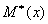 < 10,6.
< 10,6.
При
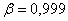 ;
; 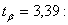 7,3 <
7,3 <
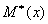 < 11,1.
< 11,1.
Найдем доверительные интервалы для дисперсии X.
При
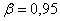 ;
; 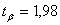 : 29,1
<
: 29,1
< 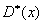 < 31,3.
< 31,3.
При
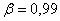 ;
; 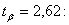 28,8
<
28,8
< 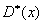 < 31,6.
< 31,6.
При
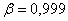 ;
; 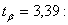 28,3
<
28,3
< 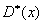 < 32,1.
< 32,1.
Заключение
В данной работе при помощи статистических методов были прослежены
закономерности и связи между двумя дискретными случайными величинами: X - количество эритроцитов в крови
(десятков тысяч) и Y - возраст
человека (лет).
Для этих величин были посчитаны числовые характеристики дискретных
случайных величин, построены полигоны и гистограммы распределения частот, приведены
диаграммы рассеивания с линиями регрессии, а также корреляционная таблица и
таблица статистической зависимости между случайными величинами X и Y.
В результате была научно доказана в принципе очевидная закономерность: с
взрослением человека количество красных клеток крови его увеличивается
соответственно.
Собственно «научная полезность» данной работы состоит в том, что
примерное количество эритроцитов в крови человека определенного возраста можно
вычислить при помощи линий регрессии, что гораздо менее трудоемко, чем
использование медицинских методов анализа крови.
Список
литературы
1. Б.В.
Петровский. Популярная медицинская энциклопедия. - Таллин: Советская
Энциклопедия, 1993.
2. С.Г.
Мамонов. Общая биология. - М.: Высшая школа, 1996.
. С.Ф.
Гилберт. Биология развития. - М.: Мир, 1993.
. Г.Закс.
Строение и деятельность человеческого тела. - СПб: Издательство В.В. Битнера,
1905.
. Э.В.
Семенов. Анатомия и физиология человека. - М.: АНМИ, 1995.
. Н.А.
Фомин. Физиология человека. - М.: Просвещение; ВЛАДОС, 1995.
. Н.В.
Бойчук. Курс гистологии. - Казань: Поволжский книжный центр, 1995.
. П.
Зенгбум. Молекулярная и клеточная биология. - М.: Мир, 1982.
. Ю.
Аккерман. Биофизика. - М.: Мир, 1964.
. М.
Циммерман. Физиология человека. - М.: Мир, 1996.
. В.Е.
Гмурман. Теория вероятностей и математическая статистика: Учеб. пособие для
вузов. - Изд. 7-е, стер. - М.: Высшая школа, 2001.
. В.Е.
Гмурман. Руководство к решению задач по теории вероятностей и математической
статистике: Учеб. пособие для студентов вузов. Изд. 5-е, стер. - М.: Высшая
школа, 2001.