Колебания линейной системы с одной степенью свободы
Введение
Цель работы
- закрепить знания студентов, получаемые при изучении
раздела "Теория колебаний" курса "Механика сплошной среды"
и привить навыки самостоятельного исследования колебательных процессов в
механических системах.
Содержание задания:
1. Составить дифференциальное уравнение малых колебаний системы.
2. Получить
решение этого уравнения и, используя заданные начальные условия, определить
постоянные интегрирования 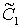 и
и 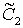 .
.
. Определить
период установившихся вынужденных колебаний 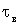 и
добротность системы Д, а для вариантов с малым линейно-вязким
сопротивлением (n<k) дополнительно:
и
добротность системы Д, а для вариантов с малым линейно-вязким
сопротивлением (n<k) дополнительно: 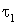 -
условный период затухающих колебаний,
-
условный период затухающих колебаний, 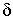 -
логарифмический декремент колебаний,
-
логарифмический декремент колебаний, 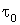 -
постоянную времени затухающих колебаний.
-
постоянную времени затухающих колебаний.
. Исследовать
амплитудно-частотную и фазочастотную характеристики системы.
. Оценить
процесс перехода от начального возмущенного движения системы к установившимся
вынужденным колебаниям, построив графики 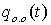 и
и 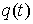 .
.
В курсовой работе рассматриваются малые колебания механической системы с
одной степенью свободы около положения устойчивого равновесия. Требуется
составить дифференциальное уравнение движения и найти его решение при заданных
начальных условиях. Для вынужденных колебаний провести исследование процесса
перехода от начального возмущенного движения к установившимся вынужденным
колебаниям и построить амплитудно-частотную и фазочастотную характеристики
системы.
Механические системы, рассматриваемые в курсовой работе - плоские
механизмы, расположенные в вертикальной плоскости и состоящие из твердых тел,
нитей, демпферов и упругих элементов.
Линейно-вязкое
сопротивление при движении системы возникает в демпфере, сила сопротивления
которого 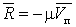 пропорциональна скорости движения поршня
пропорциональна скорости движения поршня 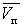 ,
, 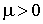 -
коэффициент сопротивления демпфера; массой демпфера можно пренебречь.
-
коэффициент сопротивления демпфера; массой демпфера можно пренебречь.
Силы
и моменты сил воздействия упругих элементов на тела пропорциональны удлинению
пружин или углу закручивания спиральных пружин.
Выполненная
курсовая работа оформляется по ГОСТ 7.32-2001 и представляется на защиту
комиссии в форме доклада с использованием средств мультимедийной аудитории.
колебание механический равновесие фазочастотный
1. Условие
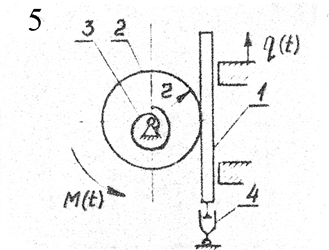
Рис.1
Сила
с моментом 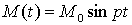 (М0=1 Н·м, p=15 рад/с) действует на однородный
сплошной цилиндр 2 массой m2=4кг и радиусом r=0,1м, вращению которого
препятствует спиральная пружина 3 со статической деформацией
(М0=1 Н·м, p=15 рад/с) действует на однородный
сплошной цилиндр 2 массой m2=4кг и радиусом r=0,1м, вращению которого
препятствует спиральная пружина 3 со статической деформацией 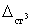 =0,25 рад.
=0,25 рад.
Движению
стержня 1 массой m1=2 кг вниз вдоль вертикальной оси препятствует демпфер 4 с
коэффициентом сопротивления 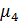
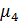 =67,2
=67,2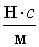 .
.
В
момент времени t=0 цилиндру 2 в положении равновесия была сообщена
начальная скорость 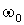 = -0,5 рад/с.
= -0,5 рад/с.
2.
Решение
.1
Составление дифференциального уравнения движения
Составим
дифференциальное уравнение движения системы, используя уравнения Лагранжа II
рода, выбрав в качестве обобщенной координаты q(t)
угол поворота 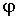 стержня 3 вокруг оси B(z)
(рис.2) с положительным направлением отсчета против хода часовой стрелки.
стержня 3 вокруг оси B(z)
(рис.2) с положительным направлением отсчета против хода часовой стрелки.
Кинетическая
энергия системы:
Т
= Т1 + Т2 , (1)
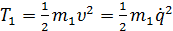
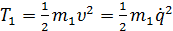 (2)
(2)
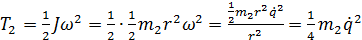
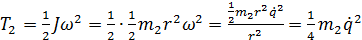 (3)
(3)
Тогда
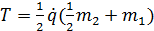
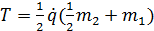 (4)
(4)
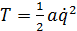
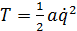 , где
, где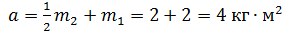
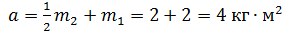 (5)
(5)
Обобщенную
силу Q представим в виде
=
QП + QФ + QВ (t) .
(6)
Из
условия равновесия системы
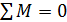
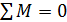 (7)
(7)
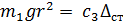
Запишем
выражение, определяющее изменение потенциальной энергии системы при повороте
цилиндра на угол 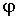 от положения статического равновесия
от положения статического равновесия
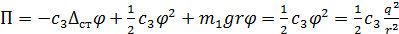
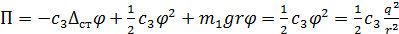 (8)
(8)
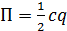
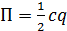 ,
, 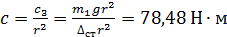
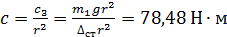 ,
, 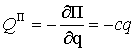 (9)
(9)
Диссипативная
функция Рэлея
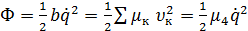
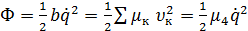 (10)
(10)
Откуда
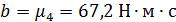
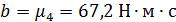 ,
, 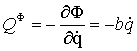 . (11)
. (11)
И,
наконец, определим 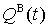
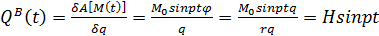
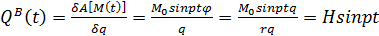 (12)
(12)
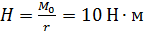
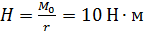 (13)
(13)
Дифференциальное
уравнение движения системы с учетом (5), (9), (11) и (13) имеет вид
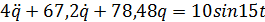
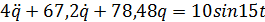 (14)
(14)
или
в канонической форме
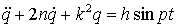 , (15)
, (15)
2.2
Решение и исследование уравнения
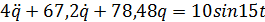
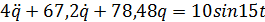
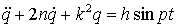 ,
,
где
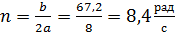
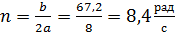 (16)
(16)
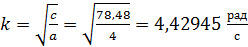
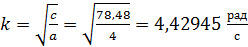 (17)
(17)
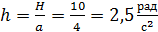
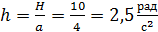 (18)
(18)
Имеем
случай большого линейно-вязкого сопротивления n > k,
поэтому общее решение однородного уравнения qо.о (t) запишем
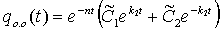 (19)
(19)
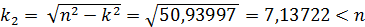
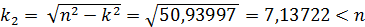 (20)
(20)
Частное
решение уравнения
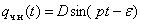 , (21)
, (21)
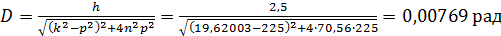
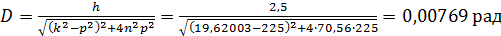 (22)
(22)
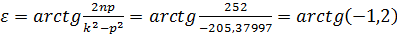
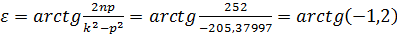 (23)
(23)
поскольку
ε
меняется в пределах от 0 до x,
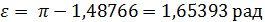
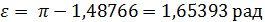 (24)
(24)
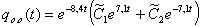 (25)
(25)
Найдем
постоянные 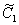 и
и 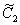 :
:
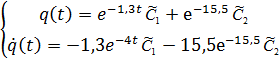
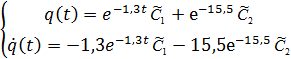 (26)
(26)
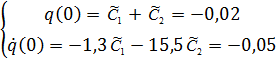
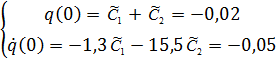 (27)
(27)
Отсюда
следует,
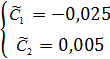
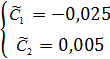 (28)
(28)
Окончательный
вид решения:
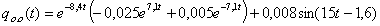
Вычислим
добротность системы Д и период вынужденных колебаний 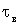 :
:
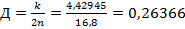
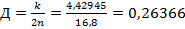 ,
, 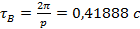
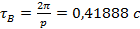 (29)
(29)
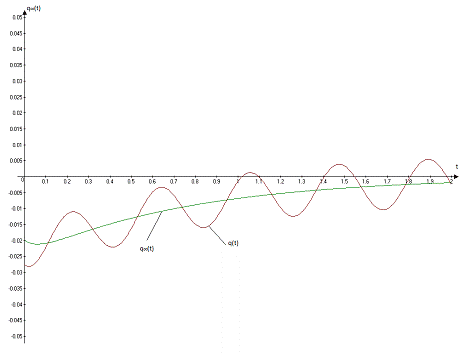
Рис.
2
Для
оценки перехода от движения системы, возникшего в начальный момент t=0 в
результате начального возмущения (q0= -0,02,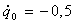 рад/с), к
установившимся вынужденным колебаниям построим графики
рад/с), к
установившимся вынужденным колебаниям построим графики 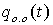 и q(t) на интервале времени
и q(t) на интервале времени 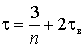 ,
достаточном для этого перехода:
,
достаточном для этого перехода:
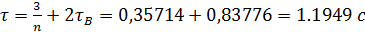
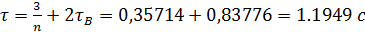 (30)
(30)
На
рис.2 представлены графики 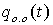 и q(t).
Видно, что на выбранном интервале времени при
и q(t).
Видно, что на выбранном интервале времени при 
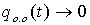 , а q(t) переходит в установившиеся вынужденные колебания.
, а q(t) переходит в установившиеся вынужденные колебания.
2.3
Характеристики системы
Амплитудно-частотная
 и фазочастотная
и фазочастотная 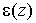 характеристики
системы, построенные по значениям, приведенным в табл.1, даны на рис.3 и рис.4.
характеристики
системы, построенные по значениям, приведенным в табл.1, даны на рис.3 и рис.4.
Таблица
1
|
z
|
λ
|
ε
|
|
0
|
1
|
0
|
|
0,5
|
0,5
|
1,2
|
|
1,0
|
0,27
|
1,57
|
|
1,5
|
0,18
|
1,79
|
|
2,0
|
0,12
|
1,95
|
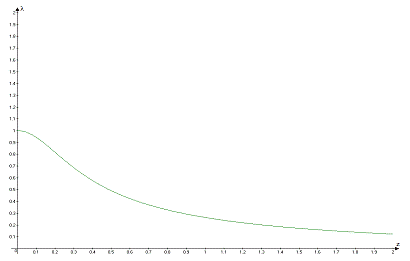
Рис.
3 Амплитудно-частотная
характеристика 
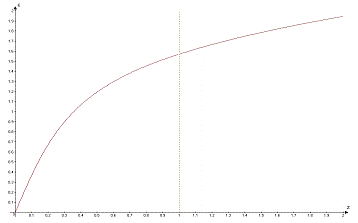
Рис.
4Фазочастотная характеристика 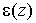
Поскольку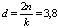 , максимальное значение
, максимальное значение 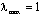 и
соответствует z=0.
и
соответствует z=0.
Заключение
1. При выполнении курсовой работы проанализирована колебательная
система, составленная из однородного сплошного цилиндра, стержня, спиральной
пружины и демпфера.
2. Составлено
дифференциальное уравнение малых колебаний линейной системы с одной степенью
свободы, получены его решения. В результате решений определено, что заданная
система обладает большим линейно-вязким сопротивлением (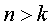 ). На выбранном интервале времени при
). На выбранном интервале времени при 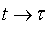
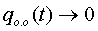 , а
, а 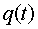 переходит
в установившиеся вынужденные колебания.
переходит
в установившиеся вынужденные колебания.
. Для
систем с большим линейно-вязким сопротивлением движение без вынужденной силы
(общее однородное решение) имеет не колебательный, затухающий характер, что
представлено на рис. 2, потому что коэффициент затухания n=8,4
рад/с больше круговой частоты собственных колебаний системы k=4,42945
рад/с. В момент начала движения (при 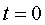 с) величина
с) величина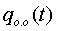 =-0,02 рад/с.
=-0,02 рад/с.
. График
окончательного решения (величина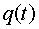 )
представлен также на рис. 2. По графику q(t)
можно сказать, что возбужденные колебания системы не будут затухающими, т.е.
амплитуда D=0,00769 рад. постоянна как при отсутствии резонанса,
так и при резонансе. Линейное сопротивление не влияет на частоту вынужденных
колебаний, которая совпадает с частотой возмущающей силы p=15
рад/с.
)
представлен также на рис. 2. По графику q(t)
можно сказать, что возбужденные колебания системы не будут затухающими, т.е.
амплитуда D=0,00769 рад. постоянна как при отсутствии резонанса,
так и при резонансе. Линейное сопротивление не влияет на частоту вынужденных
колебаний, которая совпадает с частотой возмущающей силы p=15
рад/с.
. Определены
период установившихся вынужденных колебаний 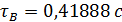
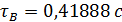 и
добротность системы Д= 0,26366.
и
добротность системы Д= 0,26366.
. На
рис. 3 представлена амплитудно-частотная, а на рис. 4 - фазочастотная
характеристики системы. Можно судить о том, что амплитуда вынужденных
колебаний стремится к нулю, и не будет превышать величины статического смещения
при увеличении частоты возмущающей силы.
. Фазочастотная
характеристика показывает нам то, как система, с начальным фазовым сдвигом 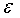 =1,65393 рад. будет откликаться на изменение частоты
возмущающей силы.
=1,65393 рад. будет откликаться на изменение частоты
возмущающей силы.
Список литературы
1. Добронравов
В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. - М.: Высшая
школа, 1974, 1983, 1989. -575 с.
2.Методические указания по выполнению курсовой работы по теме
"Колебания линейной системы с одной степенью свободы" по курсу
"Механика сплошной среды" Москва,2008.