Использование мультимедийных средств на начальном этапе изучения обыкновенных дробей и процентов в 5-6 классах общеобразовательной школы

Использование мультимедийных средств на начальном этапе изучения обыкновенных дробей и процентов в 5-6 классах общеобразовательной школы

Департамент образования города Москвы

Государственное образовательное учреждение высшего профессионального образования города Москвы

«Московский городской педагогический университет»

Математический факультет

Кафедра математического анализа и методики его преподавания

ДИПЛОМНАЯ РАБОТА

По теме: «Использование мультимедийных средств на начальном этапе изучения обыкновенных дробей и процентов в 5-6 классах общеобразовательной школы»

По специальности 050201.65 «Математика» с дополнительной специальностью «Информатика»

Студентки

курса очной формы обучения

Гармышевой Е.С.

Научный руководитель:

ст. преподаватель

Кирюшкина О.В.

Москва 2010

Содержание

Введение

Глава 1. Психолого-педагогические основы использования средств мультимедиа на начальном этапе изучения темы «Обыкновенные дроби и проценты»

1.1 Психолого-педагогические аспекты реализации принципа наглядности в обучении

1.1.1 Наглядность как один из основных принципов обучения

1.1.2 Мышление и его механизмы

1.1.3 Визуальное мышление, как формирование образов теоретических понятий

1.1.4 Средства формирования визуального мышления на уроках математики

.1.5 Визуальные задачи

1.2 Использование информационных технологий в современном учебном процессе

1.2.1 История внедрения компьютерных средств обучения в систему образования

1.2.2 Психологические особенности использования информационных технологий

.2.3 Методика применения информационных технологий в обучении

1.2.4 Использование технологии Macromedia Flash при разработке учебных пособий

.2.5 Научно-педагогические требования к компьютерным учебным пособиям

Глава 2. Методика изучения темы «Обыкновенные дроби и проценты»

2.1 Анализ учебной литературы по теме «Обыкновенные дроби и проценты»

.2 Методические основы изучения тем «Обыкновенные дроби и проценты» в школе

Глава 3. Мультимедийное пособие по теме «Обыкновенные дроби и проценты»

3.1 Основные характеристики пособия

3.2 Методические рекомендации к использованию пособия

Заключение

Библиография

Введение

На протяжении многих лет учителя стараются повысить качество усвоения знаний учащихся по теме «Обыкновенные дроби» и «Проценты» с помощью различных форм и методов. В настоящее время все большее и большее внимание на начальном этапе обучения отводится использованию средств наглядности, визуализации базовых элементов. Это обеспечивает разностороннее формирование образов, способствуют прочному усвоению знаний, пониманию связи научных знаний с жизнью. Каждый учитель математики ставит перед собой задачу не только сообщить школьникам определенную информацию, наполнить их память некоторым набором фактов и образов, но и научить учащихся думать, развить их мысль, творческую инициативу, самостоятельность.

Наиболее актуальным и современным направлением решения этой проблемы является внедрение в школы информационных технологий. В частности, использование компьютера позволяет реализовать принцип наглядности на более совершенном уровне, а именно использование компьютера позволяет создавать различные динамические иллюстрации, которые способствуют более эффективному усвоению и осмыслению содержания обучения.

Глубокое понимание и осмысление основ изучаемого материала порождает интерес к дальнейшему приобретению знаний, связанных с ним. Поэтому крайне важно, чтобы основные понятия по теме «Обыкновенные дроби» и «Проценты» были успешно усвоены учащимися.

Впервые учащиеся сталкиваются с понятиями «Обыкновенные дроби» и «Проценты» в пятом классе. И на протяжении всего дальнейшего обучения тесно взаимодействуют с ними. Именно начальный этап изучения этих тем определяет дальнейшее успешное обучение учащихся, формирует умение переносить полученные знания в новую ситуацию на протяжении изучения всего курса математики 5-6 класса, а в последствии при изучении в 7-11 классах курса алгебры и геометрии. Понятия «Обыкновенной дроби» и «Процентов» являются базовыми понятиями всего курса математики, поэтому необходимо уже на начальном этапе обучения добиться наиболее глубокого и прочного усвоения этих понятий.

Такому уровню усвоения способствует предъявление учащимся рационально организованной наглядности, визуализирующей эти понятия. Современные информационные технологии позволяют сделать такую наглядность динамичной.

Основной целью данной дипломной работы является создание мультимедийного пособия по теме “Обыкновенные дроби и проценты”, содержащего динамические иллюстрации, посредством которых визуализируется представление о дробях и процентах, для обеспечения более качественного подхода при введении соответствующих базовых понятий школьного курса математики. Для достижения данной цели, были поставлены следующие задачи:

1.  изучить психолого-педагогические аспекты реализации принципа наглядности в обучении, особенности визуального мышления учащихся на уроке;

2.       исследовать психолого-педагогические аспекты применения мультимедийных средств в процессе обучения, в частности, установить роль и виды компьютерной наглядности в обучении, требования, предъявляемые к компьютерным средствам обучения;

.        проанализировать учебную и методическую литературу по теме «Обыкновенные дроби» и «Проценты» для определения структуры и отбора содержания нашего пособия;

.        разработать мультимедийное пособие по теме «Обыкновенные дроби и проценты»;

.        разработать методические рекомендации по использованию этого мультимедийного пособия в учебном процессе.

Решение поставленных задач определило структуру дипломной работы. Она состоит из трех глав, введения, заключения, списка литературы и приложения. Первая глава посвящена изучению психолого-педагогических основ использования средств мультимедиа на начальном этапе изучения темы «Обыкновенные дроби и проценты». Обоснованы средства формирования и использования визуального мышления учащихся на уроках математики при изучении тем «Обыкновенные дроби» и «Проценты» в 5-6 классах. Рассматривается целесообразность использования компьютерной наглядности. Так же необходимо выделить возможности использования современных компьютерных средств в процессе обучения, определить требования предъявляемые к ним. При разработке необходимо учитывать и принципы обучения: такие как наглядность, доступность и т. п.

Во второй главе рассматривается методика введения понятий «обыкновенная дробь» и «процент». С этой целью проводится анализ методической литературы и, в частности, учебников математики для 5-6 классов общеобразовательной школы.

В третьей главе описывается мультимедийное пособие по теме «Обыкновенные дроби и проценты», задача которого состоит в визуализации учебного материала, связанного с изучением основных понятий, а также методические рекомендации по применению дидактического пособия.

К работе прилагается компакт-диск, содержащий мультимедийное пособие по теме «Обыкновенные дроби и проценты».

Глава 1. Психолого-педагогические основы использования средств

мультимедиа на начальном этапе изучения темы «Обыкновенные

дроби и проценты»

.1 Психолого-педагогические аспекты реализации принципа

наглядности в обучении

.1.1 Наглядность как один из основных принципов обучения

Общеизвестно, что эффективность обучения зависит от степени привлечения к восприятию всех органов чувств человека. Чем более разнообразны чувственные восприятия учебного материала, тем более прочно он усваивается. Эта закономерность нашла свое выражение в дидактическом принципе наглядности.

Принцип наглядности, является одним из важнейших принципов обучения, теоретическое обоснование которого впервые предложил Ян Коменский, полагавший, что наглядность является одним из важнейших инструментов процесса обучения. Считал, что путь человеческого познания начинается с чувственного восприятия конкретных фактов и явлений. И.Г. Песталоцци видел в наглядности единственную основу всякого развития, рассматривал ее как средство развития у детей наблюдательности, умения сравнивать предметы, выявлять их общие и отличительные признаки и соотношения между ними. Он первым указал на роль использования наглядности для формирования логического мышления.

К.Д. Ушинский - русский педагог, придавал большое значение соблюдению принципа наглядности, говорил о наглядности, как об «инструменте», отвечающем психологическим особенностям детей. Наглядность, по его мнению, делает обучение более доступным, конкретным и интересным, что является фактором, препятствующим образованию перегрузок и возникновению усталости. Много внимания уделяли восприятию ребенком предметов и явлений окружающего мира советские психологи середины XX века. В результате большинство из них пришли к выводу, что «наглядность не изолирует восприятие и представление от целостной аналитико-синтетической умственной деятельности» [11].

В обучении необходимо следовать логике процесса усвоения знаний. Наглядность является показателем простоты и понятности того психического образа, который обучаемый создаёт в процессе восприятия, памяти, мышления и воображения. Таким образом, основная задача реализации принципа наглядности в учебном процессе - это развитие мышления учащихся, посредством опоры, главным образом, на чувственно-наглядные впечатления. Принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения учащимися изучаемого материала. Благодаря наглядности создаются условия для практического применения осваиваемого материала.

Однако характер и степень использования наглядности различны на разных этапах обучения. Излишнее увлечение наглядностью в обучении может привести к нежелательным результатам. Конкретная наглядность (например, рассмотрение моделей геометрических тел) должна постепенно уступать место абстрактной наглядности (рассмотрению плоских чертежей).

По характеру отражения окружающей действительности различают следующие виды наглядности:

1.  натуральная (естественная) наглядность, представляющая собой реальные предметы или процессы (объекты и явления, раздаточный материал и др.);

2.       изобразительная наглядность (фотографии, художественные картины, рисунки, учебные картины и др.) применяется, когда показать реальный предмет не предоставляется возможным, а созерцание конкретного образа необходимо;

.        символическая наглядность (чертежи, графики, схемы, таблицы, диаграммы) своеобразный язык, специально изучаемый.

К третьему типу относится и динамическая наглядность, которая способствует более глубокому пониманию и усвоению процессов и явлений, протекающих во времени. Например, в задачах на движение по реке - скорость по течению, против течения, введение сообразно этих понятий осуществлять таким образом, чтобы были отражены и проиллюстрированы те динамические процессы, которые лежат в основе данного понятия и составляют его сущность.

Принцип наглядности обучения обусловлен рядом факторов:

1.     наглядность обучения является средством познания учащимися окружающего мира, и поэтому процесс этот происходит более успешно, если основан на непосредственном наблюдении и изучении предметов, явлений или событий;

2.       познавательный процесс требует включения в овладение знаниями различных органов восприятия; согласно К.Д. Ушинскому, знания будут тем прочнее и полнее, чем большим количеством различных органов чувств они воспринимаются;

.        наглядность обучения основана на особенностях мышления детей, которое развивается от конкретного к абстрактному; на ранних этапах ребёнок мыслит больше образами, чем понятиями; с другой стороны, понятия и абстрактные положения осмысливаются учащимися легче, если они подкрепляются конкретными фактами, примерами;

.        наглядность повышает интерес учащихся к знаниям и делает процесс обучения более лёгким; согласно К.Д. Ушинского: «Учите ребёнка каким-нибудь пяти неизвестным ему словам, и он будет долго и напрасно мучиться над ними; но свяжите с картинками двадцать таких слов и ребёнок усвоит их на лету…».

Принцип наглядности - дидактический принцип обучения, относящийся к числу ведущих. Его необходимость обосновывается диалектикой перехода от чувственного восприятия к абстрактному мышлению в процессе познания. В соответствии с принципом наглядности обучение строится на конкретных образах, непосредственно воспринимаемых обучающимися.

В процессе наблюдения предметов и явлений реальной действительности человек обнаруживает различия и сходства между ними, определяет их общие характерные черты, обобщает свои наблюдения, создает понятия, формулирует законы и правила, которым подчинены эти явления. Таким образом, «переработанные» впечатления превращаются в понятия и абстрактные обобщения.

Выдающийся русский физиолог и мыслитель-материалист И.М. Сеченов отмечал, что мысль человека переходит из области ощущений в область внутренней речи как системы условных знаков. Без этого элементы мышления, лишенные образных форм, не имели бы возможности фиксироваться в сознании [22].

Информация, полученная человеком из окружающего мира, позволяет человеку представлять не только внешнюю, но и внутреннюю сторону предмета, представлять предметы в отсутствие их самих, предвидеть их изменение во времени, устремляться мыслью в необозримые дали и микромир. Все это возможно благодаря процессу мышления.

.1.2 Мышление и его механизмы

В познании окружающего мира значительную роль играют процессы ощущения и восприятия. Но познание действительности не заканчивается, начинаясь с ощущений и восприятия, переходит к мышлению.

В психологии под мышлением понимают процесс отражения объективной действительности, составляющий высшую ступень человеческого познания. Отталкиваясь от ощущений и восприятий, мышление, выходя за пределы чувственного опыта, расширяет границы нашего познания в силу своего характера, позволяющего опосредованно (т.е. умозаключением) раскрыть то, что непосредственно (т.е. восприятием) не дано.

Мышление представляет собой порождение нового знания, порождение такого результата, какого ни в самой действительности, ни у субъекта на данный момент времени не существует.

С позиций современной психологии механизм порождение нового знания связан с созданием образа, который может быть описан как: чувственный опыт, полученный в процессе восприятия, накладываемый на познавательные структуры человека, в результате чего приобретается образная форма.

Мышление, в отличие от других психологических процессов, почти всегда связано с наличием проблемной ситуации, задачи, которую необходимо решить, и изменением условий, в которых эта задача задана. Таким образом, мышление совершается в соответствии с определенной логикой.

Дадим краткую характеристику каждому из видов мышления.

1. Наглядно-действенное мышление - это вид мышления, при использовании которого человек непосредственно связан с практическим преобразованием действительности.

Основано на переборе действий, связанных с целями данной задачи. Наглядно-действенное мышление отражается в терминах «пощупать проблему руками», «ручное мышление». Примерами могут быть задачи типа решения головоломок, прохождения по лабиринту, завязывания морских узлов.

2. Наглядно-образное мышление - это вид мышления непосредственно связан с восприятием окружающей действительности, и без нее совершаться не может. К примерам такого типа мышления можно отнести поиск объектов и фрагментов на сложном фоне, выделение сигнала из шума, описание характеристик отдельных фрагментов реальных объектов, т.е. способы работы с реальными пространственными сценами и реальными объектами.

. Теоретическое образное мышление - это вид мышления, связанный с манипулированием образами. Образные структуры в процессе решения задачи человек извлекает непосредственно из памяти или творчески воссоздаёт воображением.

4. Теоретическое понятийное мышление - это вид мышления, пользуясь которым человек в процессе решения задачи привлекает знания, полученные другими людьми, выраженные в понятийной форме, суждениях, умозаключениях.

Виды мышления у человека сосуществуют, взаимно дополняют друг друга в процессе интеллектуальной деятельности, однако в зависимости от её характера и конечных целей преобладает тот или иной вид мышления. По степени своей сложности, по требованиям к интеллекту и другим способностям человека ни один из видов мышления не уступает другому [30, 24].

Рассмотрим более подробно механизм мышления в целом.

Любой познаваемый объект может выступать для человека как в своих достаточно известных свойствах или качествах, так и в менее известных, а то и просто неизвестных качествах и отношениях. Следовательно, в каждой новой жизненной ситуации человек ищет и открывает новые стороны объекта, опираясь в то же время на свой жизненный опыт.

В таком раскрытии познаваемого объекта через включение его в новые связи и отношения состоит основной, исходный и всеобщий «механизм» (способ) мышления. Он называется анализ через синтез [6]. Механизм заключается в следующем: в процессе мышления познаваемый объект включается во все новые связи и в силу этого выявляет новые качества, которые фиксируются в новых понятиях и понятийных характеристиках. Таким образом, из объекта выделяется все новое содержание и свойства.

Следовательно, система знаний, никогда не бывает абсолютно завершенной, а всегда развивается, обогащается все новым содержанием по мере все более глубокого познания.

Поэтому мышление и выступает, прежде всего, как процесс, т. е. как нечто становящееся, формирующееся, развивающееся, никогда полностью не завершенное в своем открытии все новых и новых свойств и отношений объекта.

Приведем пример из области математики, иллюстрирующий действие этого важнейшего способа любого мышления: при изучении в геометрии сначала полностью изучаются все свойства треугольника самого по себе. Когда все свойства изучены и треугольник не может дать никакой новой информации о себе, благодаря простому приему открывается более широкий горизонт. Треугольник больше не рассматривается обособленно, а берется в связи с некоторой другой фигурой - окружностью. Благодаря этому стороны и углы получают совершенно иные определенные взаимоотношения, которых нельзя было открыть и использовать без этого отнесения треугольника к окружности.

Таким образом, первоначально формируется образ самого треугольника, создаются система знаний, которая постепенно наращивается. Впоследствии на эту систему накладывается на новый образ, происходит перестройка определяемых структур.

.1.3 Визуальное мышление, как формирование образов

теоретических понятий

Приведенные выше виды мышления выступают одновременно и как уровни развития. В зависимости от профессии, у человека доминирует тот или иной вид мышления. Например, у художника преобладает наглядно - образное и образное теоретическое мышление. Образное мышление (теоретическое и практическое), основанное на визуальных (зрительных) образах называемых «визуальным мышлением».

Визуальное мышление - это мышление посредством визуальных операций, связанное с порождением, трансформацией предметных пространственных образов восприятия и воображения, созданием новых визуальных форм, несущих определенную смысловую нагрузку и делающих знание видимым [38].

Визуальное мышление опирается на формирование и использования зрительного образа, способствует образованию визуальных понятий. Эти визуальные понятия представляются в виде рисунков и картинок. Человек накапливает всевозможные образы в течение жизни. Таким образом, когда предметы физически отсутствуют, они представлены косвенно нашей памятью и знаниями о них.

Итак, в создание образа участвует механизмы зрительного восприятия и интерпретации цвета, света и тени, попадающих на наши глаза с ранее полученной системой знаний

Зрение - это в сильной степени истолкование, объяснение самому себе, в каком-то смысле постоянное разгадывание кроссвордов. Когда мы говорим: «Я вижу нечто» - это значит, что сработали зрительные механизмы восприятия, кроме того в узнавании этого «нечто» участвовали все зрительные образы, имеющие отношение к данному объекту и хранящиеся в памяти. Именно поэтому можно сказать, что каждый раз, когда мы видим мир, мы строим его заново из хаоса света, цвета, огромного количества уже имеющихся зрительных образов и знаний [24].

Следовательно, восприятие представляет собой часть мыслительной деятельности. В частности, зрительное восприятие является базой зрительного (визуального) мышления. То есть, визуальное мышление берет свое начало в процессе зрительного восприятия, но идет гораздо дальше:

Визуальное мышление опирается на формирование и использование зрительного образа, а значит, является составной частью того вида мышления, который делает акцент на том же: наглядно-действенного, образного и наглядно-образного.

Таким образом, визуальное мышление можно вписать в описываемую схему виды мышления:

Термин «визуальное мышление» был введен американским психологом Р. Арнхеймом, который говорил, что: «Опыт откладывается в образах, и этими образами мы оперируем так же, как если бы они были оригиналами» [10, стр. 100].

Все мы в той или иной степени мыслим визуально. Так кошка, когда собирается преодолеть коварный лабиринт, состоящий из выступов и впадин, одним элегантно рассчитанным прыжком, мыслит визуально.

В этом случае элементы проблемной ситуации изменяются, перестраиваются и трансформируются; внимание переключается; вводятся новые функции и вскрываются новые взаимосвязи. Такие операции, если их предпринимать с целью прийти к решению, составляют то, что называется мышлением формируемых теоретических образов.

Младший школьный возраст, а именно его и рассматриваем - это начало школьной жизни. Ребенок вступает в новый период своего становления, приобретает внутреннюю позицию школьника, учебную мотивацию. Учебная мотивация становится для него ведущей. На протяжении этого периода у ребенка развивается теоретическое мышление; он получает новые знания, умения, навыки - создает необходимую базу для всего своего последующего обучения [25].

.1.4 Средства формирования визуального мышления на уроках

математики

Наглядность в обучении способствует тому, что у школьников, благодаря восприятию предметов и процессов окружающего мира, формируются представления, правильно отображающие объективную действительность, и вместе с тем воспринимаемые явления анализируются и обобщаются в связи с учебными задачами.

С целью реализации принципа наглядности многие учителя используют различные наглядные пособия на своих уроках. К наглядным пособиям относятся:

–     реальные предметы и явления в их натуральном виде;

–       модели объектов и процессов;

–       муляжи (от фр. mouler - формовать, отливать в форму);

–       иллюстративные пособия: картины, рисунки, фотографии;

–       графические пособия: диаграммы, графики, схемы, таблицы;

–     различные технических средств обучения: учебные кинофильмы, средства программированного обучения, компьютерные программные средства. Наглядные средства обучения или иллюстративные материалы - это рисунки, схемы, диаграммы, фотографии, мультимедиа и другие графические изображения, поясняющие текст.

Очень важно использовать наглядные средства целенаправленно, не загромождать уроки большим количеством наглядных пособий. Когда у учащихся имеются необходимые образные представления, следует использовать их для формирования понятий, для развития отвлеченного мышления учащихся. Необходимо постепенно переходить к обобщению наглядных отношений, добиваясь их понимания в отвлеченном плане. Так, проделав умножение и деление на квадратиках или кружочках в пределах двух десятков, следует перейти к уяснению связи между умножением и делением, взаимно обратных отношений между этими арифметическими действиями.

Принцип наглядности обучения в современной дидактике - это ориентация на использование в процессе обучения разнообразных средств наглядного представления соответствующей учебной информации.

Роль учебных моделей (как вид иллюстраций) в формировании теоретических понятий широко раскрыта советским педагогом и психологом В.В. Давыдовым. Он характеризует учебные модели как своеобразный сплав наглядности и понятия, конкретного и абстрактного и предлагает рассматривать моделирование как дидактический принцип, дополняющий наглядность. Соотношение этих принципов В.В. Давыдов определяет следующим образом: «…там, где содержанием обучения выступают внешние свойства вещей, принцип изобразительной наглядности себя оправдывает. Но там, где содержанием обучения становятся связи и отношения предметов, - там наглядность далеко не достаточна. Здесь вступает в силу принцип моделирования».

В условиях технического прогресса и относительной доступности компьютерных средств нельзя не отметить бесспорное преимущество компьютерной графики и мультимедийных проектов в реализации принципа наглядности.

Благодаря современным компьютерным технологиям можно не только во всех подробностях реализовать статические модели иллюстрации, но представить эти модели в динамике, то есть в движении.

Все это позволяет говорить о том, что средства наглядности обретают новую функцию - управления познавательной деятельностью учащихся. С их помощью можно подводить учащихся к необходимым обобщениям, учить применять полученные знания.

Использование форм наглядности, которые не только дополняют словесную информацию, но и сами выступают носителями информации, способствует повышению степени мыслительной активности учащихся.

Для того чтобы формировать визуальное мышление учащихся, нужно заботиться об организации зрительной информации. От использования наглядности как средства повышения эффективности урока нужно перейти к формированию математических визуальных понятий, которые по своему объему, степени обобщенности не уступали бы привычным вербальным (словесным) понятиям.

Н.А. Резник предлагает использование следующих средств для развития визуального мышления учащихся:

1. Информационная схема

2. Визуальные задачи

3. Информационная тетрадь [35]

Согласно теории о поэтапном формировании умственных действий базовую роль при формировании зрительных понятий играет практическая работа.

В практике обучения применение наглядных средств сочетается со словом учителя. Способы сочетания слова и средств наглядности при всем их многообразии составляют несколько основных форм. Одна из них характеризуется тем, что при посредстве слова учитель руководит наблюдением, которое ведут учащиеся, а знания о внешнем облике объекта, о его строении, о протекающих процессах школьники получают из наблюдаемых объектов. Например, при решении задач на проценты, учитель только наводит учащихся на основные задачи на дроби, а сами ученики уже выявляют взаимосвязь между ними. При другой форме сочетания, сведения о предметах и процессах учащиеся получают из словесных сообщений учителя, а наглядные средства служат для подтверждения или конкретизации словесных сообщений.

Знание учителем форм сочетания слова и средств наглядности, их вариантов и сравнительной эффективности дает возможность творчески применять наглядные средства сообразно поставленной дидактической задаче, особенностям учебного материала и другим конкретным условиям.

.1.5 Визуальные задачи

Визуальные задачи выступают как средство развития визуального мышления, организации зрительного образа, нацелены на повышение мыслительной деятельности учащихся.

Под визуальной задачей понимается задача, в которой решение строиться на «живом созерцании». Как правило, исходной посылкой в них является некоторый визуальный образ.

Рассмотрим классификацию визуальных задач, предложенную Н. А. Резник, обозначив следующие параметры: дидактическое назначение, структурные особенности, диапазон применения.

Режим обучения

1. Тренажер - упражнения, восстанавливающие или формирующие определенные навыки учащегося. Задания нацелены на уточнение указанного понятия, его свойств или операций над такими однородными понятиями.

Дидактическое назначение. Решение упражнений тренажера как бы «останавливает» ученика, предоставляя ему возможность сосредоточиться на одном образе или действии.

Структурные особенности. Задачи тренажера составляются на основе единого зрительного образа, подходя к нему с различных сторон, и по степени сложности практически не отличаются друг от друга. Поэтому примеры тренажера должны быть такими, чтобы их решение не требовало громоздких обоснований, длительных рассуждений и преобразований. Устное решение задач тренажера является необходимым условием, нарушение которого значительно снизит действие данного средства обучения.

Диапазон применения. Подобные упражнения можно широко применять тогда, когда утраченные знания и навыки мешают усвоению текущего материала или формированию нового алгоритма. Тренажер может явиться дополнительным средством при подготовке класса к решению трудной задачи, натолкнуть учащихся на возможные пути ее решения.

Пример:

 

 

2. Посмотрите и найдите - задача, данные которой полностью представлены на рисунке.

Дидактическое назначение. Главное назначение данной задачи в образовании навыков поиска: распознавания образа понятия, преобразования его для нахождения ответа, формирование догадки, умения «вдумываться в слово» и «всматриваться в образ».

Структурные особенности. Развернутый текст (описание) здесь, как правило, отсутствует, все ориентиры и подсказки сосредоточены на рисунке и в вопросе. Акцент ставится на «ключевые» (направляющие мысль) слова и характерные особенности рисунка или формулы.

Визуальное представление данных должно быть простым, очевидным и лаконичным. Рисунок должен передавать существо дела и одновременно как можно больше своих данных «вводить в память».

Диапазон применения. Эту задачу можно использовать при демонстрации нового материала, для повторения пройденного, в качестве домашнего задания или в числе задач для самостоятельной работы. Подобные задания могут носить и «развлекательный» характер, побуждая учеников задумываться над правильностью своих представлений о слове, образе или формуле.

Пример: Какие из заштрихованных фигур не могут быть плоскими сечениями куба?

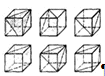
. Серия - это специальный комплект формул, текстов или рисунков, последовательно описывающих конкретное понятие, иллюстрирующих его элементы, свойства и связи. С первым заданием серии должны справиться все, последнее требует определенной сообразительности.

Дидактическое назначение. Задачи «Серии» помогают не только в формировании навыков и приобретении умений, они формируют навыки самостоятельной работы ученика. Их можно использовать как инструмент для конструирования визуального образа объекта. Визуализация трудных для восприятия и логического анализа понятий может значительно облегчить процесс усвоения учебного материала.

Структурные особенности. В основу задач «Серия» положен принцип многоуровневости, обеспеченный последовательным усложнением образа определенного понятия или его свойства. Развитие образа может сопровождаться изменением его структуры, специальным выделением деталей.

Диапазон применения. Данное средство может применяться довольно часто. «Серию» можно применить при начальном вводе понятия, при отработке навыка оперирования им, для визуализации конкретного теоретического положения, для восстановления утраченных знаний и навыков, для усвоения достаточно сложных переходов при решении трудных задач.

Пример: Продолжить серию:

 

f(x)=x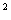+ sinx +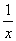

f(2)=2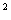+ sin2 +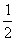

f(-x)=

f(3x+1)=

f(cosx)=

Текущий контроль

Визуальные задачи, предназначенные для текущего контроля, имеют существенную особенность: время выполнения и проверки их сведено к минимуму притом, что содержание может быть достаточно разнообразно.

1. Выберите ответ - это задача, сформированная по модели психометрических тестов.

Дидактическое назначение. Главное назначение данной задачи в образовании техники перевода: учащийся должен сопоставить исходный образ, текст или формулу с предлагаемым списком ответов.

Структурные особенности. «Выберите ответ» представляет собой частный случай теста (см. ниже) в ситуации, когда к одному из его заданий прилагается ряд вариантов различных ответов.

Учебные задания «Выберите ответ» учитель может сформировать на основе материалов учебного текста. Для повышения внимания полезно иногда исключать правильный ответ из общего списка. В таком случае ученики должны сформулировать его самостоятельно. Также в список ответов важно включать наиболее распространенные ошибки учеников, ответы с недостаточными данными и т.д. Среди предложенных ответов один или несколько могут оказаться верными.

Диапазон применения. Данная задача может широко применяться для проверки знания учащимися определения, правила, обозначений, формулы, а также для образования внутренних и межпредметных связей.

Пример:

 

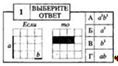
. Тест - это средство, позволяющее проверить усвоение контролируемого навыка, знание определенных фактов, усвоение содержания понятия, умение применять его свойства.

Дидактическое назначение. Главное назначение теста - образование обратной связи в системе «Учитель - ученик». Анализируя ответы учеников, преподаватель сможет выявить проблемы в понимании и усвоении изучаемого материала.

Структурные особенности. «Тест» (как и Тренажер) имеет единое общее указание. Конкретные задачи теста составляются так, чтобы поиск ответа к ним не требовал больших выкладок, громоздких вычислений и длительных рассуждений. Кроме этого не только задания теста, но и ответы к ним могут составлять специально организованную последовательность формул, рисунков или текстов. «Лишний» или отсутствующий ответ позволит избежать подгонки решения последнего по порядку решения задания под оставшееся неиспользованное отношение, заставит сделать определенный выбор.

Диапазон применения. «Тест» может быть применен на различных этапах обучения. При изучении нового материала с помощью теста ученик может выяснить сходство или различие терминов, усвоить новый для него алгоритм действий.

Тест может быть рассчитан на проверку материала конкретного урока, и выполнять функцию текущего контроля.

Пример:

 

. Посмотрите и определите - это задача, построенная на основе единого образа изучаемого объекта. Она включает 5-6 вопросов, которые позволяют исследовать его свойства.

Дидактическое назначение. Задачи «Посмотрите и определите» ориентированы на восстановление и проверку знаний, умений и навыков.

Структурные особенности. Порядок вопросов может быть организован так, чтобы предыдущий вопрос содержал дополнительную информацию к последующему. Однако отвечать на вопросы задачи ученик может и в произвольном порядке. Не всегда обязательно обосновывать ответы, иногда достаточно записи правильного результата. Сильные ученики могут выполнить такую задачу устно, мысленно преобразовывая рисунок, восстанавливая недостающие данные и проводя устные вычисления. Ученикам, которым подобные мыслительные действия на данном этапе трудны, следует перенести рисунок в тетрадь. Все пропорции, детали, обозначения должны быть сохранены, что позволит свободно оперировать ими для получения правильного ответа.

Диапазон применения. Задание «Посмотрите и определите» может оказаться полезным при проверке усвоения теоретического материала, при повторении и закреплении.

Пример:

 

Можно комбинировать задачи, используя задания последовательно в виде заданной цепочки действий, нацеленных на освоение (или проверку знания) объекта и его свойств. Выполнения такого рода заданий будет логически связано с каждым последующим, отличаясь лишь сложностью [35].

Поскольку, на основе одного и того же визуального образа (рисунок, фрагмент текста или формула) можно составить разные задания, любая из задач может быть применена как при обучении, так и при восстановлении и последующем контроле.

В настоящее время понятие «визуальный» все чаще ассоциируется с конструированием реальных моделей (ситуаций, явлений), с помощью использования средств информационных технологий. Проанализируем возможности, которые открывают новые технологии в обучении, какие задачи позволяют решать и какие ситуации моделировать.

1.2 Использование информационных технологий в современном

учебном процессе

.2.1 История внедрения компьютерных средств обучения в

систему образования

Наше время характерно стремительным развитием информационных и компьютерных технологий, которые существенно перестраивают практику повседневной жизни, проникают во все сферы человеческой деятельности. Глобальное внедрение компьютерных технологий, формирование новых коммуникаций и высокоавтоматизированной информационной среды стали не только началом преобразования традиционной системы образования, но и первым шагом к формированию информационного общества.

В истории информатизации образования выделяют четыре этапа:

I.   Период с начала 50-х и до начала 70-х годов. Характеризуется неэффективностью применения компьютерных технологий в обучении, поскольку компьютеризация в этот период не изменила традиционной системы организации обучения, в силу отсутствия возможности персонального доступа обучаемого к компьютеру. Компьютерные программы использовались лишь в качестве тренажеров и контролирующих средств.

II.      Относится к 70-80 годам и связан с внедрением персональных компьютеров в образовательные системы. Помимо контролирующих программ появляются программы информационного характера, что способствует развитию новых форм обучения.

III.    Датируется 80-90 годами и характеризуется расширением парка персональных компьютеров. Возрастают возможности индивидуализации и активности обучения. Именно третий этап дает начало инновационному обучению с помощью компьютеров, дополняя традиционные средства обучения. На этом этапе компьютеризация обучения используется в качестве поддержки самостоятельной работы учащихся в условиях сокращения количества часов по практически всем дисциплинам учебного плана и как средство для дистанционного обучения.

IV.    Начиная с 2000 года можно выделить четвертый этап в развитии информатизации образования. Этот этап связан с активным развитием сетевых технологий доступа к образовательным ресурсам и объединением информационных, обучающих и контролирующих программ в виртуальные курсы, обеспечивающие открытость образовательных процессов [48].

Применение компьютеров в образовании привело к появлению нового поколения информационных образовательных технологий, которые позволили повысить качество обучения, создать новые условия взаимодействия педагога и обучаемого с вычислительной техникой. Таким образом, можно разнообразить методы обучения в соответствии с содержанием учебного материала, что позволяет, повысит эффективность занятий, интерес к предмету.

Внедрение компьютера в сферу образования стало началом революционного преобразования традиционных методов и технологий обучения. Новым этапом глобальной технологизации передовых стран стало появление ИКТ. Примером успешной реализации ИКТ стало появление интернета - глобальной компьютерной сети с ее практически неограниченными возможностями сбора и хранения информации, передачи ее индивидуально каждому пользователю.

За последние 5 лет число детей, умеющих пользоваться компьютером, увеличилось примерно в 10 раз. Однако, как выявлено во многих исследованиях, познавательные, в частности образовательные, мотивы работы с компьютером стоят примерно на двадцатом месте, дети знакомы в основном с игровыми компьютерными программами. Для решения познавательных и учебных задач компьютер используется недостаточно.

В настоящее время в России идет становление новой системы образования, ориентированного на вхождение в мировое информационно-образовательное пространство.

Таким образом, на пути движения России к ИО и внедрения ИКТ в образование в можно выделить три этапа:

·    начальный, связанный с индивидуальным использованием компьютеров, в основном, для организации системы образования, ее административного управления и хранении информации о процессе управления;

·              современный, связанный с созданием компьютерных систем, интернета;

·              будущий, основанный на интеграции новых ИКТ с образовательными технологиями (ОТ) [45].

1.2.2 Психологические особенности использования

информационных технологий

В настоящее время применение технических средств в повседневной жизни оказывают определенное влияние на преобладающие способы мышления. Актуальным становится изучение психологических и социальных аспектов взаимодействия человека и компьютера.

Информационные технологии оказывают как прямое, так и косвенное воздействие на личность человека. Современные ТСО должны стать воплощением «золотого правила дидактики», обоснованного еще Я.А. Коменским, требовавшим, чтобы все, что только можно, представлялось для восприятия чувствами.

Из психологии известно, что зрительные анализаторы обладают значительно более высокой пропускной способностью, чем слуховые. Глаз способен воспринимать миллионы бит в секунду, ухо только десятки тысяч. Информация, воспринятая зрительно, по данным психологических исследований, более осмысленна, лучше сохраняется в памяти. Однако в процессе обучения основным источником информации продолжает оставаться речь учителя, воздействующая на слуховые анализаторы. Следовательно, учителю надо расширять арсенал зрительных и зрительно слуховых средств подачи информации, наиболее высокое качество усвоения достигается при непосредственном сочетании слова учителя и предъявляемого учащимся изображения в процессе обучения. Более полно использовать возможности зрительных и слуховых анализаторов обучаемых позволяют технические средства обучения (ТСО). Важен начальный этап процесса усвоения знаний - ощущения и восприятия. Сигналы, воспринимаемые через органы чувств, подвергаются логической обработке, попадают в сферу абстрактного мышления. В итоге чувственные образы включаются в суждения и умозаключения. Значит, более полное использование зрительных и слуховых анализаторов создает в этом случае основу для успешного протекания следующего этапа познания - осмысления. Кроме того, при протекании процесса осмысления применение наглядности (в частности, изобразительной и словесной) оказывает влияние на формирование и усвоение понятий, доказательность и обоснованность суждений и умозаключений, установление причинно-следственных связей и т.д. Объясняется это тем, что аудиовизуальные пособия влияют на создание условий, необходимых для процесса мышления, лежащего в основе осмысливания.

Большую роль ТСО играют в запоминании как логическом завершении процесса усвоения. Они способствуют закреплению полученных знаний, создавая яркие опорные моменты, помогают запечатлеть логическую нить материала, систематизировать изученный материал, посредством речевых формулировок, вынесенных на экран в виде письменной речи, классификационных схем, схем отношений понятий, круговых схем, классификационных деревьев.

Особенно необходимо учитывать эмоциональное воздействие технических средств. Если учителю важно сконцентрировать внимание учащихся на содержании предлагаемого материала, то сила их эмоционального воздействия вызывает интерес и положительный эмоциональный настрой на восприятие. Избыток эмоциональности затруднит усвоение и осмысление основного материала.

В учебно-воспитательном взаимодействии воспитателя и воспитанника одной из актуальнейших и сложнейших проблем является привлечение и сохранение детского внимания на протяжении всего урока или воспитательного занятия. К.Д. Ушинский считал внимание ученика чрезвычайно важным фактором, способствующим успешности воспитания и обучения. По его мнению, каждый воспитатель должен быть в состоянии обратить внимание ученика на желаемый предмет. Он указывает воспитателю несколько средств сохранения детского внимания: усиление впечатления, прямое требование внимания, меры против рассеянности, занимательность преподавания.

Три из четырех названных Ушинским средств присущи ТСО, которые, обладая широким диапазоном выразительных, художественных и технических возможностей, позволяют легко усилить впечатление от излагаемого материала. Обычно человек воспринимает окружающую действительность в удобном для него порядке, на экране же управление вниманием осуществляется выявлением главного изображения средствами динамики и композиции кадра, монтажной сменой планов. Из кадра убирают или ослабляют все отвлекающее от главного разными способами: соотношением главного объекта и окружающих фоновых объектов, различной интенсивностью окраски, выделением светом и т. п. Но основным приемом остаются выбор и смена планов.

Смена кадров в фильме, слайдов и т.п., демонстрируемых с помощью технических средств объектов, требует пристального внимания, иначе потом ученик не сможет ответить на вопросы, рассказать об увиденных процессах и явлениях, потому что все это на уроке, как правило, повторно не демонстрируется.

Используя ТСО, необходимо учитывать следующие психологические особенности внимания:

·  Сосредоточенность внимания - удержание внимания на одном объекте.

·        Устойчивость внимания, которая даже при активной работе с изучаемым объектом может у детей сохраняться 15 - 20 мин, а потом требуются переключение внимания, краткий отдых.

·        Объем внимания - количество объектов, символов, воспринимаемых одновременно с достаточной ясностью, что в норме составляет 7 ± 2.

·        Распределение внимания - одновременное внимание к нескольким объектам и одновременное полное их восприятие. У детей оно как раз не очень развито, поэтому часто в подготовке экранных пособий используют принцип «фон и фигура», когда изучаемый объект выделяется крупнее всего, что изображено на экране, чтобы усилить внимание именно к нему, так как на общем фоне ученик теряет многие его необходимые характеристики.

·   Переключение внимания - перемещение внимания с одного объекта на другой. Технические средства позволяют давать информацию в нужной последовательности и в нужных пропорциях, акцентируя внимание на тех частях объекта, которые в данный момент являются предметом обсуждения.

Следует отметить, что применение информационных технологий в образовании дают возможность самостоятельного обучения с открытым доступом к обширным информационным ресурсам, наличие обратной связи. С помощью компьютера учащийся может очутиться в самом разном окружении, требующем от него творческого подхода. Исследования, проводимые психологами, показали, что, работая с компьютером, учащиеся глубже вникают в суть вопроса, у них появляется интерес к предмету, они более активно пользуются учебной и технической литературой.

Но, несмотря на большое количество плюсов использования ТСО на уроке, возникает и множество негативных моментов.

Одной из негативных сторон информатизации является появление у некоторых людей компьютерной тревожности. Большинство психологов подразумевают под нею страх, возникающий при работе на компьютере или при размышлении о ней. Установлено, что уровень компьютерной тревожности позволяет предсказать успешность обучения работе на компьютере. Г. Маркулидес показал, что наличие компьютерной тревожности значительно снижает компьютерную грамотность и интерес к работе на компьютере. Люди, испытывающие высокую тревогу при выполнении какого либо задания на ЭВМ, как правило имеют отрицательное отношение к компьютеру. С другой стороны, как указывают Д. Кэмпбелл и К. Перри, отрицательные эмоции в некоторых случаях могут стимулировать рост активности, стремление выполнить задание как можно лучше и приводить тем самым к повышению успешности деятельности [8].

У учащихся компьютерная тревожность возникает зачастую как реакция на страх получить плохую отметку, показаться неспособным или глупым по сравнению с другими обучающимися. Преподаватели также сталкиваются с серьезными трудностями в процессе освоения навыков работы на компьютере. Они могут опасаться, что их рабочие места займут компьютеры или педагоги, лучше владеющие компьютером. Одним из важных факторов тревожности является также осознание ими того, что их ученики владеют компьютером намного лучше, чем они сами.

Правильная методика работы с информационными технологиями, простой интерфейс, качественное пособие и грамотное использование его - всё это поможет учителю снизить компьютерную тревожность у учащихся при использовании мультимедийного пособия.

наглядность визуальный мультимедийный дробь

1.2.3 Методика применения информационных технологий в

обучении

В настоящее время повышения эффективности учебного процесса, расширения и углубления содержания учебных предметов становится возможным благодаря применению средств информационных технологий в школьной практике обучения. Информационные технологии должны автоматизировать учебный процесс, выполняя (за учителя и учащихся) многие рутинные подготовительные функции, не связанные с изучаемым учебным материалом, позволяя более рационально расходовать учебное время, расширяя и углубляя содержание учебного предмета.

Использование средств ИКТ при изложении учебного материала позволяет поддерживать внимание учеников в течение длительного времени, способствует большей глубине осмысления изучаемого материала за счет демонстрации на экране наглядной информации.

Информационные технологии - совокупность средств и методов преобразования информационных данных для получения информации нового качества (информационного продукта). Компьютерные технологии обучения - совокупность средств и методов создания педагогических условий работы на основе компьютерной техники, средств телекоммуникационной связи и интерактивного программного продукта, которые моделируют часть функций педагога по обработке информации, организации контроля и управления познавательной деятельностью.

Известно, что учитель в процессе своей работы должен не только передавать учащимся определенный объем информации, но и стремиться сформировать у своих подопечных потребность самостоятельно добывать знания, применяя различные средства, в том числе компьютерные. Чем лучше организована самостоятельная познавательная активность учащихся, тем эффективнее и качественнее проходит обучение. Компьютер позволяет повысить самостоятельность работы учащихся, которая необходима для перевода знаний извне во внутреннее достояние школьника, учитель может варьировать формы контроля над усвоением учебного материала.

Реализация идей информатизации образования требует разработки специальных подходов и организационных форм обучения, обеспечивающих переход от иллюстративно-объяснительных методов и механического усвоения знаний к овладению умением самостоятельно приобретать новое знание, пользуясь современными способами представления и извлечения учебного материала и технологиями информационного взаимодействия. Расширяется спектр применения возможностей средств ИКТ в учебном процессе, разрабатываются новые методы и формы обучения, модифицируются традиционные методики обучения различным предметам [21].

В новых программных продуктах не всегда эффективно используются дидактические возможности ИКТ, а значит использовать такой продукт в педагогической деятельности не всегда целесообразно.

Возможности современного презентационного оборудования (проекторы, экраны, интерактивные доски), намного выше, чем у традиционного лекционного оборудования, что позволяет педагогу единовременно опираться на всю триаду восприятия: слышу, вижу, пишу.

Наибольшая эффективность обучения достигается за счет демонстрации презентаций, при изучении тем, требующих использования значительного и разнородного учебного материала. Необходимо создавать избыточную базу данных, из которой можно было бы компоновать содержание урока по вкусу учителя и ожидаемому уровню аудитории. При изложении учебного материала учителя могут использовать широкий набор различных демонстраций, которые позволяют:

·  проиллюстрировать излагаемый материал видеоизображением, анимационными роликами с аудиосопровождением;

·        использовать фрагменты лекций или полностью лекции известных педагогов;

·        с помощью проекции на экран или интерактивную доску облегчить процесс восприятия информации благодаря использованию интересных, красочных, запоминающихся образов;

·        хранить, систематизировать, готовить новые демонстрационные материалы [21].

Традиционные средства обучения не позволяющие воспроизводить явления действительности, заменяются моделирующими программами, что делает занятия более насыщенными и интересными.

Использование средств информационных и коммуникационных технологий при изложении учебного материала дает возможность:

·  демонстрировать протекание сложных явлений и процессов, которые нельзя представить в реальных условиях или которые необходимо подчинить определенной методической позиции;

·        имитировать лабораторные работы, с возможность задания и изменения начальных и граничных условий;

·        представлять объект (модель объекта) и выделять его свойства;

·        получать статическое и (или) динамическое отображение результатов расчета при использовании наборов произвольных параметров в виде графиков, диаграмм, таблиц, моделей;

·        одновременно использовать средства трехмерного изображения, анимацию, видеосюжет и звук.

Таким образом, информатизация образования приводит к существенным изменениям форм и методов, содержания обучения. Внедрение средств ИКТ не приводит к вытеснению педагога, снижению его роли. Средства ИКТ становятся существенным дополнением к традиционным:

·   использование готовых мультимедийных программ;

·        создание собственных разработок с помощью стандартного программного обеспечения, с соблюдением основных требований целесообразного использования.

Применение компьютера в учебном процессе может быть следующим:

Где применять?	Для чего? (какие задачи?)	Что именно использовать?	Как?
На уроке вводного, текущего и итогового контроля.	Для автоматизации процесса, экономии времени на обработку данных.	Контролирующие и тестирующие программы.	Оборудованный класс ПО.
Ведение нового материала, закрепления, обобщения и систематизации знаний.	Для обучения на разных этапах урока. Демонстрация учебного материала.	Обучающие программы, мультимедийные продукты.	Оборудованный класс ПО. ПО и проектор.
Проведение внеклассных мероприятий.	Для реализации (развития) творческих способностей учащихся.	Компьютерные версии интеллектуальных и развивающих игр.	Оборудованный класс ПО. ПО и проектор.

Это можно проиллюстрировать использованием компьютера при изучении темы «Основные задачи на проценты» на уроках математики. Подходящим программным средством в качестве компьютерной поддержки темы может использоваться электронные таблицы EXCEL. Разработка в ней задачи на проценты позволяет, во-первых, освоить многие операции, изучаемые в программном средстве по предмету информационных технологий, и, во-вторых, закрепить материал по данной теме. Тем самым значительно сокращаются затраты учебного времени по общим предметам.

Программная разработка в EXCEL состоит из набора изучаемых функций; нахождение процента от числа, числа по проценту. В соседний столбец для каждой функции выведены данные числа. На диаграмме отмечается соответствующее процентное содержание. Таким образом, имеется возможность графически и численно проанализировать тип задачи, то есть выполнить компьютерное моделирование.

Кроме описанной технологии применения популярного программного обеспечения, на уроках математики возможно применение специализированных программ, таких как Macromedia Flash. При изучении темы «Основные задачи на дроби и проценты», в 5-6 классах можно использовать обучающую программу «Обыкновенные дроби и проценты», в частности мультимедийное пособие, в котором демонстрируются основные виды решаемых задач. Дается теоретический материал, тренировочная работа.

Применение таких программных продуктов позволяет визуализировать и сделать более наглядными многие математические понятия и абстракции, позволяют развивать пространственное воображение, организовывать контроль знаний. При применении их наряду с традиционными формами работы на уроке позволяют получать хорошие педагогические результаты.

1.2.4 Использование технологии Macromedia Flash при разработке

учебных пособий

Современный мир сложно представить без компьютера, информационных технологий, которые в последнее время стремительно развиваются: появляются новые версии программ, программные продукты разных фирм получают распространение на рынке. Большое внимание уделяется пакету Macromedia Flash как средству создания интерактивных мультимедиа-презентаций, применяемых в учебном процессе, а также всевозможных виртуальных лабораторных работ и демонстраций.технологии - одно из наиболее востребованных направлений современного интернета и анимации. Flash анимация на сегодняшний день является одной из самых популярных технологий создания мультимедийных вставок.

Технология Flash основана на использовании векторной графики в формате Shockwave Flash (SWF). Векторная графика - чистое математическое описание каждого объекта на экране. В то время как растровая графика представляет собой массив из точек разного цвета. Векторная нетребовательна к ресурсам для воспроизведения, занимает очень мало места, не искажается при масштабировании и поворотах. Анимация выполняется не в каждом кадре, а только в ключевых. Недостающие кадры не хранятся непосредственно в файле, а дорисовываются компьютером по заранее заданному закону. Это позволяет получать файлы малых размеров [47].

С помощью Flash можно создавать:

·    анимированные изображения и целые мультипликационные фильмы;

·              интерактивные мультимедийные документы. Такие документы взаимодействуют с пользователем, содержат текст, графику (в том числе анимацию) и звук;

·              Web-страницы и даже Web-сайты, включающие в себя чаты, гостевые книги, голосования и форумы;

·              элементы интерфейса, которым потом можно назначать какие-либо действия. Например, кнопки, меню, флажки, радиокнопки и т.д.

Основными преимуществами Flash - технологий являются:

·    маленький размер получающихся файлов и, соответственно, более быстрая загрузка из сети. Flash использует векторный формат изображений и сжимает растровые и звуковые файлы;

·              В Macromedia Flash используется специальный язык - Action Script, при помощи которого можно управлять любым элементом ролика и менять любые его свойства, менять ролик в зависимости от действий пользователя;

·              красота. Flash имеет автоматическую поддержку anti-aliasing (антиалайсинг, сглаживание контуров с помощью смешения соседних цветов);

·              удобство. Создавать страницы во Flash под силу даже неподготовленному пользователю;

·              универсальность. В случаях, где необходима широкая интерактивность, графика, звук, и маленький размер, Flash незаменим.

Macromedia Flash удобно использовать при создании учебных материалов по различным предметам.

В частности, Flash целесообразно использовать на занятиях по математике при изучении функций, исследовании функций. На таких занятиях, преподавателю, как правило, приходится рисовать на доске множество различных графиков и дополнительных построений к ним. Это занимает много времени и достаточно утомительно. Применение Flash в таких случаях экономит время на уроке. Векторный подход к рисованию может повысить точность изображения (графики функций, касательные, площади криволинейных трапеций и пр.), и вызвать интерес за счет анимации. В нужное время масштабируемый и динамично прорисовывающийся график гораздо наглядней статичной картинки на доске. При помощи интерактивности появляется возможность варьировать параметры кривых и других элементов чертежа.

Преимущества векторной графики могут наглядно применяются на занятиях геометрией. Снова экономиться время за счёт готовых чертежей, демонстрируемых с компьютера. Анимация особенно пригодиться при изучении преобразований, в стереометрии. Решение задач на построения становится более наглядным.

При изучении понятия дроби, процента зачастую возникают трудности, связанные с непониманием основных его элементов. Введение понятия дроби в школьном курсе математики в большинстве учебников опирается на наглядное представление части целого, доли. В ходе рассмотрения такой задачи, приводящего к понятию обыкновенной дроби, описывается процесс, который носит динамический характер и для более глубокого усвоения и осмысления требует динамической иллюстрации. При использовании Flash-технологии становится возможным смоделировать такого рода процессы, тем самым повысив уровень их осмысления.

При помощи технологий Macromedia Flash и было разработано интерактивное дидактическое пособие для учеников 5-6 классов по теме «Обыкновенные дроби и проценты». Выбор данной темы, для представления её как интерактивного пособия, обусловлен тем, что есть реальная необходимость в визуализации материала и его динамическом представлении, что затруднительно реализовать посредством обычного учебника. Важен не только инструмент создания, но и, в первую очередь, содержание пособия, которое подчиняется ряду требований, предъявляемых к учебным пособиям такого рода.

1.2.5 Научно-педагогические требования к компьютерным

учебным пособиям

В последнее время появляется огромное количество более или менее удачных компьютерных и мультимедийных продуктов, где практически всегда отсутствуют методические материалы по их использованию. Такие компьютерные учебные продукты, как утверждает Розов Н.Х. в своей статье, не являются полноценными компьютерными продуктами. Разработка учебного пособия должна производиться по блокам, или модулям. Так как в целостном продукте могут быть использованы лишь какие-то отдельные фрагменты. Поэтому весьма перспективно создавать «набор миниатюр». Компьютер в этом плане открывает совершенно неограниченные возможности познать красоту и разнообразие геометрии мира (Н.Х. Розов) [37].

Еще немало важный момент - это сложность обучающих компьютерных продуктов. Чем меньше времени учитель-предметник затратит на предварительное изучение правил работы с продуктом, тем легче ему будет освоить и эффективно внедрить его в учебный процесс. «Высший профессионализм разработчика как раз в том и должен заключаться, чтобы созданная им программа автоматически выполняла максимум нужных манипуляций с материалом при минимуме простых команд пользователя».

При создании таких учебных продуктов очень важно учитывать психолого-педагогические особенности учеников. Отметим психолого-педагогические требования, которым должна удовлетворять обучающая программа:

·  научность содержания: обеспечение возможности построения содержания учебной деятельности с учетом основных принципов педагогики, психологии, теории системного дизайна;

·        открытость: возможность реализации любого способа управления учебной деятельностью, выбор которого обусловлен, с одной стороны, теоретическими воззрениями разработчиков обучающей программы, а с другой - целями обучения; обеспечение возможности модификации, внесения изменений в способы управления учебной деятельностью;

·        целенаправленность: обеспечение обучаемого постоянной информацией о ближайших и отдалённых целях обучения, степени достижения целей; стимуляция тех видов познавательной активности обучаемых, которые необходимы для достижения основных учебных целей;

·        обеспечение мотивации: стимулирование постоянной высокой мотивации обучаемых, подкрепляемой целенаправленностью, активными формами работы, высокой наглядностью, своевременной обратной связью, причем мотивация не должна идти за счет интереса к самому компьютеру;

·        наличие входного контроля: диагностика обучаемого перед началом работы с целью обеспечения индивидуализации обучения, а также оказания требуемой первоначальной помощи;

·        индивидуализация обучения: содержание учебного предмета и трудность учебных задач должны соответствовать возрастным возможностям и индивидуальным особенностям обучаемых и строиться с учетом уже приобретенных, знаний, умений и навыков; для реализации индивидуального подхода программа должна включать динамическую модель изучаемого объекта;

·        обеспечение обучения в сотрудничестве: программа должна по возможности моделировать совместную субъект-субъектную деятельность;

·        креативность: программа должна формировать логическое и системное мышление, обеспечивать подготовку специалистов с творческим потенциалом, способных видеть противоречия, а также самостоятельно ставить и решать проблемы; исключение таких нежелательных последствий компьютеризации, как чрезмерная алгоритмизация мыслительной деятельности, пассивность мышления, отказ от самостоятельных усилий в достижении целей;

·        обеспечение систематической обратной связи; обратная связь должна быть, педагогически оправданной, не только сообщать о допущенных ошибках, но и содержать информацию, достаточную для их устранения;

·        наличие развитой системы помощи: система помощи должна быть многоуровневой, педагогически обоснованной, достаточной для того, чтобы решить задачу и усвоить способ ее решения; помощь должна оказываться с учетом характера затруднения и модели обучаемого;

·        наличие многоуровневой организации учебного материала, базы знаний и банка заданий: соблюдение данных требований позволяет организовать систему повторов по спирали с постоянной опорой на зону ближайшего развития, добавлением на каждом уровне повторения нового, более расширенного, конкретизированного материала и использованием неповторяющихся задач;

·        педагогическая гибкость: программа должна позволять обучаемому самостоятельно принимать решение о выборе стратегии обучения, характера помощи, последовательности и темпа подачи учебного материала; должна быть обеспечена возможность доступа к ранее пройденному учебному материалу, выхода из программы в любой ее точке;

·        возможность возврата назад; при самостоятельной работе должна быть предусмотрена отмена обучаемым ошибочных действий;

·        наличие специально отведённого места для рефлексии обучаемых; программа должна накапливать результаты рефлексии с целью последующей корректировки обучающих воздействий;

·        наличие интуитивно понятного дружелюбного интерфейса; программа должна адекватно использовать все способы предъявления информации в виде текста, графики, анимации, гипертекста, мультимедиа; обучаемый должен иметь возможность пролистывания информационного материала в обоих направлениях «вперед-назад» с возможностью установления типа и размера шрифта, а также повторения любого фрагмента желаемое число раз;

·        обеспечение возможности получения твердой копии статических (текстовых, графических, иллюстративных) разделов программы; возможность копирования выбранной информации в личный электронный конспект, ее редактирования и распечатки без выхода из самого программного продукта;

·        наличие развитой поисковой системы, режимов «лупы», «автопоказа»;

·        наличие блока контроля утомления обучаемого, блока релаксации; последний должен содержать тематически однородные небольшие «банки» шуток, анекдотов, музыкальные фрагменты и т. д.;

·        надёжность работы и системная целостность; техническая корректность;

·        защита от случайного или неправильного нажатия; обеспечение адекватной реакции на любые, даже самые неожиданные ответы обучаемых; программа не должна «зависать» из-за непредвиденной последовательности срабатывания отдельных ее модулей или других причин; необходимо использовать иерархическую древовидную структуру различных программ и возможность отступления на предыдущий уровень в случае возникновения сбоя в работе системы.

Компьютер наряду с другими средствами обучения, а также методами и формами обучения является одним из способов реализации дидактических принципов, следовательно, последние должны задавать направление в решении вопросов использования компьютеров, а не наоборот.

При формировании дидактических требований к обучающим программам следует, прежде всего, ориентироваться на принципы обучения, содержание которых базируется на современных теоретических достижениях в области педагогики и психологии, что и позволяет использовать их в качестве системы дидактических требований:

. Принцип научности диктует целый ряд требований к обучающим программам:

·  обучающие программы целесообразно наполнять таким содержанием, которое наиболее эффективно может быть усвоено только с помощью компьютера;

·        содержание программ должно соответствовать современному состоянию научного знания;

·        способы усвоения учебного материала, предусмотренные программой, должны быть адекватны современным научным методам познания и динамично меняться, обеспечивая быстрое перенастраивание программного продукта в соответствии с изменяющимися требованиями.

. Принцип наглядности формирует следующие требования к обучающим программам:

·  в них при отражении чувственного объекта не следует увлекаться натурализмом: в программе должна быть представлена не любая модель, а только та, которая способствует реализации дидактических целей данной обучающей программы;

·        модель, содержащуюся в программе, следует предъявлять в форме, позволяющей наиболее четко раскрыть существенные связи и отношения объекта; существенные признаки, связи и отношения модели должны быть в программе адекватно зафиксированы цветом, миганием, звуком и т. д.;

·        наиболее важное требование, состоит в том, что с помощью обучающих программ необходимо не только предъявлять объект изучения, но и организовывать деятельность учащихся по его преобразованию.

. Принцип систематичности и последовательности может быть наиболее оптимально реализован с помощью обучающих программ следующим образом:

·  в объектах или явлениях, представляемых с помощью компьютерных программ, должны быть выделены основные структурные элементы и существенные связи между ними, позволяющие представлять этот объект или языковое явление в виде целостного образования;

·        наряду с этим, алгоритм, в соответствии, с которым строится деятельность обучаемого по усвоению материала, должен отражать логику его системного анализа.

. Принцип активности. Поскольку активность обусловлена сознательностью, при разработке обучающих программ необходимо ориентироваться на следующие требование:

·  целесообразно в структуру программы вводить ориентировочный компонент, который должен включать два вида знаний - знание о деятельности, реализуемой с помощью программы (цель деятельности, ее предмет, средства и основные этапы осуществления), и предметные знания, необходимые для успешной работы с программой (правила, справочно-информационные данные и т.д.).

Сегодня компьютер позволяет индивидуализировать процесс обучения, гарантирует интимность успехов и неудач учеников, а его замечания и комментарии воспринимаются ими как дружелюбные и необидные. Открываются широкие перспективы создания учебных программ с дифференцированным учетом психологических типов детей (и особенно для детей с ограниченными интеллектуальными возможностями) [33].

Технически грамотно выполненный учебный продукт должен отвечать и определенным требованиям, предъявляемым к содержательной стороне. Обратимся к анализу учебной литературы, для выявления структуры учебного пособия.

Глава 2. Методика изучения темы «Обыкновенные дроби и

проценты»

.1 Анализ учебной литературы по теме «Обыкновенные дроби и

проценты»

Изучение обыкновенных дробей и процентов начинается в 5 классе и продолжается на протяжении всего курса алгебры. Начиная с 6 класса, знания о дробях и процентах обобщаются, расширяются и систематизируются.

И, следовательно, анализ учебной литературы необходимо проводить за 5-6 классы, чтобы на основе этого анализа построить содержание дидактического пособия. Цель нашего пособия состоит в визуализации базовых понятий, лежащих в основе тем «обыкновенные дроби» и «проценты». Поэтому, в первую очередь, обратим внимание на визуальные задачи, способствующие формированию этих понятий. При анализе учебных пособий будем применять классификацию визуальных задач, предложенную Н.А. Резник.

Тема «Обыкновенные дроби» в данном учебном пособии изложена в главе II «Дробные числа». Учащиеся 5 класса знакомятся с простейшими дробями: ; ;  … Образование долей происходит на наглядной основе. Происхождение дробей разбирается как результат деления на любое число равных частей.

Например:

Мама купила арбуз и разрезала его на 6 равных частей: бабушке дедушке, папе, двум детям и себе. Эти равные части называют долями.

Так как арбуз разрезали на 6 долей, то каждый получит «одну шестую долю арбуза», или короче, «одну шестую арбуза».

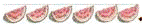
Затем вводится определение обыкновенной дроби, где выделяют числитель и знаменатель, делая акцент на соотношении взятых долей к количеству долей, на которое делят целое. Записи вида  называют обыкновенными дробями. В дроби  число 5 называют числителем дроби, а число 8 - знаменателем дроби. Знаменатель показывает, на сколько долей делят, а числитель - сколько таких долей взято.

Образование дробей, как и образование долей рассматривается с помощью наглядных примеров.

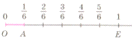
После ряда обучающих визуальных задач типа «посмотрите и найдите», например:

№884. Какая часть фигуры закрашена?

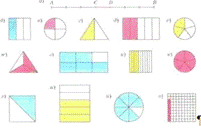
Предложены задачи на дроби, включенные в рассмотрение этого пункта 23 «Доли. Обыкновенные дроби». Выделяют три типа задач: задачи на доли; нахождение части от числа; нахождение числа по его части. Сначала решаются задачи и примеры на нахождение одной части от числа (числа по его части): ;  и т. п.

Например:

№889. Купили кусок ткани длиной 2 м 50 см и из  куска сшили платье для куклы. Сколько сантиметров ткани ушло на это платье?

№891. Петя готовил уроки 1 ч 40 мин. На математику он потратил  этого времени, а на историю -  оставшегося времени. Сколько минут Петя готовил уроки по математике и сколько по истории?

Дальше переходят к задачам и примерам на отыскание нескольких частей целого. Дается задача - математическая модель, на основе которой рассматриваются все три типа задач. Каждая из задач имеет иллюстративное приложение и решение, описанное в учебнике.

Например:

№896. Дорога от Фабричного до Ильинского равна 8 км. Лена прошла по этой дороге 3 км. Какую часть дороги она прошла?

Решение. Длина всей дороги равна 8 км. Поэтому 1 км составляет  всей дороги, а 3 км -  дороги. Значит, Лена прошла  дроги.

№900. Дорога от Фабричного до Отдыха составляет  дороги от Фабричного до Ильинского. Чему равно расстояние от фабричного до Отдыха, если от Фабричного до Ильинского 8 км?

Решение. Разделим всю дорогу на 4 доли. Тогда длина одной доли дороги равна 8 : 4, то есть 2 км. А длина  дороги, то есть трех таких долей, равна 2 3, то есть 6 км. Значит, от Фабричного до Отдыха 6 км.

№905. Дорога от Фабричного до Кратова равна 5 км, что составляет  дороги от Фабричного до Ильинского. Найдите расстояние от Фабричного до Ильинского.

Решение. Так как пять восьмых дороги составляют 5 км, то одна восьмая этой дороги равна 5 : 5, то есть 1 км. А тогда вся дорога в 8 раз длиннее, чем 1 км, то есть имеет длину 1 · 8, или 8 км. Итак, от Фабричного до Ильинского 8 км.

Решение основных задач на дроби выполняется двумя действиями: делением на знаменатель (числитель) и умножением на числитель (знаменатель). Умножение или деление на дробь не рассматривается.

Пункт 24 «Сравнение дробей». При рассмотрении алгоритма сравнения дробей используются визуальные задачи.

Пирог разрезали на 5 долей и 2 доли положили на одну тарелку, а 3 доли - на другую. Две доли составляют  пирога, а три доли -  пирога. Так как 2 доли меньше, чем 3 такие же доли, то  < .

Затем формулируется правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.

Также, сравнивают дроби при помощи точек расположенных на координатном луче.

 

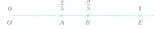
Точка на координатном луче, имеющая меньшую координату, лежит слева от точки, имеющей большую координату.

Здесь же авторы оговаривают случай равенства дробей, наглядно представляя деление круга на 4 равные части.

Две такие части вместе составляют половину круга. На координатном луче равные дроби соответствуют одной и той же точке.

Однако ни о каком основном свойстве дроби не упоминается. Равенство дробей основано лишь на наглядном представлении каждой из дробей. Выделяется ряд визуальных задач «серия»:

№940. Объясните с помощью рисунка, почему

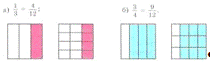
№941. Начертите в тетради отрезок длиной в 18 клеток. С помощью этого отрезка объясните, почему:

а)       = ;

б)      = .

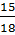
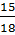Заметим, что авторы уделяют внимание произношению: «По тому, как человек говорит, можно судить о его культуре и интеллекте, об умении думать. Поэтому учитесь говорить правильно. В этом вам помогут примеры и пояснения, данные в рубрике, отмеченной славянской буквой «глаголь».

Введение понятий правильной и неправильной дробей осуществляется за счет ряда визуальных задач: разрезание пирога на несколько равных частей.

Разрезали пирог на 8 равных частей и 3 части положили на тарелку. На ней оказалось  пирога, положив 8 частей, окажется  пирога = 1.

Затем рассматривают 11 частей, соответствующие 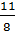 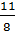пирога, на основе чего вводится понятие правильной и неправильной дробей.

Дальше проводится знакомство с неправильными дробями, равными единице и большими единицы. Сравнение таких дробей с единицей производится с помощью изображения точек на координатном луче.

После чего формулируется правило: правильная дробь меньше единицы, а неправильная дробь больше или равна единице.

После ознакомления с неправильными дробями переходят к их преобразованию в целые и смешанные числа. Преобразование неправильной дроби в целое или смешанное число производят путем исключения целого числа из неправильной дроби. Далее решается обратная задача: целое или смешанное число заменить неправильной дробью.

Использование визуальных задач в данном пособии осуществляется, в основном, на начальном этапе изучения каждой из тем главы: «Обыкновенные дроби».

Усвоение курса дробей имеет большое значение для средней школы, так как знание учащимися дробей необходимо для всего последующего курса математики, оно тесно связано с изучением процента.

Тема «Проценты» предложена авторами для изучения в конце 5 класса. Данный материал рассматривается в §8 «Инструменты для вычислений и измерений» в главе II «Дробные числа». Перед изучением этой темы, ученики познакомились с обыкновенными и десятичными дробями, и операциями над ними. Что является необходимой теоретической «базой» для изучения процентов.

Знакомство с процентами начинается традиционным образом. Вначале вводится определение. Понятие «процент» рассматривается на примере сравнения различных величин, как сотая часть числа и вводится обозначение.

Пункт 40 «Проценты»: «Сотую часть центнера называют килограммом, сотую часть метра - сантиметром, сотую часть гектара - аром или соткой. Принято называть сотую часть любой величины или числа процентом. Значит 1 кг - один процент центнера, 1 см - один процент метра, 1 а - один процент гектара, 0,02 - один процент от 2.

Процентом называют одну сотую часть.

Для краткости слово «процент» после числа заменяют знаком «%».

Далее рассматриваются задачи на проценты с решениями. Выделяют три типа задач на проценты.

Например:

Задача 1-го типа (нахождение процента от числа). Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Решение.

Так как 1200 костюмов - это 100% выпуска, то, чтобы найти 1% выпуска, надо 1200 разделить на 100. Получим, что 1200 : 100 = 12, значит, 1% выпуска равен 12 костюмов. Чтобы найти, чему равны 32% выпуска, надо умножить 12 на 32. Так как 12 · 32 = 384, то фабрика выпустила 384 костюма нового фасона.

Задача 2-го типа (нахождение числа по проценту). За контрольную по математики отметку «5» получили 12 учеников, что составляет 30% всех учеников. Сколько учеников в классе?

Решение.

Сначала узнаем, чему равен 1% всех учеников для этого разделим 12 на 30. Так как 12 : 30 = 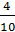 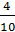= 0,4, то 1% равен 0,4. Чтобы узнать, чему равны 100% учащихся, надо умножить 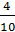 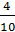на 100. Так как 0,4 · 100 = 40, то в классе 40 учеников.

Задача третьего типа - это задача на процентное отношение и поэтому они являются сложными. Однако авторы рассматривают эти задачи вместе с 1 и 2 типом в 5 классе.

Задача 3-го типа. Из 1800 га колхозного поля 558 га засажено картофелем. Какой процент засажен картофелем?

Решение.

Картофелем засажено  всего поля. Обратим дробь  в десятичную. Для этого разделим 558 на 1800. Получаем 0,31. Значит, картофелем засажена 31 сотая всего поля. Каждая сотая равна 1% поля, поэтому картофелем засажен 31% всего поля.

Для закрепления полученных знаний имеется перечень вопросов, которые помогут в дальнейшем при решении задач:

Что называется процентом?

Как называют 1% от центнера, метра, гектара? …

После сделанных выводов предлагаются задания для работы в классе.

Рассмотрим систему упражнений на основе классификации Н.А. Резник, с целью выделить класс визуальных задач, представленных в этом учебнике.

Задача типа «Посмотрите и определите».

№1533. Заполните таблицу:

Дроби
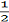
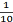
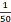
Десятичные		0,25					0,05
дроби
Проценты				20%		100%		1%

Введение процентов опирается на предметно практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. Используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения. С помощью таких наглядных приемов можно сослаться на раннее изучаемый материал об обыкновенных дробях, где и был представлен целый ряд таких упражнений.

С помощью ряда задач устанавливается связь между процентами и обыкновенными дробями, в основном это задачи на нахождение части от числа, например:

№1572. Поле на рисунке 158 разбито на 100 долей. Закрашенная на рисунке часть засеяна горохом. Найдите площадь всего поля, если горохом засеяно 24,8 га.

№1575. Двор разбит на 100 равных частей. Часть площади двора, закрашенная на рисунке 159, отведена под стоянку машин. Найдите площадь двора, если стоянка занимает 146, 4 м².

 

   

Решение основных задач на проценты выполняется с помощью двух действий: делением на знаменатель (числитель) и умножением на числитель (знаменатель), поскольку процент выражается обыкновенной дробью, таким образом, исходная задача решается путем нахождения части от числа (числа по его части).

№1537 (1 тип). В палатку завезли 850 кг огурцов. Первый покупатель взял для соления 1% всех огурцов, а второй 3% всех огурцов. Сколько килограммов огурцов купил каждый из них?

Решение.

Всего - 850 кг огурцов

покупатель - 1% всех огурцов

покупатель - 3% всех огурцов

: 100 · 1 = 8,5 кг

: 100 · 3 = 25,5 кг

Ответ: 8,5 кг и 25,5 кг.

№1544 (2 тип). Сколько человек было в кино, если 1% всех зрителей составил 7 человек?

Решение.

7 - это 1% (1% = )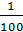

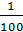Тогда 7 · 100 : 1 = 700

Ответ: 700 человек.

Система упражнений выстроена по схеме: «от простого к сложному». О процентах также упоминается при изучении материала «Круговые диаграммы». Здесь они используются при решении следующих задач.

№1676. Молоко даёт 25% сливок, сливки дают 20% масла. Сколько масла получится из молока, надоенного за 15 дней от 360 коров, если каждая корова в среднем даёт 15 кг молока в день.

С помощью диаграмм осуществляется графическая иллюстрация различных процентных баз.

В 6 классе задачи на проценты встречаются при изучении темы пропорция.

В данном учебном пособии визуальные задачи используются при начальном этапе изучения следующих тем: обыкновенные дроби, проценты. Задачи используются как при введении новых понятий, так и в системе упражнений, направленных на закрепление материала 5 класса. В 6 классе визуальные задачи используются в системе упражнений на повторение.

Учебник: Зубарева И.И, Мордкович А.Г. Математика, 5-6 Кл.: Учеб. для общеобразоват. учреждений. - 2-е изд. - М.: Мнемозина, 2003. - 293 с. [19, 20]

Тема «Обыкновенные дроби» начинается с §18 «Деление с остатком», что подготавливает учащихся к восприятию понятия дроби, вводимого, как результат деления натуральных чисел.

Введение понятия «Обыкновенная дробь» осуществляется посредством задач, где требуется целое разделить на несколько частей.

Например:

№330. Кусок проволоки длиной 1 метр разрезали на три равные части. Какова длина каждой части?

 

 

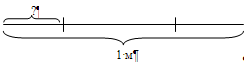
Ниже приводится решение этой задачи, в ходе которого возникает необходимость обозначения каждой новой полученной части, как обыкновенной дроби.

Решение: Осуществляем переход к более мелким единицам длины:

м = 10 дм, 10 : 3 = 3 (остаток 1)

м = 100 см, 100 : 3 = 30 (остаток 10)

м = 1000 мм, 1000 : 3 = 300 (остаток 100)

Во всех случаях получаем остатки, но по условию задачи, проволоку разрезали на три части и ничего не осталось. Таким образом, разрезав кусок проволоки длиной 1 м на три равные части, мы получаем три куска проволоки, длиною в треть метра каждый. Треть записывают в виде дроби .

Далее рассматриваются аналогичные задачи, затем вводится определение: Частное от деления натуральных чисел m и n можно записать в виде дроби , где m - числитель, а n - знаменатель:

.

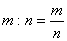Затем дробь рассматривается как количество равных долей. Представлена визуальная задача типа «проверь себя»:

№332. Кусок проволоки длиной 2 м разрезали на 3 равные части. Какова длина одной части?

Проверьте, так ли вы рассуждали при решении этой задачи.

Чтобы найти длину одной части, надо длину всего куска разделить на число частей: 2 : 3.

Частное удобно записывать в виде дроби: .

Решение: 2 м : 3 =  м.

Ответ: длина одной части -  м.

Далее следует ряд заданий, отмеченных знаком «У», выполняя которые ученики узнают что-нибудь новое (правило, свойство уже известного понятия).

№338 (У).

)        Ленту длиной 1 м разрезали пополам, а ленту длиной 2 м разрезали на 4 части. Какова длина одной части в каждом случае (в метрах)?

)        Сделайте рисунок к задаче, изобразив ленты в виде прямоугольников шириной 5 мм, а длиной, соответственно, 4 и 8 см. Выполните задания:

a)       Сравните отрезки длиной  м и  м;) Сравните дроби  и .

«Проверьте себя».

Если вы все сделали правильно, то у вас должны получиться такие рисунки:

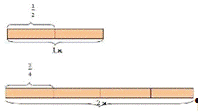
Из рисунков видно, что  =

Таким образом, учащиеся знакомятся с интересным и важным свойством дробей: «одну и ту же дробь можно записывать несколькими способами». Здесь не приводится формулировка основного свойства, подробное изучение вынесено в отдельный параграф 21 «Основное свойство дроби». Перед этим разбирается вопрос о происхождении дробей, как одна или несколько равных долей:

1)      Чтобы получить дробь 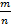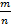, надо единицу разделить на n равных частей и взять m таких частей.

)        Чтобы получить дробь 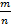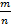, надо число m разделить на число n.

Представлен ряд обучающих визуальных задач:

№341 («Посмотрите и найдите»).

а) В семье четверо детей - одна девочка и трое мальчиков. Праздничный торт был разрезан на 6 одинаковых кусков: по одному на каждого ребенка и на каждого из родителей. Какая часть торта досталась девочке, а какая - мальчикам (рис. 36)?

б) Участок площадью 1 а был поделен на 10 грядок. На двух грядках был посажен лук, на трех - свекла, на четырех - морковь и на одной - чеснок. Найдите площадь (в арах) под каждой из этих овощных культур (рис. 37).

№342 («Тренажер»). Запишите в виде дроби, какая часть фигуры закрашена голубым цветом:

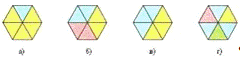
№344 («Тренажер»). Запишите, какая часть фигуры закрашена, а какая - не закрашена:

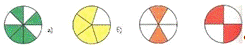
№343 («Серия»). Определите, какая часть фигуры закрашена голубым цветом. Постарайтесь дать несколько вариантов ответа.

№345

(«Серия»). Сделайте в тетради такой же рисунок и закрасьте  квадрата. Постарайтесь найти разные способы.

а)               б)               в)              г)

Предложенные упражнения нацелены на осознание учащимися понятия дроби, как одной из равных долей или нескольких равных долей единицы (целого). После того как учащиеся решили класс задач на соотнесение дроби - части закрашенной фигуры, авторы предлагают перейти к рассмотрению текстовых задач на отыскание части от целого и целого по его части, 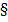 20.

Сначала решаются задачи на нахождение одной части от целого (целое по его части), например две взаимно-обратные задачи:

№350 (У). 1) Решите задачи.

В пятом классе 36 человек. В школьной математической олимпиаде участвовали  всех учащихся этого класса. Сколько учащихся пятого класса приняли участие в олимпиаде по математике?В школьной математической олимпиаде приняли участие четверо учеников пятого класса, что составило  всех учащихся этого класса. Сколько всего учащихся в пятом классе?

После чего авторы предлагают ответить на вопросы:

·        какая величина принята за целое в каждой задаче?

·        в какой из задач эта величина известна, а в какой - нет?

·        в какой из задач требуется найти часть от целого, а в какой - целое по его части?

·        можно ли утверждать, что это взаимно-обратные задачи?

Проводя, аналогию с задачей №350 учащиеся переходят к выполнению заданий на отыскание нескольких частей целого, которым предшествует подробно разобранные задачи двух типов: на отыскание части от целого и целое по его части.

№354 (У) («Проверь себя»). 1) Прочитайте задачи и ответьте на вопросы:

Площадь поля - 50 га. За день бригада трактористов вспахала  поля. Сколько гектаров вспахала бригада за день?За день бригада вспахала 20 га, что составило  площади всего поля. Какова площадь поля?

·что принято за целое в первой задаче; что - во второй?

·в какой из задач эта величина известна, а в какой - нет?

·в какой из задач требуется найти часть от целого, а в какой целое по его части?

как найти величину, которая приходится на 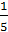 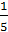в первом случае и как - во втором?

2)Решите данные задачи.

3)Проверьте правильность ответов и решения:

·в обеих задачах за целое принята площадь всего поля;

·в первой задаче целое известно - это 50 га, а во второй - целое не известно;

·в первой задаче требуется найти часть от целого, а во второй - целое по его части.

Решение:

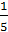
1) 50 : 5 = 10 (га) - площадь, 1 которая приходится на  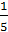часть всего поля;

) 10 ∙ 2 = 20 (га) - площадь, 2 которая приходится на 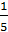 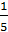всего поля.

Ответ: 20 га.1) 20 : 2 = 10 (га) - площадь, 1 которая приходится на 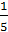 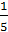часть всего поля;

) 10 ∙ 5 = 50 (га) - площадь всего поля.

Ответ: 50 га.

Таким образом, учащиеся могут сравнить две решаемые задачи, после чего сделать вывод: 1) чтобы найти часть от целого, надо число, соответствующее целому разделить на знаменатель и результата умножить на числитель дроби, которая выражает эту часть; 2) чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Заметим, что прежде чем приступать к решению таких задач авторы просят ответить на вспомогательные вопросы:

·   что принято за целое?

·        известна ли эта величина?

·        что теребуется найти в задаче: часть от целого или целое по его части?

·        как найти величину, которая приходится на одну часть?

Система упражнений выстроена от простого к сложному, где задания сложнее отмечены специальным значком «о»:

№367 (о) («Серия»). Сделайте в тетради такой же рисунок и закрасьте указанную часть соответствующей фигуры:

                

а)  ;                б)  ;                   в) .

№396. Запишите, какая часть фигуры закрашена:

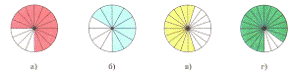
Основное свойство дроби выводится из рассмотрения примеров на увеличение или уменьшение величины дроби в связи с увеличением и уменьшением ее членов в несколько раз. Рассмотрение примеров иллюстрируется чертежом, на котором учащиеся проверяют, что равные дроби могут быть выражены в различных видах.

№371 (У) («Серия»). Запишите, какая часть фигуры закрашена оранжевым, какая - желтым и какая - зеленым цветом. Постарайтесь найти разные способы.

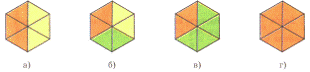
№372 (У) («Серия»). Запишите, какая часть фигуры закрашена, а какая - не закрашена. Найдите разные способы.

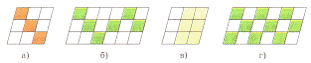
№390 (о) («Серия»). Запишите, какая часть фигуры закрашена:

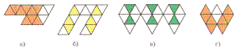
После решения примеров делаются выводы: величина дроби не изменится, если числитель и знаменатель увеличить в одинаковое число раз; величина дроби не изменится, если числитель и знаменатель уменьшить в одинаковое число раз. Основное свойство представлено символьной записью:

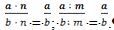
При изучении сокращения дробей авторы добиваются, чтобы учащиеся поняли а) на каком свойстве дробей основано их сокращение; б) цель этого преобразования (вид дроби упрощается, так как числитель и знаменатель выражаются меньшими числами). Осуществляется это с помощью вспомогательных вопросов: Какое свойство дроби для этого можно использовать? После чего авторы предлагают прочитать рубрику «Проверь себя». Здесь же проводится сравнение дробей, опираясь на основное свойство дроби.

Дальше проводится знакомство с правильными и неправильными дробями, равными единицы и большими единицы. Переход к преобразованию неправильных дробей в целые и смешанные числа осуществляется наглядно, посредством задачи, где необходимо разделить поровну пять одинаковых яблок между тремя детьми.

Выделяется ряд обучающих визуальных задач.

№416 («Серия»). Запишите двумя способами, в виде неправильной дроби и в виде смешанного числа, какая часть фигур закрашена:

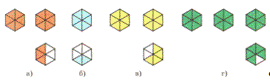
№417 («Серия»). Запишите двумя способами, в виде неправильной дроби и в виде смешанного числа, какая часть фигур закрашена:

Использование визуальных задач в данном пособии осуществляется, в основном, на начальном этапе изучения каждой из тем главы: «обыкновенные дроби». Введение основных понятий осуществляется на наглядной основе.

В банк визуальных задач входят задания на повторения, представленные в 6 классе, относящиеся к категории «Серия»:

№46. Определите, какая часть фигуры закрашена:

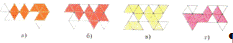
№51. Определите, какая часть фигуры закрашена:

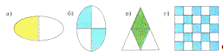
№104 (о). Определите, какая часть фигуры закрашена. Запишите ответ разными способами, если возможно.

№144. Флаг Нигерии поделен на три равные части.  флага белая, а  - зеленые. Определите, какая часть флага закрашена зеленым цветом в каждом случае и найдите флаг Нигерии.

№145. Катя закрасила  квадрата, а Даша - 1 . Определите, где рисунок Кати, а где - Даши.

Уровень наглядности (учебники полноцветные) способствует возможности изучения в 5-м классе ряда тем, ранее традиционно рассматривавшихся в курсе 6-го класса: основное свойство дроби, сложение и вычитание дробей с разными знаменателями (простейшие случаи).

Рассмотрим тему «Проценты». В учебнике И.И. Зубаревой и А.Г. Мордковича тема «Проценты» изучается в конце, в главе IV «Десятичные дроби». На проценты выделено 2 параграфа: §47 «Понятие процента». §48 «Задачи на проценты».

В начале §47 «Понятие процента» идет актуализация знаний. Ученикам предлагается прочитать следующие предложения:

-  всхожесть семян составляют 98 процентов;

-       концентрация раствора кислоты - 50 процентов;

-       в выборах президента России приняли участие 65 процентов избирателей.

Затем раскрывается смысл слова «процент», которое заменяется символом «%».

Далее следует ряд заданий, отмеченных знаком «У», выполняя которые ученики узнают что-нибудь новое (правило, свойство уже известного понятия).

Например:

№929 (У). Математический кружок посещает 1% учащихся школы. Сколько процентов учащихся не посещают математический кружок?

Если вы затрудняетесь ответить, подумайте, сколько процентов составляет число всех учащихся школы.

Проверь себя.

1% - это 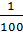 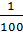от целого. Целое составляет 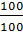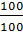. Значит, целое, в данном случае это число всех учащихся школы, составляет 100%.

К задаче 930 составлены вспомогательные вопросы. При решении следующих задач ученикам следует давать ответы на эти вопросы.

Формированию связей между частью числа, выраженной словом (словами), и соответствующим этой части процентам помогает следующее задание:

№933 («Посмотри и определите»). Заполните таблицу по образцу:

Сотая часть числа	1%
Десятая часть числа
Пятая часть числа
Четвертая часть числа
Половина
Три четверти числа
Треть числа

Система упражнений §47 направлена на усвоение двух важных вопросов: понятие «процент» и того факта, что целое - это 100%. Кроме того, школьники учатся правильно отвечать на вопрос, что принято за 100%.

§48 «Задачи на проценты». Параграф начинается с простых задач (со значком У) для устного решения, на отыскание 1%, 2% и т. д. от числа.

№939 (У). Прочитайте предложения и ответьте на вопросы:

-  что принято за 100% в каждом случае?

-       известна ли эта величина?

-       известна ли величина, которая приходится на 1%?

1) В коллекции филателиста 35 марок, посвященных знаменательным датам, что составляет 1% всех марок его коллекции.

) В школе 700 учеников. Шахматный кружок при Доме детского творчества посещает 1% всех учащихся этой школы.

Учащимся предлагается каждый раз установить, что надо найти - число по его проценту, или процент от числа.

В данном учебном пособии рассматриваются только два типа задач на проценты (нахождение процента от числа, нахождение числа по его проценту), решать которые учащиеся должны в два действия или, составляя выражение, где одним из первых шагов является отыскание величины, которая приходится на 1%.

С помощью ряда задач устанавливается связь между процентами и обыкновенными дробями, в основном это задачи на нахождение части от числа, например:

№934. Половину коллекции энтомолога составляют бабочки. Сколько процентов его коллекции приходится на остальных насекомых?

№935. Десятую часть коллекции нумизмата составляют монеты, выпущенные в XVIII в. Сколько процентов его коллекции приходится на остальные монеты?

№936. Четвертая часть книг городской библиотеки - произведения зарубежных писателей. Какой процент библиотечного фонда приходится на отечественную литературу?

№937. Найдите:

% от 245 20% от 24,5 40% от 240 4% от 350

% от 150 50% от 650 60% от 300 12,5% от 40

% от 700 10% от 750 70% от 150 1,5% от 400

Тему «Проценты» продолжают изучать в 6 классе. Вначале 6 класса в главе положительные и отрицательные числа», в §8 «Правило вычисления значения алгебраической суммы двух чисел». Здесь представлены задачи двух типов: на нахождение процента от числа и числа по его проценту, однако более сложные, чем те, которые решали ранее.

№290(У). Мотоциклист проехал 120 км, 30% из которых - по шоссе. 60% оставшегося расстояния он ехал по грунтовой дороге, а далее - по лесной тропе.

Прочитайте первое предложение и ответьте на вопросы:

Что принято за 100%? Известна ли эта величина? Какая величина приходится на 1%? Сколько километров мотоциклист проехал по шоссе? Прочитайте второе предложение и ответьте на вопросы:

Что принято за 100%? Известна ли эта величина? Сколько всего километров проехал мотоциклист по грунтовой дороге и по лесной тропе? Чему равен 1% этой величины? Сколько километров мотоциклист проехал по грунтовой дороге? Сколько километров мотоциклист проехал по лесной тропе?

До задач 290 и 291, включены задачи, направленные на повторение сведений о процентах, полученных в 5 классе.

Самые сложные задачи на проценты рассматриваются в конце 6 класса, когда изучают пропорцию.

Учебник: Дорофеев Г.В., Петерсон Л.Г. Математика, 5-6 Кл. В 2 ч. - М.: Издательство «Ювента», 2004. - 176 с. [12, 13]

В главе 3, § 1, п. 1 разбирается вопрос о происхождении дробей. Приводится историческая справка «Человечеству понадобилось придумать новые - дробные - числа, придумать дроби». В природе существует величины, которые могут быть разделены на любое число равных частей. Измерение таких величин какой-либо единицей не всегда дает в результате целые числа. Рассуждая, таким образом, авторы вводят дробное число на примере деления яблок между детьми. Приходят к выводу, что применение дробных чисел позволяет ответить на вопрос «Сколько?» и в тех случаях, когда натуральных чисел недостаточно. Выводится следующее равенство:

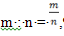
для любых натуральных чисел m и n.

Используя символьную запись, вводятся понятия правильной и неправильной дроби: если числитель m меньше знаменателя n, то дробь называют правильной, а если он больше или равен знаменателю, то дробь называют неправильной. Приводится наглядный пример:

 

Правильные дроби меньше 1, а неправильные - больше или равны 1.

Возвращаясь, к примеру, о делении яблок авторы приходят к ответу другим способом «целое число + дробь». Таким образом, вводится понятие смешанного числа (смешанной дроби):

Ясно, что при любом способе дележа каждый получит одно и то же количество яблок, значит числа  и 3 равны:  = 3. Показываются приемы обращения смешанной дроби в неправильную и выделения целой части из неправильной дроби. На примерах показываются способы выполнения действий со смешанными дробями. Формируются умения выполнять оценку и прикидку результатов.

Прежде чем сравнивать дроби авторы рассматривают изображение таких величин на числовом луче (координатном луче), с помощью такого чертежа и проводят сравнение, основываясь на расположении точек.

 

Большее из двух чисел расположено правее, а меньшее - левее.

Авторы оговаривают тот случай, когда числовой луч не позволяет выполнять сравнение: числа «неудобно» изобразить. Таким образом, мотивируя дальнейшее изучение дробей.

Затем, авторы предлагают ряд упражнений для классной работы, среди которых можно выделить задания на применение полученных знаний.

Класс визуальных задач «Посмотри и найди»:

№17. Какую часть отрезка АВ составляет отрезок CD? Какую часть отрезка CD составляет отрезок АВ?

№18. Какую часть каждый из отрезков АВ, CD и EF составляет от других отрезков? Сделай записи.

Авторы «приучают» детей сознательно разбираться в особенностях дробей, чтобы использовать эти свойства в различных преобразованиях.

Глава 3, § 1, п. 2. «Основное свойство дроби. Преобразование дробей». Основное свойство дроби выводится из рассмотрения примеров на увеличение или уменьшение величины дроби в связи с увеличением и уменьшением ее челнов в несколько раз. Рассмотрение примеров иллюстрируется чертежом.

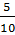
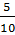 = , числитель и знаменатель второй дроби в 5 раз превышает числитель и знаменатель первой дроби. Вывод из рассуждений записывают в виде правила, основного свойства дроби: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь:

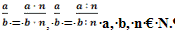
Приводится замечание: основное свойство дроби показывает, что всякое целое или дробное число можно записать в виде дроби бесконечным числом способов, например:

=  =  =  =  = …

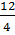
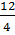Выделяют обучающие визуальные задачи «Посмотри и определи»:

№60. Объясните равенство дробей сначала с помощью рисунка, а потом с помощью основного свойства дроби:

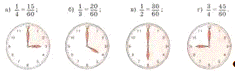
№115. Перерисуйте фигуры в тетрадь. Закрасьте части фигур, соответствующие указанным дробям. Какими еще дробями можно выразить закрашенные части фигур? Запиши ответ с помощью равенств.

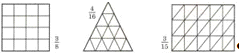
Опираясь на основное свойство дроби, авторы отмечают, что всегда можно добиться, чтобы дроби имели или один и тот же знаменатель, или один и тот же числитель, что затем их можно было сравнить. Правило сравнение дробей очевидно из самого понятия дроби: ясно, если мы делим какую-то сумму денег на несколько равных частей, то чем больше мы возьмем таких частей, тем больше денег нам достанется; если делим предмет на большее число частей, то каждая часть получается меньше. Отсюда правила:

из двух дробей с одинаковыми знаменателями меньше та дробь, у которой числитель меньше;

из двух дробей с одинаковыми числителями меньше та дробь, у которой знаменатель больше.

В качестве специального вопроса рассматриваются примеры решения задач на нахождение части целого и целого по его части.

Выделяют три задачи:

1.  Задачи на нахождение части от числа, выраженной дробью.

2.       Задачи на нахождение числа по его части, выраженной дробью.

.        Задачи на нахождение дроби, которую одно число составляет от другого.

Тип задачи определяется тем, что неизвестно - a, b или , где а - некоторая величина, принятая за единицу («целое»), b - некоторая часть целого, выраженная дробью .

Учащиеся решают такие, опираясь на смысл понятия дроби. Затем показываются формальные приемы решения этих задач умножением или делением на дробь.

Перевод алгоритма решения всех трех задач на математический язык можно представить в виде одного равенства:

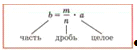
Полученное равенство верно как для случая, когда дробь  является правильной (b - правильная часть а), так и случая, когда эта дробь является неправильной (b - неправильная часть а).

Линия задач продолжается при рассмотрении комбинированных задач на дроби.

Закреплению задач на дроби способствуют следующая визуальная задача:

№508. Составь и реши задачи по схеме. Придумай и реши для них обратные задачи.

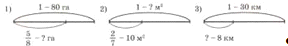
Учебное пособие содержит упражнения на дроби, которые необходимо записать в виде знака процента.

№14. Запишите с помощью дробей, какие части фигур закрашены. Какую дробь можно записать в виде натурального числа, а какую - с помощью знака процента?

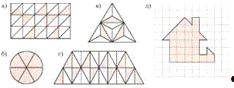
Рассмотрим проценты в контексте темы «Обыкновенные дроби».

Данная тема предложена авторами для изучения в начале 6 класса. §2 «Проценты» рассматривается в Главе 2. Арифметика. К этому времени ученики уже познакомились с дробями и действиями над ними. Изучение процентов идет в 4 этапа:

1.       Понятие о проценте.

.        Задачи на проценты.

.        Простой процентный рост.

.        Сложный процентный рост.

В пункте 1 «Понятие о проценте», авторы описывают что такое «проценты»: «Процентом от любой величины называется одна сотая часть. Обозначается -%.

1% = 0,01 =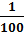

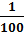
Один процент от минимальной заработной платы (1997 г) 83490 руб. - это 834,9 руб.».

После основного понятия представлена историческая справка о происхождении «процента» и правила выражения процента десятичной дробью или натуральным числом. А так выражение числа в процентах. «Чтобы выразить проценты десятичной дробью или натуральным числом, нужно число, стоящее перед знаком %, разделить на 100. А чтобы выразить число в процентах, надо его умножить на 100».

Затем, авторы предлагают ряд упражнений для классной работы на применение сформулированных правил.

№308. Найди 1% от: а) 340 руб.; б) 1 км.; в) 0,3 л. …

Рассмотрим систему таких упражнений в соответствии с классификацией Н. А. Резник.

№313 («Посмотри и определи»). Какую часть числа составляют 5%, 10%, 20%, 25%, 40%, 50%, 60%, 75%, 80% ? Перерисуй в тетрадь, заполни и выучи таблицу:

Проценты	5%	10%	20%	40%	50%	60%	75%	80%
Десятичная дробь
Обыкновенная дробь

№319 («Посмотри и определи»). Расшифруйте название европейского государства, подобрав указанные доли величины. Выразите в процентах, какую примерно часть площади Москвы оно составляет и какую часть населениям Москвы составляет его население? (Необходимые числовые данные узнай в энциклопедии.)

№328 («Посмотри и определи»). Фонд общественного мнения города N опубликовал следующие данные о зрителях популярных телесериалов:

Можно ли на основании этих данных утверждать, что:

1)  хотя бы один житель города N смотрит оба телесериала;

2)      хотя бы один житель города N смотрит дважды в день телесериал «Петербургские тайны»;

)        хотя бы один житель города N смотрит дважды в день телесериал «Санта-Барбара»;

)        телесериал «Санта-Барбара» смотрит меньшее число жителей города N;

)        телесериал «Петербургские тайны» смотрит большее число жителей города N?

Какие еще выводы позволяют сделать приведенные данные?

№339 («Выбери ответ»). Определите по каждому рисунку, какой примерно процент фигуры закрашен, и выбери наиболее подходящий ответ из трех данных. Прочитай название столицы европейского государства. Какое это государство?

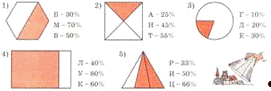
После несложных упражнений на закрепление, рассматриваются задачи.

Например:

№323. Три человека организовали предприятие и договорились, что первый из них будет получать третью часть прибыли, двое других по 20%, а остальные деньги они будут вкладывать в развитие своего предприятия. Сколько процентов от прибыли они будут вкладывать в развитие предприятия? Вырази эту часть числом и в процентах.

Решение.

Вся прибыль составляет 100%: 100% = 1

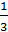
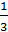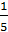
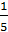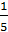
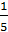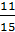
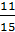 +  +  = , где 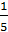 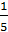= 20% ()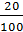

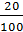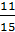
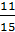-  = , тогда  · 100% = 26 %.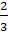

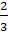Ответ:  или 26 %.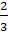

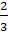Чтобы ученики не забывали понятие дроби, после классных упражнений представлены задачи на повторение.

Пункт 2 «Задачи на проценты». Авторы говорят: «поскольку проценты выражаются дробями, то задачи на проценты являются по существу теми же задачами на дроби». Задачи делятся на 3 типа:

.        Нахождение процента от числа.

2.       Нахождение числа по проценту.

.        Нахождение процентного отношения двух чисел.

Для каждого типа сформулировано правило. В простейших задачах на проценты некоторая величина «а» принимается за 100%, а ее часть «b» выражается числом «p%». Например, чтобы найти процент от числа, надо это число умножить на соответствующую дробь, т.е. чтобы найти 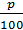 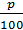от а, надо а умножить на .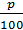

    

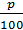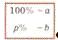
Задача 1. У Ани было 12 000 р. Из них 40% она затратила на завтрак в буфете, а на остальные деньги купила 10 тетрадей. Сколько рублей стоит 1 тетрадь?

Из расчетных задач основное внимание здесь уделяется нахождению процента от некоторой величины. Заметим, что изучение процентов будет продолжено в теме «Отношения и проценты», а также в последующих классах.

Учебник: Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Арифметика, 5-6 Кл.: Учеб. для общеобразоват. учреждений. - 2-е изд. - М.: Просвещение, 2000. - 255 с. [1, 2]

Введение понятия дроби рассматривается в последней главе IV «Обыкновенные дроби» учебника за 5 класс. Появление дроби происходит в результате деления на любое число равных отрезков, в качестве примера приводится деление длины отрезка. Измерение, которого не всегда дает в результате целые числа. Записи чисел , , , , , … называют обыкновенными дробями или короче дробями. 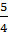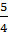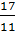Таким образом, смысл дробей , ,  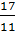- это одна из равных долей или несколько равных долей единицы, дробь обозначается через , где p и q - натуральные числа, а дробь  означает пэ части единицы, называют дробью или рациональным числом. Авторы сообщают, что дробь можно получить, записав любое натуральное число p с числителем p и знаменателем 1: p = .

После небольшой теоретической справки приводится ряд упражнений, направленных на закрепления понятия дроби, выделим из них лишь некоторые:

№737 («Посмотри и определи»). На рисунке изображены часы.

а) Какая часть окружности заключена между часовой и минутной стрелками, считая от минутной стрелки к часовой по их ходу, в 6 ч 00 мин; в 3 ч 00 мин?

б) Какую часть окружности пройдет конец минутной стрелки: за 30 мин; за 15 мин; за 20 мин; за 45 мин; за 40 мин?

в) Какую часть часа составляет: 10 мин; 5 мин; 25 мин; 55 мин?

№738 («Тренажер»). Перечертите в тетрадь квадрат 4 x 4 клетки рисунок. Закрасьте:

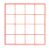   а)  квадрата; б)  квадрата; в)  квадрата.

№739 («Посмотри и найдите»). На рисунке отрезок АВ разделен на 6 равных частей. Какую часть отрезка АВ составляет отрезок AD?

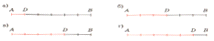
Пункт 4.2 «Равенство дробей». Авторы говорят о дробях, определяющих одно и то же число, записанное разными способами:  = .

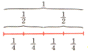
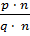
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится равная ей дробь:  =  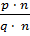или наоборот: 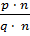 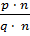=  - основное свойство дроби. Авторы придерживаются одного обозначения дроби на протяжении всего курса. Из основного свойства следует правило сокращение дробей: если числитель и знаменатель дроби имеют общий множитель (n), то дробь можно сократить на этот множитель, т. е. разделить на него и числитель и знаменатель. Здесь же отмечается что, если числитель дроби делится на знаменатель, то дробь равна частному от деления числителя на знаменатель. Таким образом, дробь представляется результат деления числителя на знаменатель.

Закрепить основное свойство предлагается примерами:

№761. Объясните с помощью рисунка, почему  =  =  = .

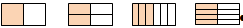
При вычислениях с дробями допускается сокращение дроби на любой общий делитель ее числителя и знаменателя (необязательно наибольший), а также приведение дробей к любому общему знаменателю (необязательно к наименьшему). Но в этом и в другом случае разъясняется, когда вычисления будут наиболее рациональными.

Формирование понятия дроби сопровождается обучением решению простейших задач на нахождение части числа и числа по его части. В пункте 4.3 «Нахождение части числа и числа по его части» соответственно рассматриваются только две задачи:

Задача 1. Было 1000 рублей,  этой сумы истратили. Сколько денег истратили?

Решение. Будем считать, что 1000 р. Состоит из пяти пятых долей. Тогда на одну пятую приходится 1000 : 5 = 200 р., а на две пятых - в два раза больше: 200 · 2 = 400 р. Эти два действия можно объединить: 1000 : 5 · 2 = 400 р.

Чтобы найти  числа 1000, можно это число разделить на знаменатель дроби и результат умножить на числитель.

Задача 2. Потратили 600 рублей, что составило  имевшейся суммы денег. Сколько было денег?

Решение. Будем считать, что искомое число состоит из трех третьих долей. По условию его две трети равны 600. Тогда на одну треть приходится 600 : 2 = 300 р., а на три трети 300 · 3 = 900 р. Эти два действия можно объединить: 600 : 2 · 3 = 900 р.

Чтобы найти число,  которого равны 600, можно 600 разделить на числитель дроби и результат умножить на знаменатель.

После приведения дробей к общему знаменателю появляется потребность в сравнении дробей. Сравнение осуществляется при помощи чертежа.

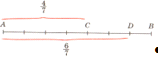
Из двух дробей с общим знаменателем больше та дробь, у которой числитель больше. Вводятся обозначения: если p > r, то  > .

Здесь же авторы вводят определение правильной и неправильной дробей. Доказывается следующее утверждение: если первая дробь меньше второй, а вторая дробь меньше третьей, то первая дробь меньше третьей.

После чего приводятся примеры для решения.

№807. Сравните правильную и неправильную дроби:

а) с 1; б) между собой.

№808. С помощью рисунка объясните, почему  > ,  < .

Смешанная дробь рассматривается как другая запись обыкновенной неправильной дроби.

Заключительный этап изучения темы - изображение дробей точками на координатной прямой.

В данной теме решаются задачи на умножение и деление дробей, а также обращается особое внимание на то, что рассмотренные ранее задачи на дроби можно решать с помощью умножения и деления на дробь.

Перейдем к рассмотрению темы «Проценты». Учебник 6 класса открывает глава 1. «Отношения, пропорции, проценты». Поскольку тема предшествует теме «Десятичные дроби», то понятие процента определяется через обыкновенную дробь и только: процент - это одна сотая часть числа, 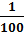 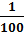= 1%.

С процентами связаны задачи трех основных типов на нахождение:

-       процентов данного числа;

-       числа по его процентам;

-       процентного отношения двух чисел.

Задача 1. Найти 1% от 600 м.

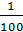
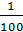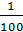
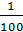Решение. 1% от 600 м равен  от 600 м:  · 600 = 6 (м).

Ответ: 6 м.

Задача 2. Найти число, 1% которого равен 5.

Решение. Так как 1% числа равен 5, то само число в 100 раз больше: 5 · 100 = 500.

Ответ: 500.

Задача 3. Из 30 учащихся класса в различных кружках занимается 12. Сколько процентов учащихся класса занимается в кружках?

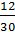
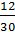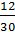
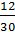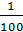
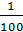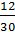
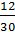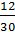
Решение. В кружках занимается  всех учащихся класса. Задача заключается в том, чтобы выразить отношение  в процентах, т. е. узнать, сколько раз  (процент) содержится в числе :  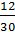= % = 40%.

Сначала решаются задачи на нахождение одного процента от данного числа и числа по его одному проценту. Затем задачи усложняются.

Так как задачи на проценты являются задачами на дроби, то авторы предлагают решать известным способом - умножением или делением на обыкновенную дробь. Таким образом, более сложные задачи рассматриваются в пунктах 1.7 «Задачи на проценты», 1.8 «Круговые диаграммы». Например:

№137. На круговой диаграмме показан процентный состав населения города N. Сколько мужчин, женщин и детей живет в городе N, если всего в нем 48 тыс. жителей?

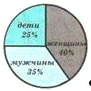
Более глубоко и подробно рассмотрение процентов проходит после изучения десятичных дробей.

В данном учебном пособии использование визуальных задач преимущественно приведено на начальном этапе введения основных понятий дроби и достаточно мало при рассмотрении темы «Проценты».

Вывод.

Проанализировав учебные пособия по математики для 5 - 6 классов таких авторов как: Н.Я. Виленкина, И.И. Зубарева, В.Г. Дорофеева, С.М. Никольского можно сделать следующий вывод, что визуальные задачи при изучении темы «Проценты» используются крайне редко.

Хотелось бы отметить, что наиболее распространенное применение визуальных задач реализовано в учебных пособиях таких авторов как: И.И. Зубарева, Г.В. Дорофеев. В данных учебниках визуальные задачи используются, как правило, при введении новых понятий, а так же используются в системе упражнений на закрепление изученного материала.

Так же хотелось бы отметить, что в учебнике Г.В. Дорофеева прослеживается связь между процентами и обыкновенными дробями.

.2 Методические основы изучения тем «Обыкновенные дроби и

проценты» в школе

Умение решать задачи на дроби и проценты в значительной мере определяются тем, как понятия дроби и процента предварительно сформированы у учащихся. Усвоение же этих понятий для многих учащихся связано с большими трудностями. Трудности в освоении дробей заключаются, в частности, в том, что ученику надо одновременно осмыслить количество долей (числитель), величину их (знаменатель) и осознать их отношение (числителя к знаменателю). Оперируя дробями, ученику приходится одновременно пользоваться правилами, которые распространяются на целые числа и противоположные им. Так, например, при сложении дробей с одинаковым знаменателем числители складываются, а знаменатели нет; с увеличением числителя (при том же знаменателе) дробь увеличивается, а с увеличением знаменателя (при том же числителе) дробь уменьшается; величина дроби не зависит от абсолютной величины числителя и знаменателя. Все это противоречит прошлому опыту ученика, а поэтому и усваивается с трудом. Формирование понятия дроби связано с отвлечением от ряда признаков, которые входили в понятие целого числа как существенные, и с выделением тех зависимостей, которые существуют между числителем и знаменателем (выделение отношений).

Необходимо правильно ввести понятие дроби, ее обозначение, научить сравнивать дроби, научить решать задачи на нахождение дроби числа. Все названные вопросы становятся для учащихся яснее, если раскрывать их на наглядной основе. Ознакомить детей с долями - значит сформировать у них конкретные представления о долях, т.е. научить детей образовывать доли практически. Например, чтобы получить одну четвертую долю круга, надо круг разделить на четыре равные части и взять одну такую часть.

Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий: геометрические фигуры, вырезанные из бумаги; рисунки фигур, выполненные на бумаге или в диапозитивах (круги, прямоугольники, треугольники, бруски, отрезки и т.п.); ТСО (технические средства обучения).

Эффективным упражнением для формирования представлений о долях является сравнение долей одной и той же величины, которое выполняется чисто практически.

Например, предлагается сравнить доли  и  и поставить знак “>”, ”<”.

Учащиеся изображают доли, например, с помощью деления квадрата на 3 и 2 равные части (рис. 1). Сравнивают соответствующие части квадрата и убеждаются, что  меньше, чем .

    Рис. 1    

Для сравнения дробей обычно используются иллюстрации с равными прямоугольниками (рис. 2). Учащимся предлагают начертить в тетради прямоугольник, длина которого 16 см, а ширина 1 см. Это один прямоугольник. Запишем (в первом прямоугольнике записывают число 1). Начертите под первым прямоугольником такой же второй и разделите его на 2 равные части (выполняют). Какие доли получили (вторые, половины). Сколько вторых долей в целом прямоугольнике? Подпишите. Ниже начертите такой же прямоугольник и разделите его на 4 равные части. Как называется каждая часть? Сколько четвертых долей в целом прямоугольнике? Сколько четвертых долей в половине? Что больше: одна вторая или две четвертые? Начертите четвертый такой же прямоугольник и разделите его на 8 равных частей.

Рис. 2

Как называются полученные доли? Сколько восьмых долей в целом? Сколько восьмых долей в четверти, в половине прямоугольника? Что больше: три восьмых или одна четвертая? Какой дроби равна одна вторая?

Ответы на все перечисленные вопросы дети дают, глядя на рисунок.

Образование дробей, как и образование долей рассматривается на практике.

Пример: Разделите круг на 4 равные части.

Как назвать каждую такую часть?

Запишите.

Покажите три четвертые доли.

Вы получили дробь - три четвертых.

Кто сможет записать эту дробь?

Что показывает число 4 (на сколько равных частей разделили круг)? Что показывает число 3 (сколько таких частей взяли)? [46]

Аналогичным образом учащиеся получают и записывают другие дроби, объясняя, что показывает каждое число.

Для закрепления полученных знаний выполняются такие же упражнения, как и при ознакомлении с долями: по данным иллюстрациям называют и записывают, какие дроби изображены, или же изображают дробь с помощью чертежа, рисунка. Уяснению конкретного смысла дроби помогают упражнения на сравнение дробей, а также решение задач на нахождение дроби числа.

Для ребенка 7-8 лет «часть» - кусок, немного и т. п. Он еще плохо разбирается даже в отношениях между видимыми конкретными явлениями. Тем труднее для него, конечно, разбираться в отношениях между отвлеченными числами, а так как дробь есть как раз такое отношение, то изучение дробей начинается сравнительно поздно и представляет значительные трудности.

Многочисленные исследования, произведенные различными исследователями (Липман и Боген, Пиаже, Штерн и др.), притом часто по различной методике, почти единодушно утверждают, что особенно быстрый рост способности устанавливать отношения бывает у детей приблизительно около 10-11 лет. Как раз с этого возраста школа начинает изучение дробей. На трудность их для детей указывает тот факт, что когда дети изучают дроби, неуспеваемость их по арифметике значительно увеличивается. При оперировании с дробями детей в особенности затрудняет: 1) обращение со знаменателями и 2) понимание значения умножения и деления дробей [5, стр. 210].

Умножать и делить на дробь необходимо при решении текстовых задач на нахождение части от числа и числа по данной величине его части. Эти задачи, в отличие от задач, решаемых до изучения дробей, обладают некоторыми своими специфическими особенностями. Так, если до изучения дробей одно арифметическое действие всегда соответствовало одной арифметической операции (сложить, вычесть, умножить, разделить), то теперь при решении рассматриваемых задач, одно арифметическое действие выполняется с помощью двух операций (при умножении и делении на дробь).

Кроме того, в начальной школе число по данной одной какой-нибудь части его находится умножением, а часть данного числа находится делением. В V же классе при изучении дробей происходит расширение понятий «умножить» и «разделить»; теперь часть от числа находится не делением, а умножением, число же по известной его части не умножением, а делением. Следовательно, для решения тех же простых задач надо выполнять действия, обратные тем, которые выполнялись раньше.

Помимо всего этого для учеников до изучения дробей, умножение было равнозначно увеличению, а деление - уменьшению; при умножении же на правильную дробь число не увеличивается, а уменьшается, а при делении не уменьшается, а увеличивается. Всё это противоречит прошлому опыту учащихся.

Чтобы подготовить учащихся к наиболее трудному случаю умножения - умножению на дробь, необходимо повторить нахождение части от числа делением или двумя действиями. Сначала решаются задачи и примеры на нахождение одной части числа: ;  и т. п.

Например: «Поле занимает 720 га; 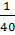 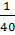его занята горохом. Какая площадь занята горохом?»

Решение: чтобы найти 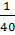 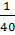часть площади 720 га, надо 720 разделить на 40 равных частей: 720 : 40 = 18 (га).

Учащимся можно предложить самим придумать задачи и примеры аналогичного содержания, с последующим объяснением и решением. Решение такого рода задач и примеров желательно сопровождать графической иллюстрацией. Для этого, например, чертят прямоугольник на клетчатой бумаге, где отмечают дроби, обозначающие какую-либо часть целого, т. е.

     

 

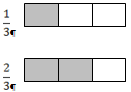
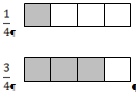
Дальше переходим к задачам на отыскание нескольких частей от целого: «Скорость полета стрижа 1600 м в минуту, скворца  и ястреба 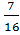 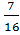скорости полета стрижа. Найти скорость полета скворца и ястреба в минуту».

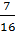
Решение: Надо найти ,  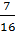от числа 1600 м. Начинать решение целесообразно со следующих вопросов:

Сколько четвертых частей числа можем (умеем) найти? (.)

Как это сделать? (1600 разделить на 4 равные части.)

Сколько получится? (1600 : 4 = 400 м.)

Как найти  от числа 1600 м? (Надо 400 м умножить на 3.)

Почему? ( больше  в 3 раза.)

Сколько получится? (400 ∙ 3 = 1200 м.)

Что показывает число 1200 м? (Скорость полета скворца в минуту.)

Применяя правила увеличения и уменьшения дробей в несколько раз, учащиеся могут решать задачи на нахождение части от дробного числа, осуществляя наглядно нахождение одной или нескольких долей от дроби.

Например,  от .

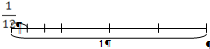
Нахождение неизвестного числа по его дроби (части), когда известно, какая именно часть дана и сколько единиц она составляет, тоже рассматривают, опираясь на наглядность, что приводит к лучшему усвоению детьми данного материала. Проиллюстрируем задачу: «В колхозе засеяно 52 га, что составляет  часть всего поля. Как велика площадь поля?» [42, с. 237]

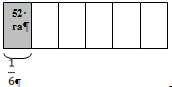
Таким образом, с введением дробных чисел в курс математики происходит расширение числовой области:

– новое понятие числа требует введения нового определения понятия равенства чисел, суммы и произведения;

–       введение дробных чисел снимает ограничения с действия деления целых чисел (кроме деления на нуль);

–       дробные числа подчиняются всем законам арифметических действий, установленным для чисел натуральных.

Изучение дробных чисел в школьном курсе продолжается с появлением процента. Тему «проценты» тоже нельзя отнести к легко усеваемым. Это связано, прежде всего, с путаницей изучаемых понятий, поскольку процент представляет собой обыкновенную дробь. Ее традиционное изучение сосредоточено в строгих временных рамках курса V - VI классов, что не позволяет расширить спектр практических приложений и полноценно учитывать возрастные возможности учащихся в формировании ряда практических умений в работе с процентами.

Тема разворачивается по спирали и изучается в несколько подходов с V по IX класс включительно. При каждом проходе учащиеся возвращаются к процентам на новом уровне, их знания пополняются, добавляются новые типы задач и приемы решения. Такое многократное обращение к понятию приводит к тому, что постепенно оно усваивается прочно и осознано.

Вопросы, связанные с процентами, позволяют сделать курс практически-ориентираванным, показать учащимся, что приобретаемые ими математические знания применяются в повседневной жизни. Интерес в значительной степени поддерживается также и содержанием задач, что служит достаточно сильным мотивом для решения предлагаемых задач.

Введение процентов опирается на предметно практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. С самого начала освоения понятия учащиеся выполняют много заданий, в которых требуется заштриховать, закрасить, начертить, вырезать часть фигуры. Широко используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения.

При изложении этой темы могут быть реализованы широкие возможности для дифференцированного обучения учащихся. Использованы задачи широкого диапазона сложности - от самых простых, базовых, до достаточно трудных. Учитель может подобрать материал, соответствующий возможностям учащихся.

При обучении решению задач на проценты учащиеся знакомятся с разными способами решения задач. Ученик овладевает разнообразными способами рассуждения, обогащая свой арсенал приемов и методов. Но при этом также важно, что он имеет возможность выбора и может пользоваться тем приемом, который ему кажется более удобным.

Впервые о процентах учащиеся узнают в V классе. В одних учебных пособиях проценты рассматриваются в начале учебного года, то есть до изучения десятичных дробей (при повторении и систематизации материала, связанного с обыкновенными дробями), в других в середине учебного года после изучения десятичных дробей.

«Что такое процент» - это первая тема изучаемой линии. Основная цель данного этапа - сформировать понимание процента как специального способа выражения доли величины, выработать умение выражать процент соответствующей обыкновенной дробью. Учащиеся должны понять, что проценты это универсальная величина измерения, которая появилась из практической необходимости измерения различных величин и не только денежных.

Учащиеся осваивают фактически другую терминологию, к которой ученики привыкают через систему упражнений, нацеленных на «перевод» задач с языка долей и дробей на язык процентов и обратно. В результате еще до решения основных задач на проценты, учащиеся прочно овладевают достаточно большим набором фактов, которые помогают им в дальнейшем при изучении как темы проценты, так и математики в целом. Так, они усваивают некоторые «эквиваленты»:

25% величины - это  этой величины;

половина некоторой величины - это ее 50%;

% величины втрое больше, чем ее 10% и т.п.

Ребята учатся сравнивать доли величины, заданные разными способами:

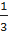
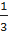 больше, чем 25%;

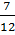
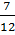 некоторой величины больше 50% этой величины;

% меньше четверти; вся величина - это 100%. И т. д. [14]

Выработке навыков может помочь работа учащихся с серией практических заданий, способствующих усвоению учащимися понятия процента. Приведем несколько примеров.

Пример: Заштрихуйте на рисунки указную часть круга:

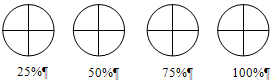
Среди упражнений, направленных на сознательное усвоение материала, могут предлагаться такие задачи:

Примеры:

1.  Для каждой фразы из первого столбца подберите соответствующую фразу во втором:

1.  100% учащихся школы

2.       25% учащихся школы

3.  10% учащихся школы

4.  50% учащихся школы

а) половина всех учащихся школы

б) все учащихся школы

в) четверть всех учащихся школы

г) десятая часть всех учащихся школы.

2. Туристы проехали 50% пути на поезде и 40% пути на автобусе. Весь ли путь они проехали?

3. В классе 40% девочек. Кого в классе больше - мальчиков или девочек?

4. Что больше:

а) 60% всего класса или половина класса?

б) 10% зарплаты или четверть зарплаты?

в) половина или 45% всего населения страны? [46]

Для формирования понятия процента очень полезны следующие задания.

Задание 1. Закрасьте: а) 10% сердечек (рис. 3); б) 60% птичек (рис. 4).

Рис. 3                     Рис. 4

Задание 2. На рис. 5 изображена указанная часть фигур. Дополните рисунок так, чтобы получилось 120% фигур.

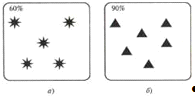
Рис. 5

 

Теперь, когда учащиеся достаточно свободно и осознано, владеют понятием процента, можно перейти к задаче на нахождение процентов некоторой величины. Методически целесообразно сначала находить один процент величины, а потом - несколько процентов этой величины (желательно чтобы у педагога уже были сформированы основные алгоритмы по методике нахождению процентов). Что касается второго приема решения (путем умножения на обыкновенную дробь), то конечно, его рассмотрение необходимо, но в более поздние сроки [17].

Рассмотрим, как развертывается соответствующая линия задач.

Умение решать задачи на проценты тесно связано с умением решать задачи на отыскание части от целого, а также целого по его части. Анализируя условия и тех и других задач, сначала надо определить, какая величина принята за целое (в задачах на проценты - за 100%). Далее следует выяснить, известна ли эта величина. После этого уже нетрудно определить, какая величина приходится на одну долю, и выполнить действия, необходимые для нахождения ответа на вопрос задачи.

В своей статье И. И. Зубарева говорит, что в учебниках и V и VI классов перед набором задач, в которых надо найти часть от целого по его части, целесообразно давать учащимся указание.

Прежде чем приступать к решению задачи необходимо ответить на вопросы:

·  Какая величина принята за целое?

·        Известна ли эта величина?

·        Как найти величину, которая приходится на одну долю?(этот вопрос формулируется только в V классе)

·        Что требуется найти - часть от целого или целое по его части?

Перед задачами на проценты дается аналогичное указание.

Прежде чем приступать к решению задачи ответьте на вопросы:

·  Какая величина принята за 100%?

·        Известна ли эта величина?

·        Как найти величину, которая приходится на 1%?(этот вопрос ставится в V классе и в VI классе до изучения §21 «Нахождение части от целого и целого по его части»)

·        Что требуется найти - процент от числа или число по его проценту?

При этом важно, чтобы учащиеся в случае, если величина, принятая за 100%, известна, при ответе на первый вопрос называли бы не числовое ее значение, а описывали бы величину словами. Например, вместо «50 га» говорили бы «площадь всего поля», а вместо «230 км» - «длина всего пути».

Замечание. В V классе мы рассматриваем задачи на проценты лишь двух типов: на нахождение процента от числа и нахождение числа по его проценту. Задачи на процентное отношение рассматриваются только в VI классе после изучения пропорций.

Это обусловлено многолетними наблюдениями за усвоением темы «Проценты» учениками V классов, обучавшимися по учебнику Н. Я. Виленкина и др. Опыт показывает, что задачи первых двух типов учащиеся в той или иной мере решают, а задачи третьего типа для абсолютного большинства из них недоступны. Сталкиваясь с задачами третьего типа, пятиклассники, как правило, обращаются за помощью к родителям, которые решаю задачи с помощью той же пропорции.

Итак, в V классе при изучении темы «Проценты» главное - приучить детей при анализе условия задачи определять, какая величина принята за 100% и известна ли эта величина. Если этого не происходит, учащиеся зачастую начинают действовать наугад, что приводит к неверному решению.

В VI классе уровень сложности задач повышается. Сначала возникают задачи с разными процентными базами. Приведем примеры.

Задача 1 (№281). Мотоциклист проехал 120 км, 30% из которых - по шоссе.

% оставшегося расстояния он проехал по грунтовой дороге, а далее - по лесной тропе.

Прочитайте первое предложение и ответьте на вопросы.

Что принято за 100%? Известна ли эта величина?

Какая величина приходится на 1%?

Сколько километров мотоциклист проехал по шоссе?

Прочитайте второе предложение и ответьте на вопросы.

Что принято за 100%? Известна ли эта величина?

Сколько километров составляет путь, пройденный мотоциклистом по грунтовой дороге и по лесной тропе?

Чему равен 1% этой величины?

Сколько километров мотоциклист проехал по грунтовой дороге? Сколько километров мотоциклист проехал по лесной тропе?

Задача 2 (№282). Мотоциклист проехал по шоссе 8 км, что составило 20% всего пути. 45% оставшегося пути он ехал по грунтовой дороге, а далее - по лесной тропе.

Ответьте на вопросы.

Что принято за 100% в первом предложении, а что во втором? Известны ли эти величины? Чему равен 1% всего пути? Какова длина всего пути?

Сколько километров составляет путь, пройденный мотоциклистом по грунтовой дороге и по лесной тропе?

Чему равен 1% этой величины?

Сколько километров проехал мотоциклист по грунтовой дороге? Сколько километров проехал мотоциклист по лесной тропе?

Что общего в условиях предыдущих двух задач и чем они отличаются?

Замечание. Для учеников основная трудность при выполнении этих заданий заключается в том, чтобы понять: в первом предложении за 100% принята длина всего пути, а во втором - длина грунтовой дороги и лесной тропы вместе (оставшийся путь). Результатом выполнения таких упражнений является осознание учениками того, что в одной и той же задаче за 100% могут быть приняты разные величины.

Многие учителя, обучая детей решению задач на проценты, уже в V классе знакомят их с методом решения путем умножения (если надо найти процент от числа) или деления (если надо найти число по его проценту) числа на десятичную дробь, соответствующую данному числу процентов. Для этого достаточно показать, что, решая задачу в два этапа: сначала находим величину, которая приходится на 1%, затем отвечаем на вопрос задачи, получаем тот же результат, что и в случае умножения (деления) на десятичную дробь.

Такой подход к формированию умений решать задачи на проценты находится в единстве с подходами к изучению других тем программы. Знания по изучаемому вопросу формализуются только после того, как учащиеся полностью усвоили все понятия, свободно оперируют терминами, демонстрируют понимание смысла условий и вопросов тех или иных задач и упражнений по данному разделу, осознанно осуществляют поиск решения задач (Зубарева И. И.) [17].

Таким образом, методика изучения дробей и процентов в 5-6 классе строится, опираясь на:

·  логику построения содержания начального курса математики, в основе которой лежит тематический принцип, позволяющий сориентировать курс на усвоение системы понятий и общих способов математических действий.

·  методические подходы к усвоению школьниками математических понятий, в основе которых лежит установление соответствия между предметными, вербальными, схематическими (графическими) и символическими моделями, а также формирование у учащихся представлений об изменении, правиле (закономерности) и зависимости.

·  систему учебных заданий, процесс выполнения которых носит продуктивный характер и, исходя из психологических особенностей младших школьников, определяется соблюдением баланса между логикой и интуицией, словом и наглядным образом, осознанным и подсознательным, догадкой и рассуждением.

Учащиеся в результате практических действий, анализа ситуаций, соотнесения различных моделей подходят к осознанию основных понятий их свойств, формулируют их и применяют при выполнении различных заданий.

С учетом требований, предъявляемых к дидактическим программным средствам, было разработано мультимедийное пособие, отражающее системный подход к изучению обыкновенных дробей и процентов, которое может применяться на начальном этапе формирования основных понятий в рамках данной темы школьного курса математики.

Глава 3. Мультимедийное пособие по теме «Обыкновенные дроби и

проценты»

.1 Основные характеристики пособия

Информационная функция средств обучения, применяемых на уроке, в современном мире меняется. Слово учителя, учебник перестали быть единственным источником информации.

С расширением видов и форм представления информации, с развитием возможностей электроники и техники, с появлением телевидения и компьютеров, статические изображения в значительной мере утрачивают свое значение и уступают место динамическим картинам. Подвижные изображения способны дольше и крепче удерживать внимание зрителей, отображать действительность более полно и объемно.

Реализовать динамическое сопровождение урока можно посредством Flash-технологий, на основе которых школьный учитель может создавать электронные учебники, виртуальные лабораторные работы, демонстрации, интерактивные мультимедиа-презентации. Такое интерактивное дидактическое пособие, разработанное при помощи программы Macromedia Flash, является компьютерным программным средством, не требующим никаких специальных и дополнительных программных или технических средств. Запуск файла пособия может быть осуществлен при помощи программы Internet Explorer, которая имеется на большинстве персональных компьютеров, а маленький размер файла позволяет размещать его на странице Интернета. Таким образом, можно реализовать использование данного пособия не только в классе, но и на удалённых компьютерах.

Этим и обусловлен выбор формы пособия - Flash-фильм, просматривая который, пользователь имеет возможность либо наблюдать за происходящими изменениями, либо изменять картинку самостоятельно, выделяя закономерности и приходя к определенным умозаключениям.

Выбор темы Flash-фильма обусловлен трудностью усвоения многими учащимися понятий дроби и процента. Восприятие предложенного материал противоречит прошлому опыту ученика, а поэтому и усваивается с трудом. Формирование понятий связано с отвлечением от ряда признаков, которые входили в понятие целого числа как существенные. Кроме того, введение дроби, процента в школьном курсе математики в большинстве учебников опирается на ряд визуальных задач. То есть в ходе решения таких задач описывается процесс, который носит динамический характер и для более глубокого усвоения и осмысления требует динамической иллюстрации. При использовании Flash-технологии становится возможным смоделировать такого рода процессы, тем самым, повысив уровень их осмысления.

Интерактивное пособие разрабатывалось с учётом требований, предъявляемых компьютерным программным средствам, использующимся в учебном процессе: дидактических, методических и эргономических.

Предложенный Flash-фильм является наглядным пособием к уроку математики. Способ подачи материала с опорой на визуальное мышление, представленный в этом пособии, мог бы облегчить восприятие учащимися довольно сложной для них теории.

Данное пособие можно использовать на различных этапах урока: в первую очередь - на уроках изучения нового материала, проводимых объяснительно-иллюстративным методом в качестве вспомогательного демонстрационного пособия, кроме того, можно использовать его и на уроках закрепления, а так же при обобщении и систематизации знаний, при этом просматривая лишь его фрагменты, используя тест. Пособие может применяться не только в процессе фронтальной работы учителя с классом, но и предлагаться учащемуся для самостоятельного просмотра, в качестве дополнения к учебнику.

Объем Flash ролика составляет 1,25 МБ.

Системные требования:

Pentium;

CD ROM x 4

-Windows 95/98/2000/XP

Macromedia Flash Player 7

Структура Flash-фильма.

Flash-фильма состоит из четырех блоков:

1.       Обыкновенные дроби.

2.       Задачи на дроби.

.        Проценты.

.        Тест: «Порешаем задачи».

Тема «Обыкновенные дроби и проценты» выбрана не случайно. Эта тема изучается не компактно, а блоками, и потому встречается фрагментарно в различных разделах учебников математики 5 и 6 классов. Данное пособие группирует основные понятия и типовые задачи на дроби и проценты в единую структуру. Поэтому пособие можно использовать как при изучении конкретного раздела темы, так и на этапе обобщения и систематизации представлений о дробях и процентах.

Интерактивное дидактическое пособие является компьютерным программным средством, разработанным при помощи программы Macromedia Flash. Предназначено для работы на персональном компьютере. Для работы с пособием не требуется никаких специальных и дополнительных программных или технических средств.

Flash-фильм может просматриваться учащимися самостоятельно, без помощи и управления со стороны преподавателя. Предполагаемый просмотр сцен осуществляется в порядке, указанном в содержании, где выделены два направления: линия дроби и линия процента. Пользователь просматривает теоретическую информацию, содержащуюся во Flash-фильме, используя в основном кнопки перехода на следующую страницу или возращения к содержанию Flash-фильма.

Просмотр охватывает сначала первую тематическую линию и начинается с введения понятия дроби, после чего выделяются основные теоретические вопросы, связанные с обыкновенными дробями:

·  дробь, как часть целого;

·        правильные и неправильные дроби. Смешанные числа;

·        сравнение дробей;

·        основное свойство дроби;

·        нахождение части от числа;

·        нахождение числа по его части;

·        нахождение дроби, которую одно число составляет от другого.

Последующий просмотр выделяет вторую тематическую линию, связанную с понятием процента:

·        понятие процента;

·        нахождение процента от числа;

·        нахождение числа по его проценту.

Каждый раздел подкреплен конкретными примерами, на основе которых учащиеся могут попробовать применить теорию к практике. Причем, решая эти задачи, ученик может проверить свой ответ или получить подсказку. Затем учащийся может перейти к выполнению заданий теста: «Порешаем задачи». Кроме того, каждое теоретическое обоснование понятия или свойства подкрепляется соответствующим определением понятия или правилом выполнения действий, ключевым для данного раздела.

С другой стороны просмотр может быть организован учителем на уроке математики. В этом случае учитель вызывает сцены в порядке, соответствующем методике изложения материала. Переход от одной сцены к другой при таком порядке просмотра осуществляется возвратом к содержанию с последующим переходом к нужной сцене.

Ниже подробнее рассмотрим способы организации работы с пособием.

Управление данным мультимедийным пособием осуществляется с помощью следующих элементов навигации:

 или  - кнопки, при нажатии которых осуществляется переход от титульной страницы на сцену «Содержание».

 - данная кнопка позволит вернуться из любой сцены на сцену «Содержание».

 - эта кнопка позволит вам листать мультимедийное пособие вперед, как книгу, в соответствии с предложенным содержанием.

 - кнопка, позволяющая вернуться к началу текущей сцены.

 - кнопка обозначающая продолжение просмотра в данной сцене.

 - кнопка продолжения просмотра, переход к следующей сцене.

 - появляющаяся кнопка, указывающая на ответ в примере.

 - появляющаяся кнопка, позволяющая повторить то или иное действие.

 - кнопка демонстрирующая правило, которым следует воспользоваться при решении того или иного примера (задачи).

 - кнопка всплывающей подсказки.

 - кнопка проверки решенного примера и в случае положительного результата перехода к следующему примеру.

 - кнопка перехода к решению рассматриваемой задачи.

Перейдем к рассмотрению каждой части интерактивного пособия.

 «Дробь, как часть целого»

При просмотре сцены «Дробь, как часть целого» учащиеся знакомятся с дробным числом. На этом этапе осуществляется подготовка учащихся к изучению нового материала, здесь возможно обсудить понятие обыкновенной дроби; ее составляющие: числитель и знаменатель.

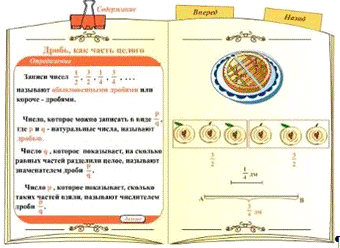
Визуально сцена разбита на две зоны: левую и правую. Правый лист представляемой книги отведен под динамическую картинку, левый под сопровождающий ее текст. В последующих сценах структура сохраняется. Данная сцена включает в себя ряд примеров, на основе которых выводится определение обыкновенной дроби. Сразу же вводится символика, буквенное обозначение числителя и знаменателя. Это удобно, поскольку, как уже отмечалось, тема обширная, и данное пособие охватывает лишь ключевые моменты, завязанные на специальном обозначении и терминологии.

После просмотра данной сцены, предлагается подкрепить теорию наглядными примерами, с интерактивными элементами. Предлагается ряд задач, представленных в разной форме: теста или безвариативной форме ответа, на предлагаемое задание, но с осуществляемой проверкой. Однако переход к таким примерам-задачам возможен лишь после теоретической справки, и не осуществляется через содержание. Задачи не выступают как самостоятельная практическая часть, а служат первичным закреплением данного в первой сцене понятия.

        

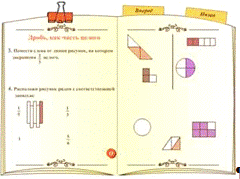
Основная мысль, объединяющая эти задания - разбиение фигур на равные части, где закрашенная часть обозначает взятую долю. Первый пример в данной серии является примером-шпаргалкой.

Форма проверки таких заданий безоценочная, что вполне объясняется типом таких упражнений и поставленной целью: первично закрепить введенное понятие.

Перейдем к рассмотрению сцены “Правильные и неправильные дроби, смешанные числа”. Еще раз хочется отметить, что данное пособие не отвечает точной тематической линии ни одного из учеников. В данной сцене определения появляются поэтапно, что позволяет лучше увидеть суть данных понятий. После появления определенных фраз появляется картинка - внимание переходит с текста на графическую иллюстрацию, что позволяет свести воедино, наглядно-образное и словесно-логическое мышление.

Динамически отмечен момент перехода неправильной дроби через единицу при преобразовании в смешанное число - момент, вызывающий особые трудности у учащихся. Схема перехода показана на простых фигурах и подкреплена соответствующим выводимым текстом, записью примера.

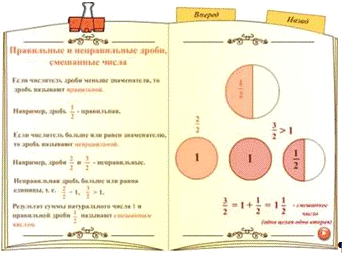
После чего целесообразно рассмотреть преобразование неправильной дроби в смешанное число и, наоборот, из смешанного числа в неправильную дробь.

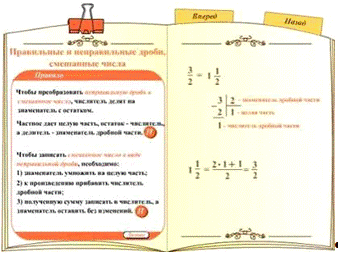
Переход к правилу осуществляется за счет нажатия на кнопку, после чего включается соответствующий ролик с пошаговой анимацией. Некоторые фрагменты анимации в этой части пособия можно повторить, осуществив запуск одного или второго преобразования. Преобразования представлены конкретными примерами, взятыми из теоретической справки предыдущего текста. Таким образом, можно видеть, что одна сцена разбита на две логические составляющие.

После нажатия на кнопку «Дальше» или перехода («Вперед») на следующую сцену, пользователю предлагается прейти к выполнению задания по преобразованию обыкновенных дробей. Однако, можно отказаться от решения данного задания и вернуться в содержание. Как и в случае с понятием дроби, преобразования являются первичным закреплением полученных знаний. Система оценки отсутствует. Учащиеся раскрепощаются, так как не боятся получить плохую отметку, показаться неспособным или глупым по сравнению с другими обучающимися. Но, в отличие от предыдущей сцены с задачами, эта сцена выстроена несколько иначе.

Упражнение подразумевает ввод с клавиатуры в соответствующие ячейки числа. Ученику предоставляется помощь в виде правила или подсказки, которыми можно воспользоваться в любой момент прохождения задания. Проверкой такого упражнения служит соответствующая кнопка: если пример решен неверно, то появляется надпись: «нет, неверно!», в противном случае: «да, верно!». Только в случае положительного ответа появляется кнопка, дающая возможность перехода к следующему примеру. Таким образом, учащийся лишен возможности случайного выбора правильного ответа.

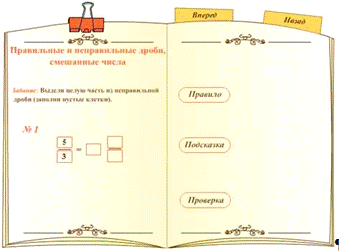
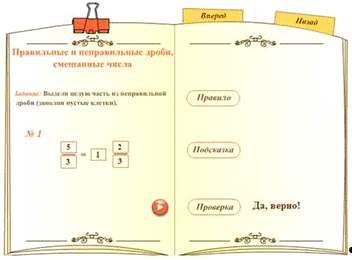
Задания на преобразования разделены на две группы. Первая включает примеры на выделение целой части из неправильной дроби, вторая - примеры на представление смешанного числа в виде неправильной дроби. Каждая группа имеет свою систему подсказок и правил. Такого рода упражнения содержат функцию самопроверки.

 

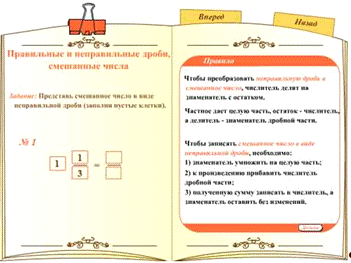
Сцена «Сравнение дробей».

Эта сцена пособия так же содержит две части: теоретическую и практическую. В теоретической части сначала рассматривается сравнение дробей по расположению соответствующих им точек на числовом луче, затем - сравнение дробей с одинаковыми знаменателями и сравнение дробей с одинаковыми числителями. Каждый из этих способов поясняется примером, формулируются правила сравнения. Теоретическая часть сцены завершается представлением общего алгоритма сравнения обыкновенных дробей, в том числе и смешанных.

    

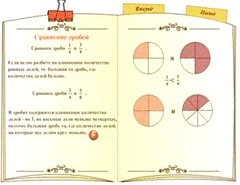
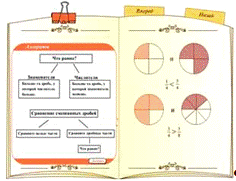
В практических задачах этой сцены пользователю предлагается ввести в соответствующую ячейку подходящий случаю знак сравнения: >, < или =. При этом ему снова становятся доступны режимы «Правило», «Подсказка» и «Проверка».

 

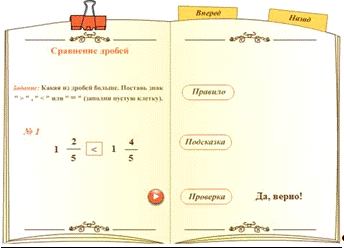
Основное свойство дроби.

Основное свойство дроби вводится на конкретном практическом примере.

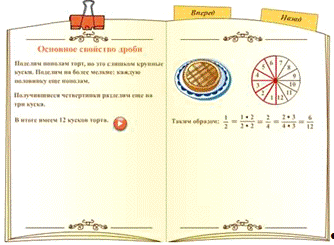
Для сравнения величины дробей ограничиваемся пока только устным объяснением получаемого результата - ответом на поставленный вопрос, на основании наблюдений над дробями.

В результате двух изменений дробь сохранила свою величину, но приняла более громоздкий вид, ее числитель и знаменатель выражены теперь большими числами. Таким образом, используя динамическую картинку, объясняется последовательность изменения вида дроби при увеличении числителя и знаменателя в одинаковое число раз. После чего подводится итог, формулируется основное свойство дроби.

Для усвоения выводов предлагается рассмотреть примеры, решение которых сопровождается рядом динамических картинок.

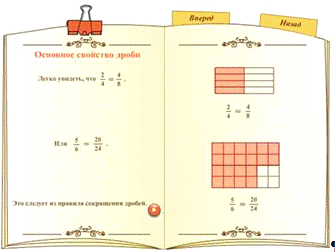
Используя эти примеры, решение которых, опирается на основное свойство дроби, можно говорить о преобразовании, где вид дроби упрощается, так как числитель и знаменатель выражаются меньшими числами. Таким образом, говорим о сокращении дроби, которое возможно тогда, когда члены дроби имеют общий множитель.

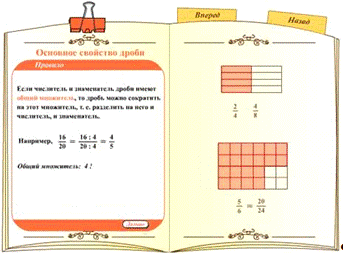
При изучении сокращения дробей надо добиться, чтобы учащиеся поняли а) на каком свойстве дробей основано их сокращение; б) цель этого преобразования (вид дроби упрощается, так как числитель и знаменатель выражаются меньшими числами). Для закрепления и самостоятельной работы можно перейти по кнопке «Дальше» (при нажатии всплывает наводящая подсказка «Порешаем?») на сцену, где предлагается ряд заданий на сокращение дробей.

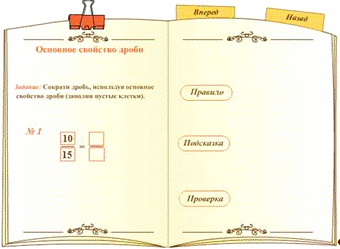
При этом пользователю снова становятся доступны режимы «Правило», где возможно вспомнить алгоритм сокращения дробей, «Подсказка», где приводится формулировка основного свойства дроби, и «Проверка».

Перейдем к рассмотрению следующего 2 раздела тематической линии «Обыкновенные дроби», «Задачи на дроби».

Нахождение части от числа.

Отыскания части от целого рассматривается на конкретном примере задачи. Формулировка условия задачи сопровождается динамической иллюстрацией, с переносом ключевых моментов на рисуемую картинку.

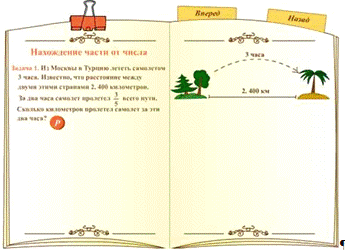
Переход к подробному описанию решения осуществляется посредством кнопки «Р». После чего можно проследить логику построения разбора данного типа задачи. Каждое утверждение, размещаемое в левой части рабочего поля, подкрепляется созданием динамической картинки или выполняемым арифметическим действием в правой части визуального поля.

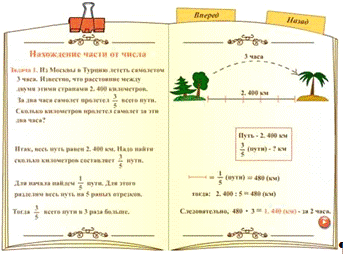
Важно сопоставить краткую запись условия с данной величиной, выраженной натуральным числом и величиной, которую надо найти. Таким образом, схематическая запись самого условия задачи, вначале этой сцены, отображается в достаточно емкую таблицу с «дано» и «найти». Процесс схематизации условия обычно вызывает затруднения у учащихся, поэтому визуализация такого процесса кажется нам весьма полезной. Следующий этап - это осознание того, на сколько равных частей разделен весь путь и сколько таких частей необходимо найти, какая дробь в итоге будет соответствовать искомому участку пути, и какой протяженностью (в км) этот участок пути окажется. Представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Отыскание части от числа (целого)».

Затем приводится алгоритм решения задач данного типа.

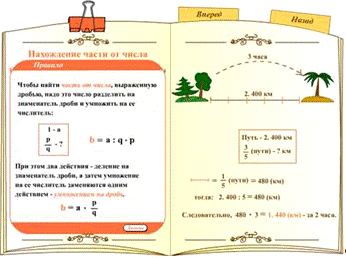
Здесь же представлено правило нахождения части от числа с помощью умножения на дробь, как обобщение выше сказанного. Формула имеет буквенную запись, обозначения компонентов в которой были введены еще в самом начале просмотра мультимедийного пособия.

Далее по кнопке перехода «Дальше» или по закладке «Вперед» попадаем в сцену «Нахождение числа по его части».

Отыскания числа (целого) по его части так же рассматривается на конкретном примере задачи. Формулировка условия задачи сопровождается динамической иллюстрацией, с переносом ключевых моментов на рисуемую картинку. Переход к подробному описанию решения осуществляется посредством кнопки «Р». После чего можно проследить логику построения разбора данного типа задачи. Каждое утверждение, размещаемое в левой части рабочего поля, подкрепляется созданием динамической картинки или выполняемым арифметическим действием в правой части визуального поля.

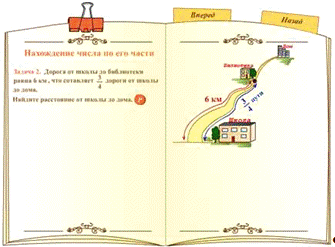
Краткая запись условия сопоставляется с данной величиной, выраженной обыкновенной дробью и величиной, которую надо найти. Таким образом, схематическая запись самого условия задачи, вначале данной сцены, отображается в достаточно емкую таблицу с «дано» и «найти». Следующий этап - это осознание того на сколько равных частей разделен путь, известный по условию задачи и сколько таких равных частей он составляет. Затем необходимо узнать какой части не хватает для отыскания всего пути (маршрута), что является связующим моментом для отображения единого алгоритма решения такого рода задач. Таким образом, представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Отыскание части от числа (целого)».

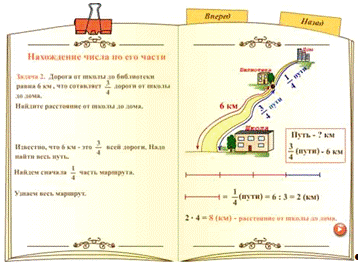
Затем приводится алгоритм решения задач данного типа.

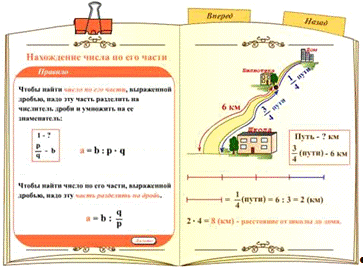
Здесь же представлено правило нахождения части от числа с помощью деления на дробь, как обобщение выше сказанного. Формула имеет буквенную запись, обозначения компонентов в которой были введены еще в самом начале просмотра мультимедийного пособия.

Серию задач продолжает задача на доли, рассмотренная в следующей сцене «Нахождение дроби, которую одно число составляет от другого».

Нахождение долей так же рассматривается на конкретном примере задачи [12]. Формулировка условия задачи сопровождается динамической иллюстрацией, с переносом ключевых моментов на рисуемую картинку. Переход к подробному описанию решения осуществляется посредством кнопки «Р». После чего можно проследить логику построения разбора данного типа задачи. Каждое утверждение, размещаемое в левой части рабочего поля, подкрепляется созданием динамической картинки или выполняемым арифметическим действием в правой части визуального поля.

Краткая запись условия сопоставляется с данной величиной, выраженной натуральным числом и величиной, которую надо найти, в данном случае мы ищем дробь. Таким образом, схематическая запись самого условия задачи, вначале рисуемого мульта, отображается в достаточно емкую таблицу с «дано» и «найти». Следующий этап - это осознание того, на сколько равных частей разделено целое. Затем необходимо узнать какую часть составляет эта величина от целого (именно этим мы занимались, рассматривая предыдущие типы задач). Таким образом, представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Нахождение дроби, которую одно число составляет от другого». Затем приводится алгоритм решения задач данного типа.

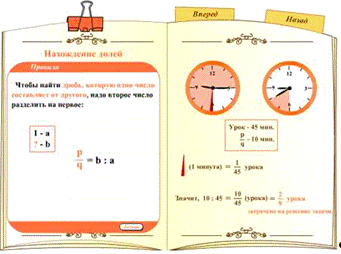
Порядок рассмотрения задач устанавливает логику следования применяемых знаний для решения следующего типа задачи.

Серия задач не имеет практической части, а лишь отражена в итоговом тесте, который следует после линии «Процента».

Рассмотрим 3 раздел мультимедийного пособия «Проценты», который начинается с пункта «Понятие процента».

Перейти к рассмотрению понятия «процент» возможно после серии задач на дроби, или вернувшись на страницу «Содержание», запустив соответствующий пункт 3.1.

Введение понятия «процент» начинается с примера, где требуется найти часть от целого, представленного в виде квадрата со стороной в 10 клеток. Без труда приходим к ответу, вводим новые обозначения. После чего формулируется определение.

Продолжение просмотра включает пример на определение процента закрашенной фигуры с поэтапным разбором и динамической картинкой. Разбирается вопрос о том, какую часть составляет целое. На основе определения делается вывод, который приводит к ответу.

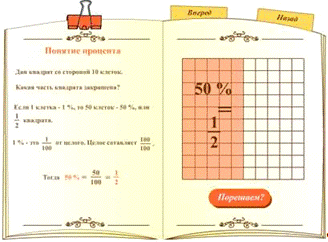
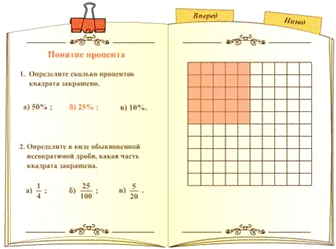
После закрепления понятия «процент» следует раздел «Задачи на проценты». В этом разделе 3.2 представлены две задачи на нахождение: процента от числа и числа по его проценту. Это две основные задачи, рассматриваемые в курсе математики 5 класса. Содержательная линия задач схожа с задачами на дроби, где сохранена логическая структура построения решения, соответствующая каждому из типов.

Рассмотрим подробнее сцену «Нахождение процента от числа».

Смысл задачи остался тем же, что и в задаче на дроби, однако соответствующая дробь, выражающая отрезок пути заменена на количество процентов, составляющее часть пути. Таким образом, задача превратилась в задачу на проценты, не теряя содержательного смысла.

Формулировка условия задачи сопровождается динамической иллюстрацией, с переносом ключевых моментов на рисуемую картинку. Переход к подробному описанию решения осуществляется посредством кнопки «Р». После чего можно проследить логику построения разбора данного типа задачи. Каждое утверждение, размещаемое в левой части рабочего поля, подкрепляется созданием динамической картинки или выполняемым арифметическим действием в правой части визуального поля.

Краткая запись условия сопоставляется с данной величиной, выраженной натуральным числом и величиной, которую надо найти. Таким образом, схематическая запись самого условия задачи, вначале данной сцены, отображается в таблицу с «дано» и «найти». Следующий этап - это осознание того что принято за 100%, какая величина приходится на 1%, какой дробью выражается данная в условии величина процента. Затем необходимо переформулировать задачу так, чтобы понять какую часть от числа необходимо найти.

Представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Нахождение процента от числа (целого)».

Затем приводится алгоритм решения задач данного типа. В алгоритме-правиле используется тот факт, что неизвестное число находится умножением на дробь, а способ решения этой задачи был уже ранее представлен в теме «дроби».

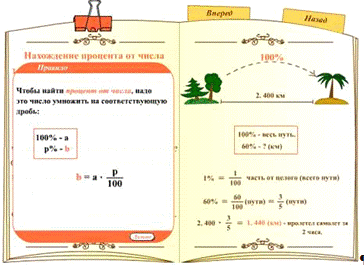
Эту серию задач продолжает задача на нахождение числа по его проценту, представленная сценой по названию типа задачи.

«Нахождение числа по его проценту».

Смысл задачи остался тем же, что и в задаче на дроби, однако соответствующая дробь, выражающая отрезок пути заменена на количество процентов, составляющее часть пути. Таким образом, задача превратилась в задачу на проценты, не теряя содержательного смысла.

Формулировка условия задачи сопровождается динамической иллюстрацией, с переносом ключевых моментов на рисуемую картинку. Переход к подробному описанию решения осуществляется посредством кнопки «Р». После чего можно проследить логику построения разбора данного типа задачи. Каждое утверждение, размещаемое в левой части рабочего поля, подкрепляется созданием динамической картинки или выполняемым арифметическим действием в правой части визуального поля.

Краткая запись условия сопоставляется с данной величиной, выраженной процентом и величиной, которую надо найти. Таким образом, схематическая запись самого условия задачи, вначале данной сцены, отображается в таблицу с «дано» и «найти». Следующий этап - это осознание того что принято за 100%, известна ли эта величина, чему равен 1%, чем он выражается, какую часть составляет величина, выраженная процентом. Затем необходимо переформулировать задачу так, чтобы понять какое число (целое) будет соответствовать данному проценту, и что для этого нужно сделать (найти целое по его части).

Представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Нахождение числа (целого) по его проценту». Затем приводится алгоритм решения задач данного типа. В алгоритме-правиле используется тот факт, что неизвестное число находится делением на дробь, а способ решения этой задачи был уже ранее представлен в теме «дроби».

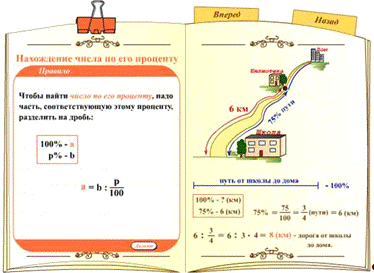
Перейдем к рассмотрению последнего раздела 4 «Порешаем задачи», где представлены задачи на дроби и проценты.

Тест содержит шесть задач по три на каждый из разделов, на два основных типа [6, 38, 40]. К каждой задаче предлагается четыре варианта ответа, один из которых верный, а так же подсказка, где это требуется. При выборе правильного ответа тестирующийся попадает на кадр со словами «Верно!», в котором при нажатии на кнопку можно перейти к следующему вопросу, при выборе неправильного ответа - тестирующийся попадает на кадр со словами «Неверно!» и с предложением повторить попытку ответа. Данный тест предлагается в качестве самопроверки знаний приобретенных после просмотра или до просмотра мультимедийного пособия.

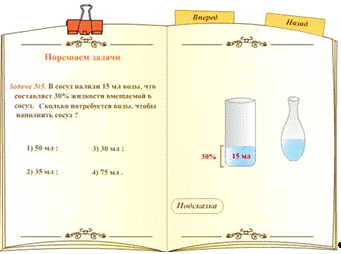
После того как мы рассмотрели основные характеристики интерактивного пособия, возникают следующие вопросы: «А как именно и где данное мультимедийное пособие можно применять на уроках математике? В каких классах, в какой теме?» На все эти вопросы мы постарались ответить в следующем параграфе.

.2 Методические рекомендации к использованию пособия

Значительная роль в образовании, развитии, подготовке учащихся к труду и их социальной адаптации принадлежит усвоению математических понятий, в частности обыкновенных дробей и процентов. Получая знания об обыкновенных дробях и процентах, школьники расширяют свои представления о числе и границе вычислительных возможностей. На примере изучения дробей они узнают то общее, что свойственно всем числам, то особенное, что свойственно только дробным числам. Это способствует развитию аналитико-синтетической деятельности, формированию логического мышления, умения находить причинно-следственные связи.

Включение темы процента в интерактивное пособие, содержащее обыкновенные дроби не случайно, а предпринято с целью установить взаимосвязь двух, изучаемых в разное время, понятий. Обыкновенная дробь является, по существу, одной из первых математических абстракций, которая встречается в школьном курсе. Соблюдение постепенности перехода от конкретного к отвлеченному, установление связи с прошлым опытом, позволяет проследить динамику развития двух математических понятий в рамках одного курса.

Пренебрежение учителем содержательной стороны изучаемых понятий, быстрый переход к формальному оперированию дробями (процентами) без надежной опоры на наглядность приводит к тому, что слабые, а то и средние ученики не понимают изучаемого материала.

Использование компьютерных технологий на уроках позволяет не только формировать и развивать познавательную мотивацию школьников к получению новых знаний, но и помогает создавать условия успешности каждого ученика на уроке, значительно улучшает чёткость в организации работы учащихся, наглядно отражая содержательную сторону изучаемого материала. Таким образом, учащиеся в результате практических действий, соотнесения различных моделей, анализа ситуаций подходят к осознанию основных понятий и операций, связанных с ними, формулируют их и применяют при выполнении различных заданий.

Разработанный Flash-фильм играет роль демонстрационного пособия с интерактивными элементами: позволяет осуществлять проверку и самоконтроль, полученных учащимися знаний. После изучения теоретического материала учащиеся могут проверить свои знания при прохождении теста или при выполнении заданий на первичное закрепление понятий.

Основной дидактической целью пособия является содержательный подход к введению понятий «обыкновенной дроби» и «процента», их взаимосвязь:

·  дробь, как часть целого;

·        правильные и неправильные дроби. Смешанные числа;

·        сравнение дробей;

·        основное свойство дроби;

·        нахождение части от числа;

·        нахождение числа по его части;

·        нахождение дроби, которую одно число составляет от другого.

·        понятие процента;

·        нахождение процента от числа;

·        нахождение числа по его проценту.

Данное пособие можно использовать при изучении раздела «Обыкновенные дроби» и «Проценты» в курсе математики 5 класса. Мультимедийное пособие содержит основной понятийный материал, соответствующий этим темам.

Так как ни один школьный учебник не ставит изучение обыкновенных дробей и процентов рядом, то первоначально учитель может демонстрировать учащимся на уроке отдельные сцены пособия, подходящей к данному уроку тематики. А затем, на уроках обобщения и систематизации знаний учащихся, использовать это пособие в более полном объеме.

Рассмотрим примеры поурочного планирования изучения данного раздела школьного курса математики с указанием возможностей использования мультимедийного пособия «Обыкновенные дроби и проценты» на отдельных уроках.

Примерное планирование по математике 5 класса (математика 5 кл. Зубарева И. И., Мордкович А. Г.) (5 часов в неделю) [18].

Тема урока	Кол-во часов	Комментарии к использованию мультимедийного пособия.
Глава II. Обыкновенные дроби
Обыкновенные дроби	2 ч	Учитель может обратиться к первому разделу «Обыкновенные дроби», пункту 1.1 интерактивного пособия, где рассмотреть предлагаемые примеры. Воспользоваться сформулированным определением обыкновенной дроби и перейти к решению нетрудных заданий, нацеленных на первичное закрепление знаний. При сравнении дробей, возможно, использовать пошаговый алгоритм, приведенный в пункте 1.3 данного программного продукта. И закрепить полученные знания рядом несложных примеров. Рассмотреть задачи на доли можно с помощью приведенного в пособии примера, который соответствует пункту 2.3 «нахождение дроби, которую одно число составляет от другого» раздела 2: «задачи на дроби». Там же можно воспользоваться сформулированным правилом, относительно нахождения долей.
Отыскание части от целого и целого по его части	3 ч	Способы отыскания части от целого и целого по его части рассматриваем на примере задач, которые приведены в интерактивном пособии в разделе «задачи на дроби» пунктах 2.1 и 2.2, запускаемых из содержания. Задачи детально разобраны и подкреплены динамическими иллюстрациями сюжета. После каждого примера приводится алгоритм решения задач данного типа. Закреплению навыка решения задач на отыскание части от числа и числа по его части могут служить первые три задачи теста (раздел «Порешаем задачи»). А весь тест полностью будет способствовать обобщению и систематизации навыков решения задач не только на дроби, но и на проценты.
Основное свойство дроби	4 ч	Основное свойство дроби выводится из рассмотрения примера на увеличение величины дроби, в связи с увеличением ее членов в несколько раз. Последовательное изменение вида дроби при уменьшении числителя и знаменателя в одинаковое число раз, представлено правилом сокращения дробей. Таки образом, учитель может как целиком, так и частично использовать сцену 1.4. Воспользоваться сформулированным основным свойством и правилом сокращения дробей. Закреплению навыка решения задач на сокращения дробей могут служить примеры, представленные в практической части пункта 1.4, следующей сразу после теории. Полезно будет рассмотреть процедуру изменения величины дроби, представленной в первой части сцены, перед выполнением заданий из учебника, где требуется сравнить дроби, не приводя их к общему знаменателю ([19], стр. 114).
Правильные и неправильные дроби. Смешанные числа	3 ч	Сначала полезно будет вернуться к понятию обыкновенной дроби, пункту 1.1, рассмотрев там пример дележа яблок, где обыкновенная дробь выражена записью: . Заодно актуализировать знания учащихся, относительно членов входящих в обыкновенную дробь. Затем перейти к сцене 1.2, где уточняется число, записанное таким образом. Здесь же воспользоваться примером перехода через единицу, определив смешанное число. Рассмотреть алгоритм преобразования дроби из неправильной в смешанное число и из смешанного в неправильную дробь. Закрепить полученные знания можно рядом несложных примеров, следующих после приведенного алгоритма.
Глава IV. Десятичные дроби
Понятие процента	3 ч	Учитель может обратиться ко второму разделу «проценты», пункту 3.1 интерактивного пособия, где рассмотреть предлагаемые примеры. Воспользоваться сформулированным определением процента и перейти, сначала к рассмотрению решения примера: отыскание процента от целого. Затем приступить к решению нетрудных заданий, нацеленных на первичное закрепление знаний. В примеры такого типа включены так же задания на отыскание части от целого, где ответ выражен обыкновенной дробью. Таким образом, прослеживается взаимосвязь процента с обыкновенной дробью.
Задачи на проценты	5 ч	Способы отыскания процента от целого и целого по его проценту рассматриваем на примере задач, которые приведены в интерактивном пособии в разделе «Задачи на проценты» пунктах 3.2.1 и 3.2.2, запускаемых из содержания. Задачи детально разобраны и подкреплены динамическими иллюстрациями сюжета, в них так же прослеживается связь с обыкновенными дробями, которая выражена сюжетной линией и структурной особенностью отыскания части от числа, числа по его части. После каждого примера приводится алгоритм решения задач данного типа. Закреплению навыка решения задач на отыскание процента от числа и числа по его проценту могут служить последние три задачи теста (раздел «Порешаем задачи»). А весь тест полностью будет способствовать обобщению и систематизации навыков решения задач не только на проценты, но и на дроби.

Примерное планирование по математике 5 класса (математика 5 кл. Части 1-2. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбург С.И.) (5 часов в неделю) [15].

Тема урока	Кол-во часов	Комментарии к использованию мультимедийного пособия.
Глава II. §5. Обыкновенные дроби
Обыкновенная дробь	1 ч	Учитель может обратиться к первому разделу «обыкновенные дроби», пункту 1.1 интерактивного пособия, где рассмотреть предлагаемые примеры. Воспользоваться сформулированным определением обыкновенной дроби и перейти к решению нетрудных заданий, нацеленных на первичное закрепление знаний.
Основные задачи на дроби	4 ч	Способы отыскания части от целого и целого по его части рассматриваем на примере задач, которые приведены в интерактивном пособии в разделе «задачи на дроби» пунктах 2.1 и 2.2, запускаемых из содержания. Задачи детально разобраны и подкреплены динамическими иллюстрациями сюжета. После каждого примера приводится алгоритм решения задач данного типа. Рассмотреть задачи на доли можно с помощью приведенного в пособии примера, который соответствует пункту 2.3 «Нахождение дроби, которую одно число составляет от другого» раздела 2: «Задачи на дроби». Там же можно воспользоваться сформулированным правилом, относительно нахождения долей. Закреплению навыка решения задач на отыскание части от числа и числа по его части могут служить первые три задачи теста (раздел «Порешаем задачи»). А весь тест полностью будет способствовать обобщению и систематизации навыков решения задач не только на дроби, но и на проценты.
Сравнение обыкновенных дробей	2 ч	Учитель может воспользоваться теоретическими сведениями, где представлено сравнение посредством числового луча, а так же посредством алгоритма сравнения членов обыкновенной дроби, в которых либо числители одинаковые, либо знаменатели. Для этого необходимо запустить сцену 1.3 соответствующего раздела 1 «Обыкновенные дроби». Закрепить полученные знания помогут примеры, представленные после теоретической справки пункта 1.3. Полезно будет рассмотреть процедуру изменения величины дроби, представленной в первой части сцены пункта 1.4, при этом использовать пошаговый алгоритм данного программного продукта. И закрепить полученные знания рядом несложных примеров.

Обыкновенная дробь (правильные и неправильные дроби) 2 ч          Сначала полезно будет вернуться к понятию обыкновенной дроби, пункту 1.1, рассмотрев там пример дележа яблок, где обыкновенная дробь выражена записью: . Заодно актуализировать знания учащихся, относительно членов входящих в обыкновенную дробь. Затем перейти к сцене 1.2, где уточняется число, записанное таким образом. Здесь же воспользоваться примером перехода через единицу, определив тот факт, что неправильная дробь больше или равна единице. Так же на примере показано, что правильная дробь меньше единицы.

При рассмотрении смешанных чисел следует вернуться к началу сцены 1.2., определив смешанное число, просмотрев пример перехода через единицу. Затем воспользоваться алгоритмом преобразования дроби из неправильной в смешанное число и из смешанного в неправильную дробь. Закрепить полученные знания можно рядом несложных примеров, следующих после приведенного алгоритма.
§8. Инструменты для вычислений и измерений
Проценты	1 ч	Учитель может обратиться ко второму разделу «проценты», пункту 3.1 интерактивного пособия, где рассмотреть предлагаемые примеры. Воспользоваться сформулированным определением процента и перейти, сначала к рассмотрению решения примера: отыскание процента от целого. Затем приступить к решению нетрудных заданий, нацеленных на первичное закрепление знаний. В примеры такого типа включены так же задания на отыскание части от целого, где ответ выражен обыкновенной дробью. Таким образом, прослеживается взаимосвязь процента с обыкновенной дробью.
Основные задачи на проценты	4 ч	Способы отыскания процента от целого и целого по его проценту рассматриваем на примере задач, которые приведены в интерактивном пособии в разделе «Задачи на проценты» пунктах 3.2.1 и 3.2.2, запускаемых из содержания. Задачи детально разобраны и подкреплены динамическими иллюстрациями сюжета, в них так же прослеживается связь с обыкновенными дробями, которая выражена сюжетной линией и структурной особенностью отыскания части от числа, числа по его части. После каждого примера приводится алгоритм решения задач данного типа. Закреплению навыка решения задач на отыскание процента от числа и числа по его проценту могут служить последние три задачи теста (раздел «Порешаем задачи»). А весь тест полностью будет способствовать обобщению и систематизации навыков решения задач не только на проценты, но и на дроби.

Примерное планирование по математике 5, 6 класса (математика 5, 6 кл. Части 1-2. Дорофеев Г.В., Петерсон Л.Г.) (6 часов в неделю) [7].

Тема урока	Количество часов	Комментарии к использованию мультимедийного пособия.
5 класс, часть 2. Глава III. Дроби

Натуральные числа и дроби           3 ч          Учитель может обратиться к первому разделу «обыкновенные дроби», пункту 1.1 интерактивного пособия, где рассмотреть предлагаемые примеры. Воспользоваться сформулированным определением обыкновенной дроби и перейти к решению нетрудных заданий, нацеленных на первичное закрепление знаний. Затем полезно будет вернуться к понятию обыкновенной дроби, пункту 1.1, рассмотрев там пример дележа яблок, где обыкновенная дробь выражена записью: . Заодно актуализировать знания учащихся, относительно членов входящих в обыкновенную дробь. Затем перейти к сцене 1.2, где уточняется число, записанное таким образом. Здесь же воспользоваться примером перехода через единицу, определив тот факт, что неправильная дробь больше или равна единице. Так же на примере показано, что правильная дробь меньше единицы.

При рассмотрении смешанных чисел следует вернуться к началу сцены 1.2., определив смешанное число, просмотрев пример перехода через единицу. Затем воспользоваться алгоритмом преобразования дроби из неправильной в смешанное число и из смешанного в неправильную дробь. Закрепить полученные знания можно рядом несложных примеров, следующих после приведенного алгоритма.
Основное свойство дроби. Преобразование дробей	4 ч	Основное свойство дроби выводится из рассмотрения примера на увеличение величины дроби, в связи с увеличением ее членов в несколько раз. Последовательное изменение вида дроби при уменьшении числителя и знаменателя в одинаковое число раз, представлено правилом сокращения дробей. Таки образом, учитель может как целиком, так и частично использовать сцену 1.4. Воспользоваться сформулированным основным свойством и правилом сокращения дробей. Закреплению навыка решения задач на сокращения дробей могут служить примеры, представленные в практической части пункта 1.4, следующей сразу после теории.
Сравнение дробей	5 ч	Учитель может воспользоваться теоретическими сведениями, где представлено сравнение посредством числового луча, а так же посредством алгоритма сравнения членов обыкновенной дроби, в которых либо числители одинаковые, либо знаменатели. Для этого необходимо запустить сцену 1.3 соответствующего раздела 1 «Обыкновенные дроби». Закрепить полученные знания помогут примеры, представленные после теоретической справки пункта 1.3.
Задачи на дроби	10 ч	Способы отыскания части от целого и целого по его части рассматриваем на примере задач, которые приведены в интерактивном пособии в разделе «задачи на дроби» пунктах 2.1 и 2.2, запускаемых из содержания. Задачи детально разобраны и подкреплены динамическими иллюстрациями сюжета. После каждого примера приводится алгоритм решения задач данного типа. Рассмотреть задачи на доли можно с помощью приведенного в пособии примера, который соответствует пункту 2.3 «Нахождение дроби, которую одно число составляет от другого» раздела 2: «Задачи на дроби». Там же можно воспользоваться сформулированным правилом, относительно нахождения долей. Закреплению навыка решения задач на отыскание части от числа и числа по его части могут служить первые три задачи теста (раздел «Порешаем задачи»). А весь тест полностью будет способствовать обобщению и систематизации навыков решения задач не только на дроби, но и на проценты.
6 класс, часть 1. Глава II. Арифметика
Понятие о проценте	4 ч	Учитель может обратиться ко второму разделу «проценты», пункту 3.1 интерактивного пособия, где рассмотреть предлагаемые примеры. Воспользоваться сформулированным определением процента и перейти, сначала к рассмотрению решения примера: отыскание процента от целого. Затем приступить к решению нетрудных заданий, нацеленных на первичное закрепление знаний. В примеры такого типа включены так же задания на отыскание части от целого, где ответ выражен обыкновенной дробью. Таким образом, прослеживается взаимосвязь процента с обыкновенной дробью.
Задачи на проценты	10 ч	Способы отыскания процента от целого и целого по его проценту рассматриваем на примере задач, которые приведены в интерактивном пособии в разделе «Задачи на проценты» пунктах 3.2.1 и 3.2.2, запускаемых из содержания. Задачи детально разобраны и подкреплены динамическими иллюстрациями сюжета, в них так же прослеживается связь с обыкновенными дробями, которая выражена сюжетной линией и структурной особенностью отыскания части от числа, числа по его части. После каждого примера приводится алгоритм решения задач данного типа. Закреплению навыка решения задач на отыскание процента от числа и числа по его проценту могут служить последние три задачи теста (раздел «Порешаем задачи»). А весь тест полностью будет способствовать обобщению и систематизации навыков решения задач не только на проценты, но и на дроби.

Таким образом, просмотр данного Flash-фильма можно осуществлять как на различных этапах изучения разделов «Обыкновенные дроби» и «Проценты», так и на различных этапах в рамках одного урока. Так как ключевые понятия данного раздела достаточно сложны в восприятии и осмыслении, то особенно важно именно на начальном этапе освоения понятия представить учащимся соответствующую наглядную динамическую иллюстрацию.

Обыкновенные дроби и проценты - одни из самых важных математических абстракций в курсе 5-6 классов, расширяющие представление учащихся о числе. Знакомство с этими понятиями строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил.

Поэтому особенно эффективно использовать данное пособие при введении новых понятий, что будет способствовать более глубокому пониманию и осмыслению абстрактных понятий и созданию визуального представления. Также возможен просмотр сцен фильма на этапах закрепления и актуализации опорных знаний школьников.

Кроме того, учащиеся могут использовать мультимедийное пособие для самостоятельного просмотра после изучения на уроке как дополнение к учебнику с целью повторения или устранения пробелов в знаниях и умениях, связанных с понятиями «обыкновенная дробь» и «процент».

Показ составляющих частей фильма можно организовать в произвольном порядке, что обеспечивает возможность применения пособия независимо от используемого преподавателем учебника по математике.

Также в мультимедийном пособии присутствует тест, способствующий формированию у учащихся навыка решения основных типов задач на дроби и проценты. В данном тесте учащимся необходимо выбрать величину, соответствующую части числа (проценту числа), а так же часть (процент), выраженную величиной. Тест состоит из шести анимационных заданий и не предполагает оценки за него. Он предназначен для того, чтобы учитель смог понять, как дети усвоили материал, а также для самопроверки.

Пособие позволяет конкретизировать изучаемые теоретические вопросы, и призвано стимулировать интерес к учению. В связи с тем, что обучаемые, как правило, в большей степени обладают одним из двух типов преимущественного мышления, словесно-логическим или наглядно-образным, наше пособие направлено на оба типа восприятия. Представленная информация поступает по нескольким каналам, которые, дополняя друг друга, дают наиболее полное представление о вводимых понятиях. Опираясь на зрительные и чувственные компоненты восприятия, можно добиться более глубокого понимания материала. Таким образом, визуализацию данного материала мы считаем возможной и полезной.

Заключение

Основная цель дипломной работы - создание мультимедийного дидактического пособия по теме «Обыкновенные дроби и проценты» курса математики в 5-6 классах. Для достижения данной цели, были:

1.  изучены психолого-педагогические аспекты реализации принципа наглядности в обучении, особенности визуального мышления учащихся на уроке, которые показали, что включение визуального ряда задач способствует улучшению восприятия преподносимого учебного материала;

2.       проведены исследования психолого-педагогических аспектов применения мультимедийных средств в процессе обучения, в частности, установлены роль и виды компьютерной наглядности в обучении, требования, предъявляемые к компьютерным средствам обучения, с учетом чего было разработано программное учебное пособие;

.        проанализирована учебная и методическая литература по теме «Обыкновенные дроби» и «Проценты», на основе чего определена структура и отобрано содержание пособия;

.        разработано соответствующее мультимедийное пособие по теме «Обыкновенные дроби и проценты»;

.        разработаны методические рекомендации по использованию этого мультимедийного пособия в учебном процессе.

Важность основных понятий, изучаемых в темах «Обыкновенные дроби» и «Проценты» заключается в том, что они являются базовыми понятиями курса математики в 5-6 классах, то есть являются «фундаментом» дальнейшего успешного обучения учащихся. Поэтому роль необходимости формирования образов, соответствующих этим понятиям на начальном этапе изучения очень велика.

Одним из способов создания наглядного образа является динамическая наглядность, которая способствует более глубокому пониманию и усвоению процессов и явлений, протекающих во времени.

При создании предлагаемого мультимедийного пособия была изучена различная литература по психологии и педагогике. Ее анализ показал, что визуальное мышление опирается на формирование и использование зрительного образа, а значит, является составной частью того вида мышления, который делает акцент на том же: наглядно-действенного, образного и наглядно-образного. И для того чтобы формировать визуальное мышление учащихся, нужно заботиться об организации зрительной информации. Была обоснована необходимость использования динамической наглядности при изучении данной темы. Для реализации динамической наглядности мы использовали компьютер, поэтому были рассмотрены компьютерные средства в образовании, классификации компьютерных средств обучения. Были учтены требования, предъявляемые учебным компьютерным средствам.

Изучение возможностей использования компьютерных средств в обучении, а также классификации компьютерных средств позволили определить выбор программного продукта для разработки представленного мультимедийного пособия.

В дипломной работе была проанализирована учебная литература по теме «Обыкновенные дроби» и «проценты». Определено, что ряд учебных пособий в той или иной мере содержит визуальные задачи по темам «Обыкновенные дроби» и «Проценты», что является прямым доказательством необходимости использования данных задач. В соответствии с представленной линией визуальных задач рассмотренных учебников было отобрано содержание интерактивного дидактического пособия.

В результате в данной работе предложено мультимедийное пособие по теме «Обыкновенные дроби и проценты», выполненное с помощью компьютерной программы Macromedia Flash. Пособие представляет собой информационно - обучающий анимированный ролик, предназначенный для использования в качестве демонстрационного материала, из которого учитель может выбирать задачи, применение которых на уроке могло бы облегчить восприятие базовых понятий, содержащихся в темах «Обыкновенные дроби» и «Проценты» курса математики в 5-6 классах. Flash-фильм может просматриваться учащимися самостоятельно, без помощи и управления со стороны преподавателя. Предполагаемый просмотр сцен осуществляется в порядке, указанном в содержании, где выделены два направления: линия дроби и линия процента. Имеется методическое описание ролика, а также разработаны методические рекомендации к его использованию.

Данное пособие представляет собой дополнительное средство обучения, которое возможно использовать наряду с традиционными средствами и методами по усмотрению преподавателя полностью или частично.

Разработанный Flash-фильм играет роль демонстрационного пособия с интерактивными элементами: позволяет осуществлять проверку и самоконтроль полученных учащимися знаний. После изучения теоретического материала учащиеся могут проверить свои знания при прохождении теста или при выполнении заданий на первичное закрепление понятий.

Основной дидактической целью пособия является содержательный подход к введению понятий «обыкновенной дроби» и «процента», их взаимосвязь. Данное пособие можно использовать при изучении разделав «Обыкновенные дроби» и «Проценты» в курсе математики 5 класса. Мультимедийное пособие содержит основной понятийный материал, соответствующий этим темам.

К работе прилагается компакт-диск, содержащий мультимедийное пособие по теме: «Обыкновенные дроби и проценты».

Библиография

1.   Арифметика 5 кл. [Текст]: Учеб. для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др. - 5-е изд., дораб. - М.: Просвещение, 2005. - 255 с.: ил.

.     Арифметика 6 кл. [Текст]: Учеб. для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др. - 5-е изд. - М.: Просвещение, 2007. - 256 с.: ил.

3.    Арнхейм, Р. Визуальное мышление [Текст]: Хрестоматия по общей психологии / Р. Арнхейм. - М.: изд-во МГУ, 1981. - 107 с.

4.       Беспалов, Б.И. Действие [Текст]: Психологические механизмы визуального мышления / Б.И. Беспалов. - М.: изд-во МГУ, 1984. - 192 с.

5.    Блонский, П.П. Педология [Текст]: Кн. для преподават. и студ. высш. пед. учеб. заведений / П.П. Блонский; под ред. В.А. Сластенина. - М.: ВЛАДОС, 1999. - 288 с.

.     Брушлинский, А.В. Субъект [Текст]: Мышление, учение, воображение / А.В. Брушлинский. - М.: Воронеж, 1996. - 392 с.

.     Бурмистрова, Т.А. Математика [Текст]: 5-6 кл.: Программы общеобразоват. учреждений / Т.А. Бурмистрова. - М.: Просвещение, 2009.

8.   Васильева, И.А. Психологические аспекты применения информационных технологий [Текст] / И.А. Васильева Е.М. Осипова, Н.Н. Петрова // Вопросы психологии. - 2002. - №3. - С. 80-88.

9.    Высоцкий, И.Н. Компьютер в образовании [Текст] / И.Н. Высоцкий // Информатика и образование. - 2000. - №1. - С. 86-87.

.     Гиппенрейтер, Ю.Б. Хрестоматия по общей психологии. Психология мышления [Текст] / Ю.Б. Гиппенрейтер, В.В. Петухова; под ред. Ю.Б. Гиппенрейтер. - М.: изд-во МГУ, 1981. - 672 с.

.     Давыдов, В.В. Виды обобщения в обучении [Текст]: Логико-психологические проблемы построения учебных предметов / В.В. Давыдов. - М.: Педагогика, 1972. - 424 с.

12.  Дорофеев, Г.В. Математика 5 кл.: В 2 ч. Ч. 2. [Текст] / Г.В. Дорофеев, Л.Г. Петерсон. - М.: Ювента, 2008. - 240 с.: ил.

13.     Дорофеев, Г.В. Математика 6 кл.: В 2 ч. Ч. 1. [Текст] / Г.В. Дорофеев, Л.Г. Петерсон. - 2-е изд., перераб. - М.: Ювента, 2010. - 112 с.: ил.

14. Дорофеев, Г.В. Учебный комплект по математике для 5-6 кл. [Текст] / Г.В. Дорофеев, С.Б. Суворова, И.Ф. Шарыгин; под ред. Г.В. Дорофеева. - 9-е изд. - М.: Просвещение, 2007. - 302 с.

15.  Жохов, В.И. Преподавание математики в 5-6 кл. [Текст]: Методические рекомендации для учителей к учеб. Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда / В.И. Жохов. - М.: Вербум-М, 2000. - 176 с.

.     Занков, Л.В. Наглядность и активизация учащихся в обучении [Текст] / Л.В. Занков. - М.: Учпедгиз, 1960. - 162 с.

.     Зубарева, И.И. Еще раз о процентах [Текст] / И.И. Зубарева // Математика в шк. - 2006. - №10. - С. 26-31.

.     Зубарева, И.И. Математика. 5-6 кл. [Текст]: Методическое пособие для учителя / И.И. Зубарева, А.Г. Мордкович. - 2-е изд. - М.: Мнемозина, 2005. - 104 с.

19.  Зубарева, И.И. Математика, 5 кл. [Текст]: Учеб. для общеобразоват. Учреждений / И.И. Зубарева, А.Г. Мордкович. - 8-е изд.- М.: Мнемозина, 2008. - 270 с.: ил.

20.  Зубарева, И.И. Математика 6 кл. [Текст]: Учеб. для общеобразоват. Учреждений / И.И. Зубарева, А.Г. Мордкович - 8-е изд. - М.: Мнемозина, 2009. - 264 с.: ил.

.     Информационные и коммуникационные технологии в образовании: Учебно-методическое пособие [Текст] / И.В. Роберт, С.В. Панюкова, А.А. Кузнецов, А.Ю. Кравцова; под ред. И.В. Роберт. - М.: Дрофа, 2008. - 312c.: ил.

22.     Клуб программистов. [Электронный документ] - (http://www.programmersclub.ru/alar-technology-flash/). 13.03.2010.

.        Киселев, А.П. Арифметика [Текст] / А.П. Киселев. - М.: ФИЗМАТЛИТ, 2002. - 168 с.

24.  Кроль, В.М. Психология и педагогика [Текст] / В.М. Кроль. - М.: Высш. шк., 2001. - 319 с.

25.  Кулагина, И.Ю. Возрастная психология [Текст]: Полный жизненный цикл развития человека: Учеб. пособие для студ. высших учебных заведений / И.Ю. Кулагина, В.Н. Колюцкий. - М.: Сфера, 2005. - 464 с.

26. Математика 5 кл.: В 2 ч. [Текст]: Учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. - 23-е изд., испр. - М.: Мнемозина, 2008. - 280 с.: ил.

27.  Математика 6 кл.: В 2 ч. [Текст]: Учеб для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. - 20-е изд. - М.: Мнемозина, 2007. - 288 с.: ил.

.     Математика [Текст]: Учебник-собеседник для 5 кл. средней шк. / Л.Н. Шеврин, А.Г. Гейн, И.О. Коряков, М.В. Волкой. - М.: Просвещение, 1994. - 223 с.

.     Математика и информатика: Типы обучающих программ. [Электронный документ] - (http://sdo.uspi.ru/mathem&inform/lek20/lek_20.htm# типы_обучающих_программ). 29.01.2010.

.     Немов, Р.С. Общие основы психологии [Текст] / Р.С. Немов. - М.: ВЛАДОС, 1997. - 688 с.

.     Осмоловская, И.М. Наглядные методы обучения [Текст]: Учеб. пособие для студ. высш. учеб. заведений / И.М. Осмоловская. - М.: Академия, 2009. - 192 с.

32.     Панина, Т.С. Современные способы активизации обучения [Текст]: учеб. пособие для студ. высш. учеб. заведений / Т.С. Панина, Л.Н. Вавилова; под ред. Т.С. Паниной.- 4-е изд., стереотип. - М.: Академия, 2008. - 176 с.

.        Проблемы методики использования компьютерных продуктов в учебном процессе [Электронный документ]: Пленарный доклад / Л.Я. Боревский, С.А. Кругликов, Н.Х. Розов и др. // Информационные технологии в образовании (ИТО): Материалы научно-практической конференции. - М., 2001.- (http://ito.edu.ru/2001/ito/P/P-0-1.html).

.        Рабочая тетрадь для 5 кл. общеобразоват. учреждений. В 2 ч. Ч. 1. [Текст] / Е.А. Бунимович, К.А. Краснянская, Л.В. Кузнецова, и др. - 8-е изд., дораб. - М.: Просвещение, 2007. - 64 с.

35.  Резник, Н.А. Визуальная среда обучения [Электронный документ] / Н.А. Резник // ЦПО. Дистанционное обучение. (http://ipo.spb.ru/internet-school/a/84.htm). 13.12.2009.

.     Резник, Н.А. Методические основы обучения математике в средней школе с использованием средств развития визуального мышления [Электронный документ]: Автореферат диссертации на соискание ученой степени доктора педагогических наук: 13.00.02 / Н.А. Резник. - Защищена 21.01.1998 - (http://www.vischool.rxt.ru-/avtoref/Rez_aref.htm). 2.02.2010.

37.     Розов, Н.Х. Некоторые проблемы применения компьютерных технологий и продуктов при обучении в средней школе [Электронный документ] / Н.Х. Розов // Вестник МГУ. Информатика и информатизация образования. - 2003. - №1. - С. 102-106.

38.  Рысь, Ю.И. Психология и педагогика [Текст]: Учеб. пособие для студ. вузов / Ю.И. Рысь, В.Е. Степанов, В.П. Ступницкий. - М.: Академический проект, 1999. - 308 с.

.     Теория и методика обучения математике в шк.: Учебно-методическое пособие для студентов математического факультета по специальности 050202.65 (032100) - математика [Текст]. Ч. 1 / Л.О. Денищева, А.Е. Захарова, М.Н. Кочагина, и др. - М.: МГПУ, 2008. - 190 с.

.     Технологии создания электронных обучающих средств [Текст] / Г.А. Краснова, М.И. Соловов, М.И. Беляев и др. - М.: МГИУ, 2001. - 224 с.

.     Фокин, Ю.Г. Теория и технология обучения [Текст]: Деятельностный подход: Учеб. пособие для студ. высш. учеб. заведений / Ю.Г. Фокин. - 3-е изд., испр. - М.: Академия, 2008. - 240 с.

42. Чекмарев, Я.Ф. Методика преподавания арифметики в V-VI классах восьмилетней школы [Текст] / Я.Ф. Чекмарев. - М.: Просвещение, 1962. - 412 с.

43.  Шлыкова, О.В. Культура мультимедиа [Текст]: Учеб. пособие для студ. МГУКИ / О.В. Шлыкова. - М.: ФАИР-ПРЕСС, 2004. - 416 с.

.     Юрченко, Е.В. Математика. Тесты 5-6 кл. [Текст]: Учебно-методическое пособие / Е.В. Юрченко. - 2-е изд. - М.: Дрофа, 1998. - 160 с.

45.     Яковлев, А.И. Информационно-коммуникационные технологии в образовании. [Электронный документ] / А.И. Яковлев. - http://emag.iis.ru/arc/infosoc/emag.nsf/BPA/bce6d4452-de1cad0c3256c4d005253d0. 13.03. 2010.

.        Якутина, Е.Ю. Актуальные вопросы изучения «Обыкновенные дроби» в школьном курсе математики [Электронный документ]: Выпускная квалификационная работа / Е.Ю. Якутина.- М., 2001.- (http://www.history.ru/index.php?option=com_ewriting&Itemid-=0&func= chapterinfo&chapter=4487&story=3573). 20.01.2010.

47.  (http://www.arttour-media.ru/news/view/11.htm). 20.04.2010.

.     (http://www.tspu.tula.ru/res/informat/aosit/Lection4.htm). 06.03.2010.