Процесс обучения математике на факультативных занятиях в классах основной школы

Процесс обучения математике на факультативных занятиях в классах основной школы

Содержание

Введение

. Психолого-педагогические особенности применения факультативных занятий в основной школе

.1 Типологические и возрастные особенности развития личности

.2 Психолого-педагогические особенности среднего школьного возраста

.3 Особенности учебной деятельности подростка

.4 Отбор форм и методов проведения факультативного курса

.5 Методы проведения факультативных занятий

.6 Анализ учебной литературы

. Историческая справка

.1 Евклидовы «Начала»

.2 Джованни Чева

.3 Леонард Эйлер

.4 Карл Фридрих Гаусс

.5 Янош Больяи

.6 Якоб Штейнер

. Математическая часть

.1 Обобщенная теорема синусов

.2 Теорема Чевы

.3 Замечательные точки

.4 Вписанная и вневписанная окружность

.5 Теорема Штейнера-Лемуса

.6 Ортотреугольник

.7 Серединный треугольник и прямая Эйлера

.8 Окружность девяти точек

.9 Педальный треугольник

. Методическая часть

.1 Структура факультативного курса

.2 Планы занятий

.2.1 Обобщенная теорема синусов

.2.2 Теорема Чевы

.2.3 Замечательные точки

.2.4 Вписанная и вневписанная окружность

.2.5 Теорема Штейнера-Лемуса

.2.6 Ортотреугольник

.2.7 Серединный треугольник и прямая Эйлера

.2.8 Окружность девяти точек

.2.9 Педальный треугольник

.2.10 Контрольная работа

. Описание эксперимента

Заключение

Введение

«Ни один наставник не должен забывать, что его главнейшая обязанность состоит в приучении воспитанников к умственному труду, и что эта обязанность более важна, нежели передача самого предмета» [К.Д. Ушинский, т.2, стр.360, изд. 1960].

Усиление связи науки, техники и производства характеризуются взаимозависимостью работников. Эти объективные условия требуют рабочих и специалистов с широким политехническим образованием. Оно необходимо не только для приспособления к постоянно изменяющимся орудиям труда и технологическим процессам, но и для социальной защищенности при конкуренции на рынке труда.

Математическое образование стало значительным средством повышения уровня подготовки будущих специалистов как естественно - научных и технических, так и гуманитарных дисциплин.

Цели преподавания математики в средней школе следующие: общеобразовательные, воспитательные и практические.

Преподавание математики, как и любого другого предмета, подвержены определенным изменениям в зависимости от задач, которые ставит перед школой современное общество.

Изучение математики вносит заметный вклад в умственное развитие человека. В процессе обучения в арсенал приемов и методов мышления естественным образом включаются анализ и синтез, индукция и дедукция, обобщение и конкретизация, аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умение формировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. «От живого созерцания, к абстрактному мышлению и от него к практике…»

Обучение математике способствует развитию нравственных черт личности - настойчивости, и целеустремленности, познавательной активности и самостоятельности, дисциплины и критичности мышления, способности аргументировано отстаивать свои взгляды и убеждения.

Слабое развитие логического мышления и геометрической интуиции дает о себе знать уже в школе, затрудняя изучение ряда школьных предметов, а в деятельности взрослого человека оно иногда оказывается причиной многих неудач.

В результате реформы школьного математического образования в учебные планы общеобразовательных школ включены факультативные занятия, являющиеся составной частью всей учебно-воспитательной работы. Факультативные занятия учитывают интересы и наклонности учащихся, расширяют и углубляют изучение программного материала, знакомят учащихся с некоторыми общими математическими идеями, раскрывают приложение математики в практике.

Факультативные занятия стали составной частью школьного математического образования для той категории школьников, которые проявляют интерес к предмету.

Объектом данного исследования является процесс обучения математике на факультативных занятиях в классах основной школы.

Целью дипломной работы являются разработка факультативного курса по теме «Замечательные точки и линии треугольника» и разработка методики его преподавания для учащихся основной школы.

Для достижения поставленной цели решались следующие задачи:

. Анализ психолого-педагогической, методической литературы.

. Анализ имеющегося методического обеспечения процесса обучения.

. Анализ учебников по геометрии 7-9, 7-11 классов средней школы.

. Определение роли и места факультативных занятий в процессе обучения математике.

. Разработка плана факультативных занятий «Замечательные точки и линии треугольника» и конспекты конкретных занятий.

В ходе работы применялись различные методы исследования:

-    изучение и анализ методической, педагогической и психологической литературы по теме работы;

-        учебники по геометрии 7-9 кл., авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина: геометрии 7-11 кл. автор А.В. Погорелов;

         беседы с опытными учителями;

         эксперимент;

         пробное преподавание элементов курса.

Изучение вопросов на факультативных занятиях по теме «Замечательные точки и линии треугольника» способствуют воспитанию устойчивого интереса к математике, знакомят учащихся с историей развития геометрии. При изучении материала осуществляется повторение и углубление имеющихся знаний, умений и навыков и овладение новыми знаниями.

Данная работа состоит из введения, четырех глав и заключения.

Глава 1 раскрывает психолого-педагогические особенности подросткового возраста и специфику обучения.

Глава 2 описывает историю развития математики.

В главе 3 представлены доказательства утверждений, образующих материал факультативных занятий.

В главе 4 показаны методы и приемы проведения факультативных занятий.

Заключение содержит выводы и результаты проведенного исследования.

Практическая ценность работы определяется тем, что в ней разработаны: учебные материалы для проведения факультативного курса «Замечательные точки и линии треугольника»; методические рекомендации для его проведения; подобраны задачи по указанной теме.

обучение математика школа факультативный

1. Психолого-педагогические особенности применения факультативных занятий в основной школе

.1 Типологические и возрастные особенности развития личности

Человек обладает огромным количеством степеней свободы - возбуждения и торможения, условных рефлексов и других психических процессов. Это огромный потенциал для» «величайших вариантов приспособлений» человека к разнообразным экстремальным условиям жизни, труда и общественной деятельности, выполнять множество вариаций творчества.

Кроме того, человеческий мозг обладает возможностями иррадиировать (распространять) раздражители, поступающие из различных рецепторных органов. Это создает условия для развития общих способностей. В то же время специфические функции различных образований коры головного мозга с их рецепторными органами создают основу для развития специальных способностей. В свою очередь, общие способности позволяют учащимся получить широкое общее и политехническое образование, а специальные - профессиональную подготовку, овладеть музыкой, литературой, искусством и т.д.

Эффективность использования потенциальных возможностей учащихся зависит от глубокого понимания закономерностей развития личности каждого ученика, индивидуальных и возрастных особенностей учащихся.

Каждый учитель должен хорошо знать, что фенологические особенности человека формируются под влиянием генотипа и внешних условий жизнедеятельности, совокупность которых и придает личности ученика индивидуальный характер.

Индивидуальные различия проявляются в особенностях слухового, зрительного, двигательного и других анализаторов, а также соответствующих им образований коры головного мозга, их пластичности или консервативности. Различия проявляются в общих типологических особенностях нервной системы (сангвиник, холерик, флегматик, меланхолик): в различной силе нервных процессов (возбуждения, торможения): в разных соотношениях между первичной и вторичной сигнальной системами. Эти врожденные особенности являются функциональной основой различия задатков, проявляющихся в скорости и прочности образования, перестройки системы связей (ассоциаций), условных рефлексов, мыслительных операций и т.д. Все это имеет фундаментальное значение для мыслительной деятельности, формирования умений и навыков, воспитания необходимых черт личности учащегося.

В конечном счете, типологические особенности образуют целостную личность как саморегулирующий организм, определяющий индивидуальные черты. Отсюда происходит и разное отношение к отдельным предметам, к теоретическим и практическим занятиям.

В зависимости от индивидуальных особенностей одни ученики тяготеют к творческому решению учебно-познавательных задач, другие - к решению по шаблону. Индивидуальными чертами определяются интересы и потребности каждой личности и формированию на их основе духовного мира - мировоззрения и идеалов, с особыми переживаниями и чувствами.

Таким образом, можно утверждать, что среди учащихся нет похожих друг на друга. Но при всем различии у них есть много схожего - и в общечеловеческих данных, и в их развитии и воспитании. Это сходство предопределяется сенситивными периодами, т.е. биологической предрасположенностью к той или иной деятельности. Граница между сенситивными периодами характеризуется новообразованиями.

Например, ребенок начинает сидеть только после укрепления первоначальной костно-мышечной структуры организма, ходить начинает только с развитием нижних конечностей, жевать пищу - после появления зубов, говорить - развитием речевого аппарата, мыслить - при условии развития коры головного мозга. В последующем развитии время от времени появляются условия для выполнения тех или других видов труда, уровня спортивных достижений и интеллектуальной деятельности.

Половое созревание происходит тоже в определенное время и создает для самих подростков и воспитателей немало проблем во взаимоотношениях мальчиков и девочек. В определенный период наступает потребность в самовыражении и самовоспитании, вызванной необходимостью самоутверждения в коллективе.

Как видим, у всех детей, подростков и юношеского возраста много типичного. Эти типологические особенности отражают возрастные закономерности, которые в педагогической науке и школьной практике делятся на возрастные периоды.

Развитие ребенка и школьника подразделяется на ряд возрастных периодов:

. Младенческий возраст - до 1 года.

. Ранний возраст от 1 до 3 лет.

. Дошкольный возраст - от 3 до 6,5 лет.

. Младший школьный возраст - от 6,5 лет до 10(1- 4 классы).

. Средний школьный возраст - от 10 до 15 лет (5- 9 классы).

. Старший школьный возраст - от 15- 17 лет (10 - 11 классы).

Психологи рассматривают дошкольный возраст и младший школьный возраст как детский, средний - как подростковый и старший школьный - как юношеский.

Учителю и воспитателю нужно хорошо знать возрастные особенности не для того, чтобы к ним приспосабливаться, а для того, чтобы на основе знания закономерностей возрастного развития учитывать особенности каждого ученика, обучать и воспитывать с наилучшими результатами.

1.2 Психолого-педагогические особенности среднего школьного возраста

Средний школьный возраст, особенно 5-7 классы, является наиболее ответственным для учителей и переломным в развитии подростка. В этот период происходит бурный биологический как количественный, так и качественный рост организма.

В физиологическом развитии подростковый возраст характеризуется тремя особенностями:

а) бурным ростом массы тела и отставанием в развитии сердечно- сосудистой системы, что приводит к диспропорции, обуславливающей быструю утомляемость, раздражительность:

б) половым созреванием, которое сопровождается развитием желез внутренней секреции, повышенной возбудимостью, что усложняет работу с подростками:

в) развитием и завершением окостенения скелета и костно-мышечной системы, что оказывает существенное влияние на развитие телосложения подростка.

В психическом развитии подростков происходят большие изменения. Восприятие носит целенаправленный характер, а наглядность служит в большей степени для понимания не только внешних, но и внутренних процессов. Наблюдательность становиться устойчивой чертой личности. В результате учебной деятельности все больше развивается анализирующее восприятие, растет удельный вес восприятия отвлеченного материала, усиливается роль символической наглядности.

Память - форма психического отражения, заключающаяся в закреплении, сохранении и последующем воспроизведении прошлого опыта, делающая возможным его повторное использование в деятельности или возвращение в сферу сознания. Память связывает прошлое субъекта с его настоящим и будущим и является важнейшей, показательной функцией, лежащей в основе развития и обучения. И если в младшем школьном возрасте память механическая, а мышление характеризуется соотношением конкретных предметов и явлений, то память подростка носит переходный характер: от механического запоминания предметов и явлений к абстрактно - логической памяти. Связь памяти с мыслительной деятельностью, с интеллектуальными процессами в подростковом возрасте на переходном этапе онтогенеза, приобретает самостоятельное значение. «Если у ребенка интеллект - это функция памяти, то у подростка память - функция интеллекта», писал Л.С. Выготский. Рассматривая предпосылки дальнейшего развития памяти в подростковом возрасте, Л.С. Выготский писал, что ключ к пониманию этого процесса «надо искать не в тех изменениях, которые происходят в самой памяти, а в тех, которые охватывают отношения памяти с другими функциями».

Мышление - это социально обусловленный, неразрывно связанный с речью психический процесс поисков и открытий нового, т.е. процесс опосредованного и обобщенного отражения действительности в ходе ее анализа и синтеза.

Существует одна особенность мышления подростка, важная для понимания работы его памяти. На этом переходном этапе развития человека мышление представлено двумя формами: конкретным (образным) и абстрактным (вербально-логическим). По мере развития подростка содержание его мыслительной деятельности изменяется в направлении перехода к мышлению в понятиях, которые, в свою очередь, более углубленно и всесторонне отражают взаимосвязи между явлениями действительности.

Эта особенность мышления подростка предъявляет свои требования и к организации процесса усвоения знаний. При подаче учебного материала педагогу следует использовать как конкретно - образные характеристики, логические, абстрактные, понятийные связи и отношения. Причем, использование характеристик, как тех, так и других должно четко соответствовать сложности материала. Вредно как излишне упрощение излагаемого материала, так и его усложнение. «Восход от конкретного к абстрактному, от особенного к общему. Мышление в процессе применения анализа и синтеза и других мыслительных операций вновь возвращается к конкретному, но уже обогащенному знанием общего, знанию многосторонних связей и отношений объектов».

Мотивами отношения к учению служит сочетание интереса к учебному процессу с социальной значимостью обучения.

Задача учителя в процессе обучения - сформировать потребность познания учащихся, которая обеспечивает:

Заинтересованность учащегося в освоении действий и понятий, через увязывание их, с трудовой мотивацией и мотивацией общения.

Обеспечить «проблемное включение» учащегося через стимулирование потребности в ориентировке, в новизне.

Поддерживать новизну не только за счет освоения той или иной исполнительской деятельности, но также и контроля, коррекции и оценки.

Примером для воспитания служат внешние черты людей - их одежда, должность, положение в обществе, в том числе и учителя.

Положение в коллективе утверждается самовыражением, любыми средствами.

Подростки характеризуются повышенной возбудимостью нервной системы и повышенной чувствительностью.

Психомоторика неодинаково развита у подростков. Одни малоподвижны, с трудом выполняют практические, познавательные и трудовые операции. Но, возможно у них хорошо развита память и мышление как компенсаторы малоподвижности организма. И, наоборот, другие с трудом воспроизводят изученный материал и решают задачи, тяжело выполняют мыслительные операции и пользуются знаниями, но они оперативно, легко выполняют практические действия на лабораторных и практических занятиях, в процессе трудовой деятельности. Эти особенности тоже учитываются учителем.

Психические качества сложнее учитывать, чем состояние здоровья. Но при изучении психических процессов нужно уделять им должное внимание. Например, восприятие, с помощью которого ученики по-разному получают информацию. Одни используют зрительный аппарат, а, следовательно, для них следует использовать средства наглядности: другие внимательно слушают учителя и получают звуковую информацию из его слов: третьи - лучше усваивают материал из учебника: четвертые - если они сами напишут или нарисуют, начертят, выполнят самостоятельную практическую работу.

Формируя самого себя, свои отношения с миром, подросток ищет и утверждает свою позицию в изменившихся условиях жизни, преодолевает внутренние тревоги, кризисы внешние сложности жизни. Мощные сдвиги происходят во всех областях жизнедеятельности ребенка, не случайно этот возраст называют «переходным».

В это время складываются, оформляются устойчивые формы поведения, черты характера и способы эмоционального реагирования, которые в дальнейшем во многом определяют жизнь взрослого человека, его физическое и психическое здоровье, общественную и личную зрелость.

1.3 Особенности учебной деятельности подростка

Учение для подростка является главным видом деятельности. От того, как учится подросток, во многом зависит его психическое развитие, становление как гражданина. В учебной деятельности подростка имеются свои трудности и противоречия, но есть и преимущества, которые может и должен использовать педагог. Преимущества учебной деятельности заключается в избирательной готовности, повышенной восприимчивости (сенситивности) к тем или иным сторонам обучения. Большим достоинством подростка является его готовность ко всем видам учебной деятельности, которые делают его взрослым в собственных глазах. Его привлекают самостоятельные формы организации занятий на уроке, сложный учебный материал, возможность строить самому свою познавательную деятельность за пределами школы.

Проблемы подростка связаны с тем, что эту готовность он еще не умеет реализовать; т.к. не владеет способами выполнения новых форм учебной деятельности. Обучить этим способам, не дать угаснуть интересу к ним - важная задача педагога. Нередко у подростков снижается общий интерес к учению, происходит «внутренний отход от школы». (А.Н. Леонтьев) Этот отход выражается в том, что школа перестает быть для ученика центром его духовной жизни, и, прежде всего изменением ведущей деятельности подростка.

Отсутствие учебной деятельности у учащихся является основной причиной «отхода от школы», что не дает возможности удовлетворить актуальную проблему возраста - потребность в самоутверждении.

Деятельность учащихся, когда они, побуждаясь прямыми мотивами самого учения, могут самостоятельно определять учебные задачи, выбирать рациональные приемы и способы решения, контролировать и оценивать свою работу - характеризуя ее сформированность учебной деятельности.

Целенаправленное формирование мотивов учения является одним из резервов повышения эффективности обучения подростков. Познавательная потребность подростка связана с удовлетворением потребности возраста. При ее удовлетворении у него формируются устойчивые познавательные интересы, которые определяют его положительное отношение к учебным предметам. Подростков привлекает возможность расширить, обогатить свои знания, проникнуть в сущность изучаемых явлений, установить причинно- следственные связи.

Подростки испытывают большое эмоциональное удовлетворение от исследовательской деятельности. Им нравится мыслить, делать самостоятельные открытия. Неудовлетворение познавательной потребности и познавательных интересов вызывает у подростков не только состояние скуки, апатии, безразличия, но порой и отрицательное отношение к предмету. При этом у подростка в равной степени имеет значение, как содержание, так и процесс, способы приема и овладения знаниями. Очень важно, что бы учитель давал материал не только тот, что есть в учебнике. «Ни один наставник не должен забывать, что его главнейшая обязанность состоит в приучении воспитанников к умственному труду, и что эта обязанность более важна, нежели передача самого предмета».

Интересы подростков различают по направленности их познавательной деятельности. Одни учащиеся предпочитают описательный материал, их привлекают отдельные факты, другие стремятся разобраться в сущности изучаемых явлений, объяснить их с точки зрения теории, третьи проявляют большую активность при использовании знаний в практической деятельности. Одни учащиеся склонны к репродуктивной деятельности, другие - к творческой, исследовательской деятельности. При положительном отношении подростков к учению существенное значение имеет понимание значимости знаний. Для подростка очень важно осознать, осмыслить жизненное значение знаний, и, прежде всего их значение для развития личности. Это связано с усиленным ростом самосознания современного подростка. Многие учебные предметы нравятся подростку потому, что они отвечают его потребностям не только много знать, но и уметь, быть культурным, всесторонне развитым человеком.

Убеждения и интересы, сливаясь воедино, создают у подростка повышенный эмоциональный тонус и определяют их активное отношение к учебе.

Если же подросток не видит жизненного значения знаний, то у него могут сформироваться негативные убеждения и отрицательное отношение к существующим предметам. Неуспех, как правило, вызывает у подростка бурные, отрицательные эмоции и нежелание выполнять трудные учебные задания. И если неуспех повторяется, то у подростка закрепляется отрицательное отношение к предмету.

Ситуация успеха обеспечивает подростку эмоциональное благополучие, которое во многом зависит от оценки его учебной деятельности взрослыми.

Оценки для подростков имеют различный смысл. В одних случаях оценка дает возможность выполнить свой долг, занять достойное место среди товарищей, в других - заслужить уважение учителей и родителей. Нередко смысл оценки для подростка выступает в стремлении добиться успеха в учебном процессе и тем самым получить уверенность в своих умственных способностях и возможностях. Это связано с потребностью возраста, оценить себя как личность, свои слабые и сильные стороны. Для эмоционального благополучия подростка очень важно, чтобы оценка и самооценка совпадали. Только при этом условии они могут выступать как мотивы, действующие в одном направлении и усиливающие друг друга. В противном случае возникает внутренний, а иногда и внешний конфликт.

Учителю необходимо знать не только мотивы учения, но и условия их формирования. Отношение подростков к учению обусловлено, прежде всего, качеством работы учителя и его отношением к учащимся. Учитель должен быть требовательным, добрым, (не добреньким) справедливым и чутким, и тогда подростки будут учиться в полную силу своих способностей.

1.4 Отбор форм и методов проведения факультативного курса

Основным методом обучения в средней школе было формальное ведение теории, которая состояла из определенных математических понятий, догматически преподносимых доказательств теорем и решения задач, в большей части носящих искусственный характер.

Сложившаяся традиционная система математического образования в школе перестала удовлетворять возросшим потребностям общества. Еще в 1865 году ученик М. В. Остроградского (1801-1862) военный педагог В.Н. Шкларевич опубликовал в майском номере «Педагогического сборника» статью «Некоторые соображения о методе преподавания начальной математике», в которой были указаны основные пути реформы школьного математического образования.

Главная задача преподавания математики заключалась, по мнению автора, в развитии у школьника функционального мышления. Идейными последователями Шкларевича, в 80-90-х г.г. стали видные педагоги - математики С.И.Шохор - Троцкий (1853-1923), В.П. Шереметевский 1851- 1919) и др. «…Если вся математика есть, в сущности, учение о функциях, то ясно, что и элементарный курс должен группироваться вокруг основного понятия о функциональной зависимости».

Эти мысли спустя 9 лет после выступления В.П. Шереметевского повторил немецкий педагог-математик Ф. Клейн (1849-1925) на конференции в Братиславе. В 1908 году на IV Международном математическом конгрессе в Риме с участием России была образована комиссия по реформе математического образования.

Движение за реформу преподавания математики в школе возникло давно. Вопросы, связанные с ней, широко обсуждались на исторических Всероссийских съездах преподавателей математики. Результаты съездов поражают обилием интересных решений, идей и находок.

Среди обсуждаемых на 1-ом съезде (1913) в России вопросов была проблема возможного сближения школьного курса математики с математической наукой, доступное введение в школьную программу важнейших идей современной математики.

Перестройка всей системы народного образования, ликвидация неграмотности, тяжелые годы войны приостановили реформу математического образования. В конце пятидесятых годов прошлого столетия движение за реформу продолжилось. Выразилось это в выделении специальных часов на факультативные занятия. Первые факультативные курсы назывались «Дополнительные главы и вопросы математики».

В современной школе накоплен большой научный и практический опыт в решении дифференцированного обучения, истоком которого является фуркация обучения в средней школе.

Под фуркацией понимаем - разделение учебных планов с целью такой специализации учащихся, которая совместима с сохранением общеобразовательного характера школы.

ноября 1966 года было принято постановление» О мерах дальнейшего улучшения работы средней школы», в котором были предложены новые формы обучения. В частности, формы дифференцированного обучения, учитывающие индивидуальные склонности и способности учащихся. К этому моменту школа накопила опыт по организации и проведению таких форм обучения, как:

а) классы с углубленным изучением ряда предметов:

б) специализированные школы.

Факультативные занятия не только не противоречат указанным формам, но и дополняют их, являясь самой подвижной, доступной и массовой формой, т.к. могут быть введены в каждой школе. Учитель со своими учениками, пожелавшими посещать факультативные занятия, опираясь на примерные программы факультативного курса, может создать свой факультативный курс, отвечающий интересам конкретных учеников, что очень важно.

Экспериментальные проверки на факультативных занятиях позволили некоторые темы включить в основной курс математики. Например, «Метод координат» (7 класс), «Производная» (9класс) В практику работы школы факультативные занятия вошли в 1967-1968 учебном году.

К 1980 году был завершен переход средней школы на новую программу по математике. Новый факультативный курс состоял из трех разделов:

1.  Избранные вопросы математики (7-10 класс)

2.       Математика в приложениях (9-10класс)

.        Алгоритмы и программирование (8-10класс).

В настоящее время развернулось движение за новую реформу общеобразовательной и профессиональной школы. Реформой предусматривается дальнейшее развитие дифференциации обучения для учащихся 8-11 классов - как возможность углубленного изучения отдельных предметов, в том числе и математики.

Практика работы школы показала невозможность решение образовательных задач обучения в отрыве от воспитания и развития школьников и, наоборот, невозможность воспитания и развития в отрыве от процесса обучения. Таким образом, целью обучения на современном этапе развития государства должно быть не только формирование личности учащихся, а усвоение знаний, умений, навыков - как особая цель в общей системе целей формирования, и как средство воспитания.

В современной педагогике разработаны общие критерии отбора содержания учебного материала, удовлетворяющего требованиям комплексного подхода к обучению, воспитанию и развитию учащихся.

. Критерий целостности содержания образования, предполагает достаточно полное отражение в нем требований современного общества к всестороннему, гармоническому развитию личности и охват всех основных направлений современной науки, производства, общественной жизни и культуры.

. Критерий научной и практической весомости элементов содержания образования, который обеспечивает широкое политехническое образование и высокую профессиональную подготовку, которые тем самым обеспечат социальную защищенность подрастающего поколения в условиях рыночных отношений. Факультативный курс не может охватить всех направлений современной науки.

Критерий соответствия возрастным возможностям учеников, предполагает выявление элементов содержания, которые вызывают большие затруднения у значительной части школьников соответствующего возраста, поиск возможных путей устранения этих затруднений.

. Критерий соответствия имеющемуся времени на изучение данного учебного материала, предполагающий затраты времени, необходимые для углубленного и прочного усвоения соответствующих тем содержания, соответствуют критериям качества усвоения знаний, практических умений и навыкам.

. Критерий соответствия содержания имеющейся учебно-методической и математической базе современной школы.

. Критерий соответствия международному опыту построения содержания школьного образования.

Перечисленные критерии отбора содержания материала указывают лишь общее направление, следуя которым и учитывая специфику факультативных занятий, можно сформировать критерии отбора содержания учебного материала для факультативных занятий.

В методической литературе вопрос о критериях отбора факультативных занятий, направленных на комплексное решение образовательных, развивающих и воспитательных задач обучения не ставился. Различные авторы, в зависимости от целей факультативных курсов, высказывают различные рекомендации для отбора содержания.

Анализ, проведенный соответствующей литературы, в ходе которого выделены следующие рекомендации по отбору содержания факультативных занятий.

. Преемственность основного и факультативного курса. Опрос учащихся показывает, что они предпочитают факультативные курсы, содержание которых связано с основным курсом, основываются на понятиях, известных учащимся из основного курса, как бы расширяют и углубляют материал основного курса математики. В этом случае факультативные курсы имеют большую эффективность, что, прежде всего, связано с экономией времени, учащихся не надо вводить в круг основных понятий и методов темы, знакомить с терминологией и обозначениями. Углубленное изучение темы основного курса дает возможность для обобщения и систематизации обязательных знаний, показа их развития и применения к решению более сложных задач в математике и других науках.

2. Целостность содержания. Использование термина целостности является естественным для отбора содержания факультативного курса в смысле внутренней взаимосвязи содержания, концентрации его вокруг нескольких основных понятий, законов и методов. Это позволяет сосредоточить усилия учащихся в одном направлении, повышает доступность материала, позволяет за короткое время добиться наибольшей эффективности и качества обучения.

. Научная и практическая значимость элементов содержания. В решении этой задачи большая помощь может быть оказана, если в факультативный курс будет включена:

-    сведения об ученых, занимавшихся решением проблемы:

-        история возникновения и постановка той или иной проблемы;

         поиски решения, трудности на пути решения проблемы;

         значимость решения проблемы для развития науки;

         применение полученного результата в других областях знаний;

         применение полученного результата к решению прикладных задач.

Реализация критерия научной и практической значимости содержания факультативных занятий - « раскрытие межпредметных связей изучаемого материала» [А.Д. Александров О геометрии Математика в школе 1980 н3 с 56-62 с 58] ученику нужно показать реальные связи и воплощение геометрии в жизни, в природе, в искусстве, в науке и технике. Геометрия должна предстать перед учениками - «не как сухой предмет, подлежащий зубрежке и сдаче на экзамене, а как полное содержания, значения и красоты явление культуры, как наука в ее связях с реальными вещами».

. Соответствие содержания факультативного курса воспитательным и развивающим целям обучения.

Не всякое содержание способствует достижению целей воспитания и развития учащихся. Надо специальным образом конструировать содержание факультативного курса, включая в него элементы истории, современности, занимательности, красоты математики Занимательность в смысле показа занимательных элементов в самом содержании математики. К ним можно отнести: неожиданный факт, аналогии, примеры, исторические материалы, решение поучительных задач. Еще Н.И. Лобачевский обосновал дидактический принцип» «преподавание, приноровленное к возрасту». Ученый считал, что занимательность - необходимое средство возбуждать, поддерживать внимание, без которого преподавание не будет успешным.

. Формирование мировоззрения ускоряет у учащихся гражданскую и политическую зрелость. С 5-го класса школьники приобщаются к систематическому изучению научных знаний основ наук. Опираясь на представления о природе, обществе, полученные в начальных классах, учащиеся средней и старшей школы на уроках, во внеклассной и внешкольной работе углубляют и обобщают знания об окружающем мире, объединяют их в целостное представление о природе. Но главное для мировоззрения - комплексный подход к интеграции знаний, развитие диалектического мышления школьников.

. Соответствие содержания факультативного курса возрастным и индивидуальным особенностям. Эта рекомендация предполагает не только доступность изучаемого материала, уровня трудности изучаемого материала, но и включение в содержание материала, вызывающего повышенный интерес, стимулирующий творческую деятельность, соответствующую уровню развития школьников.

. Соответствие содержания учебно-методическому обеспечению. Тем самым предполагается что, факультативные занятия охватываются учебными пособиями, научно-популярной литературой, наглядными пособиями и техническими средствами обучения в объеме, достаточном для успешного решения поставленных задач познания.

. Соответствие содержания имеющемуся времени. Планирование содержания факультативного курса по занятиям, а также соответствие всего объема факультативного курса времени, отведенного на его прохождение.

Рекомендации отбора содержания факультативного курса требуют применения таких методов и форм обучения, которые бы побуждали учащихся к самостоятельной, поисковой, исследовательской деятельности, активизировали бы творчество учащихся.

Выбор форм и методов обучения на факультативных занятиях должны отвечать [Кадыров, с.17]:

-    организации самостоятельной работы учащихся на всех этапах обучения:

-        построение процесса изучения материала как совместной исследовательской деятельности каждого учащегося:

         индивидуализация и увеличение объема самостоятельной работы каждого учащегося.

Анализ методической литературы дал возможность выделить следующие критерии отбора методов проведения факультативных занятий.

1.5 Методы проведения факультативных занятий

Методы проведения факультативных занятий должны обеспечивать:

. Преемственность методов, применяемых на основных и факультативных занятиях, по математике означает, что методы, используемые на факультативных занятиях, являются естественным продолжением методов, используемых на основных уроках.

. Соответствие целей и задач обучения, предполагает выбор методов обучения и целей для учета задач образования, воспитания и развития, которые будут реализовываться на данном этапе и на протяжении изучения всего материала факультативного курса.

. Соответствие содержания факультативных занятий предполагает, использование тех или иных методов обучения, зависящих от содержания изучаемого материала. Различное содержание требует применения различных форм и методов обучения.

. Соответствие возрастным и индивидуальным особенностям развития подростков предполагает такой выбор методов обучения, которые в наибольшей степени помогли лучше развить «интеллектуальные операции в познавательной деятельности», формировать технику самообразования, рациональной работе с учебным материалом, (конспектирование, рефераты, использование тезисов, работа с учебником).

. Методическая классификация методов обучения должна соответствовать трактовке методов обучения математике. Математическое содержание учебного предмета развивается главным образом посредством индукции, дедукции и обобщения, а способы взаимодействия учителя и ученика выражаются через репродукцию, эвристику и исследование.

По характеру учебно-познавательной деятельности и организации материала можно выделить следующие методы обучения:

1)  индуктивно-репродуктивный:

2)      индуктивно-эвристический:

)        индуктивно-исследовательский:

)        дедуктивно-репродуктивный:

)        дедуктивно-эвристический:

)        дедуктивно-исследовательский:

)        обобщенно- репродуктивный:

)        обобщенно-эвристический:

)        обобщенно-исследовательский.

Суть индуктивно-репродуктивного метода заключается в том, что учитель создает такую ситуацию, в которой ученик воспроизводит понятие или теорему в процессе частных случаев, например, посредством решения задач на выделение ситуаций, удовлетворяющих условиям теоремы, или решению задачи (изучение теоремы) осуществляется по плану, предложенному учителем.

Пример. Перед выполнением упражнения на умножение чисел с разными знаками учащиеся получают предписание: «Произведение двух чисел с разными знаками есть число отрицательное. Чтобы найти модуль произведения, надо перемножить модули этих чисел». Пользуясь этим предписанием, ученик выполняет упражнения, соотнося свои действия с указанными рекомендациями. Например, умножая -1,5 на 7, ученик указывает, что даны числа с разными знаками, читает по частям предписание и выполняет соответствующие действия.

Дедуктивно-репродуктивный метод предполагает воспроизведение частных случаев в процессе решения задач, где используется общее положение. Например, теорема о сумме смежных углов воспроизводится посредством решения задач на нахождение одного из смежных углов, если задан другой.

При обобщенно-репродуктивном методе цель достигается путем воспроизведения изученных фактов. Например, выполняя упражнения на воспроизведение умножения двучлена вида (а - в) на двучлен вида (а + в) на основе правила умножения многочлена на многочлен, учащиеся получают известную формулу: 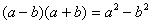. Или поэлементное овладение некоторым действием осуществляется в процессе усвоения его компонентов и их совокупностей. Так, усвоение векторного метода предполагает овладение действиями перевода геометрического языка на алгебраический векторный и обратно, сложение и вычитание векторов, представления вектора в виде суммы, разности векторов и т.п.

Индуктивно-эвристический метод предполагает самостоятельное открытие фактов в процессе рассмотрения частных случаев. Примеры. Упражнения на умножение степеней с одинаковым основанием приводят к открытию определения произведения степеней с одинаковыми основаниями. Выполнение цепочки упражнений на построение образов треугольника и точки пересечения его высот в гомотетии с к=-0,5 относительно точки пересечения медиан этого треугольника приводит к открытию известной теоремы Эйлера.

Дедуктивно-эвристический метод заключается в открытии частностей любого факта при рассмотрении общего случая. Примером проявления этого метода может служить решение любой конкретной задачи на применение какой-либо теоремы. Пусть учителем предложена задача на применение свойств и признаков параллелограмма: «На диагонали ВД параллелограмма АВСД отмечены две точки Р и О так, что РВ = ОД. Докажите, что четырехугольник АВСО - параллелограмм». Её решение позволяет открыть частный случай, заключающийся в том, что указанное в задаче условие обусловливает тот факт, что полученный четырехугольник является параллелограммом. Или: решение конкретного квадратного уравнения по общей формуле приводит к зависимости между заданными коэффициентами при Х₂, Х и свободным членом и корнями данного уравнения.

Эвристическое обобщение предполагает создание учителем такой ситуации, в которой ученик самостоятельно (или с небольшой помощью учителя) приходит к обобщению. Например, измеряя стороны и углы произвольных треугольников, ученики могут открыть следующую зависимость между углами и сторонами треугольника: против большей стороны треугольника лежит больший угол и наоборот.

Индуктивно-исследовательский метод заключается в проведении исследований различных феноменов посредством изучения их конкретных проявлений. Пример, изучая свойства четырехугольников в зависимости от наличия у них симметрии, приходим к таким видам четырехугольника, как прямоугольник, ромб, квадрат.

Дедуктивно-исследовательский метод заключается в организации исследований посредством дедуктивного развития учебного материала. Он проявляется в таких формах, как аксиоматический метод, метод моделирования, решение задач на применение теорем.

Обобщенное исследование предполагает наличие в учебном материале ситуаций, исследование которых приводит к обобщенному знанию

Например, рассматривая различные случаи расположения вписанных в окружность углов, можно прийти к известной теореме о том, что вписанный угол измеряется половиной дуги, на которую он опирается.

Наряду с традиционной системой обучения, в которой лежит совокупность дидактических принципов, наиболее распространены проблемное и программированное обучение, система обучения Л.В. Занкова.

В качестве основы проблемного обучения предлагается следующая система дидактических принципов:

-    научности и систематичности обучения;

-        активности и самостоятельности учащихся в обучении;

         единство образования, воспитания и развития;

         связь теории с практикой;

         проблемности.

Организация проблемного обучения предполагает качественно иное взаимодействие учителя и учащихся, специфическое построение учебного материала. Специфика построения учебного материала основывается на выделении ведущих идей курса, их развитии, роли «человеческого фактора» в этом процессе. Важнейшим моментом взаимодействия учителя и обучающихся становится организуемое и руководимое учителем самостоятельное овладение учащимися знаний.

Познание учащихся осуществляется как исследование в процессе интеллектуальной учебной деятельности. В основной школе обеспечивается эвристическим и исследовательским методами.

Под проблемной ситуацией понимаем осознанное затруднение, порождаемое несоответствием, несогласованностью между имеющимися знаниями и теми, которые необходимы для решения предложенной задачи. Задача, создающая проблемную ситуацию, называется проблемной задачей или проблемой. Проблема должна быть доступной пониманию учащихся, а ее формулировка - вызвать интерес, постановка проблемы должна быть естественной. Проблемную ситуацию нужно готовить, она должна создаваться всем ходом урока, быть ее органической частью. Пути создания проблемной ситуации:

Предварительная постановка практической проблемы:

. Разбор возможностей использования изученного материала:

. Поиск средств выполнения решения:

. Решение нешаблонных задач.

В первом случае мы можем предложить учащимся проверить вертикальную кирпичную кладку стен с помощью отвеса. ЕЕ анализ порождает проблему выяснения математической основы этого приема.

Во втором случае мы можем после доказательства тождества .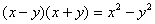

Возникает вопрос, как использовать его для вычислений. Учащиеся, прежде всего, обращают внимание на применение этой формулы при умножении. С ее помощью можно вычислять квадраты чисел.

Подводя итоги, выделяем следующие вопросы методического обеспечения факультативного курса:

. Отбор содержания факультативного курса, отвечающего поставленным целям обучения.

. Разработка программы факультативного курса, в которой предусматривается:

-    распределение содержания по занятиям:

-        указание вопросов для самостоятельного изучения:

         перечень рефератов, носящих самостоятельный, творческий характер:

         литература, в которую входят: учебно-методические пособия, статьи, книги по тематике факультативного курса.

3. Разработка программ каждого занятия с указанием:

-    содержания материала, рассматриваемого на занятии:

-        домашнее задание:

         индивидуальные задания:

         темы докладов и сообщений для учащихся:

         литература:

         формы и методы проведения занятий.

4. Составление индивидуальных планов работы школьников, посещающих факультатив, в которых предусматривается:

-    выполнение заданий, носящих образовательный воспитательный и развивающий характер:

-        работа с научно- популярной литературой:

         подготовка докладов и сообщений:

         написание реферата.

.6 Анализ учебной литературы

Первой русской учебной книгой по математике была «Арифметика» Л.Ф. Магницкого (1703): в 1739 переведены на русский язык «Начала» Евклида. В 1740 издана «Универсальная арифметика» Л. Эйлера, в 1757 - «Универсальная арифметика» Н.Г. Курганова, вытеснившая из школ учебник Магницкого.

В 1-й четверти 19 века преподавание математики велось по трем учебникам: «Начальные основания математики» А.Г. Кестнера (перевод с немецкого, 1792-1794): «Курс математики» Т.Ф. Осиповского (т. 1-3, 1801-1823) до 1812 был основным учебным пособием для гимназий, отличался полнотой и ясностью изложения, превышал по объему гимназический курс: учебник Н.И. Фусса «Начальные основания чистой математики» (ч. 1-3, 1810 - 1812), стал первым стабильным учебником для гимназий. В 30 годы для употребления в гимназиях рекомендовались «Руководство к арифметике» и «Собрание арифметических задач» Ф.И. Буссе, которые по простоте изложения превосходили существовавшие учебники. Они были продуманы и в методическом отношении: обучение начиналось с простых и наглядных истин, соблюдался постепенный переход к трудным понятиям, объяснение проводилось раньше правил. В качестве задачника применялись «Арифметические листки» П.С. Гурьева, которые содержали 2523 задачи с решениями, расположенными последовательно от «легчайших к труднейшим».

Во второй половине 19 века в гимназиях использовалась «Элементарная геометрия в объеме гимназического курса» (1864) А.Ю. Давидова. С 90-х годов в школе используются учебники А.П. Киселева.

Перестройка системы среднего образования, проводившаяся в связи с реформой средней и профессиональной школы, потребовала усиления мировоззренческой направленности курса математики, его воспитывающего значения, роли самостоятельной деятельности учащихся. Трактовка основных геометрических понятий ориентирована на их широкое применение в смежных дисциплинах. Построение курса геометрии стало традиционным, близким к курсу А.П. Киселева.

Действующей программой по математике предусмотрено систематическое изучение курса геометрии в основной и средней школе. С 1982 года в школах Российской Федерации используется учебник по геометрии для 7-11классов А.В. Погорелова, учебник по геометрии Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняк, И.И. Юдиной с 1988. Изданы учебники для профильных физико-математических классов по геометрии А.Д. Александрова, А.Л. Вернера и В. И. Рыжик, И.Ф. Шарыгина, для гуманитарного профиля - учебник геометрии В.Ф. Бутузова и др.

Учебники по геометрии А.В. Погорелова и Л.С. Атанасяна учат школьников основной школы систематическому изучению свойств геометрических фигур на плоскости, формированию пространственных представлений, развитию логического мышления и подготовку головного мозга для изучения смежных дисциплин (физика, черчение и т.д.) и курса стереометрии в старших классах. Несколько разное расположение теорем не сказывается на сегодняшних требованиях к математической подготовке учащихся основной и средней школы.

Хочется отметить, что учебник по геометрии Л.С. Атанасяна разработан так, что его можно использовать и для учащихся желающих продолжать углубленное изучение математике. «Содержание дополнительных глав расширяет и углубляет геометрические сведения, представленные в главах основного учебника: вводятся новые понятия, рассматриваются интересные геометрические факты, дается обоснование некоторых утверждений, которые в основном учебнике принимаются на основе наглядных представлений либо предлагались в виде задач повышенной трудности». Л.С. Атанасян и другие Геометрия дополнительные главы к учебнику Москва Просвещение 1990 г.

Курс школьной геометрии является традиционным курсом евклидовой геометрии, дополненным простейшими вопросами векторной алгебры и аналитической геометрии.

2. Историческая справка

Положение математики в современном мире далеко не то, каким оно было сто или даже шестьдесят лет назад. Математика превратилась в повседневное орудие исследования в физике, астрономии, биологии, инженерном деле, организации производства и многих других областях теоретической и прикладной деятельности. Многие крупные врачи, экономисты и специалисты в области социальных исследований считают, что дальнейший прогресс их дисциплин связан с более широким и полнокровным использованием математических методов, чем это было до настоящего времени. Там, где недавно царил чисто качественный подход, теперь отыскиваются строгие количественные закономерности и строятся математические модели изучаемых явлений. И чем грандиознее замыслы познания, относятся ли они к макро - или микромиру, тем более значительной становится роль математики [Б.В. Гнеденко Математика в современном мире. - М.: «Просвещение», 1980].

За тысячелетия своего существования математика прошла большой и сложный путь, на протяжении которого неоднократно изменялся ее характер, содержание и стиль изложения.

Еще в древности геометрия превратилась в дедуктивную, строго логическую науку, построенную на основе систем аксиом.

Первичные математические представления были в обиходе у людей на самых ранних стадиях развития человеческого общества. Хозяйственные потребности вынуждали людей совершенствовать правила счета, измерения расстояний, а также расширять объем математических понятий. Следует отметить, что на этой ступени развития математические сведения различных народов, практически не общавшихся между собой, поразительно близки по форме и содержанию. Правила вычисления объемов и площадей, использовавшиеся в Древнем Вавилоне и Египте, тождественны аналогичным правилам Древнего Китая. Свойство сторон прямоугольного треугольника, известное под именем теоремы Пифагора, было найдено для частных случаев треугольников с целочисленными сторонами задолго до Пифагора в Древнем Вавилоне. Оно было известно и в Древнем Китае. Все народы, обращаясь к изучению геометрических форм, исходят фактически из одних и тех же практических задач. Людям необходимо было различать прямоугольники, круги, треугольники, цилиндры, параллелепипеды и тетраэдры. Хозяйственные потребности вынудили постепенно выработать правила вычисления площадей и объемов наиболее простых плоских фигур и пространственных тел. Этого требовали нужды передела земель, вычисления объемов дворцов, строений, земляных работ. В начальный период развития математики были подмечены не только правила сложения целых чисел, но и многие другие закономерности, сохранившиеся в арифметике и геометрии до наших дней.

В Древней Греции были школы, в которых будущие купцы и ремесленники обучались математическим сведениям, необходимых для их предстоящей повседневной деятельности, как выражался Платон «для бытных нужд». Также существовали и такие школы, в которых математика излагалась как система научных знаний, логически выводимых из некоторых первичных положений, принимаемых за истинные, из аксиом. Древнегреческим философам был известен афоризм: «Не знающий геометрии не допускается», который, как говорят, принадлежал знаменитому Платону, повесившему его на дверях своей школы.

.1 Евклидовы «Начала»

В течение двух тысяч лет геометрию узнавали из «Начал» Евклида, либо из учебников, написанных не основе этой книги. Лишь профессиональные математики обращались к трудам других великих греческих геометров: Архимеда, Апполония - и геометров более позднего времени. Классическую геометрию стали называть евклидовой в отличие от появившихся в Х1Х веке «неевклидовых геометрий».

Об этом поразительном человеке история сохранила настолько мало сведений, что нередко высказываются сомнения в самом его существовании. Что же дошло до нас: Каталог греческих геометров Прокла Диадоха Византийского, жившего в V веке нашей эры, - первый серьезный источник сведений о греческой геометрии. Из каталога следует, что Евклид был современником царя Птолемея, который царствовал с 306 до 283г. до нашей эры. Евклид должен быть старше Архимеда, который ссылался на «Начала». До нашего времени дошли сведения, что он преподавал в Александрии столице Птолемея 1, начинавшийся превращаться в один из центров научной жизни. Евклид был последователем древнегреческого философа Платона, и преподавал он, вероятно, четыре науки, которые должны предшествовать занятиям философией: арифметику, геометрию, теорию гармонии, астрономию. Кроме «Начал» до нас дошли книги Евклида, посвященные гармонии и астрономии.

Что касается места Евклида в науке, то оно определяется не столько собственными его научными исследованиями, сколько педагогическими заслугами. Евклиду приписывается несколько теорем и новых доказательств, но их значение не может быть сравнимо с достижениями великих греческих геометров: Фалеса и Пифагора, Евджокса и Тиэтета.

Величайшая заслуга Евклида в том, что он подвел итог построению геометрии и придал изложению столь совершенную форму, что на две тысячи лет «Начала» стали энциклопедией геометрии.

В период возрождения европейской математики (XVI в.) «Начала» изучали и воссоздавали заново. Логическое построение «Начал», аксиоматика Евклида воспринималась математиками как нечто безупречное до Х1Х века, когда начался период критического отношения к достигнутому, который закончился новой аксиоматикой евклидовой геометрии - аксиоматикой Д. Гильберта. Изложение геометрии в началах считалось образцом, которому стремились следовать ученые и за пределами математики.

Именно в Древней Греции появились знаменитые «Начала» Евклида, (Евклид жил и работал приблизительно две тысячи двести лет назад), где отдельные осмысленные факты были объединены в общую логическую систему.

Евклид был выдающейся личностью. Помимо «Начал» у этого мыслителя имеется много других трудов, но все же самым крупным вкладом в математику были его «Начала». До Евклида занимались подбором и обобщением фактов многие мыслители. Наиболее ранним сочинением такого рода считается книга Гиппократа Хиосского (IV в. до н.э.). Однако основы теории Евклида по своему содержанию, по глубине мысли заметно отличались, и книга Гиппократа, как впрочем, труды других мыслителей прошлого не шла в сравнение с «Началами». Как писал Прокл (V в.), Евклид многое взял от Евдокса (408-350 гг. до н.э.: ученик Платона), многое усовершенствовал в трудах Теэтета (415-369 гг. до н.э.: группа Платона) и затем, проанализировав труды своих предшественников, возвысился до создания невиданной по тем временам точно обоснованной теории.

Теория Евклида удивляет и сложным построением, и четкостью мысли, и живостью изложения. Это - первый образец построения научной системы. Теория Евклида оказала большое влияние на формирование науки в Греции, став фундаментом развития таких областей знания, как математика, философия и другие, тем культурным наследием, которое считается гордостью греческой нации.

Египтяне, например Пифагор (ок. 600-500 гг. до н.э.), использовали свойства прямоугольных треугольников со сторонами 3,4,5. По скудным сведениям, дошедшим до нас, Пифагор, покинув свой родной остров Самос, некоторое время жил в Египте [Мацуо Камацо. Многообразие геометрии: «Знание», 1981, стр.13].

Таким образом, уже в те далекие времена люди владели различными познаниями в области геометрии, но они не были в состоянии свести их в единую систему. Фалес (примерно 600 г.до н.э.) путешествуя по Египту, познакомился с местными методами измерений и, вернувшись в Грецию, рассказал о них своим соотечественникам. У него были и собственные исследования: в современных школьных курсах математики есть теорема Фалеса. И, только Пифагор, дав доказательство своей теоремы, тем самым отделил геометрию от искусства измерения. К возникшей впоследствии школе Пифагора принадлежали многие ученые, среди которых выделялся Гиппократ Хиосский. Именно он составил систематическое изложение основ геометрии.

Затем наступила эпоха многочисленных геометрических исследований знаменитой платоновской Академии. Платон (427-347гг. до н.э.) наряду с философией серьезное внимание уделял геометрии. Евклид был моложе учеников Платона, но старше Архимеда (ок.287-212 гг. до н.э.), так как был платоником и хорошо знал философию Платона (именно поэтому он закончил «Начала» изложением так называемых Платоновых тел, т.е. пяти правильных многогранников), а с другой стороны его имя упоминается в первом из двух писем Архимеда к Досифею «О шаре и цилиндре».

Евклид жил в Александрии примерно 365 до 300 г. до нашей эры.

Евклид при написании «Начал» не использовал слова «геометрия», но оно, как известно, в то время применялось довольно широко. Его «Начала» представляют собой полное и систематическое изложение основ геометрии. Они состоят из 13 книг, причем не все книги посвящены геометрии: в пятой, седьмой, восьмой девятой и десятой книгах рассматриваются вопросы арифметики. В остальных восьми книгах излагаются основы геометрии.

Открываются «Начала» определениями основных понятий и формулировками некоторых основных положений геометрии, которые принимаются без доказательств.

Далее идут в строгой последовательности «предложения», которые являются теоремами или задачами на построение. Каждая книга «Начал» имеет ту же структуру.

В первую книгу входят теоремы о равенстве треугольников, соотношениях между сторонами и углами треугольников, теории параллельных линий, условия равновеликости треугольников и многоугольников, теорема Пифагора. Во второй книге рассматривается превращение многоугольников в равновеликий квадрат. Третья книга посвящена изучению свойств окружности, четвертая - вписанным и описанным многоугольникам, шестая - подобным фигурам. Наконец, в последних трех книгах излагается стереометрия, которая заканчивается построением циркулем и линейкой ребер правильных многогранников.

Первая книга, как уже было сказано, начинается с определений. Вот некоторые из них:

Определение 1. Точка есть то, часть чего есть ничто.

Определение 2. Линия есть длина без ширины.

Определение 4. Прямая есть такая линия, которая одинаково расположена по отношению ко всем своим точкам и т. д. Всего подряд 23 определения.

Теория Евклида опирается на ряд определений и аксиом. Исходной точкой его логической системы является положение о том, что выдвигаемые им постулаты очевидны, их справедливость признается всеми несомненной.

Имеется пять постулатов:

a.  Через две точки проходит единственная прямая.

b.      Ограниченную прямую линию можно непрерывно продолжать..        Из любой точки как из центра можно описать окружность любого радиуса..       Все прямые углы равны между собой..     Всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых углов, эти прямые пересекаются и при том с той стороны, с которой эта сумма меньше двух прямых.

Пятый постулат известен как постулат о параллельных прямых.

Евклид приводит также девять аксиом, представляющих собой общие положения.

Теоремы геометрии, изложенные Евклидом, располагаются в такой последовательности, чтобы каждую теорему можно было доказать, используя предыдущие теоремы, постулаты, аксиомы.

Перечисление определений и аксиом, которые достаточны для проведения логического доказательства всех следующих за ними теорем геометрии, принято называть обоснованием геометрии.

Таким образом, «Начала» Евклида - первый, дошедший до нас труд по обоснованной геометрии, и в этом огромная историческая заслуга античного геометра перед наукой. «Начала» Евклида не потеряли своей ценности и поныне, несмотря на то, что со дня появления их прошло более 2000лет.

Благодаря, в первую очередь, трудам выдающегося русского математика Н.И. Лобачевского было установлено, что евклидова геометрия не является единственно возможной. 23 февраля 1826 года на заседании физико-математического отделения Казанского университета Н.И. Лобачевский сделал доклад «Сокращенное изложение начал геометрии с точным доказательством теоремы о параллельных». По образному выражению А.П. Котельникова, это было днем рождения неевклидовой геометрии.

Большая заслуга в расширении представлений о геометрических пространствах принадлежит математику Х1Х века Б..Риману. Он открыл, параллельно с Лобачевским, способ построения бесконечно многих» геометрий», которые локально, «в малом» устроены почти так же, как и евклидова геометрия, но обладают кривизной. К. Гаусс, обогативший математику замечательными открытиями, ушел после доклада Римана: глубоко задумавшись, над ошеломляющими его новыми геометрическими идеями. Карл Гаусс сразу оценил новые идеи, разобрался в них, понял, но сказать в слух не решался.

Он добился избрания Н. И. Лобачевского в члены Геттенского ученого общества, но своего отношения к новой науке не высказал. Он был прозорлив в науке, но осторожен в жизни. Только после смерти из дневников и писем узнали, как высоко ценил Гаусс гениальное творение Лобачевского.

2.2 Джованни Чева

Третьего марта 1648 года в Милане родился будущий итальянский инженер и математик Джованни Чева.

Окончил Пизанский университет. Основные работы по механике, гидравлике и математике.

В 1678 году Джованни Чева доказал теорему о соотношении отрезков некоторых прямых, пересекающих треугольник (Теорема Чевы). Построил учение о секущих, которое положило начало синтетической геометрии: оно изложено в сочинении «О взаимно пересекающихся прямых». Прежде чем сформулировать теорему расшифруем используемое в ней понятие «чевиана» - отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне

Эта теорема гласит: если три чевианы пересекаются в одной точке, то отношения, в которых их основания делят стороны треугольника, удовлетворяют равенство:

.

И теорема обратная: Если точки X, Y, Z на прямых, ограничивающих треугольник АВС, удовлетворяют условию Чевы, причём собственно на его сторонах лежат все три либо ровно одна из них, то соответствующие чевианы пересекаются в одной точке или параллельны.

декабря 1734 года Джованни Чева скончался в городе Мантуя, в Италии.

Простейший из многоугольников - треугольник - играет в геометрии особую роль. Без преувеличения можно сказать, что вся (или почти вся) геометрия со времен «Начал» Евклида покоится на «трех китах» - трех признаках равенства треугольников. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника». Как о самостоятельном разделе элементарной геометрии.

.3 Леонард Эйлер

В Базеле на берегу Рейна 15 апреля 1707 года в семье ученого-теолога Пауля Эйлера родился сын, названный Леонардом. Состав семьи пастора вскоре вырос до шести душ, семья располагала только одной жилой комнатой и отцовским кабинетом. Благодаря мягкому климату члены семьи большую часть времени проводили под открытым небом.

Начальное обучение будущий ученый прошел дома под руководством отца, учившегося некогда математике у Якоба Бернулли. Добрый пастор готовил старшего сына к духовной карьере, однако занимался с ним математикой для развития логического мышления. Мальчик увлекся математикой.

Когда у Леонарда появился интерес к учебе, его направили в базельскую латинскую гимназию - под надзор бабушки, вдовы госпитального священника. В те годы гимназия была в плохом состоянии: грубые и малоквалифицированные учителя, с одной стороны, и запущенные ученики - с другой, портили жизнь друг другу. Разумеется, серьезных знаний эта гимназия дать не могла.

Но чиновничья карьера требовала получение аттестата, знания некоторых разделов математики: поэтому многим брали репетиторов. У Леонарда тоже появился частный учитель - Иоганн Буркгардт, впоследствии небезызвестный математик и теолог, который сразу же предсказал своему ученику блестящее будущее.

октября 1720 года 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета: отец желал, чтобы он стал священником. Но любовь к математике, блестящая память и отличная работоспособность сына изменили эти намерения и направили Леонарда по иному пути.

Леонард Эйлер давно интересовался математикой. Теперь, став студентом, он благодаря своей блестящей памяти легко усваивал учебные предметы, отдавая основное время математике. И немудрено, что способный мальчик обратил на себя внимание Бернулли.

В то время не существовало учебников по высшей математике, а заниматься с Леонардом индивидуально Бернулли не имел времени. И он нашел единственно правильный метод, который очень высоко оценил впоследствии сам Эйлер: предложил юноше читать математические мемуары, а по субботам приходить к нему домой, чтобы совместно разбирать непонятные вопросы.

В доме своего учителя Эйлер познакомился и подружился с сыновьями Бернулли - Николаем и Даниилом, также увлеченно занимавшимися математикой. А 8 июня 1724 года 17-летний Леонард Эйлер произнес по- латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона - и был удостоен ученой степени магистра(в Х1Х веке в большинстве университетов Западной Европы ученая степень магистра была заменена степенью доктора философии).

Небольшая по численности населения Швейцария, готовила гораздо больше образованных людей, чем могла содержать и обеспечить службой. Да и во всей Западной Европе спрос на ученых был невелик. Ни Эйлер, ни его друзья братья Бернулли не могли найти приложения своим силам. Однако у братьев было достаточно известное ученым Европы имя, служившее им лучшей рекомендацией, - и вскоре обоих пригласили во вновь создаваемую в Петербурге Академию наук.

«Я возымел неописуемое желание, - пишет Эйлер в автобиографии, - отправиться вместе с ними в 1725г. в Петербург. Однако дело не могло быть тогда осуществлено».

В последующие два года юный Эйлер написал несколько научных работ. Объявленный конкурс, Парижской Академией, на оптимальное решение количества, высоты и расположения мачт, выиграл всем не известный юноша из Базеля, откуда «хоть три года скачи, ни до какого моря не доскачешь». По существу проблемы нужно было представить себе корабль - парусник.

Эйлер был молод и полон энергии. Ни в магистрате, ни в университете он не мог найти применения своим силам и способностям. 5 апреля 1727 года Эйлер навсегда покидает Швейцарию, отправляясь в далекий Петербург по приглашению «Ее Императорского величества» и рекомендации братьев Бернулли.

Петербургская Академия с самого сначала своего существования была государственным учреждением, цели и задачи ее определялись потребностями государства, научные достижения широко публиковались в изданиях Академии.

В августе 1727 года молодой ученый уже читал в Академии свой первый доклад «О количестве истекающей из отверстия воды». Со следующего года ни один том трудов Академии не выходил без нескольких сочинений Эйлера по математике, механике, физике.

В уставе Академии содержалось требование, чтобы, «не только слава государства для размножения наук…. Распространялась, но и через обучение и распространение оных польза в народе была». Из числа учеников Эйлера в русской науке успешно работали В. Адуров, С. Котельников, С. Румовский, М. Сафронов, М. Головин, а позднее также А. Лексель, Ф. Шуберт и другие. С августа 1728года по 1736 год молодой ученый издал 11 трудов по математике в «Трудах Академии».

За первые 14 лет пребывания в Петербурге он написал более 80 крупных научных работ, более 50 работ из которых тогда же были опубликованы.

Ему часто давались поручения по практическим проблемам. Он читал лекции студентам академического университета, принимал экзамены в Кадетском корпусе, занимался вопросами пожарных насосов и механических пил, работал в Комиссии мер и весов, в Географическом департаменте. Не ограничиваясь чисто математической частью, он непосредственно занялся картографией и сам вычертил немало карт, испортив при этом зрение.

«Стараниями Гейнзисуса и Винсгейма, под руководством бессмертного Эйлера, составлен был, наконец, и издан в 1745году тот превосходный атлас империи, который был в общем употреблении…» писал сто с лишним лет спустя директор Пулковской обсерватории академик О.В. Струве. Впрочем, ценность и важность выполненной работы понимал и сам Эйлер.

Академия обратилась к своим членам с просьбой: составить руководства для первоначального обучения наукам. И Эйлер, не считаясь со временем, составил на немецком языке прекрасное «Руководство к арифметике», которое вскоре было переведено на русский язык и сослужило добрую службу многим учащимся. Перевод первой части выполнил в 1740году русский адъюнкт Академии, ученик Эйлера Василий Адуров. На русском языке это было первым изложением арифметики как математической науки.

В 1730 году на русский престол вступила Анна Иоанновна, страной фактически стали править ее приближенные. Поползли слухи о скором закрытии Академии.

Адмирал Сиверс, начальник русского флота, понимая, какую пользу может принести флоту способный ученый-математик, выхлопотал Эйлеру чин лейтенанта и обещал немедленное продвижение по службе. И 23-х летний Эйлер, готов был принять это предложение.

Однако Академия продолжала существовать. Правда, делами ее правил теперь Иоганн-Даниил Шумахер, тщеславный карьерист, но к Эйлеру относившийся с большим уважением. Многие ученые терпеть не могли Шумахера и, не чувствуя поддержки, стали покидать Россию. В 1733 году Д. Бернулли покинул Россию, Эйлер стал академиком и профессором чистой математики.

В один из последних дней 1733 года 26-летний Леонард Эйлер женился на дочери живописца Екатерине Гзель, которой в это время тоже было 26 лет. Вся Академия сердечно поздравляет молодоженов.

Оказывается, великий математик может не только вычислять и анализировать, он не чужд и мирской жизни. Молодоженами преподнесли сочиненные к случаю стихи.

В 1735 году Академия получила задание выполнить срочное и очень громоздкое астрономическое вычисление. Группа академиков просила на эту работу 3 месяца, а Эйлер взялся за эту работу и выполнил ее за три дня - справился самостоятельно. Перенапряжение не прошло бесследно, он заболел и потерял зрение на правый глаз. Однако ученый отнесся к несчастью с величайшим спокойствием: «Теперь я меньше буду отвлекаться от занятий математикой», - философски заметил он. До этого времени Эйлер был известен узкому кругу ученых. Но двухтомное сочинение «Механика, или наука о движении, в аналитическом изложении», изданное в 1736году, принесло ему мировую славу. Эйлер блестяще применял методы математического анализа к решению проблем движения в пустоте и в сопротивляющейся среде. Применение аналитического метода позволило упростить многие проблемы механики и привело к новым открытиям.

Обстоятельства ухудшились, когда в 1740 году умерла императрица Анна Иоанновна. Сложилась неустойчивая политическая обстановка, которую особенно почувствовали иностранцы. Поэтому Эйлер принял предложение прусского короля, который приглашал его в Берлинскую Академию на весьма выгодных условиях.

В соответствии с поданным прошением Эйлер «был отпущен от Академии в 1741 году», и утвержден почетным академиком. Он обещал по мере своих сил помогать Петербургской Академии - и действительно помогал весьма существенно все 25 лет, пока не вернулся в Россию обратно.

В феврале 1748 года Эйлер писал Гольдбаху, что доказал теорему, которая кажется любопытной.

Школьникам старших классов известно, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Эйлер доказал, что в четырехугольнике, не являющемся параллелограммом, вторая сумма всегда больше первой.

.

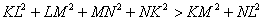В Берлинской Академии было издано двухтомное «Введение в анализ бесконечных», которое содержало не столько анализ, сколько алгебру, аналитическую геометрию и другие вопросы. Главной идеей сочинения было учение о функциях и обоснование важнейшей роли этого понятия в математике и ее приложениях. С появлением этих книг математический анализ становится методически разработанной учебной дисциплиной.

В 1766 году Эйлер возвращается в Петербург, к этому времени у него образовалась катаракта второго, левого глаза - и он перестал видеть. Приехавший с ним из Берлина мальчик-портной, понятия не имевший о математике, писал под его диктовку по-немецки. И Эйлер очень быстро продиктовал ему свои «Элементы алгебры», которые были сразу же переведены П. Иноходцевым и Юдиным на русский язык и вышли в двух томах в 1768 и 1769 гг. под названием «Универсальная арифметика».

Трудно даже перечислить все отрасли науки, в которых весьма успешно трудился Эйлер. Но в первую очередь он был математиком. Его сочинения по механике, физике, астрономии большей частью представляют собой математическую формулировку и математическое решение прикладных проблем.

В последние годы жизни ученый продолжал усердно работать, пользуясь для чтения «глазами старшего сына» и ряда своих учеников: Н. Фусса, М. Головина (племянника М. В. Ломоносова), Ф. Шуберта и других.

В 1783г. ученый стал ощущать головные боли и слабость. 18сентября, беседуя с А.И. Лекселем об открытой недавно планете Уран и ее орбите, он почувствовал себя плохо. Эйлер успел произнести «Я умираю» - и потерял сознание. Он скончался от кровоизлияния в мозг.

По образному выражению французского ученого Кондорсе, «Эйлер перестал жить и вычислять». Его похоронили на Смоленском кладбище в Петербурге.

Через несколько дней после смерти Эйлера состоялось траурное заседание конференции Академии. В начале 1785года в зале заседаний Академии против президентского кресла был укреплен бюст Эйлера на мраморной колонне. После переезда Президиума Академии наук СССР в Москву, этот бюст этот бюст установлен в одном из московских залов Президиума Академии.

Эйлер привил любовь к математике и своим трем сыновьям. Наиболее способным был старший сын Иоганнн Альбрехт - однако, и он главным образом разрабатывал идеи отца.

Учеными секретарями Санкт-Петербургской Академии наук в течение целого века были потомки и родственники Эйлера.

.4 Карл Фридрих Гаусс

В Броауншвейге 30 апреля 1777 года родился будущий великий математик. Сын водопроводчика в 1795 году поступил в Геттингенский университет, который с успехом закончил в 1798 году.

В 1799 году Карл Фридрих получил доцентуру в Брауншвейге, а в 1807 году кафедру математики и астрономии в Геттингенском университете.

Немецкий математик, внесший фундаментальный вклад также в астрономию и геодезию, иностранный член - корреспондент (1802) и иностранный, почетный член (1824) Петербургской Академии наук.

Отличительными чертами творчества Гаусса являются глубокая органическая связь в его исследованиях между теоретической и прикладной математикой, необычайная широта проблематики. Работы Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии. Во многих областях математические труды Гаусса содействовали повышению требований к логической отчетливости доказательств, однако сам Гаусс оставался в стороне от работ по строгому обоснованию математического анализа.

Первое крупное сочинение по теории чисел и высшей алгебре («Арифметические исследования», 1801) во многом предопределило дальнейшее развитие этих дисциплин. В конце книги излагается теория уравнений деления круга (то есть уравнений Хⁿ - 1 =0), которая во многом была прообразом теории Галуа. Помимо общих методов решения этих уравнений Гаусс установил связь между ними и построением правильных многоугольников. Он, впервые после древнегреческих ученых, сделал значительный шаг вперед в этом вопросе, а именно: Гаусс нашел все значения n, для которых правильный n-угольник можно построить циркулем и линейкой. В частности, решив уравнение Х17 - 1 = 0, он дал построение правильного 17-угольника при помощи циркуля и линейки. Гаусс придавал этому открытию большое значение и завещал выгравировать правильный 17- угольник, вписанный в круг, на своем надгробном памятнике, что и было исполнено. Алгебраические интересы Гаусса связаны с основной теоремой алгебры: он дал несколько ее доказательств - первое из них в 1799г. В 1801 немецкий ученый доказал, что всякое натуральное число представимо в виде суммы не более трех треугольных чисел (числа - числа последовательности).

;

;

;

…

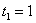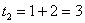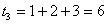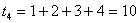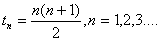
Обобщением треугольных чисел являются многоугольные (к-угольные) числа.

В 19 веке роль математической символики возрастает, Гаусс вводит математический знак отношений, например, сравнимости «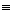(mod а)».

Замечательное приложение нашла геометрия в начале 19 века. С ее помощью было измерено все вокруг. В частности, наша Земля. Проблемы геодезии были самыми актуальными проблемами в прикладной математике особенно в первой трети столетия.

Изучение формы земной поверхности потребовало углубленного общего геометрического метода для исследования поверхностей. Выдвинутые Гауссом в этой области идеи получили выражение в сочинении «Общие исследования о кривых поверхностях» (1827). Руководящая мысль этого сочинения заключается в том, что при изучении поверхности как бесконечно тонкой гибкой пленки основное значение имеет не уравнение поверхности в декартовых координатах, а дифференциальная квадратичная форма, через которую выражается квадрат элемента длины и инвариантами которой является все собственные свойства поверхности - прежде всего ее кривизна в каждой точке.

В 1855 году 23 февраля великого ученого не стало. Похоронен Карл Фридрих Гаусс в Геттенгене.

Очень многие исследования Гаусса остались неопубликованными и в виде очерков, незаконченных работ, переписки с друзьями входят в его научное наследие. Вплоть до 2ой мировой войны 1939-1945 оно тщательно разрабатывалось Геттенгенским ученым обществом, которое издало 12 томов сочинений Гаусса.

Наиболее интересными в этом наследии являются дневник Гаусса и материалы по неевклидовой геометрии и теории элиптических функций. Дневник содержит 146 записей, относящихся к периоду от 30 марта 1796, когда 19-летний Гаусс отметил открытие построения правильного 17-угольника, по 9июля 1814.

Материалы, относящиеся к неевклидовой геометрии, обнаруживают, что Гаусс пришел к мысли о возможности построения наряду с евклидовой геометрией и геометрии неевклидовой в 1818. Опасение, что эти идеи не будут поняты, было причиной того, что Гаусс их не разрабатывал далее и не опубликовывал. Когда вне всякого отношения к этим попыткам Гаусса, неевклидова геометрия была построена и опубликована российским ученым Н.И. Лобачевским, Гаусс был инициатором избрания его членом - корреспондентом Геттенгенского ученого общества, но своей оценки великого открытия не дал.

.5 Янош Больяй

В семье венгерского математика Фаркаша Больяй родился сын Янош 15 декабря 1802 года в местечке Коловожар, ныне Клуж Напока.

С детских лет сын мечтал продолжить работу отца, который занимался проблемами геометрии, пытался доказать пятый постулат Евклида.

Еще будучи студентом Военно-инженерной академии в Вене, стал заниматься доказательством постулата о параллельных линиях. По окончании академии Янош Больяй продолжает усиленно работать в том же направлении. Обработав свои исследования, издал их в 1832году в виде приложения («Аппендикс») к 1-му тому сочинений своего отца.

Изложение «Аппендикса» отличается крайней сложностью и схематичностью, но по продуманности каждого слова и обозначения, «Аппендикс» принадлежит к числу наиболее совершенных произведений математической литературы.. «Аппендикс» - приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности Х1 аксиомы Евклида.

Один из творцов неевклидовой геометрии Больяй Янош, не получил признания при жизни, что отразилось на его психике. Скончался Янош Больяй 27 января 1860 года в больнице в Марошвангархей (Тиргу-Муран).

2.6 Якоб Штейнер

Якоб Штейнер родился в 1796 году в Швейцарии в семье крестьянина. В молодости был пастухом. Грамоте Якоб научился лишь в возрасте 19 лет в школе своего знаменитого соотечественника, педагога - демократа Иоганна Генриха Песталоцци (1746-1827).

В общей педагогической системе Песталоцци геометрия как учение о формах занимала особо важное место: ей придавалось исключительное значение в деле общего образования и развития мыслительной деятельности учащихся.

Идеи Песталоцци оказали большое влияние на Штейнера и в дальнейшем склонили его к занятиям синтетической проективной геометрией. Впоследствии, будучи уже членом Берлинской Академии наук, Штейнер в предисловии к важнейшей своей работе «Систематическое развитие зависимости геометрических образов друг от друга» (ч.1, 1896) писал: «Предлагаемое произведение пытается вскрыть тот механизм, которым связаны друг с другом разные разнообразнейшие явления в пространстве. Существует весьма ограниченное количество весьма простых основных соотношений, выражающих ту схему, по которой остальная масса предложений развивается последовательно и без всяких затруднений. Посредством надлежащего усвоения этих немногих основных соотношений делаешься хозяином всего предмета: порядок заступает место хаоса, и видишь, как все части, естественно опираются друг на друга, располагаются в прекрасном порядке и соединяются в удачно ограниченные группы. Таким образом, удается овладеть теми элементами, из которых исходит природа, чтобы с возможной экономией и простейшим образом придать фигурам несчетное множество свойств».

В 1833 году Штейнер охотно изучал построения различными неклассическими средствами. Рассматривались, в частности, построения с помощью двухсторонней линейки, (иными словами разрешалось пользоваться двумя краями линейки), или угольником - прямого угла. Угольник можно было расположить так, что бы его края проходили через данные точки, а вершина попадали на данную линию. Каждое из этих замысловатых приспособлений заменяют циркуль и линейку, причем позволяют получить более простые решения. Если на плоскости нарисован круг с отмеченным центром, выполненный циркулем, то любое построение можно осуществить только линейкой. Другими словами, если задачу можно решить с помощью циркуля и линейки, циркуль достаточно применять только раз. Позднее оказалось, что и от окружности достаточно иметь любую самую малую дугу и центр.

В истории математики С. Л. Лемус остался исключительно потому, что в 1840 году он обратился к Я. Штйнеру с просьбой дать геометрическое доказательство одного из признаков равнобедренного треугольника. В последующем эта теорема получила название - Теорема Штейнера-Лемуса.

Если в равнобедренном треугольнике равны две медианы или две высоты, или две биссектрисы, то такой треугольник равнобедренный.

Первые два признака доказываются просто. Однако последний или теорема о том, что треугольник имеющий две равные биссектрисы является равнобедренным доказать довольно сложно - это теорема Штейнера-Лемуса.

Если на плоскости нарисован круг с отмеченным центром. То любое построение выполняемое циркулем и линейкой можно выполнить только линейкой, что было доказано в 1833 году Штейнером.

Показано два построения такого рода из точки А проведены касательные к кругу и перпендикуляр к его диаметру (в этих построениях центр круга не нужен) другими словами, если задачу можно решить с помощью циркуля и линейки.

В отличие от теоремы Ферма-Торричели, Штейнер рассматривал ту же проблему в несколько общем виде: он пытался найти кратчайшую сеть дорог, соединяющую три пункта.

Оказывается, что такая сеть должна состоять из трех сходящихся в одной точке прямолинейных дорог, причем, одна из этих дорог может сжаться в точку (как в задаче Ферма).

В такой формулировке, но уже для произвольного числа пунктов, задача приобретает и чисто практическое значение, например, ее приходится решать при прокладке кабельных сетей.

Если радиус катящейся окружности в. три раза меньше радиуса опорной, то точка описывает дельтоиду или кривую Штейнера (гипоциклоида с модулем m=3).

Уравнение кривой Штейнера в прямоугольной декартовой системе координат:

.

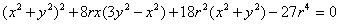Имеются три точки возврата. Длина дуги от точки А: 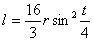. Длина всей кривой 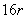. Радиус кривизны 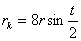. Площадь, ограниченной кривой .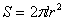

3. Математическая часть

3.1 Обобщенная теорема синусов

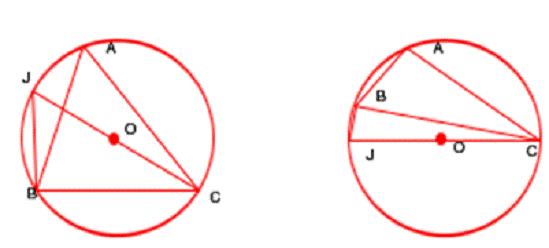
Теорема 1.1: Для треугольника АВС с радиусом описанного круга R выполнены соотношения:

.

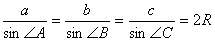3.2 Теорема Чевы

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой.

Теорема 2.1: Если три чевианы AX, BY, CZ (по одной из каждой вершины) треугольника АВС конкурентны, то:

.

Три прямые (или отрезка) конкурентны, если все они проходят через одну точку.

Площади треугольников с равными высотами пропорциональны основаниям треугольников.

Ссылаясь на рисунок, имеем: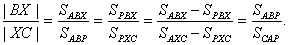

Аналогично:

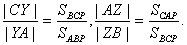
Если их перемножить, то получим:

Теорема, обратная к этой теореме, также верна:

Теорема 2.2: Если три чевианы AX, BY, CZ удовлетворяют нижеприведенное соотношение, то они конкурентны:

.

Чтобы это показать, предположим, что две первые чевианы пересекаются в точке Р, как и прежде, а третья чевиана, проходящая через точку Р, будет CZ`. Тогда по теореме 2.1: .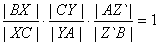

Но по предположению: .

Следовательно: .

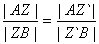Точка Z` совпадает с Z, т.е. отрезки AX, BY и CZ конкурентны.

3.3 Замечательные точки

Центр окружности, описанной вокруг треугольника. О - её обозначение. Она является точкой пересечения трех перпендикуляров, делящих пополам стороны треугольника. R - радиус описанной окружности.

Чевианы, которые связывают вершины треугольника с серединами противоположных сторон, называются медианами. На рисунке отрезки АА`, BB` и CC` - медианы, так что |BA`|=|A`C|, |CB`|=|B`A| и |AC`|=|C`B|. Применяя теорему 2, делаем вывод, что медианы конкурентны. Их общая точка G называется центроидом треугольника. Если бы треугольник был вырезан из однородного материала, то он оставался бы в равновесии, будучи подвешенным в этой точке. Другими словами, центроид есть «центр тяжести» треугольника.

Теорема 3.1: Треугольник делится своими медианами на шесть меньших треугольников равной площади.

Теорема 3.2: Медианы треугольника делят одна другую в отношении 2:1. Другими словами, каждая медиана отсекает треть другой медианы.

Чевианы AD, BE, CF, перпендикулярные прямым BC, CA, AB, соответственно, называются высотами треугольника АВС. Теорема, обратная теореме Чевы, устанавливает их конкурентность. Их общая точка Н называется ортоцентром.

Сами точки D, E, F называются основаниями высот. Соединяя их попарно, мы получим треугольник DEF - ортотреугольник треугольника АВС.

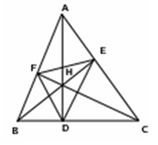
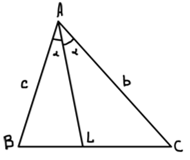
Другое важное семейство чевиан образуют биссектрисы внутренних углов. На рисунке показана одна такая биссектриса AL. Применяя теорему 1 к двум треугольникам ABL и ALC (углы которых в точке L, равные синусы), мы получаем:

.

Так как можем получить аналогичные результаты для биссектрис внутренних углов B и C, то таким образом доказали теорему.

Теорема 3.3: Каждая биссектриса внутреннего угла в треугольнике делит противоположную сторону на отрезки, длины которых пропорциональны длинам прилегающих сторон.

Любая точка на прямой AL равноудалена от прямых CA и AB. Аналогично, любая точка на биссектрисе внутреннего угла В равноудалена от прямых ВА и ВС. Следовательно, точка I, в которой эти две биссектрисы пересекаются, находится на равных расстояниях r от трех сторон:

Теорема 3.4: Биссектрисы трех внутренних углов треугольника конкурентны.

Окружность с центром в точке I и радиуса r касается всех трех сторон и поэтому является вписанной окружностью.

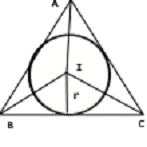
3.4 Вписанная и вневписанная окружности

На рисунке изображена вписанная окружность, касающаяся сторон ВС, СА и АВ в точках X, Y, Z. Так как две касательные к окружности, проведенные из внешней точки, равны, то получаем, что |AY|=|AZ|, |BZ|=|BX|, |CX|=|CY|. На рисунке длины этих отрезков обозначены x, y, z так что y+z=a, z+x=b, x+y=c.

Складывая эти равенства и используя введенное Эйлером обозначение s для полупериметра (от «semiperimetr»), получим 2x+2y+2z= a + b + c=2s, поэтому x + y + z=s, т.е. справедлива.

Теорема 4.1: Для треугольника, изображенного на рисунке, выполняются соотношения:

x=s-a,=s-b,=s-c.

Так как треугольник IBC имеет основание равное а, высоту r, то его площадь равна: 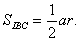 Прибавив к нему аналогичные выражения для  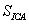и  мы получим: 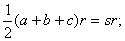 следовательно, теорема доказана.

Теорема 4.2: Для треугольника, изображенного на рисунке, выполняется соотношение:

_ABC = sr.

На рисунке изображен треугольник 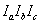, стороны которого являются биссектрисами внешних углов треугольника АВС. Любая точка на биссектрисе угла В равноудалена от прямых АВ и ВС. Аналогично: любая точка на прямой  равноудалена от прямых ВС и СА.

Следовательно, точка I, в которой эти биссектрисы пересекаются, находится на одинаковом расстоянии r от всех трех сторон. Так как I равноудалена от сторон АВ и АС, то она должна принадлежать множеству точек, равноудаленных от этих прямых, то есть она должна лежать на прямой А₁, внутренней биссектрисе угла А.

Теорема 4.3: Внешние биссектрисы любых двух углов треугольника конкурентны с внутренней биссектрисой третьего угла.

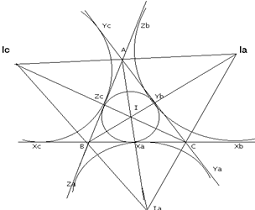
Окружность с центром в точке I радиуса r, касающаяся всех трех сторон треугольника, является одной из трех вневписанных окружностей. Каждая из вневписанных окружностей касается одной из сторон треугольника внутри, а двух других сторон (продолженных) извне.

Обозначив точки касания как на рисунке,  две касательные из одной точки к окружности имеют одинаковые длины, то: ;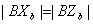

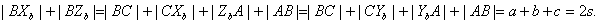
Следовательно, касательная из точки В (или любой другой вершины) к вневписанной окружности, расположенной за противолежащей стороной, имеет длину s. Действительно: .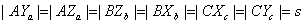

Кроме того, так как: .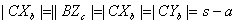

И так далее, то также и:   .

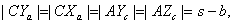
3.5 Теорема Штейнера-Лемуса

Теорема 5.1: Любой треугольник, у которого равны длины биссектрис двух углов (измеряемые от вершины до противоположной стороны), является равнобедренным.

Одно из простейших доказательств этой теоремы опирается на следующие две леммы:

Лемма 5.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно, меньший острый угол с вершинами на окружности.

Лемма 5.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

Доказательство: Пусть АВС - треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки BM и CN делят пополам углы В и С. Мы хотим доказать, что |BM|>|CN|. Возьмем точку М` на отрезке ВМ так, чтобы ÐM`CN=1/2 ÐB. Так как это угол равен углу M`BN, то четыре точки N, B, C, M` на одной окружности.

Поскольку ÐB < 1/2(ÐB+ÐC) < 1/2(ÐA+ÐB+ÐC), то ÐCBN < M`CB <90°.

По лемме 5.1.1 |CN|<|M`B|. Следовательно, |BM|>|BM`|>|CN|.

Доказательство теоремы: Часто бывает, что теорема может быть выражена в форме «противоположной к обратной» - эквивалентной к обратной. Вместо доказательства теоремы 1.51 для нас будет достаточно доказать, что если в треугольнике АВС В ¹ С, то |BM| ¹ |CN|. Но это есть прямое следствие леммы 5.1.2.

3.6 Ортотреугольник

Теорема 6.1: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Одно из простейших доказательств опирается на две следующие леммы:

Лемма 6.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают равные углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно; меньший угол с вершиной на окружности.

Лемма 6.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

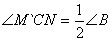Доказательство: Пусть АВС - треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки ВМ и CN делят пополам углы В и С. Мы хотим доказать, что . Возьмём точку М` на отрезке ВМ так, чтобы . Так как этот угол равен углу M`BN, то четыре точки N, B, C, M` лежат на одной окружности. Поскольку  то . По лемме 6.1.1 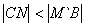. Следовательно,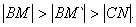

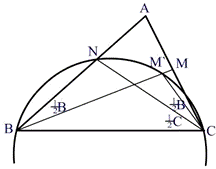
Доказательство теоремы 6.1: Часто случается, что теорема может быть выражена в форме «противоположной к обратной» - эквивалентной первоначальной.

Вместо доказательства самой теоремы 6.1. нам достаточно доказать, что если в треугольнике АВС 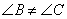, то . Но это есть прямое следствие леммы 6.1.2.

Теорема 6.2: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Мы уже отметили на рисунке, чт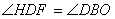о . А так как отрезок HD перпендикулярен отрезку DB, то и отрезок FD должен быть перпендикулярен отрезку OB. Перпендикулярность отрезков DE и OC, а также EF и OA показывается аналогично.

.7 Серединный треугольник и прямая Эйлера

Треугольник, полученный соединением середин сторон данного треугольника, назовем серединным треугольником. На рисунке A`B`C` есть срединный треугольник треугольника АВС. Рассмотрим так же две медианы AA` и BB`, пересекающиеся в точке G, две высоты треугольника ABC, пересекающиеся в точке H, и две высоты треугольника A`B`C` пересекающиеся в точке O.

Во-первых, стороны треугольника A`B`C` параллельны сторонам треугольника АВС, поэтому эти треугольники подобны.

Далее, |C`B`|=1/2|BC|, поэтому отношение длин любых двух соответствующих отрезков (а не только соответствующих сторон) будет равно 1:2. В действительности, отрезки B`C`, C`A`, A`B` разбивают треугольник ABC на четыре конгруэнтных треугольника. Кстати, точка P -середина отрезка B`C` - также является и серединой отрезка AA`.

Далее мы видим, что AC`A`B` - параллелограмм, следовательно, прямая AA` делит пополам отрезок B`C`. Поэтому медианы треугольника A`B`C` лежат на медианах треугольника ABC, а это значит, что оба треугольника имеют один и тот же центроид G.

Высоты треугольника A`B`C`, изображенные на рисунке, являются срединными перпендикулярами сторон AB и BC треугольника ABC. Отсюда делаем вывод, что точка O - ортоцентр треугольника A`B`C` - является время и центром окружности, описанной вокруг треугольника ABC.

Так как точка H - ортоцентр треугольника ABC, а точка O - ортоцентр подобного ему треугольника A`B`C`, то |AH| = 2 |OA`|. По теореме 3.2. |AG| + 2 |GA`|. И так как оба отрезка, AD и OA`, перпендикулярны стороне BC, то они параллельны. Следовательно, ÐHAG = ÐOA`G, Ñ HAG ¥ Ñ OA`G и ÐAGH = Ð A`GO.

Этим показано, что точки O, G, H коллинеарны и |HG| = 2 |GO|, то есть справедлива.

Теорема 7.1: Ортоцентр, центроид и центр описанной окружности произвольного треугольника лежат на одной прямой. Центроид делит расстояние от ортоцентра до центра описанной окружности в отношении 2:1.

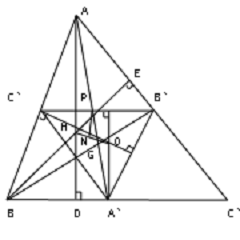
.8 Окружность девяти точек

Рассмотрим рисунок. На нем точки K, L, M - середины отрезков AH, BH, CH, лежащих на высотах. Так как BC - общая сторона двух треугольников ABC и HBC, а точки C`, B` и L, M являются серединами других их сторон соответственно, то отрезки C`B` и LM параллельны прямой BC. Аналогично, так как AH - общая сторона двух треугольников BAH и CAH, то оба отрезка C`L и B`M параллельны прямой AH. Следовательно, B`C`LM - параллелограмм. Так как отрезки BC и AH - перпендикулярны, то этот параллелограмм - прямоугольник. Аналогично, A`B`KL - прямоугольник. Следовательно, A`K, B`L, C`M являются тремя диаметрами окружности, как показано на рисунке.

Так как ÐA`DK - прямой, то эта окружность проходит через точку D. Точно также она проходит через точки E и F.

Теорема 8.1: Основания трех высот произвольного треугольника, середины трех его сторон и середины трех отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности радиуса (Ѕ)R.

Теорема 8.2. Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.

.9 Педальный треугольник

Ортотреугольник и серединный треугольник являются примерами сопутствующих треугольников более общего типа. Пусть Р - любая точка внутри данного треугольника АВС, и пусть из точки Р на стороны АВ, АС, ВС опущены перпендикуляры РА₁, РВ₁, РС₁. Треугольник, А₁В₁С₁ вершинами которого являются основания этих перпендикуляров, называется педальным треугольником треугольника АВС для педальной точки Р.

Теорема 9.1: Если расстояния от педальной точки до вершин треугольника АВС равны x, y, z, то длины сторон педального треугольника равны

В частном случае, когда 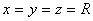, это утверждение общеизвестно.

Теорема 9.2: Третий педальный треугольник подобен исходному.

Доказательство следует из чертежа.

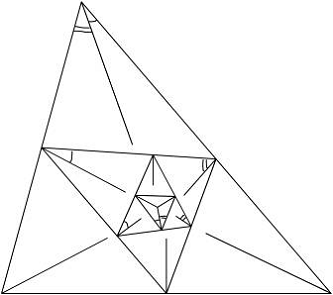
4. Методическая часть

Методика обучения математике впервые выделилась как самостоятельная дисциплина в книге швейцарского ученого И.Г. Песталоцци «Наглядное учение о числе» (1803, русский перевод 1806). В 18 веке - начале 19 века методические вопросы излагались в основном в учебниках. Первым пособием по методике математики в России стала книга Ф.И. Буссе «Руководство к преподаванию арифметики для учителей» (1831). Создателем русской методики арифметики для народной школы считается П.С. Гурьев, который критерием правильности решения методических проблем признавал опыт и практику.

.1 Структура факультативного курса

В данной работе разработана методика изучения геометрии замечательных точек и линий треугольника для учащихся старших нематематических классов.

1.  Данный курс предполагается проводить в 9-10 классах с углубленным изучением математики, так как материал достаточно сложен и для качественного усвоения материала, заложенного в данном курсе, необходимы знания, полученные при изучении курса геометрии 7-9 классов, в частности разделов посвященных геометрии n-угольников и окружности. Сложность данного материала заключается в его глубине. То есть знания учащихся по данной теме поверхностны, они имеют некоторые представления о самых распространенных положениях этой темы, но не знают, что эти, на первый взгляд неважные моменты, несут в себе очень глубокий смысл, интереснейшую историю своего возникновения и огромное практическое применение для решения ряда задач в более простой форме.

2.       Замечательные точки и линии треугольника целесообразно изучать совместно с геометрией Евклида и общими вопросами аксиоматики, в силу того, что данная тема является неотъемлемой частью геометрии на плоскости и одной из составных частей геометрии треугольника. Так как в школьной программе по геометрии рассматривается только малая часть замечательных точек и линий треугольника, то данный курс направлен на расширение знаний учащихся по данной теме, формирование новых пространственных представлений, способов логического мышления и, как результат, новых путей решения уже известных задач.

.        Этот курс рассчитан на третью четверть 9 - 10 класса. Он состоит из 14 занятий, по два часа каждое. Десятое занятие - контрольная работа. Формы изложения материала предполагаются быть динамическими, что бы максимально интересно и адаптировано передать смысл всего курса. Предполагается, что в процессе изучения данного курса учащиеся будут выполнять очень важную роль для самих себя, то есть одной из форм работы учащихся будет их самостоятельная работа с материалом и его предварительный поиск. После этапа поиска и обработки материала, учащимся предлагается выбрать форму сообщения собранного материала. (Хотя, если учесть сегодняшнее положение вещей, то в лучшем случае можно рассчитывать только на несколько докладов или рефератов, а вся остальная работа будет выполняться самим учителем практически в лекционно-семинарской форме). Конечно, данный курс не ограничивается только самостоятельной работой учащихся, так же предполагается наличие лекционных и семинарских занятий по отдельным темам. Иначе говоря, формы деятельности учителя и учащихся рассматривается с двух сторон: со стороны учителя - объяснительная деятельность, а со стороны учащихся - исследовательская.

.        Методы, применяемые учителем на занятиях:

i.   индуктивно-репродуктивный;

ii.       индуктивно-эвристический;. индуктивно-исследовательский;.         дедуктивно-репродуктивный;.       дедуктивно-эвристический;.         дедуктивно-исследовательский;.    обобщенно-репродуктивный;.         обобщенно-эвристический;. обобщенно-исследовательский.

5.  Тематическое планирование:

План занятий

4.2 Планирование занятий

.2.1 Обобщенная теорема синусов

Теорема синусов - это тригонометрическая теорема, которой мы будем часто пользоваться.

К сожалению, в учебниках она обычно появляется в урезанной форме, и в этом виде она не приносит всей той пользы, которую могла бы дать обобщенная теорема. Поэтому докажем эту теорему в желательной для нас форме.

Давайте вспомним формулировку теоремы синусов, о чем в ней говориться?

Учащиеся формулируют известную им теорему синусов (если требуется, то с помощью учителя).

Формулировка: стороны треугольника пропорциональны синусам противолежащих углов:

.

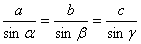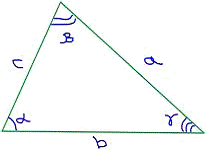
Мы начинаем с треугольника АВС и описываем вокруг его окружность с центром в точке О и радиусом R, как показано на рисунке. Проведем диаметр CJ и хорду BJ.

Что можно сказать про угол CBJ?

Он прямой.

Почему?

Потому что он вписан в окружность и опирается на диаметр.

Да, в обоих случаях ÐCBJ - прямой, так как он вписан в полукруг.

Следовательно, как тогда можно выразить sinÐJ?

Рассмотрим рисунок.

Что вы можете сказать про углы J и A, какие они?

Они равны.

Почему?

Потому что они опираются на одну и ту же дугу окружности.

На рисунке ÐJ=ÐA, поскольку углы J и A опираются на одну и ту же дугу окружности.

А на втором рисунке, что вы можете сказать про углы J и A, какие они?

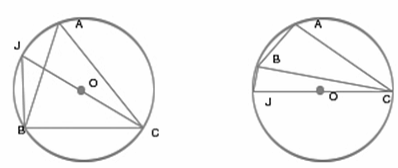
Скажите, вот вы сделали дополнительные построения, какую фигуру вы видите на рисунке.

Треугольник.

Скажите, какие дополнительные построения вы сделали?

Вокруг имеющегося треугольника мы описали окружность, построили диаметр CJ и хорду BJ.

Какая в итоге получилась фигура?

Четырехугольник, вписанный в окружность.

Так что можно сказать про углы J и A данного четырехугольника, какие они?

Противоположные.

А что вам известно про противоположные углы вписанного четырехугольника?

Они являются дополнительными.

Что это значит? Какой можно из этого сделать вывод? Как это можно записать?

ÐJ = 180⁰ - ÐА

Давайте посчитаем синус ÐJ.

ÐJ = sin(180⁰ - ÐА)

А это почему?

Потому что противоположные углы вписанного четырехугольника являются дополнительными.

И что из этого следует? Какой можно сделать вывод? Чему же равен sinÐJ?

ÐJ=sinÐA

Чем вы воспользовались, чтобы получить это равенство?

Мы воспользовались равенством sin q = sin (180⁰ - q).

Скажите, этот вывод относится к какому рассматриваемому случаю, 1 или 2?

К обоим.

Почему к обоим?

Потому что данное равенство sin q = sin (180⁰ - q) справедливо для этих двух случаев.

Теперь на основании сделанных умозаключений давайте сделаем вывод, что sinÐA = a/2R, так как sin q = sin (180⁰ - q), и получим что a/sinÐA=2R.

Аналогично, если проведем подобные рассуждения, получим такие же результаты для остальных углов.

Объединяя результаты, мы можем сформулировать обобщенную теорему синусов следующим образом:

Запишем обобщенную теорему синусов.

Теорема 1.1: Для треугольника АВС с радиусом описанного круга R выполнены соотношения:

/ sinÐA = b / sinÐB = c / sinÐC = 2R.

Решение задач:

Приведенные ниже задачи разделены на 2 блока. Задачи из блока 1 - это задачи на применение теоремы синусов, задачи из блока 2 - задачи на применение обобщенной теоремы синусов.

Задачи блока 1 можно предложить для решения учащимся до введения нового материала.

Блок 1.

. С помощью теоремы синусов решите треугольник, если:

а) ÐА=60⁰, ÐВ=40⁰, с =14

б) ÐА=30⁰, ÐС=75⁰, b = 4,5

в) ÐА=80⁰, a = 16, b = 10

г) ÐB=45⁰, ÐC=70⁰, a = 24,6

д) ÐА=60⁰, a = 10, b = 7

. В треугольнике АВС АС=12, ÐА=75⁰, ÐС=60⁰. Найдите АВ и SABC.

. Найдите стороны треугольника АВС, если ÐА=45⁰, ÐВ=30⁰, а высота AD равна 3 метрам.

4. В параллелограмме . Найдите ÐBDC и ÐDBC.

. Найдите биссектрисы треугольника, если одна из его сторон равна а, а прилежащие к этой стороне углы равны 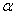 и .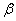

Блок 2.

. Найдите угол А треугольника АВС, если известно, что радиус описанной около этого треугольника окружности равен 6, а сторона ВС равна 3.

. Найдите сторону ВС треугольника АВС, если известно, что угол А равен 70 градусам и радиус описанной окружности равен 4.

. Найдите радиус описанной около треугольника окружности, если одна его сторона равна 4, противоположный ей угол равен 55 градусам.

Домашнее задание:

Учить новый материал.

Задачи: Придумать 3 задачи на применение обобщенной теоремы синусов.

Сделать доклад на тему: «Джованни Чева - его теоремы и тд.»

Так же нужно вспомнить, как связаны площади треугольников с равными высотами и их основания.

Задание «Сделать доклад» дается 2 группам учащихся (каждая группа состоит максимум из 3 человек), предполагается соревновательная форма работы.

.2.2 Теорема Чевы

Этап 1. Организационный момент. Проверка домашнего задания. Повторение изученного материала.

Этап 2. Введение нового материала.

Вы уже хорошо знакомы с понятием треугольник. Давайте вспомним, какие линии в треугольнике вам известны?

Учащиеся перечисляют известные им линии треугольника. Особое внимание учитель обращает на медиану, высоту и биссектрису. Далее учитель просит учащихся проанализировать эти три линии и найти их общие черты и различия. Учащиеся должны увидеть, что каждая из этих линии это отрезок, выходящий из вершины треугольника, соединяющий вершину с точкой на противоположной стороне.

Вводится определение.

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой.

Краткая историческая справка.

Этот термин происходит от имени итальянского математика Джованни Чевы, который в 1678 году опубликовал следующую очень полезную теорему:

Учащиеся записывают

Теорема 2.1: Если три чевианы AX, BY, CZ (по одной из каждой вершины) треугольника АВС конкурентны, то:

.

Когда мы говорим, что три прямые (или отрезка) конкурентны, то имеем в виду, что все они проходят через одну точку, которую обозначим через Р.

Как результат выполненного домашнего задания учащиеся под руководством учителя формулируют факт о том, что площади треугольников с равными высотами пропорциональны основаниям треугольников.

Для доказательства этой теоремы (как только что было уточнено) вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников.

Далее, путем построения простой логической цепочки рассуждений ученики выводят следующие факты:

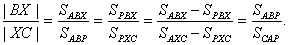
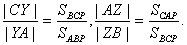
Для доказательства справедливости утверждения теоремы классу предлагается проверить ее утверждение, используя уже полученный результат.

Классу сообщается, что теорема, обратная к этой теореме, также верна.

Ученикам предлагается сформулировать теорему обратную к исходной. Ученики формулируют и записывают:

Теорема 2.2: Если три чевианы AX, BY, CZ удовлетворяют нижеприведенному соотношению, то они конкурентны:

.

Доказательство этой теоремы можно предложить ученикам выполнить дома, в случае, если на дом ученикам дается другое задание, то доказательство можно провести на занятии. В зависимости, от планов учителя, доказывать теорему могут ученики или он сам.

Решение задач:

Следующим этапом предлагаются задачи с нарастающей трудностью:

Доказать, что в треугольнике АВС в одной точке пересекаются:

1.  медианы треугольника

2.       биссектрисы внутренних углов треугольника

.        высоты треугольника

.        прямые, выходящие из вершины треугольника с точками касания вписанной в него окружности

.        прямые, которые выходят из вершины треугольника и делят противоположные стороны пропорционально одним и тем же самым тригонометрическим функциям прилежащих углов

.        прямые, которые соединяют вершины треугольника с точками касания соответственных вневписанных окружностей.

Задачи 1-6 являются вспомогательными задачами, готовящими ученика к самостоятельной деятельности. Схематично задача А вместе с серией вспомогательных задач А₁, А₂, ……Аn изображается так: А₁ - А₂ - А₃ - …-Аn. Самостоятельная деятельность ученика начинается с решения задачи А (тригонометрическая теорема Чевы). Если ученик за определенное время не может решить её, то приступает к решению первой вспомогательной задачи А₁: А-А₁ (теорема Чевы). В случае решения задачи А₁ ученик возвращается к задаче А₁: А - А₁. Если задача А снова не решается, то ученик обращается к задаче А₂. Решив задачу А₂, возвращается к задаче А и т.д.

Возможен случай, когда школьник не сможет решить вспомогательную задачу А₁. Тогда он приступает к решению задачи А₂. От задачи Аn ученик последовательно возвращается к задаче А.

Вернемся к тригонометрической форме теоремы Чевы, которая является основной задачей и предлагается доказать ученику самостоятельно.

Домашнее задание:

Решить задачи 5-6.

По учебнику найти, какие точки называются замечательными. Подготовить доклад о найденных замечательных точках.

Вырезать из плотного картона остроугольный треугольник.

4.2.3 Замечательные точки

Этап 1. Проверка домашнего задания. Повторение.

Этап 2. Введение нового материала (метод - объяснительно-иллюстративный и частично поисковый).

Слова учителя:

Существует много специальных точек и линий, связанных с треугольником. Мы уже упоминали одну такую точку - центр окружности, описанной вокруг треугольника.

Условимся обозначать ее О. Она является точкой пересечения трех перпендикуляров, делящих пополам стороны треугольника. Радиус описанной окружности был уже обозначен буквой R. Эти 2 чертежа заранее приготовлены на доске.

Ученики конспектируют определения, понятия и делают записи и чертежи. Чевианы, которые связывают вершины треугольника с серединами противоположных сторон, называются медианами. На рисунке отрезки АА`, BB` и CC` - медианы, так что |BA`|=|A`C|, |CB`|=|B`A| и |AC`|=|C`B|. Применяя теорему 2, делаем вывод, что медианы конкурентны. Их общая точка G называется центроидом треугольника. Если бы треугольник был вырезан из однородного материала, то он оставался бы в равновесии, будучи подвешенным в этой точке. Другими словами, центроид есть «центр тяжести» треугольника. Для наглядности учащиеся берут сделанные дома заготовки и проверяют последнее утверждение.

Рассмотрим 2 треугольника S_GBA`= S<sub>GA`C.</sub>

Что вы можете сказать про эти 2 треугольника?

Равны они или нет?

Нет.

Почему?

Они не равны, так как у них разные длины боковых сторон, а основания равны.

У них равны только основания?

Нет.

Какие еще элементы у них равны?

У них равны высоты.

Почему?

Их высоты равны, потому что вершины этих треугольников находятся в одной точке, а их основания лежат на основании треугольника АВС.

А что вам известно про треугольники с равными основаниями и высотами?

Их площади равны.

И так, мы обнаружили, что S_GBA`= S<sub>GA`C</sub>, так как эти треугольники имеют одинаковые основания и одну и ту же высоту. На рисунке обозначим эти площади одной и той же буквой х.

А что можно сказать про треугольники BGC`, AGC`, CGB`, AGB`?

Площади треугольников BGC`, AGC` и CGB`, AGB` равны, так как у этих треугольников равны высоты и основания.

То есть, делаем вывод, что S_GCB` = S<sub>GB`A</sub> и S_GAC` = S<sub>GC`B</sub>.

Обозначим эти площади через y и z, и отметим это на чертеже.

А что вы можете сказать про треугольники CAC` и CC`B?

Их площади S_{CAC`</sub> = S<sub>CC`B} так же равны между собой.

Чему равна площадь треугольника S_CAC`?

_CAC` = 2y + z.

Чему равна площадь треугольника S_CC`B?

_CC`B = 2x + z.

Но так как S_{CAC`</sub> = S<sub>CC`B,} то 2y + z = 2x + z, сократим слева и справа равные элементы, получим 2y = 2x, а следовательно x = y.

А что вы можете сказать про треугольники S_{ABA`</sub> и S<sub>AA`C}?

Какой можно сделать вывод из 2 последних рассуждений?

= y = z.

Прекрасно вы показали, что x = y = z.

Теорема 3.1: Треугольник делится своими медианами на шесть меньших треугольников равной площади.

Далее ученикам сообщается уже известный факт.

Продолжая рассмотрение рисунка, отмечаем, что S_GAB = 2S<sub>GBA`</sub>. Так как эти треугольники имеют общую высоту, то отсюда следует, что |AG|=2|GA`|. Аналогично, |BG|=2|GB`| и |CG|=2|GC`|.

Теорема 3.2: Медианы треугольника делят одна другую в отношении 2:1.

Другими словами, каждая медиана отсекает треть другой.

Чевианы AD, BE, CF, перпендикулярные прямым BC, CA, AB, соответственно, называются высотами треугольника АВС. Теорема, обратная теореме Чевы, устанавливает их конкурентность. Их общая точка Н называется ортоцентром.

Ученики записывают определение

Сами точки D, E, F называются основаниями высот. Соединяя их попарно, мы получим треугольник DEF - ортотреугольник треугольника АВС.

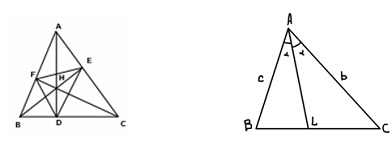
Следующий блок информации дается учителем, ученики записывают теоремы, определения и делают чертежи.

Другое важное семейство чевиан образуют биссектрисы внутренних углов. На рисунке показана одна такая биссектриса AL.

В данный момент можно попросить учеников сформулировать теорему 1.1 и спросить - почему ее можно применить в данном случае?

Применяя теорему 1.1 к двум треугольникам ABL и ALC (углы которых в точке L, равные синусы), мы получаем:

.

Так как можем получить аналогичные результаты для биссектрис внутренних углов B и C, то таким образом доказали.

Теорема 3.3: Каждая биссектриса внутреннего угла в треугольнике делит противоположную сторону на отрезки, длины которых пропорциональны длинам прилегающих сторон.

Следующие три момента нужно отдельно выделить, после их предварительного воспроизведения учащимися.

Любая точка на прямой AL равноудалена от прямых CA и AB. Аналогично, любая точка на биссектрисе внутреннего угла В равноудалена от прямых ВА и ВС. Следовательно, точка I, в которой эти две биссектрисы пересекаются, находится на равных расстояниях r от трех сторон:

Из последнего вывода делается вывод (он хорошо известен учащимся из курса планиметрии и проверен на практике, заодно можно вспомнить понятие конкурентности).

Теорема 3.4: Биссектрисы трех внутренних углов треугольника конкурентны.

Окружность с центром в точке I и радиуса r касается всех трех сторон и поэтому является вписанной окружностью.

Решение задач:

1. В остроугольном треугольнике АВС высоты АА₁ и ВВ₁ пересекаются в точке О. Найдите угол ОВА, если угол ОСА = 38°.

. В треугольнике АВС биссектрисы ВВ₁ и СС₁ пересекаются в точке О. Найдите отношение площадей треугольника ВОА и АОС, если АВ = 10, АС = 15.

. В остроугольном треугольнике АВС серединные перпендикуляры сторон АВ и АС пересекаются в точке О и ОА = 8. Найдите площадь треугольника ОВС, если угол ОВС = 60°.

. В остроугольном треугольнике АВС высоты ВВ1 и СС1 пересекаются в точке О. Найдите угол ОАВ, если ВС = 2ВС₁.

. В треугольнике АВС медианы ВВ₁ и СС₁ пересекаются в точке О и взаимно перпендикулярны. Найдите ОА, если ВВ₁ = 36, СС₁ = 15.

Домашнее задание:

Решить задачи:

. В остроугольном треугольнике АВС серединные перпендикуляры сторон ВС и АС пересекаются в точке О. Найдите строну Ос, если АВ = 10, а угол ВОА = 120°.

. Во внутренней области треугольника АВС взята точка О, равноудаленная от его сторон. Найдите угол АОС, если угол АВО = 39°.

. Найдите углы треугольника, если известно, что одна из биссектрис этого треугольника разбивают его на два равнобедренных треугольника.

Доделать задачи, которые не сделаны на уроке.

Подготовить доклад на тему «Вневписанная окружность»

4.2.4 Вписанная и вневписанная окружности

Этап 1. Проверка домашнего задания.

Этап 2. Введение нового материала.

Перед введением нового материала выслушивается доклад сделанный учениками по теме урока. В это время остальной класс делает конспект делаемого доклада. После завершения того, как доклад будет заслушан подводятся итоги по полученной информации и делаются выводы самими учениками под руководством учителя. А после этого уже сам учитель дополняет и корректирует материал текущего урока.

На рисунке изображена вписанная окружность, касающаяся сторон ВС, СА и АВ в точках X, Y, Z. Обозначим через x длины отрезков AY и AZ, через y длины отрезков BZ и BX, через z длины отрезков CX и CY.

Почему AY = AZ, BZ = BX, CX = CY?

Они равны. Так как две касательные к окружности, проведенные из внешней точки, равны, и мы получаем, что |AY|=|AZ|, |BZ|=|BX|, |CX|=|CY|.

На рисунке длины этих отрезков обозначены x, y, z так что y + z=a, z + x=b, x + y=c.

Сложим эти равенства. Что получим?

Получим 2x + 2y + 2z = a + b + c = Р, то есть периметр.

Для нужного нам обозначения используем введенное Эйлером обозначение s для полупериметра (от «semiperimetr»), получим 2x + 2y + 2z = a + b + c = 2s, поэтому х + y + z=s, т.е. справедлива

Теорема 4.1: Для треугольника, изображенного на рисунке, выполняются соотношения:

x=s-a,=s-b,=s-c.

Здесь x, y, z - длины равных отрезков касательных проведенных из точек А, В и С (А, В,С - вершины треугольника АВС) к окружности с центром в точке I и радиусом r, s - полупериметр треугольника АВС.

Дальнейшие рассуждения направлены на рассмотрение и доказательство следующей теоремы.

Рассмотрим треугольник IBC.

Чему равна площадь треугольника IBC с основанием а и высотой r?

Так как треугольник IBC имеет основание а и высоту r, то его площадь равна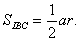

А чему равны площади треугольников ICA и IAB?

Какое равенство будет получено, если сложить все три выражения для площадей треугольников IBC, ICA, IAB?

Мы получим: .

Тем самым вы доказали теорему.

Теорема 4.2: Для треугольника, изображенного на рисунке, выполняется соотношение:

_ABC = sr.

Площадь треугольника АВС равна произведению полупериметра этого треугольника на радиус вписанной в него окружности.

Учащиеся под руководством учителя выполняют построения, фиксируют алгоритм построения и записывают следующие факты.

Построим произвольный остроугольный треугольник АВС. Продлим каждую из его сторон за вершины треугольника. Введем обозначения для продолжений сторон проведем дополнительные построения: а) построим биссектрисы внутренних треугольника и продлим их за стороны треугольника, б) построим биссектрисы внешних углов треугольника АВС, полученных продлением сторон треугольника за его вершины, в) точки пересечения биссектрис внутренних углов треугольника с соответствующими биссектрисами внешних углов обозначим как на рисунке, г) соединим полученные точки пересечения.

Мы получили изображение треугольника 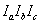, стороны которого являются биссектрисами внешних углов треугольника АВС. Любая точка на биссектрисе угла В равноудалена от прямых АВ и ВС. Аналогично, любая точка на прямой  равноудалена от прямых ВС и СА. Следовательно точка I_a, в которой эти биссектрисы пересекаются, находится на одинаковом расстоянии r_a от всех трех сторон. Так как I_a равноудалена от сторон АВ и АС, то она должна принадлежать множеству точек, равноудаленных от этих прямых, то есть она должна лежать на прямой А1, внутренней биссектрисе угла А.

Теорема 4.3: Внешние биссектрисы любых двух углов треугольника конкурентны с внутренней биссектрисой третьего угла.

Для закрепления понимания понятия «конкурентности» у учащихся рекомендуется спросить расшифровку этого понятия.

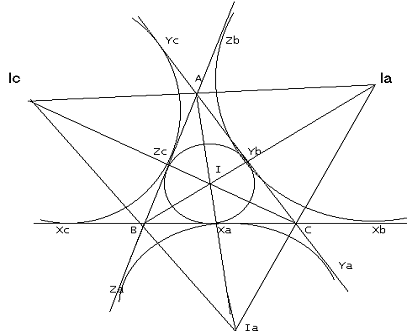
Окружность с центром в точке I_a радиуса r_a, касающаяся всех трех сторон треугольника, является одной из трех вневписанных окружностей. Каждая из вневписанных окружностей касается одной из сторон треугольника внутри, а двух других сторон (продолженных) извне.

Обозначив точки касания как на рисунке, т.к. две касательные из одной точки к окружности имеют одинаковые длины, то: ;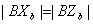

Следовательно, касательная из точки В (или любой другой вершины) к вневписанной окружности, расположенной за противолежащей стороной, имеет длину s. Действительно: .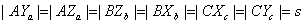

Кроме того, так как: .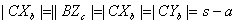

И так далее, то также и:   .

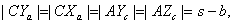
Решение задач:

1. Пусть М - точка на стороне АС треугольника АВС. Обозначим через R₁ и R₂ радиусы окружностей, описанных около треугольников АВМ и СВМ соответственно. Докажите, что R₁ относится к R₂, как АВ к ВС.

. Даны окружность и точка А вне ее. АВ и АС - касательные к окружности (В и С - точки касания). Докажите, что середины двух дуг, на которые разделена данная окружность точками В и С, являются центром вписанной и вневписанной окружности треугольника АВС.

. Пусть J - центр окружности, вписанной в треугольник АВС, Ja - центр вневписанной окружности (касающейся сторон ВС и продолжений сторон АВ и АС). Докажите, что точки В, С, J, Ja - расположены на одной прямой.

. Пусть J - центр окружности, вписанной в треугольник АВС. Докажите, что прямая AJ проходит через центр окружности, проходящей через точки В, С и J.

. Пусть Ja - центр вневписанной окружности. Найдите угол AJaB, если угол АВС равен b.

. Три окружности радиусам 1, 2, 3 попарно касаются друг друга внешним образом. Найдите радиус окружности, проходящей через точки касания этих окружностей.

Домашнее задание:

Решить задачи 5-6 и доделать задачи из классной работы.

Сделать доклад о Штейнере и Лемусе.

4.2.5 Теорема Штейнера-Лемуса

Этап 1. Проверка домашнего задания.

Этап 2. Повторение ранее изученного материала.

Учащиеся формулируют определения и теоремы, изученные на прошлых уроках.

Этап 3. Введение нового материала (объяснительно иллюстративный способ).

Учащиеся рассказывают подготовленную историческую справку о Штейнере и о Лемусе.

Ученики записывают формулировку теоремы.

Теорема 5.1: Любой треугольник, у которого равны длины биссектрис двух углов (измеряемые от вершины до противоположной стороны), является равнобедренным.

Одно из простейших доказательств этой теоремы опирается на следующие две леммы:

Лемма 5.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух не равных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно, меньший острый угол с вершинами на окружности.

Учащиеся дома должны записать это доказательство в символьной форме

Лемма 5.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

Доказательство: Пусть АВС - треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки BM и CN делят пополам углы В и С. Мы хотим доказать, что |BM|>|CN|. Возьмем точку М` на отрезке ВМ так, чтобы ÐM`CN=1/2 ÐB. Так как это угол равен углу M`BN, то четыре точки N, B, C, M` на одной окружности. Поскольку ÐB < 1/2(ÐB+ÐC) < 1/2(ÐA+ÐB+ÐC), то ÐCBN < M`CB <90°.

По лемме 5.1.1 |CN|<|M`B|. Следовательно, |BM|>|BM`|>|CN|.

Доказательство теоремы: Часто бывает, что теорема может быть выражена в форме «противоположной к обратной» - эквивалентной к обратной. Вместо доказательства теоремы 5.1 для нас будет достаточно доказать, что если в треугольнике АВС: В ¹ С, то |BM| ¹ |CN|. Но это есть прямое следствие леммы 5.1.2.

В силу того, что теоретическая часть этого занятия носит исключительно ознакомительный характер, то на этапе решения задач предполагается решение задач подготавливающих к введению нового материала следующего занятия и повторение ранее изученного материала.

Решение задач:

1. Докажите, что прямые, содержащие высоты треугольника, пересекаются в одной точке, которая называется ортоцентром треугольника.

2. В остроугольном треугольнике АВС проведены высоты 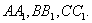 Докажите, что треугольники  подобны треугольнику АВС.

. Треугольник , вершинами которого являются основания высот 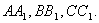 треугольника АВС. Найдите углы ортоцентрического треугольника остроугольного треугольника АВС, если углы треугольника АВС равны А, В, С.

. Докажите, что высоты остроугольного треугольника являются биссектрисами его ортоцентрического треугольника.

. Найдите углы ортоцентрического треугольника тупоугольного треугольника, если углы треугольника АВС равны А, В, С (угол С тупой).

. Найдите углы всех треугольников, которые подобны своим ортоцентрическим треугольникам.

. Дан остроугольный треугольник АВС. Докажите, что точки, симметричные ортоцентру треугольника АВС относительно его сторон, лежат на окружности, описанной около этого треугольника.

. Продолжения высот остроугольного треугольника АВС пересекают описанную окружность в точках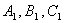. Докажите, что а) треугольник  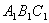подобен ортоцентрическому треугольнику треугольника АВС и коэффициент подобия равен 2, б) высоты треугольника АВС являются биссектрисами треугольника .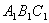

. Пусть Н - ортоцентр треугольника АВС. Докажите, что радиусы окружностей, описанных около треугольников АВН, ВСН и САН равны между собой и равны радиусу окружности, описанной около треугольника АВС.

Домашнее задание:

Решить задачи 6-9 и дорешать задачи из классной работы.

Подготовить доклад на тему «Ортотреугольник»

4.2.6 Ортотреугольник

Этап 1. Проверка домашнего задания и разбор не решенных задач.

Этап 2. Повторение ранее изученного материала.

Этап 3. Введение нового материала (объяснительно иллюстративный метод).

Прежде всего, учащиеся формулируют определение ортоцентра треугольника и ортоцентрического треугольника. Далее учащиеся записывают формулировку теоремы.

Теорема 6.1: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Одно из простейших доказательств опирается на две следующие леммы:

Две следующие леммы, используемые для доказательства теоремы 6.1 уже хорошо известны учащимся из курса планиметрии.

Лемма 6.1.1: Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.

Доказательство: Две равные хорды стягивают равные углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно; меньший угол с вершиной на окружности.

Лемма 6.1.2: В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой.

Доказательство:

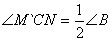Пусть АВС - треугольник, в котором угол В меньше угла С, как на рисунке; пусть отрезки ВМ и CN делят пополам углы В и С. Мы хотим доказать, что . Возьмём точку М` на отрезке ВМ так, чтобы . Так как этот угол равен углу M`BN, то четыре точки N, B, C, M` лежат на одной окружности. Поскольку  то . По лемме 1.6.1 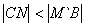. Следовательно,

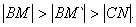
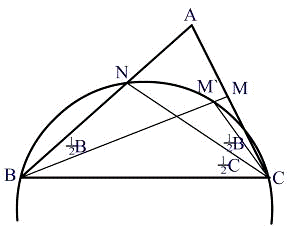
Доказательство теоремы 6.1:

При доказательстве этой теоремы важно обратить внимание учащихся на построении структуры логических рассуждений, которые делают доказательство данной теоремы более коротким.

Часто случается, что теорема может быть выражена в форме «противоположной к обратной» - эквивалентной первоначальной.

Например, вместо того, чтобы сказать: «Все люди смертны», мы можем также сказать «Бессмертные не есть люди».

Вместо доказательства самой теоремы 6.1. нам достаточно доказать, что если в треугольнике АВС: 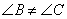, то . Но это есть прямое следствие леммы 6.1.2.

Теорема 6.2: Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Учащимся предлагается самостоятельно показать доказательство этой теоремы дома.

Мы уже отметили на рисунке, что . А так как отрезок HD перпендикулярен отрезку DB, то и отрезок FD должен быть перпендикулярен отрезку OB. Перпендикулярность отрезков DE и OC, а также EF и OA показывается аналогично.

Решение задач:

Задачи 1-7 из задачника.

Домашнее задание:

Решить задачи 8-11 из задачника.

4.2.7 Серединный треугольник и прямая Эйлера

Этап 1. Проверка домашнего задания. Особое внимание уделяется проверке доказательства теоремы 6.2.

Этап 2. Повторение ранее изученного материала. Проводится сначала письменный опрос учащихся по материалу предыдущих уроков. После окончания работы ученики сдают листочки со своими ответами, и начинается устный опрос по тем же самым вопросам, что дает возможность учащимся проверить их работы.

Этап 3. Введение нового материала.

Учащиеся записывают определение:

Треугольник, полученный соединением середин сторон данного треугольника, назовем серединным треугольником.

На доске по заготовленному за ранее чертежу ведется объяснение.

На рисунке A`B`C` есть срединный треугольник треугольника АВС. Рассмотрим так же две медианы AA` и BB`, пересекающиеся в точке G, две высоты треугольника ABC, пересекающиеся в точке H, и две высоты треугольника A`B`C` пересекающиеся в точке O.

Что вы можете сказать про треугольники АВС и А`B`C`? Какие они?

Стороны треугольника A`B`C` параллельны сторонам треугольника АВС, поэтому эти треугольники подобны.

Далее, |C`B`|=1/2|BC|, поэтому отношение длин любых двух соответствующих отрезков (а не только соответствующих сторон) будет равно1:2. В действительности, отрезки B`C`, C`A`, A`B` разбивают треугольник ABC на четыре конгруэнтных треугольника. Кстати, точка P -середина отрезка B`C` - также является и серединой отрезка AA`

Далее мы видим, что AC`A`B` - параллелограмм, следовательно, прямая AA` делит пополам отрезок B`C`. Поэтому медианы треугольника A`B`C` лежат на медианах треугольника ABC, а это значит, что оба треугольника имеют один и тот же центроид G.

Высоты треугольника A`B`C`, изображенные на рисунке, являются срединными перпендикулярами сторон AB и BC треугольника ABC. Отсюда делаем вывод, что точка O - ортоцентр треугольника A`B`C` - является время и центром окружности, описанной вокруг треугольника ABC.

Так как точка H - ортоцентр треугольника ABC, а точка O - ортоцентр подобного ему треугольника A`B`C`, то |AH| = 2 |OA`|. По теореме 3.2 |AG| + 2 |GA`|. И так как оба отрезка, AD и OA`, перпендикулярны стороне BC, то они параллельны. Следовательно,

ÐHAG = ÐOA`G, Ñ HAG ¥ Ñ OA`G и ÐAGH = Ð A`GO.

Этим показано, что точки O, G, H коллинеарны и |HG| = 2 |GO|, то есть справедлива

Теорема 7.1: Ортоцентр, центроид и центр описанной окружности произвольного треугольника лежат на одной прямой. Центроид делит расстояние от ортоцентра до центра описанной окружности в отношении 2:1.

Решение задач:

№55 из задачника.

Домашнее задание:

Учить все определения и теоремы.

4.2.8 Окружность девяти точек

Рассмотрим рисунок. На нем точки K, L, M - середины отрезков AH, BH, CH, лежащих на высотах.

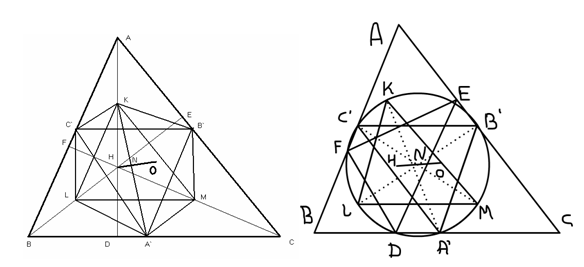
Так как BC - общая сторона двух треугольников ABC и HBC, а точки C`, B` и L, M являются серединами других их сторон соответственно, то отрезки C`B` и LM параллельны прямой BC. Аналогично, так как AH - общая сторона двух треугольников BAH и CAH, то оба отрезка C`L и B`M параллельны прямой AH. Следовательно, B`C`LM - параллелограмм. Так как отрезки BC и AH - перпендикулярны, то этот параллелограмм - прямоугольник. Аналогично, A`B`KL - прямоугольник. Следовательно, A`K, B`L, C`M являются тремя диаметрами окружности, как показано на рисунке.

Так как ÐA`DK - прямой, то эта окружность проходит через точку D. Точно также она проходит через точки E и F.

В итоге получаем:

Теорема 8.1. Основания трех высот произвольного треугольника, середины трех его сторон и середины трех отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности радиуса (Ѕ)R.

Теорема 8.2. Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.

Решение задач:

Задача № 54, 56-58 из задачника.

Домашнее задание:

Решить задачи №№59-63.

4.2.9 Педальный треугольник

Ортотреугольник и серединный треугольник являются примерами сопутствующих треугольников более общего типа. Пусть Р - любая точка внутри данного треугольника АВС, и пусть из точки Р на стороны АВ, АС, ВС опущены перпендикуляры РA₁, РB₁, РС₁. Треугольник, А₁В₁С₁ вершинами которого являются основания этих перпендикуляров, называется педальным треугольником треугольника АВС для педальной точки Р.

Теорема 9.1: Если расстояния от педальной точки до вершин треугольника АВС равны x, y, z, то длины сторон педального треугольника равны

В частном случае, когда 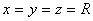, это утверждение общеизвестно.

Теорема 9.2: Третий педальный треугольник подобен исходному.

Доказательство следует из чертежа.

Решение задач:

Задачи №36-41.

Домашнее задание:

Подготовиться к контрольной работе. Решить задачи №№ 16-25.

4.2.10 Контрольная работа

Данная контрольная работа состоит из 2 вариантов, каждый вариант содержит 4 задачи.

. Вариант

1.  Докажите, что биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной в этот треугольник окружности.

2.  Докажите, что серединные перпендикуляры сторон треугольника пересекаются в одной точке, совпадающей с центром описанной около этого треугольника окружности.

3.       Докажите, что биссектрисы внутреннего и внешнего углов при вершине С треугольника АВС равны тогда и только тогда, когда .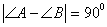

.        Дан треугольник АВС. Известно, что биссектриса СС₁ внутреннего угла при вершине С равна биссектрисе СС₂ внешнего угла при той же вершине. Может ли прямая СВ быть биссектрисой угла С₁СС₂?

2. Вариант

1.  Докажите, что медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершин треугольника.

2.  Докажите, что точка М, лежащая внутри треугольника АВС является точкой пересечения его медиан тогда и только тогда, когда треугольники АВМ, ВСМ, САМ равновелики.

3.  Может ли центр описанной окружности треугольника АВС лежать на его: а) стороне, б) высоте, в) биссектрисе, г)средней линии?

4. Докажите, что в прямоугольном треугольнике медиана и высота, проведенные из вершины прямого угла, образуют равные углы с катетами.

Все предложенные задачи взяты из части «Задачи для самостоятельного решения» приложения (В1: №1 - 1, №2 - 2, №3 - 8, №4 - 9, В2: №1 -15, №2 - 16, №3 -20, №4 - 21).

5. Описание эксперимента

Экспериментальная часть данной дипломной работы проводилась на базе ГОУ СОШ ЦО №1406, в десятых классах переводчиков и педагогов. В содержание апробации факультативного курса входило 12 занятий: по 9 основным темам, 2 занятия увеличенных по времени (1 занятие - 3 урока) специально отведенные для дополнительного решения задач и одно занятие - контрольная работа для проверки качества усвоения материала. Из каждого класса на факультативные занятия приходили практически все учащиеся. Надо отметить, что среди посещавших занятия учащихся был замечен огромный интерес к изучаемому материалу. Интерес учащихся выражался в их заинтересованности. Новизна изучаемого материала узнаваемого ими на основе уже имеющихся у них знаний и их новая интерпретация особенно нравилась ученикам. Учащиеся с огромным интересом делали чертежи предлагаемых теоретических фактов и решаемых на занятиях задач, и искали их модификации, а также выполняли задания направленные на их самостоятельную деятельность в подготовке исторических справок по изучаемому материалу. Еще один важный результат - учащиеся вне факультативных занятий, на уроках геометрии, искали пути применения новых знаний, и им это иногда очень успешно удавалось. Так же особый интерес у учащихся вызвало электронное сопровождение курса, специально для него разработанное. Электронное сопровождение курса особенно понравилось учащимся, так как в нем можно было самостоятельно создавать чертежи к содержанию занятий и произвольно их модифицировать, тем самым рассматривать различные случаи рассмотрения изучаемых фактов.

По результатам проведенного эксперимента были внесены изменения в содержание факультативного курса: общее количество занятий увеличилось, за счет добавления 4 занятий, отводимых для решения большего объема задач.

Заключение

В данной работе показано, что основные новообразования подростка самостоятельность, самосознание, самовоспитание в процессе обучения развивают познавательный интерес. Главное психологическое образование - это открытие своего внутреннего мира. У подростка учебные интересы определяют выбор профессии.

Факультативные занятия - одна из форм дифференцированного обучения, которая позволяет осуществлять личностно - ориентированный подход к обучению в основной школе.

Факультативный курс по геометрии формирует у учащихся устойчивый интерес к предмету, развивает творческие способности, формирует мировоззрение, показывает содержательную связь с историей развития науки.

Использование на занятиях эвристического, проблемного, частично - поискового метода включают учащихся в различные формы самостоятельной деятельности. Совмещение математической строгости изложения материала с математической красотой и занимательностью способствуют формированию культуры мышления учеников.

Анализ психолого-педагогической литературы дал возможность выделить требования к построению факультативных занятий. Соотношение факультативных занятий с основным курсом математики, соответствие содержания учебно-методическому обеспечению, воспитательным и развивающим задачам обучения, преемственность факультативных занятий к другим формам внеклассной работы по математике в сторону приложения математики - основные требования.

В результате исследования разработан факультативный курс - «Замечательные точки и линии треугольника», состоящий из 16 занятий и методика его проведения.

Изучение замечательных точек и линий треугольника подразумевает, что школьники в процессе занятий повторяют основные факты геометрии. Воспроизведение зрительных образов оказывается не пассивным отпечатком зрительного восприятия, а итогом анализа, синтеза, абстракции и обобщения.

Решение задач позволяет развивать логическое мышление, геометрическую интуицию, формировать математический склад ума.

Проведенный эксперимент подтвердил сказанное выше.

Все поставленные в ведении задачи выполнены.