Обработка лесоводственной информации
Содержание
Введение
1 Обработка лесоводственной информации
1.1 Исходные данные и их характеристика
1.2 Группировка результатов наблюдения
1.3 Графическое изображение рядов распределения
1.4 Виды средних
1.5 Показатели вариации признаков
1.6 Ошибки и надёжность статистических показателей
2 Анализ лесоводственной информации
Заключение
Библиографический список
Введение
В лесохозяйственных и
биологических исследованиях постоянно имеют дело с оценкой массовых явлений.
Эти явления нередко представляются сложными, с первого взгляда беспорядочными,
вследствие разнообразия (варьирования) в размерах, весе в поведении отдельных
единиц или индивидуумов составляющих массовые явления.
Чтобы разобраться в
сущности таких явлений и дать им оценку, необходимо располагать соответствующим
методом и теорией.
Вариационная статистика
излагает методы изучения массовых явлений и построения для них количественных
оценок. Отдельные единицы или индивидуумы, подлежащие наблюдению (измерению,
взвешиванию или подсчёту), называют вариантами. Коллективы отдельных единиц,
характеризующихся определённой общностью, называют статистическими
совокупностями.
Различают совокупности
выборочные и генеральные. Генеральной совокупностью является весь коллектив
единиц, подлежащих изучению. Число единиц в таком коллективе бесконечно
большое. Выборочной совокупностью или выборкой называют часть единиц, выбранных
для наблюдения.
При статистических
наблюдениях в биологии практически всегда имеют дело с выборками и по
результатам их судят о совокупности.
В настоящей работе
приводится обработка и анализ определённой лесоводственной информации.
1 Обработка
лесоводственной информации
1.1 Исходные данные и их
характеристика
Исходные данные для
обработки представляют собой информацию о линейных размерах деревьев (диаметре
ствола на высоте 1,3 метра, диаметра кроны) и их пространственных показателях
(площади роста). Отбор данных был производён в количестве 50 вариант
(деревьев). Изначальным номером отбора, был номер варианты данный моим
глубокоуважаемым преподавателем, да и просто хорошим человек А.Г. Неповинных.
На рисунке 1 представлены
показатели, характеризующие отдельное дерево.
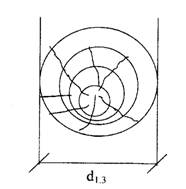
а) диаметр ствола на
высоте 1,3 метра (d1,3)
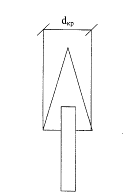
б) диаметр кроны дерева (dкр)
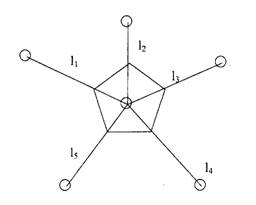
в) площадь роста дереве (S)
Рисунок 1 –Показатели,
характеризующие отдельное дерево
В таблице 1 представлены
морфолого-пространственные показатели смешанных пихтовых насаждений
Большемуртинского лесхоза.
Таблица 1 –
Морфолого-пространственные показатели деревьев смешанных пихтовых насаждений
Большемуртинского лесхоза
|
№ п.п.
|
№ дерева
|
Порода
|
Диаметр ствола, см
|
Диаметр кроны, м
|
Площадь роста, м2
|
|
1
|
5
|
Ос
|
21,3
|
1,0
|
15,75
|
|
2
|
6
|
П
|
7,5
|
2,9
|
57,78
|
|
3
|
7
|
Б
|
19,9
|
3,9
|
106,83
|
|
4
|
8
|
Л
|
14,7
|
1,9
|
97,83
|
|
5
|
9
|
Е
|
16,8
|
3,7
|
26,19
|
|
6
|
20
|
С
|
51,3
|
7,4
|
16,11
|
|
7
|
21
|
Е
|
41,3
|
4,2
|
47,79
|
|
8
|
22
|
П
|
9,0
|
3,0
|
21,98
|
|
9
|
23
|
Л
|
13,6
|
3,8
|
5,22
|
|
10
|
24
|
Е
|
22,0
|
3,0
|
3,51
|
|
11
|
35
|
Е
|
22,1
|
3,6
|
3,42
|
|
12
|
36
|
Б
|
22,1
|
3,2
|
15,3
|
|
13
|
37
|
П
|
10,3
|
3,6
|
22,95
|
|
14
|
38
|
П
|
13,2
|
4,0
|
14,94
|
|
15
|
39
|
П
|
9,2
|
2,9
|
3,15
|
|
16
|
50
|
П
|
12,3
|
4,3
|
23,22
|
|
17
|
51
|
Ос
|
22,7
|
3,0
|
60,66
|
|
18
|
52
|
П
|
9,4
|
3,3
|
17,01
|
|
19
|
53
|
П
|
22,4
|
2,2
|
23,85
|
|
20
|
54
|
Е
|
21,8
|
3,1
|
17,1
|
|
21
|
65
|
П
|
6,3
|
3,4
|
1,17
|
|
22
|
66
|
П
|
12,2
|
4,1
|
5,76
|
|
23
|
67
|
Б
|
18,0
|
3,2
|
0,09
|
|
24
|
68
|
С
|
15,1
|
2,9
|
22,95
|
|
25
|
69
|
П
|
13,5
|
4,8
|
4,14
|
|
26
|
80
|
П
|
12,8
|
2,9
|
21,33
|
|
27
|
81
|
П
|
9,6
|
2,8
|
2,52
|
|
28
|
82
|
П
|
10,6
|
3,5
|
0,09
|
|
29
|
83
|
П
|
8,7
|
2,8
|
0,36
|
|
30
|
84
|
Б
|
14,9
|
2,2
|
16,38
|
|
31
|
95
|
П
|
12,5
|
3,1
|
0,09
|
|
32
|
96
|
Л
|
7,4
|
1,8
|
0,36
|
|
33
|
97
|
П
|
12,4
|
3,5
|
12,78
|
|
34
|
98
|
Б
|
8,9
|
3,5
|
25,56
|
|
35
|
99
|
Л
|
16,6
|
3,4
|
0,09
|
|
36
|
110
|
Ос
|
26,2
|
4,0
|
17,1
|
|
37
|
111
|
Ос
|
23,9
|
4,8
|
0,36
|
|
38
|
112
|
С
|
15,6
|
2,0
|
0,09
|
|
39
|
113
|
Ос
|
27,2
|
5,3
|
5,04
|
|
40
|
114
|
Е
|
10,5
|
2,3
|
0,09
|
|
41
|
125
|
П
|
8,5
|
2,6
|
0,09
|
|
42
|
126
|
Е
|
7,7
|
2,3
|
18,9
|
|
43
|
127
|
Б
|
26,5
|
4,6
|
3,42
|
|
44
|
128
|
Ос
|
29,0
|
5,2
|
0,18
|
|
45
|
129
|
П
|
8,8
|
3,7
|
0,09
|
|
46
|
140
|
Л
|
42,3
|
7,0
|
0,36
|
|
47
|
141
|
П
|
9,3
|
3,7
|
59,04
|
|
48
|
142
|
Е
|
32,6
|
3,7
|
4,59
|
|
49
|
143
|
Е
|
15,8
|
2,3
|
0,81
|
|
50
|
144
|
Ос
|
24,4
|
4,7
|
0,9
|
1.2 Группировка
результатов наблюдения
Для того что, чтобы
придать опытным материалам определённую наглядность и извлечь из них
необходимую статистическую информацию о наблюдённом признаке, материалы
наблюдений подвергают сводке в статистические ряды и таблицы.
Статистическим рядом или
рядом распределения называю ряд значений признака, размещённых в порядке
возрастания или убывания, с указанием числа повторений.
Значения признака,
сведённые в ряд, называют классовыми вариантами, а число повторений их в
классах – численностями, или частотами классов. Общее число вариант (Х)
называют объёмом ряда (n).
Число классов определяли
исходя из следующего выражения:
к=1+3.32*LOG10(n). (1)
Величину интервала
определяли по формуле:
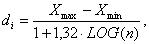 (2)
(2)
где di – классовый интервал по признаку;
Хмах, Хmin – максимальные и минимальные
значения признака;
n – объём ряда, выборки.
Нижняя и верхняя границы
первого класса устанавливались по следующим формулам:
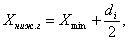 (4)
(4)
где Xниж.г, Xверх.г – нижняя и верхняя границы первого класса.
Сгруппированный ряд
распределения признака является интервальным, когда между классами нет
промежутков, поэтому за первым интервалом идёт второй и т.д.
Основные характеристики
интервальных рядов по морфолого-пространственным показателям представлены в
таблице 2.
В целях исключения
перекрытия верхней границы предыдущего класса с нижней границей последующего
класса, нижние границы классов увеличивают на величину, равную точности
измерения признака. В данном случае для всех 3-х показателей мы её приняли
равной 0,1 см, м, м2.
Серединой класса является
среднее значение указанного интервала. Ряд делился на классы до тех пор, пока
максимальная не попадала в последний класс.
Были получены группировки
данных по 3-м признакам (диаметру ствола (таблица 3), диаметру кроны (таблица
4), площади роста (таблица 5)).
Таблица 2 – Основные
характеристики интервальных рядов
|
Показатель
|
Морфолого-пространственные
показатели
|
|
Диаметр ствола, см
|
Диаметр кроны, м
|
Площадь роста, м2
|
|
N=
|
50
|
50
|
50
|
|
к=
|
7
|
7
|
7
|
|
Xmax=
|
51,3
|
7,4
|
106,8
|
|
Xmin=
|
6,3
|
1,0
|
0,1
|
|
di=
|
6,8
|
1,0
|
16,1
|
|
Xниж.гр.=
|
2,9
|
0,5
|
0,0
|
|
Xверх.гр.=
|
9,7
|
1,5
|
8,1
|
Таблица 3 – Группировка
ряда распределения по диаметру ствола
|
Границы классов
|
Середины классов
|
Частоты
|
|
нижняя
|
верхняя
|
в числах
|
накопленные
|
|
2,9
|
9,7
|
6,3
|
13
|
13
|
|
9,8
|
16,5
|
13,1
|
16
|
29
|
|
16,6
|
23,2
|
19,9
|
11
|
40
|
|
23,3
|
30,0
|
26,7
|
6
|
46
|
|
30,1
|
36,8
|
33,5
|
1
|
47
|
|
36,9
|
43,6
|
40,2
|
2
|
49
|
|
43,7
|
50,3
|
47,0
|
0
|
49
|
|
50,4
|
57,1
|
53,8
|
1
|
50
|
Таблица 4 – Группировка
ряда распределения по диаметру кроны
|
Границы классов
|
Середины классов
|
Частоты
|
|
нижняя
|
верхняя
|
в числах
|
накопленные
|
|
0,5
|
1,5
|
1,0
|
1
|
1
|
|
1,6
|
2,4
|
2,0
|
8
|
9
|
|
2,5
|
3,4
|
3,0
|
17
|
26
|
|
3,5
|
4,4
|
3,9
|
16
|
42
|
|
4,5
|
5,3
|
4,9
|
6
|
48
|
|
5,4
|
6,3
|
5,9
|
0
|
48
|
|
6,4
|
7,3
|
6,8
|
1
|
49
|
|
7,4
|
8,2
|
7,8
|
1
|
50
|
Таблица 5 – Группировка
ряда распределения по площади роста
|
Границы классов
|
Середины классов
|
Частоты
|
|
нижняя
|
верхняя
|
в числах
|
накопленные
|
|
0,0
|
8,1
|
4,1
|
26
|
26
|
|
8,2
|
24,2
|
16,2
|
16
|
42
|
|
24,3
|
40,3
|
32,3
|
2
|
44
|
|
40,4
|
56,3
|
48,4
|
1
|
45
|
|
56,4
|
72,4
|
64,4
|
3
|
48
|
|
72,5
|
88,5
|
80,5
|
0
|
48
|
|
88,6
|
104,6
|
96,6
|
1
|
49
|
|
104,7
|
120,6
|
112,7
|
1
|
50
|
В таблице 3, 4, 5 частота
представлена: в числах и в накопленном виде. Частота это количество значений
признака, которые попадают в границы данного класса. Все значения
представленных признаков были распределены по классам. Накопленные частоты
представляют собой сумму частот, когда к предыдущей накопленной сумме
прибавляется очередная частота.
Важно отметить, что
таблицы группировок данных по указанным выше признакам позволят нам установить
характер распределения и упростить дальнейшую обработку материала (количество
данных ограничивается количеством классов).
1.3 Графическое
изображение рядов распределения
После группировки данных
наблюдений в классы вариационные ряды изображались графически (рисунок 2). Они
иллюстрировались тремя видами кривых: гистограммой, полигоном распределения и
кумулятой. По визуальной оценке рисунка, можно произвести в дальнейшем анализ,
который включал бы в себя: отмечается наличие максимумов, характера возрастания
или убывания частот, обращается внимание на симметричность и растянутость ряда.
Пользуясь кумулятой, можно подразделить вариационный ряд на две равные части
(медиану).
1.4 Виды средних
Ряды распределения численностей,
приведённых в таблице 3, 4, 5 и изображённые на рисунке 2, показывают, что
варианты концентрируются около некоторого их значения. Следовательно, можно
найти такое значение варианты или абстрактное среде число, которое будет
наиболее представительной характеристикой какой либо совокупности.
Показателем, дающим
возможность сопоставлять изучаемые совокупности, является обобщённое значение признака
– средняя его величина, последняя для качественно однородной совокупности
представляет типичное значение признака, обобщённый центр, вокруг которого колеблются
значения признака отдельных единиц совокупности, так и действием всевозможных
факторов и их сочетанием, различным для разных единиц.
Средние значения
используют в статистике для характеристики ряда распределения одним числом.
В данной работе были
вычислены значения некоторых средних и по показателям сведены в таблицу 6:
- среднее арифметическое
(простое) (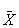 ). Оно равно
сумме отдельных значений (Xi), поделённой на их число (n)
(формула 5). Формула простого среднего арифметического применяется обычно в тех
случаях, когда каждое значение признака наблюдается только один раз;
). Оно равно
сумме отдельных значений (Xi), поделённой на их число (n)
(формула 5). Формула простого среднего арифметического применяется обычно в тех
случаях, когда каждое значение признака наблюдается только один раз;
- средняя гармоническая (Xгарм.) представляет собой обратную
величину средней арифметической из обратных величин (формула 6). Она
применяется в тех случаях, когда имеются данные об индивидуальных значениях
признака и общем объёме совокупности, но не известны частоты;
- среднее геометрическое
(Xгеом.) (формула 7) применяется при
вычислении средней доли относительных изменений и индексов.
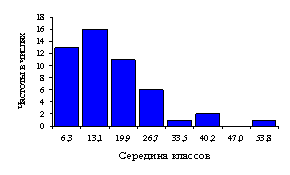
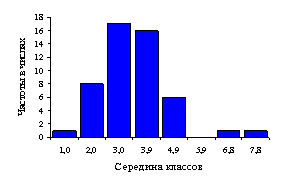
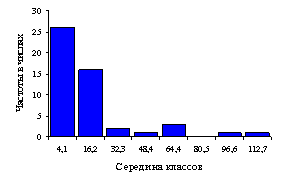
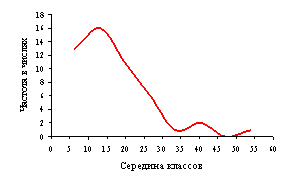
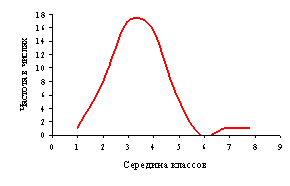
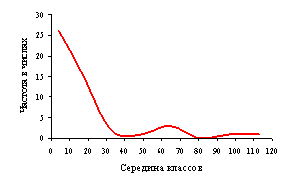
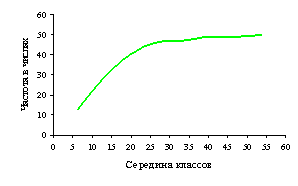
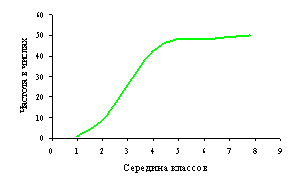
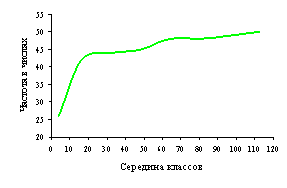
Рисунок 1 – Гистограмма
(а), полигон (б), кумулята (в) ряда распределения по диаметру ствола (1), по
диаметру кроны (2), по площади роста (3)
Медиана (Ме) и мода (Мо)
представляют собой группу структурных средних.
- медианой называется
величина признака, которая находится в середине упорядоченного вариационного
ряда, где варианты расположены в порядке возрастания или убывания.
- модой называется
наиболее часто встречающаяся величина признака. Поскольку мода является
величиной конкретной, она имеет важное значение для характеристики структуры
изучаемой совокупности;
- средняя квадратическая
величина (формула 8) используется в лесном хозяйстве при расчётах средних
признаков, имеющих квадратичную величину при переходе на линейные признаки
(площадь поперечного сечения ствола, площадь роста).
После расчёта средних
значений, медианы и моды было установлено соотношение средних значений (то есть
соблюдение свойства мажорантности параметрических средних согласно выражению Xкв.>Хср.ариф. >Хгеом.
>Хгарм). Соотношение данных выполняется – расчёты были выполнены
правильно!
Таблица 6 – Расчёт
средний для несгруппированных рядов распределения
|
Виды средних
|
Значения для:
|
|
диаметра ствола, см
|
диаметра кроны, м
|
площади роста, м2
|
|
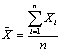
, (5)
|
17,4
|
3,5
|
16,51
|
|
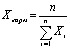
, (6)
|
13,6
|
3,1
|
0,44
|
|
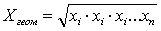
, (7)
|
15,3
|
3,3
|
3,81
|
|
Ме
|
14,8
|
3,4
|
5,49
|
|
Мо
|
22,1
|
2,9
|
0,09
|
|
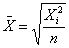
, (8)
|
19,9
|
3,7
|
28,64
|
1.5 Показатели вариации
признаков
Средняя величина не даёт
достаточного представления о свойствах изучаемой совокупности. Являясь
показателем центральной тенденции, т.е. наиболее представительной
характеристикой изучаемого коллектива, она не характеризует степени
разнообразия (варьирования) отдельных единиц в этом коллективе.
Наиболее употребляемые
статистическими характеристиками вариации являются размах варьирования, дисперсия,
средне-квадратическое отклонение, коэффициент вариации. Расчёт этих показателей
по признакам был сведён в таблицу 7.
Таблица 7 – Статистики
изменчивости (вариации)
|
Показатели вариации признаков
|
Значения для:
|
|
диаметра ствола, см
|
диаметра кроны, м
|
площади роста, м2
|
|
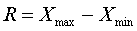
, (9)
|
45,0
|
6,4
|
106,7
|
|
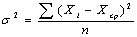
, (10)
|
93,8
|
1,4
|
559,1
|
|
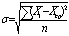
, (11)
|
9,7
|
1,2
|
23,6
|
|
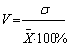
, (12)
|
55,6
|
33,9
|
143,2
|
|
Мера изменчивости признака
|
оч. Большая
|
Большая
|
оч. Большая
|
Размах (R), или широта (степень) разброса,
является простейшей мерой рассеивания. Он определяется как разность между
наибольшим (Хmax) и
наименьшим значениями (Хmin) распределения в упорядоченной последовательности значений признака
(формула 9). Понятие размаха опирается, следовательно, только на два
экстремальных значения. Соответственно этому его информативное содержание
невелико.
Важнейшей мерой
рассеивания является дисперсия (δ2). При её
вычислении определяются отклонения значений признака (Xi) или соответственно середин классов
от арифметического среднего (Xср.) и возведением в квадрат (формула
10).
Среднее квадратическое
отклонение (стандартное отклонение) (δ) – показывает среднее отклонение
вариант от центра ряда распределения. Оно равно квадратному корню из дисперсии
(формула 11). В то время как в теоретической статистике находит применение
главным образом дисперсия как мера рассеяния, в практической статистике
используется преимущественно стандартное отклонение.
В отличие от
рассмотренных и найденных параметров коэффициент вариации (V) определяет не абсолютную, а
относительную меру рассеивания. С помощью коэффициента вариации можно
сравнивать рассеяние у различных частотных распределений. Коэффициент вариации
находили по формуле 12. Он характеризует те же свойства совокупности, что и
среднее квадратическое отклонение, и представляет средний процент отклонения вариант
рядя от их среднего значения. Так как коэффициент изменчивости выражается в
процентах, то его величина не зависит от единиц измерения.
Нормированное отклонение
показывает на сколько сигм (δ) отклоняется какая-либо варианта от среднего
значения:
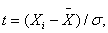 (13)
(13)
где t – нормированное отклонение;
Хi – варианты ряда распределения;
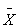 – среднее значение.
– среднее значение.
С помощью нормированного
отклонения можно определить местоположение варианты по отношению к центру ряда
распределения, проверить соответствие ряда нормальному распределению. Для каждой
варианты было найдено нормированное отклонение (таблица 8).
Таблица 8 – Расчёт
нормированного отклонения
|
№ дерева
|
5
|
6
|
7
|
8
|
9
|
20
|
21
|
22
|
23
|
24
|
|
Диаметр ствола, см
|
0,40
|
-1,02
|
0,26
|
-0,28
|
-0,06
|
3,50
|
2,47
|
-0,87
|
-0,39
|
0,47
|
|
Диаметр кроны,м
|
-2,10
|
-0,49
|
0,35
|
-1,34
|
0,18
|
3,32
|
0,61
|
-0,41
|
0,27
|
-0,41
|
|
Площадь роста, м2
|
-0,03
|
1,75
|
3,82
|
3,44
|
0,41
|
-0,02
|
1,32
|
0,23
|
-0,48
|
-0,55
|
|
№ дерева
|
35
|
36
|
37
|
38
|
39
|
50
|
51
|
52
|
53
|
54
|
|
Диаметр ствола, см
|
0,48
|
0,48
|
-0,73
|
-0,44
|
-0,53
|
0,55
|
-0,83
|
0,51
|
0,45
|
|
Диаметр кроны,м
|
0,10
|
-0,24
|
0,10
|
0,44
|
-0,49
|
0,69
|
-0,41
|
-0,15
|
-1,09
|
-0,32
|
|
Площадь роста, м2
|
-0,55
|
-0,05
|
0,27
|
-0,07
|
-0,56
|
0,28
|
1,87
|
0,02
|
0,31
|
0,03
|
|
№ дерева
|
65
|
66
|
67
|
68
|
69
|
80
|
81
|
82
|
83
|
84
|
|
Диаметр ствола, см
|
-1,15
|
-0,54
|
0,06
|
-0,24
|
-0,40
|
-0,48
|
-0,81
|
-0,70
|
-0,90
|
-0,26
|
|
Диаметр кроны,м
|
-0,07
|
0,52
|
-0,24
|
-0,49
|
1,12
|
-0,49
|
-0,58
|
0,02
|
-0,58
|
-1,09
|
|
Площадь роста, м2
|
-0,65
|
-0,45
|
-0,69
|
0,27
|
-0,52
|
0,20
|
-0,59
|
-0,69
|
-0,68
|
-0,01
|
|
№ дерева
|
95
|
96
|
97
|
98
|
99
|
110
|
111
|
112
|
113
|
114
|
|
Диаметр ствола, см
|
-0,51
|
-1,03
|
-0,52
|
-0,88
|
-0,08
|
0,91
|
0,67
|
-0,19
|
1,01
|
-0,71
|
|
Диаметр кроны,м
|
-0,32
|
-1,43
|
0,02
|
0,02
|
-0,07
|
0,44
|
1,12
|
-1,26
|
1,54
|
-1,00
|
|
Площадь роста, м2
|
-0,69
|
-0,68
|
-0,16
|
0,38
|
-0,69
|
0,03
|
-0,68
|
-0,69
|
-0,48
|
-0,69
|
|
№ дерева
|
125
|
126
|
127
|
128
|
129
|
140
|
141
|
142
|
143
|
144
|
|
Диаметр ствола, см
|
-0,92
|
-1,00
|
0,94
|
1,20
|
-0,89
|
2,57
|
-0,84
|
1,57
|
-0,17
|
0,72
|
|
Диаметр кроны,м
|
-0,75
|
-1,00
|
0,95
|
1,46
|
0,18
|
2,98
|
0,18
|
0,18
|
-1,00
|
1,03
|
|
Площадь роста, м2
|
-0,69
|
0,10
|
-0,55
|
-0,69
|
-0,69
|
-0,68
|
1,80
|
-0,50
|
-0,66
|
-0,66
|
Показатели вариации
характеризуют общую изменчивость признака, а также отклонения (размещения)
отдельных вариант распределения по отношению к центру ряда. По величине
коэффициента вариации установили меру изменчивости каждого признака (таблица
7), по следующей схеме (шкала М.Л. Дворецкого), рисунок 3.
|
коэффициент
изменчивости:
|
до 5%
|
6-10%
|
11-20%
|
21-50%
|
больше 50%
|
|
Изменчивость:
|
слабая
|
умеренная
|
значительная
|
большая
|
очень большая
|
|
|
Рисунок 3 – Шкала вида
изменчивости по М.Л. Дворецкого
|
1.6 Ошибки и надёжность
статистических показателей
Расчёт значений ошибок и
показателей надёжности и их формулы представлен в таблице 9.
Таблица 9 – Ошибки и
надёжность статистических показателей
|
Показатели надёжности и ошибок
|
Значения для:
|
|
диаметра ствола
|
диаметра кроны
|
площади роста
|
|
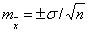
, (14)
|
1,37
|
0,17
|
3,34
|
|
-1,37
|
-0,17
|
-3,34
|
|
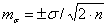
, (15)
|
0,97
|
0,12
|
2,36
|
|
-0,97
|
-0,12
|
-2,36
|
|
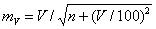
, (16)
|
6,24
|
2,35
|
41,09
|
|
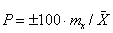
, (17)
|
7,87
|
4,79
|
20,26
|
|
-7,87
|
-4,79
|
-20,26
|
|
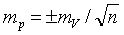
, (18)
|
0,88
|
0,33
|
5,81
|
|
-0,88
|
-0,33
|
-5,81
|
|

, (19)
|
по X
|
12,71
|
20,87
|
4,94
|
|
-//-
|
по δ
|
10,00
|
10,00
|
10,00
|
|
-//-
|
по V
|
8,92
|
14,44
|
3,49
|
|
-//-
|
по P
|
8,92
|
14,44
|
3,49
|
|
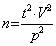
, (20)
|
уровень вероятности 0,683
|
50
|
50
|
50
|
|
-//-
|
уровень вероятности 0,954
|
200
|
200
|
200
|
|
-//-
|
уровень вероятности 0,977
|
450
|
450
|
450
|
Выборочная совокупность
довольно точно воспроизводит свойства и соотношения в генеральной совокупности,
но не абсолютно точно вследствие колеблемости изучаемых признаков. Поэтому
между статистическими показателями выборочной совокупности и действительными
значениями этих показателей генеральной совокупности всегда будут некоторые
расхождения, которые являются случайными ошибками выборки и называются
основными ошибками того или иного статистического показателя. На основании
величины этой основной ошибки и значения соответствующего показателя выборки
можно судить о действительном значении данного показателя в генеральной
совокупности. Так, с вероятностью, равной 0,68, можно утверждать, что
расхождение между действительным значением данного показателя в генеральной
совокупности и вычисленным его значением для выборки не превышает однократного
значения основной ошибки этого показателя (со знаком плюс или минус);
предельное же расхождение не превышает трёхкратного значения основной ошибки (о
чём можно утверждать с вероятностью 0,997).
Ошибкой выборочной
средней называют средней ошибкой средней величины, обозначают её буквой 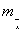 , находили эту ошибку по
формуле 14.
, находили эту ошибку по
формуле 14.
Ошибка
среднеквадратического отклонения (стандартного отклонения - 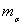 ) рассчитывали по формуле 15, ошибку
коэффициента варьирования по формуле 16.
) рассчитывали по формуле 15, ошибку
коэффициента варьирования по формуле 16.
В практике исследований
значение μ (средняя величина в генеральной совокупности) неизвестна.
Принято записывать значение выборочной средней вместе с её ошибкой, т.е. 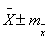 .
.
Точность опыта, или
процент ошибки наблюдения – это процент расхождения между генеральной и
выборочной средней, который вычислялся по формуле 17.
В 68 % случаях
расхождения между генеральной и выборочной средней не превышает однократного
значения точности опыта (в ту или другую сторону), а предельное расхождение –
не превосходит трёхкратного значения.
Точность опыта (P) показывает, насколько процентов
можно ошибиться, если утверждать, что генеральная средняя равна полученной
выборочной средней.
Полученный процент ошибки
сопоставляется с заданным: если он больше заданного, точность достаточная, а
если он не больше заданного, точность достаточная, а если больше, то точность
результата является неудовлетворительной; значит, следует увеличить число
наблюдений.
Ошибка точности опыта
была вычислена через ошибку коэффициента изменчивости (формула 18).
Выборочная средняя тем
точнее, т.е. тем меньше будет отличаться от генеральной средней, чем больше
объём выборки n.
Госсет (псевдоним
Стьюдент) для различных N, точнее N-1, рассчитал значения отклонений выборочных
средних от генеральной средней величины. Были вычислены по некоторому выражению
значения показателя t. Были получены пограничные значения. Такими пограничными
уровнями t можно пользоваться как предельными (критическими) значениями,
которые с определённой вероятностью могут быть следствием случайных причин.
Отметим, что значение t=3,25
и более при числе степеней свободы, равным 9 (N-1), практически встречается так редко, что событие является
крайне маловероятным.
Если найденное в
каком-либо опыте t превзойдёт по
величине табличное значение, то его нельзя уже объяснить случайными причинами.
С помощью критерия t и значения выборочного
статистического показателя и его средней ошибки можно дать оценку
соответствующего параметра с определённой вероятностью.
Во многих опытах
целесообразно оценить параметр путём проверки некоторой статистической гипотезы
в отношении его размера. Наиболее часто проверяется предположение, что
полученная выборочная средняя незначимо отличается от гипотетической
(теоретически установленной) или вообще известной величины средней в
генеральной совокупности μ. Выдвигается гипотеза H0, что
истинная разность равна нулю. В таком виде гипотеза часто называется нулевой.
Проверка гипотезы состоит
в выяснении совместимости наблюдённых данных с этой гипотезой. Применим критерии
t. Формула (19) обобщена в том отношении, что она применима для оценки
значимости любого статистического показателя T, к которому нулевая гипотеза
разумна. Она была применена для расчёта оценки ряда статистических показателей,
таблица 9.
Критерий t обычно
называют критерием значимости (или существенности).
При t<ti (ti-критическое значение этого критерия, взятое из таблиц
для уровня значимости в 5% или в 1%) опытные данные совместимы с гипотезой H0 подтверждается. При t>ti, т.е. t0,01 или t0,05
они несовместимы H0 отвергается.
Если частное t получается равным и больше трёх, то
значение показателя является надёжным, достоверным, и им можно пользоваться для
разных сопоставлений и выводов. Если же это отношение t будет меньше трёх, то данный показатель оказывается
ненадёжным, величина его достоверна и является лишь в той или иной мере
вероятной (в зависимости от величины отношения t-показателя достоверности).
При планировании опыта
приходится решать вопрос о числе наблюдений или объёме выборки, достаточном для
получения оценки средней величины или другого статистического показателя с
определённой точностью. Этот вопрос решается с помощью формулы 20. Формула
указывает число наблюдений для уровня значимости средней в 0,32 (вероятность
безошибочного заключения p=0,68).
Такой уровень редко признаётся достаточным. Обычно принимают уровень значимости
0,05 или 0,01. В формулу вводят соответствующее принимаемому уровню значение t (t0,05 или t0,01). Расчёты объёма выборки при
различных вероятностях заключения помещены в таблицу 9.
2 Анализ лесоводственной
информации
При проведённых
исследованиях нами была взята выборка в количестве 50 деревьев, у которых
замерены и определены следующие показатели: диаметр дерева на высоте 1,3 метра; диаметр кроны и площадь роста. Исходные данные были подвергнуты статистическому анализу. В
результате можно сделать следующие выводы.
Среднее значение
выборочной совокупности по диаметру – 17,4, см; по диаметру кроны – 3,5, м и
площади роста – 16,51 м2. Среднее значение деревьев в лесном массиве
(генеральная совокупность) по диаметру – 17,4 ± 2,74 см; по диаметру кроны – 3,5 ± 0,34 м; по площади роста – 16,51 ± 6,68 м2. Об этом можно утверждать с достоверной вероятностью в 0,954.
Размах варьирования
вариант в выборке и в генеральной совокупности имеют одинаковые значения:
по диаметру ствола – 45,0 см;
по диаметру кроны – 6,4 м;
по площади роста – 106,7 м2.
Каждое значение дерева по
диаметру отклоняется от среднего на величину – 9,7, см; по диаметру кроны
отклоняется от среднего на величину – 1,2 м; по площади роста отклоняется от центра на величину – 23,6 м2. Для всех деревьев в лесном массиве:
по диаметру ствола – 9,7
± 1,94 см;
по диаметру кроны – 1,2 ±
0,24 м;
по площади роста – 23,6 ±
4,72 м2.
Об этом можно утверждать
в вероятностью 0,954. При этом изменчивость деревьев в выборке составляет по
диаметру ствола – 55,6, %; по диаметру кроны – 33,9, %; по площади роста –
143,2, %. Для всех деревьев вариация составляет – по диаметру ствола – 55,6 ±
1,76 %; по диаметру кроны – 33,9 ± 0,66 % и по площади роста – 143,2 ± 11,62 %.
Об этом можно утверждать с вероятностью 0,954.
Согласно шкале М.Л.
Дворецкого [ ] изменчивость по диаметру ствола очень большая, диаметру кроны
большая и по площади роста очень большая.
Расхождение между средним
значением выборочной совокупности и средним значением всех деревьев составляет:
для диаметра ствола – 7,87, %; диаметра кроны – 4,79, % и площади роста –
20,26, %. При этом для всех деревьев в лесном массиве:
диаметр ствола – 7,87 ±
1,76 %;
диаметр кроны – 4,79 ±
0,66 %;
площадь роста – 20,26 ±
11,62 %.
Исходя из полученных
результатов, можно рассчитать необходимое количество наблюдений по диаметру
ствола при уровне доверительной вероятности 0,683 – 50; при 0,954 – 200, а при
0,977 – 450.
О степени надёжности
судим по показателю t. Так как t для найденных показателей по 3
признакам больше 3, значение рассчитанных нами показателей достоверны.
Большую часть
статистических показателей можно получить с помощью пакета анализа электронной
таблицы «Excel». Что и было проделано (таблица 10).
Таблица 10 – Расчёт
статистических показателей по морфолого-пространственным показателям
|
Статистические показатели
|
Диаметр ствола, см
|
Диаметр кроны, м
|
Площадь роста, м2
|
|
Среднее
|
17,4
|
3,5
|
16,5
|
|
Стандартная ошибка
|
1,4
|
0,2
|
3,3
|
|
Медиана
|
14,8
|
3,4
|
5,5
|
|
Мода
|
22,1
|
2,9
|
0,1
|
|
Стандартное отклонение
|
9,7
|
1,2
|
23,6
|
|
Дисперсия выборки
|
93,8
|
1,4
|
559,1
|
|
Эксцесс
|
2,6
|
2,6
|
5,9
|
|
Асимметричность
|
1,5
|
1,1
|
2,3
|
|
Интервал
|
45,0
|
6,4
|
106,7
|
|
Минимум
|
6,3
|
1,0
|
0,1
|
|
Максимум
|
51,3
|
7,4
|
106,8
|
|
Сумма
|
870,7
|
174,1
|
825,3
|
50,0
|
50,0
|
50,0
|
|
Уровень надежности (95,0%)
|
2,8
|
0,3
|
6,7
|
Заключение
Внедрение современных
компьютерных технологий во многом упростило обработку данных. В тоже время процесс
большей частью автоматизирован (таблица 10) и происходит потеря интереса к
научным изысканиям в силу непонимания сущности обработки исходных данных.
В процессе обработки и
анализа представленной выше информации мы в какой то мере научились, во всяком
случае имеем теперь представление о способах обработки лесоводственной
информации, ознакомились с необходимыми математическими методами, которые
используются в лесном хозяйстве.
А как «бонус» научились
придерживаться определённых стандартов, которые имеют место при оформлении
печатных работ.
А свободное общение с
преподавателем (чуть ли не понибратство) и уверенность в том, что зачёт
«выхватим» в лёт, позволило нам чувствовать на занятиях достаточно свободно и в
тоже время «мимо» ходом что-то уловить. Считаем, что выражение «не знал, а ещё
и забыл» это не про нас. Считаем, что легче «въехать» в определённую тему можно
и без отличного знания теории, конечно азы кой-какие нужны, здесь этот вопрос
даже не обсуждается, но легче учиться, если ты не связан какими либо
ограничениями. Мы учимся в первую очередь для себя и поэтому на нашей совести
усидчивость, трудолюбие, желание познания чего-либо.
В заключении хотелось бы
сказать спасибо Артёму Геннадьевичу Неповинных, за добросовестный труд))))))),
за то что он «крутился» возле нас в силу своей энергичности, за его взгляд на
каждого студента как на перспективного молодого человека, даже на самого отпетого
лентяя))))) И он прав, мы самые лучшие, целеустремлённые и готовые жить
полноценной жизнью, преодолевать жизненные трудности, верить в лучшее,
стремится изменить себя к лучшему и в конечном итоге и общество в целом в
котором мы обитаем.
Библиографический список
1. Вайс, А.А. Математические методы в
лесном хозяйстве: Лабораторный практикум для студентов специальности 260400,
260500 и 320800 очной формы обучения [Текст] / А.А. Вайс, Н.В. Павлов, А.В.
Подколзин. – Красноярск: СибГТУ, 2005.-32 с.
2. Дворецкий, М.Л. Практическое
пособие по вариационной статистике [Текс] / М.Л. Дворецкий. – Йошкар-Ола, 1961.
– 100 с.
3. Кюн, Ю. Описательная и индуктивная
статистика [Текс] / Ю. Кюн. – М.: Финансы и статистика, 1981. – 126 с.
4. Свалов, Н.Н. Вариационная
статистика [Текс] / Н.Н. Свалов. – М.: Московский лесотехнический институт,
1975. – 84 с.
5. Свалов, Н.Н. Вариационная
статистика: учебное пособие для вузов [Текс] / Н.Н. Свалов. – М.: Лесная
промышленность, 1977. – 176 с.
6. Фалалеев, Э.Н. Математическая
статистика: учебное пособие [Текс] / Э.Н. Фалалеев, А.С. Смольянов. –
Красноярск: КГУ, 1981. – 128 с.
7. Хазанов, Ю.С. Статистика [Текс] /
Ю.С. Хазанов. – М.: Статистика, 1974. – 192 с.