Технико-экономический анализ. Анализ выпуска и объемов продаж продукции
Министерство образования и науки
Российской Федерации
Государственное образовательное
учреждение высшего профессионального образования
Кафедра прочности летательных
аппаратов
Курсовая работа
по курсу: “Строительная механика
самолетов”
“Расчет
оболочек вращения по безмоментной теории ”
Самара
Реферат
Курсовой
проект.
Пояснительная
записка: 16 с., 3 источника
Произведен
расчет оболочки вращения согласно заданию, построены эпюры изменения
нормального давления вдоль образующей составной оболочки, рассчитаны
меридиональные и окружные погонные усилия в оболочке по безмоментной теории и
построены эпюры этих сил
Содержание
Определение закона изменения нормального давления вдоль образующей
составной оболочки и построение его эпюры
Расчет меридиональных и окружных погонных усилий в оболочке по
безмоментной теории и построение их эпюр
Сечение
I-I
Сечение
II-II
Сечение
III-III
Сечение
IV-IV
Сечение
V-V
Эпюра
меридиональных и окружных погонных усилий
Определение максимальных значений окружных и меридиональных напряжений во
всех частях составной оболочки
Эпюра меридианальных и окружных напряжений
Определение
закона изменения нормального давления вдоль образующей составной оболочки и
построение его эпюры
Для
определения закона изменения нормального давления вдоль образующей составной
оболочки, разделим ее на две части. Построим эпюру нормального давления (рис. 2.2 ).
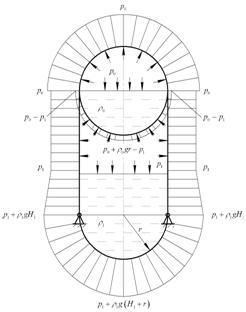
Рис.
1.2
Расчет меридиональных и окружных погонных усилий в оболочке
по безмоментной теории и построение их эпюр
В
основе расчета усилий в оболочке по безмоментной теории лежат следующие два
уравнения:
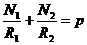 ,
,
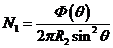 ,
,
где
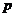 - интенсивность внутреннего давления;
- интенсивность внутреннего давления; 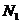 и
и 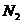 -
меридиональные и окружные погонные нормальные усилия;
-
меридиональные и окружные погонные нормальные усилия; 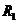 и
и 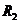 -
главные радиусы кривизны срединной поверхности оболочки в меридиональном и
окружном направлениях соответственно;
-
главные радиусы кривизны срединной поверхности оболочки в меридиональном и
окружном направлениях соответственно; 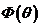 -
равнодействующая внешней нагрузки, приложенной к оболочке выше параллельного
круга, определяемого углом
-
равнодействующая внешней нагрузки, приложенной к оболочке выше параллельного
круга, определяемого углом  .
.
Уравнение
носит название уравнения Лапласа,
второе – уравнение равновесия зоны.
Рассмотрим
следующие сечения оболочки на рисунке 2.3: I, II, III, IV и V.
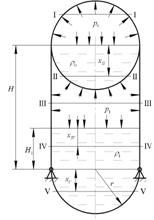
Рис.
1.3
Сечение I-I
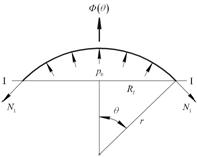
Рис.
1.4
В
силу того, что в сечении I-I  , перепишем уравнения и в следующем виде:
, перепишем уравнения и в следующем виде:
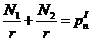

Где
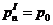 ,
, 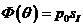 ,
,
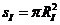 ,
, 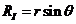 ,
,
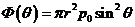
Тогда
меридиональное усилие 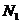 в сечении I-I будет вычислено следующим образом:
в сечении I-I будет вычислено следующим образом:
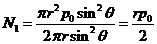
Окружное
усилие 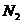 , с учетом найденного
, с учетом найденного 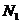 и уравнения :
и уравнения :
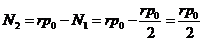
В
итоге имеем:
 .
. 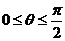 :
: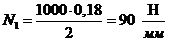 ,
,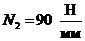
Сечение
II-II
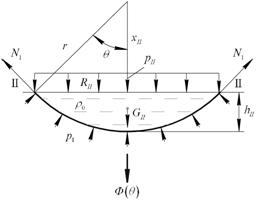
Оболочка
в сечении II-II имеет следующие геометрические характеристики:
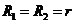 .
.
Уравнения
и принимают вид:
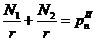

Где
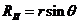
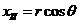
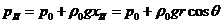 ,
,
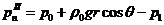
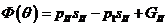 ,
,
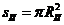 ,
, 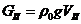
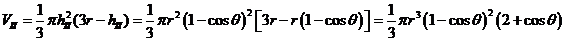 ,
,
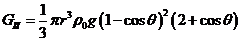 ,
,
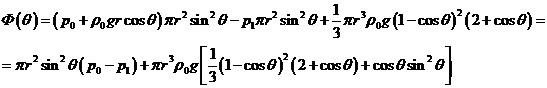
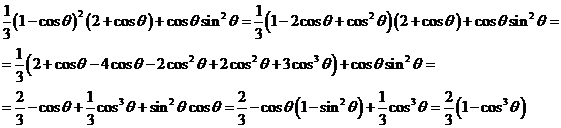
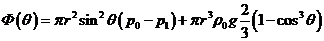
Подставим
в:
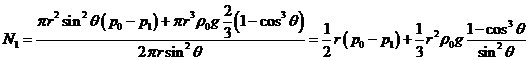 ,
,
Полученное
выражение для 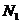 подставим в и выразим
подставим в и выразим 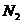 :
:
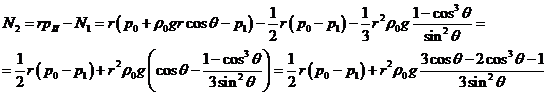
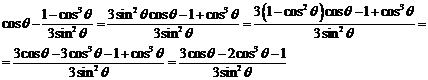
Запишем
полученные выражения для 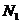 и
и 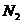 :
:
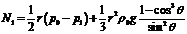 ,
,
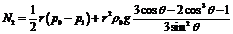 .
.
Вычислим
численные значения 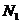 и
и 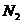 при
при 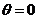 и
и
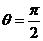 предварительно подсчитав
следующие пределы при
предварительно подсчитав
следующие пределы при 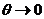 .
.
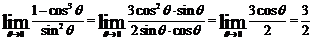
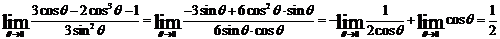
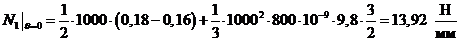
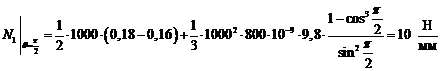
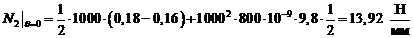
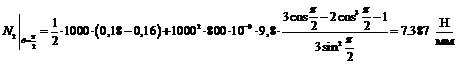
Сечение III-III
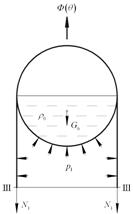
Рис.
1.6
Оболочка
в сечении III-III имеет следующие геометрические характеристики:
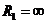 ,
, 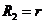 .
.
Уравнения
и принимают вид:
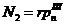
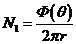
Где

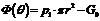 ,
,
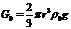
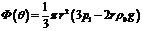
Подставим
в и получим выражение для 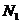 :
:
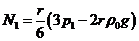
Найдем
выражение для 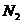 используя формулу :
используя формулу :
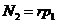
Меридиональное
и окружное усилия в сечении III-III будут иметь значения:
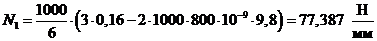 ,
,
 .
.
Сечение IV-IV
Рис.
1.7
Геометрические
характеристики оболочки в сечении IV-IV: 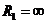 ,
,
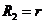 .
.
Уравнения
и принимают вид:

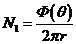
Где
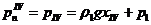
 ,
,
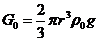
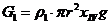
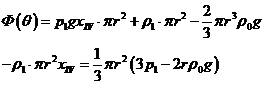
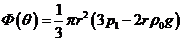
Подставим
полученное 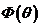 в :
в :
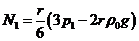
Теперь
найдем окружное усилие в сечении:
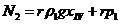
Вычислим
численные значения 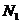 и
и 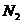 при
при 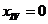 и
и
 :
:
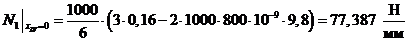
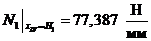
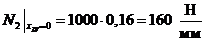
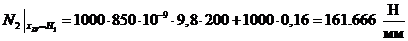
Сечение
V-V
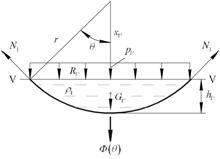
Рис.
1.8
Оболочка
в сечении V-V имеет следующие геометрические характеристики:
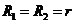 .
.
Уравнения
и принимают вид:

Где
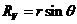

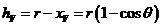
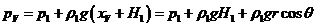 ,
,
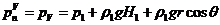
 ,
,
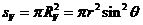 ,
,
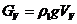
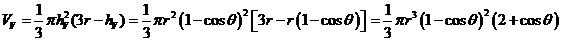 ,
,
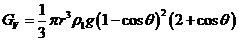 ,
,

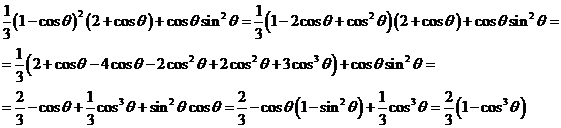
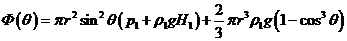
Подставим
в :
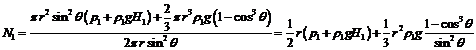 ,
,
Полученное
выражение для 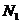 подставим в и выразим
подставим в и выразим 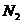 :
:
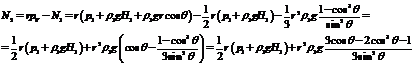
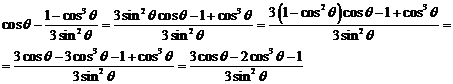
Запишем
полученные выражения для 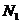 и
и 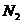 :
:
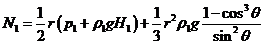 ,
,
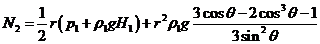 .
.
Вычислим
численные значения 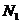 и
и 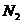 при
при 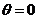 и
и
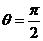 предварительно подсчитав
следующие пределы при
предварительно подсчитав
следующие пределы при 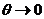 .
.
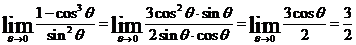
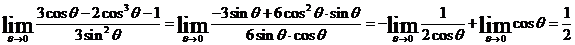
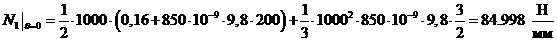
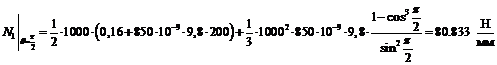
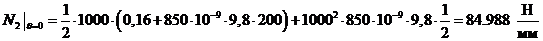
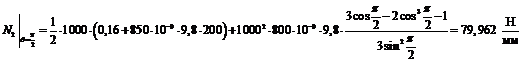
В
общем, для построения эпюры мы имеем следующие значения в соответствующих
сечениях:
сечение
I-I: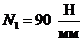 ,
,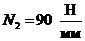 ;
;
сечение
II-II: 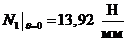 ,
,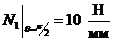 ,
,
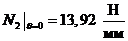 ,
,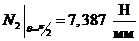 ;
;
сечение
III-III: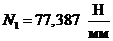 ,
,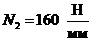 ;
;
сечение
IV-IV: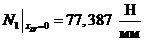 ,
,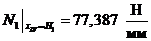
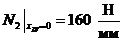 ,
,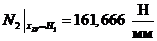
сечение
V-V: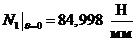 ,
,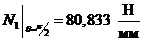
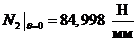 ,
,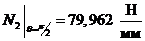
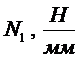
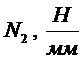
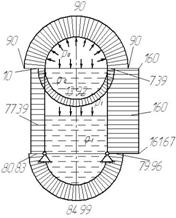
Рис.
1.9
Определение максимальных значений окружных и меридиональных
напряжений во всех частях составной оболочки
Окружные
и меридиональные напряжения можно подсчитать по формулам:
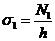
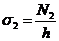
Вычислим
значения этих напряжений для всех сечений:
сечение
I-I:
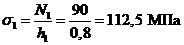 ,
,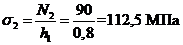 ;
;
сечение
II-II:
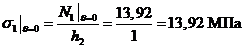 ,
,
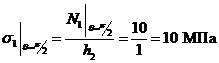 ,
,
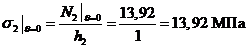 ,
,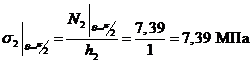 ;
;
сечение
III-III:
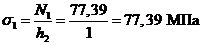 ,
, ;
;
сечение
IV-IV:
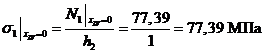 ,
,
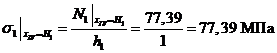
 ,
,
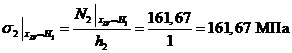
сечение
V-V:
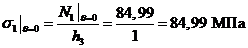 ,
,
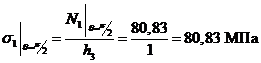
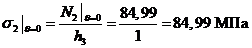 ,
,
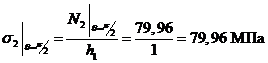
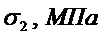

Рис.
1.10
По
виду эпюры можно сказать, что максимальное меридиональное напряжение возникнет
в днище бака: 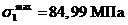 , а максимальные
окружные напряжения в опорах:
, а максимальные
окружные напряжения в опорах:  .
.