Інтегральні характеристики векторних полів
інтегральні характеристики векторних полів
1.
Диференціальні операції другого порядку
Нехай в області  задані скалярне поле
задані скалярне поле 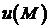 і векторне поле
і векторне поле 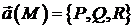 , причому функції
, причому функції 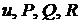 мають в області
мають в області  неперервні частинні похідні
другого порядку. Тоді
неперервні частинні похідні
другого порядку. Тоді 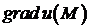 і
і
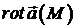 є диференційовними
векторними полями, а
є диференційовними
векторними полями, а 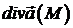 –
диференційовним скалярним полем.
–
диференційовним скалярним полем.
До векторних
полів 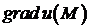 і
і 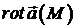 можна застосувати операції
обчислення дивергенції і ротора, а до скалярного поля
можна застосувати операції
обчислення дивергенції і ротора, а до скалярного поля  – операцію обчислення градієнта. Таким чином,
отримуємо повторні операції:
– операцію обчислення градієнта. Таким чином,
отримуємо повторні операції:
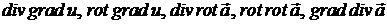 .
.
Операцію 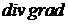 називають оператором
Лапласа і позначають також символом
називають оператором
Лапласа і позначають також символом 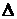 :
:
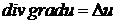 .
.
З допомогою
оператора Гамільтона оператор Лапласа записується у вигляді
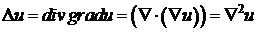 .
.
Враховуючи, що
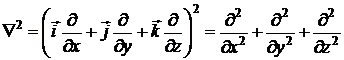 ,
,
дістаємо
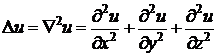 .
.
Функція 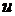 , яка задовольняє в деякій
області рівняння Лапласа
, яка задовольняє в деякій
області рівняння Лапласа 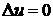 ,
називається гармонічною в цій області. Наприклад, лінійна функція
,
називається гармонічною в цій області. Наприклад, лінійна функція 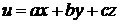 є гармонічною в довільній
області. Оператор Лапласа широко застосовується в рівняннях математичної
фізики. Відзначимо, зокрема, що потенціал електричного поля точкового заряду
або поля тяжіння точкової маси, який має вигляд
є гармонічною в довільній
області. Оператор Лапласа широко застосовується в рівняннях математичної
фізики. Відзначимо, зокрема, що потенціал електричного поля точкового заряду
або поля тяжіння точкової маси, який має вигляд 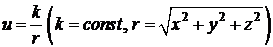 , при
, при 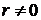 задовольняє рівняння Лапласа:
задовольняє рівняння Лапласа:
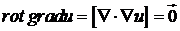
(потенціальне
векторне поле 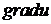 є
безвихровим) і
є
безвихровим) і
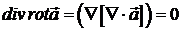
(векторне поле 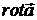 є соленоїдальним).
є соленоїдальним).
1. Дві інші
повторні операції 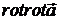 і
і 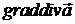 пов’язані співвідношенням
пов’язані співвідношенням
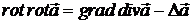 , (1)
, (1)
де 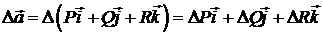 – вектор-функція,
координатами якої є результати застосування оператора Лапласа до функцій
– вектор-функція,
координатами якої є результати застосування оператора Лапласа до функцій 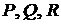 .
.
2. Розкладання
векторного поля на суму потенціального і соленоїдального полів
Довільне
неперервно диференційовне векторне поле  може бути зображено у вигляді
може бути зображено у вигляді
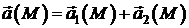 , (2)
, (2)
де 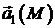 – потенціальне поле,
– потенціальне поле, 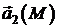 – соленоїдальне поле.
– соленоїдальне поле.
Дійсно, за
означенням потенціальне векторне поле 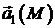 є градієнтом деякого скалярного поля
є градієнтом деякого скалярного поля 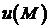 :
: 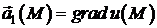 . Тому для вектора
. Тому для вектора 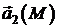 із рівності (2) маємо
із рівності (2) маємо
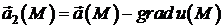 . (3)
. (3)
Щоб векторне поле
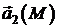 було соленоїдальним,
воно має задовольняти умову
було соленоїдальним,
воно має задовольняти умову 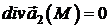 , звідси, враховуючи рівність (3), знаходимо
, звідси, враховуючи рівність (3), знаходимо
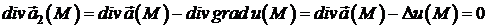 .
.
Таким чином, для
скалярного потенціала поля 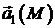 отримуємо рівняння
отримуємо рівняння
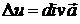 , (4)
, (4)
де 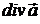 – відома функція даного поля
– відома функція даного поля  .
.
Отже, якщо
функція 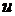 є розв’язком
рівняння (4), то, поклавши
є розв’язком
рівняння (4), то, поклавши 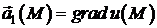 ,
, 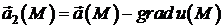 , отримаємо зображення поля
, отримаємо зображення поля  у вигляді (2), де
у вигляді (2), де 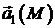 – потенціальне поле,
– потенціальне поле, 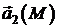 – соленоїдальне поле.
– соленоїдальне поле.
Рівняння (2) –
неоднорідне рівняння в частинних похідних другого порядку, яке називається
рівнянням Пуассона:
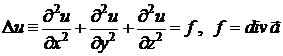 .
.
Відзначимо, що це
рівняння має (нескінченну) множину розв’язків, тому зображення поля  у вигляді (2) не є єдиним.
у вигляді (2) не є єдиним.
2. Потік
векторного поля
Розглянемо
векторне поле  ,
визначене в просторовій області
,
визначене в просторовій області  , і деяку кусково-гладку орієнтовну поверхню
, і деяку кусково-гладку орієнтовну поверхню 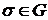 . Нехай
. Нехай 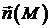 – поле одиничних нормалей на обраній стороні
поверхні
– поле одиничних нормалей на обраній стороні
поверхні  .
.
Як було
відзначено в п. 4.2, поверхневий інтеграл
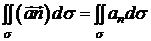 (5)
(5)
називається
потоком векторного поля  через
поверхню
через
поверхню  в сторону,
яка визначається вектором
в сторону,
яка визначається вектором 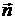 (кажуть також «потік через обрану сторону
поверхні
(кажуть також «потік через обрану сторону
поверхні  »).
»).
Якщо взяти іншу
сторону поверхні (змінити орієнтацію), то вектор 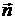 змінить напрям на протилежний; тому скалярний
добуток
змінить напрям на протилежний; тому скалярний
добуток 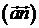 , а отже, і
потік (поверхневий інтеграл (5)) змінить знак.
, а отже, і
потік (поверхневий інтеграл (5)) змінить знак.
Якщо 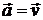 – швидкість рухомої рідини,
то
– швидкість рухомої рідини,
то 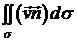 є кількістю
(об’ємом) рідини, яка протікає через поверхню
є кількістю
(об’ємом) рідини, яка протікає через поверхню  у напрямі нормалі
у напрямі нормалі 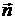 за одиницю часу. Ця величина називається у
фізиці (гідродинаміці) потоком рідини через поверхню
за одиницю часу. Ця величина називається у
фізиці (гідродинаміці) потоком рідини через поверхню  . Тому і у випадку довільного векторного поля
. Тому і у випадку довільного векторного поля  інтеграл (5) називається
потоком векторного поля через поверхню
інтеграл (5) називається
потоком векторного поля через поверхню  .
.
Розглянемо
електричне поле 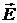 точкового
заряду
точкового
заряду 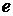 , який міститься
в точці
, який міститься
в точці 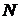 . Знайдемо
потік векторного поля
. Знайдемо
потік векторного поля 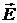 через
зовнішню сторону сфери
через
зовнішню сторону сфери  радіуса
радіуса
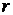 з центром у точці
з центром у точці 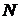 . Нехай
. Нехай 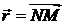 (
(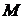 – точка на сфері
– точка на сфері  ); тоді
); тоді 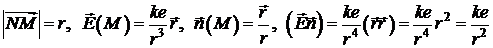 . Тому
. Тому
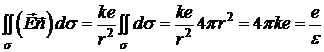 ,
,
де 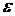 – діелектрична проникність
середовища,
– діелектрична проникність
середовища, 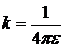 .
.
Якщо в системі
координат 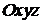
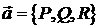 , а
, а 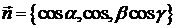 , то вираз (5) для потоку векторного
поля
, то вираз (5) для потоку векторного
поля  можна записати у
вигляді
можна записати у
вигляді
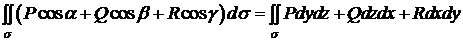 . (6)
. (6)
Кожен доданок у
правій частині рівності (6) залежить від вибору системи координат, проте їх
сума, тобто потік 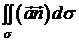 ,
очевидно, не залежить від вибору системи координат.
,
очевидно, не залежить від вибору системи координат.
3. Формула
Остроградського-Гаусса в векторній формі
Нехай в області  визначено векторне поле
визначено векторне поле 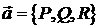 ;
;  – замкнена поверхня, яка обмежує область
– замкнена поверхня, яка обмежує область  ;
; 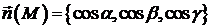 – одиничний вектор зовнішньої нормалі до
поверхні
– одиничний вектор зовнішньої нормалі до
поверхні  у точці
у точці 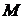 .
.
Нехай, далі, 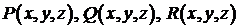 та їхні частинні похідні
та їхні частинні похідні 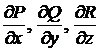 неперервні в області
неперервні в області  . Тоді справедлива формула
Остроградського-Гаусса:
. Тоді справедлива формула
Остроградського-Гаусса:
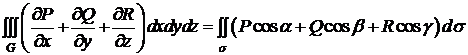 . (7)
. (7)
Підінтегральна
функція в потрійному інтегралі є 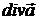 , а поверхневий інтеграл – потік векторного
поля
, а поверхневий інтеграл – потік векторного
поля 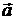 через поверхню
через поверхню  . Тому формулу (7) можна
записати у векторній формі:
. Тому формулу (7) можна
записати у векторній формі:
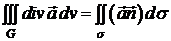 . (8)
. (8)
Фізичний зміст
формули Остроградського-Гаусса: потік векторного поля 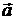 через замкнену поверхню в сторону зовнішньої
нормалі дорівнює потрійному інтегралу по області, обмеженій цією поверхнею, від
дивергенції векторного поля
через замкнену поверхню в сторону зовнішньої
нормалі дорівнює потрійному інтегралу по області, обмеженій цією поверхнею, від
дивергенції векторного поля 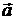 . Щоб потік був відмінним від нуля, всередині
області
. Щоб потік був відмінним від нуля, всередині
області  мають бути
джерела (або стоки) поля. Із формули Остроградського-Гаусса випливає, що тоді
мають бути
джерела (або стоки) поля. Із формули Остроградського-Гаусса випливає, що тоді 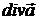 є відмінною від нуля. Таким
чином,
є відмінною від нуля. Таким
чином, 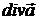 характеризує
джерела поля. Само векторне поле як би розходиться від джерел. Звідси і
походить назва «розбіжність» або «дивергенція».
характеризує
джерела поля. Само векторне поле як би розходиться від джерел. Звідси і
походить назва «розбіжність» або «дивергенція».
4. Властивості
соленоїдального поля
Як відомо,
векторне поле  , яке
задовольняє в області
, яке
задовольняє в області  умову
умову
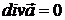 , називається
соленоїдальним в цій області. Нехай область
, називається
соленоїдальним в цій області. Нехай область 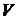 є об’ємно однозв’язною. Це означає, що, якщо
кусково-гладка замкнена поверхня
є об’ємно однозв’язною. Це означає, що, якщо
кусково-гладка замкнена поверхня  лежить в області
лежить в області  , то і область, яка обмежує поверхню
, то і область, яка обмежує поверхню  , цілком належить області
, цілком належить області  . Прикладами об’ємно однозв’язних
областей є куля, паралелепіпед, тор. Відзначимо, що тор не є поверхнево
однозв’язною областю. Область, яка знаходиться між двома сферами, не є об’ємно
однозв’язною (але є поверхнево однозв’язною).
. Прикладами об’ємно однозв’язних
областей є куля, паралелепіпед, тор. Відзначимо, що тор не є поверхнево
однозв’язною областю. Область, яка знаходиться між двома сферами, не є об’ємно
однозв’язною (але є поверхнево однозв’язною).
Із формули
Остроградського-Гаусса випливає, що соленоїдальне поле в взаємно однозв’язній
області має таку властивість: потік соленоїдального поля через довільну
замкнену поверхню, яка знаходиться в цій області, дорівнює нулю.
Відзначимо, що,
якщо область не є об’ємно однозв’язною, то потік соленоїдального (в цій
області) поля через замкнену поверхню, яка знаходиться в області, може бути
відмінним від нуля. Так електричне поле 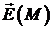 точкового заряду, який міститься в точці
точкового заряду, який міститься в точці 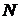 , є соленоїдальним в кулі з
викинутим центром (
, є соленоїдальним в кулі з
викинутим центром (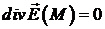 при
при 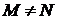 ).
).
Слово
«соленоїдальне» означає «трубасте». Для соленоїдального поля є справедливим
закон збереження інтенсивності векторної трубки. З’ясуємо суть цього закону.
Нехай  – соленоїдальне поле.
Розглянемо відрізок «векторної трубки», тобто область, обмежену двома
перерізами
– соленоїдальне поле.
Розглянемо відрізок «векторної трубки», тобто область, обмежену двома
перерізами 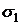 і
і 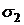 та боковою поверхнею
та боковою поверхнею 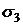 , яка складається із
векторних ліній (рис. 1). Застосуємо до такої області формулу
Остроградського-Гаусса (8). Оскільки в
соленоїдальному полі
, яка складається із
векторних ліній (рис. 1). Застосуємо до такої області формулу
Остроградського-Гаусса (8). Оскільки в
соленоїдальному полі 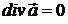 , то
потік векторного поля
, то
потік векторного поля  через
поверхню області дорівнює нулю:
через
поверхню області дорівнює нулю: 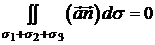 (
(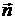 – одиничний вектор зовнішньої нормалі). На
боковій поверхні
– одиничний вектор зовнішньої нормалі). На
боковій поверхні 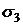 маємо
маємо
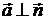 , тому
, тому 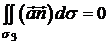 .
.
Отже,
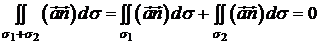 .
.
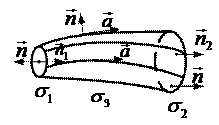
Рисунок 1 –
Відрізок «векторної трубки»
Змінимо на
перерізі 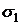 напрям
нормалі
напрям
нормалі 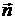 на протилежний
(
на протилежний
(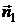 – внутрішня нормаль
до
– внутрішня нормаль
до 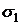 ). Тоді отримаємо
). Тоді отримаємо
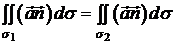 ,
,
де обидва потоки
через перерізи 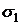 і
і 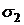 обчислюються в напрямі
векторних ліній.
обчислюються в напрямі
векторних ліній.
Таким чином, у
соленоїдальному (трубчастому) векторному полі 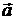 потік через будь-який переріз векторної трубки
набуває одного й того самого значення. Це і є закон збереження інтенсивності
збереження векторної трубки.
потік через будь-який переріз векторної трубки
набуває одного й того самого значення. Це і є закон збереження інтенсивності
збереження векторної трубки.
Нехай в області  , обмеженій поверхнею
, обмеженій поверхнею  , визначено векторне поле
, визначено векторне поле  . Запишемо формулу (8) для
векторного поля
. Запишемо формулу (8) для
векторного поля 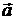 в
області
в
області  . Застосовуючи
до лівої частини цієї формули теорему про середнє, отримаємо
. Застосовуючи
до лівої частини цієї формули теорему про середнє, отримаємо
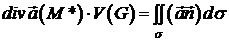
або
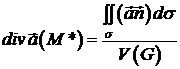 ,
,
де 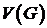 – об’єм області
– об’єм області  , а
, а 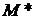 – деяка точка області
– деяка точка області  .
.
Зафіксуємо точку 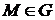 і стягуватимемо область
і стягуватимемо область  до точки
до точки 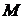 так, щоб
так, щоб 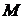 залишалася внутрішньою точкою області
залишалася внутрішньою точкою області  . Тоді
. Тоді 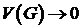 , а
, а 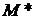 прямуватиме до
прямуватиме до 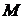 . Внаслідок неперервності
. Внаслідок неперервності 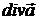 значення
значення 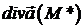 прямуватиме до
прямуватиме до 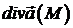 . Таким чином, отримуємо
. Таким чином, отримуємо
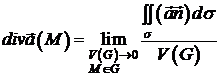 . (9)
. (9)
У праву частину
формули (9) входять величини, інваріантні відносно вибору системи координат
(потік векторного поля через поверхню і об’єм області). Тому формула (9) дає
інваріантне означення дивергенції векторного поля. Отже, дивергенція векторного
поля залежить тільки від самого поля і не залежить від вибору системи
координат.
6. Циркуляція
векторного поля
Розглянемо
векторне поле  , визначене
в просторовій області
, визначене
в просторовій області  ,
і деяку кусково-гладку криву
,
і деяку кусково-гладку криву 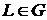 , на якій вказано напрям обходу (вибір напряму
обходу називають також орієнтацією кривої). Нехай
, на якій вказано напрям обходу (вибір напряму
обходу називають також орієнтацією кривої). Нехай 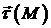 – одиничний дотичний вектор до кривої
– одиничний дотичний вектор до кривої 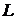 у точці
у точці 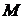 , напрямлений в сторону обходу
кривої.
, напрямлений в сторону обходу
кривої.
Криволінійний
інтеграл
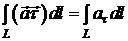 (10)
(10)
називається
циркуляцією векторного поля 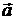 вздовж кривої
вздовж кривої 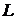 у заданому напрямі.
у заданому напрямі.
Якщо взяти інший
напрям обходу кривої (змінити орієнтацію), то вектор 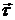 змінить напрям на протилежний, тому скалярний
добуток
змінить напрям на протилежний, тому скалярний
добуток 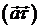 , а, отже, і
циркуляція (криволінійний інтеграл (10)) змінить знак.
, а, отже, і
циркуляція (криволінійний інтеграл (10)) змінить знак.
Якщо 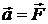 – силове векторне поле,
тобто
– силове векторне поле,
тобто 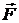 – вектор сили,
то циркуляція
– вектор сили,
то циркуляція 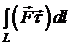 визначає
роботу силового векторного поля вздовж кривої
визначає
роботу силового векторного поля вздовж кривої 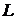 в заданому напрямі.
в заданому напрямі.
Якщо в
прямокутній системі координат 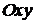
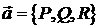 , а
, а 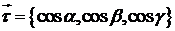 , то вираз (10) для циркуляції векторного поля
, то вираз (10) для циркуляції векторного поля 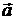 можна записати в вигляді
можна записати в вигляді
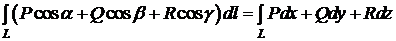 . (11)
. (11)
Кожний доданок у
правій частині (11) залежить від вибору системи координат, проте їхня сума,
тобто циркуляція 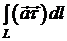 ,
очевидно, не залежить від вибору системи координат.
,
очевидно, не залежить від вибору системи координат.
Якщо ввести
вектор 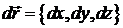 , то циркуляцію
можна записати у вигляді
, то циркуляцію
можна записати у вигляді 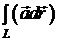 (порівняйте
з правою частиною рівності (11)).
(порівняйте
з правою частиною рівності (11)).
7. Формула
Стокса у векторній формі
Нехай в області  визначено векторне поле
визначено векторне поле 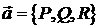 ;
; 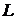 – замкнений контур, який лежить в області
– замкнений контур, який лежить в області  ;
;  – довільна поверхня, межею якої є контур
– довільна поверхня, межею якої є контур 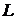 ;
; 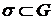 («поверхня
(«поверхня  натягнута на контур
натягнута на контур 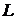 »);
»); 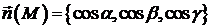 – одиничний вектор нормалі на обраній стороні
поверхні
– одиничний вектор нормалі на обраній стороні
поверхні  .
.
Нехай функції 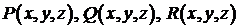 та їхні частинні похідні
першого порядку неперервні на поверхні
та їхні частинні похідні
першого порядку неперервні на поверхні  . Тоді справедлива формула Стокса
. Тоді справедлива формула Стокса
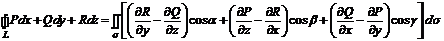 ,
,
де орієнтація
контуру 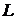 узгоджена з
орієнтацією поверхні
узгоджена з
орієнтацією поверхні  .
Ліва частина формули Стокса є циркуляцією векторного поля
.
Ліва частина формули Стокса є циркуляцією векторного поля 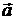 вздовж контура
вздовж контура 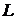 , а права частина визначає потік
через поверхню
, а права частина визначає потік
через поверхню  векторного
поля з координатами
векторного
поля з координатами 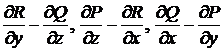 ,
тобто потік
,
тобто потік 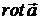 через
поверхню
через
поверхню  . Тому формулу
Стокса можна записати у векторній формі:
. Тому формулу
Стокса можна записати у векторній формі:
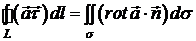 (12)
(12)
або
 . (13)
. (13)
Фізичний зміст
формули Стокса: циркуляція векторного поля 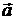 вздовж замкненого контуру дорівнює потоку
ротора векторного поля
вздовж замкненого контуру дорівнює потоку
ротора векторного поля 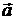 через
поверхню, натягнуту на цей контур.
через
поверхню, натягнуту на цей контур.
8. Властивості
потенціального поля
Як відомо,
векторне поле  , яке
задовольняє в області
, яке
задовольняє в області  умову
умову
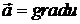 , називається
потенціальним у цій області (
, називається
потенціальним у цій області (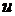 – скалярний потенціал поля
– скалярний потенціал поля  ). Якщо поле
). Якщо поле 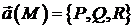 потенціальне в області
потенціальне в області  , то
, то 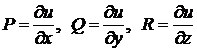 і вираз
і вираз 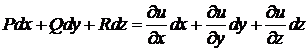 є повним диференціалом функції
є повним диференціалом функції 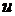 в області
в області  . Це означає, що виконана умова незалежності
криволінійного інтеграла від шляху інтегрування в просторі.
. Це означає, що виконана умова незалежності
криволінійного інтеграла від шляху інтегрування в просторі.
Таким чином,
потенціальне в області  поле
має такі властивості.
поле
має такі властивості.
1. Циркуляція
потенціального поля  вздовж
довільного замкненого контуру
вздовж
довільного замкненого контуру 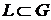 дорівнює нулю:
дорівнює нулю:
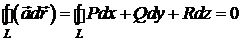 .
.
2. Для довільних
точок 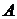 і
і 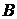 області
області  циркуляція потенціального поля
циркуляція потенціального поля 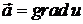 вздовж кривої
вздовж кривої 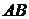 не залежить від вибору кривої
не залежить від вибору кривої 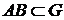 і дорівнює різниці значень
потенціала
і дорівнює різниці значень
потенціала 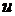 в точках
в точках 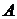 і
і 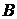 :
:
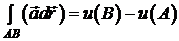 .
.
У випадку
силового потенціального поля ця властивість означає, що робота такого поля
вздовж кривої 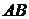 не
залежить від вибору кривої, а залежить тільки від початкової і кінцевої точок
не
залежить від вибору кривої, а залежить тільки від початкової і кінцевої точок 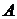 і
і 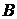 .
.
3. Потенціальне
поле  є безвихровим,
тобто
є безвихровим,
тобто 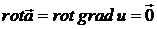 .
.
Нехай тепер дано
векторне поле 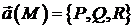 , яке
задовольняє в області
, яке
задовольняє в області  умову
умову
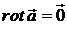 . Чи випливає звідси,
що поле
. Чи випливає звідси,
що поле  є
потенціальним в області
є
потенціальним в області  ?
Відповідь на це запитання залежить від форми області
?
Відповідь на це запитання залежить від форми області  . Якщо область
. Якщо область  є поверхнево однозв’язною, то із умови
є поверхнево однозв’язною, то із умови 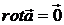 випливає, що існує функція
випливає, що існує функція 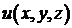 така, що
така, що
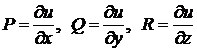 .
.
Отже, 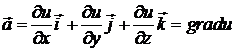 , тобто поле
, тобто поле 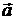 є потенціальним в області
є потенціальним в області  .
.
Таким чином,
умова 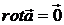 є необхідною і
достатньою умовою потенціальності поля
є необхідною і
достатньою умовою потенціальності поля  у поверхнево однозв’язній області.
у поверхнево однозв’язній області.
Потенціал 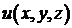 потенціального поля
потенціального поля 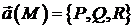 у поверхнево однозв’язній
області можна обчислити за формулою:
у поверхнево однозв’язній
області можна обчислити за формулою:
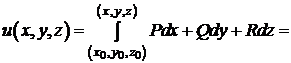
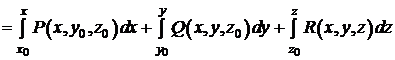 . (14)
. (14)
Якщо область  не є поверхнево однозв’язною,
то умова
не є поверхнево однозв’язною,
то умова 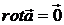 не є
достатньою для потенціальності поля
не є
достатньою для потенціальності поля  в області
в області  .
.
9. Інваріантне
означення ротора
Нехай в області  визначено векторне поле
визначено векторне поле  . Зафіксуємо точку
. Зафіксуємо точку 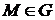 і деяку площину, яка
проходить через цю точку. Нехай
і деяку площину, яка
проходить через цю точку. Нехай 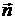 – одиничний вектор нормалі до площини,
– одиничний вектор нормалі до площини, 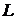 – замкнений контур, який
лежить в площині і обмежує область
– замкнений контур, який
лежить в площині і обмежує область  таку, що
таку, що 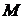 – внутрішня точка області
– внутрішня точка області  . Запишемо формулу (12) для
векторного поля
. Запишемо формулу (12) для
векторного поля 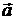 в
області
в
області  . Застосовуючи
до правої частини цієї формули теорему про середнє, отримуємо
. Застосовуючи
до правої частини цієї формули теорему про середнє, отримуємо
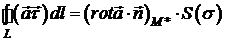 ,
,
диференціальне
векторне поле формула соленоїдальне
звідки
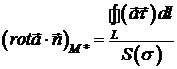 ,
,
де 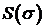 – площа області
– площа області  ,
, 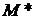 – деяка точка області
– деяка точка області  .
.
Стягуватимемо
область  до точки
до точки 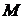 так, щоб
так, щоб 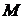 залишалася внутрішньою точкою
області
залишалася внутрішньою точкою
області  . Тоді
. Тоді 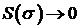 , а
, а 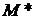 прямуватимемо до
прямуватимемо до 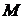 . Внаслідок неперервності
. Внаслідок неперервності 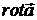 значення
значення 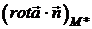 прямуватимемо до
прямуватимемо до 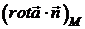 . Таким чином, отримуємо
. Таким чином, отримуємо
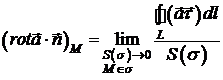 .
.
У праву частину
формули входять величини, інваріантні відносно вибору системи координат
(циркуляція векторного поля вздовж замкненого контура і площа плоскої області).
Тому дана формула дає інваріантне означення проекції 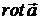 в точці
в точці 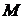 на напрям, який виражається заданим вектором
на напрям, який виражається заданим вектором 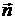 .
.
Отже, проекція
ротора векторного поля на довільний напрям, а отже, і сам 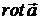 залежить тільки від векторного поля
залежить тільки від векторного поля 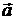 і не залежить від вибору
системи координат.
і не залежить від вибору
системи координат.
Для означення
вектора 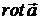 вищезазначеним
способом достатньо розглянути в заданій точці
вищезазначеним
способом достатньо розглянути в заданій точці 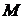 проекції
проекції 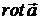 на три довільних некомпланарних напрями.
Такими трьома проекціями
на три довільних некомпланарних напрями.
Такими трьома проекціями 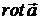 визначається
однозначно.
визначається
однозначно.