Складність деяких методів експоненціювання точки кривої
Складність деяких методів експоненціювання точки кривої
Найпоширенішою операцією у всіх криптографічних
алгоритмах є 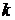 - кратне додавання
точки
- кратне додавання
точки 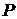 , позначуване як
, позначуване як 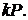
Цю операцію звичайно називають скалярним множенням,
або, звертаючись до термінології мультиплікативної групи, експоненціюванням точки
кривої.
З метою підвищення продуктивності під час обчислення
точки 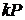 багатьма авторами
запропоновано різні методи. Дамо стислий опис й оцінку складності найпоширеніших
з них.
багатьма авторами
запропоновано різні методи. Дамо стислий опис й оцінку складності найпоширеніших
з них.
Підхід до розрахунку точки 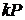 може відрізнятися залежно від того, чи
є точка
може відрізнятися залежно від того, чи
є точка 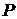 фіксованою (заздалегідь
відомою) або довільною точкою. У першому випадку завжди можна користуватися передрозрахунками
точок, наприклад,
фіксованою (заздалегідь
відомою) або довільною точкою. У першому випадку завжди можна користуватися передрозрахунками
точок, наприклад, 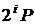 , які
зберігаються в пам'яті. Двійкове подання числа
, які
зберігаються в пам'яті. Двійкове подання числа 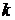 дозволяє селектрувати ті з них, які в результаті
підсумовування утворять точку
дозволяє селектрувати ті з них, які в результаті
підсумовування утворять точку 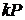 . У другому, більш загальному випадку, всі обчислення
доводиться проводити в реальному часі.
. У другому, більш загальному випадку, всі обчислення
доводиться проводити в реальному часі.
Нехай порядок 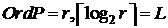 і число
і число 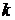 подано у двійковій системі
подано у двійковій системі
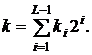
Розглянемо спочатку основні алгоритми експоненціювання
при невідомій заздалегідь точці 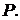
експоненціювання алгоритм скалярне множення
Алгоритм подвоєння-додавання
Це найприродніший і найпростіший метод, при якому
обчислення здійснюються за формулою
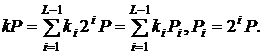
Ці обчислення на основі методу розрахунку ліворуч-праворуч
здійснюються за допомогою наступного алгоритму.
Алгоритм 1.
Вхід: 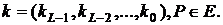
Вихід: 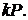
1. 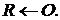
2. 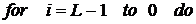
2.1 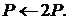
2.2 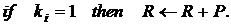
3. 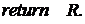 .
.
Реалізація методу вимагає 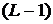 операцій
операцій 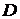 подвоєння точки й
подвоєння точки й 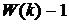 додавань
додавань 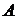 , де
, де 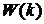 - вага Хеммінга двійкового вектора
- вага Хеммінга двійкового вектора 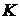 (число одиниць цього вектора).
Оскільки в середньому число одиниць випадкового вектора дорівнює
(число одиниць цього вектора).
Оскільки в середньому число одиниць випадкового вектора дорівнює 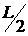 , загальне число групових операцій оцінюється
величиною
, загальне число групових операцій оцінюється
величиною 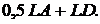
Алгоритм подвоєння-додавання-віднімання
Попередній алгоритм можна вдосконалити, якщо вести
додаткову операцію-віднімання точки. Цей метод запропонований в 1990 році Ф. Морейном
і Дж. Олівосом. Наприклад, число 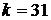 у двійковій системі має вага у
у двійковій системі має вага у 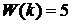 , але його можна подати як
, але його можна подати як 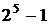 з вагою
з вагою 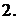 Ця ідея знижує вагу Хеммінга і, відповідно,
число групових операцій. Реалізувати алгоритм подвоєння - додавання віднімання можна
переходом від двійкового подання числа
Ця ідея знижує вагу Хеммінга і, відповідно,
число групових операцій. Реалізувати алгоритм подвоєння - додавання віднімання можна
переходом від двійкового подання числа 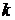 до трійкового
до трійкового 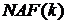 з коефіцієнтами
з коефіцієнтами 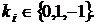
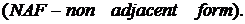 Одне із властивостей подання
Одне із властивостей подання 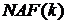 - відсутність у ньому суміжних пар ненульових
елементів, завдяки чому зростає питома вага нульових елементів
- відсутність у ньому суміжних пар ненульових
елементів, завдяки чому зростає питома вага нульових елементів 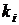 . Для розрахунку
. Для розрахунку 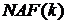 використовується наступний алгоритм.
використовується наступний алгоритм.
Алгоритм 2.
Вхід: позитивне ціле число 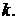
Вихід: 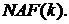
1. 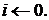
2. 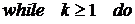
2.1 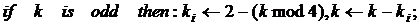
2.2 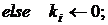
2.3 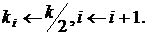
3. 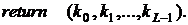
Після розрахунку 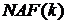 обчислюється точка
обчислюється точка 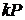 методом ліворуч-праворуч за допомогою алгоритму
3.
методом ліворуч-праворуч за допомогою алгоритму
3.
Алгоритм 3.
Вхід: 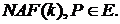
Вихід: 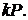
1. 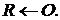
2. 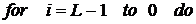
2.1 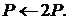
2.2 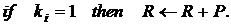
2.3 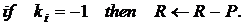
3. 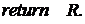 .
.
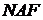 -подання числа
-подання числа 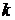 може виявитися на один біт більше двійкового. Водночас,
для випадкового
може виявитися на один біт більше двійкового. Водночас,
для випадкового 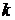 ймовірність
ненульових елементів
ймовірність
ненульових елементів 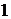 і
і
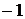 знижується від
знижується від 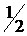 до
до 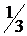 , тобто, у середньому, для
, тобто, у середньому, для 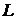 - розрядного числа їхня кількість оцінюється
величиною
- розрядного числа їхня кількість оцінюється
величиною 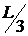 . Тоді загальне
середнє число групових операцій додавання
. Тоді загальне
середнє число групових операцій додавання 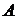 й подвоєння
й подвоєння 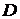 в алгоритмі 3 можна оцінити як суму
в алгоритмі 3 можна оцінити як суму 
Метод вікон з алгоритмом подвоєння - додавання - віднімання
Якщо в криптосистемі є резерви пам'яті, їх можна
задіяти для подальшого збільшення швидкості обчислень. Ідея в тому, що замість точки
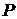 можна експоненціювати і
надалі складати суміжні блоки або вікна шириною
можна експоненціювати і
надалі складати суміжні блоки або вікна шириною 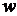 в
в  - поданні точки
- поданні точки 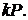
Для цього розраховується за допомогою алгоритму
2 трійкове число 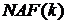 , що потім
може розбиватися на блоки довжиною, не менше
, що потім
може розбиватися на блоки довжиною, не менше 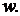
Назвемо 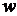 - вікном числа
- вікном числа 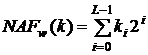 непарний коефіцієнт
непарний коефіцієнт 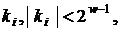 утримуючий хоча б один ненульовий елемент. Зазначимо,
що
утримуючий хоча б один ненульовий елемент. Зазначимо,
що 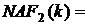
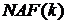 . Наприклад, при
. Наприклад, при 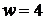 маємо вісім різних значень
маємо вісім різних значень 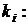
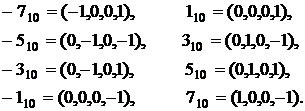
Цих вікон достатньо для формування числа 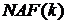 довільної довжини
довільної довжини 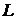 . Зазначимо, що парні коефіцієнти
в
. Зазначимо, що парні коефіцієнти
в 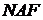 - поданні числа
- поданні числа 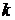 надлишкові, тому що вони утворяться
подвоєнням непарних. На першому етапі передрозрахунків розраховуються й записуються
на згадку вісім точок:
надлишкові, тому що вони утворяться
подвоєнням непарних. На першому етапі передрозрахунків розраховуються й записуються
на згадку вісім точок: 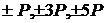 і
і 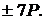
У загальному випадку в пам'яті зберігається 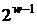 точок. Число
точок. Число 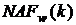 може бути визначене за допомогою модифікованого
алгоритму 2. Модифікація полягає в тому, що: на кроці 2.1 замість
може бути визначене за допомогою модифікованого
алгоритму 2. Модифікація полягає в тому, що: на кроці 2.1 замість 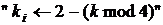 необхідно записати
необхідно записати 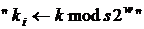 , де
, де 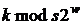 означає ціле число
означає ціле число 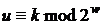 , певне в інтервалі
, певне в інтервалі 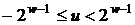 . Далі обчислюється точка
. Далі обчислюється точка 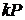 згідно з алгоритмом 4.
згідно з алгоритмом 4.
Алгоритм 4.
Вхід: 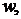
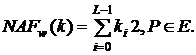
Вихід: 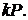
1. 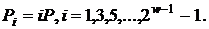
2. 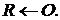
3. 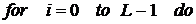
3.1 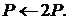
3.2 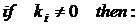
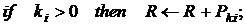
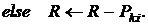
4. 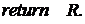 .
.
Нехай, наприклад,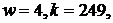 при цьому
при цьому 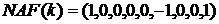 й
й 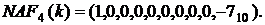 Використання трійкового
Використання трійкового 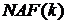 вимагає, мабуть, двох додавань точок,
тоді як у другому випадку за рахунок попереднього розрахунку точки
вимагає, мабуть, двох додавань точок,
тоді як у другому випадку за рахунок попереднього розрахунку точки 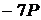 достатньо одного додавання.
Число подвоєнь однаково в обох випадках. Зрозуміло також, що виграш за рахунок вікна
з'являється лише при порівняно більших довжинах
достатньо одного додавання.
Число подвоєнь однаково в обох випадках. Зрозуміло також, що виграш за рахунок вікна
з'являється лише при порівняно більших довжинах 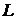 числа
числа 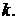
Перший крок алгоритму 4 у загальному випадку вимагає
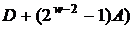 групових операцій із точками
кривої. На третьому кроці складність обчислень оцінюється середнім числом
групових операцій із точками
кривої. На третьому кроці складність обчислень оцінюється середнім числом 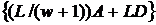 групових операцій додавання
й подвоєння. Збільшення ширини
групових операцій додавання
й подвоєння. Збільшення ширини 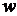 вікна веде до збільшення складності обчислень на
першому кроці (і об'єму пам'яті) і зниження тимчасової складності на третьому кроці.
Для значень
вікна веде до збільшення складності обчислень на
першому кроці (і об'єму пам'яті) і зниження тимчасової складності на третьому кроці.
Для значень 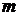 розширення
поля порядку 180-260 оптимальним виявляється вікно шириною
розширення
поля порядку 180-260 оптимальним виявляється вікно шириною 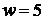 , а при
, а при 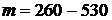 - вікно шириною
- вікно шириною 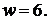
Метод Монтгомері
Розглянемо метод Монтгомері. Нехай 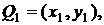
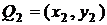 з
з  Позначимо
Позначимо 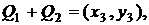
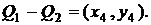 Можна перевірити, що
Можна перевірити, що
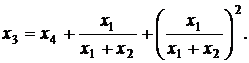 (1)
(1)
Отже, знаючи 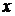 - координати точок
- координати точок 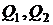 й
й 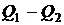 , можна обчислити
, можна обчислити 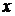 координати точок
координати точок 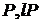 й
й 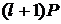 , перейти до пари
, перейти до пари 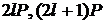 , або до пари
, або до пари 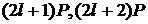 .
.
Кожна така ітерація вимагає одного подвоєння й
одного додавання з використанням формули (1).
Після останньої ітерації, 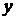 - координата точки
- координата точки 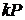 може бути відновлена з
може бути відновлена з 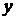 - координати точки
- координати точки 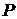 й
й 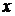 - координат точок
- координат точок 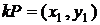 і
і 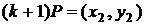 за формулою
за формулою
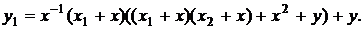
Використовуючи проективні координати, можна позбутися
від інвертування, і кожна ітерація вимагатиме шість множень. Усього ж трудомісткість
алгоритму 5, що реалізує метод експоненціювання Монтгомері, дорівнює 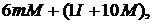 причому алгоритм не вимагає
додаткової пам'яті на зберігання попередньо обчислених змінних, а час його роботи
не залежить від значення
причому алгоритм не вимагає
додаткової пам'яті на зберігання попередньо обчислених змінних, а час його роботи
не залежить від значення 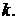
Алгоритм 5. Метод експоненціювання Монтгомері.
Вхід: 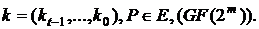
Вихід: 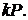
2. 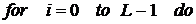
2.1 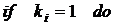
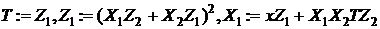
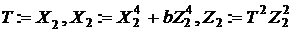
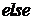
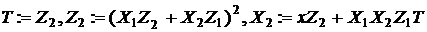
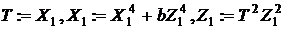
3.1 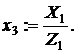
3.2 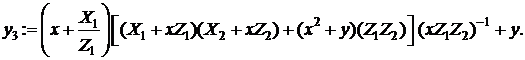
4. 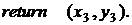
Алгоритм 5 вимагає однієї інверсії, а не двох,
тому що можна обчислити
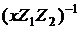 , а
, а 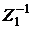 потім отримати множенням на
потім отримати множенням на 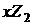 . Можна домогтися істотного збільшення
продуктивності, якщо операцію подвоєння замінити операцією ділення точки на два.
Виграш до 40% при цьому досягається у зв'язку з відсутністю операції інверсії елемента
в полі. Крім того, групові операції послідовних ділень у НБ зводяться практично
до однієї операції множення в полі.
. Можна домогтися істотного збільшення
продуктивності, якщо операцію подвоєння замінити операцією ділення точки на два.
Виграш до 40% при цьому досягається у зв'язку з відсутністю операції інверсії елемента
в полі. Крім того, групові операції послідовних ділень у НБ зводяться практично
до однієї операції множення в полі.
Методи експоненціювання при фіксованій точці
Фіксованою точкою в криптосистемі завжди є генератор
або базова точка криптосистеми порядку 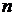 . Такі точки - це відкриті ключі користувачів. Якщо
в системі є резерв пам'яті, його можна використати для зберігання заздалегідь розрахованих
точок. Наприклад, якщо обчислити й записати в пам'яті точки
. Такі точки - це відкриті ключі користувачів. Якщо
в системі є резерв пам'яті, його можна використати для зберігання заздалегідь розрахованих
точок. Наприклад, якщо обчислити й записати в пам'яті точки 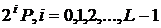 , то для визначення скалярного добутку
, то для визначення скалярного добутку
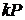 залишиться лише обчислити
суми точок відповідно до двійкового подання
залишиться лише обчислити
суми точок відповідно до двійкового подання 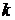 . У середньому для цього буде потрібно лише
. У середньому для цього буде потрібно лише 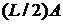 операцій. Їхнє число можна зменшити
до
операцій. Їхнє число можна зменшити
до 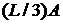 операцій додавання й
віднімання, якщо скористатися трійковим поданням
операцій додавання й
віднімання, якщо скористатися трійковим поданням 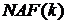 .
.
Другим досить витонченим підходом є підхід на основі
вікон з фіксованою базою. Замість двійкового подання числа використовується 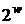 -е із передобчислюванням точок
-е із передобчислюванням точок
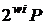 . Дійсно, нехай
. Дійсно, нехай 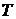 -е подання числа
-е подання числа 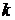 має вигляд
має вигляд
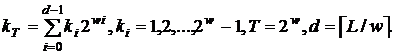
Тоді
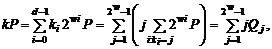
де 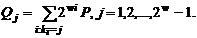
Ці обчислення здійснюються за допомогою наступного
алгоритму.
Алгоритм 6.
Вхід: ширина вікна 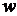 ,
, 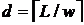 ,
,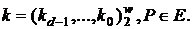
Вихід: 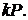
1. Передрозрахунки: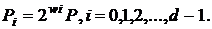
2. 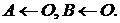
3. 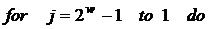
3.1 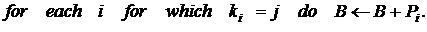
3.2 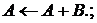
4. 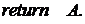
Середня обчислювальна складність алгоритму оцінюється
кількістю додавань :
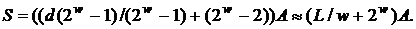 .
.
Метод вікон у цьому випадку більше продуктивний,
ніж при невідомій точці, тому що передрозрахунки не входять в алгоритм експоненціювання.
Якщо використати поряд з додаванням подвоєння точки, реалізувати алгоритм можна
інакше. Два вікна точки 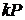 шириною
шириною
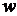 кожне можна подати у вигляді:
кожне можна подати у вигляді:
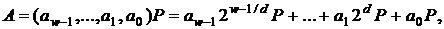
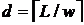 ;
;
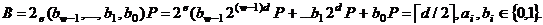
Всі можливі точки 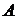 й
й  обчислюються на етапі передрозрахунків і записуються
на згадку. Загальна кількість цих точок
обчислюються на етапі передрозрахунків і записуються
на згадку. Загальна кількість цих точок 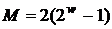 зростає експоненційно зі збільшенням ширини вікна
зростає експоненційно зі збільшенням ширини вікна
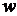 . Двійкове подання точки
. Двійкове подання точки
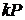 розбивається далі на
розбивається далі на 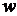 фрагментів шириною
фрагментів шириною 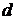 . У кожному такому фрагменті
відбираються старші розряди й розряди зі зрушенням вправо на
. У кожному такому фрагменті
відбираються старші розряди й розряди зі зрушенням вправо на 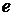 (тобто на половину фрагмента).
(тобто на половину фрагмента).
Їхні двійкові подання дають першу пару точок 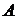 й
й 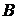 , які складаються, після чого їхня сума подвоюється.
, які складаються, після чого їхня сума подвоюється.
Далі реалізується алгоритм послідовних додавань
і подвоєнь праворуч із двома вікнами, описаний нижче.
Алгоритм 7.
Вхід: ширина вікна 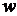 ,
, 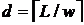 ,
,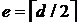 ,
,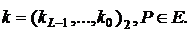
Вихід: 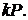
1. Передрозрахунки: обчислити всі точки 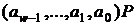 й
й
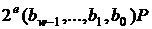 ,
, 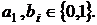
2. Подати число 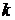 у вигляді конкатенації фрагментів шириною
у вигляді конкатенації фрагментів шириною 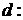
 Нехай
Нехай 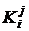 означає
означає 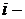 й біт фрагмента
й біт фрагмента 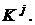
3. 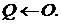
4. 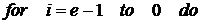
4.1 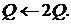
4.2 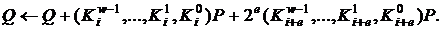
5. 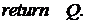
Обчислювальна складність цього алгоритму оцінюється
числом групових операцій
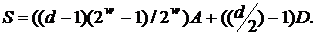
Обмінюючи час обчислень на пам'ять, можна й далі
підвищувати продуктивність експоненціювання точки кривої. Наприклад, для кожного
вікна шириною 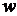 можна заздалегідь
розрахувати
можна заздалегідь
розрахувати 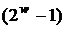 точок, при
цьому на згадку рийдеться записати
точок, при
цьому на згадку рийдеться записати 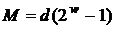 точок. Операція подвоєння в цьому випадку не використовується,
а складність оцінюється числом
точок. Операція подвоєння в цьому випадку не використовується,
а складність оцінюється числом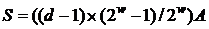 додавань. Цей алгоритм назвемо алгоритмом максимальної
пам'яті. У табл.13.1 дані для порівняння величини пам'яті
додавань. Цей алгоритм назвемо алгоритмом максимальної
пам'яті. У табл.13.1 дані для порівняння величини пам'яті 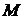 й тимчасової складності
й тимчасової складності 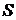 (числа групових операцій) алгоритму
6 й алгоритму максимальної пам'яті при
(числа групових операцій) алгоритму
6 й алгоритму максимальної пам'яті при 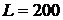 . В обох випадках зі збільшенням ширини вікна збільшується
пам'ять і знижується число групових операцій. Очевидно, що останній алгоритм за
наявності більших резервів пам'яті дозволяє істотно прискорити операцію експоненціювання
фіксованої точки
. В обох випадках зі збільшенням ширини вікна збільшується
пам'ять і знижується число групових операцій. Очевидно, що останній алгоритм за
наявності більших резервів пам'яті дозволяє істотно прискорити операцію експоненціювання
фіксованої точки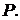
Таблиця
1 - Об'єм пам'яті
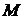 й тимчасова складність
й тимчасова складність 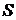 (число групових операцій) алгоритму
6 й алгоритму максимальної пам'яті при
(число групових операцій) алгоритму
6 й алгоритму максимальної пам'яті при 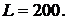
|
Метод
|
W = 3
|
W = 4
|
W = 5
|
W = 6
|
|
M
|
S
|
M
|
S
|
M
|
S
|
M
|
S
|
|
Алгоритм 6
|
14
|
900
|
30
|
62
|
632
|
126
|
529
|
|
Алгоритм
максимальної пам'яті.
|
469
|
58
|
750
|
46
|
1280
|
38
|
2079
|
33
|
A