|
N
|
Координаты точек
|
|
Вар
|
A1
|
A3
|
A4
|
|
2.19
|
(8;6;4)
|
(10;5;5)
|
(5;6;8)
|
(8;10;7)
|
Решение:
Воспользуемся
формулой для вычисления расстояние между двумя точками:
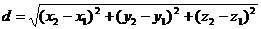
Наши
точки А1(8; 6; 4) и A2(10; 5; 5):
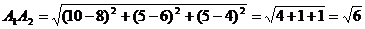ед.
Длина ребра А1А2 равна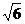 
ед.
Составим уравнение прямой
проходящей через точки А1(8; 6; 4) и A4(8; 10; 7).
Для этого воспользуемся
уравнением: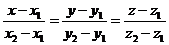 
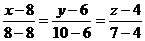, т.е. А1А4: 
.
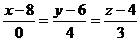Найдем
уравнение плоскости, проходящей через точки А1(8; 6; 4), A2(10;
5; 5), А3(5; 6; 8).
Воспользуемся
формулой: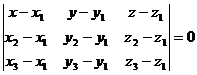 
Подставим
данные:
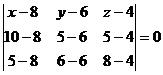или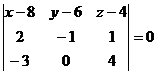 
Т.е. уравнение грани А1А2А3:
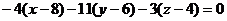или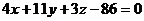 
Искомая высота проходит через точку A4(8;
10; 7) и перпендикулярна плоскости 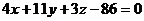, имеющей вектор нормали 
.
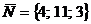Направляющий вектор
высоты совпадает с вектором нормали плоскости, к которой проведена высота,
следовательно, т.к. каноническое уравнение прямой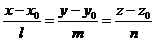 
, то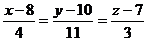 
уравнение искомой высоты.
Площадь треугольника А1А2А3
можно найти по формул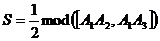е: 
,
где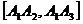 
- векторное
произведение двух векторов
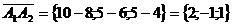и 
.
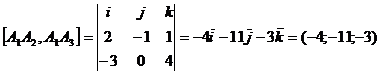
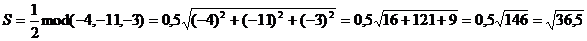кв.ед.
Объем пирамиды можно найти по
формул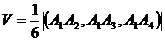е: 
, где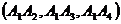 
- смешанное произведение
трех векторов 
, 
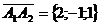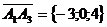и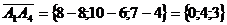 
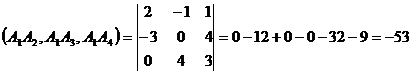
Тогда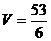 
куб.ед.
Ответ:
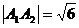ед.; А1А4: 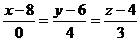; А1А2А3:
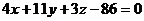
h: ;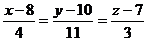 
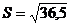кв.ед.; 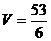куб.ед.
4. Найти собственные числа и собственные векторы матрицы
А.
;
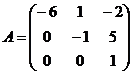Решение:
Найдем характеристическое
уравнение матрицы А – определитель матрицы А -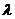
Е, где Е – единичная
матрица, 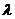– независимая
переменная.
А –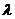Е =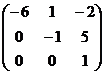 
– 
= 
.
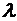
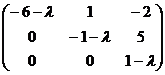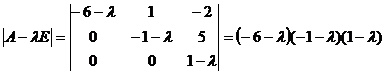
Найдем теперь собственные
числа матрицы А – корни характеристического уравнения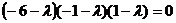 
. Получаем:
Получаем:
, 
, 
.
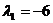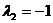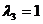Далее найдем собственные
векторы матрицы А, соответствующие каждому из собственных чисел.
Пусть Х =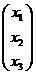 
– искомый собственный
вектор.
Тогда система однородных
уравнений (А -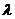Е)
= 0 выглядит так:
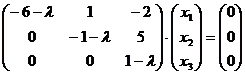или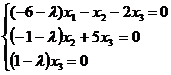 
Эта однородная система
линейных уравнений имеет множество решений, так как ее определитель равен нулю.
При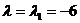 
система принимает вид:
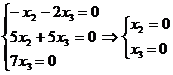
Общее решение этой
системы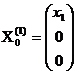 
, где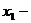 
любое число.
В качестве собственного
вектора достаточно взять любое частное решение.
Пусть, например,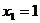 
, тогда собственный вектор,
соответствующий собственному числу 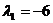, имеет вид: 
.
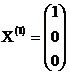При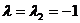 
система принимает вид:
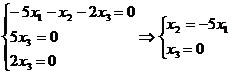
Общее решение этой
системы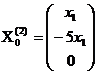 
, где 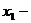любое число.
Пусть, например, 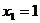, тогда собственный вектор,
соответствующий собственному числу 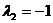, имеет вид: 
.
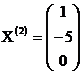Аналогично при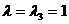 
получаем систему
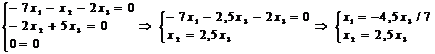
общее решение которой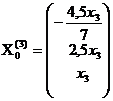 
, где 
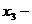любое число.
Пусть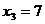 
, тогда собственный вектор,
соответствующий собственному числу 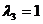, имеет вид: 
.
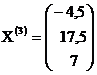Ответ: , , .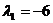
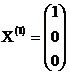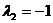
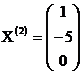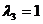
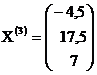5. Решить систему методом Жорданa - Гаусса. Найти общее решение и два частных. Сделать
проверку общего решения.
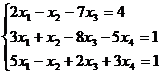
Решение:
Преобразуем расширенную матрицу
системы к диагональному виду:
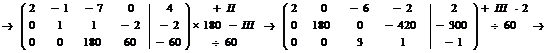
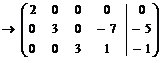
откуда получаем следующую систему
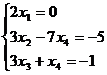и
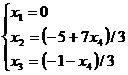- общее решение исходной системы уравнений.
Частные решения получим присвоив
конкретные значения переменной х4:
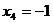тогда: 
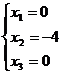, т.е. решением будет вектор (0; -4; 0; -1)
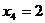тогда: 
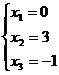, т.е. решением будет вектор (0; 3; -1; 2).
Выполним проверку общего решения:
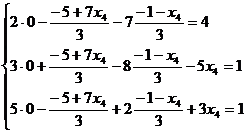
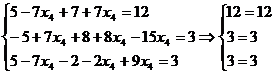- верные равенства.
Ответ: 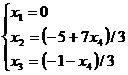; (0; -4; 0; -1); (0;
3; -1; 2).
к/р № 2
1.
Найти следующие
пределы.
а)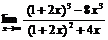 
б) 
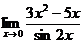
Решение:
а)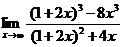 
- неопределенность с бесконечностью. Раскроем
скобки, приведем подобные и разделим числитель и знаменатель дроби на
максимальную степень х. Получим:
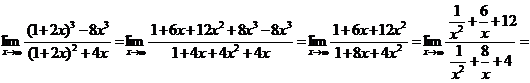
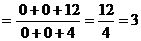
б) 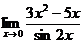- неопределенность 
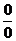. Избавимся от обнуляющего множителя, для этого
числитель разложим на множители, а к знаменателю применим эквивалентную
бесконечно малую: при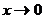 
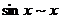. Получим:
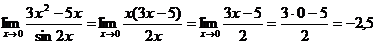
Ответ: а) 3; б) -2,5.
2.
Найти производные
функций, заданных в явном и неявном виде.
а)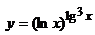 
б) 
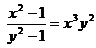
Решение:
а) Перепишем функцию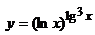 в виде экспоненты: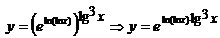 
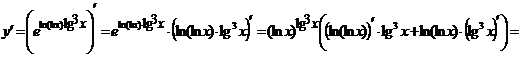
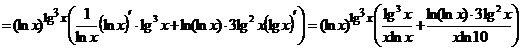
б) 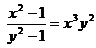- продифференцируем обе части равенства по х.
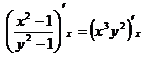
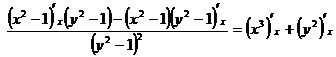
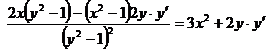
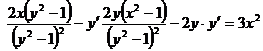
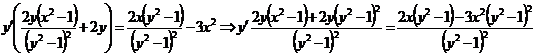
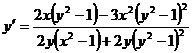
Ответ: решение выше.
3.
Исследовать
функцию методами дифференциального исчисления и построить ее график.
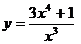
Решение:
1) Область определения функции: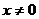 
.
2) Четность, периодичность: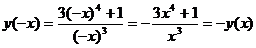 
, т.е. функция нечетная
(симметричная относительно начала координат), не периодическая.
3) Пересечение с осями:
с осью ОY: х = 0 – не принадлежит
области определения.
с осью OX: y = 0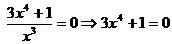 
- решения нет, точек пересечения с
осью ОХ нет.
4) Асимптоты и поведение на
бесконечности:
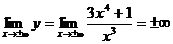
Наклонные асимптоты: y = kx + b, где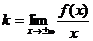 
b =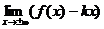 
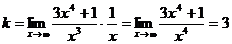
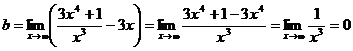
т.е. существует наклонная асимптота y
= 3х.
5) Поведение возле точки разрыва:
Наша точка разрыва x = 0.
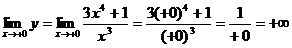
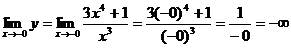
6) Критические точки:
Найдем производную функции y и решим
уравнение y´ = 0.
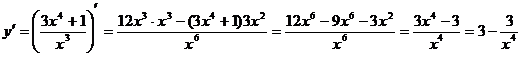
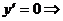
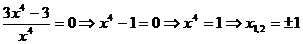
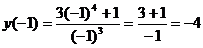
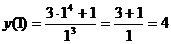
т.е. точка: (-1; -4) – точка максимума
и (1; 4) - точка минимума.
7) Точки перегиба:
Найдем вторую производную функции y и
решим уравнение y´´ = 0.
При x > 0 функция выпуклая, при x < 0 вогнутая.
8) Построим график функции:
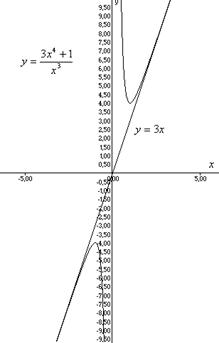
4.
Найти
градиент функции Z в точке М.
уравнение
матрица функция вектор дифференциальный
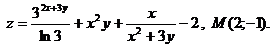
Решение:
Градиентом функции z в точке М является вектор grad (z) =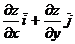 
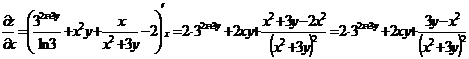
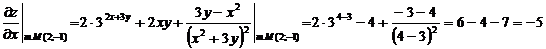
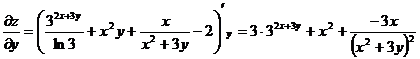
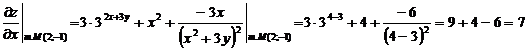
Т.е. grad(z) =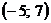 
.
Ответ: grad (z) = .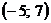
5.
Вычислить
неопределенные интегралы.
а)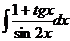 
б) 
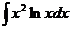с)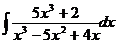 
.
Решение:
а)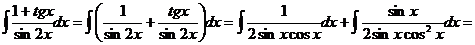 
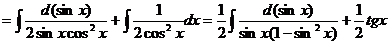
Рассмотрим интеграл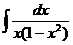 
:
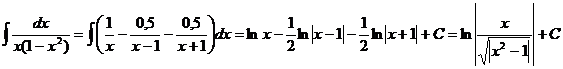
Тогда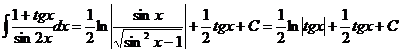 
б) Воспользуемся формулой
интегрирования по частям: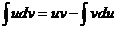 
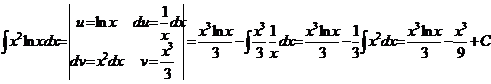
с) Разложим
подинтегральное выражение на простые дроби:
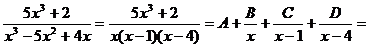
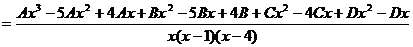, т.е.
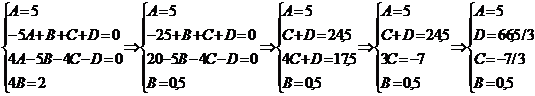
Тогда:
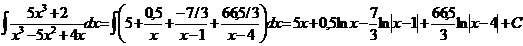
Ответ: решения выше.
6.
Вычислить объем
тела, образованного вращением фигуры, ограниченной графиками функций вокруг оси
OY
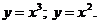
Решение:
Построим в координатной плоскости
заданную фигуру.
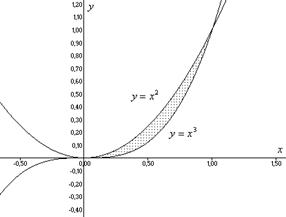
Объем тела, полученного вращением
плоской фигуры около оси ОХ найдем по формуле:
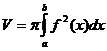
В нашем случае получаем:
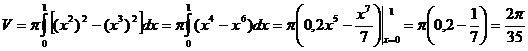куб.ед.
Ответ: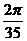 
куб.ед.
7.
А) Найти общее решение дифференциального уравнения.
Б) Найти решение задачи Коши
В) Найти общее решение дифференциального уравнения.
а)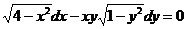 
;
б) 
; 
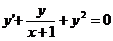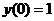; в)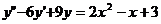 
.
Решение:
а) -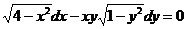
уравнение с разделяющимися переменными.
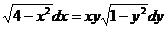
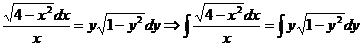
Возьмем интегралы:
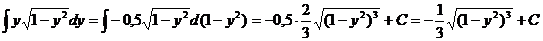
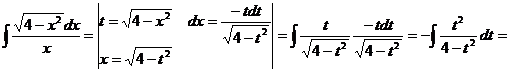
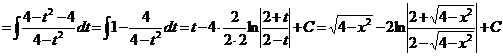
Таким
образом
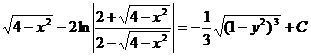- общее решение уравнения,
где С – произвольная константа.
б)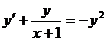 
- уравнение Бернулли.
Решим его, выполнив замену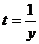 
. Тогда 
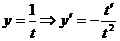и исходное уравнение примет вид: 
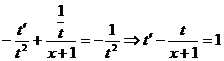- линейное неоднородное
уравнение первого порядка. Будем искать его решение в виде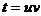 
, тогда 
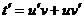и
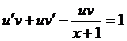
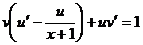
Функцию u будем искать такую, что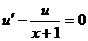 
, т.е.
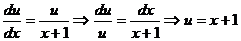
Тогда: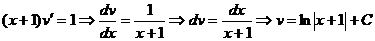 
В итоге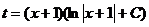 
и подставляя 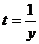получаем 
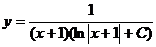- общее решение уравнения.
Найдём решение задачи Коши для :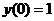
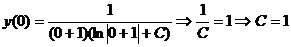
в) 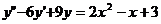- неоднородное уравнение
второго порядка с постоянными коэффициентами.
Его решение представляет собой сумму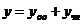 
, где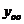 
- общее решение однородного
уравнения,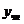 
- частное
решение неоднородного уравнения, зависящее от 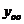и вида правой части неоднородного уравнения.
Решением уравнения вида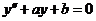 
будет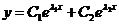 
, где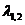 
- корни характеристического уравнения 
.
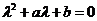Запишем характеристическое уравнение
для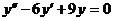 
:
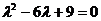и найдем его корни: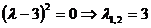 
Тогда решение уравнения имеет вид: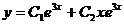 
, где С1 и С2
– произвольные константы.
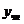будем искать в виде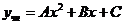 
Тогда:
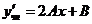
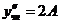и подставляя в уравнение 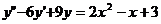получаем:
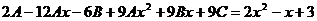
откуда, приравнивая коэффициенты при
соответствующих степенях х, получаем:
,
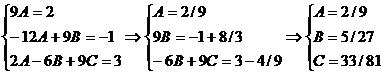т.е.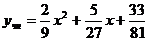 
Общее решение неоднородного уравнения
есть
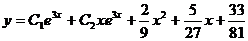
Ответ: а) ;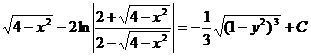
б)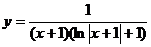 
;
с) .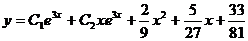
8.
а) Исследовать сходимость ряда.
б) Определить область сходимости
ряда.
а)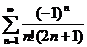 
б) 
.
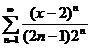Решение:
а) 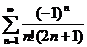- рассмотрим ряд из абсолютных
величин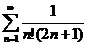 
.
Поскольку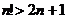 
, то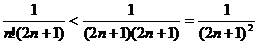 
.
Ряд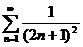 
сходится как обобщенный
гармонический ряд степени р = 2 >1, следовательно и меньший ряд 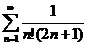также сходится.
Исходный ряд 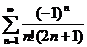сходится абсолютно.
б) Для степенного ряда вида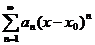 
интервалом сходимости будет
интервал (x0 – R; x0 + R),
где 
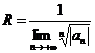- радиус
сходимости степенного ряда.
Для нашего ряда 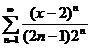получим: x0 = 2 и общий член 
.
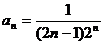Тогда: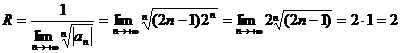 
Получили интервал сходимости (2 – 2;
2 + 2) или (0; 4).
Рассмотрим концы
интервала.
х = 4: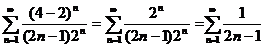 
- расходящийся гармонический ряд.
х = 0: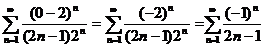 
- условно сходящийся ряд Лейбница.
Ответ: а) сходится абсолютно; б) [0;
4).