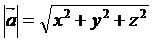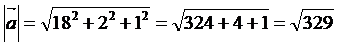Определитель матрицы

Оглавление

Задача 1

Задача 2

Задача 3

Задача 4

Задача 5

Задача 1

Вычислить определитель 4-го порядка.

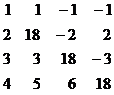
Решение:

Определитель 4-го порядка находится по формуле:

 ,

где

a_ij – элемент матрицы;

М_ij – минора элемента a_ij. Минора элемента a_ij матрицы А называется определитель матрицы, которая была получена путем удаления из матрицы А строк и столбцов, которые содержат элемент a_ij

Задача 2

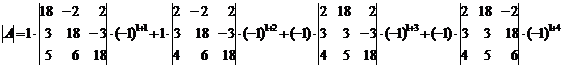
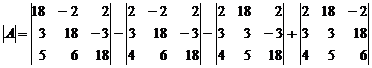
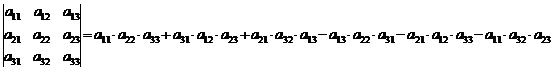
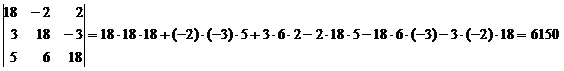
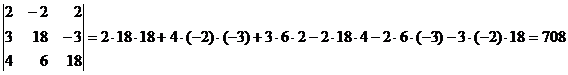
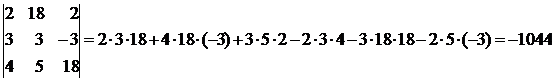
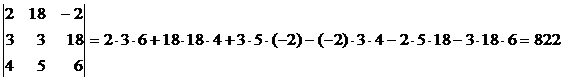
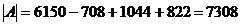
Решить систему матричным способом.

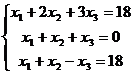
Решение:

1.   Введем обозначения:

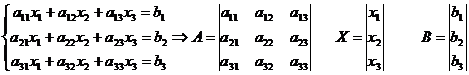
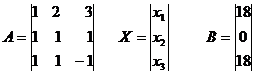
Тогда в матричной форме система имеет вид 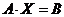, т.е.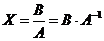

А^-1-обратная матрица, которая существует только тогда, когда исходная матрица А невырожденная, т.е.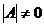

2.   Найдем определитель матрицы по формуле:

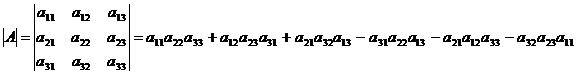
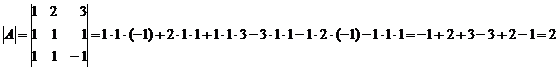
Так как 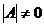, то матрица А – невырожденная и обратная матрица А^-1 существует и единственная.

3.   Найдем обратную матрицу по формуле:

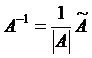, где

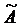- присоеденненая матрица, элементы которой 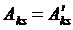 равны алгебраическим дополнениям элементов матрицы 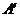, и затем транспонированная.

a.   найдем алгебраического дополнения всех элементов матрицы:

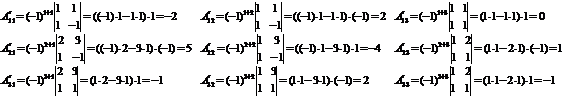
Получается матрица

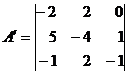
b. транспонируем матрицу (т.е. матрица A^T, полученная из исходной матрицы заменой строк на столбцы)

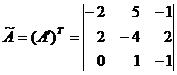
c.   обратная матрица равна:

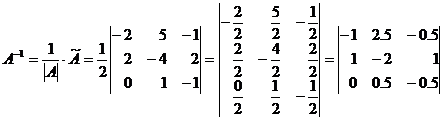
4.   Находим значение переменных х₁,х₂,х₃:

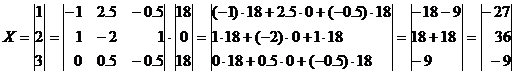
Х₁=-27,  Х₂=36,  Х₃=-9

Задача 3

Решить систему методом Крамера

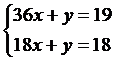
Решение:

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно)

1. Данную систему представим в виде матрицы:

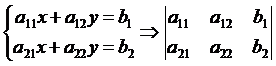
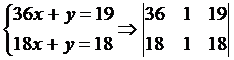
2. Найдем определители:

,

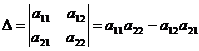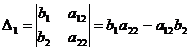
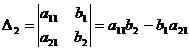
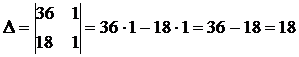
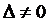(, т.е. можно применить метод Крамера)

;

.

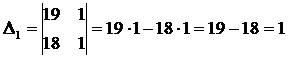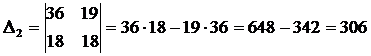3. Найдем значение x, y:

,

,

Задача 4

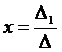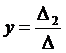
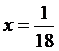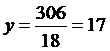
Найти общее решение системы, используя метод Жордана-Гаусса:

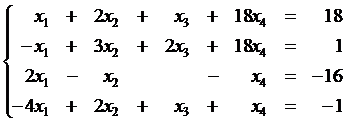
Решение:

Данную систему представим в виде матрицы:

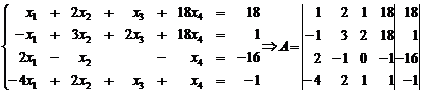
Шаг 1.  

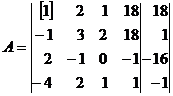
В качестве разрешающего элемента удобнее взять элемент а₁₁=1 (т.к. при делении на «1» число остается без изменения). Делим элементы строки на разрешающий элемент а₁₁. Разрешающие переменную х₁ следует исключить из остальных уравнений, поэтому в новой матрице 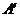в первом столбце во всех строках (кроме 1 строки) необходимо поставить значение «0». Другие элементы новой матрицы находим по правилу прямоугольника:

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

; 

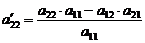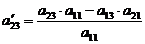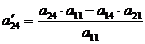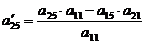
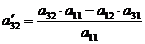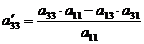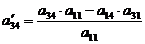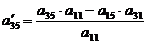
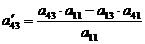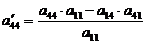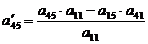
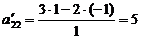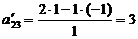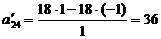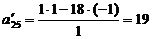
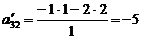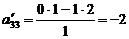
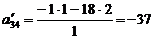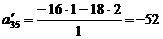
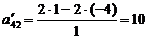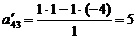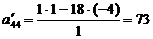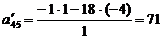
Шаг 2.  

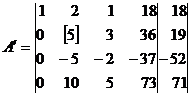
В полученной матрице в качестве разрешающего элемента берем не равный нулю элемент из любой строки, кроме первой, например а₂₂=5. Делим элементы разрешающей второй строки на «5». Все элементы первого столбца, кроме а₁₁ берем равные «0», а остальные элементы находим по правилу прямоугольника:

;      ;        

; ;

;               

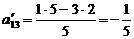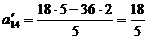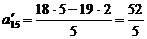
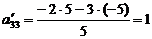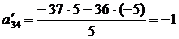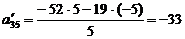
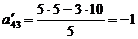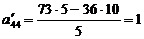
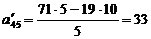
Шаг 3.  

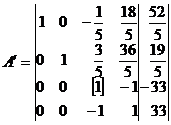
В полученной матрице в качестве разрешающего элемента берем не равный нулю элемент из любой строки, кроме первой и второй, например а₃₃=1. Делим элементы разрешающей второй строки на «1». Все элементы первого и второго столбца, кроме а₁₁=1 и а₂₂=1 берем равные «0», а остальные элементы находим по правилу прямоугольника:

;

;     

;       

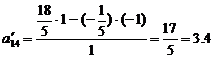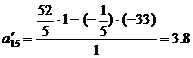
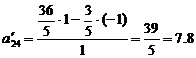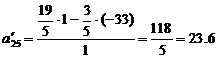
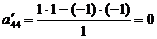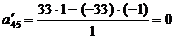
Шаг 4.  

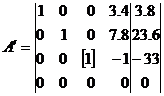
Так как больше строк в качестве разрешающих не осталось, выписываем систему уравнений, которая соответствует последней матрице:

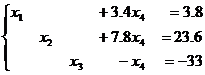
Предполагаем, что х₄ – это любое число С, тогда

Х₁=3,8-3,4С;                 Х₂=23,6-7,8С;               Х₃=-33+С

Задача 5

Даны векторы.

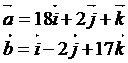
Найти:

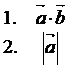
Решение:

Вектором называется направленный отрезок АВ с начальной точкой А и конечной точкой В.

Из данных уравнений выделим координаты векторов:

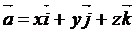, где координатами являются (x,y,z)

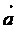т.е. координатами вектора  являются (18,2,1), а координатами вектора 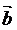являются (1,-2,17).

1. Скалярное произведение векторов находится по формуле:

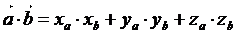
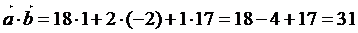
2. Длина 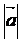 вектора  определяется по формуле: