Вивчення поняття відносин залежності
Курсова робота
Вивчення поняття відносин залежності
Зміст
Введення
1. Визначення й приклади
2. Простір залежності
3. Транзитивність
4. Зв'язок транзитивних
відносин залежності з операторами замикання
5. Матроїди
Висновок
Список літератури
Введення
Метою курсової роботи є вивчення поняття відносини
залежності, розгляд відносини залежності на різних множинах.
Поставлена мета припускає рішення наступних задач:
Вивчити й дати визначення поняттю відношення
залежності.
Розглянути деякі приклади відносини залежності.
Сформулювати й довести властивості й теореми як для
довільних, так і для транзитивних просторів залежності.
Розглянути теорему про зв'язок транзитивного
відношення залежності й алгебраїчного оператора замикання.
Вивчити поняття матроїда, привести приклади матроїдів.
Розглянути жадібний алгоритм і його зв'язок з
матроїдами.
На підставі поставлених цілей і задач кваліфікаційна
робота розбивається на 5 параграфів.
У першому параграфі наведені основні визначення й
розглянуті деякі приклади відносини залежності.
У другому - розглядаються довільні простори
залежності, їхньої властивості й деяких теорем.
Третій – присвячений транзитивним і кінцеве мірним просторам
залежності. Тут розглянуті властивості транзитивних просторів залежності й
доведені теореми, які підтверджують існування базису й інваріантність
розмірності в будь-якому кінцеве мірному транзитивному просторі залежності.
У четвертому параграфі формулюються основні визначення
дотичного оператора замикання й розглянута теорема про подання транзитивного
відношення залежності за допомогою алгебраїчного оператора замикання.
П'ятий параграф присвячений матроїдам, прикладам матроїдів
і їхньому застосуванню при вивченні теоретичною основою аналізу «жадібних»
алгоритмів.
Основною літературою при написанні кваліфікаційної
роботи стали монографії: Кона П. «Універсальна алгебра» [2] і Куроша О. Г.
«Курс вищої алгебри» [3].
1. Визначення й приклади
Визначення 1.
Множина Z підмножин
множини A назвемо відношенням залежності на A, якщо виконуються наступні
аксіоми:
Z1: 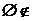 Z ;
Z ;
Z2: 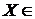 Z
Z  Z ;
Z ;
Z3: 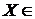 Z
Z 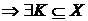 (
(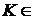 Z
Z 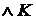 - звичайно).
- звичайно).
Підмножина множини A називається залежною,
якщо вона належить Z, і незалежною у противному випадку.
Легко переконатися в незалежності аксіом Z1 -
Z3..
Модель 1: 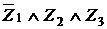 . Думаємо Z = B (А) для
будь-якої множини
. Думаємо Z = B (А) для
будь-якої множини  .
.
Модель 2: 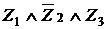 . Нехай Z =
. Нехай Z = 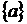 при
при 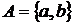 .
.
Модель 3: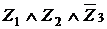 . Нехай Z =
. Нехай Z = 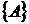 для нескінченної множини
для нескінченної множини  .
.
Визначення 2.
Простором залежності назвемо пари 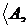 Z
Z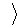 , де Z – відношення
залежності на A.
, де Z – відношення
залежності на A.
Визначення 3.
Елемент 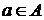 називається залежним від множини
називається залежним від множини 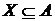 , якщо а Î X або існує
така незалежна підмножина Y множини X, що
, якщо а Î X або існує
така незалежна підмножина Y множини X, що 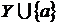 залежно, тобто
залежно, тобто 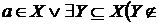 Z
Z 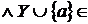 Z ).
Z ).
З визначення 1 випливає, що якщо елемент 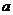 залежить від множини
залежить від множини 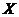 , то він залежить від деякої
кінцевої підмножини
, то він залежить від деякої
кінцевої підмножини 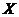 .
.
Визначення 4.
Множина всіх елементів, що залежать від X,
називається оболонкою множини X і позначається через 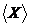 .
.
Ясно, що 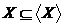 й включення
й включення 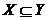 тягне включення їхніх оболонок:
тягне включення їхніх оболонок: 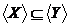 .
.
Визначення 5.
Якщо 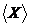 = A, то X називається множиною, що
породжує, множини A.
= A, то X називається множиною, що
породжує, множини A.
Визначення 6.
Незалежна підмножина, що породжує, множини A називається
базисом множини A.
Визначення 7.
Множина 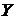 залежить від
залежить від  , якщо будь-який елемент із
, якщо будь-який елемент із 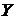 залежить від
залежить від  , тобто
, тобто 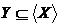 .
.
Визначення 8.
Відношення залежності Z на A будемо називати транзитивним
відношенням залежності, якщо 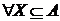
 .
.
Визначення 9.
Транзитивним простором залежності назвемо
простір залежності, у якому відношення залежності має властивість
транзитивності.
Як теоретико-множинний постулат будемо використовувати
наступний принцип, еквівалентний відомій аксіомі вибору.
Лема Цорна.
Непуста впорядкована множина, у якому кожне лінійно
впорядкована підмножина має верхню грань, має максимальний елемент.
Далі доцільно розглянути деякі приклади відносини
залежності:
Приклад 1.
Поняття лінійної залежності у векторному просторі V
над полем 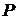 . Система
векторів векторного простору V називається лінійно залежної, якщо існує
кінцева лінійно залежна її підсистема, у противному випадку – лінійно
незалежної.
. Система
векторів векторного простору V називається лінійно залежної, якщо існує
кінцева лінійно залежна її підсистема, у противному випадку – лінійно
незалежної.
Поняття лінійної залежності в кінцеве мірних векторних
просторах дається в курсі алгебри. Кінцева система векторів 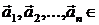 V називається лінійно залежної,
якщо існують елементи поля
V називається лінійно залежної,
якщо існують елементи поля 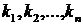 одночасно не рівні нулю й такі, що лінійна
комбінація
одночасно не рівні нулю й такі, що лінійна
комбінація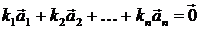 . Множина
лінійних комбінацій множини
. Множина
лінійних комбінацій множини  векторів векторного простору V з коефіцієнтами
з поля P називається лінійною оболонкою цих векторів і позначається
векторів векторного простору V з коефіцієнтами
з поля P називається лінійною оболонкою цих векторів і позначається 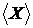 . При цьому
. При цьому 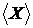 - є підпростором у
просторі V, породженим
- є підпростором у
просторі V, породженим  . Одержуємо транзитивне відношення залежності.
. Одержуємо транзитивне відношення залежності.
Приклад 2.
Нехай поле 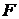 є розширенням основного поля Р, а
є розширенням основного поля Р, а 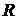 мінімальне підкольце
утримуючі елементи
мінімальне підкольце
утримуючі елементи 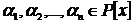 й
поле Р. Підкольце
й
поле Р. Підкольце 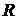 складається
із всіх елементів поля
складається
із всіх елементів поля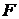 ,
які виражаються через елементи
,
які виражаються через елементи 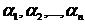 й елементи поля Р за допомогою
додавання, вирахування й множення: це будуть усілякі багаточлени від
й елементи поля Р за допомогою
додавання, вирахування й множення: це будуть усілякі багаточлени від 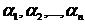 з коефіцієнтами з поля Р.
Тоді, якщо для всякого елемента
з коефіцієнтами з поля Р.
Тоді, якщо для всякого елемента 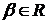 існує єдиний запис у вигляді багаточлена від
існує єдиний запис у вигляді багаточлена від 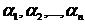 як невідомих з
коефіцієнтами з поля Р, тобто якщо різні багаточлени від
як невідомих з
коефіцієнтами з поля Р, тобто якщо різні багаточлени від 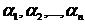 будуть різними елементами підкольца
будуть різними елементами підкольца 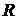 , те система елементів
, те система елементів 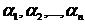 , буде називатися алгебраїчно
незалежної над полем Р, у противному випадку алгебраїчно залежної.
Довільна множина елементів поля Р називається залежним, якщо воно
містить кінцеву залежну підмножину. У першому випадку кільце
, буде називатися алгебраїчно
незалежної над полем Р, у противному випадку алгебраїчно залежної.
Довільна множина елементів поля Р називається залежним, якщо воно
містить кінцеву залежну підмножину. У першому випадку кільце 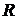 ізоморфно кільцю багаточленів
ізоморфно кільцю багаточленів 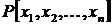 . Відношення алгебраїчної
залежності над полем Р є транзитивним відношенням залежності.
. Відношення алгебраїчної
залежності над полем Р є транзитивним відношенням залежності.
Приклад 3.
Нехай на множині A задане рефлексивне й
симетричне бінарне відношення 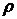 (називане відношенням подібності). Підмножина
X множини A будемо вважати залежним, якщо воно містить два різних
елементи, що перебувають у відношенні
(називане відношенням подібності). Підмножина
X множини A будемо вважати залежним, якщо воно містить два різних
елементи, що перебувають у відношенні 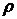 .
.
Оболонкою множини 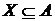 служить множина
служить множина
У цьому випадку можна підсилити аксіому 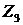 відносини залежності в такий спосіб:
відносини залежності в такий спосіб:
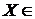 Z
Z 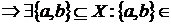 Z.
Z.
Тоді оболонкою множини 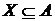 буде множина всіх елементів, що
перебувають відносно подібності хоча б з одним елементом із множини
буде множина всіх елементів, що
перебувають відносно подібності хоча б з одним елементом із множини  .
.
Уведене відношення залежності буде транзитивним тоді й
тільки тоді, коли відповідне бінарне відношення 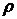 буде транзитивне, тобто є відношенням
еквівалентності на
буде транзитивне, тобто є відношенням
еквівалентності на  .
.
У випадку, коли 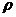 - відношення еквівалентності
- відношення еквівалентності 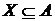 буде незалежним тоді й
тільки тоді, коли
буде незалежним тоді й
тільки тоді, коли 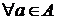 множина
множина
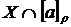 містить не більше
одного елемента. Будь-яка максимальна незалежна підмножина буде містити рівно
по одному елементі з кожного класу еквівалентності
містить не більше
одного елемента. Будь-яка максимальна незалежна підмножина буде містити рівно
по одному елементі з кожного класу еквівалентності 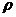 .
.
Приклад 4.
Розглянемо чотирьох елементну множину 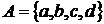 .
.
Назвемо підмножину 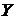 множини
множини  залежним тоді й тільки тоді, коли
залежним тоді й тільки тоді, коли 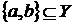 або
або 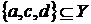 .
.
Z 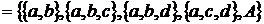 .
.
Розглянемо підмножину 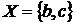 множини
множини  , по уведеному визначенню воно буде
незалежно. Розглянемо оболонку множини
, по уведеному визначенню воно буде
незалежно. Розглянемо оболонку множини 
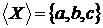 й знайдемо оболонку оболонки нашої множини
й знайдемо оболонку оболонки нашої множини 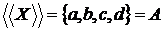 . Таким чином, ми одержали
. Таким чином, ми одержали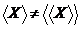 , тобто розглянуте нами
відношення залежності не є транзитивним.
, тобто розглянуте нами
відношення залежності не є транзитивним.
Приклад 5.
Розглянемо довільну множину  й
й 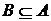 . Множина
. Множина  будемо вважати залежним, якщо
будемо вважати залежним, якщо 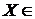 B (А)\ B (В), тобто
B (А)\ B (В), тобто 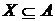 , але
, але 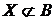 . Таким чином, одержали наступний
транзитивний простір залежності:
. Таким чином, одержали наступний
транзитивний простір залежності: 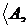 B (А)\ B (В.
B (А)\ B (В.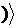 Оболонкою
Оболонкою 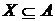 буде множина
буде множина 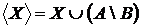 .
.
Зокрема можна розглянути 2 випадки:
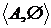 ,
тобто всі множини незалежні, тоді
,
тобто всі множини незалежні, тоді 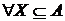
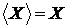 .
.
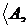 B
(А)
B
(А)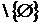
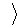 , тобто всі множини, крім
порожнього, будуть залежними, у цьому випадку
, тобто всі множини, крім
порожнього, будуть залежними, у цьому випадку 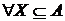
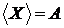 .
.
Приклад 6.
Розглянемо довільну множину  і його непусту кінцеву
підмножину
і його непусту кінцеву
підмножину 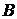 . Уведемо на
множині А наступне відношення залежності
. Уведемо на
множині А наступне відношення залежності
Z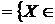 B (А)
B (А)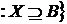 .
.
Таким чином, залежними будуть всі надмножини множини 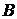 .
.
Якщо 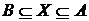 , то
, то 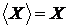 .
.
Якщо 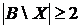 , то
, то 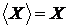 .
.
Якщо 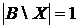 , то
, то 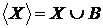 .
.
Одержуємо транзитивний простір залежності.
Приклад 7.
Підпростір простору залежності 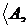 Z
Z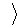 . Розглянемо
. Розглянемо 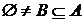 , де діє те ж відношення залежності Z. Тоді
одержимо індукований простір залежності
, де діє те ж відношення залежності Z. Тоді
одержимо індукований простір залежності 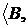 Z
Z 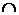 B
B 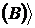 . У цьому випадку залежними будуть тільки
ті підмножини множини
. У цьому випадку залежними будуть тільки
ті підмножини множини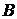 ,
які були залежні в просторі
,
які були залежні в просторі 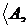 Z
Z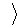 . І якщо простір
. І якщо простір 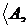 Z
Z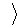 транзитивне, те транзитивним буде й
підпростір
транзитивне, те транзитивним буде й
підпростір 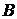 .
.
Приклад 8.
Нехай 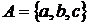 і Z =
і Z = 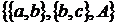 . Такий простір залежності
. Такий простір залежності 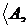 Z
Z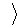 не транзитивне, тому що
не транзитивне, тому що 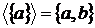 й
й 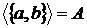 . Простір А має два базиси
. Простір А має два базиси 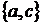 й
й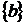 , які є і єдиними мінімальними множинами, що
породжують
, які є і єдиними мінімальними множинами, що
породжують  в.
в.
Цей приклад показує, що існують не транзитивні
простори залежності, у яких мінімальні множини, що породжують, незалежні, тобто
є базисами.
Приклад 9.
Задамо на множині N натуральних чисел
наступне відношення залежності:
Z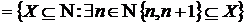 .
.
Одержуємо нескінченну строго зростаючий ланцюжок
оболонок в 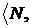 Z
Z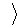 . При
. При 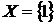 одержуємо
одержуємо
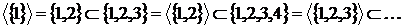 .
.
Таким чином, маємо 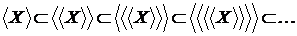 .
.
Зауваження.
Поняття простору залежності можна й зручно визначати
через базу залежності. Саме, множина B всіх мінімальних залежних
множин простору залежності 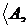 Z
Z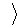 назвемо його базою. Ясно, що
множини з B не порожні, кінцеві й не втримуються друг у другу.
Крім того, будь-яка незалежна множина містить деяка множина бази B.
Простір
назвемо його базою. Ясно, що
множини з B не порожні, кінцеві й не втримуються друг у другу.
Крім того, будь-яка незалежна множина містить деяка множина бази B.
Простір 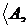 Z
Z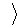 має єдину базу й
однозначно визначається їй. Тому простору залежності можна задавати базами.
має єдину базу й
однозначно визначається їй. Тому простору залежності можна задавати базами.
Легко бачити, що вірно наступне твердження:
Непуста множина B підмножин множини  задає на
задає на  відношення залежності тоді й тільки
тоді, коли множини з B не порожні, кінцеві й не включений друг у друга.
відношення залежності тоді й тільки
тоді, коли множини з B не порожні, кінцеві й не включений друг у друга.
У термінах бази B можна сформулювати
умова транзитивності відповідного простору залежності.
2. Простір залежності
Теорема 1.
Нехай 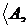 Z
Z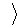 - довільний простір залежності. Розглянемо
наступні три твердження:
- довільний простір залежності. Розглянемо
наступні три твердження:
X — базис в A;
X — максимальна
незалежна підмножина в A;
X — мінімальна множина, що породжує, в A.
Тоді 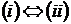 й
й 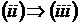 .
.
Доказ:
(i) 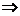 (ii) Якщо X
– базис, то по визначенню 6 X – незалежна підмножина, що породжує.
Доведемо від противного, що воно максимальне. Нехай існують незалежні множини
(ii) Якщо X
– базис, то по визначенню 6 X – незалежна підмножина, що породжує.
Доведемо від противного, що воно максимальне. Нехай існують незалежні множини 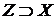 . Візьмемо
. Візьмемо 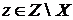 , тоді
, тоді 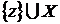 незалежно, тому що будь-яка підмножина
незалежної множини незалежно. Тому по визначеннях 3 і 5
незалежно, тому що будь-яка підмножина
незалежної множини незалежно. Тому по визначеннях 3 і 5 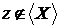 , звідки
, звідки 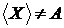 , одержали протиріччя з умовою. Тому X є
максимальною незалежною підмножиною в A.
, одержали протиріччя з умовою. Тому X є
максимальною незалежною підмножиною в A.
(ii) 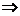 (i) Доведемо від противного,
нехай
(i) Доведемо від противного,
нехай  не базис в
не базис в  , тобто
, тобто 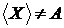 . Тоді
. Тоді 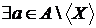 таке, що
таке, що 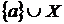 незалежно й лежить в
незалежно й лежить в  , одержали протиріччя з максимальністю
, одержали протиріччя з максимальністю  .
.
(ii) 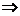 (iii) Якщо X —
максимальна незалежна множина в A, те всякий елемент в
(iii) Якщо X —
максимальна незалежна множина в A, те всякий елемент в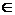 A або належить X, або
такий, що
A або належить X, або
такий, що 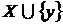 залежно, а
тому
залежно, а
тому 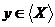 в тім і
іншому випадку, тобто
в тім і
іншому випадку, тобто 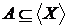 Оскільки
Оскільки
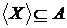 , те X -
множина, що породжує. Виходить,
, те X -
множина, що породжує. Виходить,  - базис простору
- базис простору  .
.
Доведемо тепер, що воно мінімально. Нехай множина 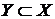 . Доведемо, що воно не є
породжує для A. Візьмемо
. Доведемо, що воно не є
породжує для A. Візьмемо 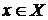 , але
, але 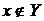 . Тоді
. Тоді 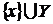 незалежно, як підмножина множини X.
Тому по визначеннях 3 і 5
незалежно, як підмножина множини X.
Тому по визначеннях 3 і 5 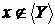 і
і 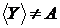 , а це значить, що Y не є множиною, що
породжує. Висновок: X – мінімальна множина, що породжує, в A.
, а це значить, що Y не є множиною, що
породжує. Висновок: X – мінімальна множина, що породжує, в A.
(i) 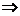 (iii) Справедливо, по
доведеним вище твердженнях (i)
(iii) Справедливо, по
доведеним вище твердженнях (i)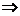 (ii) і (ii)
(ii) і (ii) 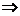 (iii). :
(iii). :
Визначення - позначення 10.
Для довільної множини  простору залежності
простору залежності 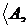 Z
Z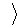 позначимо
позначимо 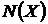 множину всіх максимальних незалежних
підмножин, а через
множину всіх максимальних незалежних
підмножин, а через 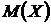 -
множину всіх мінімальних підмножин, що породжують, цієї множини.
-
множину всіх мінімальних підмножин, що породжують, цієї множини.
З теореми 1 випливає, що 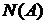 збігається із множиною всіляких базисів простору
збігається із множиною всіляких базисів простору
 й
й 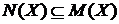 для кожного
для кожного 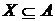 .
.
Наступний приклад показує, що зворотне включення 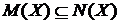 вірно не завжди.
вірно не завжди.
Приклад 10.
Розглянемо дев'яти елементну множину 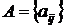 , що записана у вигляді матриці
, що записана у вигляді матриці 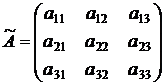 . Залежними
будемо вважати підмножини множини
. Залежними
будемо вважати підмножини множини  , що містять «прямі лінії»: стовпці, рядки або
діагоналі матриці
, що містять «прямі лінії»: стовпці, рядки або
діагоналі матриці 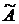 .
.
Розглянемо множини 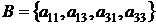 й
й 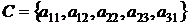 , вони буде максимальними незалежними, тому що
не містять прямих і при додаванні будь-якого елемента з
, вони буде максимальними незалежними, тому що
не містять прямих і при додаванні будь-якого елемента з  , що не лежить у них, стають
залежними. Тут максимальні незалежні множини містять різна кількість елементів.
, що не лежить у них, стають
залежними. Тут максимальні незалежні множини містять різна кількість елементів.
Розглянемо ще одну множину 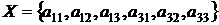 , вона є мінімальним що породжує, тому що якщо
виключити з нього хоча б один елемент, то воно вже не буде множиною, що
породжує. Легко помітити, що
, вона є мінімальним що породжує, тому що якщо
виключити з нього хоча б один елемент, то воно вже не буде множиною, що
породжує. Легко помітити, що  залежно, тому не є базисом. Даний приклад
ілюструє, що (iii)
залежно, тому не є базисом. Даний приклад
ілюструє, що (iii)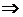 (i)
не вірно в загальному випадку, тобто для довільних просторів залежності.
(i)
не вірно в загальному випадку, тобто для довільних просторів залежності.
Для будь-якого простору залежності 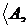 Z
Z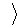 виконуються наступні властивості:
виконуються наступні властивості:
Заміщення. Якщо 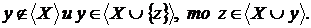
Доказ:
Вкладеність. Об'єднання будь-якої системи вкладених друг у друга незалежних множин є
незалежною множиною, тобто 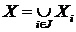 - незалежно, де
- незалежно, де 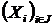 також незалежні й
також незалежні й 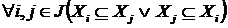
Доказ:
Доведемо від противного. Припустимо, що  залежно, тоді в ньому найдеться
кінцева залежна підмножина
залежно, тоді в ньому найдеться
кінцева залежна підмножина 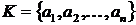 :
: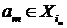 . Маємо
. Маємо 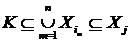 , одержали протиріччя з незалежністю
, одержали протиріччя з незалежністю 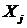 .
.
Максимальність. Будь-яка незалежна множина втримується в максимальній незалежній
множині.
Доказ:
Нехай  - довільна незалежна множина в.
- довільна незалежна множина в.  Утворимо множину
Утворимо множину 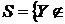 Z :
Z :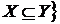 всіх незалежних множин, що містять
всіх незалежних множин, що містять  . Відносно
. Відносно 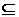 множина
множина 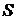 є впорядкованою множиною, що задовольняє по
властивості вкладеності, умові леми Цорна. Тоді по лемі Цорна в
є впорядкованою множиною, що задовольняє по
властивості вкладеності, умові леми Цорна. Тоді по лемі Цорна в 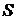 існує максимальний елемент
існує максимальний елемент  .
.
Теорема 2.
Будь-який простір залежності має базис.
Доказ:
Візьмемо порожню множину, вона незалежне. По
властивості максимальності воно повинне втримуватися в деякій максимальній
незалежній множині, що по теоремі 1 є базисом.
3. Транзитивність
Особливий інтерес представляють транзитивні простори
залежності. Важливим результатом є доказ інваріантності розмірності будь-якого
транзитивного простору залежності.
Доведемо деякі властивості, справедливі для
транзитивних просторів залежності 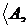 Z
Z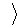 .
.
Властивість 1: 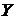 залежить від
залежить від 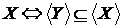 .
.
Доказ:
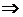
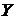 залежить від
залежить від  , тобто
, тобто 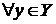
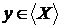 , і
, і  . Розглянемо
. Розглянемо 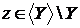 , тоді
, тоді 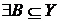
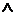
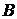 - незалежно й
- незалежно й 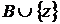 - залежно, а
- залежно, а 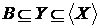 , одержуємо, що
, одержуємо, що 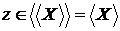 , тому
, тому 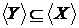 . Маємо
. Маємо 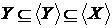 .
.
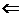 По
визначенню 8 будь-яка підмножина
По
визначенню 8 будь-яка підмножина  залежить від
залежить від 
Властивість 2: Якщо 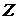 залежить від
залежить від 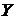 , а
, а 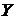 залежить від
залежить від  , те
, те 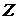 залежить від
залежить від  .
.
Доказ:
Запишемо умову, використовуючи властивість 1 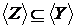 , а
, а 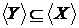 , тоді очевидно, що
, тоді очевидно, що 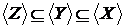 .
.
Властивість 3: Якщо X — мінімальна множина, що породжує, в A, те X - базис в A.
Доказ:
Нехай X — мінімальна множина, що породжує, в
A. Покажемо, що воно не може бути залежним, тому що в цьому випадку його
можна було б замінити власною підмножиною, що усе ще породжує A. Дійсно,
у силу транзитивності відносини залежності, будь-яка множина, що породжує
множина X, буде так само породжувати й множина A. Отже, X
- незалежна множина, що породжує, що по визначенню 6 є базисом.
Властивість 4: 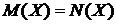 для кожного
для кожного 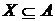 .
.
Доказ: Потрібне із
властивості 3.
Властивість 5 (про заміну.) :
Якщо X — незалежна
множина й Y — множина, що породжує, в A, то існує така 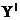 підмножина множини Y,
підмножина множини Y, 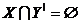 що
що 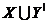 й - базис для A.
й - базис для A.
Доказ:
Розглянемо систему J таких незалежних підмножин Z
множини A, що 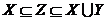 .
.
Тому що X незалежно, те такі множини існують;
крім того, якщо 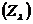 — деяке
лінійно впорядкована множина множин з J, те його об'єднання
— деяке
лінійно впорядкована множина множин з J, те його об'єднання 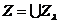 знову належить J, оскільки
Z задовольняє умові
знову належить J, оскільки
Z задовольняє умові 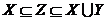 ,
і якщо Z залежне, те деяка кінцева підмножина множини Z повинне було б бути
залежним; ця підмножина втримувалося б у деякій множині
,
і якщо Z залежне, те деяка кінцева підмножина множини Z повинне було б бути
залежним; ця підмножина втримувалося б у деякій множині 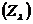 в суперечності з тим фактом, що всі
в суперечності з тим фактом, що всі 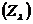 незалежні.
незалежні.
По лемі Цорна J має максимальний елемент М; у
силу максимальності кожний елемент множини Y або належить М, або
залежить від М, звідки 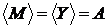 . Цим доведено, що М — базис в A. Тому
що
. Цим доведено, що М — базис в A. Тому
що 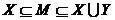 , те М має вигляд
, те М має вигляд 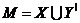 , де
, де 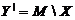 задовольняє умовам
задовольняє умовам 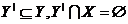 .■
.■
Визначення 11.
Простір залежності 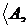 Z
Z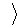 називається кінцеве мірним, якщо будь-яке його
незалежна множина кінцева.
називається кінцеве мірним, якщо будь-яке його
незалежна множина кінцева.
Теорема 3.
Нехай 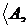 Z
Z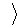 - транзитивний простір залежності. Тоді
будь-які два базиси в цьому просторі рівно потужні.
- транзитивний простір залежності. Тоді
будь-які два базиси в цьому просторі рівно потужні.
Доказ:
Розглянемо спочатку випадок кінцеве мірного простору  .
.
Нехай В, З — будь-які два базиси в А,
їхнє існування забезпечується теоремою 2, і 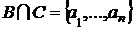 ,
, 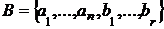 ,
, 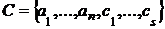 , де різні елементи позначені різними буквами
або постачені різними індексами. Застосуємо індукцію по max (r, s).
, де різні елементи позначені різними буквами
або постачені різними індексами. Застосуємо індукцію по max (r, s).
Якщо r = 0 або s = 0, то 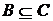 або
або 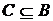 , і
, і 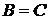 . Тому можна припускати, що r ≥ 1, s ≥
1, без обмеження спільності будемо вважати, що r > s, так що
насправді r > 1.
. Тому можна припускати, що r ≥ 1, s ≥
1, без обмеження спільності будемо вважати, що r > s, так що
насправді r > 1.
Припустимо, що базиси будуть рівне потужними для
будь-якого t < r
По лемі про заміну множина 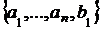 можна доповнити до базису D елементами
базису З, скажемо
можна доповнити до базису D елементами
базису З, скажемо
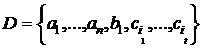 , t ≤ s < r.
, t ≤ s < r.
Тепер перетинання D c У складається з n
+ 1 елемента, і D містить, крім того, ще t (< r) елементів, тоді
як У містить, крім цього перетинання, ще r - 1 елементів, так що по
припущенню індукції 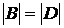 ,
тобто
,
тобто 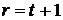 .
.
Оскільки r > 1, звідси випливає, що t ≥
1, і тому перетинання D із Із містить не менше ніж n+1
елементів. Використовуючи ще раз припущення індукції, знаходимо, що 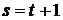 й, отже, r = s і
базиси В и С рівне потужні.
й, отже, r = s і
базиси В и С рівне потужні.
Далі, нехай В - кінцевий базис в.  Тоді й будь-який інший
базис Із простору
Тоді й будь-який інший
базис Із простору  буде кінцевим. Дійсно, У
виражається через кінцеву множину елементів
буде кінцевим. Дійсно, У
виражається через кінцеву множину елементів 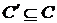 у силу транзитивності
у силу транзитивності 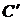 буде що породжує й незалежною множиною в
буде що породжує й незалежною множиною в  , тобто
, тобто 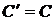 .
.
Нарешті, якщо базиси В и С нескінченні.
Кожний елемент із У залежить від деякої кінцевої підмножини базису З,
і навпаки. Потужність множини всіх кінцевих підмножин усякої нескінченної
множини дорівнює потужності самої множини. Тому потужності В и С
збігаються.
Теорема 4.
Нехай 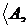 Z
Z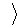 - довільний простір залежності, тоді наступні
умови еквівалентні
- довільний простір залежності, тоді наступні
умови еквівалентні
Z транзитивне;
для будь-якого кінцевого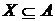
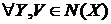
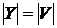 ;
;
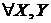 кінцевих
і
кінцевих
і 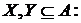
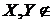 Z
Z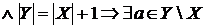
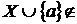 Z;
Z;
для будь-якого кінцевого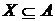
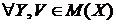
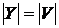 .
.
Доказ:
(i) 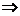 (ii) Справедливо
по теоремі 3 і прикладу 7.
(ii) Справедливо
по теоремі 3 і прикладу 7.
(ii) 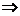 (iii) Візьмемо
(iii) Візьмемо 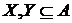 , так що
, так що 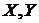 - незалежно й
- незалежно й 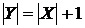 . Допустимо, що твердження
. Допустимо, що твердження 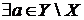
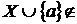 Z невірно. Тоді
Z невірно. Тоді 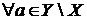
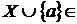 Z. Розглянемо
Z. Розглянемо  . Маємо
. Маємо 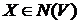 . Але
. Але 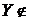 Z, тому
Z, тому 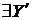
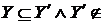 Z
Z 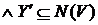 . По (ii) маємо
. По (ii) маємо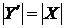 . Але
. Але 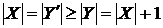 - протиріччя.
- протиріччя.
(iii) 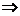 (ii) Доведемо від
противного. Нехай
(ii) Доведемо від
противного. Нехай 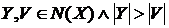 .
Можна вважати, що
.
Можна вважати, що 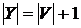 .
Тоді по (iii)
.
Тоді по (iii) 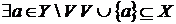 незалежно.
Одержали протиріччя з максимальністю
незалежно.
Одержали протиріччя з максимальністю 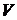
(iii)  (i) Потрібно
довести рівність
(i) Потрібно
довести рівність  для
довільного
для
довільного 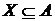 .
.
Візьмемо 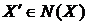 й покажемо, що
й покажемо, що 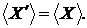 Тому що
Тому що 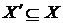 , те
, те 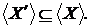 Нехай існує
Нехай існує 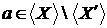 , тоді
, тоді 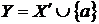 незалежно й існує
незалежно й існує 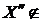 Z і
Z і 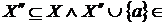 Z . Розширюючи
Z . Розширюючи  в
в  можна припустити, що
можна припустити, що 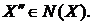 По (ii)
По (ii) 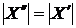 , тобто
, тобто 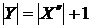 . Тому по (iii)
. Тому по (iii) 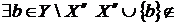 Z . бачимо, що
Z . бачимо, що 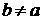 . Виходить,
. Виходить, 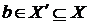 . Одержуємо протиріччя з тим, що
. Одержуємо протиріччя з тим, що 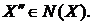 Отже,
Отже,  , те мережа
, те мережа 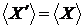 .
.
Тепер досить показати, що 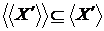 . Нехай
. Нехай 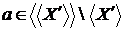 , тоді
, тоді 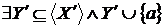 залежно, розширюючи
залежно, розширюючи 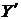 в
в 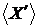 можна припустити, що
можна припустити, що 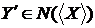 , крім того
, крім того 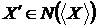 , тоді по (ii)
, тоді по (ii) 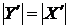 .
. 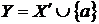 незалежно, тому
незалежно, тому 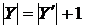 . По (iii)
. По (iii) 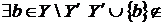 Z . бачимо, що
Z . бачимо, що 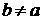 . Виходить,
. Виходить, 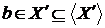 , одержали протиріччя з максимальністю
, одержали протиріччя з максимальністю 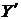 . Отже,
. Отже, 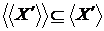 , зворотне включення очевидно, тому
, зворотне включення очевидно, тому  .
.
(iv) 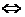 (ii) У силу теорем 1 і
3 і доведена еквівалентності
(ii) У силу теорем 1 і
3 і доведена еквівалентності
(i)  (ii).■
(ii).■
Далі будемо розглядати транзитивний простір залежності
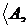 Z
Z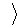 .
.
Визначення 12.
Потужність максимальної незалежної підмножини даної
множини 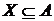 називається рангом
цієї множини:
називається рангом
цієї множини: 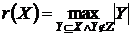 .
.
Будемо розглядати кінцеві підмножини 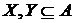 .
.
Мають місце наступні властивості.
Властивість 1о: 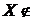 Z
Z 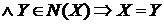 .
.
Доказ: 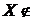 Z
Z 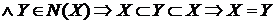 .
.
Властивість 2о: 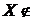 Z
Z 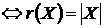 .
.
Властивості 3о – 7о
сформульовані для 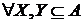
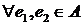 .
.
Властивість 3о: 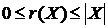 .
.
Доказ: Ясно, що 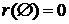 , і тому що число елементів
будь-якої підмножини не більше числа елементів самої множини, то дана
властивість виконується.
, і тому що число елементів
будь-якої підмножини не більше числа елементів самої множини, то дана
властивість виконується.
Властивість 4о: 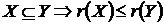 .
.
Доказ: потрібне з того, що
незалежна підмножина в 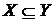 можна
продовжити до максимальної незалежної підмножини в
можна
продовжити до максимальної незалежної підмножини в 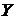 ;
;
Властивість 5о: 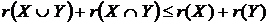 .
.
Доказ:
Нехай 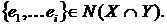 Тоді
Тоді 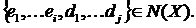 И потім
И потім 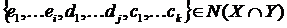 . Маємо
. Маємо 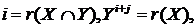
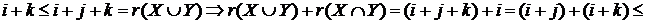
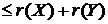 .
.
Властивість 6о: 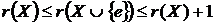 .
.
Доказ: випливає із
властивості 40;
Властивість 7о: 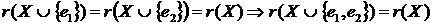 .
.
Доказ: 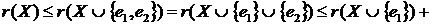
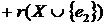
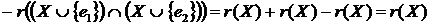 .
.
4. Зв'язок транзитивних відносин
залежності з операторами замикання
Транзитивне відношення залежності також може бути
описане за допомогою алгебраїчного оператора замикання деякого типу. Для
початку сформулюємо визначення використовуваних понять.
Визначення 13.
Множина E підмножин множини A називається системою
замикань, якщо 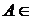 E і
система E замкнута щодо перетинань, тобто ∩D
E і
система E замкнута щодо перетинань, тобто ∩D 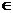 E для кожної непустої підмножини D
E для кожної непустої підмножини D 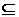 E
E
Визначення 14.
Оператором замикання на множині A називається відображення J множини B (A) у себе, що
володіє наступними властивостями:
J. 1. Якщо 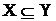 , то J(X)
, то J(X)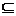 J(Y);
J(Y);
J. 2. X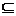 J(X);
J(X);
J. 3. JJ(X) = J(X), для всіх X, Y 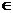 B (A).
B (A).
Визначення 15.
Оператор замикання J на множині A називається алгебраїчним,
якщо для будь-яких 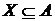 і
і 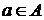
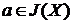 тягне
тягне 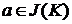 для деякої кінцевої підмножини
для деякої кінцевої підмножини 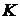 множини
множини  .
.
Визначення 16.
Система замикань називається алгебраїчної,
якщо тільки відповідний оператор замикання є алгебраїчним
Слід зазначити теорему про взаємозв'язок між системами
замикань і операторами замикань.
Теорема 5.
Кожна система замикань E на множині  визначає
оператор замикання J на
визначає
оператор замикання J на  за правилом J(X) = ∩{Y
за правилом J(X) = ∩{Y 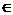 E | Y
E | Y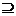 X}. Обернено, кожний оператор замикання J на
X}. Обернено, кожний оператор замикання J на  визначає систему
замикань E
визначає систему
замикань E 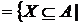 J
J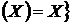 .
.
Наступна теорема показує зв'язок транзитивного
відношення залежності й алгебраїчного оператора замикання.
Теорема 6.
Для будь-якого транзитивного відношення залежності 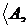 Z
Z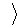 відображення
відображення 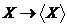 є алгебраїчним оператором замикання на А із властивістю заміщення.
є алгебраїчним оператором замикання на А із властивістю заміщення.
Обернено, будь-який алгебраїчний оператор замикання
на А із властивістю заміщення виходить таким способом з деякого транзитивного
відношення залежності Z на А.
Доказ:
Будемо називати підмножину Т множини A замкнутим,
якщо 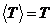 .
.
Покажемо спочатку, що замкнуті підмножини утворять
систему замикань. Якщо 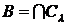 ,
де
,
де 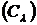 - сімейство
замкнутих множин, то нехай
- сімейство
замкнутих множин, то нехай 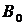 - така незалежна підмножина множини B, що
- така незалежна підмножина множини B, що 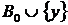 залежно; оскільки
залежно; оскільки 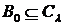 для всіх
для всіх 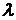 , маємо
, маємо 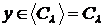 , звідки
, звідки 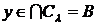 , тобто В замкнуто.
, тобто В замкнуто.
Нехай 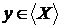 , те по визначенню 3
, те по визначенню 3 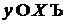
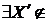 Z
Z 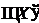 кінцеве, таке що
кінцеве, таке що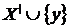 залежно. У першому випадку
залежно. У першому випадку 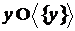 , а в другому
, а в другому 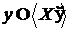 . І оскільки
. І оскільки 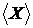 замкнуто в силу транзитивності, одержуємо
алгебраїчний оператор замикання.
замкнуто в силу транзитивності, одержуємо
алгебраїчний оператор замикання.
Цим доведено, що замкнуті підмножини утворять
алгебраїчну систему замикань.
Виконання властивості заміщення потрібне з відповідної
властивості просторів залежності.
Обернено, нехай 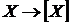 - алгебраїчний оператор замикання із
властивістю заміщення.
- алгебраїчний оператор замикання із
властивістю заміщення.
Будемо вважати  залежним, якщо
залежним, якщо 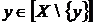 для деякого
для деякого 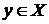 , і незалежним у противному випадку.
, і незалежним у противному випадку.
Тому що оператор алгебраїчний, то звідси випливає, що
всяка залежна множина має кінцеву залежну підмножину, і оскільки очевидно, що
всяка множина, що містить залежну підмножину, саме залежно, у такий спосіб
одержуємо відношення залежності. Умова транзитивності виконується по визначенню,
і це показує, що ми маємо транзитивне відношення залежності.
Тепер для будь-яких 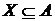 ,
, 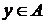 маємо
маємо  тоді й тільки тоді, коли
тоді й тільки тоді, коли 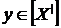 для деякої кінцевої підмножини
для деякої кінцевої підмножини 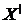 множини
множини  . Вибираючи
. Вибираючи 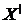 мінімальним, можемо припускати, що
мінімальним, можемо припускати, що 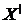 незалежно. Звідси випливає,
що
незалежно. Звідси випливає,
що 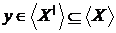 й, отже,
й, отже, 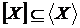 .
.
Обернено, якщо 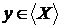 , те знову
, те знову 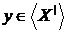 для деякої кінцевої незалежної підмножини
для деякої кінцевої незалежної підмножини 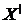 множини
множини  . Це означає, що
. Це означає, що 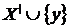 залежно, тобто
залежно, тобто 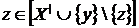 для якогось
для якогось 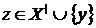 .
.
У силу властивості заміщення одержуємо, що 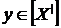 й
й 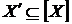 , тому
, тому 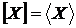 .
.
Зауваження. Існують алгебраїчні оператори замикання, що не володіють властивістю
заміщення. Для приклада візьмемо нескінченну циклічну напівгрупу 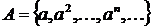 .
.
Нехай 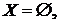
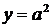 і
і 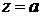 . Тоді
. Тоді 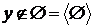 ,
, 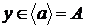 , але
, але 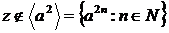 .
.
5. Матроїди
Поняття матроїда тісно пов'язане з поняттям відносини
залежності, тому ця тема розглядається в даній кваліфікаційній роботі. Однак з
іншої сторони воно є теоретичною основою для вивчення й аналізу «жадібних»
алгоритмів.
Визначення 17.
Матроїдом 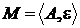 називається
кінцева множина й сімейство його підмножин
називається
кінцева множина й сімейство його підмножин 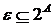 , таке що виконується три аксіоми:
, таке що виконується три аксіоми:
М1: 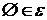 ;
;
М2: 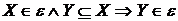 ;
;
М3: 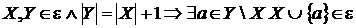
Визначення 18.
Елементи множини 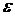 називаються незалежними, а інші
підмножини
називаються незалежними, а інші
підмножини 
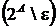 - залежними
множинами.
- залежними
множинами.
Відповідно до уведеного раніше аксіомами простору
залежності бачимо, що матроїди - це в точності кінцеві транзитивне простори
залежності.
Розглянемо наступні приклади матроїдів:
Приклад 1.
Сімейство всіх лінійно незалежних підмножин будь-якої
кінцевої множини векторів довільного непустого векторного простору є матроїдом.
Дійсно, по визначенню можна вважати, що порожня
множина лінійно незалежно. Усяка підмножина лінійно незалежної підмножини векторів
лінійно незалежно. Нехай 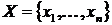 і
і 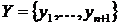 - лінійно незалежні множини. Якби всі вектори
із множини
- лінійно незалежні множини. Якби всі вектори
із множини 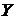 виражалися
у вигляді лінійної комбінації векторів із множини
виражалися
у вигляді лінійної комбінації векторів із множини  , то множина
, то множина 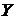 була б лінійно залежним. Тому, серед векторів
множини
була б лінійно залежним. Тому, серед векторів
множини 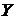 є принаймні
один вектор
є принаймні
один вектор 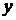 , що не
входить у множину
, що не
входить у множину  й не
виражається у вигляді лінійної комбінації векторів із множини
й не
виражається у вигляді лінійної комбінації векторів із множини  . Додавання вектора
. Додавання вектора 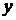 до множини
до множини  утворить лінійно незалежна множина.
утворить лінійно незалежна множина.
Приклад 2.
Вільні матроїди. Якщо  - довільна кінцева множина, то
- довільна кінцева множина, то  - матроїд. Такий матроїд називається
вільним. У вільному матроїді кожна множина незалежно, А є базисом
і
- матроїд. Такий матроїд називається
вільним. У вільному матроїді кожна множина незалежно, А є базисом
і 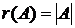 .
.
Приклад 3.
Матроїд трансверсалей. Нехай  - деяка кінцева множина, і
- деяка кінцева множина, і 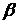 - деяке сімейство підмножин цієї
множини. Підмножина
- деяке сімейство підмножин цієї
множини. Підмножина 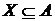 називається
часткової трансверсалью сімейства
називається
часткової трансверсалью сімейства 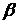 , якщо
, якщо  містить не більш ніж по одному елементі кожної
підмножини із сімейства
містить не більш ніж по одному елементі кожної
підмножини із сімейства 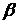 .
Часткові трансверсали над
.
Часткові трансверсали над 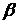 утворять матроїд на А.
утворять матроїд на А.
Перейдемо до розгляду жадібного алгоритму. Для початку
потрібно сформулювати задачу, що будемо вирішувати з його використанням.
Нехай є кінцева множина  ,
, 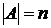 , вагова функція
, вагова функція 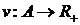 й сімейство
й сімейство 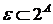 .
.
Не обмежуючи спільності, можна вважати, що 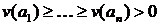
Розглянемо такий алгоритм, що вихідними даними має
множину  , сімейство
його підмножин
, сімейство
його підмножин 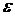 і
вагарню функцію
і
вагарню функцію 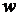 ,
причому множина
,
причому множина  впорядкована
в порядку убування ваг елементів. Після виконання цього алгоритму ми одержимо
підмножину
впорядкована
в порядку убування ваг елементів. Після виконання цього алгоритму ми одержимо
підмножину  .
.
Споконвічно шукана множина  порожньо, далі переглядаємо по черзі всі
елементи із множини
порожньо, далі переглядаємо по черзі всі
елементи із множини 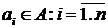 й
перевіряємо залежність множини
й
перевіряємо залежність множини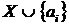 , якщо
, якщо 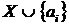 - незалежно, те елемент
- незалежно, те елемент 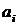 додаємо в множину
додаємо в множину  , якщо ж
, якщо ж 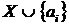 - залежне, те переходимо до елемента
- залежне, те переходимо до елемента 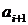 , поки всі елементи із
множини
, поки всі елементи із
множини  не будуть
перевірені.
не будуть
перевірені.
Алгоритм такого типу називається «жадібним». Зовсім
очевидно, що по побудові остаточна множина 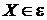 , тобто незалежно. Також очевидно, що жадібний
алгоритм є надзвичайно ефективним: кількість кроків становить
, тобто незалежно. Також очевидно, що жадібний
алгоритм є надзвичайно ефективним: кількість кроків становить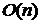 , тобто жадібний алгоритм є лінійним.
(Не вважаючи витрат на сортування множини
, тобто жадібний алгоритм є лінійним.
(Не вважаючи витрат на сортування множини  й перевірку незалежності
й перевірку незалежності 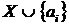 .)
.)
Приклад 4.
Нехай дана матриця 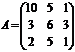 . Розглянемо наступні задачі.
. Розглянемо наступні задачі.
Задача 1. Вибрати
по одному елементі з кожного стовпця, так щоб їхня сума була
максимальна.
Тут вагова функція 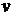 ставить у відповідність елементу матриці
ставить у відповідність елементу матриці 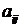 його значення. Наприклад,
його значення. Наприклад, 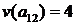 .
.
Множина  в такий спосіб:
в такий спосіб: 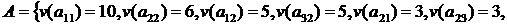
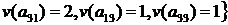 .
.
Сімейство незалежних підмножин 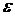 будуть утворювати такі множини, у
яких всі елементи з різних стовпців і порожня множина.
будуть утворювати такі множини, у
яких всі елементи з різних стовпців і порожня множина.
Наш алгоритм буде працювати в такий спосіб:
0 крок: 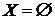 ;
;
1 крок: перевіряємо для елемента 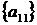 ,
, 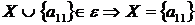 ;
;
2 крок: для 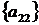 ,
,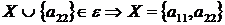 ;
;
3 крок: для 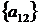 ,
,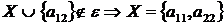 ;
;
4 крок: для 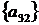 ,
,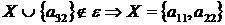 ;
;
5 крок: для 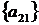 ,
,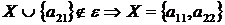 ;
;
6 крок: для 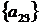 ,
,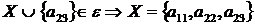 ;
;
7 крок: для 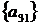 ,
,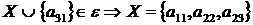 ;
;
8 крок: для 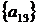 ,
,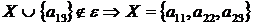 ;
;
9 крок: для 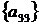 ,
,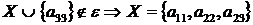 ;
;
У результаті одержали множину 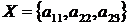 ,
, 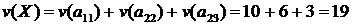 ., отриманий результат дійсно є рішенням
задачі.
., отриманий результат дійсно є рішенням
задачі.
Задача 2. Вибрати
по одному елементі з кожного рядка, так щоб їхня сума була максимальна.
Тут функція 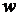 й множина
й множина  такі ж як і в попередній задачі, а сімейство
незалежних підмножин
такі ж як і в попередній задачі, а сімейство
незалежних підмножин 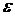 будуть
утворювати такі множини, у яких всі елементи з різних рядків і порожня множина.
будуть
утворювати такі множини, у яких всі елементи з різних рядків і порожня множина.
Використовуючи наш алгоритм одержимо наступне рішення:
множина 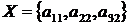 й
й 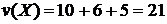 , що так само є вірним.
, що так само є вірним.
Задача 3. Вибрати
по одному елементі з кожного стовпця й з кожного рядка, так щоб їхня
сума була максимальною.
У цій задачі функція 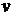 й множина
й множина  залишаються колишніми, а сімейство незалежних
підмножин
залишаються колишніми, а сімейство незалежних
підмножин 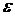 будуть
утворювати такі множини, у яких всі елементи з різних стовпців і різних рядків
і порожня множина.
будуть
утворювати такі множини, у яких всі елементи з різних стовпців і різних рядків
і порожня множина.
Неважко бачити, що жадібний алгоритм вибере наступні елементи:
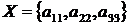 і
і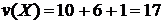 , які не є рішенням задачі, оскільки існує
краще рішення -
, які не є рішенням задачі, оскільки існує
краще рішення - 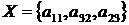 і
і 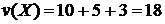 .
.
Виникає питання, у яких же випадках жадібний алгоритм
дійсно вирішує поставлену задачу? На поставлене питання допоможе відповісти
теорема, сформульована й доведена в [4, с.75-76].
Теорема 7.
Для будь-якої
функції 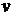 жадібний алгоритм знаходить незалежну
множину
жадібний алгоритм знаходить незалежну
множину  з найбільшою
вагою, тоді й тільки тоді, коли
з найбільшою
вагою, тоді й тільки тоді, коли 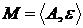 є матроїдом.
є матроїдом.
Дійсно, у нашім прикладі в задачах 1 і 2 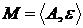 - матроїд, а в задачі 3
таким не є, тому що не виконується аксіома М3. Якщо розглянути
- матроїд, а в задачі 3
таким не є, тому що не виконується аксіома М3. Якщо розглянути 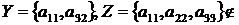
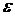 , тоді
, тоді 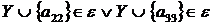 одержали протиріччя з незалежністю хоча б
одного із множин.
одержали протиріччя з незалежністю хоча б
одного із множин.
Висновок
У роботі були розглянуті такі питання, як:
Вивчення й визначення поняття відношення залежності.
Розглянуті деякі приклади відносин залежності.
Сформулювали й довели властивості теореми як для
довільних, так і для транзитивних просторів залежності. Робота дала відповіді
на всі питання, які були поставлені за мету.
Список літератури
1. Ван дер Варден Б.Л.
Алгебра. – К., 2004
2. Кон П. Універсальна
алгебра. – К., 2004.
3. Курош О. Г. Курс вищої
алгебри. – К., 2003.
4. Новиков Ф. А. Дискретна
математика для програмістів. – К., 2005
5. Фрид Е. Елементарне
введення в абстрактну алгебру. – К., 2000