Градієнтні методи

Міністерство освіти і науки України

НТУУ КПІ

Кафедра АПЕПС

Лабораторна робота

по темі "Градієнтні методи"

Виконала

ст. 3-го курсу

ТЕФ, гр. ТМ-81

Кошева А.С.

Київ 2010

1. Короткі теоретичні відомості

1.1 Про чисельні методи багатомірної оптимізації

Мета роботи: знайомство з методами багатомірної безумовної оптимізації першого й нульового порядків і їхнє засвоєння, порівняння ефективності застосування цих методів для конкретних цільових функцій.

Задача багатомірної безумовної оптимізації формулюється у вигляді:

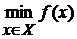
де x={x ^(1), x ^(2), …, x ⁽ⁿ⁾ } - точка в n-мірному просторі X=IRⁿ, тобто цільова функція f (x) =f (x ^(1),…,f (x ⁽ⁿ⁾⁾ - функція n аргументів.

Так само як і в першій лабораторній роботі ми розглядаємо задачу мінімізації. Чисельні методи відшукання мінімуму, як правило, складаються в побудові послідовності точок {x_k}, що задовольняють умові f (x₀) >f (x₁) >…>f (x_n) >…. Методи побудови таких послідовностей називаються методами спуску. У цих методах точки послідовності {x_k} обчислюються за формулою:

х_k+1 = x_k + a_kp_k, k=0,1,2,…,

де p_k - напрямок спуску, a_k - довжина кроку в цьому напрямку.

Різні методи спуска відрізняються друг від друга способами вибору напрямку спуска p_k і довжини кроку a_k уздовж цього напрямку. Алгоритми безумовної мінімізації прийнято ділити на класи, залежно від максимального порядку похідних функції, що мінімізується, обчислення яких передбачається. Так, методи, що використовують тільки значення самої цільової функції, відносять до методів нульового порядку (іноді їх називають також методами прямого пошуку); якщо, крім того, потрібне обчислення перших похідних функції, що мінімізується, то ми маємо справу з методами першого порядку; якщо ж додатково використовуються другі похідні, те це методи другого порядку й т.д.

1.2 Градієнтні методи

1.2.1 Загальна схема градієнтного спуску

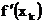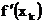Як відомо, градієнт функції в деякій точці x_k спрямований в бік найшвидшого локального зростання функції й перпендикулярний лінії рівня (поверхня постійного значення функції f (x), що проходить через точку x_k). Вектор, протилежний градієнту , називається антиградієнтом, що спрямований убік найшвидшого убування функції f (x). Вибираючи як напрямок спуска p_k антиградієнт -  у точці x_k, ми приходимо до ітераційного процесу виду:

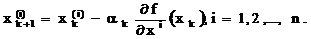
x_k+1 = x_k - a_k f’ (x_k), a_k>0, k=0, 1, 2, …

У координатній формі цей процес записується в такий спосіб:

Всі ітераційні процеси, у яких напрямок руху на кожному кроці збігається з антиградієнтом функції, називаються градієнтними методами. Вони відрізняються друг від друга тільки способом вибору кроку a_k. Існує багато різних способів вибору a_k, але найпоширеніші: метод з постійним кроком, метод із дробленням кроку й метод найшвидшого спуска.

1.2.4 Метод найшвидшого спуска

У градієнтному методі з постійним кроком величина кроку, що забезпечує убування функції f (x) від ітерації до ітерації, виявляється дуже малої, що приводить до необхідності проводити велику кількість ітерації для досягнення точки мінімуму. Тому методи спуска зі змінним кроком є більше ощадливими. Алгоритм, на кожній ітерації якого крок a_до вибирається з умови мінімуму функції f (x) у напрямку руху, тобто:

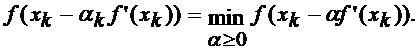
називається методом найшвидшого спуска. Зрозуміло, цей спосіб вибору a_до складніше раніше розглянутих варіантів.

Реалізація методу найшвидшого спуска припускає рішення на кожній ітерації досить трудомісткої допоміжної задачі одномірної мінімізації. Як правило, метод найшвидшого спуска, проте, дає виграш у числі машинних операцій, оскільки забезпечує рух із самим вигідним кроком, тому що рішення задачі одномірної мінімізації пов'язане з додатковими обчисленнями тільки самої функції f (x), тоді як основний машинний час витрачається на обчислення її градієнта .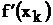

Варто мати на увазі, що одномірну мінімізацію можна робити будь-яким методом одномірної оптимізації, що породжує різні варіанти методу найшвидшого спуска.

Схема алгоритму

Крок 1.

Задаються х₀, e₃. Обчислюється градієнт 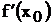, напрямок пошуку.

Привласнюється до=0.

Крок 2.

Визначається точка чергового експерименту:

х_к+1 = х_к - a_до,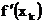

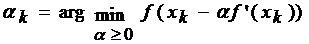
де a_до - мінімум задачі одномірної мінімізації:

Крок 3.

Обчислюється значення градієнта в точці х_к+1: .

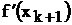Крок 4.

Якщо ||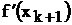||£e₃, то пошук точки мінімуму закінчується й покладається:

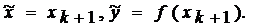
Інакше до=до+1 і перехід до кроку 2.

1.5 Методи ярів

1.5.1 Загальна характеристика

Градієнтні методи повільно сходяться в тих випадках, коли поверхні рівня цільової функції f (x) сильно витягнуті. Цей факт відомий у літературі як "ефект ярів". Суть ефекту в тім, що невеликі зміни один змінних приводять до різкої зміни значень функції - ця група змінних характеризує "схил яру", а по іншим змінним, що задає напрямок "дно яру", функція міняється незначно. На малюнку зображені лінії рівня "яружної" функції траєкторія градієнтного методу характеризується досить швидким спуском на "дно яру", і потім повільним зиґзаґоподібним рухом у точку мінімуму.

Існують різні підходи для визначення точки мінімуму функції f (x) у яружній ситуації. Більшість із них засновані на евристичні (тобто інтуїтивних, не обґрунтованих строго) міркуваннях. Їх можна застосовувати в ситуаціях, коли застосування більше зроблених методів неможливо або недоцільно, наприклад, значення цільової функції обчислюється зі значними погрішностями, інформація про її властивості недостатня, і т.д. Ці методи прості в реалізації й досить часто застосовуються на практиці, дозволяючи в ряді випадків одержати задовільне рішення задачі.

Схема яружного методу 1.

Евристичні алгоритми

Іноді, використовуючи градієнтний спуск для мінімізації функцій зі складною топографічною структурою, застосовують евристичні схеми, які ідейно близькі до методів спуска. Ми розглянемо дві такі схеми.

Перша евристична схема містить два основних етапи. Обидва етапи являють собою аналоги градієнтного спуска з постійним кроком. Тільки замість градієнта 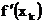 використовується вектор g (x), формований з координат 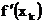, але на кожному з етапів за різними правилами.

На першому етапі задається мале число d₁<<1 і використовується градієнтний спуск, де замість градієнта 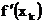 береться вектор g (x) ={g ^{(1) (}x),…,g ^{(n) (}x) }, який визначається в такий спосіб:

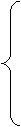
Таким чином, спуск виробляється лише по тими змінним, у напрямку яких похідна цільової функції досить велика. Це дозволяє швидко спуститися на "дно яру". Ми спускаємося доти, поки метод не зациклиться, тобто доти, поки кожна наступна ітерація дозволяє знайти точку, у якій значення функції менше, ніж значення, знайдене в попередній ітерації. Після цього переходимо до наступного етапу.

На другому етапі задається деяке велике число d₂>>1 і використовується процедура спуска, де замість градієнта 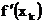 береться вектор g (x) ={g ^{(1) (}x),…,g ^{(n) (}x) }, який визначається в такий спосіб:

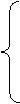
У цьому випадку переміщення відбувається по "березі" яру уздовж його "дна". Як і на першому етапі, спуск триває доти, поки метод не зациклиться.

Після виконання першого й другого етапів приймається рішення про завершення роботи або продовження. Для цього рівняється норма різниці попередньої точки, тобто точки, що ми мали до застосування першого й другого етапів, з поточною точкою, тобто отриманої після застосування з точністю рішення задачі e₁. Якщо ця норма менше e₁ і норма градієнта в поточній точці менше e₃, то пошук закінчується й остання обчислена точка приймається за наближене рішення задачі. Інакше для поточної точки знову повторюємо перший і другий етапи й т.д.

Схема алгоритму

Крок 1.

Задаються х₀, e₁, e₃,d₁,d₂,a₁ - постійний крок пункту 1 і a₂ - постійний крок пункту 2 (a₁<a₂). Привласнюється до=0.

Крок 2. (Перший етап).

Із точки х_к здійснюється спуск на "дно яру" з постійним кроком a₁.

При спуску обчислення чергової точки здійснюється з використанням формул:

x_j+1 = x_j - a₁g (x_j), де g (x) ={g ^{(1) (}x),…,g ^{(n) (}x) },

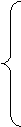Нехай цей процес зупиниться в точці x_l.

Крок 3. (Другий етап).

Із точки x_l здійснюється спуск уздовж "дна яру" з постійним кроком a₂. При спуску використовуються формули: x_j+1 = x_j - a₂g (x_j), де

g (x) ={g ^{(1) (}x),…,g ^{(n) (}x) },

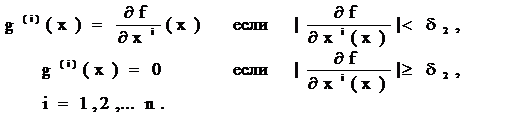
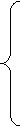Нехай цей процес зупинився в точці x_m.

Крок 4.

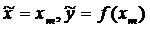
і пошук мінімуму закінчується.

Інакше k=m і переходимо до кроку 2.

2. Завдання на лабораторну роботу

1)   Вивчити викладені методи багатомірної безумовної оптимізації.

2)   У відповідність із варіантом завдання, вказаним викладачем, скласти програми для методів багатомірної безумовної мінімізації й знайти точку мінімуму цільової функції f (x) =f (x ^(1), x ⁽²⁾⁾ із заданою точністю ε зазначеними методами. Початкове наближення x₀ і точність e приводяться в умові задачі. Порівняти результати, отримані різними методами для однієї й тієї ж цільової функції (зокрема, порівняти число обчислень цільової функції і її похідних, що знадобилися для одержання заданої точності). Для кожного використаного методу побудувати траєкторію проміжних точок, які одержані на чергових кроках методу й збіжних до точки мінімуму.

3)   Оформити звіт про виконання завдання із приведенням умови задачі, алгоритмів і програм, зазначених у завданні методів мінімізації, графіків траєкторій проміжних наближень, таблиці результатів порівняння розглянутих методів, висновку за результатами порівняння методів.

Методи

1)   метод найшвидшого спуску;

2)   евристичний алгоритм;

Варіанти завдань

Цільова функція f (x) =f (x ^(1), x ⁽²⁾⁾ залежить від двох аргументів. Функція f (x) наступного виду:

f (x) =a*x ⁽¹⁾ +b*x ⁽²⁾ +e^{c* (x) +d* (x).}

Програма до методу № 1

#include <stdio.h>

#include <math.h>

#include <iostream.h>

#include <conio.h>

// ing namespace std;

double f (double x1, double x2)

{ double f;

f=3*x1-1.2*x2+exp (0.02*x1*x1+1.3*x2*x2);

return (f);

}

double df1 (double x1, double x2)

{double f1;

f1=3+0.04*x1*exp (0.02*x1*x1+1.3*x2*x2);

return (f1);

}

double df2 (double x1, double x2)

{double f2;

f2=-1.2+2.6*x2*exp (0.02*x1*x1+1.3*x2*x2);

return (f2);

}

double zsech (double a,double b,double x1k,double x2k,double z1,double z2)

{

double eps=0.0001;

double x1,x2,y1,y2,t;

t= (1+sqrt (5)) /2;

x1=a- (b-a) / (t);

y1=f (x1k-x1*z1,x2k-x1*z2);

x2=a+ (b-a) /t;

y2=f (x1k-x2*z1,x2k-x2*z2);

while ( (b-a) >eps) {

if (y1<=y2) { b=x2; x2=x1; y2=y1; x1=a+b-x2; y1=f (x1k-x1*z1,x2k-x1*z2); }

else { a=x1; x1=x2; y1=y2; x2=a+b-x1; y2=f (x1k-x2*z1,x2k-x2*z2); }

}

// if (y1<y2) b=x2;

// else a=x1;

return ( (a+b) /2);

}

void main ()

{int k, i,N,N0,N1,l1,l2;

double x [3000] [2]; double y [10];

clrscr ();

x [0] [1] =-1;

x [0] [2] =0;

e2=0.0001;

double z1,z2,y1,y2,e,p,alpmin,g1,g2;

int m;

cout<<"Metod naiskor. spuska"<<endl;

k=0; N0=0; N1=0;

z1=df1 (x [0] [1],x [0] [2]);

z2=df2 (x [0] [1],x [0] [2]);

N1=N1+2;

dalph=2.2;

mm1:

m = 0;

y1=f (x [k] [1],x [k] [2]); N0++;

metka:

y2=f (x [k] [1] - (m+1) *dalph*z1,x [k] [2] - (m+1) *dalph*z2);

N0++;

if (y2<y1)

{m++; y1=y2; goto metka; }

else

{b= (m+1) *dalph;

if (m==0)

{a=0; }

else {a= (m-1) *dalph; }

}

alpmin=zsech (a,b,x [k] [1],x [k] [2],z1,z2);

cout<<"\nk="<<k+1<<endl;

x [k+1] [1] =x [k] [1] - alpmin*z1; cout<<"\nx [1] [1] ="<<x [k+1] [1];

x [k+1] [2] =x [k] [2] - alpmin*z2; cout<<"\nx [1] [2] ="<<x [k+1] [2] <<endl; // getch ();

z1=df1 (x [k+1] [1],x [k+1] [2]);

z2=df2 (x [k+1] [1],x [k+1] [2]);

N1=N1+2;

d=pow (z1*z1+z2*z2,0.5);

if (d>e2)

{k++; goto mm1; }

else {xmin1=x [k+1] [1];

xmin2=x [k+1] [2];

ymin=f (xmin1,xmin2);

cout<<"x1="<<xmin1<<" x2="<<xmin2<<" ymin="<<ymin<<endl<<"N1="<<N1;

cout<<" N0="<<N0<<" k="<<k+1<<endl;

}

// return 0;

getch ();

}

Метод 2

include "iostream"

#include <math.h>

#include <conio.h>

#include <stdlib.h>

#include "iomanip"

#include <stdio.h>

using namespace std;

int N0=0, N1=0;

double a=3, b=-1.2, c=0.02, d=1.3;

double f (double x1, double x2)

{

double f;

N0++;

f=3*x1-1.2*x2+exp (0.02*x1*x1+1.3*x2*x2);

return (f);

}

double fdx1 (double x1,double x2)

{double fx1;

N1++;

fx1=3+0.04*x1*exp (0.02*x1*x1+1.3*x2*x2);

return (fx1); }

double fdx2 (double x1,double x2)

{ double fx2;

fx2=-1.2+2.6*x2*exp (0.02*x1*x1+1.3*x2*x2);

return (fx2); }

void evrist ()

{ double x1 [100],x2 [100],A1,A2,E2,del1,del2,f1,f2,h [4],g [4],b [4],r [4];

double d,N;

int k;

x1 [0] =-1;

x2 [0] =0;

E2=0.0001;

del1=0.01;

del2=3;

A1=0.5;

A2=2;

k=0;

label1:

do{

h [1] =fdx1 (x1 [k],x2 [k]);

if (fabs (h [1]) >del1) {g [1] =h [1]; }

else {g [1] =0; }

h [2] =fdx2 (x1 [k],x2 [k]);

if (fabs (h [2]) >del1) {g [2] =h [2]; }

else {g [2] =0; }

x1 [k+1] =x1 [k] - A1*g [1];

x2 [k+1] =x2 [k] - A1*g [2];

// cout<<":: "<<x1 [k] <<":: "<<x2 [k] <<endl;

f1=f (x1 [k+1],x2 [k+1]);

f2=f (x1 [k],x2 [k]);

k++;

}

while (f1<f2);

k--;

do{

r [1] =fdx1 (x1 [k],x2 [k]);

if (fabs (r [1]) >del2) {b [1] =0; }

else {b [1] =r [1]; }

r [2] =fdx2 (x1 [k],x2 [k]);

if (fabs (r [2]) >del2) {b [2] =0; }

else {b [2] =r [2]; }

x1 [k+1] =x1 [k] - A2*b [1];

x2 [k+1] =x2 [k] - A2*b [2];

cout<<x1 [k+1] <<":: "<<x2 [k+1] <<endl;

f1=f (x1 [k+1],x2 [k+1]);

f2=f (x1 [k],x2 [k]);

k++;

}while (f1<f2);

k--;

d=pow (r [1],2) +pow (r [2],2);

if (sqrt (d) >E2) {A1=A1/2.0; A2=A2/2.0; goto label1; }

else {cout<<"X1="<<x1 [k] <<" X2="<<x2 [k] <<" F (x) ="<<f (x1 [k],x2 [k]) <<endl;

N=N1+N0;

cout<<"Кол-во экспер.: "<<N<<" Кол-во итераций: "<<k<<":: "<<N0<<endl; }

N0=0; N1=0;

}

void main ()

{

evrist ();

getch ();

}

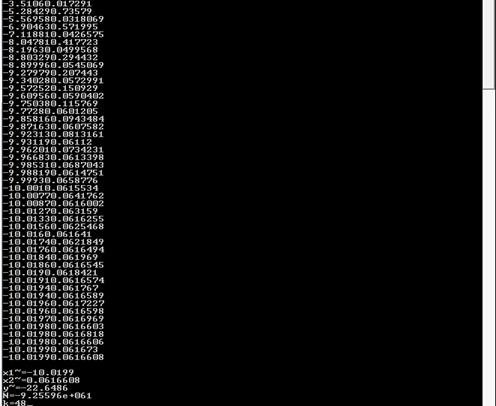
Скрин до методу 1